Abstract
Numerical simulations are a powerful tool to investigate turbulent flows, both for theoretical studies and practical applications. The reliability of a simulation is mainly dependent on the turbulence model adopted, and improving its accuracy is a crucial issue. In this study, we investigated the potential for an alternative formulation of the Navier–Stokes equations, based on the stochastic representation of the velocity field. The new approach, named pseudo-stochastic simulation (PSS), is a generalisation of the widespread classical eddy–viscosity model, where the contribution of the unresolved scales of motion is expressed by a variance tensor, modelled following different paradigms. The PSS models were compared with the classical ones mathematically and numerically in the turbulent channel flow at . The PSS and the classical models are equivalent when the variance tensor is shaped through a molecular dissipation analogy, while it is more accurate when the tensor is defined by the way of a local variance model. A near-wall damping function derived from recent advancement in the field is also proposed and was successfully validated. The analyses demonstrate the relevance of the approach proposed and provide a basis for the development of an alternative turbulence model.
1. Introduction
The use of stochastic calculus to describe fluid flows is a suitable strategy for turbulence modelling in computational fluid dynamics. The random nature of turbulence cannot be completely represented through deterministic variables, conversely it can be represented by stochastic processes. Nevertheless, the numerical solution of stochastic equations and the mathematical complexity inherent to the use of stochastic calculus pose challenging issues. Turbulence modelling with stochastic variables is of great interest in geophysical flow analysis, where the unresolved processes related to coarse spatial discretization are handled with probabilistic models. In the same spirit, stochastic models can be applied to numerical simulations of environmental and engineering flows.
In the last decades, several efforts have been made in this direction. In the context of the probability density function (PDF), the Langevin equation was used to describe the velocity of a fluid particle subjected to a turbulent flow, modelled as Brownian motion (see Pope [1]). This equation was first applied to the homogeneous isotropic turbulence, and later to the inhomogeneous case by Pope [2] and to the anisotropic diffusion case by Durbin and Speziale [3]. In the eddy-damped quasi-normal Markovian (EDQNM) models, introduced by Orszag [4], Leslie [5], the large-scale governing equations were closed in the spectral space by modelling the third/fourth-order moments through a Gaussian closure. This strategy was found to be suitable in case of strong non-linearity in the small-scale turbulence. Chasnov [6] developed a forced-dissipative model, where the large-eddy Navier–Stokes equations were corrected by eddy-viscosity and stochastic force terms. Similarly, Leith [7] studied the case of a plane shear mixing layer and improved the accuracy of large-eddy simulation (LES) with the Smagorinsky model by adding an empirical stochastic backscatter. The work of Kraichnan [8] exploited a different approach: the Navier–Stokes equations were replaced by a set of equations having the same mathematical properties but closed by a Gaussian stochastic model. This model led to valuable results when applied to the study of mathematical properties and physical effects, like turbulent diffusion and backscatter. Frederiksen et al. [9] showed that the same methodology can be used in the stochastic modelling of barotropic flows or quasi-geostrophic approximation, as well as for the description of the interactions between topography and small-scale eddies.
Such attempts to include random functions in fluid dynamics modelling had some limitations: in PDF and EDQNM models the solution was found in the spectral space and not in the physical one; the explicit introduction of a random term relied mostly on empirical considerations and led to a certain degree of arbitrariness. For example, a question arose about whether the random forcing term should be multiplicative or additive.
Here we present a different approach, based on the idea that the velocity field itself is a random process, composed of a differentiable component and a fast oscillating random term. Physically, the former describes the smooth macroscopic velocity while the latter accounts for the stochastic turbulent motion. Under this assumption, the fluid dynamics equations are re-derived using stochastic calculus, leading to a complete set of stochastic partial differential equations. Pioneering work in this field was made by Brzeźniak et al. [10]. Subsequently, Mikulevicius and Rozovskii [11], Flandoli [12] expanded his formulation and studied the mathematical properties of the resulting stochastic system. Such a model has been further developed by Mémin [13] in view of practical applications and took the name of model under location uncertainty (LU). Also, Neves and Olivera [14] theoretically investigated a similar system, while Holm [15] derived an equivalent model using Lagrangian mechanics. This last model differs from LU because an extra term appears in the momentum equation, which ensures helicity and circulation conservation but may alter the kinetic energy budget.
The LU model was tested in several cases: in a series of papers Resseguier et al. [16,17,18,19], as well as Bauer et al. [20,21], successfully used this model to study geophysical flows. It was found to be more accurate in the reproduction of extreme events and to provide a new analysis tool. Chapron et al. [22] investigated the Lorentz-63 case and stated that LU was more effective in exploring the regions of the deterministic attractor than the classical models. Furthermore, it was used in conjunction with the proper orthogonal decomposition technique by Resseguier et al. [23] for studying a wake flow past a circular cylinder at . Recently, Pinier et al. [24] performed a mathematical analysis of the turbulent boundary layer using the LU equations. They proposed a complete and explicit profile for the mean vertical velocity, including an expression for the velocity in the buffer layer, for which a rigorous theoretical model was missing so far.
Despite these encouraging results, the use of the stochastic numerical simulations for practical applications poses some difficulties; e.g., the numerical resolution techniques are not straightforward and they can require a large computational effort. To circumvent such difficulties, Mémin [13] introduced a hybrid model hereafter named pseudo-stochastic model: first, the governing equations are decomposed into two coupled system of partial and stochastic differential equations; second, the resolution of the stochastic equations is avoided and the system is closed by modelling the effects of the random velocity term through physical assumptions. Hence, the flow dynamics is described by a set of classical partial differential equations, which includes terms deriving from the stochastic representation of turbulence. Harouna and Mémin [25] used the pseudo-stochastic model to investigate the Green–Taylor vortex flow, testing several closure models. Chandramouli et al. [26] successfully employed the model to simulate the transitional wake flow with a coarse mesh resolution.
The present contribution aims at exploring the potentiality of the pseudo-stochastic model, making a direct comparison with the large-eddy simulation (LES) methodology. The mathematical model is described and discussed in details, highlighting the specific elements that are not present in the LES classical model. The turbulent kinetic energy budget for the LU model is here presented for the first time. Also, a near-wall damping function was derived from a recent analysis of the boundary layer by Pinier et al. [24] and validated. Different pseudo-stochastic models were tested in the turbulent channel flow case and compared with the classical LES results. The turbulent channel flow case is widely documented in the literature and allows a detailed analysis of the model performance.
The paper is organised as follows: in Section 2 the pseudo-stochastic model is described; in Section 3 the model equations are interpreted and compared with the classical LES turbulence models; in Section 4 the simulation settings are reported; in Section 5 the performance of the pseudo-stochastic simulation approach is analysed; Section 6 gives some final comments.
2. Pseudo-Stochastic Model
The pseudo-stochastic equations are described, together with the kinetic energy budgets (see [13,27] for a formal derivation).
2.1. Stochastic Formalism
The pathlines in a turbulent flow are modelled as a stochastic process, where a regular function is perturbed by a random (turbulent) process. Consequently, a Lagrangian fluid-particle displacement is described by a stochastic differential equation of the type:
where the index indicates respectively the x,y,z-component in the space domain (they are placed at the top or bottom indifferently) and the Einstein summation convention is adopted; is the trajectory followed by a fluid-particle initially located in ; is a differentiable function that corresponds to the drift velocity; is a stochastic process (accounting for turbulent effects) uncorrelated in time but correlated in space. This last is constructed as a combination of a cylindrical Wiener processes not differentiable in time, and a time-differentiable symmetric diffusion tensor, which acts as an integral kernel.
The velocity field in Eulerian coordinate x is derived from Equation (1):
where the second term on the right-hand side expresses the stochastic velocity defined as the weak derivative of in time. From a physical point of view, is the velocity expected value and represents a noise. This is a generalised stochastic process that has to be defined in the space of temperate distribution, see [28].
In the derivation of the stochastic model, the quadratic variation of the diffusion tensor is of particular interest since it represents the time-variation of spatial variance of the stochastic increments along time. It is named variance tensor and it is defined as:
it can be shown to be a symmetric and semi-positive definite matrix with dimension .
2.2. Pseudo-Stochastic Equations of Motion
The stochastic process (1) that describes the flow is not time-differentiable in the framework of classical analysis. Thus, the Navier–Stokes equations need to be re-derived using the stochastic calculus. To do so, the use of the Itō-Wentzell formula is crucial for computing the derivative in time, see Kunita [29]. The result is a complete system of stochastic partial differential equations that describes the fluid flow. Assuming the drift velocity is of bounded variation (deterministic) and using the unique decomposition of semi-martingale, the system can be divided into a set of stochastic equations and a set of pure deterministic equations. The former set allows to find an expression for the variance tensor , required for the resolution of the latter set. The pseudo-stochastic model is derived by neglecting the resolution of the stochastic equations and closing the system by giving an expression of the variance tensor, which is modelled through physical hypotheses. This choice gives rise to a hybrid model where the terms that depend on account for the stochastic unresolved scales (SUS) of motion.
The pseudo-stochastic equations for incompressible flows read:
they represent the momentum and mass conservation, respectively, written in the non-conservative form proposed by Resseguier et al. [16]. The effective advection velocity is defined as:
and the pressure is the sum of a hydrostatic pressure and an isotropic turbulent term:
This last term does not contribute to the flow and is included in the pressure gradient term in the same manner as the isotropic residual stress in the Smagorinsky model, see [1]. It is worthwhile to notice that the system (4) reduces to the classical Navier–Stokes equations when the variance tensor tends to the zero matrix, i.e., when the stochastic contributions disappear.
In the framework of computational fluid dynamics, the drift velocity can be interpreted as the (numerically) resolved velocity field, while the random field assembles the (turbulent) unresolved motions. Therefore, giving an expression for the variance tensor is equivalent to specifying a turbulence model.
2.3. Isotropic Constant Model
Several strategies can be adopted to model the variance tensor. The isotropic model is developed by analogy with the Smagorinsky model, e.g., see [13,30]. The variance tensor is given by:
where is a model parameter, is the strain-rate tensor norm, and is the computational cell width. The variance tensor reduces to a diagonal matrix with equal elements because turbulence is assumed to be isotropic and homogeneous in all directions. The isotropic constant model is the equivalent in the pseudo-stochastic simulation (PSS) framework of the Smagorinsky model for eddy-viscosity in the LES framework (see discussion in the following Section 3). Such an LES model has the well-known shortcoming of being too dissipative near the wall; hence, it is customary to apply a corrective function near the wall (ref. Section 3.2). After some preliminary analysis, we noticed that the same shortcoming is inherited from the isotropic constant model, therefore a corrective function based on current knowledge of the PSS model was developed and presented in the following Section 2.4.
2.4. Near-Wall Modelling for Isotropic Model
In recent work, Pinier et al. [24] studied the mean velocity profile of the turbulent boundary layer through the LU equations. They proposed a modification of the classical velocity expression for wall-bounded flow and provided an analytical formula for the buffer layer, not available till now. Notice that the modified advection velocity plays a crucial role in the mathematical derivation of this formula; therefore, such a profile cannot be deduced using the classical formulation of the Navier–Stokes equations, where the modified advection is not explicitly taken into account. Hereafter, quantities are made non-dimensional by means of the friction velocity : the non-dimensional wall-normal direction is and the non-dimensional stream-wise velocity is . In the viscous sublayer () and in the logarithm region () the linear and log–law velocity profiles (respectively) are retrieved, while in the buffer layer () an hyperbolic profile is specified:
where is the stream-wise velocity as a function of the wall-normal coordinate. The is a model constant (not to be confused with the von Kármán constant); for a plain channel flow it has been estimated to be from direct numerical simulations. The boundaries of the three regions are: , , and even if the profile is often extended till the half of the channel. Let us stress that these profiles are rigorously derived from the LU models. Figure 1-left-panel, shows the good agreement of the hyperbolic profile in the buffer region; see Pinier et al. [24] for an extensive validation on the pipe flow, turbulent boundary layer, and channel flow case.
An additional result concerns the expression of the variance tensor. In the viscous sublayer, is almost zero, while in the buffer layer the wall-normal component depends only on the distance from the wall and exhibits a linear profile:
where . In the log–law region, it scales as the square-root of the wall distance:
No estimates are provided for the other components.
Preliminary pseudo-stochastic simulations with the isotropic constant model (7) have shown an excessive energy dissipation near the solid boundaries, given by high values of in the buffer and viscous layer. This is not unexpected since the LES Smagorinsky model (that is the classical counterpart of the isotropic model) exhibits the same behaviour (see discussion in following Section 3.4).
To correct this behaviour, a damping function for variance tensor is here formulated, exploiting the above-described characterisation of wall-normal component. Away from the wall, is given by the isotropic model; at a point placed in the buffer layer, a linear decrease is imposed in such a way to reach the zero value at ; in the viscous sublayer, it is set to be zero. Hence, the LU near-wall model reads:
The coordinate is a model parameter that has to be set after theoretical or numerical estimation. No constraints are imposed on the other components; they are computed according to the isotropic model (7).
2.5. Local Variance Model
An additional model for is derived from the interpretation of variance tensor as an empirical velocity covariance. The variance tensor is estimated cell-by-cell, using the statistics of resolved velocity components computed in a local neighbourhood of the cell:
where is a model constant, is the characteristic turbulent time scale, is the velocity local mean (see also Harouna and Mémin [25]). The quantity can be estimated through scaling considerations [25]; however, in this work, it is empirically determined through a calibration procedure. The mathematical derivation of the local variance model was not reported in previous studies and it is shortly presented in Appendix A for the sake of completeness.
It is worth noticing that the local variance model corresponds to an anisotropic form of the variance tensor, where the non-diagonal components can be non-zero. Moreover, tensor is computed taking information from the local characteristic of the flow and can be more suitable for reproducing localised turbulence.
2.6. Resolved Kinetic Energy Budget
To investigate the peculiarity of the PSS model, the budget equations for the mean and the turbulent kinetic energy of the resolved scales of motion are derived and compared with the classical ones. The resolved velocity is decomposed in a mean and a fluctuating part, respectively:
where the capital letter indicates the averaged field, . The variance tensor and the pressure are decomposed in a similar way: and . The variance tensor accounts for the SUS effects on the mean flow.
The budget of resolved kinetic energy is obtained by multiplying momentum Equation (4-first) by and averaging. Applying the conservation of mass (4-second) and rearranging the terms, one gets:
The second term on the left-hand side represents the rate of change by means of the effective (mean) advection. The first four terms on the right-hand side express the energy transport by pressure, molecular and turbulent viscous stresses, resolved turbulence, and turbulent SUS motion (respectively). The fifth term is due to the non-solenoidal velocity field and is related to the compression–expansion work made by the SUS; it can be a production or a dissipation term. The sixth term represents a viscous and a turbulent dissipation (it can be proven that is positive defined), while the seventh term is a loss due to resolved turbulence; the same term but with opposite sign is present in the turbulent kinetic energy budget presented later in this section. The last term indicates dissipation/production due to SUS.
The (resolved) turbulent kinetic energy budget is obtained following the procedure described in Kundu and Cohen [31]: the equation for the resolved fluctuations is obtained subtracting expression (14) from ((4)-first), then multiplying by and averaging. Using the continuity Equation ((4)-second) to simplify the terms and rearranging them, one obtains the following expression for stochastic turbulent kinetic energy (TKE):
On the left-hand side, the second and third terms represent the TKE advection by the mean and the SUS effective advection velocity, respectively. On the right-hand side:
- the first four terms express spatial transport;
- the fifth term is a turbulent compression/expansion term due to SUS;
- the sixth and seventh terms account for dissipation by molecular viscosity, resolved turbulence, and SUS motions;
- the eight term represents the shear production, including the contribution by the fluctuations of turbulent advection velocity;
- the last term indicates a loss due to SUS; this term is also present in the resolved kinetic energy budget.
Both expressions of kinetic energy and TKE reduce to the classical ones if the stochastic contribution is negligible . Particularly, the turbulent compression and the loss due to SUS disappear in the classical formulation.
3. Physical Interpretation and Comparison with Les Models
The pseudo-stochastic Equation (4) are analysed from a physical point of view, and a comparison with the eddy-viscosity model used in LES is reported.
3.1. Physical Interpretation
Recalling the decomposition of the velocity gradient as the sum of the symmetric and the antisymmetric parts, respectively the strain-rate tensor and the rotation-rate tensor , the pseudo-stochastic Equation (4) are rearranged as:
and
The terms that depend on variance tensor account for the influence of the SUS on the resolved scales. A physical interpretation of such terms is proposed:
- Effective advection: the advection velocity is corrected by an inhomogeneous turbulence contribution. As pointed out by Resseguier et al. [16], it corresponds to a velocity induced by the unresolved eddies, that is linked to the turbophoresis phenomenon detectable in geophysical flows; i.e., the tendency of the fluid-particle to migrate in the direction of less energetic turbulence.
- Diffusion due to SUS: the last two terms on the right-hand side of Equation (19) account for the turbulent diffusion; the variance tensor plays the role of a diffusion tensor similar to a generalised eddy-viscosity coefficient. Both deformation rate and rotation-rate contribute to diffusion, unlike in the classical eddy-viscosity model.
- Turbulent compressibility: the continuity Equation (20) suggests that the flow is turbulent-compressible; i.e., the unresolved turbulence induces a local fluid compression or expansion.
The variance tensor (3) is the key parameter of the pseudo-stochastic model. It has the physical dimension of the dynamic viscosity , and carries information on the intensity of the SUS. The role played in governing Equation (4) and in kinetic energy budgets (14)–(18), suggests that can be interpreted as a generalised eddy-viscosity parameter. Implicitly, this leads to the hypothesis that the SUS influences the resolved flow as an alteration (increasing or possibly decreasing) of fluid viscosity, which is an empirical consideration largely accepted.
The divergence of the variance tensor is hereafter named turbulent advection velocity:
the divergence of the turbulent advection velocity measures the turbulent compressibility:
and it is directly proportional to the isotropic turbulent term appearing in Equation (6).
3.2. Comparison with Les Eddy-Viscosity Models
In the classical framework, the fluid velocity is a deterministic function of time and space. Adopting the LES approach, the computational grid acts on the governing equations as an implicit spatial filter (denoted by an over-bar) depending on the local cell width , see [32,33] for extended reviews. Filtering the Navier–Stokes equations, the sub-grid scale (SGS) stress tensor appears:
and it has to be modelled to close the system: a popular choice is to use the eddy-viscosity models. They are a class of turbulent models relying on the Boussinesq assumption, where the anisotropic part of is proportional to the resolved strain-rate tensor through the SGS viscosity parameter :
while the isotropic part is included in the pressure term and does not contribute to the motion. This parameter has to be specified by additional models; the classical constant Smagorinsky model is here analysed:
where is the norm of the filtered strain-rate tensor, and the parameter is set constant and can be evaluated from experiments, direct numerical simulations or analytical considerations, e.g., see Lilly [34]. The main drawback of this approach is to rely on the homogeneous turbulence assumption. This hypothesis is violated in many, even simple, cases; for example close to solid surfaces where the turbulent length-scales decrease. To cope with this shortcoming, a damping function is usually introduced to account for the reduction of turbulence intensity. After the first work by van Driest [35], several modifications of the original damping function have been proposed, e.g., see Piomelli et al. [36], Cabot and Moin [37]. They can be summarised in the following expression:
where is the von Kármán constant. The original formulation by van Driest [35] prescribes , and . Note that this damping function is based on empirical observation and does not have a theoretical basis.
3.3. Remarks on Eddy-Viscosity Model
Notice that the eddy-viscosity Equation (24) implies that the Boussinesq’s hypotheses are satisfied: (a) the anisotropic Reynolds stress tensor is aligned with the mean strain-rate tensor; (b) the two are directly proportional through a single parameter, equal for all the six independent components of .
The pseudo-stochastic model is equivalent to an eddy-viscosity model if the variance tensor is expressed by , i.e., assuming that the SUS induces an (isotropic) increase of fluid viscosity. In this sense, the pseudo-stochastic model can be considered as a generalisation of the eddy-viscosity model. Some theoretical advantages of the pseudo-stochastic model are:
- The effects of unresolved scales of motion are given by , without imposing any constraint on the directions along which the SUS acts. Hence, the hypothesis (a) is not required.
- The tensor form of allows reproducing the anisotropy of unresolved turbulence, i.e., different turbulent contributions along different directions. Thus, hypothesis (b) is not required.
- The extra terms in the governing equations account for turbulent effects, usually not considered in the classical models, namely turbulent advection and turbulent compressibility.
The eddy-viscosity models are reasonable for simple shear flows and they are largely applied in computational fluid dynamics. However, most of their shortcomings derive from the fact that hypotheses (a) and (b) are not generally satisfied; see Pope [1] for an overview of this issue.
It is worth mentioning that the eddy-viscosity parameter comes directly from the basic assumption of the velocity decomposition (2); whereas it is introduced in LES equations through an ad hoc physical assumption. Overall, the pseudo-stochastic model represents a general approach that overcomes the limitations of the Boussinesq assumption and includes turbulent effects not considered in the classical LES sub-grid scales models.
3.4. Remarks on Smagorinsky Model
It can be shown that the pseudo-stochastic isotropic model (7) reduces to the LES Smagorinsky model under two approximations:
- the rotation-rate does not contribute to turbulence effects on the mean flow;
- the norm of the strain-rate tensor is almost harmonic (Laplacian is close to zero).
Notice that with the latter hypothesis the continuity Equation ((4)-second) becomes the classical solenoidal constraint. Therefore, the LES Smagorinsky model can be interpreted as a particular case of the pseudo-stochastic isotropic model.
Approximation (1) is valid if the turbulent energy is mainly concentrated in the region where the irrotational strain dominates vorticity. Exceptions to this behaviour have been found and have motivated the development of alternative models, like the wall adaptive local-eddy viscosity (WALE) model of Nicoud and Ducros [38] or the structure-function model of Métais and Lesieur [39]. Approximation (2) implies that the flow deformation rate can be represented by a linear function in each spatial point; thus it is a particularly regular function. This is equivalent to neglecting the turbulent correction on advective velocity and continuity equation, hence the associated physical phenomena of turbophoresis and turbulent compressibility are not reproduced.
4. Simulation Methodologies
The pseudo-stochastic model was studied in detail on channel flow at . The pseudo-stochastic simulation (PSS) techniques were compared with the LES approach and the direct numerical simulation (DNS) of Moser et al. [40]. The following notation is adopted: if is a generic variable, then is the time and space averaged over -directions, is the instantaneous fluctuation and is the root-mean square.
4.1. Methodology and Implementation
Simulations were performed taking advantage of the open-source software OpenFOAM v6. This is a C++ library for computational fluid dynamics and uses the finite volume method.
The LESs were carried out using the solver pisoFoam included in the standard software distribution. The implementation details can be found in the OpenFOAM documentation and in Jasak et al. [41]. The filtered classical Navier–Stokes equations were closed by the Smagorinsky model (25), with . The van Driest function (26) for near-wall damping is used unless otherwise specified. The optimal parameters were set as , , .
The PSSs were carried out using the home-made solver pseudoStochasticPisoFoam, developed by the authors within the Fluminance research group at INRIA Rennes (France). The pseudo-stochastic Equation (4) were solved employing the pressure-implicit with splitting of operators (PISO) algorithm proposed by Issa et al. [42], Oliveira and Issa [43]. The variance tensor was expressed by the local variance model and the isotropic constant model (7), corrected by the near-wall damping function (11) unless otherwise specified. The isotropic constant was set to be in analogy with the Smagorinsky model. The damping parameter was set to be after a theoretical estimation [24], confirmed by several test simulations. In order to regularise the damped profile of , a smoothing filter was applied to the variance tensor.
Variables were discretised in space with a second-order central difference scheme, while time integration was performed using an implicit Euler backward scheme. Such a scheme employs the variables at the previous two time-steps, leading to second-order accuracy. Globally, numerical solvers were second-order accurate in time and space. The time advancement fulfils the Courant–Friedrichs–Lewy condition . For LES, the Courant number was computed as , where is the time step, is the velocity magnitude through the cell, is the cell length. For PSS, the definition was modified in order to account for the effective advection velocity: .
4.2. Case Geometry and Settings
The channel was composed of two horizontal walls between which a shear flow develops. The dimensions in stream-wise (x), vertical (y) and span-wise (z) directions were , respectively. The computational points were uniformly distributed in stream-wise and spanwise directions, while the grid was stretched along the vertical direction. The stretching was symmetric with respect to the channel centre plane , and it was obtained with a double-side stretching function based on an hyperbolic tangent function. The mesh was such that the first cell centre near the walls is below , there are 9 cells in the range , and the cell width in the wall-parallel direction was sufficient to ensure an accurate resolution of the boundary layer.
Cyclic boundary conditions were set at the vertical boundaries, while velocity no-slip condition and pressure zero-gradient were imposed at the horizontal walls. All the cases were initialised with the instantaneous fields provided by a preliminary LES with the constant Smagorinsky SGS model that has reached the statistical steady state.
Quantities were made non-dimensional by the friction velocity and molecular viscosity as follow: space , time , velocity , and variance tensor . The flow was driven by a constant pressure gradient ; Reynolds number reads . The characteristic flow time was estimated to be , where is the bulk velocity in stream-wise direction, while the large-eddy turn over time was estimated to be . After the statistical steady state was reached, statistics were collected in an interval of every .
5. Results and Discussion
Several simulations were performed adopting five turbulence models: two large-eddy simulation (LES) using the constant Smagorinsky model with and without the van Driest damping, labelled respectively LES vanDriest and LES smagConst; two PSS using the isotropic constant model with and without the LU near-wall model, labelled respectively PSS isoConst and PSS isoLUWall; one PSS using the local variance model labelled PSS variance. They were compared with the DNS by Moser et al. [40].
Figure 1-right-panel shows the non-dimensional averaged stream-wise velocity along wall-normal direction. First, we can notice that the LES smagConst and the PSS isoConst exhibit a very similar profile. This is because the isotropic model is derived by analogy with the classical Smagorisnky model. The main difference between the two is the presence in the PSS equations of turbulent advection (21) and turbulent compressibility (22); however, in this case, they are not strong enough to produce remarkable results on the mean flow (see discussion of Figure 4-left-panel). Both models underestimate the velocity: this is a well-known shortcoming of Smagorinsky model when is constant, and it is inherited by the constant isotropic model. Second, we compare the LES vanDriest and the PSS isoLUWall, which implement a near-wall damping function for and (respectively). The damping reduces the turbulent dissipation in the buffer layer, preventing the underestimation of velocity. When the near-wall models are activated, velocity is well captured in the viscous and buffer layers but is slightly overestimate in the logarithmic and far-wall regions (). Remarkably, the LU near-wall model here proposed is as accurate as the well-established van Driest wall function in reproducing the velocity profile. Further analysis of such a damping model is reported in the discussion of Figure 3. Third, the PSS variance is the most accurate model and exhibits a very good agreement with the reference profile. Notice that the local variance model is not corrected with a damping function.
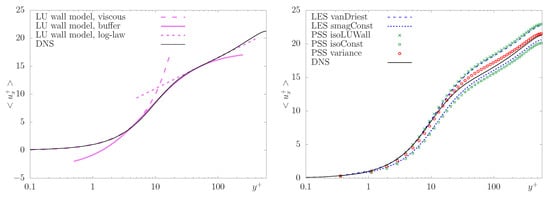
Figure 1.
Non-dimensional stream-wise velocity profiles along wall-normal direction for turbulent channel at . Left panel: solid black, direct numerical simulation (DNS) by Moser et al. [40]; dash violet, analytical profile (11) derived from location uncertainty (LU) by Pinier et al. [24]. Right panel: comparison between the large-eddy simulation (LES) and pseudo-stochastic simulation (PSS) (see label definition in the text).
Figure 2-left-panel reports the root-mean square (RMS) of velocity components. No significant differences are detectable between the LES smagConst and the PSS isoConst and between the LES vanDriest and the PSS isoLUWall; hence, just the LES profiles are displayed. The PSS with local variance model reproduces the results of the LES vanDriest, which is more accurate than the LES smagConst, as expected.
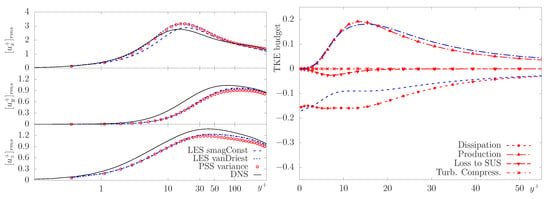
Figure 2.
Left-panel: averaged non-dimensional root-mean square of velocity components along wall-normal direction for three selected simulations (same label as Figure 1). Right-panel: non-dimensional Turbulent Kinetic Energy (TKE) budget (18) along the wall-normal direction. Blue lines, LES with van Driest damping (LES vanDriest); Red lines with symbols, PSS with local variance model (PSS variance).
The TKE budget is also scrutinised for the LES van Driest model and the PSS variance model, which are selected because they are the most accurate LES and PSS, respectively. The TKE budget for LES is obtained from (18) setting except in the dissipation term, where in order to account for the dissipative effect of the sub-grid model. Figure 2-right-panel shows selected terms of the TKE budget. The production profiles are practically the same for PSS and LES, while the dissipation ones differ in . PSS shows a larger dissipation in the buffer layer but collapses to the same value as the LES at the wall. In the PSS, the turbulent compression term is almost zero and does not contribute to the budget, while the loss due to SUS presents slightly negative values mainly localised in the viscous layer. Hence, it contributes to global energy dissipation.
Figure 3 reports the non-dimensional averaged eddy-viscosity and the variance tensor components along wall-normal direction for selected simulations. The near-wall scaling of the turbulent contribution strongly influences the overall dynamics and is crucial for obtaining accurate results. In the framework of LES, it has been shown that the highly accurate SGS models (such as the dynamic scale similarity models) follow the scaling in the proximity of the wall, e.g., see [44,45]. The in LES constant Smagorinsky (not reported) does not follow this scaling and shows a profile equal to of the PSS isoLUWall. A large SGS viscosity in the buffer layer entails an underestimation of the speed of the fluid (see Figure 1). The same shortcoming affects the PSS with isotropic constant model (not reported), where by definition. In the LES vanDriest, the van Driest function damps the SGS viscosity in the buffer layer (), increasing the accuracy of the simulation. In the PSS isoLUWall, the LU near-wall model scales the component similarly to the . As a result, the accuracy of this model is equivalent to the LES vanDriest. Surprisingly, the values of stream-wise and spanwise components and seem not to affect the overall fluid dynamics, which is mainly influenced by the wall-normal component . In the PSS variance model, the off-diagonal components () assume low values and they are not reported. The diagonal components of variance tensor have a different behaviour. The component goes to zero near the wall. The profile starts to decrease at the beginning of the buffer layer () and scales like . Instead, the components and have larger values and do not approach zero near the wall. However, as previously noticed, they do not influence the final velocity statistics.
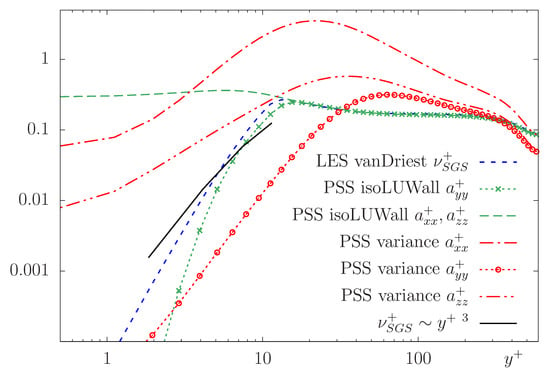
Figure 3.
Non-dimensional mean and along wall-normal direction. Three selected simulations are reported: LES with van Driest damping (LES vanDriest), PSS isotropic constant with LU near-wall model (PSS isoLUWall), and PSS with local variance model (PSS variance). Black solid line: the slope .
In order to assess the time performance of the PSS methodology, the computational time required by the pseudo-stochastic models with respect to the classical LES Smagorinsky constant model is also estimated [46]. The PSS isoConst model shows an increase in computational time of about compared to LES smagConst, while the PSS variance has an increment of . This increment is mainly ascribed to the additional computations due to the extra terms in the governing equations, along with the numerical manipulation of the variance tensor. Notice that such an estimate depends on the particular software used and on the numerical implementation; the optimisation of the numerical solver can lead to better performances.
Overall, the PSS variance model shows a moderate increase in computational time and can reproduce the mean velocity profile more accurately than the standard LES model here analysed, mainly because of the correct damping of the wall-normal variance tensor component in the vicinity of the wall. Also, the LU near-wall damping is able to reproduce the velocity profile as the LES with van Driest function. This result validates the pertinence of the LU wall-law model. It is worth noticing that the damping is imposed only at the wall-normal component of the generalised eddy-viscosity tensor (), while no modification is required for the wall-parallel components , .
PSS Extra Terms
The effects of the extra terms that characterised the PSS model are here shortly discussed. Figure 4-top-panel presents the non-dimensional turbulent advection velocity and the turbulent compressibility for the PSS isoConst. The stream-wise component of is practically zero, as well as the span-wise component; thus they are not displayed. The vertical component profile reveals low negative values, with a climax at . Quantitatively, the turbulent advection is not strong enough to produce remarkable results on the mean flow; however, it generates a weak vertical velocity directed from the centre of the channel to the wall (not reported). Hence, is qualified as a weak turbophoresis velocity: it advects the flow from the buffer region to the log–law region, i.e., in the direction of decreasing turbulence levels. The turbulent compressibility is practically zero, but it assumes slightly negative and positive values in the viscous sub-layer and the buffer layer, that can be qualitatively related to weak turbulent compression and expansion. The profiles of the other PSSs performed are not shown because the magnitude of is negligible and, overall, does not have an impact on the velocity statistics.
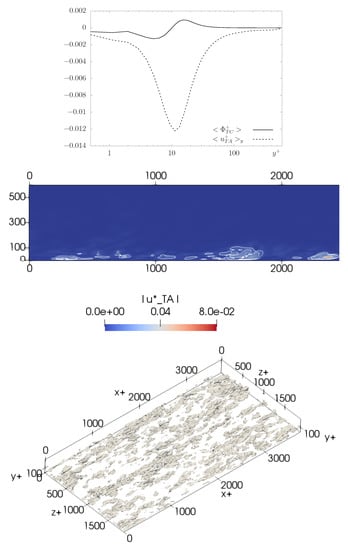
Figure 4.
Top-panel: averaged non-dimensional turbulent advection (21) and compressibility (22) appearing in PSS with constant isotropic model (PSS isoConst). Central-panel: contourplot of the instantaneous turbulent advection magnitude at a vertical slice for the simulation PSS variance. Bottom-panel: contourplot of the instantaneous turbulent compressibility at the channel bottom wall for the simulation PSS variance.
In the simulation PSS variance, the turbulent advection and compressibility assume low values, possibly because of the regular profile of . Nevertheless, the instantaneous structures linked to these quantities can be analysed. Figure 4-central-panel shows the instantaneous distribution of at a vertical slice. Spots of non-zero turbulent advection are localised in the region ; they are more intense in the buffer layer and logarithmic region . As for the PSS isoConst above discussed, the velocity generates a weak instantaneous and localised turbophoresis velocity in the direction of lower turbulent areas.
Figure 4-bottom-panel displays the instantaneous contourplot of turbulent compressibility near the bottom wall of the channel. The contourplot shows structures that are organised in spots, confined in the near-wall region and elongated in the stream-wise direction. Interestingly, the shape and the location of the isosurfaces suggest a correlation with the streak structures typical of the wall-bounded flows. The streaks are generated in a region of low velocity, very close to the wall, approximately at . They are elongated in the stream-wise direction, with a characteristic length of and a span-wise period of . This estimation can vary with respect to the wall distance, see Smith and Metzler [47]. The structures have the same stream-wise extension and span-wise period, suggesting a link with the streaks. This link will require additional investigations also because, despite multiple theories being proposed in the literature (see Chernyshenko & Baig [48]), there is no clear consensus on the streak formation mechanism so far.
6. Conclusions
In this study, we explored the potential of an alternative formulation of the Navier–Stokes equations through the use of stochastic calculus. Such formulation relies on the decomposition of the velocity field in a regular (i.e., differentiable) function and in a fast oscillating random variable, accounting for the unresolved turbulent scales of motion. The result is an alternative set of governing equations where the turbulence effects are taken into account through a variance tensor. This tensor needs to be modelled and is recognised to be a generalised form of the eddy-viscosity parameter used in the framework of large-eddy simulation (LES). The new simulation paradigm, named pseudo-stochastic simulation (PSS) approach, does not rely on the restrictive physical assumptions related to Boussinesq’s hypotheses and includes additional terms linked to physical phenomena. These additional terms are interpreted as turbophoresis and turbulent compression/expansion. A detailed comparison between the classical LES model and the PSS equations is reported and the turbulent kinetic energy budget equation is newly derived. Two PSSs were performed adopting different turbulent models for variance tensor: the isotropic constant and the local variance model. They were tested in the turbulent channel flow case at . The PSS isotropic constant model was provided with a near-wall damping function which was applied here for the first time. The results of the simulations are of the same order of accuracy as the classical LES counterpart. Differences between PSS and LES are not expected for this model because it is derived following an analogy with the Smagorisnky model for LES; nonetheless, PSS simulations successfully validated the proposed damping function. The PSS local variance model, instead, does not have a counterpart in the LES framework and exhibits a higher accuracy. This is mainly due to the correct scaling of the turbulent contribution near the wall. In conclusion, the PSS outperforms the classical LES when the local variance tensor model is chosen. Such a model is mathematically derived rather than empirically determined from physical assumptions (as the Smagorinsky model for LES). We believe that these results are encouraging and that the pseudo-stochastic formalism can foster the development of efficient turbulent models.
Author Contributions
Conceptualization, C.C. and E.M.; methodology, C.C. and E.M.; software, C.C.; validation, C.C.; formal analysis, C.C.; investigation, C.C. and E.M.; resources, E.M.; data curation, C.C.; writing–original draft preparation, C.C.; writing–review and editing, C.C. and E.M.; visualization, C.C.; supervision, E.M.; project administration, E.M.; funding acquisition, E.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Mathematical Derivation of Local Variance Model
The local variance model is derived from the definition of the variance tensor in term of fluid-particle trajectory [13]:
where the is the simulation time-step, and is the quadratic variation of a stochastic process. This can be seen as a summation along time of random increments, e.g., see Le Gall [49] for the mathematical definition. Approximating the integral with the mean value theorem, one can write
where . Considering that the time-step is small, the approximation is also done and the definition of quadratic variation for one time-step interval is applied:
The stochastic displacement can be estimated as . Subsequently, using the Eulerian coordinates and the velocity decomposition (2), one can express:
where denotes the averaged velocity and the parameter links the SUS with the fluctuations of the resolved scales. The final expression of the variance tensor reads:
which is used in the present study.
References
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Pope, S.B. A Lagrangian two-time probability density function equation for inhomogeneous turbulent flows. Phys. Fluids 1983, 26, 3448–3450. [Google Scholar] [CrossRef]
- Durbin, P.A.; Speziale, C.G. Realizability of second-moment closure via stochastic analysis. J. Fluid Mech. 1994, 280, 395–407. [Google Scholar] [CrossRef]
- Orszag, S.A. Analytical theories of turbulence. J. Fluid Mech. 1970, 41, 363–386. [Google Scholar] [CrossRef]
- Leslie, D.C. Developments in the Theory of Turbulence; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Chasnov, J.R. Simulation of the Kolmogorov inertial subrange using an improved subgrid model. Phys. Fluids A Fluid Dyn. 1991, 3, 188–200. [Google Scholar] [CrossRef]
- Leith, C.E. Stochastic backscatter in a subgrid-scale model: Plane shear mixing layer. Phys. Fluids A Fluid Dyn. 1990, 2, 297–299. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Dynamics of nonlinear stochastic systems. J. Math. Phys. 1961, 2, 124–148. [Google Scholar] [CrossRef]
- Frederiksen, J.S.; O’Kane, T.J.; Zidikheri, M.J. Subgrid modelling for geophysical flows. Philos. Trans. R. Soc. A 2013, 371. [Google Scholar] [CrossRef][Green Version]
- Brzeźniak, Z.; Capiński, M.; Flandoli, F. Stochastic partial differential equations and turbulence. Math. Model. Methods Appl. Sci. 1991, 1, 41–59. [Google Scholar] [CrossRef]
- Mikulevicius, R.; Rozovskii, B.L. Stochastic Navier–Stokes Equations for Turbulent Flows. SIAM J. Math. Anal. 2004, 35, 1250–1310. [Google Scholar] [CrossRef]
- Flandoli, F. The Interaction Between Noise and Transport Mechanisms in PDEs. Milan J. Math. 2011, 79, 543–560. [Google Scholar] [CrossRef]
- Mémin, E. Fluid flow dynamics under location uncertainty. Geophys. Astrophys. Fluid Dyn. 2014, 108, 119–146. [Google Scholar] [CrossRef]
- Neves, W.; Olivera, C. Wellposedness for stochastic continuity equations with Ladyzhenskaya–Prodi–Serrin condition. Nonlinear Differ. Equations Appl. NoDEA 2015, 22, 1247–1258. [Google Scholar] [CrossRef]
- Holm, D.D. Variational principles for stochastic fluid dynamics. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2015, 471. [Google Scholar] [CrossRef] [PubMed]
- Resseguier, V.; Mémin, E.; Chapron, B. Geophysical flows under location uncertainty, Part I: Random transport and general models. Geophys. Astrophys. Fluid Dyn. 2017, 111, 149–176. [Google Scholar] [CrossRef]
- Resseguier, V.; Mémin, E.; Chapron, B. Geophysical flows under location uncertainty, Part II: Quasi-geostrophy and efficient ensemble spreading. Geophys. Astrophys. Fluid Dyn. 2017, 111, 177–208. [Google Scholar] [CrossRef]
- Resseguier, V.; Mémin, E.; Chapron, B. Geophysical flows under location uncertainty, Part III: SQG and frontal dynamics under strong turbulence conditions. Geophys. Astrophys. Fluid Dyn. 2017, 111, 209–227. [Google Scholar] [CrossRef]
- Resseguier, V.; Li, L.; Jouan, G.; Dérian, P.; Mémin, E.; Chapron, B. New Trends in Ensemble Forecast Strategy: Uncertainty Quantification for Coarse-Grid Computational Fluid Dynamics. Arch. Computat. Methods Eng. 2020, 1–82. [Google Scholar] [CrossRef]
- Bauer, W.; Chandramouli, P.; Chapron, B.; Li, L.; Mémin, E. Deciphering the Role of Small-Scale Inhomogeneity on Geophysical Flow Structuration: A Stochastic Approach. J. Phys. Oceanogr. 2020, 50, 983–1003. [Google Scholar] [CrossRef]
- Bauer, W.; Chandramouli, P.; Li, L.; Mémin, E. Stochastic representation of mesoscale eddy effects in coarse-resolution barotropic models. Ocean Model. 2020, 151, 101646. [Google Scholar] [CrossRef]
- Chapron, B.; Dérian, P.; Mémin, E.; Resseguier, V. Large-scale flows under location uncertainty: A consistent stochastic framework. Q. J. R. Meteorol. Soc. 2017, 144, 251–260. [Google Scholar] [CrossRef]
- Resseguier, V.; Mémin, E.; Heitz, D.; Chapron, B. Stochastic modelling and diffusion modes for proper orthogonal decomposition models and small-scale flow analysis. J. Fluid Mech. 2017, 826, 888–917. [Google Scholar] [CrossRef]
- Pinier, B.; Mémin, E.; Laizet, S.; Lewandowski, R. Stochastic flow approach to model the mean velocity profile of wall-bounded flows. Phys. Rev. E 2019, 99, 063101. [Google Scholar] [CrossRef] [PubMed]
- Harouna, S.K.; Mémin, E. Stochastic representation of the Reynolds transport theorem: Revisiting large-scale modeling. Comput. Fluids 2017, 156, 456–469. [Google Scholar] [CrossRef]
- Chandramouli, P.; Heitz, D.; Laizet, S.; Mémin, E. Coarse large-eddy simulations in a transitional wake flow with flow models under location uncertainty. Comput. Fluids 2018, 168, 170–189. [Google Scholar] [CrossRef]
- Resseguier, V. Mixing and Fluid Dynamics under Location Uncertainty. Ph.D. Thesis, University of Rennes 1 and Inria Rennes, Bretagne Atlantique, France, 2017. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Kunita, H. Stochastic Flows and Stochastic Differential Equations; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Kundu, P.; Cohen, I.M. Fluid Mechanics, 3rd ed.; Elsevier Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows. An Introduction; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Piomelli, U. Large-eddy and direct simulation of turbulent flows. In Proceedings of the CFD 2001—9th Conférence Annuelle de la Société Canadienne de CFD, Waterloo, ON, Canada, 27–29 May 2001. [Google Scholar]
- Lilly, D.K. The Representation of Small-Scale Tubulence in Numerical Simulation Experiments. In Proceedings of IBM Scientific Computing Symposium on Environmental Sciences, Yorktown Heights; Goldstine, H.H., Ed.; IBM, Data Processing Division: Armonk, NY, USA, 1967; pp. 195–210. [Google Scholar] [CrossRef]
- Van Driest, E. On turbulent flow near a wall. J. Aeronaut. Sci. 1956, 23, 1007–1011. [Google Scholar] [CrossRef]
- Piomelli, U.; Ferziger, J.; Moin, P.; Kim, J. New approximate boundary conditions for large eddy simulations of wall-bounded flows. Phys. Fluids A Fluid Dyn. 1989, 1, 1061–1068. [Google Scholar] [CrossRef]
- Cabot, W.; Moin, P. Approximate Wall Boundary Conditions in the Large-Eddy Simulation of High Reynolds Number Flow. Flow Turbul. Combust. 2000, 63, 269–291. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Métais, O.; Lesieur, M. Spectral large-eddy simulation of isotropic and stably stratified turbulence. J. Fluid Mech. 1992, 239, 157–194. [Google Scholar] [CrossRef]
- Moser, R.D.; Kim, J.; Mansour, N.N. Direct numerical simulation of turbulent channel flow up to Reτ = 590. Phys. Fluids 1999, 11, 943–945. [Google Scholar] [CrossRef]
- Jasak, H.; Weller, H.; Gosman, A. High resolution NVD differencing scheme for arbitrarily unstructured meshes. Int. J. Numer. Meth. Fluids 1999, 31, 431–449. [Google Scholar] [CrossRef]
- Issa, R.I.; Gosman, A.D.; Watkins, A.P. The computation of compressible and incompressible recirculating flows by a non-iterative implicit scheme. J. Comput. Phys. 1986, 62, 66. [Google Scholar] [CrossRef]
- Oliveira, P.J.; Issa, P.I. An improved PISO algorithm for the computation of bouyancy driven flows. Numer. Heat Transf. Part B Fundam. 2001, 640, 473. [Google Scholar] [CrossRef]
- Castaño, S.L.; Petronio, A.; Petris, G.; Armenio, V. Assessment of Solution Algorithms for LES of Turbulent Flows Using OpenFOAM. Fluids 2019, 4, 171. [Google Scholar] [CrossRef]
- Armenio, V.; Piomelli, U. A Lagrangian Mixed Subgrid-Scale Model in Generalized Coordinates. Flow Turbul. Combust. 2000, 65, 51–81. [Google Scholar] [CrossRef]
- Piomelli, U. Large-eddy simulation: Achievements and challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Smith, C.R.; Metzler, S.P. The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 1983, 129, 27–54. [Google Scholar] [CrossRef]
- Chernyshenko, S.I.; Baig, M.F. The mechanism of streak formation in near-wall turbulence. J. Fluid Mech. 2005, 544, 99–131. [Google Scholar] [CrossRef]
- Le Gall, J.F. Brownian Motion, Martingales, and Stochastic Calculus; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).