Electrical Conductivity of Field-Structured Emulsions
Abstract
1. Introduction
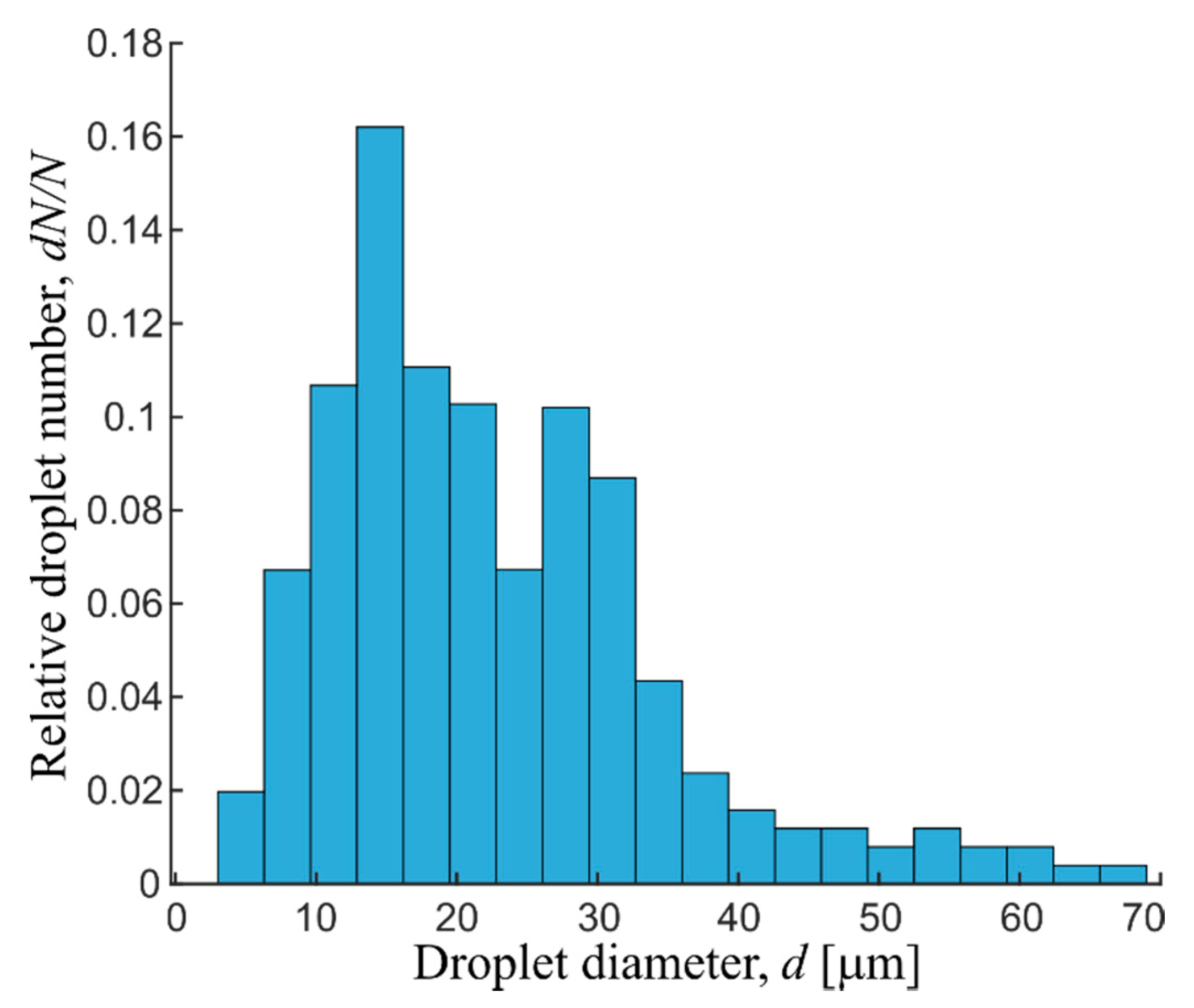
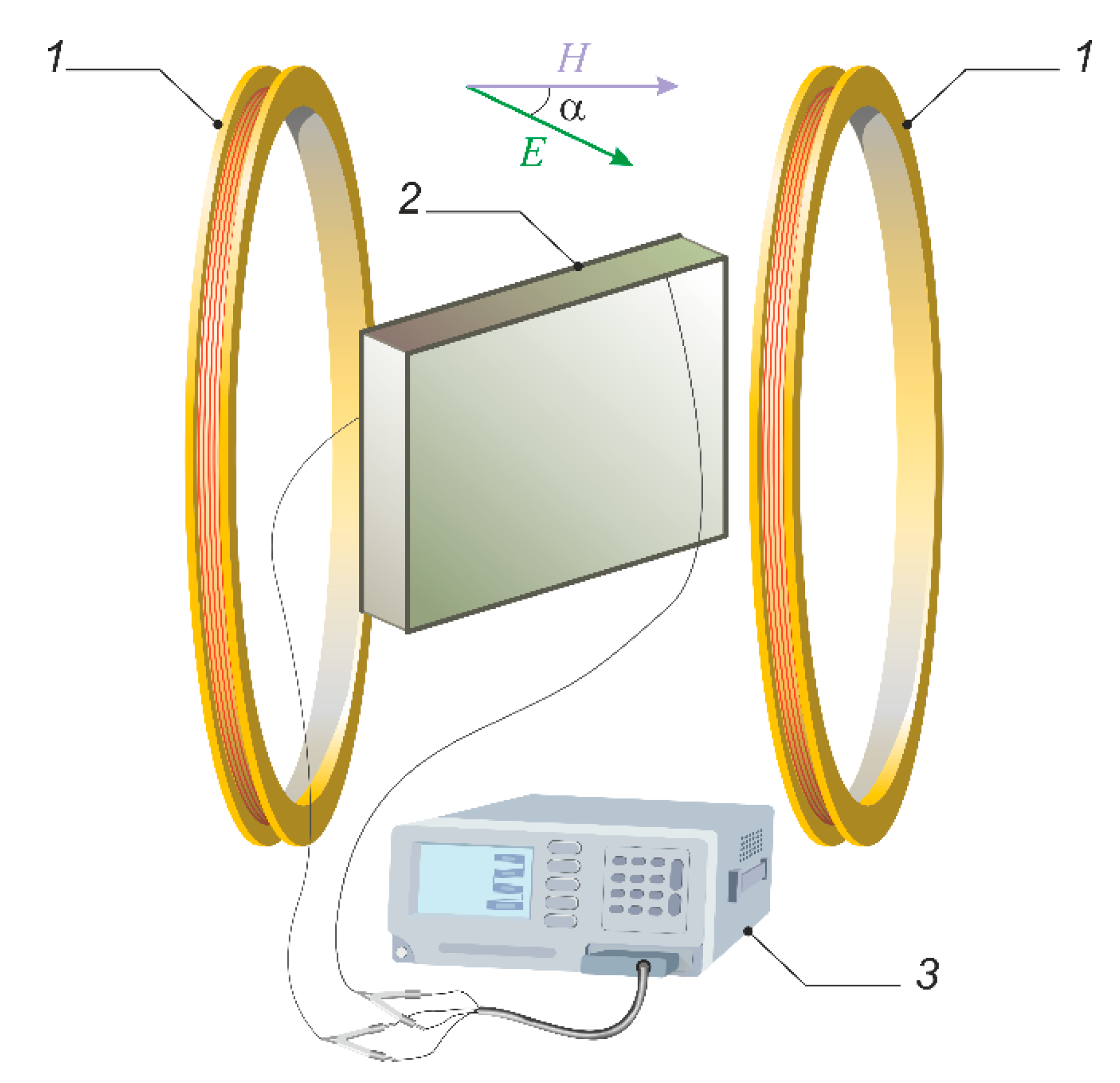
2. Materials and Methods
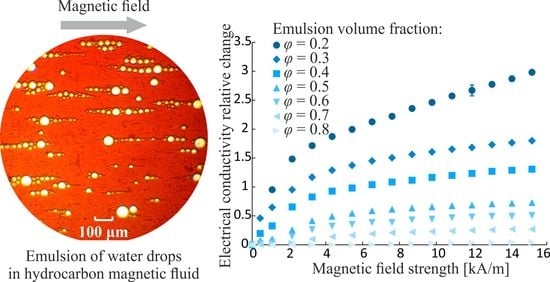
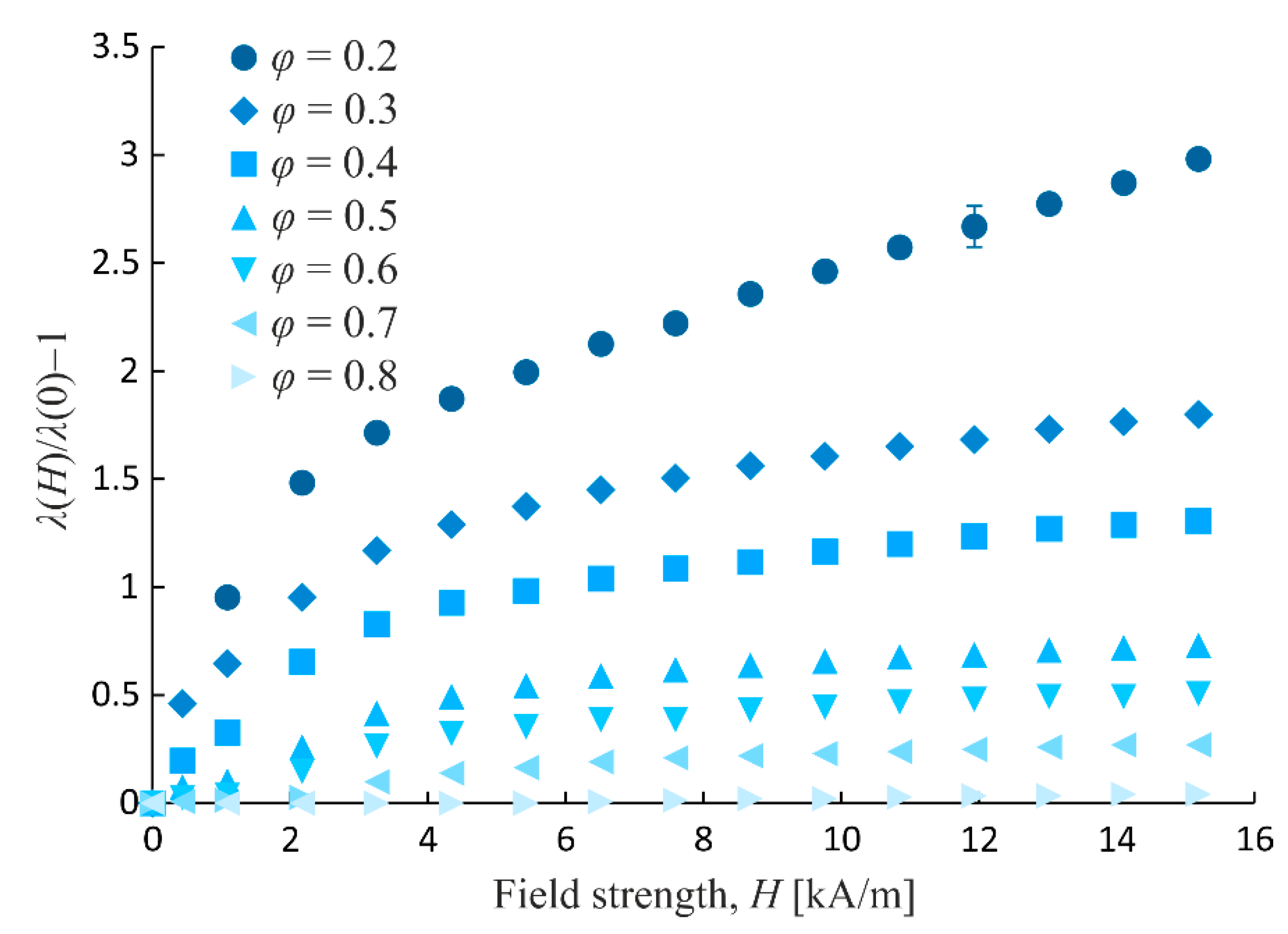
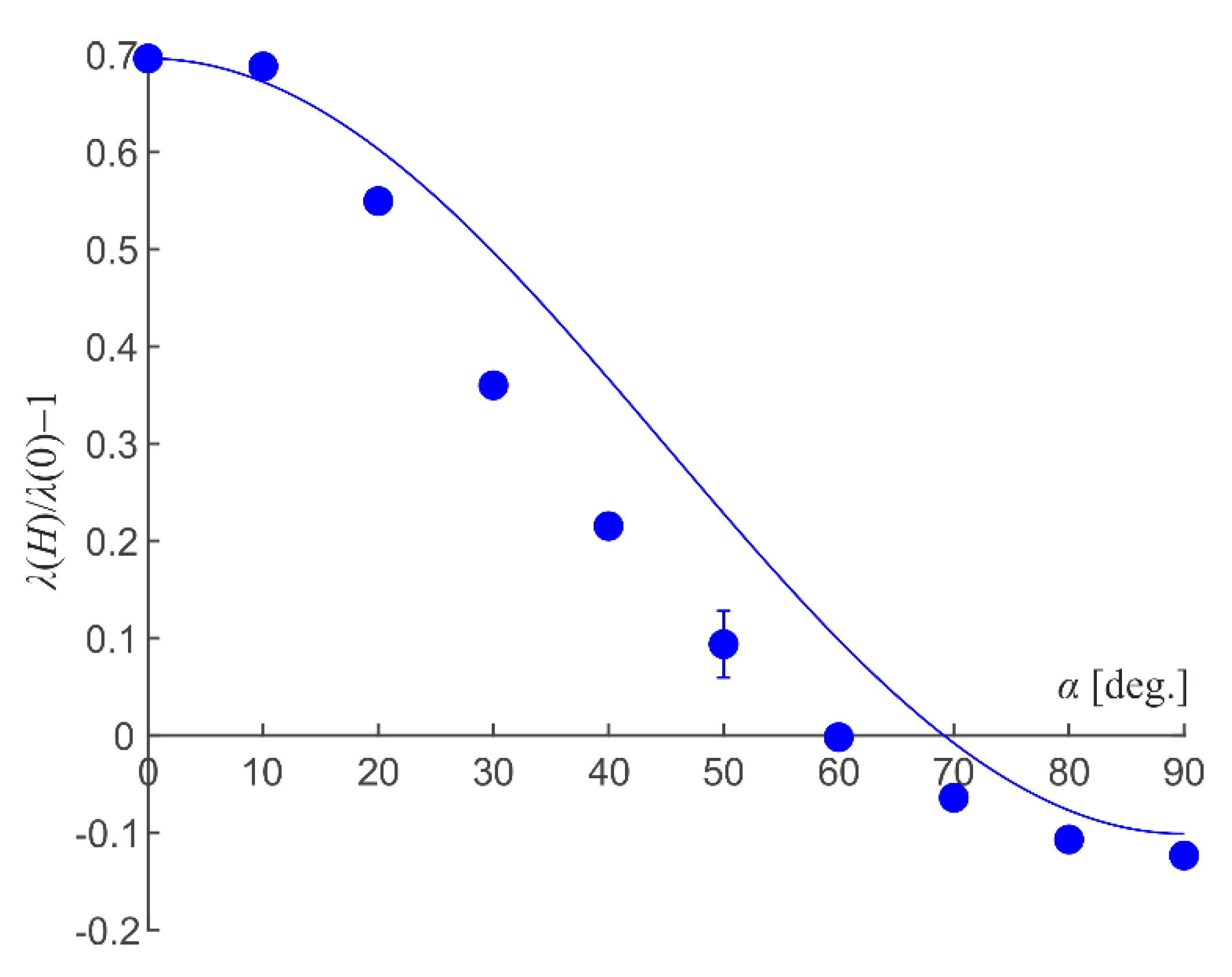
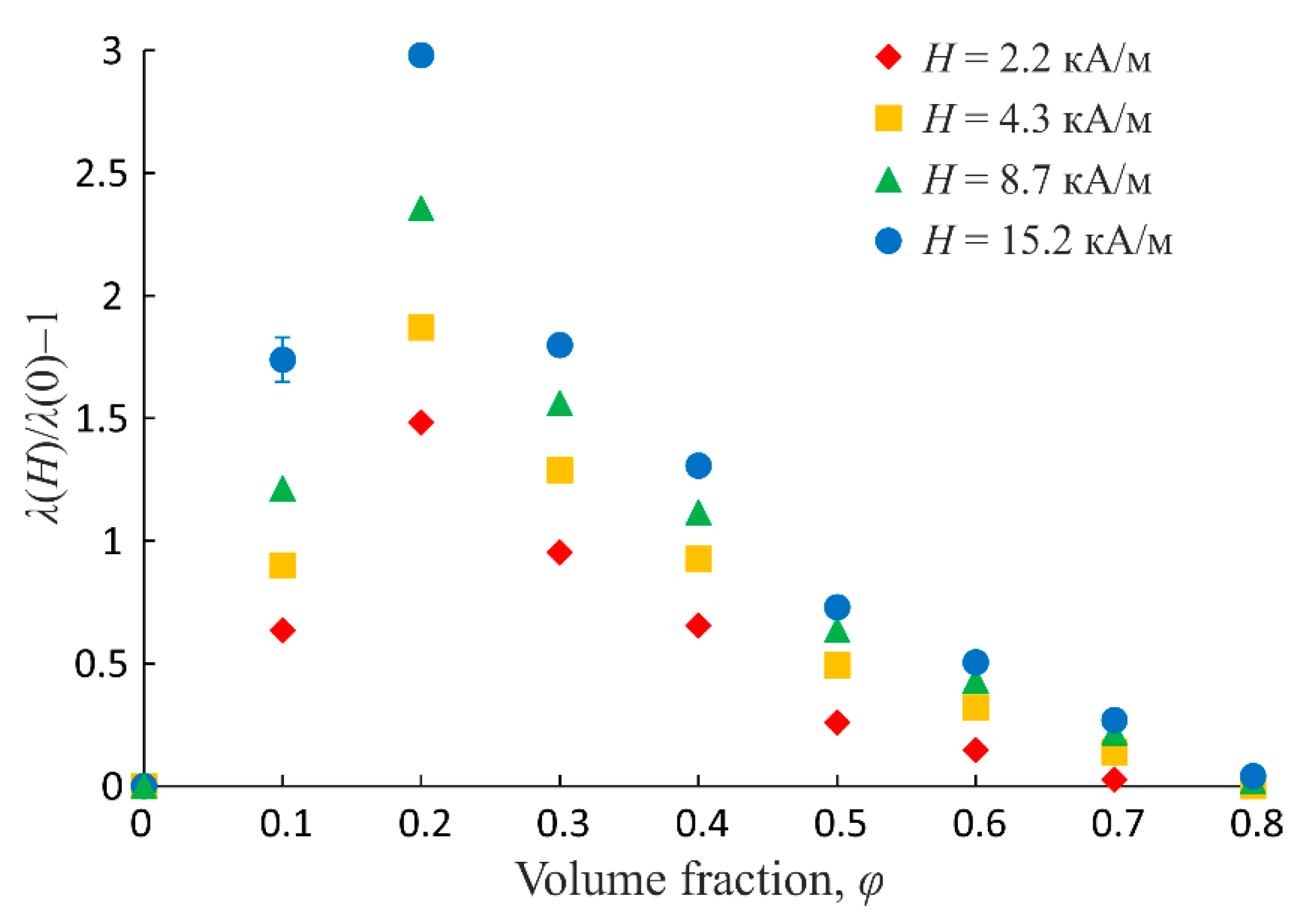
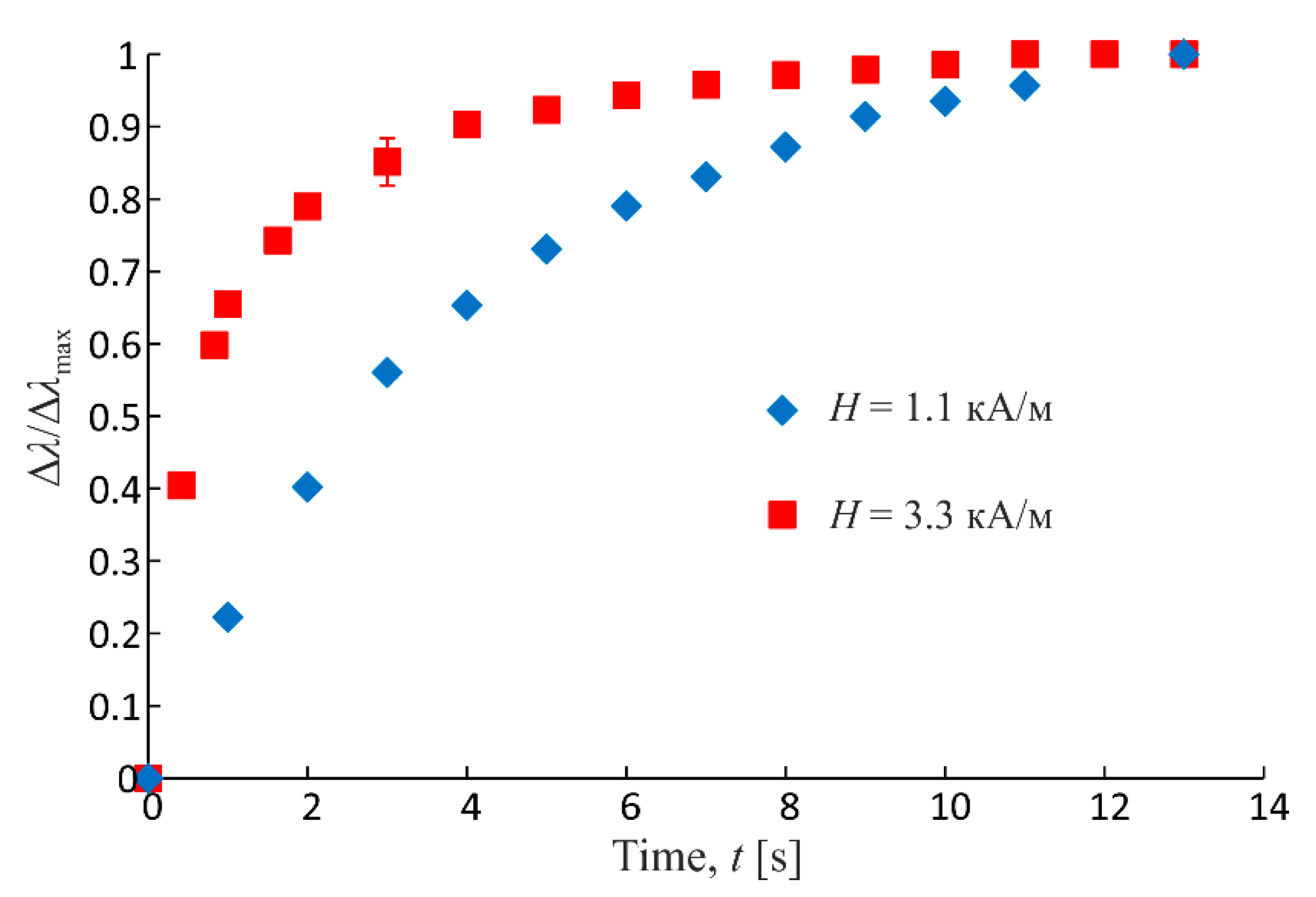
3. Experimental Results
4. Analysis and Discussion
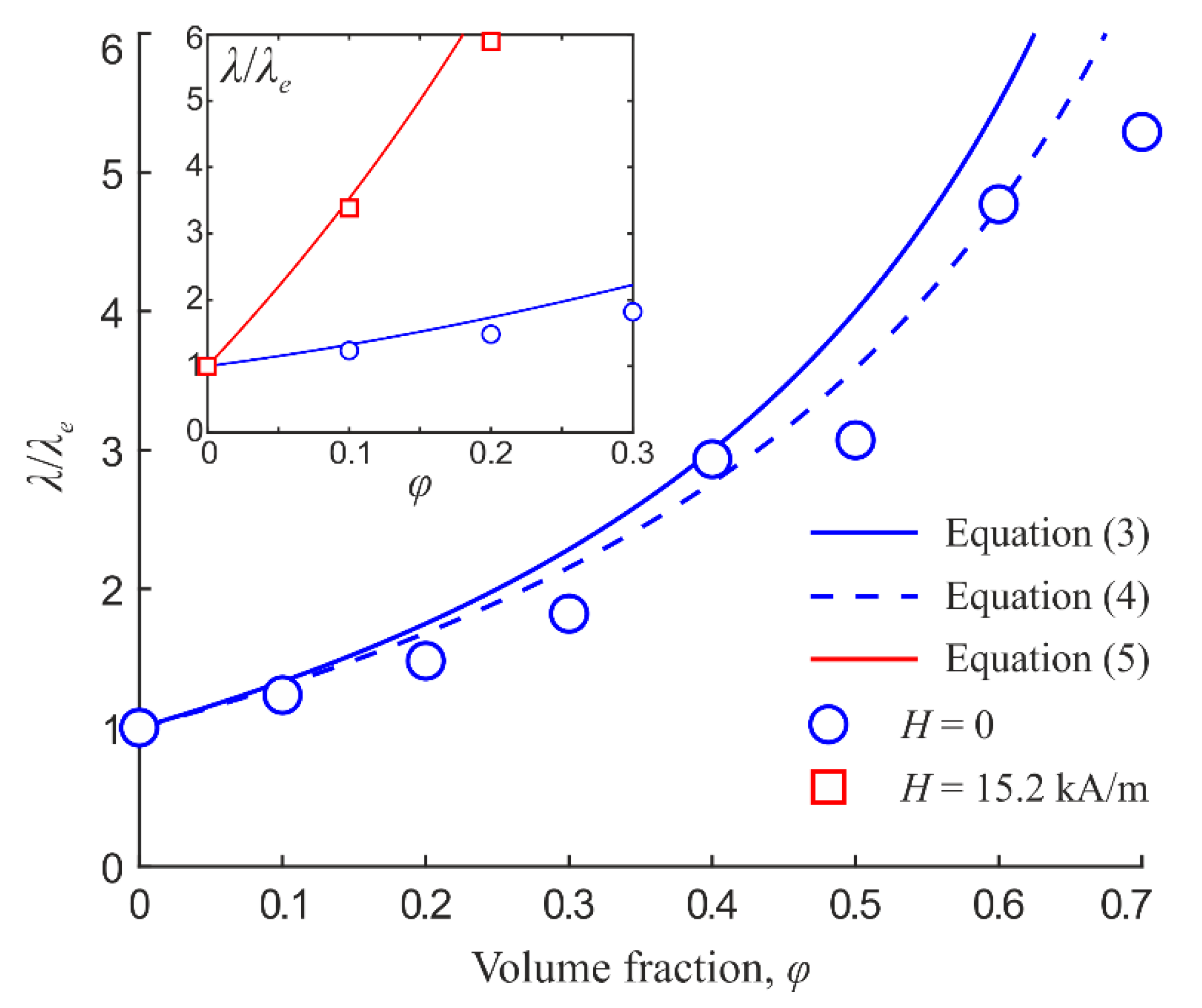
4.1. Conductivity Estimation
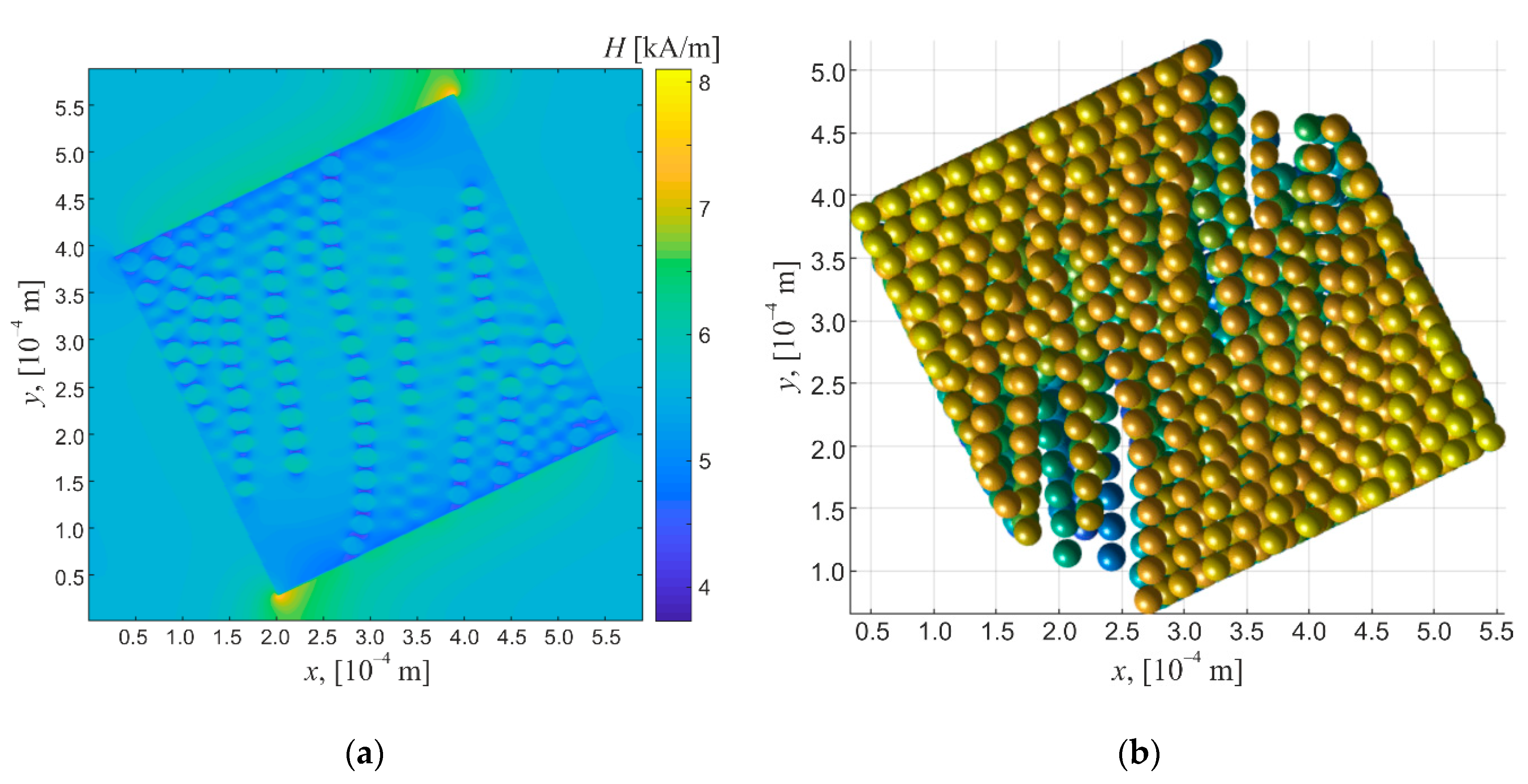
4.2. Structure Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Löwen, H. Colloidal soft matter under external control. J. Phys. Condens. Matter. 2001, 13, R415–R432. [Google Scholar] [CrossRef]
- Chiolerio, A.; Quadrelli, M.B. Smart fluid systems: The advent of autonomous liquid robotics. Adv. Sci. 2017, 4, 1700036. [Google Scholar] [CrossRef]
- Ge, J.; He, L.; Hu, Y.; Yin, Y. Magnetically induced colloidal assembly into field-responsive photonic structures. Nanoscale 2011, 3, 177–183. [Google Scholar] [CrossRef]
- Torres-Díaz, I.; Rinaldi, C. Recent progress in ferrofluids research: Novel applications of magnetically controllable and tunable fluids. Soft Matter 2014, 10, 8584–8602. [Google Scholar] [CrossRef]
- Chiew, Y.C.; Glandt, E.D. The effect of structure on the conductivity of a dispersion. J. Colloid Interface Sci. 1983, 94, 90–104. [Google Scholar] [CrossRef]
- Pelster, R.; Simon, U. Nanodispersions of conducting particles: Preparation, microstructure and dielectric properties. Colloid Polym. Sci. 1999, 277, 2–14. [Google Scholar] [CrossRef]
- Wu, C.; Cho, T.J.; Xu, J.; Lee, D.; Yang, B.; Zachariah, M.R. Effect of nanoparticle clustering on the effective thermal conductivity of concentrated silica colloids. Phys. Rev. E 2010, 81, 011406. [Google Scholar] [CrossRef] [PubMed]
- Ammar, A.; Chinesta, F.; Heyd, R. Thermal conductivity of suspension of aggregating nanometric rods. Entropy 2017, 19, 19. [Google Scholar] [CrossRef]
- Timofeeva, E.V.; Gavrilov, A.N.; McCloskey, J.M.; Tolmachev, Y.V.; Sprunt, S.; Lopatina, L.M.; Selinger, J.V. Thermal conductivity and particle agglomeration in alumina nanofluids: Experiment and theory. Phys. Rev. E 2007, 76, 061203. [Google Scholar] [CrossRef] [PubMed]
- Bica, I.; Choi, H.J. Preparation and electro-thermoconductive characteristics of magnetorheological suspensions. Int. J. Mod. Phys. B 2008, 22, 5041–5064. [Google Scholar] [CrossRef]
- Bica, I.; Liu, Y.D.; Choi, H.J. Physical characteristics of magnetorheological suspensions and their applications. J. Ind. Eng. Chem. 2013, 19, 394–406. [Google Scholar] [CrossRef]
- Heine, M.C.; de Vicente, J.; Klingenberg, D.J. Thermal transport in sheared electro- and magnetorheological fluids. Phys. Fluids 2006, 18, 023301. [Google Scholar] [CrossRef]
- Shima, P.D.; Philip, J. Tuning of thermal conductivity and rheology of nanofluids using an external stimulus. J. Phys. Chem. C 2011, 115, 20097–20104. [Google Scholar] [CrossRef]
- Ruan, X.; Wang, Y.; Xuan, S.; Gong, X. Magnetic field dependent electric conductivity of the magnetorheological fluids: The influence of oscillatory shear. Smart Mater. Struct. 2017, 26, 035067. [Google Scholar] [CrossRef]
- Forero-Sandoval, I.Y.; Vega-Flick, A.; Alvarado-Gil, J.J.; Medina-Esquivel, R.A. Study of thermal conductivity of magnetorheological fluids using the thermal-wave resonant cavity and its relationship with the viscosity. Smart Mater. Struct. 2017, 26, 025010. [Google Scholar] [CrossRef]
- Song, D.-X.; Ma, W.-G.; Zhang, X. Anisotropic thermal conductivity in ferrofluids induced by uniform cluster orientation and anisotropic phonon mean free path. Int. J. Heat Mass Transf. 2019, 138, 1228–1237. [Google Scholar] [CrossRef]
- Hanai, T. Electrical properties of emulsions. In Emulsion Science; Sherman, P., Ed.; Academic Press: London, UK, 1968; pp. 353–478. [Google Scholar]
- Bumajdad, A.; Eastoe, J. Conductivity of water-in-oil microemulsions stabilized by mixed surfactants. J. Colloid Interface Sci. 2004, 274, 268–276. [Google Scholar] [CrossRef]
- Yan, Y.-L.; Shan, C.; Wang, Y.; Deng, Q. Effects of oil on aqueous foams: Electrical conductivity of foamed emulsions. ChemPhysChem 2014, 15, 3110–3115. [Google Scholar] [CrossRef]
- Leal-Calderon, F.; Thivilliers, F.; Schmitt, V. Structured emulsions. Curr. Opin. Colloid Interface Sci. 2007, 12, 206–212. [Google Scholar] [CrossRef]
- McClements, D.J. Advances in fabrication of emulsions with enhanced functionality using structural design principles. Curr. Opin. Colloid Interface Sci. 2012, 17, 235–245. [Google Scholar] [CrossRef]
- Liu, J.; Lawrence, E.M.; Wu, A.; Ivey, M.L.; Flores, G.A.; Javier, K.; Bibette, J.; Richard, J. Field-induced structures in ferrofluid emulsions. Phys. Rev. Lett. 1995, 74, 2828–2831. [Google Scholar] [CrossRef] [PubMed]
- Ivey, M.; Liu, J.; Zhu, Y.; Cutillas, S. Magnetic-field-induced structural transitions in a ferrofluid emulsion. Phys. Rev. E 2000, 63, 011403. [Google Scholar] [CrossRef] [PubMed]
- Montagne, F.; Braconnot, S.; Mondain-Monval, O.; Pichot, C.; Elaïssari, A. Colloidal and physicochemical characterization of highly magnetic O/W magnetic emulsions. J. Dispers. Sci. Technol. 2003, 24, 821–832. [Google Scholar] [CrossRef]
- Zakinyan, A.; Dikansky, Y. Drops deformation and magnetic permeability of a ferrofluid emulsion. Colloids Surf. A 2011, 380, 314–318. [Google Scholar] [CrossRef]
- Subbotin, I.M. Magnetic permeability of inverse ferrofluid emulsion: Nonlinear ferrofluid magnetization law. J. Magn. Magn. Mater. 2020, 502, 166524. [Google Scholar] [CrossRef]
- Nguyen, N.-T. Micro-magnetofluidics: Interactions between magnetism and fluid flow on the microscale. Microfluid. Nanofluid. 2012, 12, 1–16. [Google Scholar] [CrossRef]
- Yang, R.-J.; Hou, H.-H.; Wang, Y.-N.; Fu, L.-M. Micro-magnetofluidics in microfluidic systems: A review. Sens. Actuators B Chem. 2016, 224, 1–15. [Google Scholar] [CrossRef]
- Mahendran, V.; Philip, J. Sensing of biologically important cations such as Na+, K+, Ca2+, Cu2+, and Fe3+ using magnetic nanoemulsions. Langmuir 2013, 29, 4252–4258. [Google Scholar] [CrossRef]
- Mahendran, V.; Philip, J. A methanol sensor based on stimulus-responsive magnetic nanoemulsions. Sens. Actuators B Chem. 2013, 185, 488–495. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Thanh, N.T.K.; Jones, S.K.; Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224001. [Google Scholar] [CrossRef]
- Sander, J.S.; Erb, R.M.; Denier, C.; Studart, A.R. Magnetic transport, mixing and release of cargo with tailored nanoliter droplets. Adv. Mater. 2012, 24, 2582–2587. [Google Scholar] [CrossRef] [PubMed]
- Mefford, O.T.; Woodward, R.C.; Goff, J.D.; Vadala, T.P.; Pierre, T.G.S.; Dailey, J.P.; Riffle, J.S. Field-induced motion of ferrofluids through immiscible viscous media: Testbed for restorative treatment of retinal detachment. J. Magn. Magn. Mater. 2007, 311, 347–353. [Google Scholar] [CrossRef]
- Hu, H.; Chen, C.; Chen, Q. Magnetically controllable colloidal photonic crystals: Unique features and intriguing applications. J. Mater. Chem. C 2013, 1, 6013–6030. [Google Scholar] [CrossRef]
- Brojabasi, S.; Lahiri, B.B.; Philip, J. External magnetic field dependent light transmission and scattered speckle pattern in a magnetically polarizable oil-in-water nanoemulsion. Phys. B 2014, 454, 272–278. [Google Scholar] [CrossRef]
- Belykh, S.S.; Yerin, C.V. Magneto-optic effect in water-based magnetic emulsions. Magnetohydrodynamics 2018, 54, 5–10. [Google Scholar] [CrossRef]
- Mohapatra, D.K.; Laskar, J.M.; Philip, J. Temporal evolution of equilibrium and non-equilibrium magnetic field driven microstructures in a magnetic fluid. J. Mol. Liq. 2020, 304, 112737. [Google Scholar] [CrossRef]
- Zakinyan, A.; Dikansky, Y.; Bedzhanyan, M. Electrical properties of chain microstructure magnetic emulsions in magnetic field. J. Dispers. Sci. Technol. 2014, 35, 111–119. [Google Scholar] [CrossRef][Green Version]
- Zakinyan, A.; Arefyev, I. Thermal conductivity of emulsion with anisotropic microstructure induced by external field. Colloid Polym. Sci. 2020, in press. [Google Scholar] [CrossRef]
- Darras, A.; Fiscina, J.; Pakpour, M.; Vandewalle, N.; Lumay, G. Ribbons of superparamagnetic colloids in magnetic field. Eur. Phys. J. E 2016, 39, 47. [Google Scholar] [CrossRef]
- Faraudo, J.; Andreu, J.S.; Calero, C.; Camacho, J. Predicting the self-assembly of superparamagnetic colloids under magnetic fields. Adv. Funct. Mater. 2016, 26, 3837–3858. [Google Scholar] [CrossRef]
- Fertman, V.E. Magnetic Fluids Guidebook: Properties and Applications; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Promislow, J.H.E.; Gast, A.P.; Fermigier, M. Aggregation kinetics of paramagnetic colloidal particles. J. Chem. Phys. 1995, 102, 5492–5498. [Google Scholar] [CrossRef]
- Darras, A.; Opsomer, E.; Vandewalle, N.; Lumay, G. Effect of volume fraction on chains of superparamagnetic colloids at equilibrium. Eur. Phys. J. E 2019, 42, 123. [Google Scholar] [CrossRef] [PubMed]
- Andreu, J.S.; Camacho, J.; Faraudo, J. Aggregation of superparamagnetic colloids in magnetic fields: The quest for the equilibrium state. Soft Matter 2011, 7, 2336–2339. [Google Scholar] [CrossRef]
- Darras, A.; Opsomer, E.; Vandewalle, N.; Lumay, G. Superparamagnetic colloids in viscous fluids. Sci. Rep. 2017, 7, 7778. [Google Scholar] [CrossRef] [PubMed]
- Fricke, H. The Maxwell-Wagner dispersion in a suspension of ellipsoids. J. Phys. Chem. 1953, 57, 934–937. [Google Scholar] [CrossRef]
- Martin, J.E.; Anderson, R.A.; Tigges, C.P. Simulation of the athermal coarsening of composites structured by a uniaxial field. J. Chem. Phys. 1998, 108, 3765–3787. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon Press: New York, NY, USA, 1984. [Google Scholar]
- Nagel, J.R. Numerical solutions to Poisson equations using the finite-difference method. IEEE Antennas Propag. Mag. 2014, 56, 209–224. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakinyan, A.R.; Kulgina, L.M.; Zakinyan, A.A.; Turkin, S.D. Electrical Conductivity of Field-Structured Emulsions. Fluids 2020, 5, 74. https://doi.org/10.3390/fluids5020074
Zakinyan AR, Kulgina LM, Zakinyan AA, Turkin SD. Electrical Conductivity of Field-Structured Emulsions. Fluids. 2020; 5(2):74. https://doi.org/10.3390/fluids5020074
Chicago/Turabian StyleZakinyan, Arthur R., Ludmila M. Kulgina, Anastasia A. Zakinyan, and Sergey D. Turkin. 2020. "Electrical Conductivity of Field-Structured Emulsions" Fluids 5, no. 2: 74. https://doi.org/10.3390/fluids5020074
APA StyleZakinyan, A. R., Kulgina, L. M., Zakinyan, A. A., & Turkin, S. D. (2020). Electrical Conductivity of Field-Structured Emulsions. Fluids, 5(2), 74. https://doi.org/10.3390/fluids5020074