1. Introduction
The interaction of surface waves with submerged spheres and spheroids presents a characteristic problem in the field of hydrodynamics. Considering the case of perfectly symmetric spherical geometries, Linton [
1], for example, studied the diffraction and the radiation problem of a submerged sphere in waters of finite depth, while Wu et al. [
2] extended Linton’s work by including the calculation of drift forces. Rahman [
3] studied the exciting forces of a submerged sphere, and estimated the wave elevation above the sphere due to monochromatic incident waves. All these studies employed Thorn’s [
4] multipole expansions, in order to expand the potential into series of spherical harmonics. On the other hand, in the case of spheroidal geometries, most existing studies focus on prolate spheroids, while relevant analytical solutions have been developed by utilizing the so-called system of image singularities. Briefly, the system of image singularities of an arbitrary exterior potential field within a spheroid allows the expression of the fundamental solution of the Laplace equation, i.e., the sources, in terms of spheroidal harmonics. Accordingly, it enables the implementation of a full hydrodynamic analysis based explicitly on the associated coordinate system. The analysis sought is performed by constructing the involved velocity potentials in terms of spheroidal harmonics.
The theorem on the system of image singularities for a spheroidal geometry, and the associated homonymous method, were first developed, and employed, by Havelock [
5], who studied the moment, due to surface waves, applied on a fully submerged, moving prolate spheroid. Havelock [
6] used the same method to investigate both the forces and the moments acting on a submerged moving prolate spheroid as the body is subjected to regular waves. In both cases, he studied, without a proof of the relevant theorem, the non-axisymmetric case, where the axis of symmetry of the spheroid is parallel to the undisturbed free surface. The proof of the theorem for a prolate spheroid was later given by Miloh [
7]. Subsequently, this theorem was employed by Chatjigeorgiou and Miloh [
8,
9,
10,
11,
12], who investigated the diffraction, radiation and the wave resistance problems, for immersed prolate spheroids and for the non-axisymmetric case (symmetrical axis parallel to the undisturbed free surface). It should be noted that the works of Chatjigeorgiou and Miloh [
8,
9,
10,
11,
12] preceded the studies of Wu and Eatock Taylor [
13,
14], who based their research on a Fredholm integral equation of the second type, involving a source/sink distribution over the surface of the spheroid. In terms of the “symmetric” placement of a prolate spheroid relative to the free surface, i.e., symmetrical axis normal to the free surface, it appears that the only relevant study is that of Chatjigeorgiou [
15], who, however, started from Thorn’s [
4] multipoles in spherical coordinates, and developed rigorous addition theorems to transform the governing expansions into prolate spheroidal coordinates.
The relevant theorems, associated with the system of image singularities for an oblate geometry, were first reported in the book of Chatjigeorgiou [
16]. Chatjigeorgiou et al. [
17] utilized for the first time the method of image singularities in oblate geometry, to enable the solution of the diffraction problem for an immersed oblate spheroid in infinite water depth. The axisymmetric placement of the spheroid (symmetrical axis normal to the free surface) was considered. Indeed, the diffraction problem provides the path for the solution of the radiation problem, the case that is considered herein. The present investigation is a follow-up of the study conducted in [
17], which, contrary to [
17], determines and discusses the variation of the most important hydrodynamic parameters of added masses and hydrodynamic damping. The same formulation can be effectively extended to finite water depth as well.
A question which easily arises is whether the formulation(s) developed and analyzed herein can be immediately extended to prolate geometries with symmetrical placement relative to the undisturbed free surface. The answer cannot be strict and unconditional, given the different starting points of the existing (and reported) “image singularity systems” in prolate and oblate geometries. The former (e.g., [
7]) rely on the uniform distribution of singularities along the major axis of the spheroid between the two foci, while the latter rely on the distribution of singularities on the fundamental disk of the oblate spheroid (e.g., [
16]). The formulations are not by default equivalent, while the verification that they could coincide with only simple transformations would require some further mathematical elaborations.
The present paper focuses on the semi-analytical formulation of the radiation problem, for a fully submerged axisymmetric oblate spheroid in a liquid field of infinite water depth. The study employs the theorem of image singularities connected with the concerned geometry. The body is assumed to undergo small amplitude oscillations in all three translational modes of motion, while the rotational modes are considered ideally restricted. The solution of the problem relies on the use of the governing Green’s function, and its transformation into oblate spheroidal coordinates via the evaluation of the Green’s function multipoles. The velocity potentials for the radiation problem are expressed in a series of multipoles, which are appropriately truncated; thus, a semi-analytical formulation of the examined problem is realized. Simple formulas are, finally, derived, enabling the calculation of the hydrodynamic coefficients for the translational modes of motion. For demonstrating the reliability, the accuracy, and the robustness of the developed method, results are, initially, compared with those of Wu [
18] for the limiting case of a sphere, and with those obtained using the respected Boundary Integral Equation (BIEΜ) code WAMIT [
19]. Results are also presented focusing on the effect of the immersion depth and the slenderness of the spheroid on the hydrodynamic coefficients. Although the proposed method requires several mathematical processes/computations, its value is significant since it provides results in practically ‘no time’, and thus, it is characterized by computational efficiency. Moreover, the proposed numerical formulation can be extended for calculating the hydrodynamic coefficients of a semi-immersed oblate or arrays of oblates (fully submerged or semi-immersed). This is very important, as the oblate spheroid represents a promising configuration/shape for wave energy converters [
20].
This study is organized as follows: In
Section 2, the oblate spheroidal coordinate system, utilized throughout this work, is presented.
Section 3 describes the examined boundary value problem, while in
Section 4 we derive the formulas of the radiation velocity potentials.
Section 5 includes the expressions of the added mass and the radiation damping coefficients. In
Section 6 the results of this paper are presented and discussed in detail, while, finally, in
Section 7 the main conclusions of the present investigation are cited along with suggestions for future work.
2. The Oblate Spheroidal Coordinate System
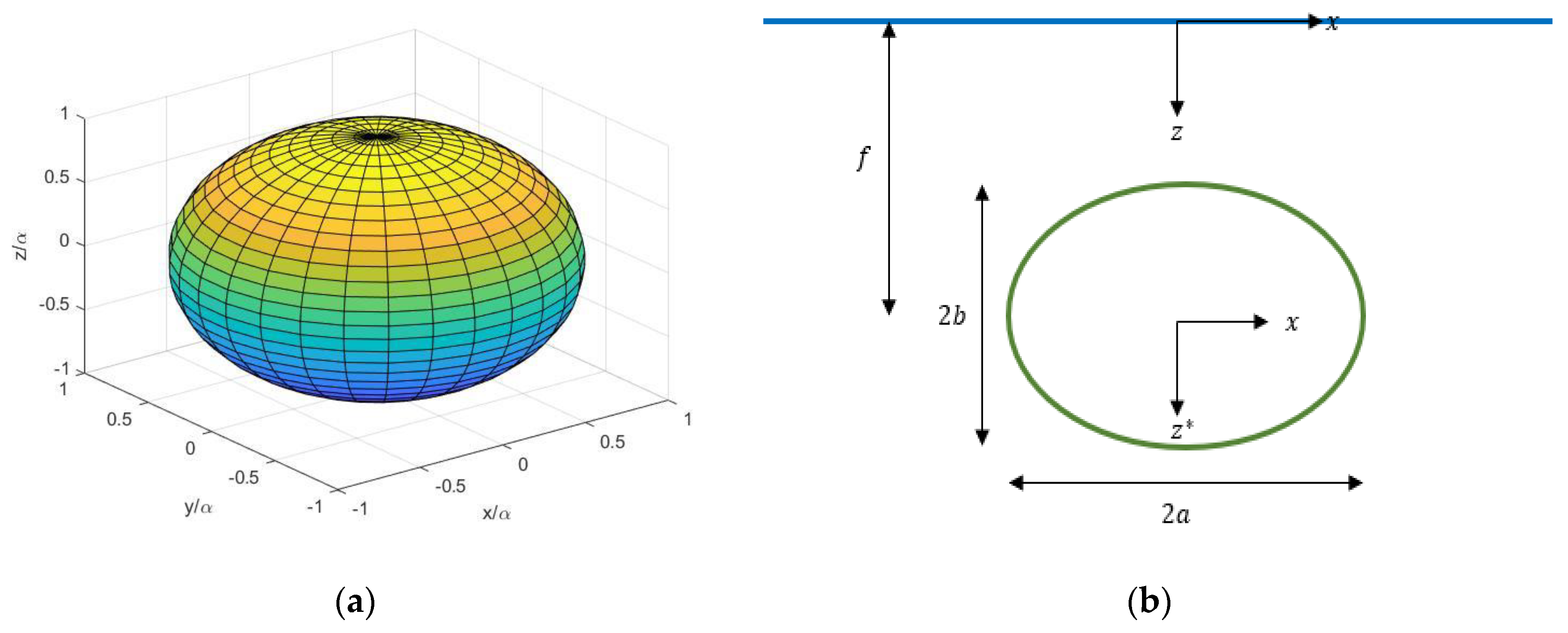
We study the axisymmetric configuration of the spheroid. The term “axisymmetric” refers to the case where the symmetrical axis of the spheroid is normal to the free surface. The center of the spheroid is assumed to be immersed at a distance
below the undisturbed free surface. A Cartesian (global) coordinate system
is assumed fixed on the undisturbed free surface, with its vertical
axis pointing in the gravity direction. The origin of the local Cartesian system
is taken fixed at the center of the body, with the vertical
axis pointing, again, downwards, so that
(
Figure 1).
The transformation formulas between local Cartesian coordinates and oblate spheroidal coordinates are (e.g., [
21]):
where
,
,
. Moreover,
denotes the semi focal distance given by
, while
correspond to the semi-major and the semi-minor axis of the spheroid, respectively (
Figure 1b).
Employing Nicolson notations [
22], namely,
and
, the transformation formulas can be written as:
3. The Boundary Value Problem
The present study deals with the radiation problem of an oblate spheroid, immersed in a liquid field of infinite water depth. The body is assumed to undergo small amplitude oscillations
in surge (
), sway, (
) and heave (
). Within the realm of the linear potential theory [
23], the resulting velocity and pressure fields can be described in terms of the velocity potential
, where
is the time,
denotes the circular frequency of body’s oscillation,
and
is the spatial complex total radiation potential, which is expressed as:
In Equation (7) correspond to the unit-amplitude radiation potentials.
The aforementioned potentials
satisfy, in the entire infinite liquid domain, the Laplace equation given by:
Moreover, the radiation potentials satisfy the following linearized boundary conditions on the free surface (Equation (9)) and on the wetted surface of the submerged body (Equation (10)):
where
,
is the gravitational acceleration and
is the unit vector normal to the boundary of the body.
In the axisymmetric configuration, the surge motions are equivalent to the sway motions, and accordingly only the
and
modes are investigated. The unit normals
and
, expressed in oblate spheroidal coordinates, will read:
where
with
and
.
Except from the above equations, the unit radiation velocity potentials must be zero at infinity away from the free surface (i.e., ). The overall boundary value problem is completed taking into account the radiation condition for outgoing waves at infinity.
4. Formulation of the Radiation Velocity Potentials
The components
and
of the total radiation potential will be formulated by utilizing the underlying Green’s function, connected with the aforementioned boundary value problem. The Green’s function (see e.g., [
8,
9,
10,
11,
12]) can be written as:
where
are the coordinates of the source point and
are the coordinates of the field point.
Clearly, Equation (12) satisfies the Laplace equation (Equation (8)), the free-surface condition (Equation (9)) and the far-field condition as
. Nevertheless, the Green’s function does not satisfy the radiation condition for outgoing waves at infinity. This task is accomplished by interpreting the infinite improper integral as a Cauchy principal value integral, namely, by introducing in Equation (12) the following notations [
16]:
where
denotes the Cauchy principal value integral.
The Green’s function (Equation (12)) must be properly elaborated in order to be expanded in multipoles. The multipoles [
4] of the Green’s function are obtained by employing the image singularity system for an oblate spheroid. The aforementioned theorem for the axisymmetric configuration of an oblate spheroid is expressed by the following formula [
16]:
where
and
are the
th degree and
th order associate Legendre functions, of the first and the second kind, respectively. In the succeeding discussion, the orientation of the local vertical
axis (
Figure 1b) will be reversed, and it will be associated with the global
axis with the relationship
.
Substituting Equation (14) into Equation (12), the multipoles of the Green’s function (auxiliary potentials), coined herein
, take the form:
It is evident that Equation (15) must be elaborated further, in order to express the second term of the equation into oblate spheroidal coordinates. This is achieved by employing the following expansion of the exponential term into spheroidal coordinates [
16]:
where
and
denotes the Bessel function of the first kind with fractional order
.
Therefore, the final expression for the auxiliary multipole expansions of the Green’s function for the oblate spheroid reads:
with
In Equation (19), is the Newman symbol (, for ), is the Kronecker’s delta function, and denotes the Cauchy principal value integral.
Having defined the auxiliary multipole expansions of the Green’s function,
, the
th velocity potential is immediately obtained from:
where
are unknown coefficients to be obtained by employing the body boundary condition.
The final form for each velocity potential
and
will read:
The velocity potentials are fully determined by calculating the coefficients
. To achieve this goal, the body boundary condition (Equation (10)) is applied for each mode of oscillation, using Equation (21) as the expression for the velocity potential. The body conditions for the radiation problem read:
Taking into account Equations (22) and (23), and making use of the orthogonality properties of the trigonometric and the associated Legendre functions (see e.g., [
16]), the following linear system of equations are obtained to be solved, using standard matrix techniques, in terms of the expansion coefficients
:
where
and the upper dot denotes differentiation with respect to the argument.
5. Hydrodynamic Coefficients in Surge and Heave
Having calculated the radiation potentials, the sought hydrodynamic parameters are obtained via the surface integral:
where
and
and
denote the added mass and hydrodynamic damping coefficients, respectively, while
is the water density. The integration is performed on the wetted surface
of the spheroid.
The differential area,
, in spheroidal coordinates for an oblate spheroid is written as:
Substituting the radiation potentials (Equation (21)) and the unit normals (Equation (11)) into Equation (26), one gets, after evaluating the surface integral over
, the following:
It is recalled that for the axisymmetric case of the spheroid, and . Clearly, the off-diagonal terms are zero. In the following section, the added mass and hydrodynamic damping coefficients are normalized by and respectively, unless otherwise mentioned.
6. Results and Discussion
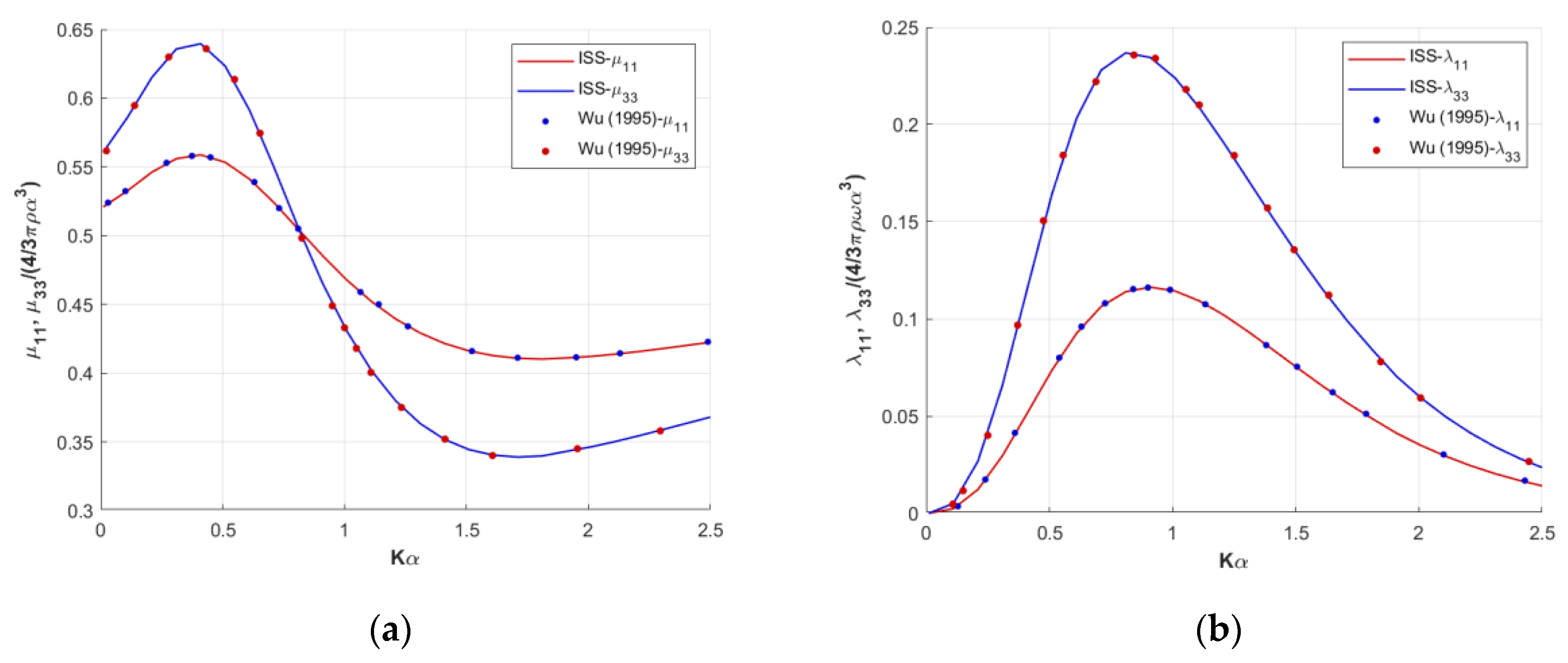
For demonstrating the accuracy of the developed semi-analytical formulation, results of the present method are compared against the results of Wu [
18] for the limiting case of a sphere, and against calculations obtained using the code WAMIT [
19], which is based on the well-known Boundary Integral Equation Method (BIEM). In the case of Wu [
18], who studied the diffraction and the radiation problem of a single and a group of immersed spheres, the oblate spheroid is simulated as a sphere assuming
, and comparisons are made for an immersion depth
equal to
. The corresponding results are shown in
Figure 2, where the added mass and the damping coefficients are normalized by
and
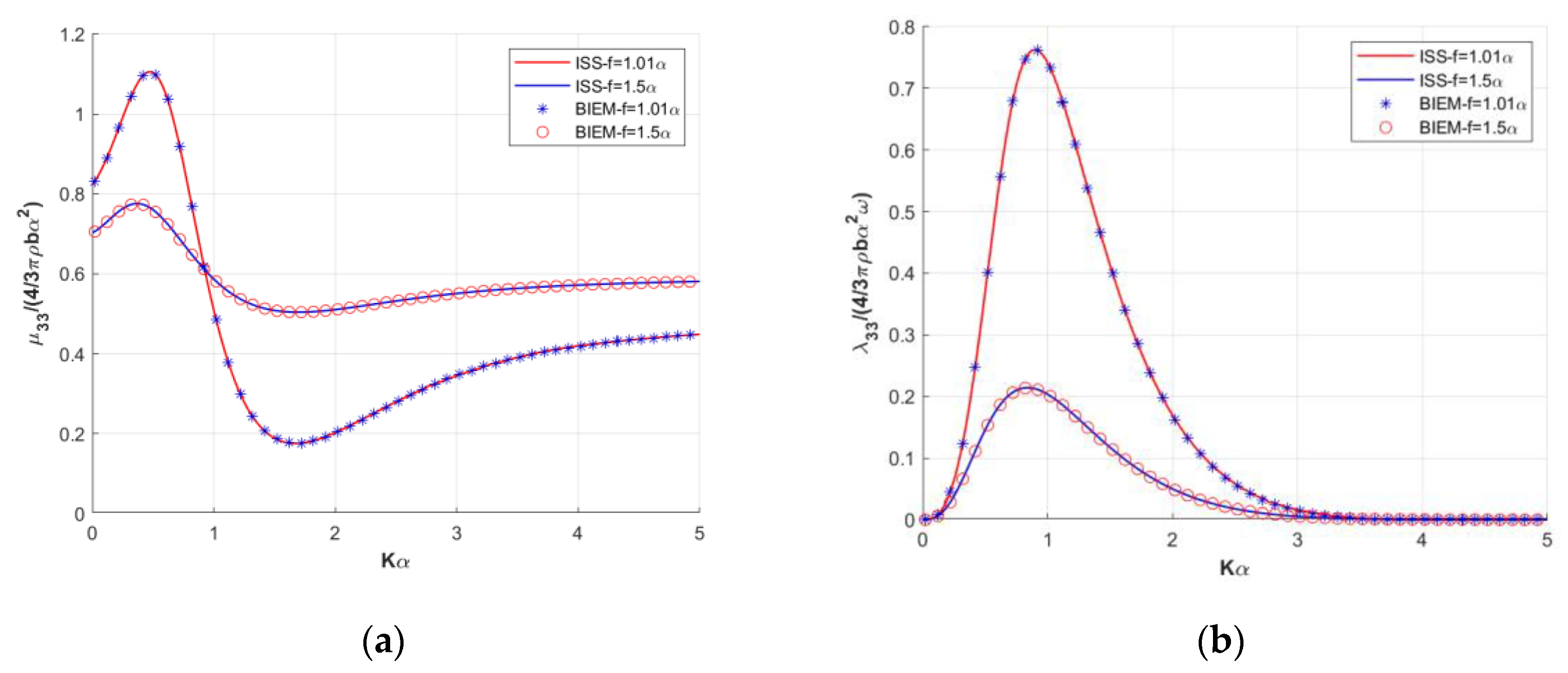
respectively. The abbreviation ISS, which stands for Image Singularity System, is used to denote the present analytical formulation. In the case of WAMIT [
19], comparisons are made for an oblate spheroid of slenderness
, and for two immersion depths,
, equal to
and
. The immersion of
has been selected so that the body touches the free surface. The relevant results are shown in
Figure 3;
Figure 4. From
Figure 2,
Figure 3 and
Figure 4, it is immediately apparent that the results of the present method demonstrate an excellent agreement with both the results of Wu [
18] for the limiting case of the sphere (average relative error smaller than
), as well as with the results obtained using WAMIT [
19].
The numerical computations of
Figure 2,
Figure 3 and
Figure 4 have been realized by utilizing
modes (in the semi-analytical formulation), which was proven sufficient to achieve a convergence up to the fifth decimal digit (
Table 1;
Table 2).
Figure 5;
Figure 6 show the effect of the immersion depth on the surge and heave hydrodynamic coefficients respectively, for an oblate spheroid with slenderness ratio
. More specifically, three different immersion depths,
, are examined equal to
and
. It can be easily observed that the increase of
leads to a smoother variation of the surge (
Figure 5a) and the heave (
Figure 6a) added mass in the examined
interval. As expected, by increasing the distance between the spheroid and the undisturbed free surface, the surge and the heave hydrodynamic damping coefficients (
Figure 5b and
Figure 6b, respectively) decrease. In general, as
increases, both added mass and damping tend to become frequency-independent hydrodynamic quantities. Analogous conclusions can be drawn for
(
Figure 3;
Figure 4). It is also interesting to note that, for a given immersion depth, the increase of the slenderness of the spheroid decreases the damping coefficients, while the added mass exhibits a reversed behavior. This can be demonstrated by comparing the curves of
and
, in
Figure 3;
Figure 4 (
), with the corresponding ones of
Figure 5;
Figure 6 (
).
7. Conclusions
In the present paper, a semi-analytical formulation has been developed for solving the radiation problem of a fully submerged oblate spheroid in a liquid field of infinite depth. The placement of the examined body is “axisymmetric”; namely, the symmetrical axis is normal to the free surface. The radiation problem is solved for all translational degrees of freedom, and formulas for calculating the corresponding hydrodynamic coefficients are derived. The employed method is based on the expansion of the governing Green’s function into spheroidal harmonics, using the method of ultimate image singularities. The excellent agreement of results with those of Wu [
18] for the limiting case of a sphere, and with those obtained using a well-known BIEM code, demonstrates the accuracy, reliability, and robustness of the developed semi-analytical solution.
Moreover, the results of the present paper illustrated that the immersion depth and the slenderness of the oblate spheroid have a direct impact on the hydrodynamic coefficients. Specifically, for a given slenderness, the placement of the spheroid at a greater distance from the free surface leads to a more smooth variation of the added mass coefficients, as well as to a reduction of the damping coefficients. The increase of the slenderness of the spheroid for a given immersion depth affects the hydrodynamic coefficients in a similar manner, i.e., the damping coefficient decreases, and the added mass exhibits a decrease of the absolute difference between the observed maximum and minimum values.
The present numerical formulation, combined with the corresponding solution of the diffraction problem [
17], could be further exploited for calculating the translational motions of submerged spheroids, with potential application to wave energy hydrodynamic problems, i.e., numerical modelling of submerged point absorbers.