Droplet Impact on Suspended Metallic Meshes: Effects of Wettability, Reynolds and Weber Numbers
Abstract
1. Introduction
2. Numerical Simulation Framework
2.1. Governing Equations
2.2. Sharpening the Interface
2.3. VOF Smoothing
2.4. Dynamic Contact Angle Treatment
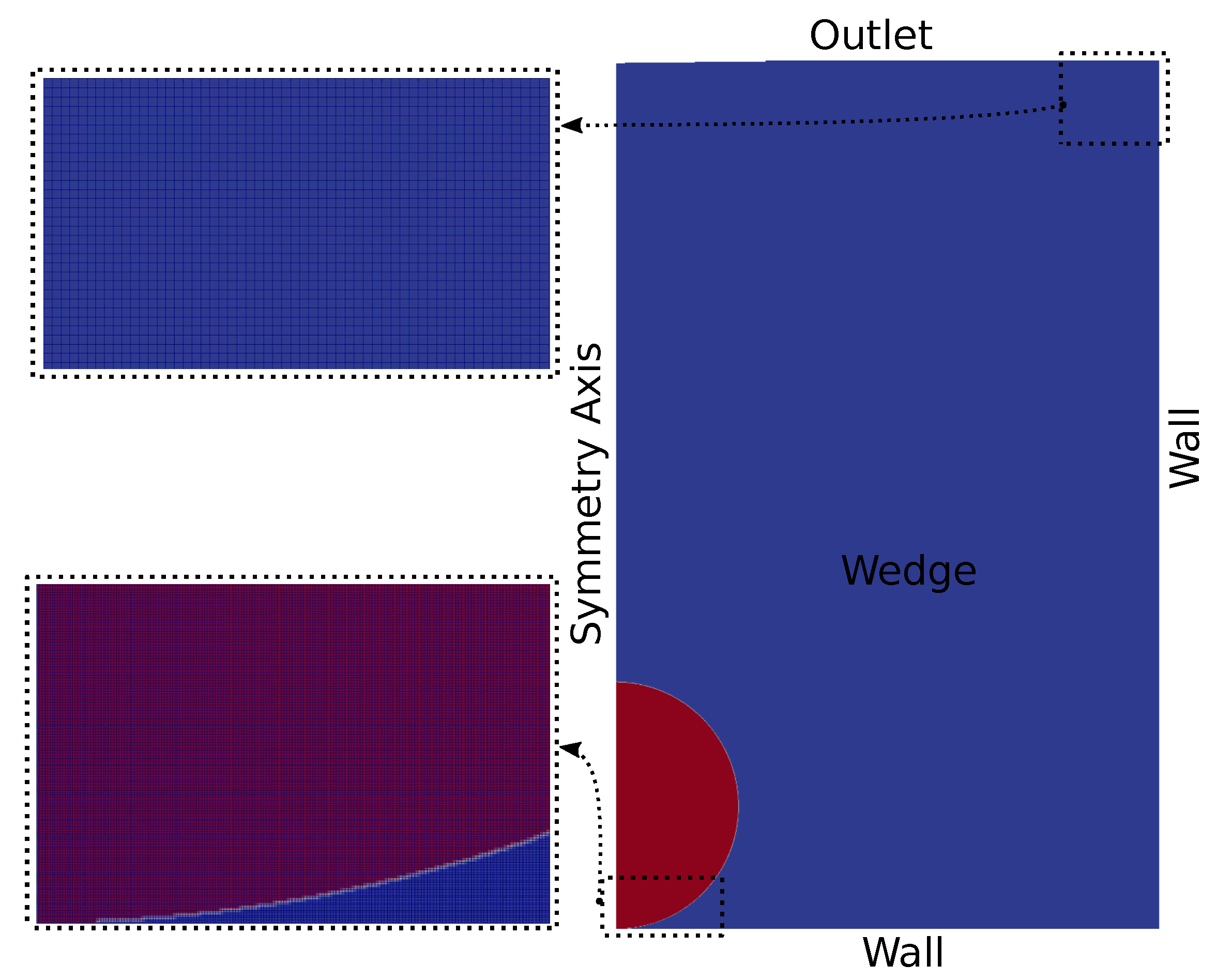
3. Validation of the Numerical Simulation Framework
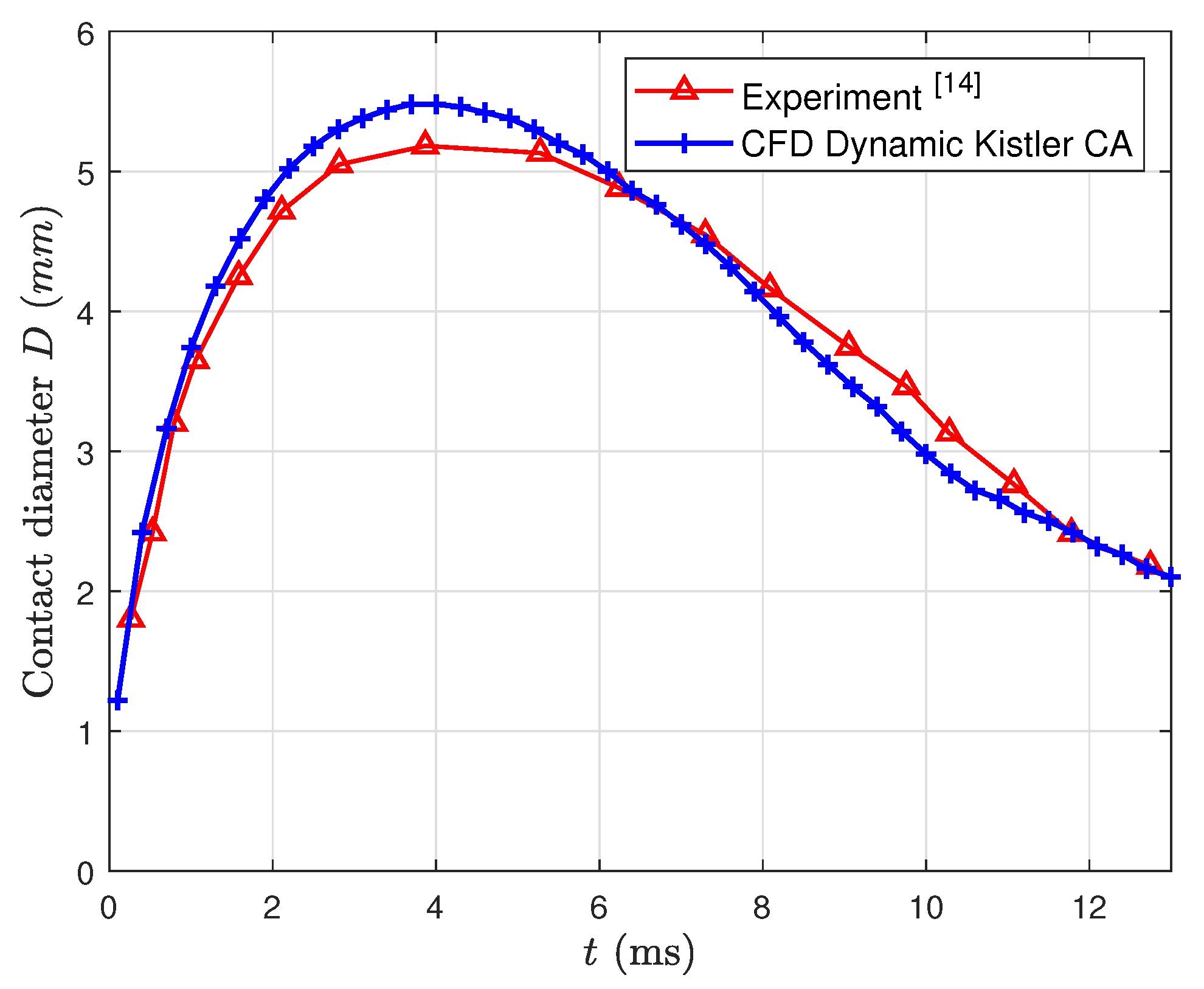
3.1. Low Weber Number Impacts
3.2. High Weber Number Impacts
4. Droplet Impact on Metallic Meshes
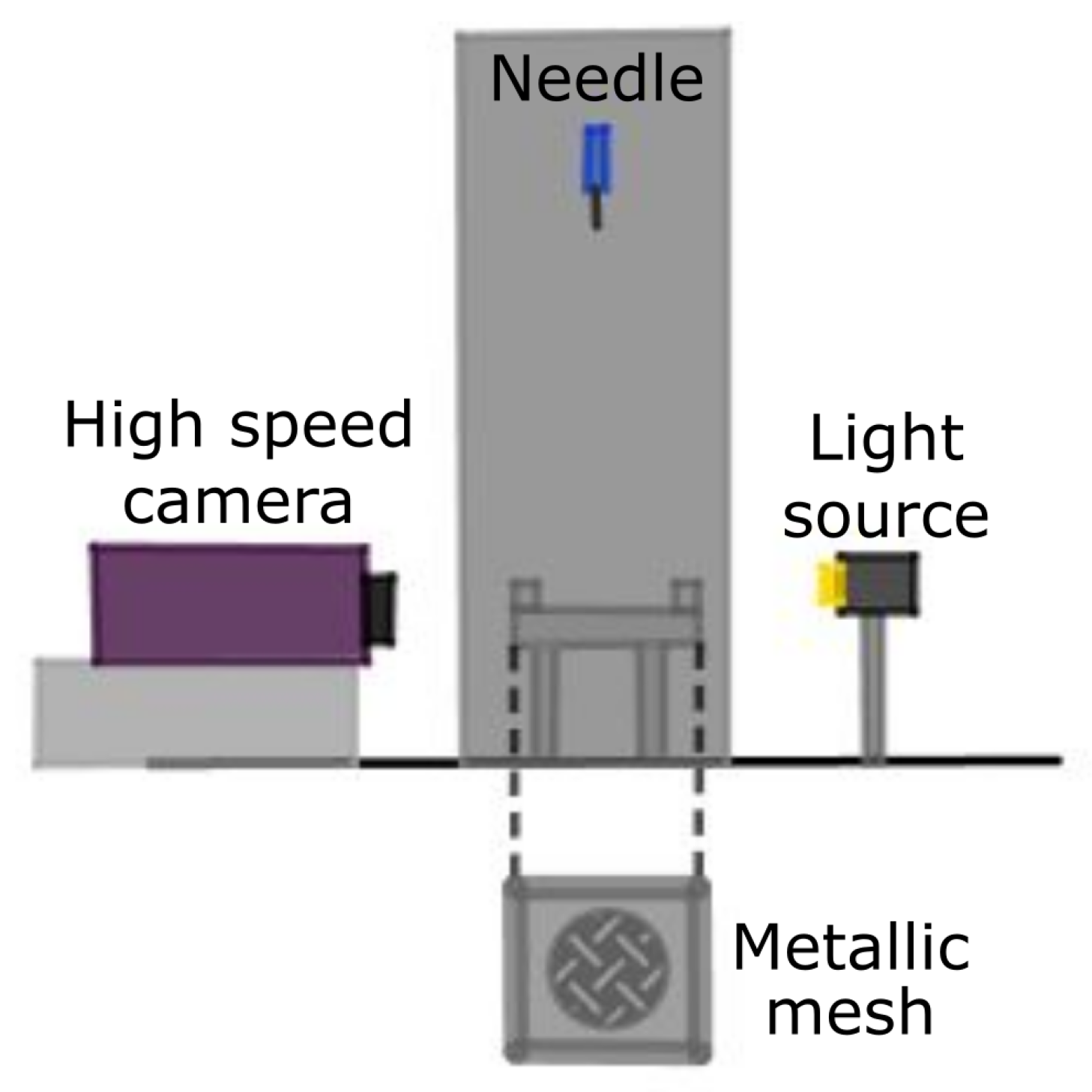
4.1. Experimental Investigation
4.2. Numerical Investigation
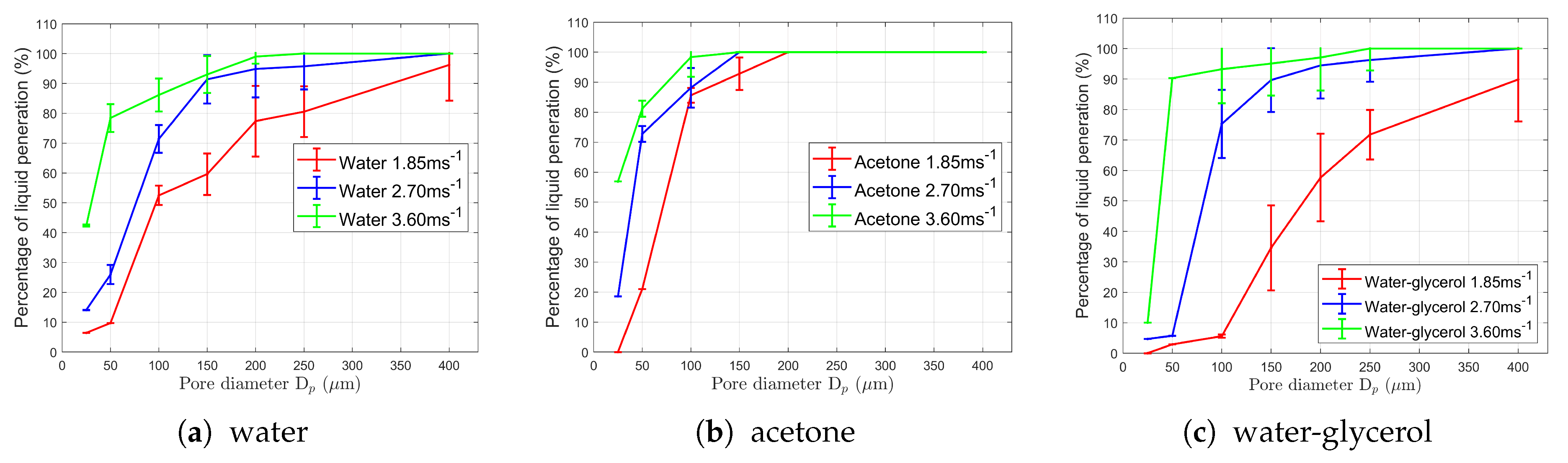
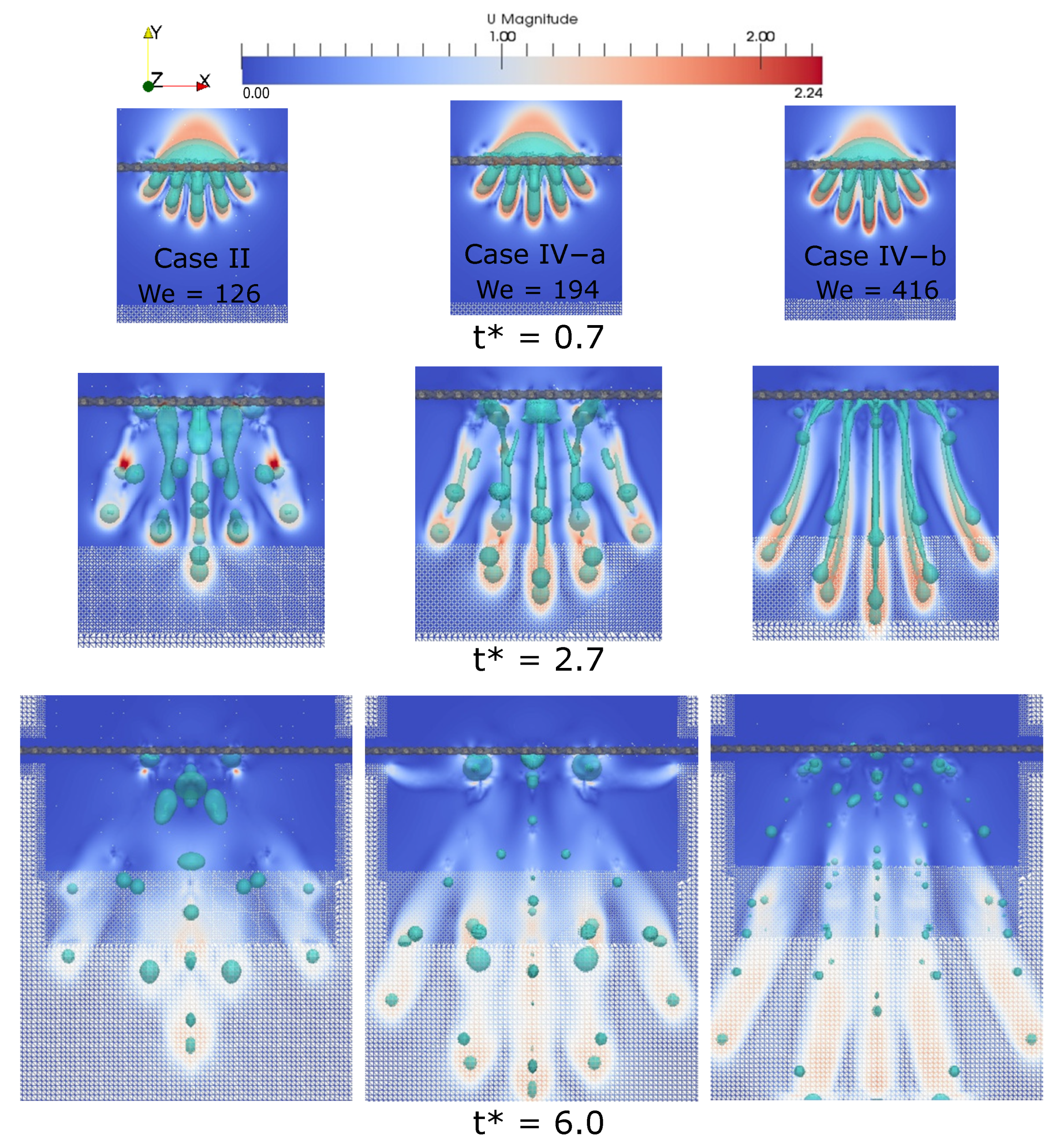
4.3. Numerical Simulation Results for Droplet Impact on Metallic Meshes
5. Parametric Numerical Simulations
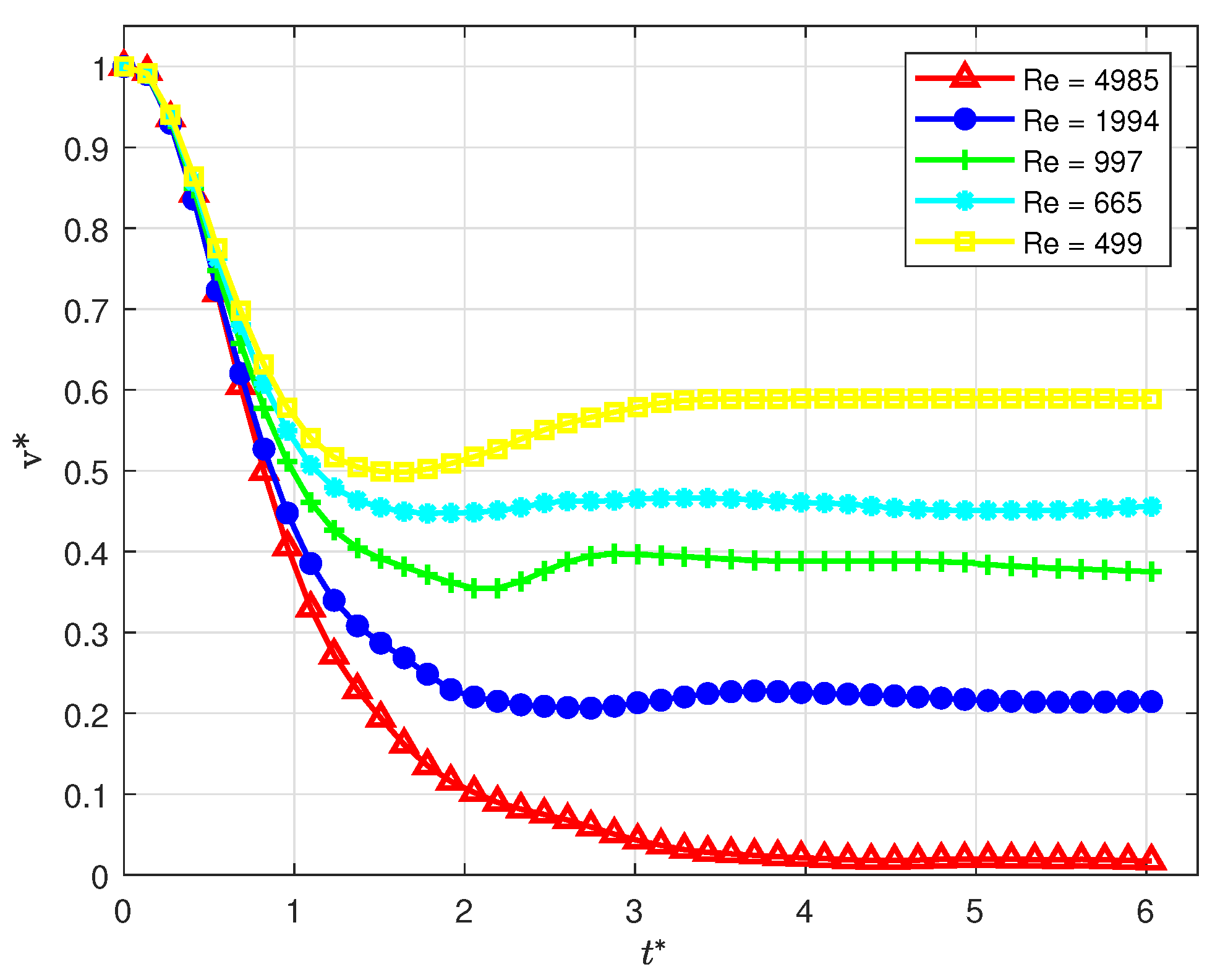
5.1. Influence of Reynolds Number
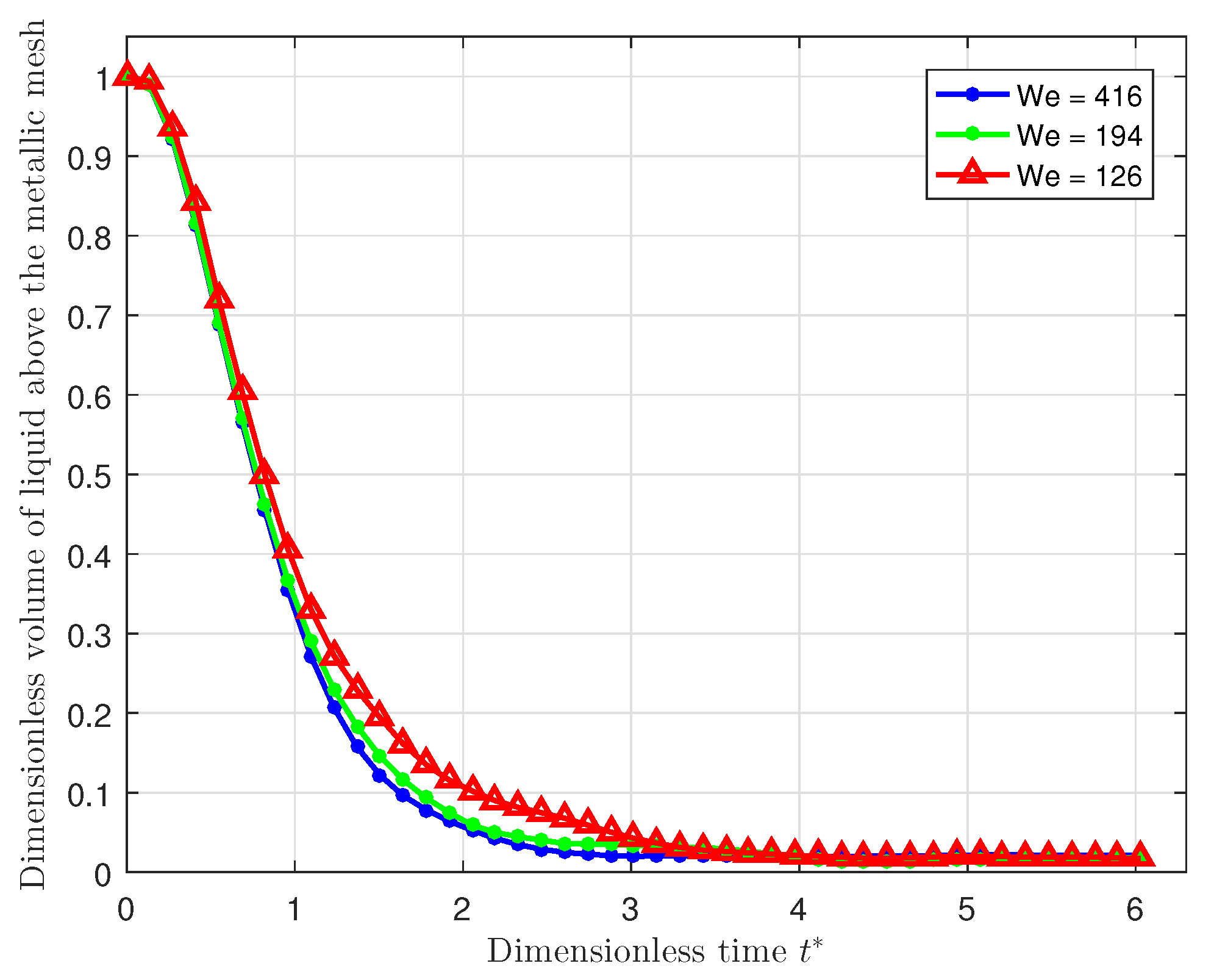
5.2. Influence of Weber Number
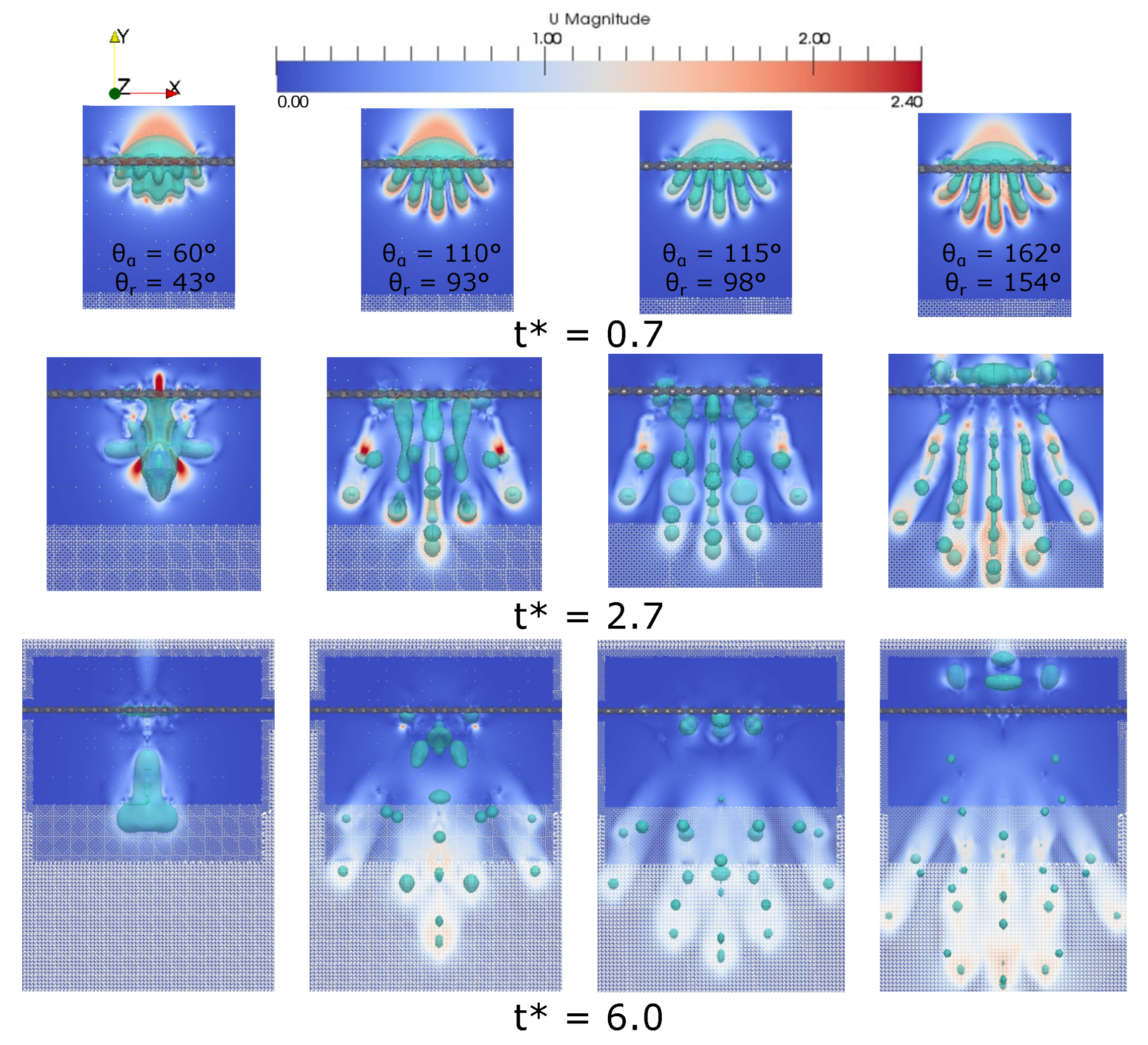
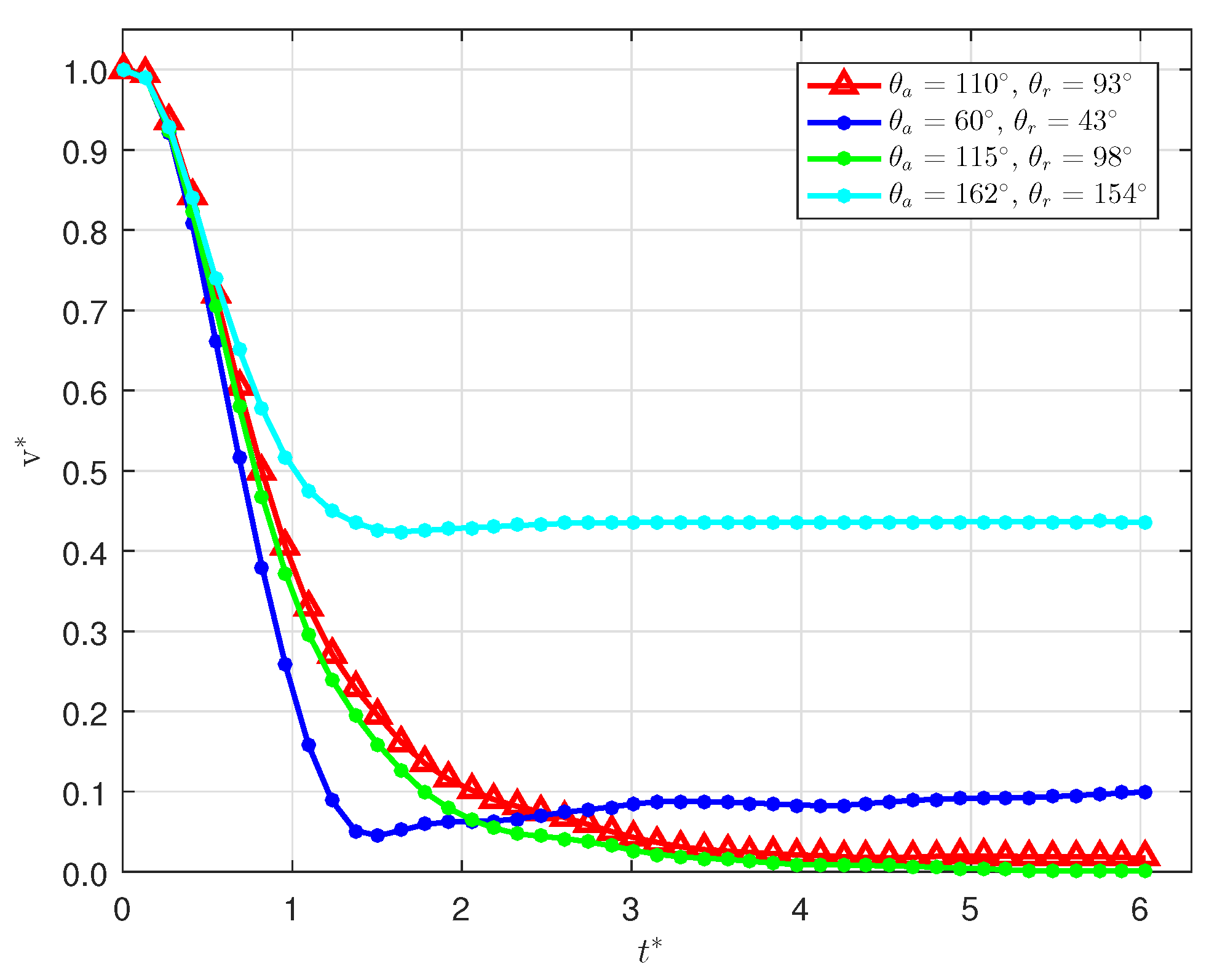
5.3. Influence of Wettability
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Josserand, C.; Thoroddsen, S. Drop Impact on a Solid Surface. Annu. Rev. Fluid Mech. 2016, 48, 365–391. [Google Scholar] [CrossRef]
- Rioboo, R.; Tropea, C.; Marengo, M. Outcomes from drop impact on solid surfaces. At. Spray 2001, 11, 155–165. [Google Scholar] [CrossRef]
- Rioboo, R.; Marengo, M.; Tropea, C. Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 2002, 33, 112–124. [Google Scholar] [CrossRef]
- Kim, H.Y.; Chun, J.H. The recoiling of liquid droplets upon collision with solid surfaces. Phys. Fluids 2001, 13, 643–659. [Google Scholar] [CrossRef]
- Roisman, I.V.; Opfer, L.; Tropea, C.; Raessi, M.; Mostaghimi, J.; Chandra, S. Drop impact onto a dry surface: Role of the dynamic contact angle. Colloids Surf. A Physicochem. Eng. Asp. 2008, 322, 183–191. [Google Scholar] [CrossRef]
- Malgarinos, I.; Nikolopoulos, N.; Marengo, M.; Antonini, C.; Gavaises, M. VOF simulations of the contact angle dynamics during the drop spreading: Standard models and a new wetting force model. Adv. Colloid Interface Sci. 2014, 212, 1–20. [Google Scholar] [CrossRef]
- Vadillo, D.C.; Soucemarianadin, A.; Delattre, C.; Roux, D.C.D. Dynamic contact angle effects onto the maximum drop impact spreading on solid surfaces. Phys. Fluids 2009, 21, 1–8. [Google Scholar] [CrossRef]
- Antonini, C.; Amirfazli, A.; Marengo, M. Drop impact and wettability: From hydrophilic to superhydrophobic surfaces. Phys. Fluids 2013, 24, 102104. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Qiao, Y.M.; Chandra, S.; Mostaghimi, J. Capillary effects during droplet impact on a solid surface. Phys. Fluids 1996, 8, 650–659. [Google Scholar] [CrossRef]
- Šikalo, Š.; Marengo, M.; Tropea, C.; Ganić, E.N. Analysis of impact of droplets on horizontal surfaces. Exp. Therm. Fluid Sci. 2002, 25, 503–510. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop Impact Dynamics: Splashing, Spreading, Receding, Bouncing …. Annu. Rev. Fluid Mech. 2006, 38, 160–192. [Google Scholar] [CrossRef]
- Antonini, C.; Innocenti, M.; Horn, T.; Marengo, M.; Amirfazli, A. Understanding the effect of superhydrophobic coatings on energy reduction in anti-icing systems. Cold Regions Sci. Technol. 2011, 67, 58–67. [Google Scholar] [CrossRef]
- Patil, N.D.; Gada, V.H.; Sharma, A.; Bhardwaj, R. On dual-grid level-set method for contact line modeling during impact of a droplet on hydrophobic and superhydrophobic surfaces. Int. J. Multiph. Flow 2016, 81, 54–66. [Google Scholar] [CrossRef]
- Yokoi, K.; Vadillo, D.; Hinch, J.; Hutchings, I. Numerical studies of the influence of the dynamic contact angle on a droplet impacting on a dry surface. Phys. Fluids 2009, 21, 1–12. [Google Scholar] [CrossRef]
- Šikalo, Š.; Wilhelm, H.D.; Roisman, I.V.; Jakirlić, S.; Tropea, C. Dynamic contact angle of spreading droplets: Experiments and simulations. Phys. Fluids 2013, 17, 1–13. [Google Scholar] [CrossRef]
- Bussmann, M.; Chandra, S.; Mostaghimi, J. Modeling the spash of a droplet impacting a solid surface. Phys. Fluids 2000, 12, 3121–3132. [Google Scholar] [CrossRef]
- Hapgood, K.P.; Litster, J.D.; Biggs, S.R.; Howes, T. Drop penetration into porous powder beds. J. Colloid Interface Sci. 2002, 253, 353–366. [Google Scholar] [CrossRef]
- Clarke, A.; Blake, T.D.; Carruthers, K.; Woodward, A. Spreading and Imbibition of Liquid Droplets on Porous Surfaces. Langmuir 2002, 18, 2980–2984. [Google Scholar] [CrossRef]
- Alam, P.; Toivakka, M.; Backfolk, K.; Sirviö, P. Impact spreading and absorption of Newtonian droplets on topographically irregular porous materials. Chem. Eng. Sci. 2007, 62, 3142–3158. [Google Scholar] [CrossRef]
- Ryu, S.; Sen, P.; Nam, Y.; Lee, C. Water Penetration through a Superhydrophobic Mesh during a Drop Impact. Phys. Rev. Lett. 2017, 118, 1–5. [Google Scholar] [CrossRef]
- Reis, N.C.; Griffiths, R.F.; Santos, J.M. Parametric study of liquid droplets impinging on porous surfaces. Appl. Math. Model. 2008, 32, 341–361. [Google Scholar] [CrossRef]
- Fu, F.; Li, P.; Wang, K.; Wu, R. Numerical Simulation of Sessile Droplet Spreading and Penetration on Porous Substrates. Langmuir 2019, 35, 2917–2924. [Google Scholar] [CrossRef] [PubMed]
- Liwei, W.; Xiao, W.; Weijie, Y.; Pengfei, H.; Feng, H.; Xiwen, Z. Numerical study of droplet fragmentation during impact on mesh screens. Microfluid. Nanofluid. 2019, 23, 1–14. [Google Scholar] [CrossRef]
- Georgoulas, A.; Koukouvinis, P.; Gavaises, M.; Marengo, M. Numerical investigation of quasi-static bubble growth and detachment from submerged orifices in isothermal liquid pools: The effect of varying fluid properties and gravity levels. Int. J. Multiph. Flow 2015, 74, 59–78. [Google Scholar] [CrossRef]
- Vontas, K.; Andredaki, M.; Georgoulas, A.; Nikas, K.S.; Marengo, M. Numerical Investigation of Droplet Impact on Smooth Surfaces with Different Wettability Characteristics: Implementation of a dynamic contact angle treatment in OpenFOAM. In Proceedings of the ILASS–Europe 2017, 28th Conference on Liquid Atomization and Spray Systems, Valencia, Spain, 6–8 September 2017. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Hoang, D.A.; van Steijn, V.; Portela, L.M.; Kreutzer, M.T.; Kleijn, C.R. Benchmark numerical simulations of segmented two-phase flows in microchannels using the Volume of Fluid method. Comput. Fluids 2013, 86, 28–36. [Google Scholar] [CrossRef]
- Kistler, S.F. Hydrodynamics of Wetting. Wettability 1993, 311–429. Available online: https://scholar.google.com/scholar?cluster=18337677993544788386&hl=en&as_sdt=0,5 (accessed on 3 March 2020).
- Antonini, C.; Carmona, F.J.; Pierce, E.; Marengo, M.; Amirfazli, A. General methodology for evaluating the adhesion force of drops and bubbles on solid surfaces. Langmuir 2009, 25, 6143–6154. [Google Scholar] [CrossRef]
- Blake, T.D.; Bracke, M.; Shikhmurzaev, Y.D. Experimental evidence of non local hydrodynamic influence on the dynamic contact angle. Phys. Fluids 1999, 11, 1995–2007. [Google Scholar] [CrossRef]
- Boscariol, C.; Chandra, S.; Sarker, D.; Crua, C.; Marengo, M. Drop impact onto attached metallic meshes: Liquid penetration and spreading. Exp. Fluids 2018, 59, 1–13. [Google Scholar] [CrossRef]
- Xu, J.; Xie, J.; He, X.; Cheng, Y.; Liu, Q. Water drop impacts on a single-layer of mesh screen membrane: Effect of water hammer pressure and advancing contact angles. Exp. Therm. Fluid Sci. 2017, 82, 83–93. [Google Scholar] [CrossRef]
- Blanchette, F.; Bigioni, T.P. Partial coalescence of drops at liquid interfaces. Nat. Phys. 2006, 2, 254–257. [Google Scholar] [CrossRef]
- Berthier, J. EWOD Microsystems. In Micro-Drops and Digital Microfluidics, 2nd ed.; William Andrew Publishing: Norwich, NY, USA, 2013; pp. 225–301. [Google Scholar] [CrossRef]
- Ding, M.; Kantzas, A. Capillary number correlations for gas-liquid systems. J. Can. Pet. Technol. 2007, 46, 27–32. [Google Scholar] [CrossRef]
- Malla, L.K.; Patil, N.D.; Bhardwaj, R.; Neild, A. Droplet Bouncing and Breakup during Impact on a Microgrooved Surface. Langmuir 2017, 33, 9620–9631. [Google Scholar] [CrossRef] [PubMed]





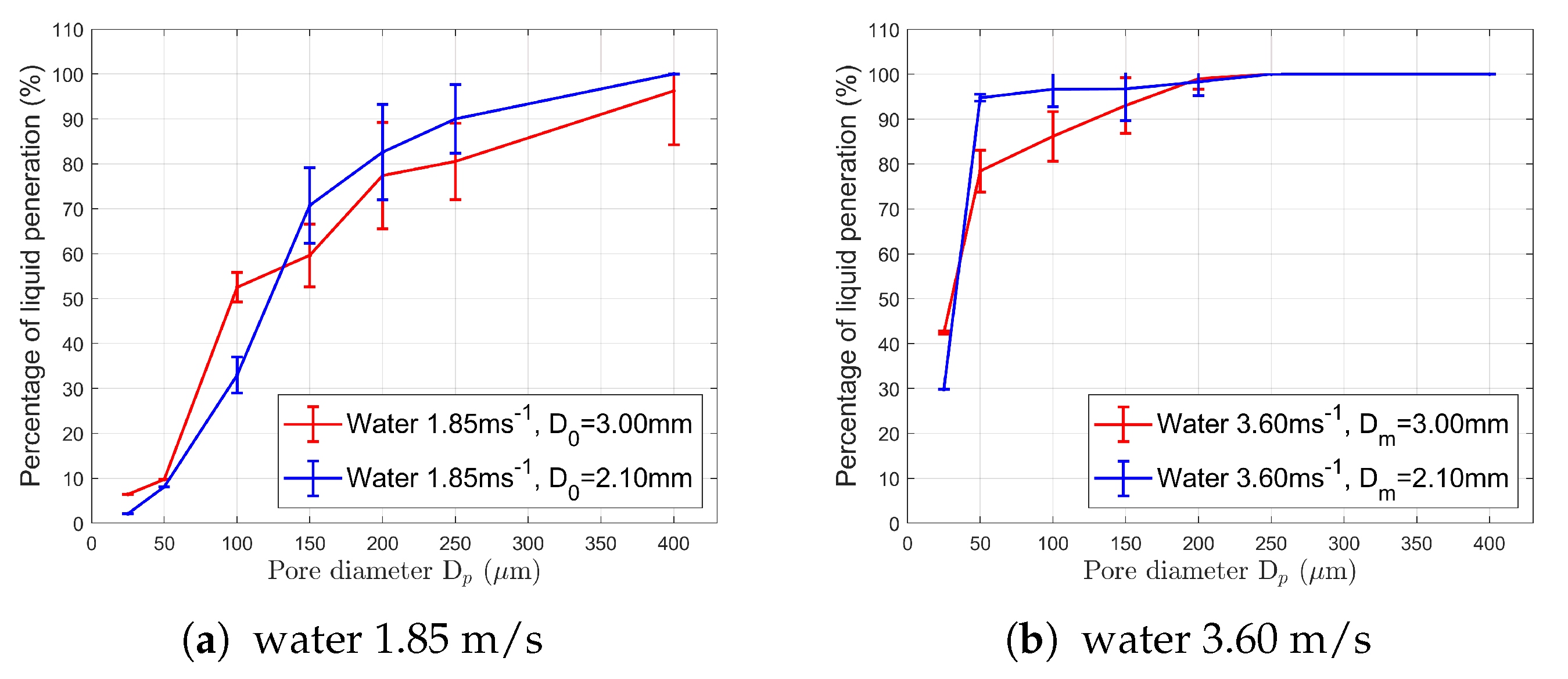
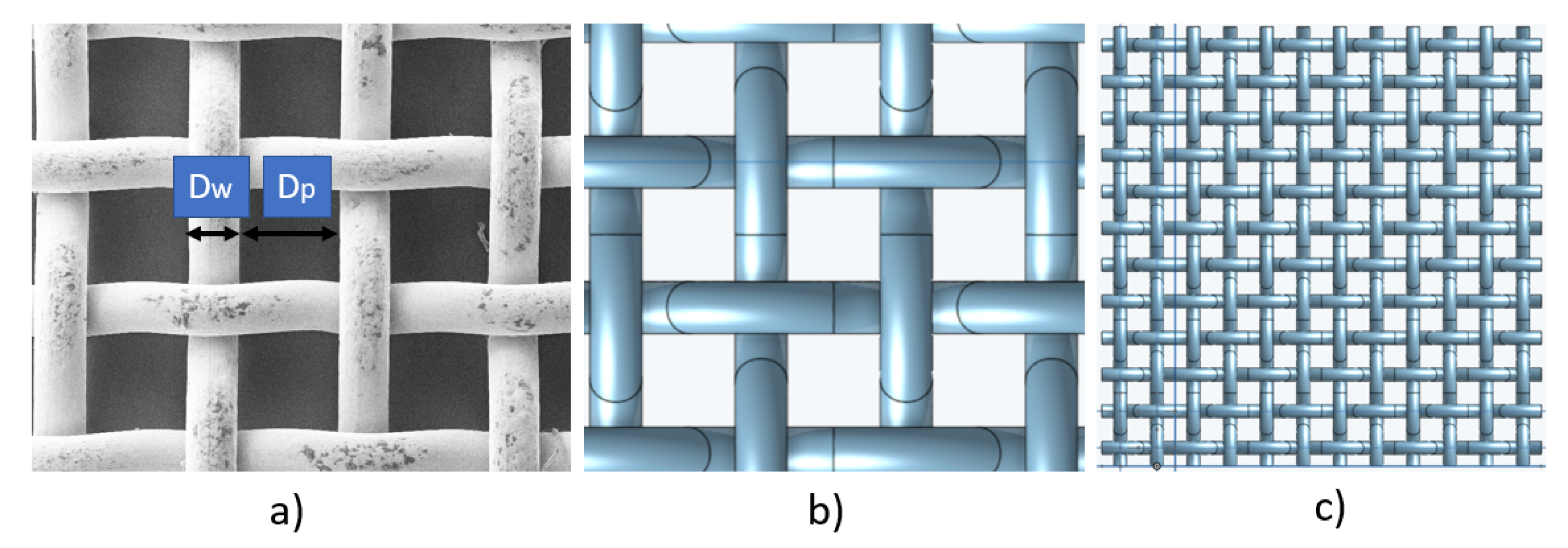


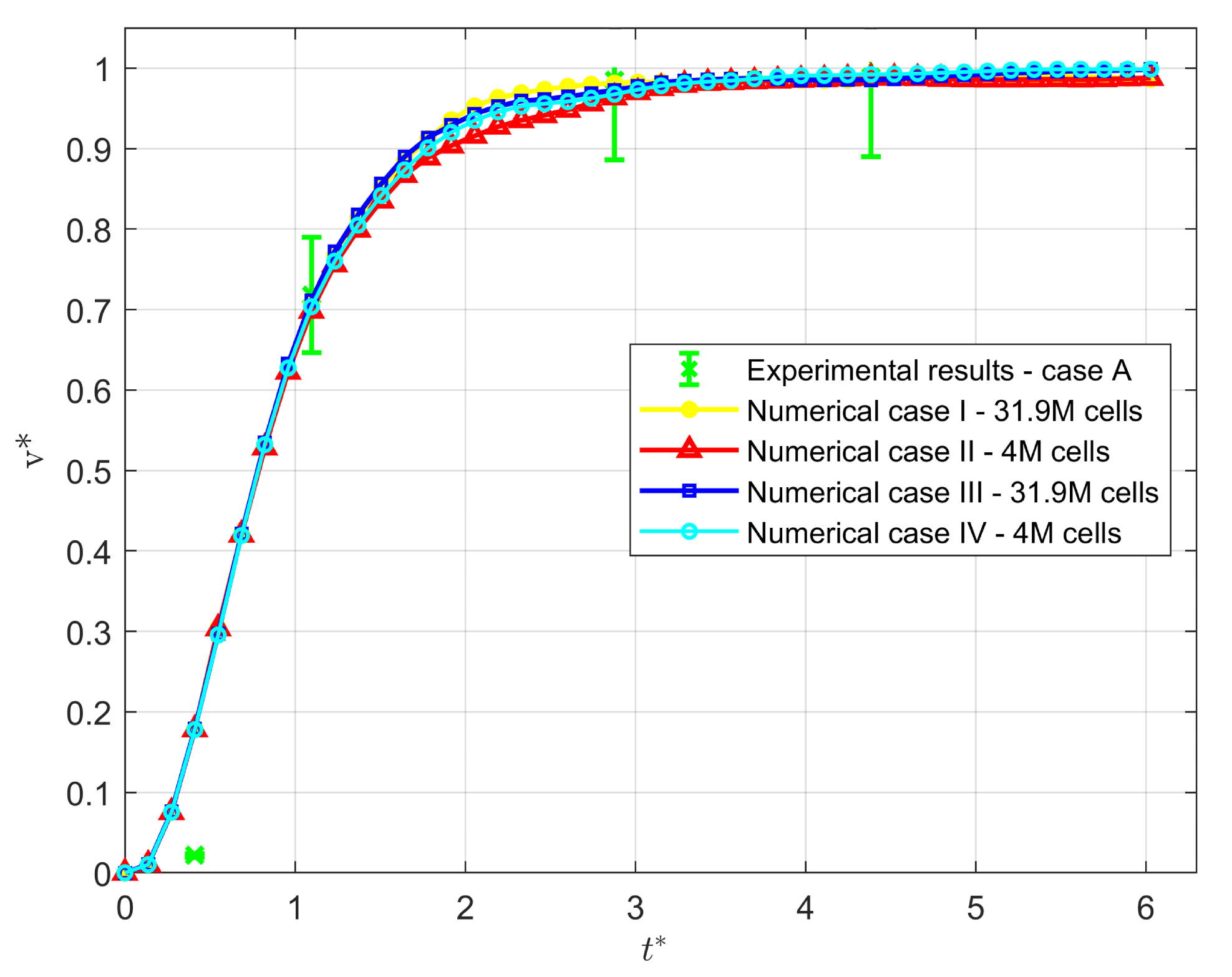

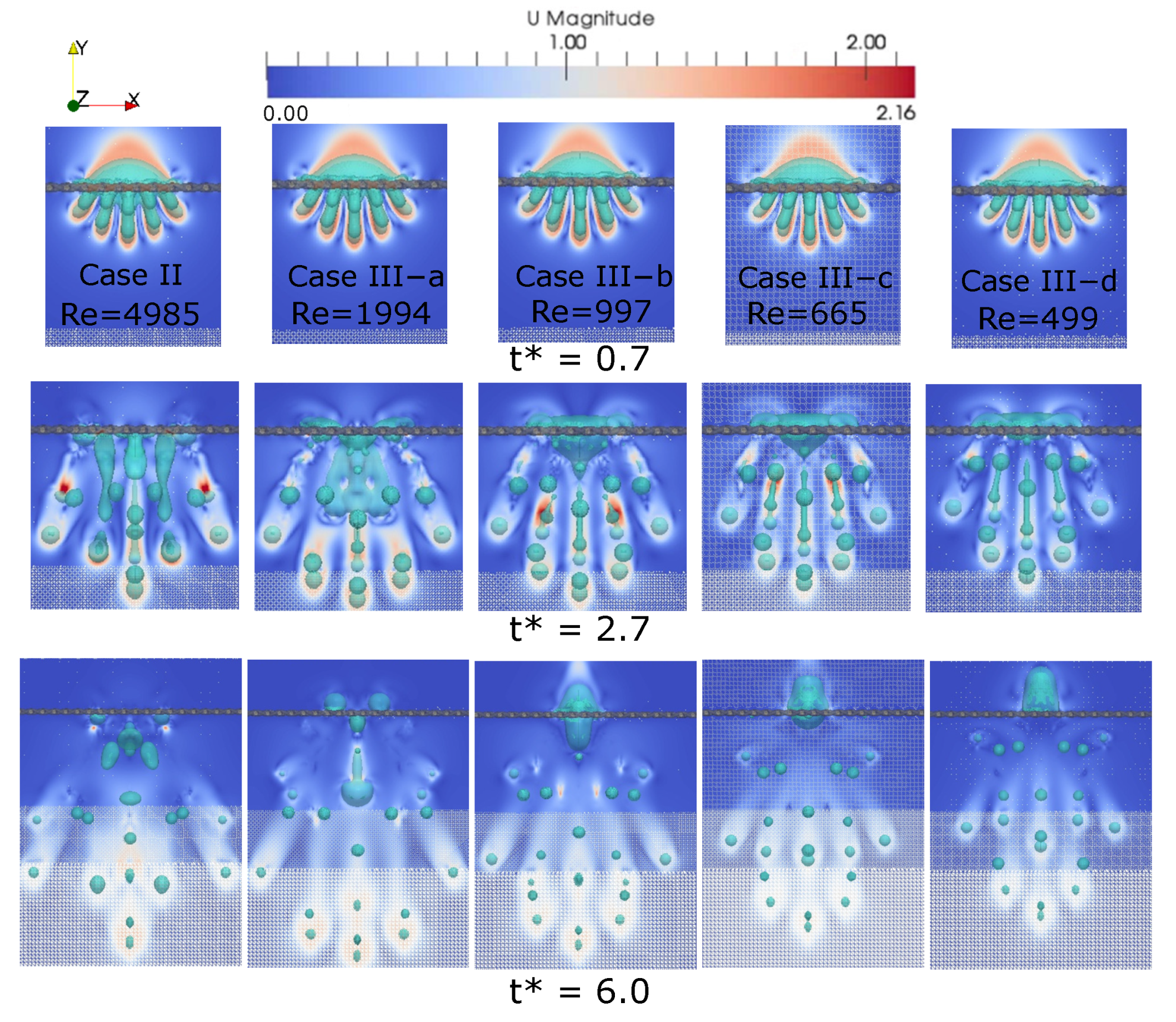
| Liquid | (kg m) | (Pa s) | (N m) | Range (-) | Range (-) |
|---|---|---|---|---|---|
| Water | 996.0 | 1.0 | 0.073 | 3501.1–9924.4 | 83.9–499.8 |
| Acetone | 793.0 | 0.3 | 0.023 | 7835.9–19,518.3 | 179.3–890.1 |
| Water and Glycerol | 1118.6 | 10.0 | 0.067 | 448.2–1042.5 | 120.0–560.3 |
| Liquid | Needle 21 (mm) | Needle 26 s (mm) |
|---|---|---|
| Water | 3.0 | 1.9 |
| Acetone | 2.0 | 1.7 |
| Water and Glycerol | 2.9 | 1.5 |
| Pore Size (m) | Impact Velocity (m s) | % Liquid Penetration Size: 1.5 cm | % Liquid Penetration Size: 2.0 cm | % Liquid Penetration Size: 2.5 cm |
|---|---|---|---|---|
| 25 | 1.86 | 7.0 | 10.0 | 7.0 |
| 25 | 2.70 | 13.0 | 11.0 | 14.0 |
| 25 | 3.60 | 46.0 | 42.0 | 43.0 |
| 200 | 1.86 | 79.0 | 76.0 | 77.0 |
| 200 | 2.70 | 90.0 | 88.0 | 95.0 |
| 200 | 3.60 | 100.0 | 98.0 | 99.0 |
| 400 | 1.86 | 96.0 | 94.0 | 96.0 |
| 400 | 2.70 | 100.0 | 100.0 | 100.0 |
| 400 | 3.60 | 100.0 | 100.0 | 100.0 |
| Pore Size (m) | Impact Velocity (m s) | % Liquid Penetration Size: 1.5 cm | % Liquid Penetration Size: 2.0 cm | % Liquid Penetration Size: 2.5 cm |
|---|---|---|---|---|
| 25 | 1.85 | 0.0 | 0.0 | 0.0 |
| 25 | 2.70 | 21.1 | 18.6 | 19.4 |
| 25 | 3.6 | 51.2 | 56.9 | 54.3 |
| 200 | 1.85 | 100.0 | 100.0 | 100.0 |
| 200 | 2.70 | 100.0 | 100.0 | 100.0 |
| 200 | 3.6 | 100.0 | 100.0 | 100.0 |
| 400 | 1.85 | 100.0 | 100.0 | 100.0 |
| 400 | 2.70 | 100.0 | 100.0 | 100.0 |
| 400 | 3.6 | 100.0 | 100.0 | 100.0 |
| Pore Size (m) | Impact Velocity (m s) | % Liquid Penetration Size: 1.5 cm | % Liquid Penetration Size: 2.0 cm | % Liquid Penetration Size: 2.5 cm |
|---|---|---|---|---|
| 25 | 1.85 | 0.0 | 0.0 | 0.0 |
| 25 | 2.70 | 0.0 | 4.7 | 0.0 |
| 25 | 3.60 | 0.0 | 10.0 | 0.0 |
| 200 | 1.85 | 58.4 | 57.6 | 60.0 |
| 200 | 2.70 | 91.2 | 94.4 | 87.3 |
| 200 | 3.60 | 95.4 | 97.1 | 97.0 |
| 400 | 1.85 | 86.4 | 89.9 | 83. 3 |
| 400 | 2.70 | 100.0 | 100.0 | 100.0 |
| 400 | 3.60 | 100.0 | 100.0 | 100.0 |
(mm) | (m s) | (-) | (-) | () | () |
|---|---|---|---|---|---|
| 2.70 | 1.85 | 126 | 4953 | 110 | 93 |
| Numerical Case | Droplet Centering at | Computational Domain (mm) | Total no. of Cells (Millions) | Levels of Refinement |
|---|---|---|---|---|
| I | above two wires | (8.00 8.00 25.00) | 31.9 | 4 |
| II | above two wires | (7.54 7.54 20.00) | 4.0 | 3 |
| III | above one wire | (8.00 8.00 25.00) | 31.9 | 4 |
| IV | above one wire | (7.54 7.54 20.00) | 4.0 | 3 |
| Case | (Pa s) | (N m) | () | () | (-) | (-) |
|---|---|---|---|---|---|---|
| II | 1 | 0.073 | 110 | 93 | 126 | 4985 |
| III-a | 2.5 | 0.073 | 110 | 93 | 126 | 1994 |
| III-b | 5.0 | 0.073 | 110 | 93 | 126 | 997 |
| III-c | 7.5 | 0.073 | 110 | 93 | 126 | 665 |
| III-d | 10.0 | 0.073 | 110 | 93 | 126 | 499 |
| IV-a | 1.0 | 0.022 | 110 | 93 | 416 | 4985 |
| IV-b | 1.0 | 0.048 | 110 | 93 | 194 | 4985 |
| V-a | 1.0 | 0.073 | 60 | 43 | 126 | 4985 |
| V-b | 1.0 | 0.073 | 115 | 98 | 126 | 4985 |
| V-c | 1.0 | 0.073 | 162 | 154 | 126 | 4985 |
| Case | 0.80 ms | 1.6 ms | 2.40 ms | 4.40 ms | 6.60 ms | 8.80 ms |
|---|---|---|---|---|---|---|
| II | 72.0 | 33.0 | 16.1 | 4.3 | 1.8 | 1.7 |
| III-a | 72.3 | 38.5 | 26.9 | 21.3 | 22.2 | 21.4 |
| III-b | 74.8 | 46.1 | 38.1 | 39.6 | 38.8 | 37.5 |
| III-c | 76.3 | 50.7 | 44.9 | 46.5 | 45.4 | 45.6 |
| III-d | 77.5 | 54.0 | 49.8 | 57.9 | 58.9 | 58.9 |
| IV-a | 68.8 | 27.2 | 9.6 | 2.0 | 2.8 | 2.2 |
| IV-b | 69.1 | 29.0 | 11.6 | 3.4 | 1.4 | 1.9 |
| V-a | 66.2 | 15.7 | 5.2 | 8.5 | 8.7 | 1.0 |
| V-b | 70.4 | 29.6 | 12.6 | 2.7 | 0.7 | 0.1 |
| V-c | 73.9 | 47.6 | 42.0 | 43.5 | 43.6 | 43.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vontas, K.; Boscariol, C.; Andredaki, M.; Georgoulas, A.; Crua, C.; Walther, J.H.; Marengo, M. Droplet Impact on Suspended Metallic Meshes: Effects of Wettability, Reynolds and Weber Numbers. Fluids 2020, 5, 81. https://doi.org/10.3390/fluids5020081
Vontas K, Boscariol C, Andredaki M, Georgoulas A, Crua C, Walther JH, Marengo M. Droplet Impact on Suspended Metallic Meshes: Effects of Wettability, Reynolds and Weber Numbers. Fluids. 2020; 5(2):81. https://doi.org/10.3390/fluids5020081
Chicago/Turabian StyleVontas, Konstantinos, Cristina Boscariol, Manolia Andredaki, Anastasios Georgoulas, Cyril Crua, Jens Honoré Walther, and Marco Marengo. 2020. "Droplet Impact on Suspended Metallic Meshes: Effects of Wettability, Reynolds and Weber Numbers" Fluids 5, no. 2: 81. https://doi.org/10.3390/fluids5020081
APA StyleVontas, K., Boscariol, C., Andredaki, M., Georgoulas, A., Crua, C., Walther, J. H., & Marengo, M. (2020). Droplet Impact on Suspended Metallic Meshes: Effects of Wettability, Reynolds and Weber Numbers. Fluids, 5(2), 81. https://doi.org/10.3390/fluids5020081








