Liquid-Cooling System of an Aircraft Compression Ignition Engine: A CFD Analysis
Abstract
1. Introduction
2. The Model
2.1. Mathematical Model
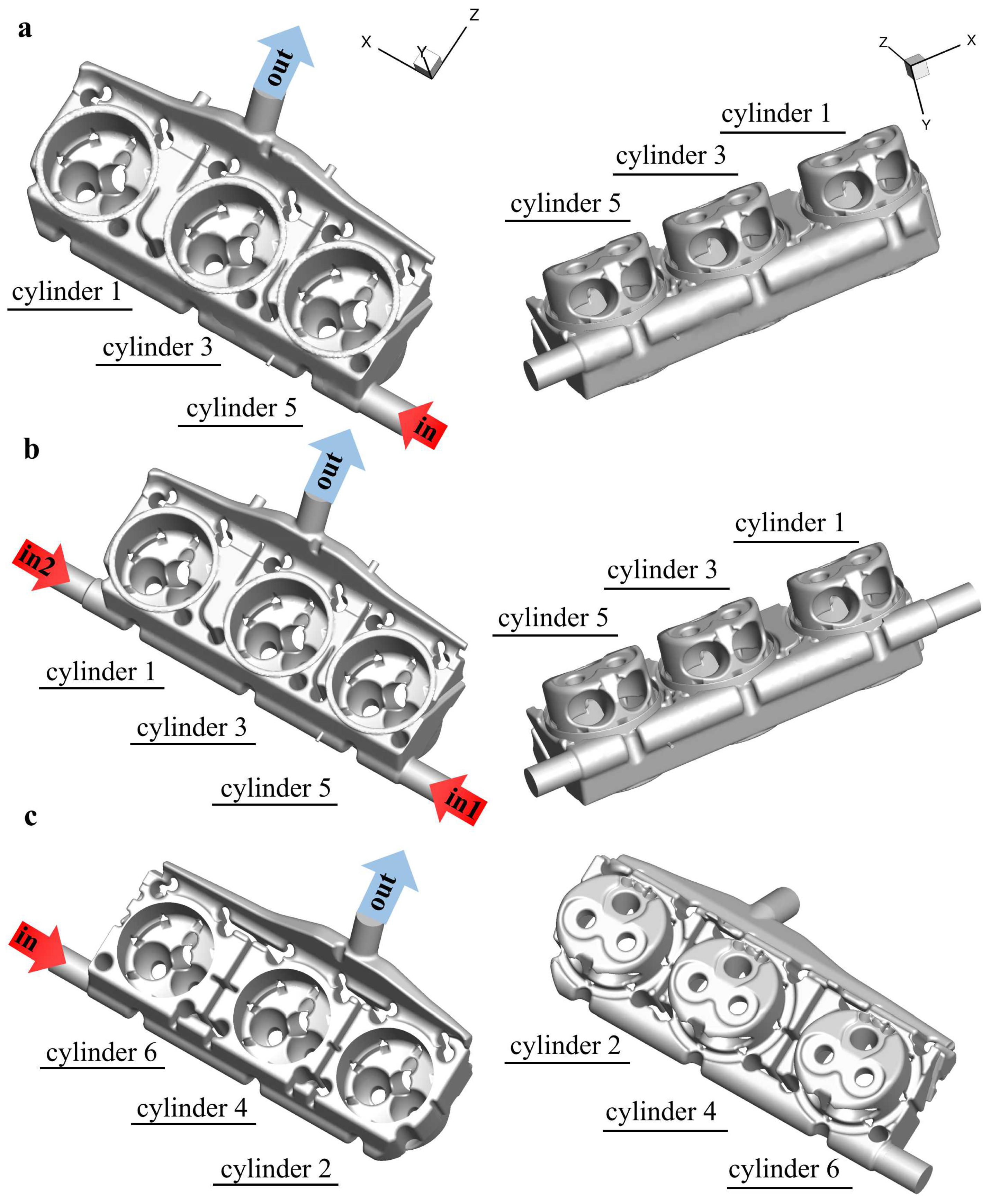
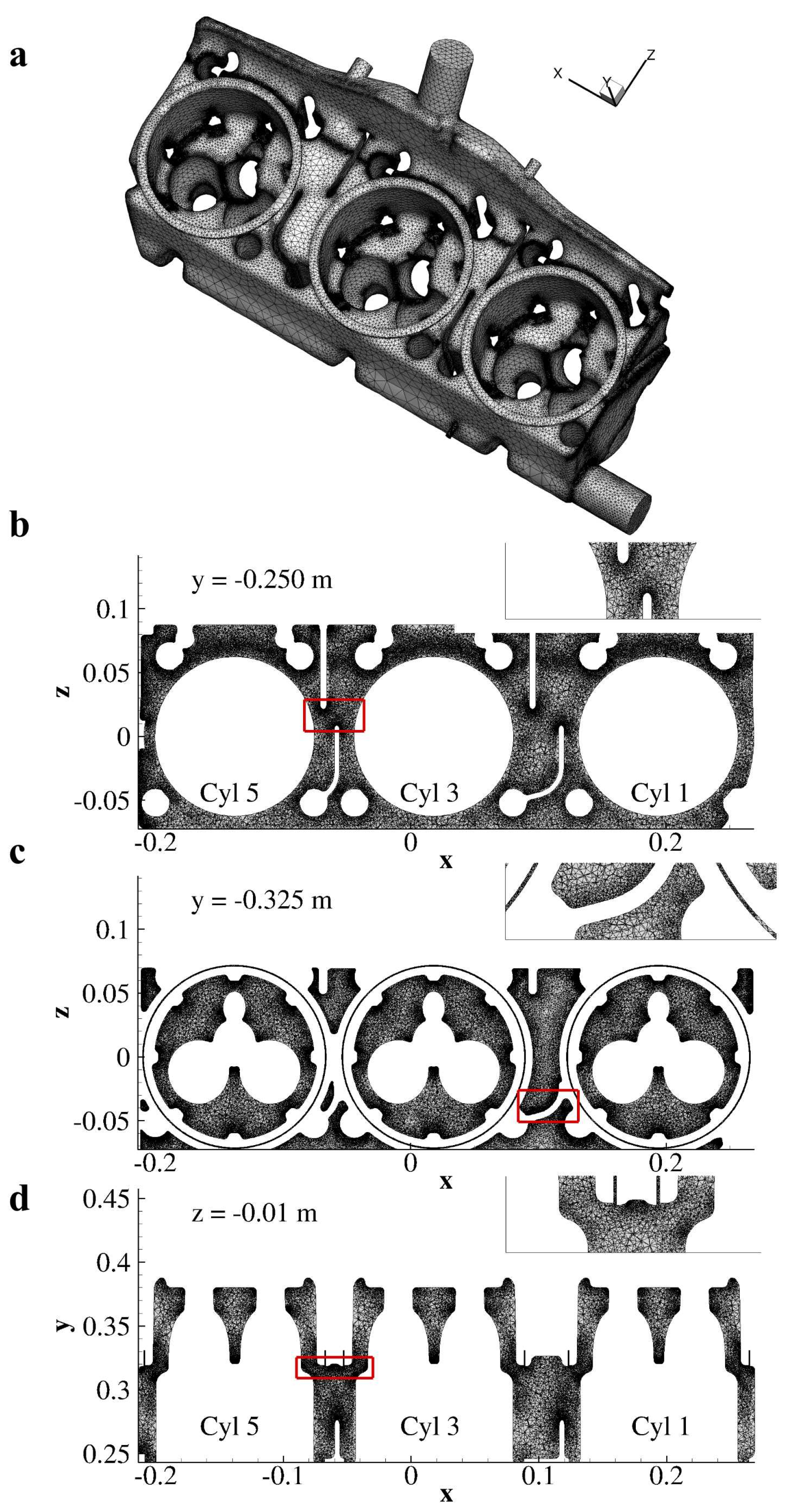
2.2. Computational Domain and Boundary Conditions
3. Results and Discussion
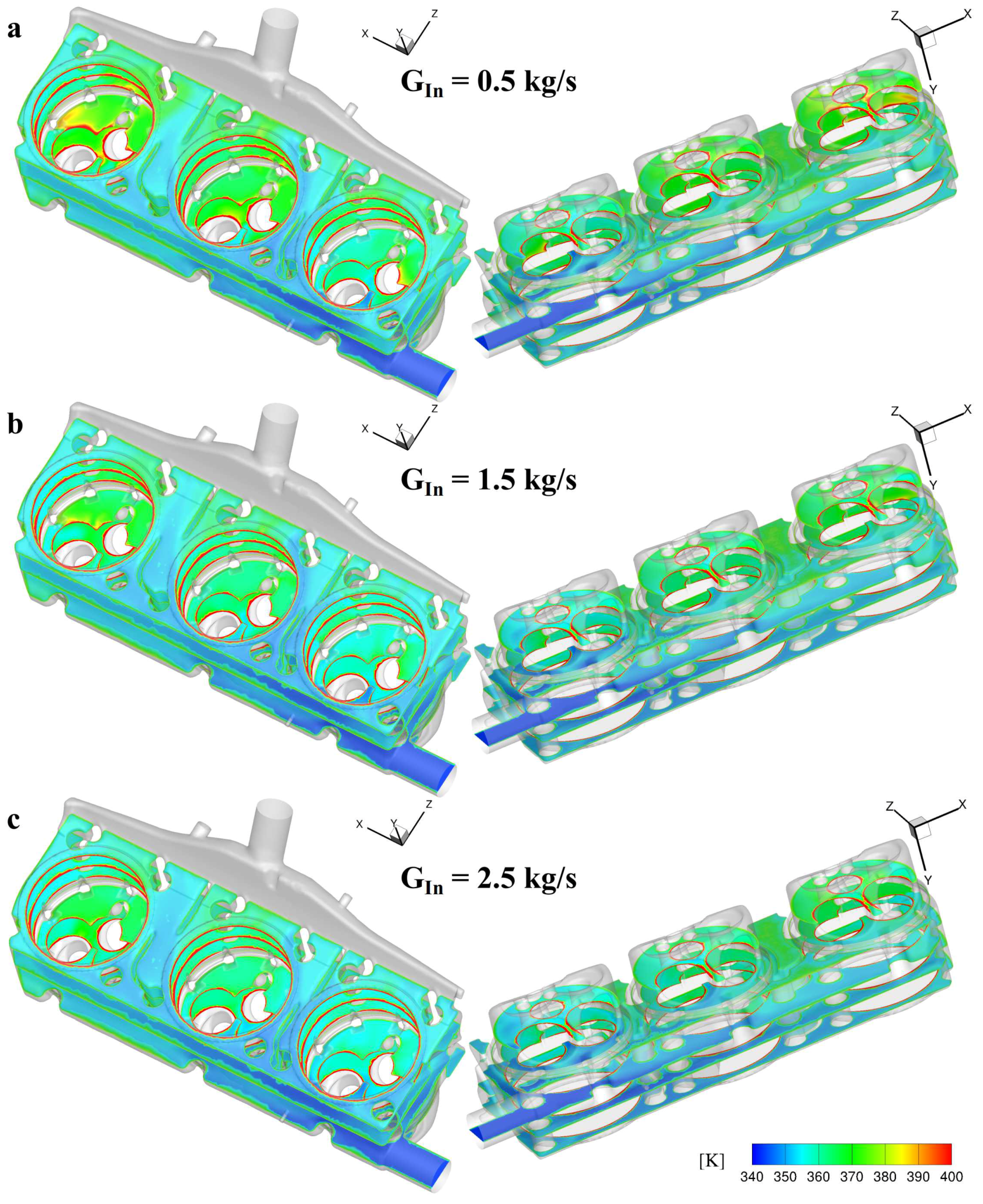
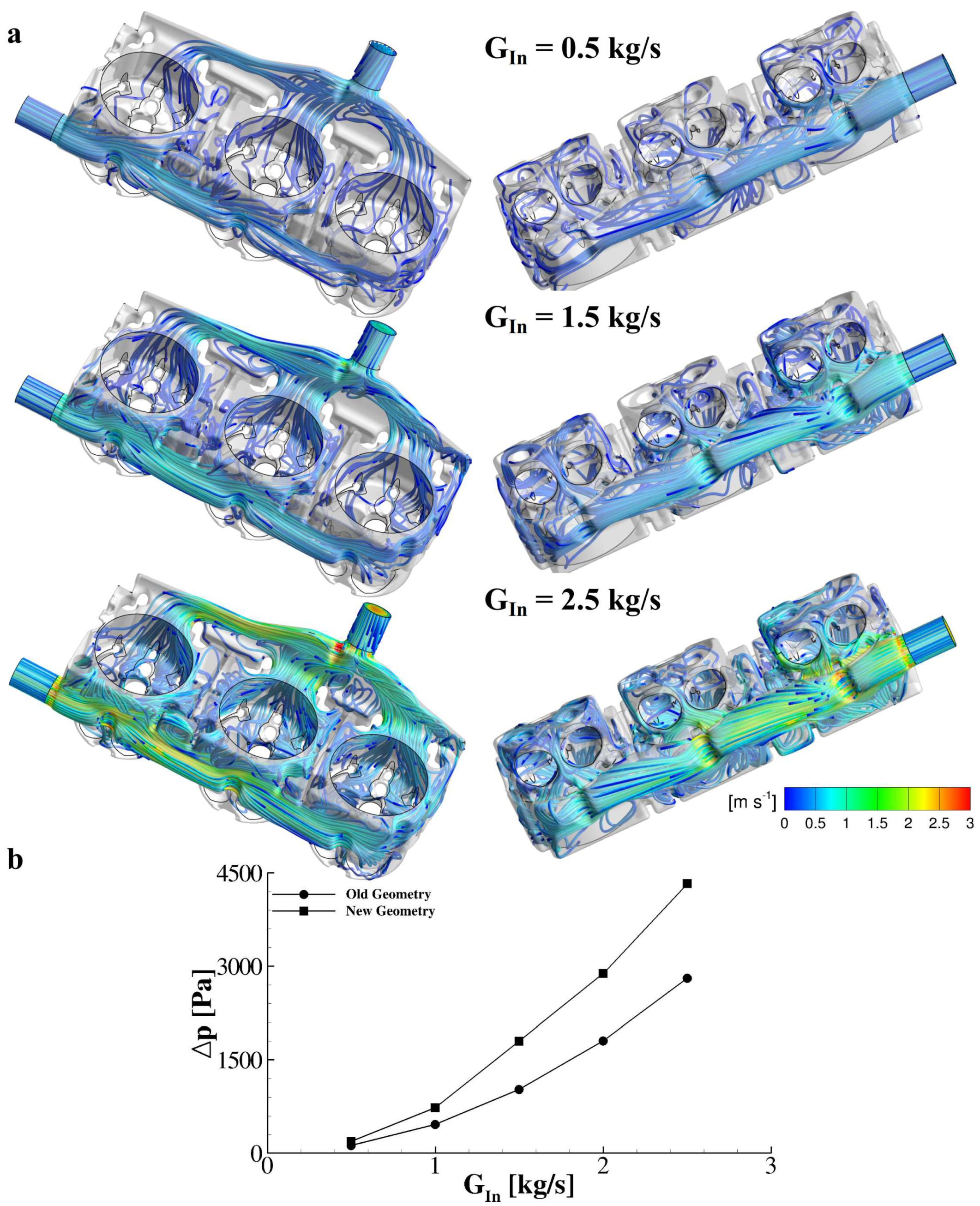
3.1. Analysis of the Single-Inlet Geometry
3.2. A First Cooling Improvement: The Double-Inlet Geometry
3.3. A New Single Inlet Geometry
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jacobs, T.J. Internal Combustion Engines, Developments in. In Fossil Energy; Malhotra, R., Ed.; Encyclopedia of Sustainability Science and Technology Series; Springer: New York, NY, USA, 2020; pp. 133–184. ISBN 978-1-4939-9762-6. [Google Scholar] [CrossRef]
- Ryuichi, M.; Toshihiko, I.; Hiroyuki, F.; Yasutoshi, Y. Internal combustion engine cooling apparatus. App. Therm. Eng. 1996, 16, 101–132. [Google Scholar] [CrossRef]
- Griffiths, J.; Barnard, J. Flame and Combustion; Routledge: Abingdon, UK, 2019; ISBN 9780203755976. [Google Scholar] [CrossRef]
- Zhukov, V.; Melnik, O.; Logunov, N.; Chernyi, S. Regulation and control in cooling systems of internal combustion engines. E3S Web Conf. 2019, 02015, 135. [Google Scholar] [CrossRef]
- Farokhi, S. Future Propulsion Systems and Energy Sources in Sustainable Aviation; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Vasilyev, A.V.; Lartsev, A.; Fedyanov, E. Evaluation of Possible Limits of Forcing of High-Capacity Air-Cooled Engines. In Proceedings of the International Conference on Industrial Engineering, Sochi, Russia, 25–29 March 2019; Springer: Berlin, Germany, 2019. [Google Scholar] [CrossRef]
- Bleier, F.; Bauer, H. Prediction of Heat Transfer in a Jet Cooled Aircraft Engine Compressor Cone Based on Statistical Methods. Aerospace 2018, 5, 51. [Google Scholar] [CrossRef]
- Jafari, S.; Nikolaidis, T. Thermal Management Systems for Civil Aircraft Engines: Review, Challenges and Exploring the Future. Appl. Sci. 2018, 8, 2044. [Google Scholar] [CrossRef]
- Wang, D.; Naterer, G.; Wang, G. Adaptive response surface method for thermal optimization: Application to aircraft engine cooling system. In Proceedings of the 8th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, St. Louis, MO, USA, 24–26 June 2002. [Google Scholar] [CrossRef]
- Jaffe, R.; Taylor, W. The Physics of Energy; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Jaffe, R.; Taylor, W. Internal Combustion Engines; Cambridge University Press: Cambridge, UK, 2019; pp. 203–218. [Google Scholar] [CrossRef]
- Aschemann, H.; Prabel, R.; Gross, C.; Schindele, D. Flatness-based control for an internal combustion engine cooling system. In Proceedings of the 2011 IEEE International Conference on Mechatronics, Istanbul, Turkey, 13–15 April 2011; pp. 140–145. [Google Scholar] [CrossRef]
- Petrov, A.P.; Bannikov, S.N. Active Shutters of the Internal Combustion Engine Cooling System of a Passenger Car. In Proceedings of the Higher Educational Institutions, Palma, Spain, 1–3 July 2019; pp. 44–51. [Google Scholar] [CrossRef]
- Razuvaev, A.; Slobodina, E. The operating conditions of the internal combustion engine with high temperature cooling. J. Phys. Conf. Ser. 2020, 1441, 120–126. [Google Scholar] [CrossRef]
- Keskinen, K.; Nuutinen, M.; Kaario, O.; Vuorinen, V.; Jann, K.; Wright, Y.M.; Larmi, M.; Boulouchos, K. Hybrid LES/RANS with wall treatment in tangential and impinging flow configurations. Int. J. Heat Fluid Flow 2017, 65, 141–158. [Google Scholar] [CrossRef]
- Krastev, V.K.; Silvestri, L.; Bella, G. Effects of turbulence modeling and grid quality on the zonal URANS/LES simulation of static and reciprocating engine-like geometries. SAE Int. J. Eng. 2018, 11, 669–686. [Google Scholar] [CrossRef]
- Krastev, V.K.; Di Ilio, G.; Falcucci, G.; Bella, G. Notes on the hybrid URANS/LES turbulence modeling for Internal Combustion Engines simulation. Energy Procedia 2018, 148, 1098–1104. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transfer 1972, 15, 54–73. [Google Scholar] [CrossRef]
- Anderson, W.K.; Bonhaus, D.L. An implicit upwind algorithm for computing turbulent flows on unstructured grids. Comput. Fluids 1994, 23, 1–21. [Google Scholar] [CrossRef]
- Barth, T.; Jespersen, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989; pp. 366–390. [Google Scholar]
- Hutchinson, B.R.; Raithby, G.D. A multigrid method based on the additive correction strategy. Numer. Heat Transf. Part A Appl. 1986, 9, 511–537. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Likhachev, E.R. Dependence of Water Viscosity on Temperature and Pressure. Tech. Phys. 2003, 48, 4. [Google Scholar] [CrossRef]






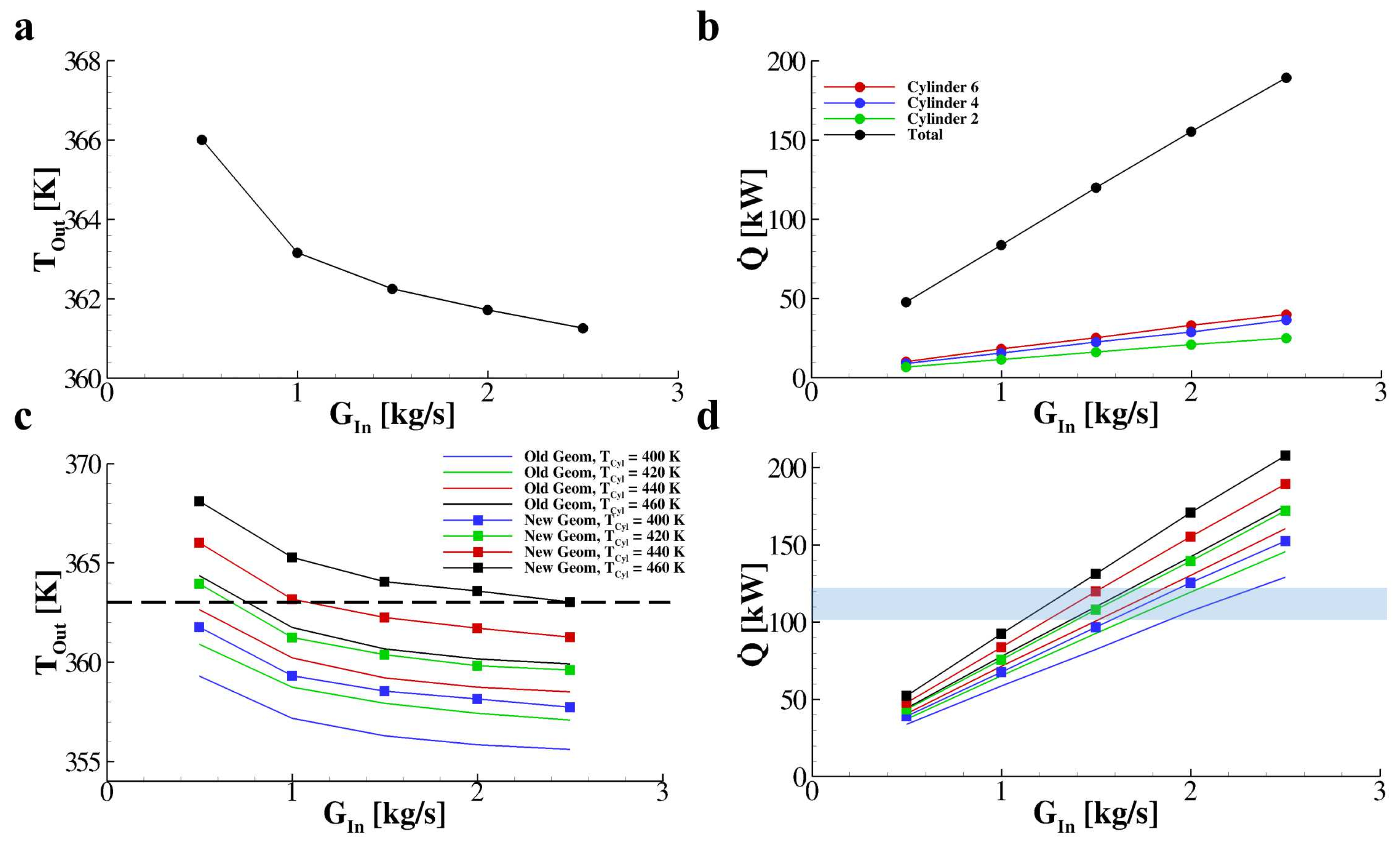
| G [kg/s] | T [K] | Q [kW] | Q [kW] | Q [kW] | Q [kW] |
|---|---|---|---|---|---|
| 0.5 | 362.6 | 9.6 | 6.9 | 4.4 | 40.8 |
| 1.0 | 360.2 | 17.5 | 11.4 | 6.7 | 71.4 |
| 1.5 | 359.2 | 25.4 | 16.3 | 9.0 | 100.7 |
| 2.0 | 358.7 | 32.9 | 21.3 | 11.4 | 130.3 |
| 2.5 | 358.5 | 40.8 | 25.9 | 13.9 | 160.5 |
| T = 400 K | T = 420 K | T = 440 K | T = 460 K | |||||
|---|---|---|---|---|---|---|---|---|
| G [kg/s] | T [K] | Q [kW] | T [K] | Q [kW] | T [K] | Q [kW] | T [K] | Q [kW] |
| 0.5 | 359.3 | 33.7 | 360.9 | 37.1 | 362.6 | 40.8 | 364.3 | 44.3 |
| 1.0 | 357.1 | 58.7 | 358.7 | 65.1 | 360.2 | 71.4 | 361.7 | 77.8 |
| 1.5 | 356.3 | 82.4 | 357.9 | 92.7 | 359.2 | 100.7 | 360.7 | 109.9 |
| 2.0 | 355.8 | 107.1 | 357.4 | 119.3 | 358.7 | 130.3 | 360.2 | 142.3 |
| 2.5 | 355.5 | 129.0 | 357.0 | 145.6 | 358.5 | 160.5 | 359.9 | 175.3 |
| G [kg/s] | T [K] | Q [kW] | Q [kW] | Q [kW] | Q [kW] |
|---|---|---|---|---|---|
| 0.5 | 361.2 | 6.0 | 6.1 | 5.8 | 35.8 |
| 1.0 | 358.1 | 9.7 | 9.9 | 9.4 | 58.9 |
| 1.5 | 357.2 | 13.9 | 13.5 | 13.3 | 82.6 |
| 2.0 | 356.5 | 17.6 | 17.2 | 17.3 | 104.5 |
| 2.5 | 356.3 | 21.5 | 20.9 | 21.2 | 128.5 |
| T = 400 K | T = 420 K | T = 440 K | T = 460 K | |||||
|---|---|---|---|---|---|---|---|---|
| G [kg/s] | T [K] | Q [kW] | T [K] | Q [kW] | T [K] | Q [kW] | T [K] | Q [kW] |
| 0.5 | 357.6 | 27.7 | 359.7 | 32.6 | 361.6 | 35.8 | 362.7 | 38.9 |
| 1.0 | 355.6 | 48.3 | 356.9 | 53.6 | 358.1 | 58.9 | 359.5 | 65.0 |
| 1.5 | 354.8 | 67.6 | 356.0 | 75.1 | 357.2 | 82.6 | 358.4 | 90.3 |
| 2.0 | 354.3 | 86.2 | 355.5 | 96.0 | 356.5 | 104.5 | 357.8 | 115.7 |
| 2.5 | 353.9 | 104.5 | 355.1 | 116.5 | 356.3 | 128.5 | 357.4 | 140.5 |
| G [kg/s] | T [K] | Q [kW] | Q [kW] | Q [kW] | Q [kW] |
|---|---|---|---|---|---|
| 0.5 | 366.0 | 10.1 | 9.0 | 6.8 | 47.9 |
| 1.0 | 363.1 | 18.3 | 15.5 | 11.4 | 83.7 |
| 1.5 | 362.2 | 25.1 | 22.5 | 16.3 | 119.9 |
| 2.0 | 361.5 | 33.2 | 28.9 | 20.8 | 155.3 |
| 2.5 | 361.2 | 39.9 | 36.4 | 25.0 | 189.4 |
| T = 400 K | T = 420 K | T = 440 K | T = 460 K | |||||
|---|---|---|---|---|---|---|---|---|
| G [kg/s] | T [K] | Q [kW] | T [K] | Q [kW] | T [K] | Q [kW] | T [K] | Q [kW] |
| 0.5 | 361.7 | 38.9 | 363.9 | 43.5 | 366.0 | 47.9 | 368.1 | 52.1 |
| 1.0 | 359.3 | 67.7 | 361.2 | 75.7 | 363.1 | 83.7 | 365.2 | 92.5 |
| 1.5 | 358.5 | 96.6 | 360.3 | 108.1 | 362.2 | 119.9 | 364.0 | 131.1 |
| 2.0 | 358.1 | 125.5 | 359.8 | 139.4 | 361.5 | 155.3 | 363.5 | 170.9 |
| 2.5 | 357.7 | 152.4 | 359.6 | 172.0 | 361.2 | 189.4 | 363.0 | 207.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coclite, A.; Faruoli, M.; Viggiano, A.; Caso, P.; Magi, V. Liquid-Cooling System of an Aircraft Compression Ignition Engine: A CFD Analysis. Fluids 2020, 5, 71. https://doi.org/10.3390/fluids5020071
Coclite A, Faruoli M, Viggiano A, Caso P, Magi V. Liquid-Cooling System of an Aircraft Compression Ignition Engine: A CFD Analysis. Fluids. 2020; 5(2):71. https://doi.org/10.3390/fluids5020071
Chicago/Turabian StyleCoclite, Alessandro, Maria Faruoli, Annarita Viggiano, Paolo Caso, and Vinicio Magi. 2020. "Liquid-Cooling System of an Aircraft Compression Ignition Engine: A CFD Analysis" Fluids 5, no. 2: 71. https://doi.org/10.3390/fluids5020071
APA StyleCoclite, A., Faruoli, M., Viggiano, A., Caso, P., & Magi, V. (2020). Liquid-Cooling System of an Aircraft Compression Ignition Engine: A CFD Analysis. Fluids, 5(2), 71. https://doi.org/10.3390/fluids5020071





