Jet Oscillation Frequency Characterization of a Sweeping Jet Actuator †
Abstract
1. Introduction
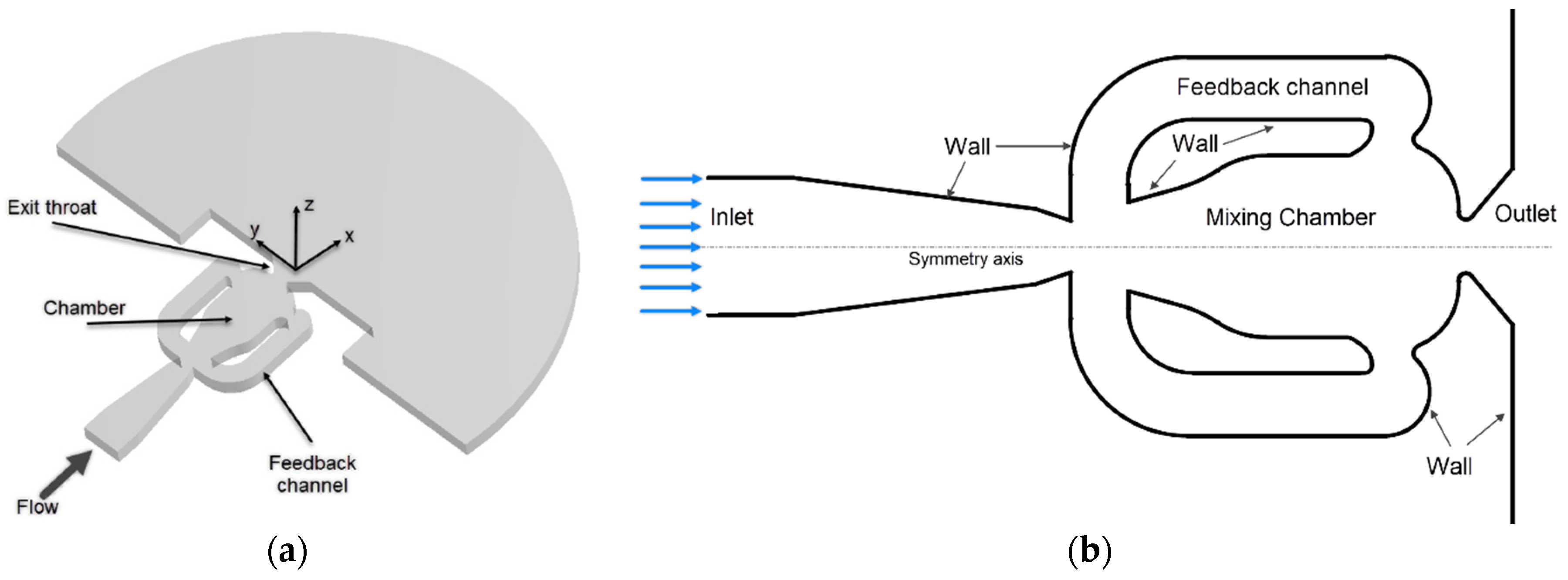
2. Numerical Methodology
3. Results
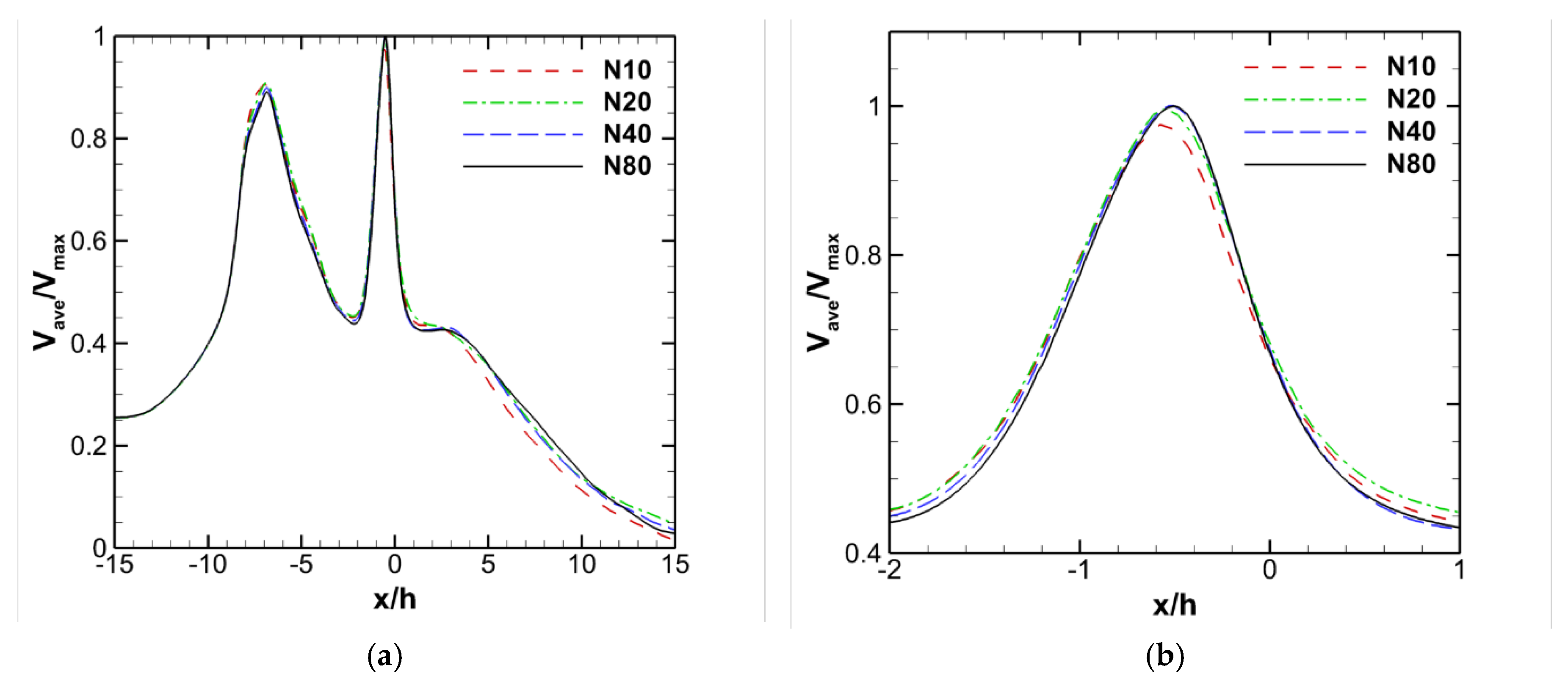
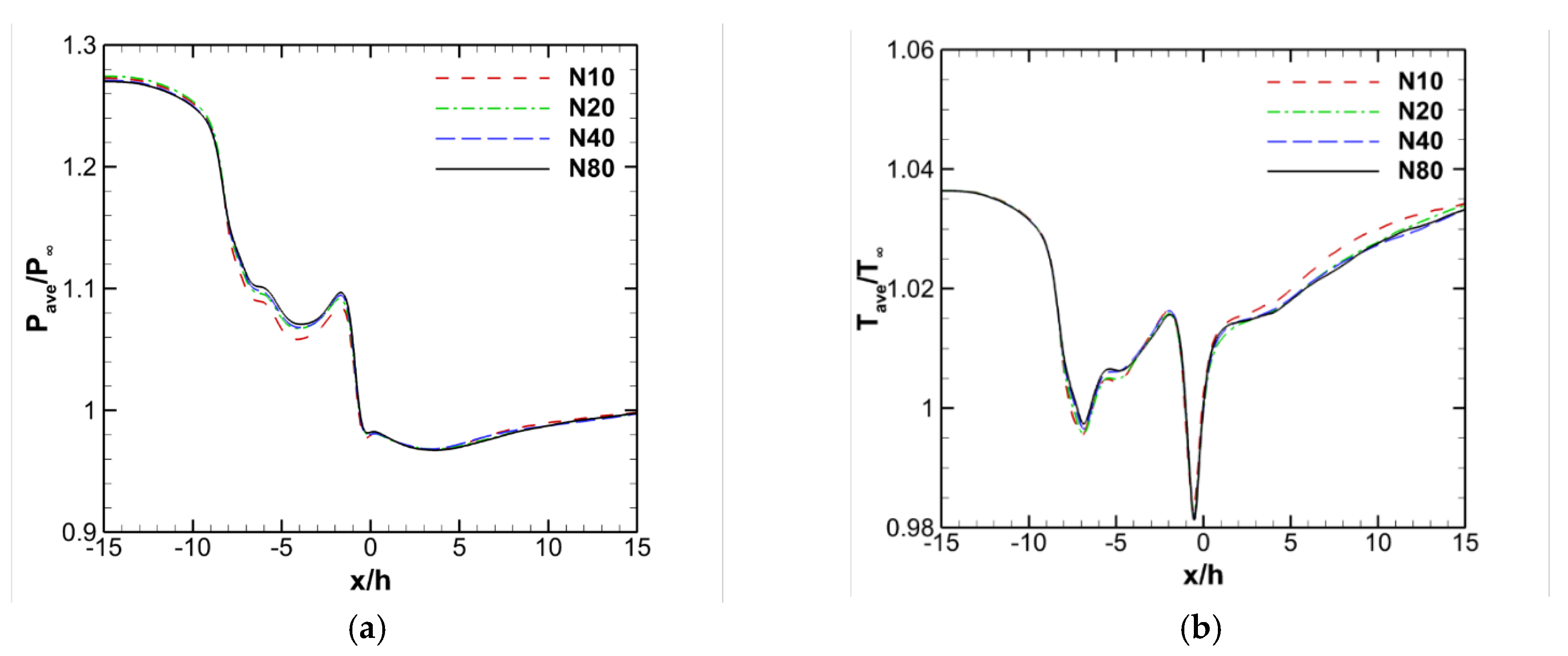
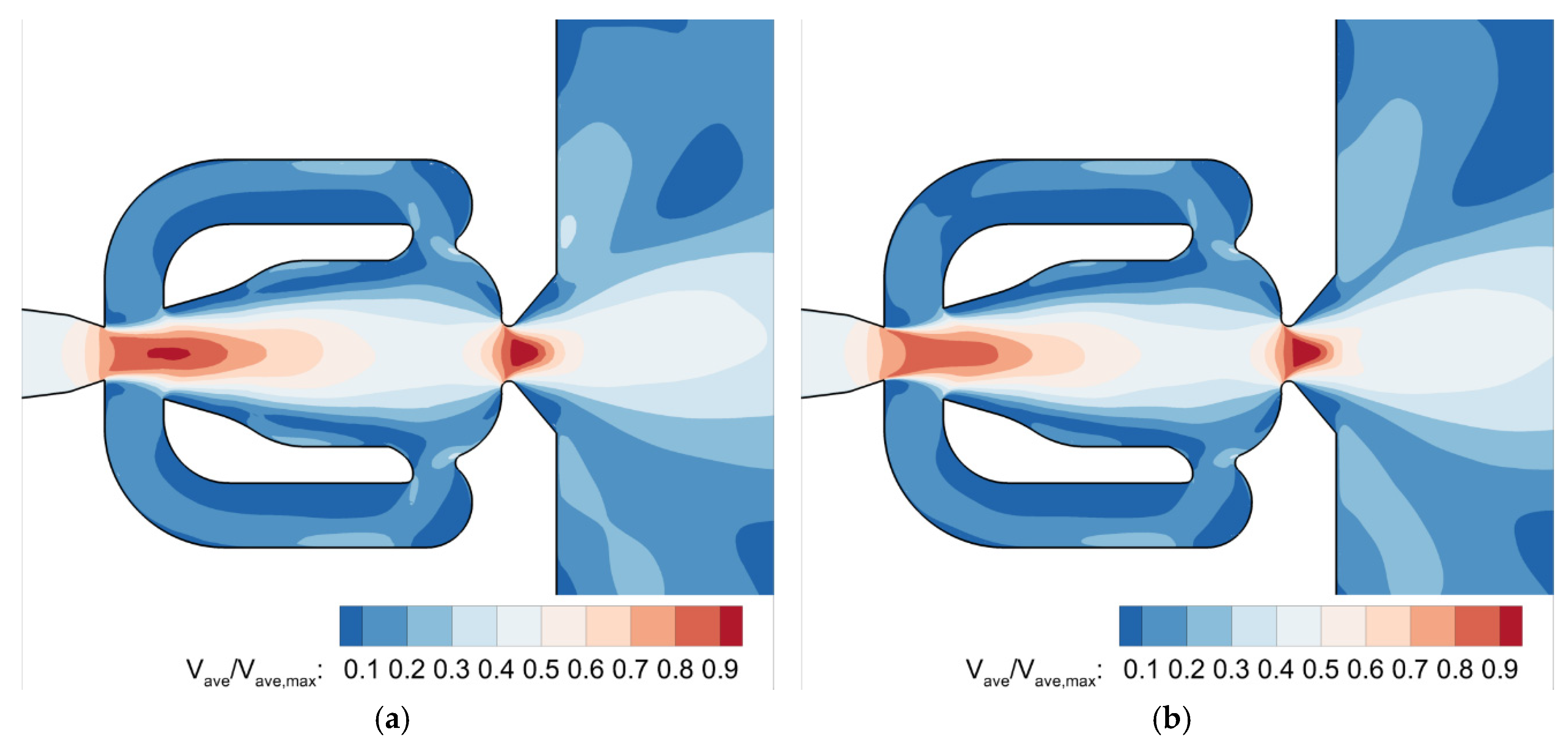
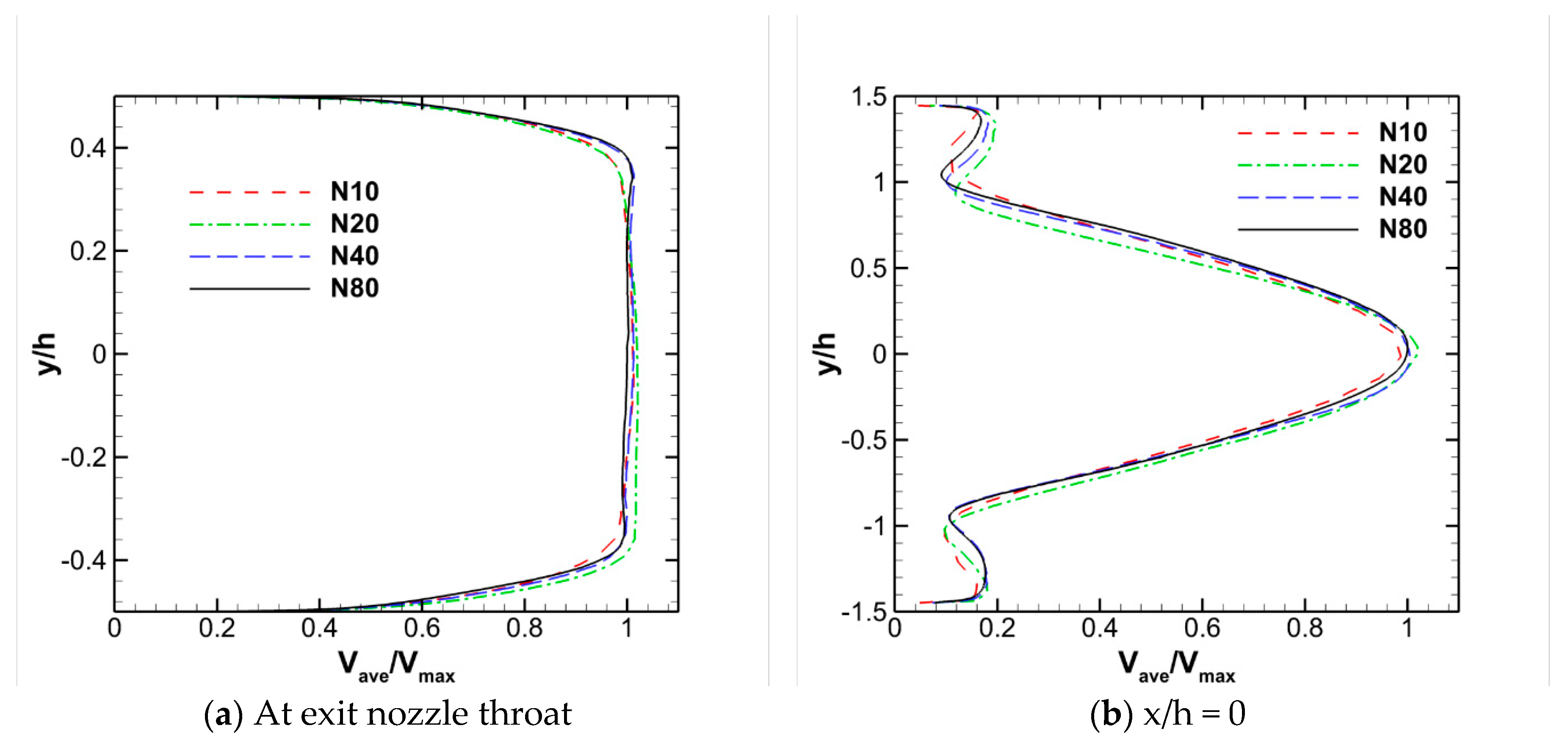
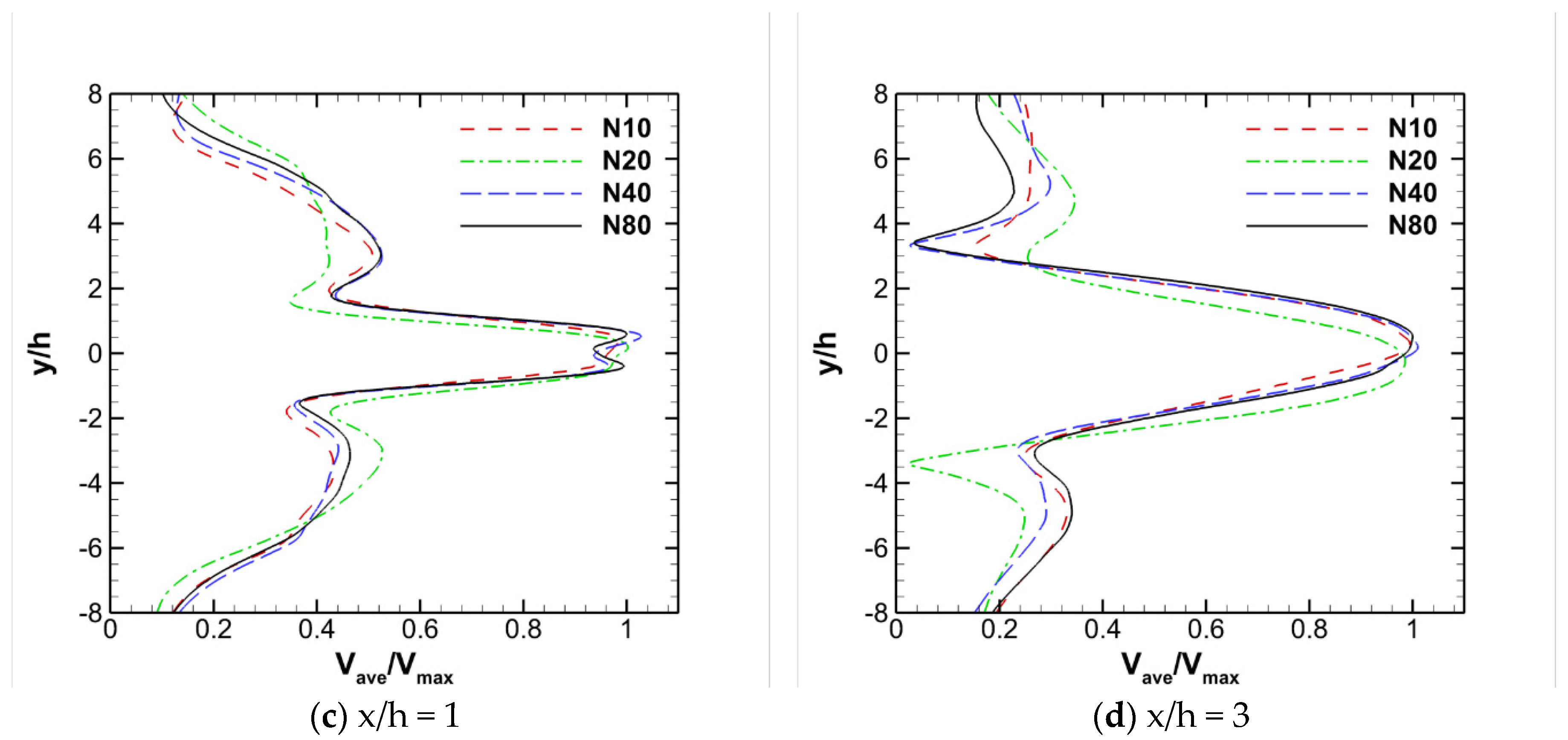
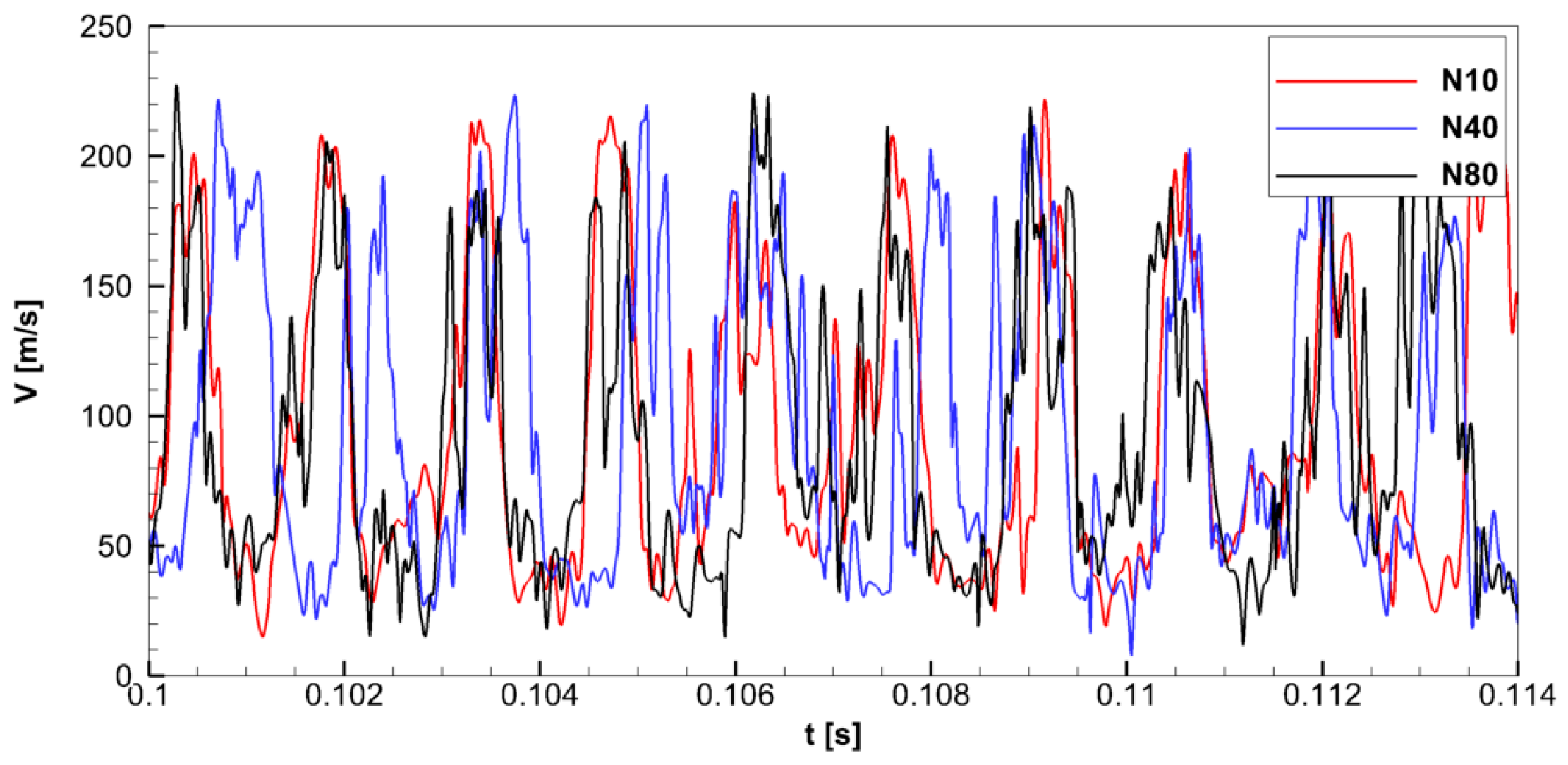
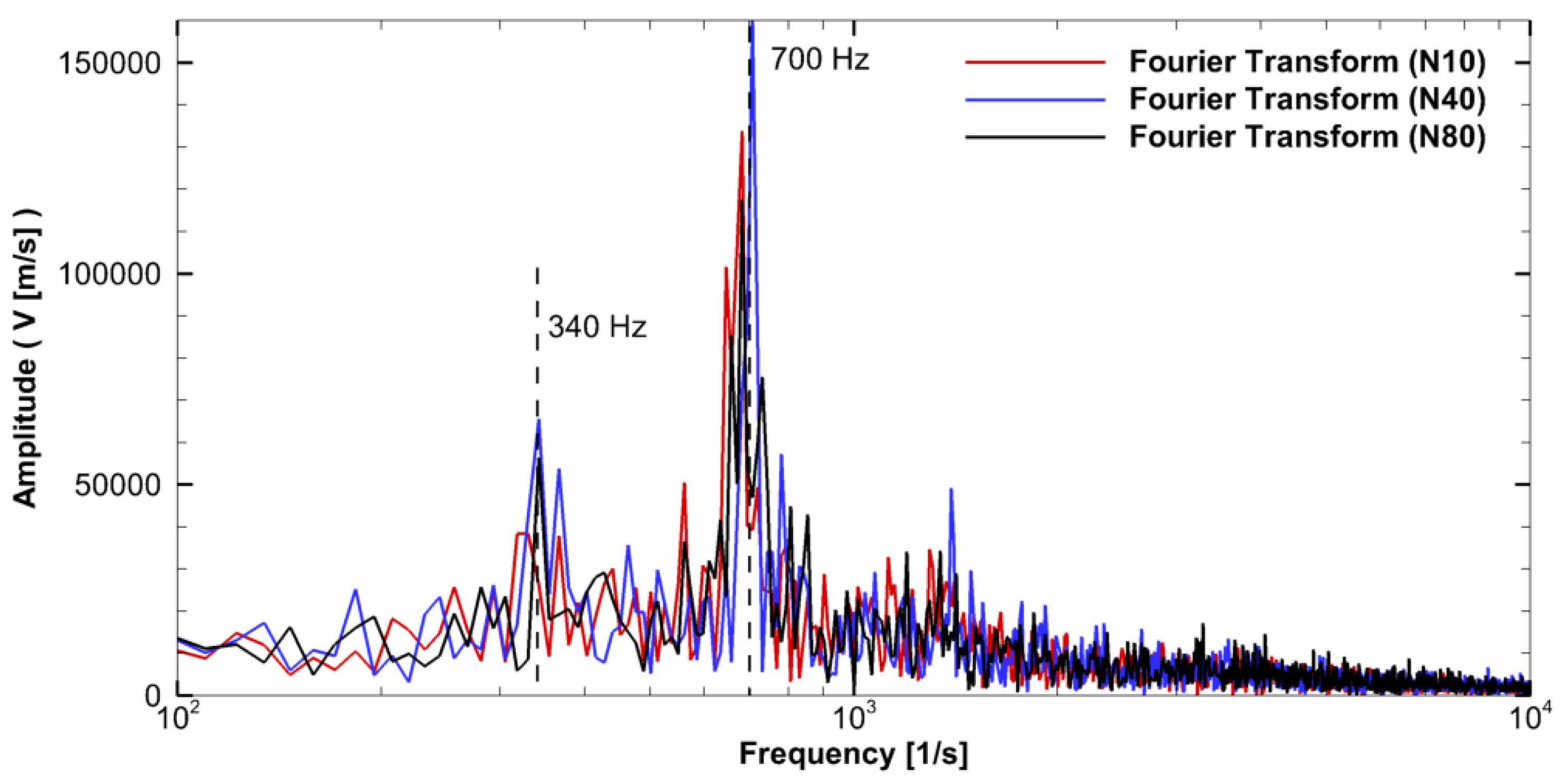
3.1. Mesh Sensitivity Analysis
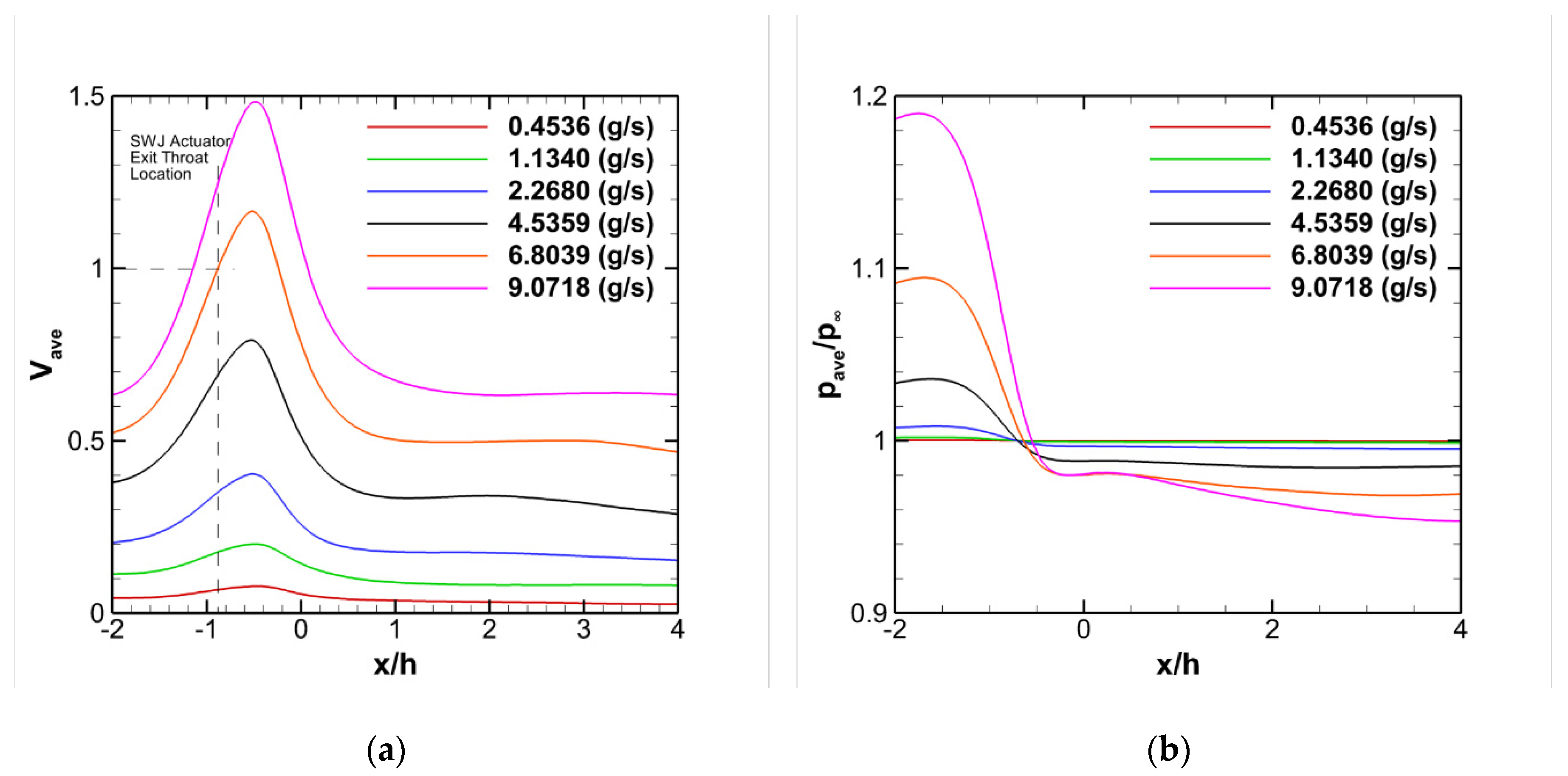
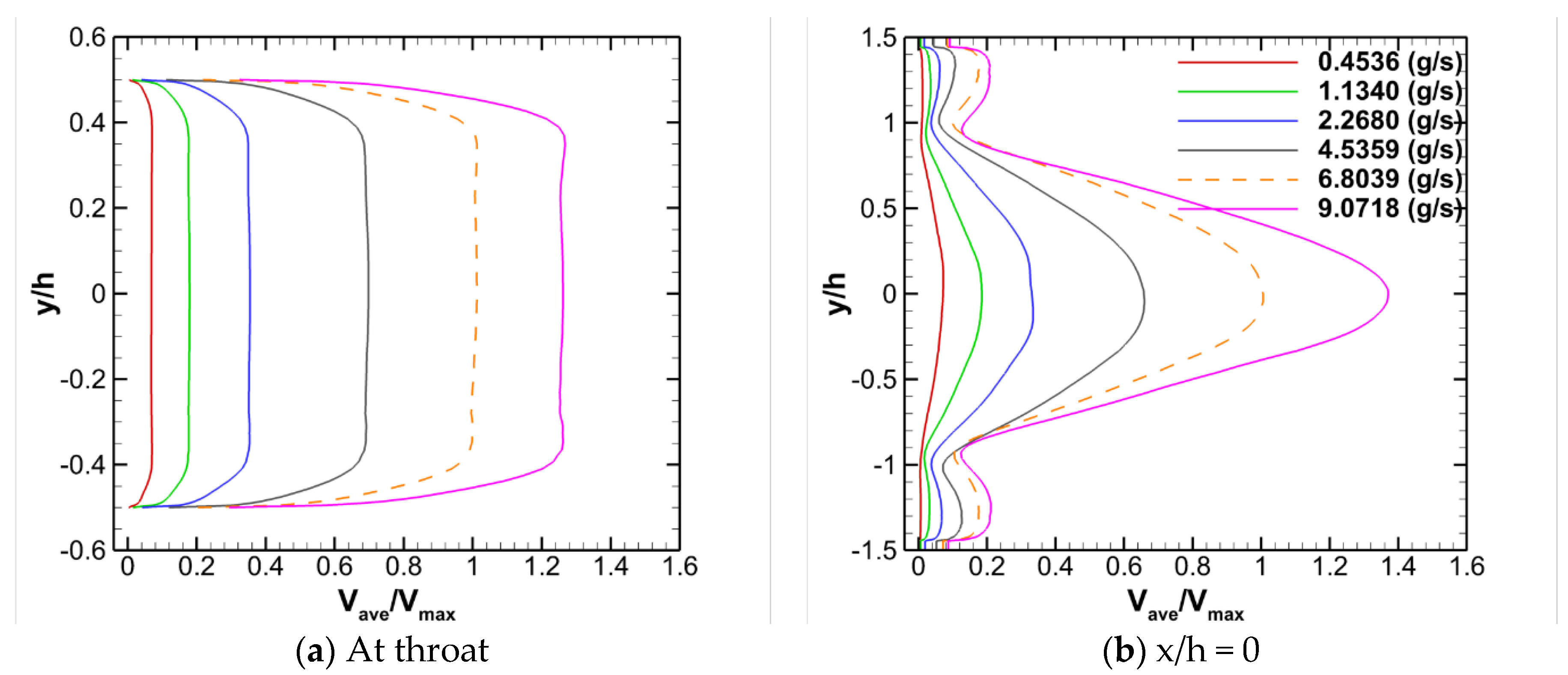
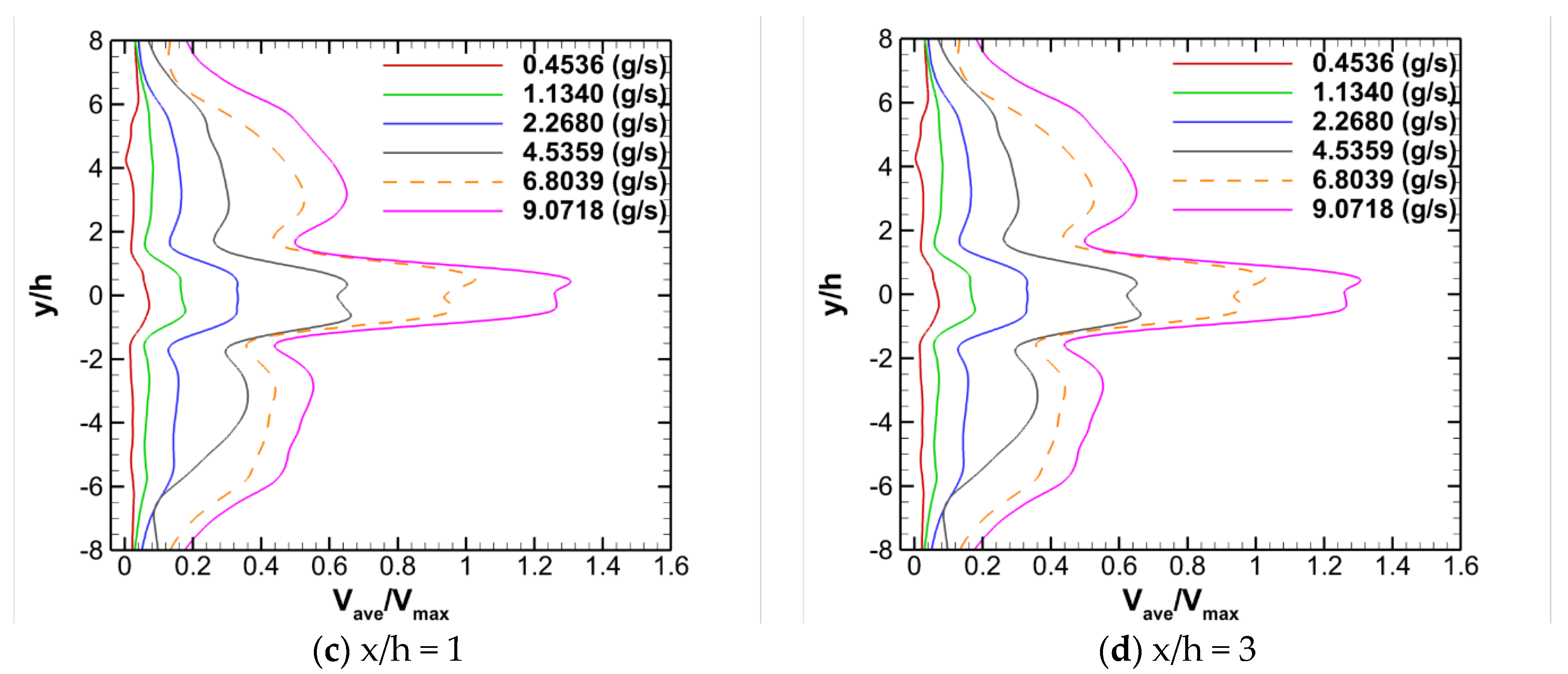
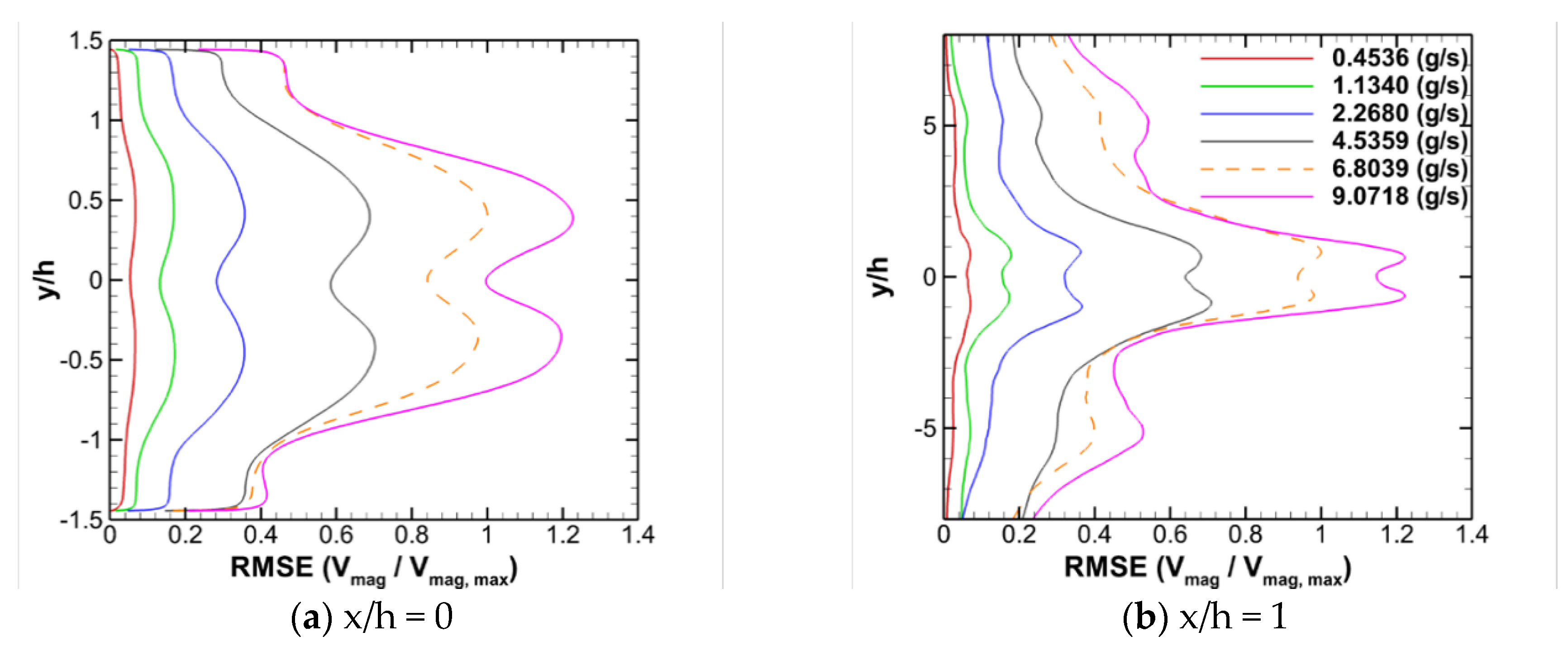
3.2. Effect of Mass Flow Rate
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Anders, S.G.; Sellers, W.L.; Washburn, A.E. Active flow control activities at NASA langley. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar]
- Whalen, E.A.; Spoor, M.; Vijgen, P.M.; Tran, J.; Shmilovich, A.; Lin, J.C.; Andino, M. Full-scale Flight Demonstration of an Active Flow Control Enhanced Vertical Tail. In Proceedings of the 8th AIAA Flow Control Conference, Washington, DC, USA, 13–17 June 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar]
- Lin, J.C.; Andino, M.Y.; Alexander, M.G.; Whalen, E.A.; Spoor, M.A.; Tran, J.T.; Wygnanski, I.J. An overview of active flow control enhanced vertical tail technology development. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; American Institute of Aeronautics and Astronautics Inc, AIAA: Reston, VA, USA, 2016. [Google Scholar]
- Stouffer, R.D. Liquid Oscillator Device. U.S. Patent 4508267, 2 April 1985. [Google Scholar]
- Beale, R.B.; Lawler, M.T. Development of a Wall-Attachment Fluidic Oscillator Applied To Volume Flow Metering. In Flow: Its Measurement and Control in Science and Industry; Instrument Society of America: Pittsburgh, PA, USA, 1974; Volume 1, pp. 989–996. [Google Scholar]
- Wang, H.; Beck, S.B.M.; Priestman, G.H.; Boucher, R.F. Fluidic pressure pulse transmitting flowmeter. Chem. Eng. Res. Des. 1997, 75, 381–391. [Google Scholar] [CrossRef]
- Lucas, N.; Taubert, L.; Woszidlo, R.; Wygnanski, I.; McVeigh, M.A. Discrete sweeping jets as tools for separation control. In Proceedings of the 4th AIAA Flow Control Conference, Seattle, WA, USA, 23–26 June 2008; Fluid Dynamics and Co-located Conferences; AIAA Paper 2008-3868. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. ISBN 9781563479427. [Google Scholar]
- Tewes, P.; Taubert, L.; Wygnanski, I. On the use of sweeping jets to augment the lift of a λ-wing. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; Fluid Dynamics and Co-located Conferences; AIAA Paper 2010-4689. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010; Volume 1, ISBN 9781617389269. [Google Scholar]
- Kara, K. Numerical simulation of a sweeping jet actuator. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016; p. 3261. [Google Scholar]
- Slupski, B.J.; Kara, K. Effects of geometric parameters on performance of sweeping jet actuator. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar]
- Duda, B.; Wessels, M.; Fares, E.; Vatsa, V. Unsteady flow simulation of a sweeping jet actuator using a Lattice-Boltzmann method. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016; p. 1818. [Google Scholar]
- Melton, L.T.P.; Koklu, M.; Andino, M.; Lin, J.C.; Edelman, L. Sweeping jet optimization studies. In Proceedings of the 8th AIAA Flow Control Conference, Washington, DC, USA, 13–17 June 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016; p. 4233. [Google Scholar]
- Koklu, M. Effect of a coanda extension on the performance of a sweeping-jet actuator. AIAA J. 2016, 54, 1125–1128. [Google Scholar] [CrossRef]
- Koklu, M.; Owens, L.R. Comparison of sweeping jet actuators with different flow-control techniques for flow-separation control. AIAA J. 2017, 55, 848–860. [Google Scholar] [CrossRef]
- Jurewicz, B.; Kara, K. Effects of Feedback Channels and Coanda Surfaces on the Performance of Sweeping Jet Actuator. In Proceedings of the AIAA SciTech Forum—55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- Aram, S.; Lee, Y.T.; Shan, H.; Vargas, A. Computational fluid dynamic analysis of fluidic actuator for active flow control applications. AIAA J. 2018, 56, 111–120. [Google Scholar] [CrossRef]
- Park, T.; Kara, K.; Kim, D. Flow structure and heat transfer of a sweeping jet impinging on a flat wall. Int. J. Heat Mass Transf. 2018, 124, 920–928. [Google Scholar] [CrossRef]
- Meng, Q.; Chen, S.; Li, W.; Wang, S. Numerical investigation of a sweeping jet actuator for active flow control in a compressor cascade. In Proceedings of the ASME Turbo Expo, Oslo, Norway, 11–15 June 2018; Volume 2A. [Google Scholar]
- Woszidlo, R.; Nawroth, H.; Raghu, S.; Wygnanski, I.J. Parametric study of sweeping jet actuators for separation control. In Proceedings of the 5th Flow Control Conference, Chicago, IL, USA, 28 June–1 July 2010. AIAA Paper 2010-4247. [Google Scholar]
- Phillips, E.; Wygnanski, I.J.; Menge, P.M.; Taubert, L. Passive and Active Leading Edge devices on a simple swept back wing. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3393. [Google Scholar]
- Aram, S.; Shan, H. Computational analysis of interaction of a sweeping jet with an attached crossflow. AIAA J. 2019, 57, 682–695. [Google Scholar] [CrossRef]
- Jentzsch, M.; Taubert, L.; Wygnanski, I. Using sweeping jets to trim and control a tailless aircraft model. AIAA J. 2019, 57, 2322–2334. [Google Scholar] [CrossRef]
- Wen, X.; Liu, J.; Li, Z.; Zhou, W.; Liu, Y. Flow dynamics of sweeping jet impingement upon a large convex cylinder. Exp. Therm. Fluid Sci. 2019, 107, 1–15. [Google Scholar] [CrossRef]
- Kim, D.J.; Jeong, S.; Park, T.; Kim, D. Impinging sweeping jet and convective heat transfer on curved surfaces. Int. J. Heat Fluid Flow 2019, 79, 108458. [Google Scholar] [CrossRef]
- Sushanth Gowda, B.C.; Vinuth, N.; Poornananda, T.; Dhanush, G.J.; Paramesh, T. Internal flow analysis on sweeping jet actuator. Int. J. Recent Technol. Eng. 2019, 8, 296–304. [Google Scholar]
- Meng, Q.; Du, X.; Chen, S.; Wang, S. Numerical Study of Dual Sweeping Jet Actuators for Corner Separation Control in Compressor Cascade. J. Therm. Sci. 2019, 1–9. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.; Meng, Q.; Zhou, Z.; Wang, S. Effects of a sweeping jet actuator on aerodynamic performance in a linear turbine cascade with tip clearance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 4468–4481. [Google Scholar] [CrossRef]
- Wen, X.; Liu, J.; Kim, D.; Liu, Y.; Kim, K.C. Study on three-dimensional flow structures of a sweeping jet using time-resolved stereo particle image velocimetry. Exp. Therm. Fluid Sci. 2020, 110, 109945. [Google Scholar] [CrossRef]
- Woszidlo, R.; Wygnanski, I. Parameters governing separation control with sweeping jet actuators. In Proceedings of the 29th AIAA Applied Aerodynamics Conference 2011, Honolulu, HI, USA, 27–30 June 2011; Fluid Dynamics and Co-located Conferences; AIAA Paper 2011-3172. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. ISBN 9781624101458. [Google Scholar]
- Koklu, M.; Melton, L.P. Sweeping jet actuator in a quiescent environment. In Proceedings of the 43rd Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]
- Seele, R.; Graff, E.; Lin, J.; Wygnanski, I. Performance enhancement of a vertical tail model with sweeping jet actuators. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition 2013, Grapevine, TX, USA, 7–10 January 2013; AIAA Paper 2013-0411. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar]
- Gärtlein, S.; Woszidlo, R.; Ostermann, F.; Nayeri, C.N.; Paschereit, C.O. The time-resolved internal and external flow field properties of a fluidic oscillator. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2014; pp. 1–15. [Google Scholar]
- Koklu, M.; Owens, L.R. Flow separation control over a ramp using sweeping jet actuators. In Proceedings of the AIAA AVIATION 2014—7th AIAA Flow Control Conference, Atlanta, GA, USA, 16–20 June 2014; AIAA Paper 2014-2367. American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2014. [Google Scholar]
- Andino, M.Y.; Lin, J.C.; Washburn, A.E.; Whalen, E.A.; Graff, E.C.; Wygnanski, I.J. Flow separation control on a full-scale vertical tail model using sweeping jet actuators. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 785. [Google Scholar]
- Peters, C.J.; Miles, R.B.; Burns, R.A.; Bathel, B.F.; Jones, G.S.; Danehy, P.M. Femtosecond laser tagging characterization of a sweeping jet actuator operating in the compressible regime. In Proceedings of the 32nd AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Washington, DC, USA, 13–17 June 2016; pp. 1–22. [Google Scholar]
- DeSalvo, M.; Whalen, E.; Glezer, A. High-lift enhancement using fluidic actuation. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Seele, R.; Tewes, P.; Woszidlo, R.; McVeigh, M.A.; Lucas, N.J.; Wygnanski, I.J. Discrete sweeping jets as tools for improving the performance of the V-22. J. Aircr. 2009, 46, 2098–2106. [Google Scholar] [CrossRef]
- Cerretelli, C.; Wuerz, W.; Gharaibah, E. Unsteady separation control on wind turbine blades using fluidic oscillators. AIAA J. 2010, 48, 1302–1311. [Google Scholar] [CrossRef]
- Seifert, A.; Stalnov, O.; Sperber, D.; Arwatz, G.; Palei, V.; David, S.; Dayan, I.; Fono, I. Large trucks drag reduction using active flow control. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; pp. 115–133. [Google Scholar]
- Woszidlo, R.; Stumper, T.; Nayeri, C.N.; Paschereit, C.O. Experimental study on bluff body drag reduction with fluidic oscillators. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2014. [Google Scholar]
- Kara, K.; Kim, D.; Morris, P.J. Flow-separation control using sweeping jet actuator. AIAA J. 2018, 56, 4604–4613. [Google Scholar] [CrossRef]
- Seele, R.; Graff, E.; Gharib, M.; Taubert, L.; Lin, J.; Wygnanski, I. Improving rudder effectiveness with sweeping jet actuators. In Proceedings of the 6th AIAA Flow Control Conference, New Orleans, LA, USA, 25–28 June 2012; AIAA Paper 2012-3244. American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2012. [Google Scholar]
- Koklu, M. Effects of sweeping jet actuator parameters on flow separation control. AIAA J. 2018, 56, 1–11. [Google Scholar] [CrossRef]
- Hirsch, D.; Gharib, M. Schlieren visualization and analysis of sweeping jet actuator dynamics. AIAA J. 2018, 56, 2947–2960. [Google Scholar] [CrossRef]
- Ott, C.; Gallas, Q.; Delva, J.; Lippert, M.; Keirsbulck, L. High frequency characterization of a sweeping jet actuator. Sens. Actuators A Phys. 2019, 291, 39–47. [Google Scholar] [CrossRef]
- Horne, W.C.; Burnside, N.J. Acoustic study of a sweeping jet actuator for active flow control applications. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; American Institute of Aeronautics and Astronautics Inc, AIAA: Reston, VA, USA, 2016. [Google Scholar]
- Seo, J.H.; Zhu, C.; Mittal, R. Flow physics and frequency scaling of sweeping jet fluidic oscillators. AIAA J. 2018, 56, 2208–2219. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows; John Wiley & Sons: Chichester, UK, 1990; Volume 2, ISBN 978-8126539239. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; D C W Industries: La Canada, CA, USA, 2006. [Google Scholar]
- Gatski, T.B.; Bonnet, J.P. Compressibility, Turbulence and High Speed Flow; Elsevier Ltd.: Amsterdam, The Netherlands, 2013; ISBN 9780123970275. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Ansys® Fluent, Release 17.1, User Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2016.
- Vatsa, V.; Koklu, M.; Wygnanski, I. Numerical Simulation of Fluidic Actuators for Flow Control Applications. In Proceedings of the 6th AIAA Flow Control Conference, New Orleans, LA, USA, 25–28 June 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar]
- Raghu, S. Fluidic oscillators for flow control. Exp. Fluids 2013, 54, 1455. [Google Scholar] [CrossRef]
- Tecplot 360 EX, 2019 Release 1, User’s Manual; Tecplot, Inc.: Bellevue, WA, USA, 2019.
- Slupski, B.J.; Tajik, A.R.; Parezanović, V.B.; Kara, K. On the impact of geometry scaling and mass flow rate on the frequency of a sweeping jet actuator. FME Trans. 2019, 47, 599–607. [Google Scholar] [CrossRef]
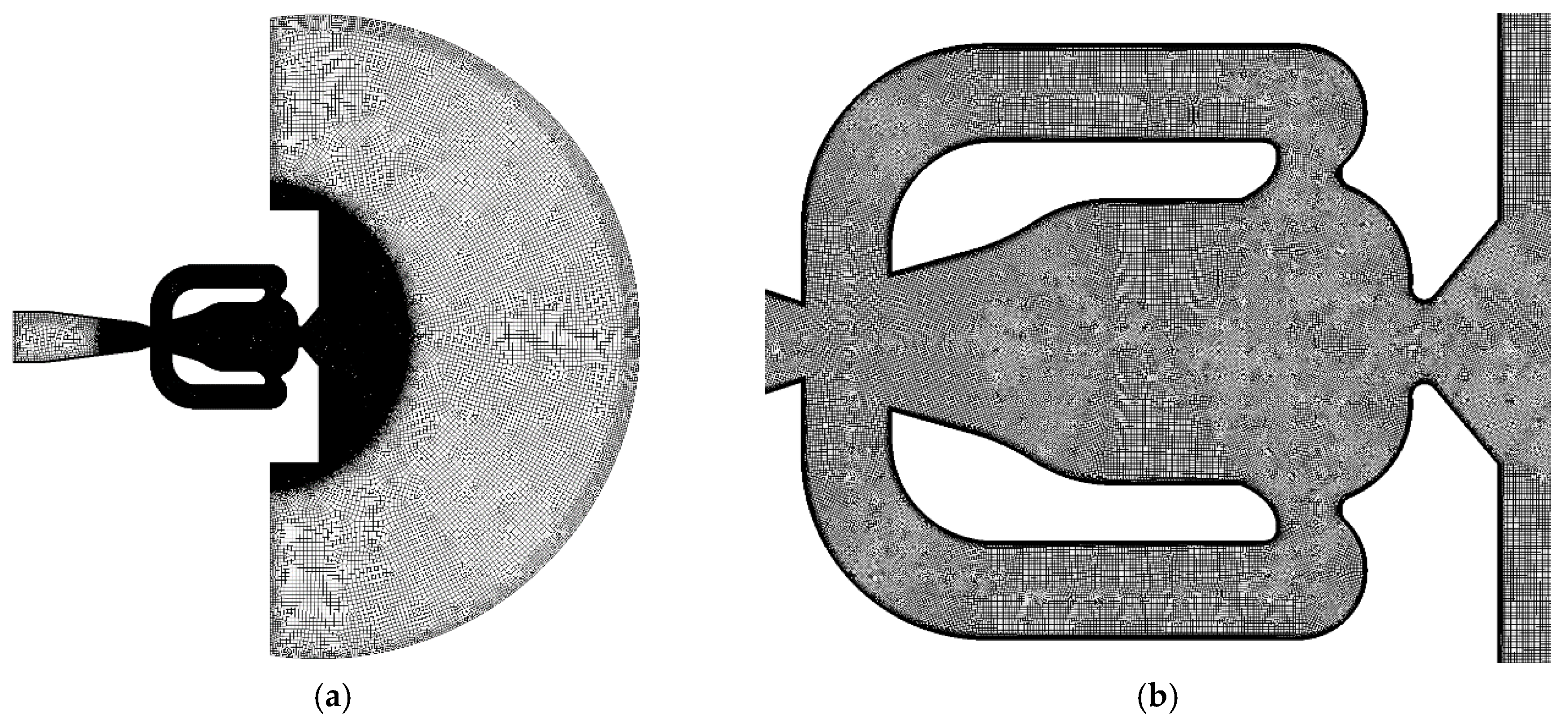




| (g/s) | (m/s) | ||
|---|---|---|---|
| 0.4536 | 3.7 | 0.01 | 2197 |
| 1.134 | 9.3 | 0.03 | 5491 |
| 2.268 | 18.6 | 0.05 | 10,983 |
| 4.5359 | 37.2 | 0.11 | 21,965 |
| 6.8039 | 55.8 | 0.16 | 32,948 |
| 9.0718 | 74.4 | 0.22 | 43,930 |
| 11.3398 | 93.0 | 0.27 | 54,913 |
| Mesh Name | Element Size (mm) | Number of Elements | Mesh Resolution |
|---|---|---|---|
| N10 | 6.3500 × 10−1 | 397,670 | Coarse |
| N20 | 3.1750 × 10−1 | 749,280 | Normal |
| N40 | 1.5875 × 10−1 | 2,023,860 | Fine |
| N80 | 7.9375 × 10−2 | 6,672,820 | Finest |
| Mesh | f (Hz.) | Error (%) |
|---|---|---|
| N10 | 329.6 | −3.6 |
| N20 | 366.2 | 7.1 |
| N40 | 341.8 | 0.0 |
| N80 | 341.8 | Assumed true solution |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oz, F.; Kara, K. Jet Oscillation Frequency Characterization of a Sweeping Jet Actuator. Fluids 2020, 5, 72. https://doi.org/10.3390/fluids5020072
Oz F, Kara K. Jet Oscillation Frequency Characterization of a Sweeping Jet Actuator. Fluids. 2020; 5(2):72. https://doi.org/10.3390/fluids5020072
Chicago/Turabian StyleOz, Furkan, and Kursat Kara. 2020. "Jet Oscillation Frequency Characterization of a Sweeping Jet Actuator" Fluids 5, no. 2: 72. https://doi.org/10.3390/fluids5020072
APA StyleOz, F., & Kara, K. (2020). Jet Oscillation Frequency Characterization of a Sweeping Jet Actuator. Fluids, 5(2), 72. https://doi.org/10.3390/fluids5020072






