Abstract
Developing accurate, efficient, and robust closure models is essential in the construction of reduced order models (ROMs) for realistic nonlinear systems, which generally require drastic ROM mode truncations. We propose a deep residual neural network (ResNet) closure learning framework for ROMs of nonlinear systems. The novel ResNet-ROM framework consists of two steps: (i) In the first step, we use ROM projection to filter the given nonlinear system and construct a spatially filtered ROM. This filtered ROM is low-dimensional, but is not closed. (ii) In the second step, we use ResNet to close the filtered ROM, i.e., to model the interaction between the resolved and unresolved ROM modes. We emphasize that in the new ResNet-ROM framework, data is used only to complement classical physical modeling (i.e., only in the closure modeling component), not to completely replace it. We also note that the new ResNet-ROM is built on general ideas of spatial filtering and deep learning and is independent of (restrictive) phenomenological arguments, e.g., of eddy viscosity type. The numerical experiments for the 1D Burgers equation show that the ResNet-ROM is significantly more accurate than the standard projection ROM. The new ResNet-ROM is also more accurate and significantly more efficient than other modern ROM closure models.
1. Introduction
Many scientific and engineering applications, such as weather forecasting, ocean modeling, and cardiovascuar flow simulation, can often be represented by multiscale systems of ordinary differential equations (ODE) in high-dimensional modal spaces. The analysis and high-fidelity simulation of such systems can be very expensive even on high-performance computing systems. Consequently, using the full order model (FOM) for such simulations can be impractical for time critical applications, such as flow control and parameter estimation. To alleviate the computation burden of the FOM simulation, reduced order models (ROMs) have been successfully used.
ROMs seek a low-dimensional approximation of the FOM with orders of magnitude reduction in computational cost. The classical projection based ROM approach is first to construct a low dimensional space using data-driven reduction methods, such as proper orthogonal decomposition (POD) or dynamical modal decomposition (DMD). The ROM dynamics can be obtained via Galerkin projection of the FOM onto the reduced space [1,2,3,4,5].
The Galerkin projection reduced order model (GP-ROM) can be very efficient and relatively accurate for many systems [3,4]. There are, however, systems (e.g., convection-dominated fluid flows) for which the GP-ROM can generate inaccurate approximations. There are several approaches to address this inaccuracy (see, e.g., [6,7,8,9]). In this paper, we focus on one of the main reasons for this inaccuracy: the ROM closure problem, i.e., modeling the interaction between the GP-ROM modes and the discarded modes. Indeed, due to the inherently drastic mode truncation required in realistic settings, the dimension of the GP-ROM space is too low to resolve the complex nonlinear interactions of the fluid system [1,2,10,11]. GP-ROMs that do not include a ROM closure model can yield inaccurate results, often in the form of spurious numerical oscillations [1,2,12,13]. Endowing GP-ROM with closure models could extend the applicability of GP-ROM in many fluid mechanics applications, such as flow control, climate modeling, and weather forecasting [1,2].
ROM closure models for nonlinear systems have been proposed in, e.g., [14,15,16,17,18,19,20,21,22,23,24]. The vast majority of the current ROM closure models aim at mitigating the numerical instability observed in GP-ROMs that do not include a closure model. Some of these ROM closure models use stabilization techniques that have been developed in standard discretization methods (e.g., in the finite element community) [25,26,27]. Other ROM closure models have imported ideas developed in standard CFD methodologies, e.g., large eddy simulation (LES) [1,24,28,29]. The overwhelming majority of the current ROM closure models can be categorized as stabilization techniques (for a notable exception, see the approximate deconvolution ROM closure model [28] that uses a mathematical framework inspired from image processing).
This is in stark contrast with classical LES, where a plethora of closure models have been proposed over the years. The main difference between ROM closure and LES closure is that the latter has been entirely built around physical insight from the statistical theory of turbulence (e.g., energy cascade and Kolmogorov’s theory), which is generally posed in the Fourier setting [30,31]. This physical insight is generally not available in the ROM setting (see, however, [32] for initial steps). Thus, current ROM closure models have generally been deprived of this powerful methodology that represents the core of most LES closure models.
We believe that machine learning represents a natural solution for ROM closure modeling. Indeed, since physical insight cannot be easily extended to the ROM setting, available data and machine learning can be utilized instead to develop ROM closure models.
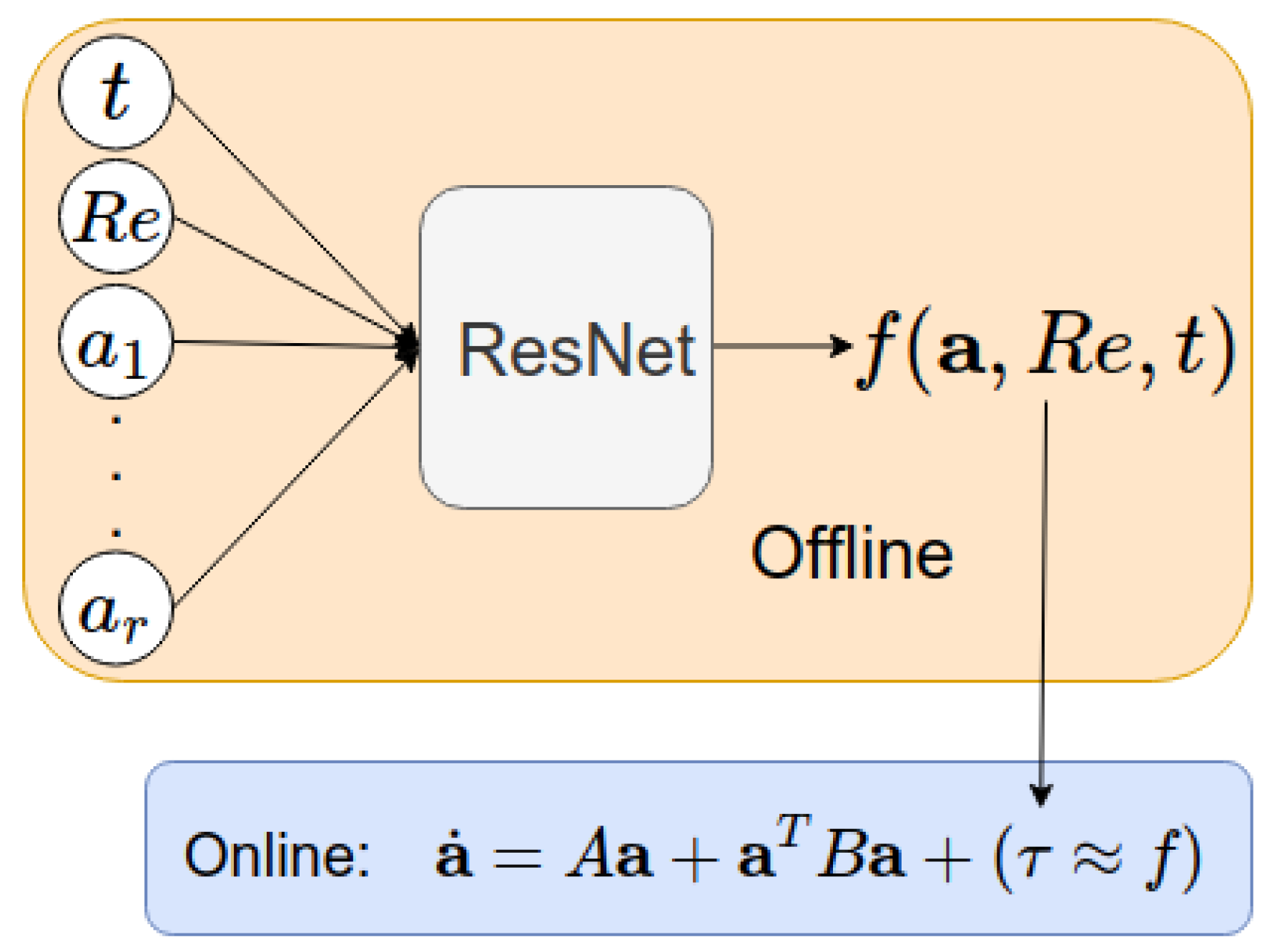
We propose a novel ROM closure modeling framework that is constructed by using available data and deep residual neural network (ResNet) (for details, see, e.g., [33,34,35,36,37]). The resulting ROM, which we call the residual neural network ROM (ResNet-ROM), is schematically illustrated in (1) and Figure 1 (see Section 3 for details). We emphasize that, in the new ResNet-ROM framework, data is used only to complement classical physical modeling (i.e., only in the closure modeling component) [29,38], not to completely replace it [39]. Thus, the resulting ResNet-ROM combines the strengths of both physical and data-driven modeling.
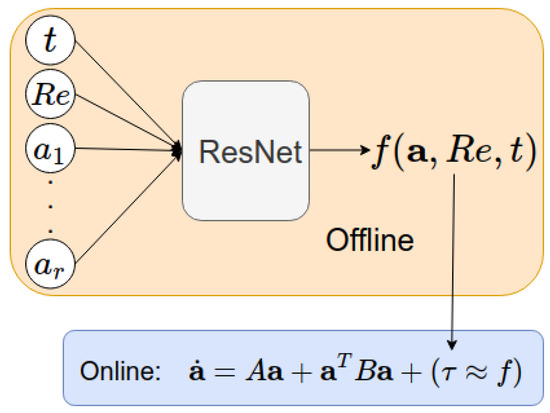
Figure 1.
Flow chart of the new ResNet-ROM.
The main contributions of this paper can be summarized as follows:
- A novel ROM closure learning framework centered around deep neural networks.
- A hybrid framework that synthesizes the strengths of physical modeling and data-driven modeling.
- Very good performance in numerical tests, in both the reconstructive and the predictive regime.
- Significant improvement in numerical accuracy compared with state of the art ROM closure models.
Machine learning has recently been utilized to construct ROM closure models (see, e.g., [22,38,40,41,42]). The ROM closure model proposed in [22] is similar to the new ResNet-ROM. There are, however, two major differences between the two ROM closure models: The first difference is that the ROM closure model in [22] uses FOM data to model both the linear and the nonlinear terms in the underlying equations (see Section 5.1 in [22]). In contrast, in the LES spirit [31], the ResNet-ROM models only the nonlinear terms (see Algorithm 1). One motivation for modeling only the nonlinear terms is given in the theoretical and numerical investigation in [43], where it was shown that the contribution of the linear terms to the ROM closure term (i.e., the commutation error) is not significant in convection-dominated problems, such as those we consider in this study. The second major difference between the ROM closure model in [22] and the ResNet-ROM is the machine learning approach used to construct the ROM closure model: Bayesian regularization and extreme learning machine approaches are used in [22], whereas a deep residual neural network (ResNet) is used to construct the ResNet-ROM.
2. Reduced Order Model
To construct the novel ResNet-ROM framework, we use the Navier-Stokes equations (NSE) for incompressible fluid flows:
which are defined on a spatial domain and on the time interval . In the NSE (2), is the velocity, p the pressure, and the Reynolds number. The ROM basis , where r is small, represents the large, energy containing structures in the flow, and is obtained by using available numerical or experimental data and, e.g., the POD or DMD methods [1,3,4]. The ROM velocity approximation is defined as
where are the sought time-varying coefficients. To determine these coefficients, we use a Galerkin procedure. We replace in (2) with the ROM approximation (3), we take the inner product between the resulting system and each ROM basis function , and then we integrate by parts:
To derive the above equation, we assumed that the ROM velocity modes are perpendicular to the discrete pressure space, which is the case if standard mixed FEs (e.g., Taylor-Hood) are used for the snapshot creation [1,29]. Using (3), we obtain the standard Galerkin projection ROM (GP-ROM):
which can be written componentwise as follows:
where and .
3. Closure Learning
3.1. Residual Neural Network (ResNet)
Deep residual neural network (ResNet) has been first introduced for image recognition in [33]. ResNet has been widely studied and applied in many supervised learning tasks. Recent mathematical understanding of deep ResNet has been achieved in the ODE representation of ResNet; for a comprehensive introduction, see, e.g., [35,36,37,44].
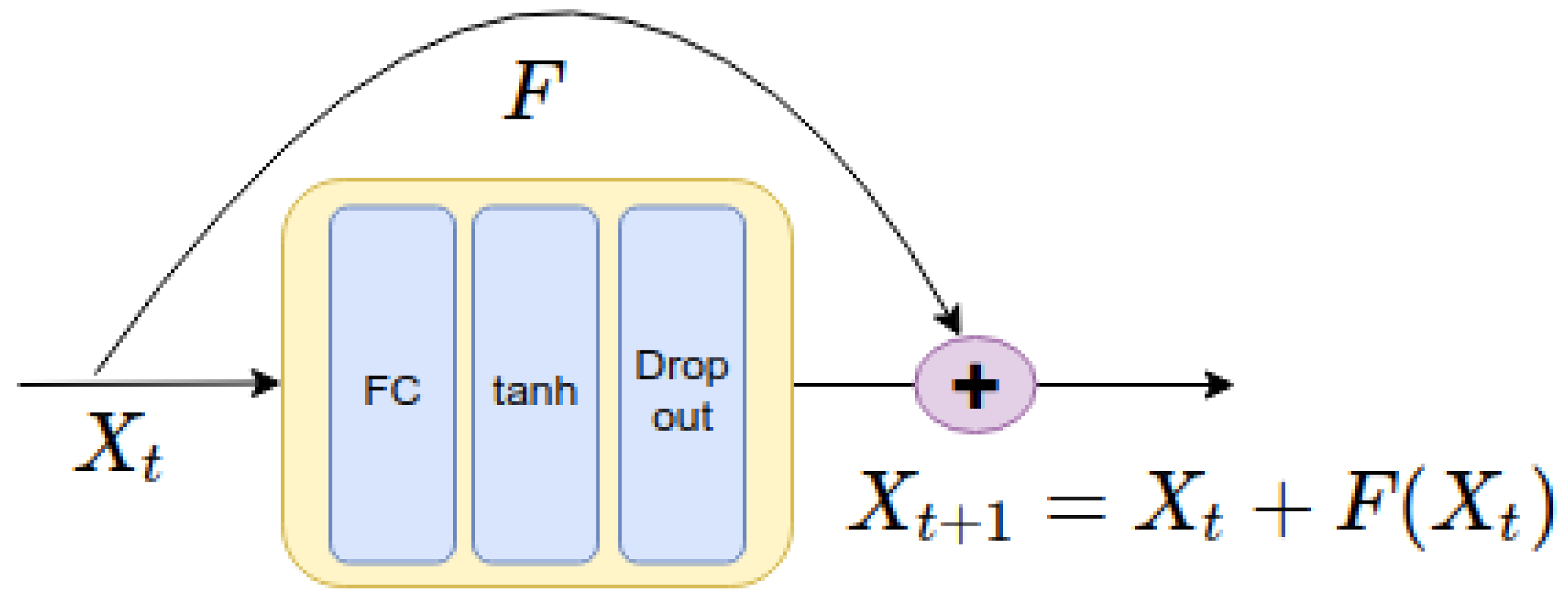
To construct the novel ResNet-ROM framework, we consider the ResNet model, which is illustrated in Figure 2.
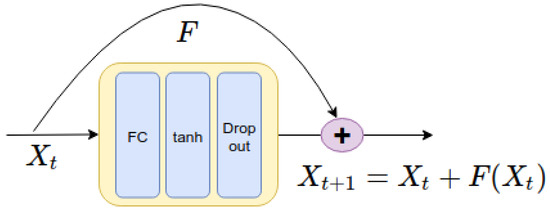
Figure 2.
ResNet block used in our training. Each ResNet block consists of a flatten fully connected layer with a tanh activation function, followed by a drop out layer to prevent overfitting. 128 neurons and 5% drop out rate are used.
The input values of forward propagation in the ResNet are given by
where N is the number of layers in the network architecture, and is the output from each ResNet block at time t. and are the weight matrix and bias at each layer, respectively. The ResNet propagation starts from step with the nonlinear activation function tanh. The initial input layer for the network is . For a standard ResNet in image classification, a convolution layer (CNN) is often included in a residual block. In our work, we use a simplified version of the ResNet that does not include CNN.
3.2. ROM Closure Modeling
In realistic nonlinear systems (e.g., convection-dominated flows), current GP-ROMs of the form (4) generally yield inaccurate results, often in the form on numerical instabilities. This inaccurate behavior is due to the fact that, in order to maintain a low computational cost, GP-ROMs are constructed with a drastically truncated ROM basis , where r is generally small (e.g., ). In realistic nonlinear systems, this extreme truncation cannot capture the complex nonlinear interactions among the various degrees of freedom of the system. Thus, current GP-ROMs are computationally efficient, but numerically inaccurate. To alleviate this inaccurate behavior, GP-ROMs are often supplemented with a ROM closure model [1,24], i.e., a model for the important interactions between the ROM basis and the discarded ROM modes , where R is the dimension of the input data. For example, for the NSE, the standard GP-ROM (4) is generally modified as follows:
where is a ROM closure model that represents the interactions between the ROM modes and the discarded modes.
We emphasize that the same closure problem needs to be addressed when classical numerical discretization schemes (e.g., finite element or spectral methods) are used in the numerical simulation of turbulent flows. In those settings, classical discretizations schemes are used in inherently under-resolved regimes (i.e., they use coarse meshes or too few spectral modes). To ensure the relative accuracy of these under-resolved simulations, various types of closure models for the unresolved (e.g., subgrid-scale) information are generally utilized. These closure models are central to, e.g., large eddy simulation (LES) [31], one of the main approaches to the numerical simulation of turbulent flows. The vast majority of LES closure models have been constructed by using physical insight from Kolmogorov’s statistical theory of turbulence. The concept of energy cascade is central in the development of LES closure models. The energy cascade states that energy enters the system at the large scales, is transferred to smaller and smaller scales through nonlinear interactions, and is dissipated at the smallest scale (i.e., the Kolmogorov’s scale). Thus, most LES closure models (e.g., of eddy viscosity type) aim at recovering the energy cascade displayed by the original system (i.e., the NSE).
This physical insight cannot be easily extended to the ROM setting (see, however, [32] for a preliminary numerical investigation). Thus, current ROM closure models have generally been deprived of this powerful methodology that represents the main tool in the development of most LES closure models.
3.3. ROM Closure Learning
Our vision is that machine learning represents a natural approach for constructing ROM closure modeling. Indeed, since physical insight cannot generally be used in a ROM setting, data and machine learning can be utilized instead to develop ROM closure models. Furthermore, data is used only to construct the ROM closure model; the other ROM operators are built by using the classical Galerkin projection. Thus, data and machine learning complement (instead of replace) physical based modeling, yielding a hybrid framework that synthesizes the strengths of both approaches [17,18,22,27,29,42,45,46,47,48].
In this section, we propose a novel ROM closure modeling framework that is constructed by using available data and the ResNet approach described in Section 3.1. The resulting ROM, which we call the residual neural network ROM (ResNet-ROM), is schematically illustrated in (1) and Figure 1, and is summarized in Algorithm 1.
To obtain the explicit formula (11) in Algorithm 1, we develop a large eddy simulation ROM (LES-ROM) framework [24,28]: First, we filter the high-resolution (R-dimensional) ROM approximation of the NSE with a low-pass ROM spatial filter, denoted by overbar in (11). In this paper, as a ROM spatial filter, we use the ROM projection onto the space spanned by the first r ROM modes [29,48] (see [28] for an alternative ROM spatial filter): For a given , the ROM projection seeks such that
where denotes the inner product. The resulting filtered equations can be cast within a variational multiscale (VMS) framework [49], yielding a two-scale VMS-ROM [50]. Equation (11) represents the explicit VMS-ROM formula for the ROM closure term in(10). In the two-scale VMS-ROM [50], the ROM closure model is developed in two steps. First, an ansatz is used to approximate the ROM closure term: . Then, FOM data for in the training time interval is used to solve a least squares problem to determine the optimal entries in and . In the new ResNet-ROM, we construct the ROM closure model in a fundamentally different way. Instead of making an ansatz on the structural form of the ROM closure term (as in the two-scale VMS-ROM [50]), in Algorithm 1 we consider a general structural formulation and use the ResNet approach to construct the ROM closure model. To this end, in (6), we make the following choices: The initial layer contains the Reynolds number (), the current time (t), and the current ROM coefficients in (3) (), i.e., . The final output layer provides an approximation for the closure term, i.e., . The optimization problem associated with this ResNet is given by
where the regularizer R penalizes undesirable parameters and can prevent overfitting, is the output from the neural network, W and b are weights in the network, is the Frobenius norm, and is a hyperparameter for the regularization to prevent overfitting [36,37]. The minimization problem (9) is over the parameters defining the structural form of the function f used to define .
| Algorithm 1 ResNet-ROM |
|
4. Numerical Experiments
4.1. Implementation
As a test problem for our new approach, we use the 1D Burgers equation, which has been used to test new ROM ideas in simplified settings [29,51,52]:
where, for consistency with the notation used for the NSE, the diffusion parameter is denoted as . In our numerical tests, is the computational domain and the time domain is . We use the same initial conditions as those utilized in [29,51,52]: , . These initial conditions yield a steep internal layer that is difficult to capture in the convection-dominated regime that we consider [29,51,52]. We first use a piecewise linear finite element discretization to generate the FOM solution. To this end, we utilize a uniform mesh with grid points (which yields a meshsize ) and the forward Euler method with for the time discretization. To construct the ROM basis, we collect 101 snapshots sampled from . We build the neural network in PyTorch and we train the ROM closure model with a 6 block ResNet with the common Adam optimizer [53]. We perform all the computational experiments on a Linux system laptop with Nvidia Geforce GTX GPU hardware.
4.2. Reconstruction
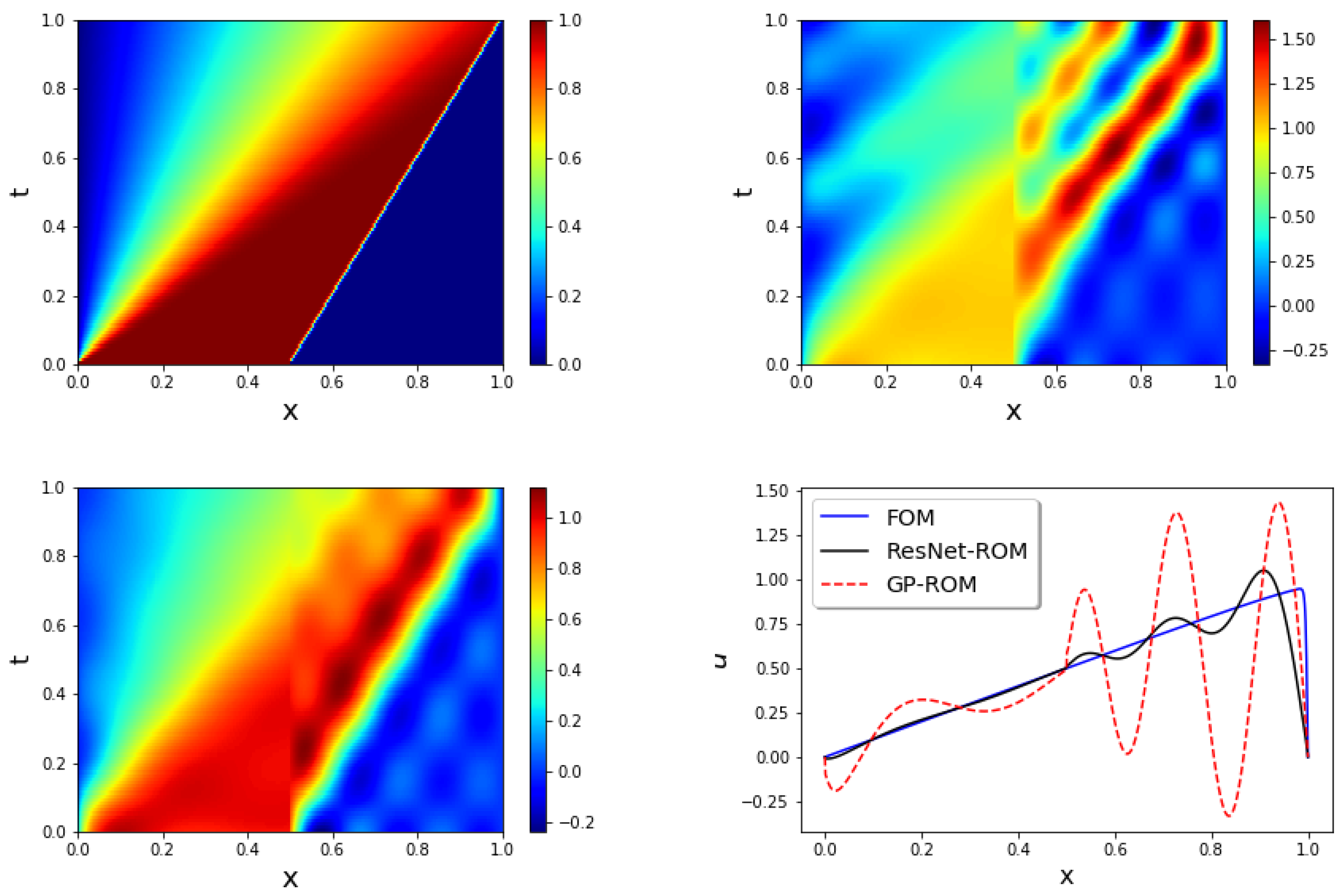
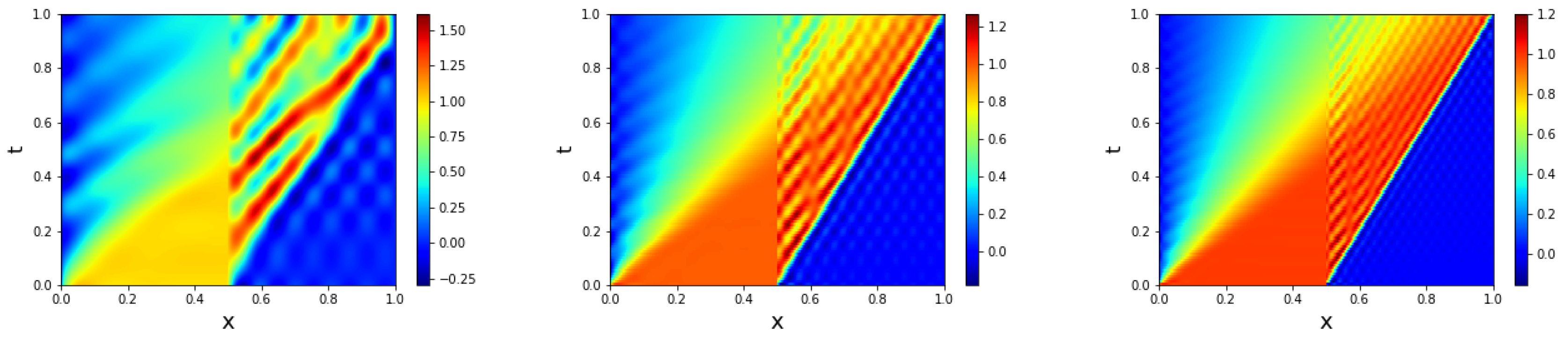
In this section, we consider the reconstructive regime, i.e., we test the ROMs at the same as the at which the ROMs are constructed. We choose in (14) and we use basis functions in all ROMs. In Figure 3, we plot the solutions of the FOM (top left), GP-ROM (top right), and ResNet-ROM (bottom left). When compared with the FOM data, the ResNet-ROM solution is significantly more accurate than the standard GP-ROM solution. In Figure 3, we also plot the FOM, GP-ROM, and ResNet-ROM solutions at the final time step (i.e., at ). This plot shows that the closure term in the ResNet-ROM plays an important role in stabilizing the ROM approximation. Indeed, the GP-ROM solution displays large, spurious numerical oscillations. These oscillations are dramatically decreased in the ResNet-ROM solution.
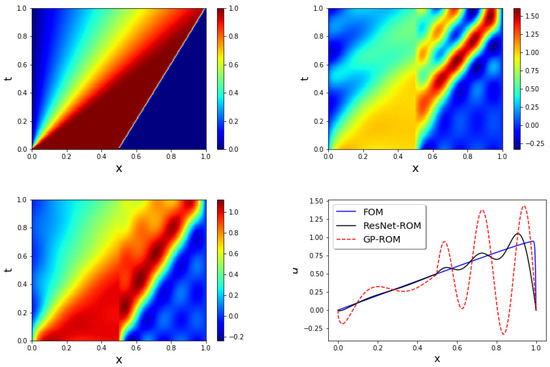
Figure 3.
Reconstructive regime, : FOM (top left), GP-ROM (top right), ResNet-ROM (bottom left), and final time solution for all three simulations (bottom right). ResNet-ROM yields the most accurate solution.
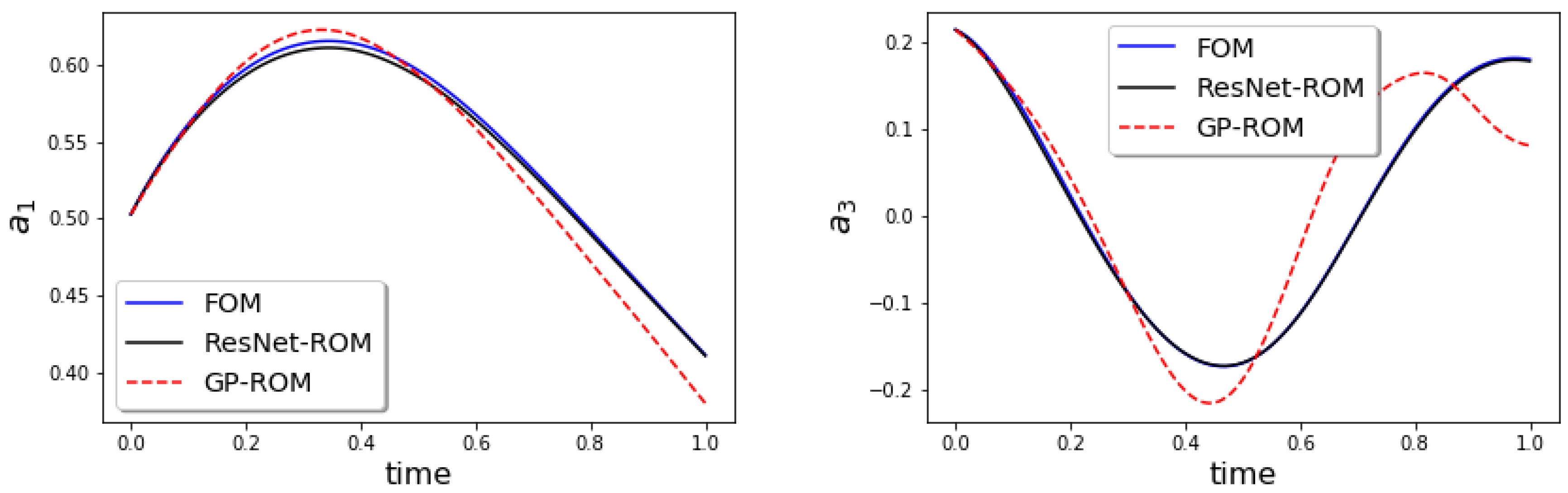
In Figure 4, we plot the the time evolution of the ROM coefficients a for the FOM, GP-ROM, and ResNet-ROM. The plots show that the ResNet-ROM is significantly more accurate than the standard GP-ROM.
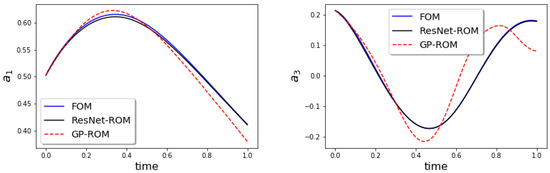
Figure 4.
Reconstructive regime, : Time evolution of ROM coefficients and for FOM, GP-ROM, and ResNet-ROM. ResNet-ROM yields the most accurate solution.
4.3. Prediction
To study the robustness of the new ResNet-ROM, we test its predictability, i.e., we train the ResNet-ROM closure term on data from multiple and we then test the ResNet-ROM to predict the ROM dynamics at different . The training data space is sampled at , and the test data contains . Note that the solution of the Burgers equation is affected by . Small values yield a slow movement of the sharp internal layer, while large values can speed up this movement.
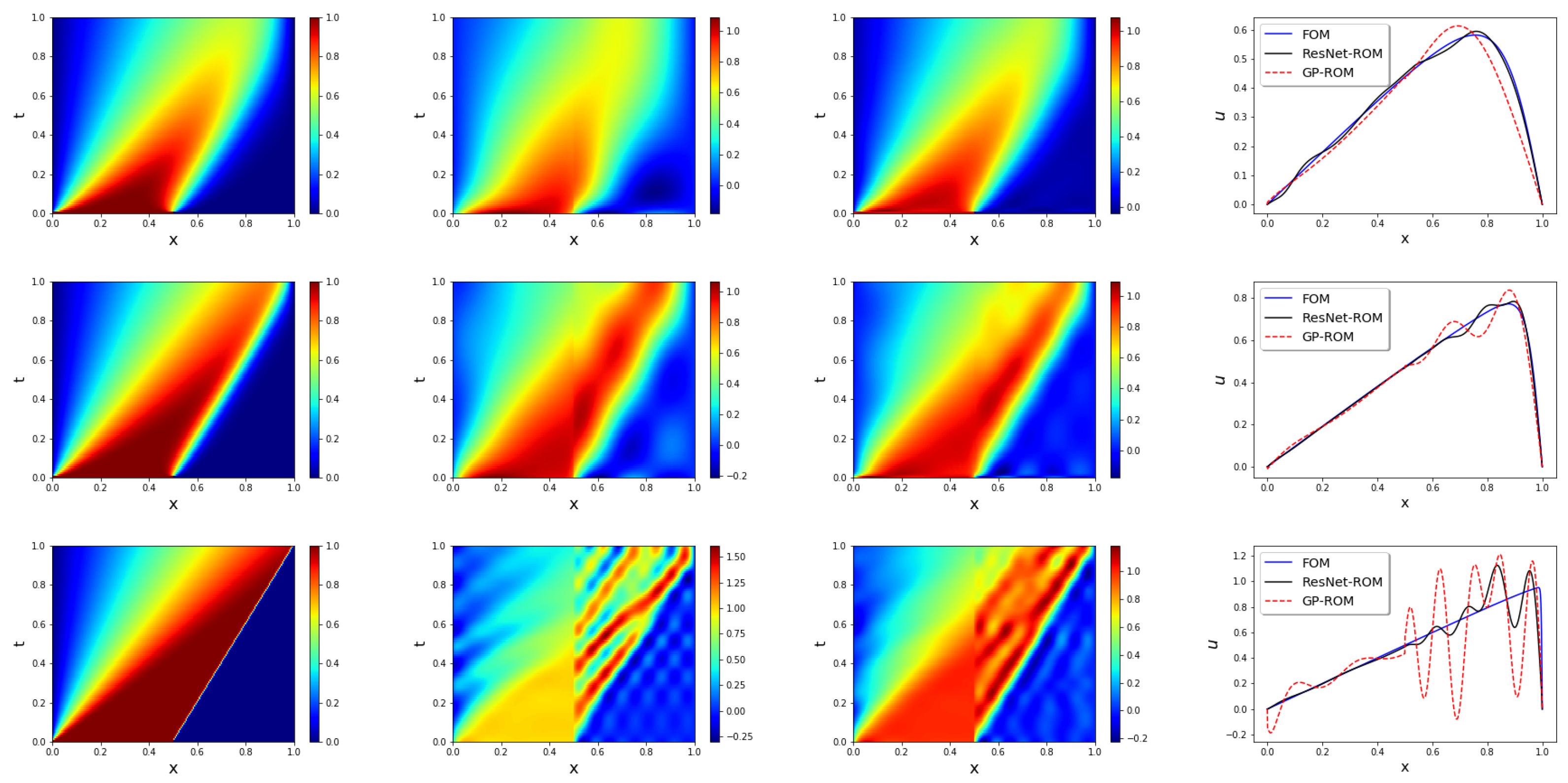
In Figure 5, for , and 1200 (which are different from the training values), we plot the solutions for the DNS (first column), GP-ROM (second column), ResNet-ROM (third column), and final time solution for all three simulations (fourth column). These plots show that the ResNet-ROM is consistently the most accurate ROM, especially for the largest value. In Figure 5, we also plot the FOM, GP-ROM, and ResNet-ROM solutions at the final time step (i.e., at ). These plots show that the closure term in the ResNet-ROM plays an important role in stabilizing the ROM approximation.
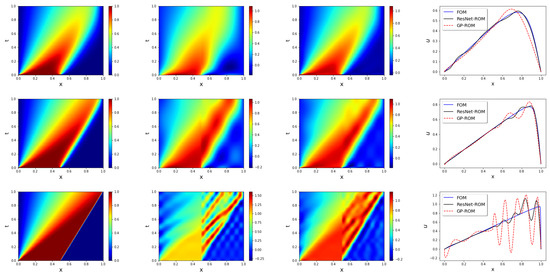
Figure 5.
Predictive regime: ROMs are trained on data from and are tested at (first row), (second row), (third row). Results presented for FOM (first column), GP-ROM (second column), ResNet-ROM (third column), and final time solution for all three simulations (fourth column).
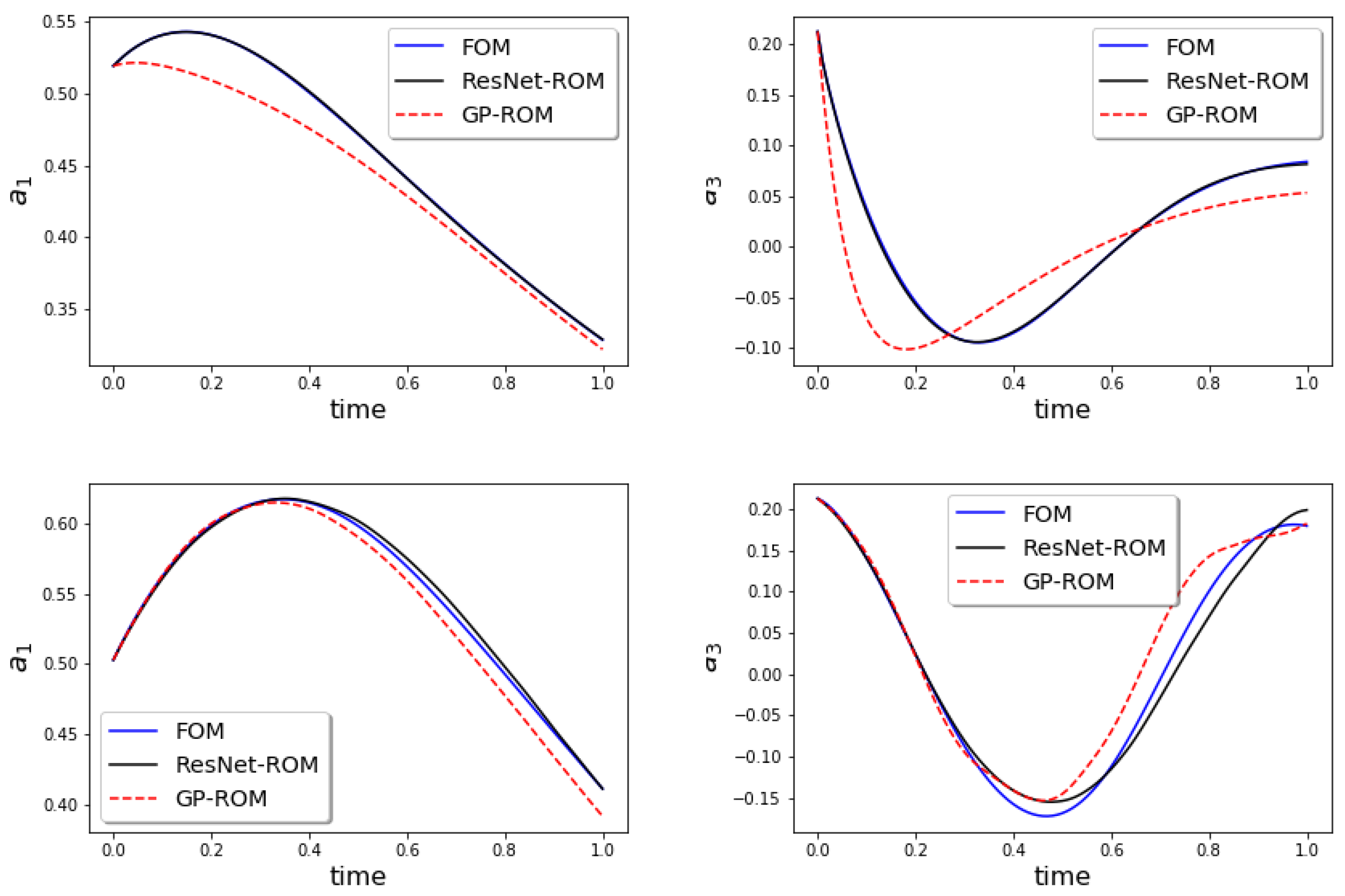
In Figure 6, we plot the the time evolution of the ROM coefficients a for the FOM, GP-ROM, and ResNet-ROM. These plots show that the ResNet-ROM is significantly more accurate than the standard GP-ROM.
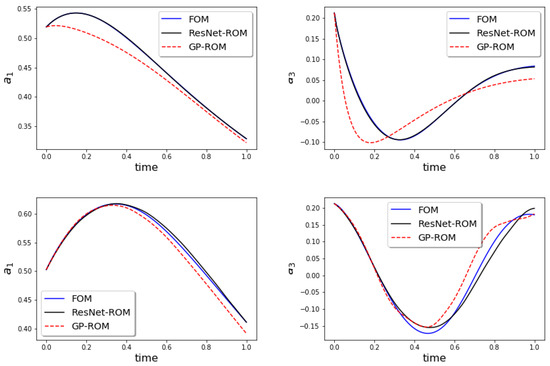
Figure 6.
Predictive regime: Time evolution of ROM coefficients and for FOM, GP-ROM, and ResNet-ROM. Results for (top) and (bottom). ResNet-ROM yields the most accurate solution.
Overall, we draw the same conclusion as in the reconstructive regime (Section 4.2): In all cases, the ResNet-ROM is significantly more accurate than the standard GP-ROM in the predictive regime.
4.4. Comparison
In this section, in the numerical simulation of the Burgers equation, we also make a numerical comparison between the new ResNet-ROM and several modern ROM closure models: the POD artificial viscosity model (POD-AV) [51], the POD Smagorinsky model (POD-L) [54], the evolve-then-filter ROM (EF-ROM) [55], the approximate deconvolution ROM (AD-ROM) [28], and the data-driven filtered ROM (DDF-ROM) [29].
In Table 1, we list the errors of the ResNet-ROM and the other closure models. These results show that the ResNet-ROM error is at least an order of magnitude lower than the errors of the other ROM closure models.

Table 1.
errors of the new ResNet-ROM and other closure models.
For the online ResNet-ROM integration, we use the scipy package with the built-in integration function odeint. In the online stage, the new ResNet-ROM is more efficient than the other ROM closure models: The online CPU time of the ResNet-ROM is s, whereas the online CPU times of the EF-ROM, AD-ROM, and DDF-ROM are and s, respectively [28,29,55].
The CPU time of the offline training of the new ResNnet-ROM is s for the current dataset with 10,000 epochs (iterations). Thus, even though the online cost for ResNet-ROM is lower than the online cost of the other closure models that are compared in this paper, the neural network training cost of ResNet-ROM is much higher than the offline training cost of the other ROM closure models [28,29,55].
4.5. Sensitivity
In this section, we perform a sensitivity study of the new ResNet-ROM with respect to two parameters: (i) the hyperparameter used in the regularization of the neural network training; and (ii) the meshsize h used in the snapshot generation. We also investigate the potential improvement in GP-ROM accuracy when the number of snapshots and the dimension r of the ResNet-ROM are increased.
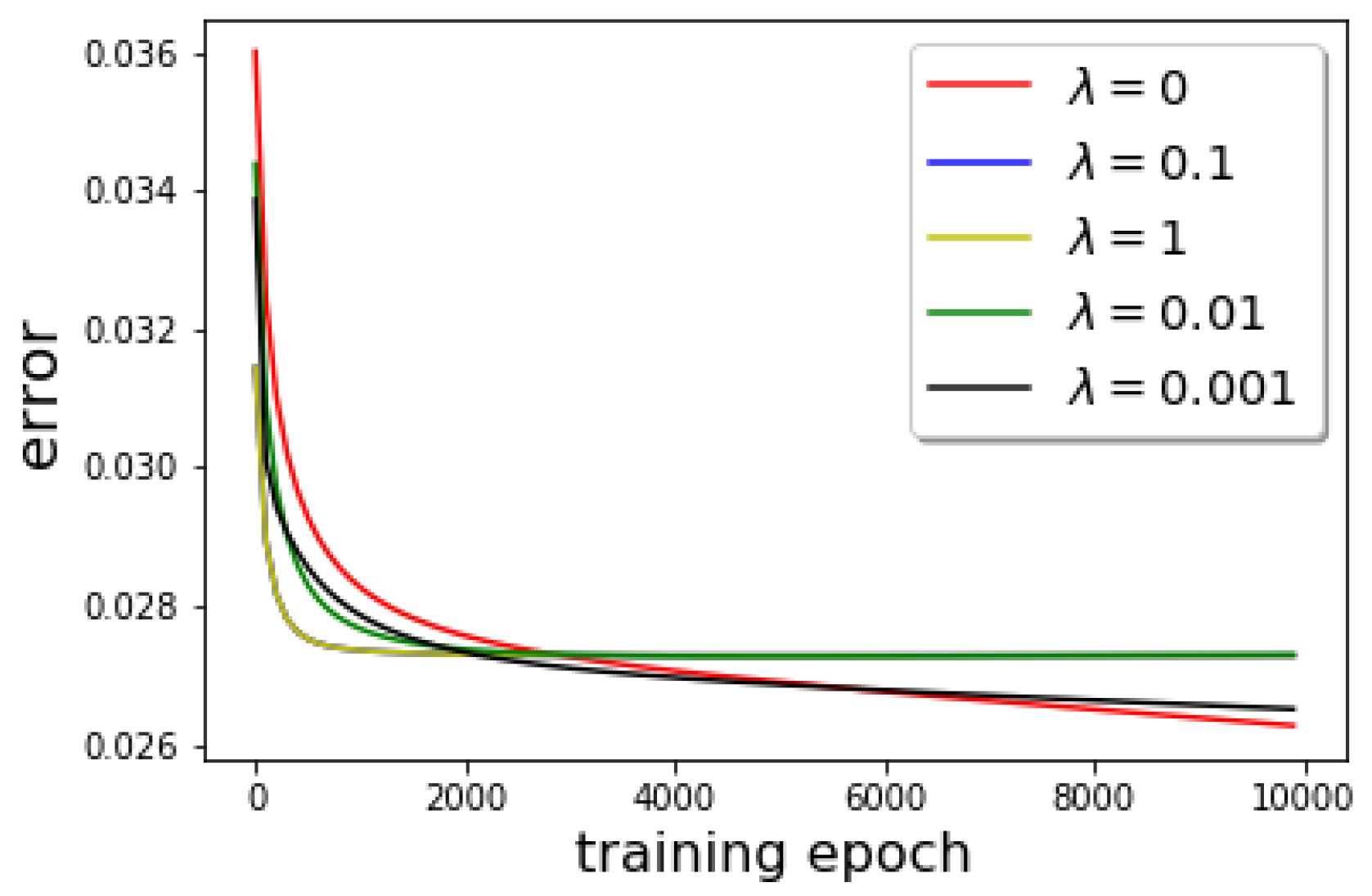
The parameter is an regularization parameter used in the neural network training to prevent overfitting. In our numerical simulations, we pick the parameter based on the validation error performance in the training phase. In our training dataset for , we test the following parameter values: . In Figure 7, we plot the ResNet-ROM error for different parameter values. The plot in Figure 7 shows that the ResNet-ROM is not very sensitive to the hyperparameter . Thus, in our numerical tests, we fix with 10,000 epochs (iterations) in the Resnet-ROM training.
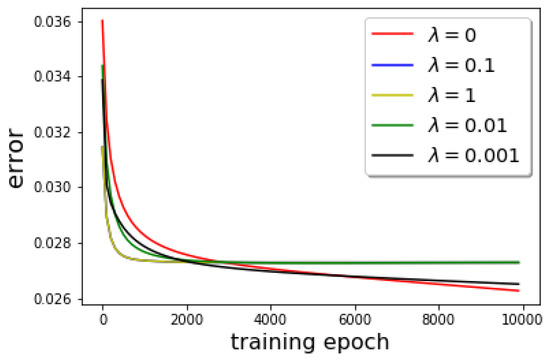
Figure 7.
Validation error performance for different values of the regularization parameter .
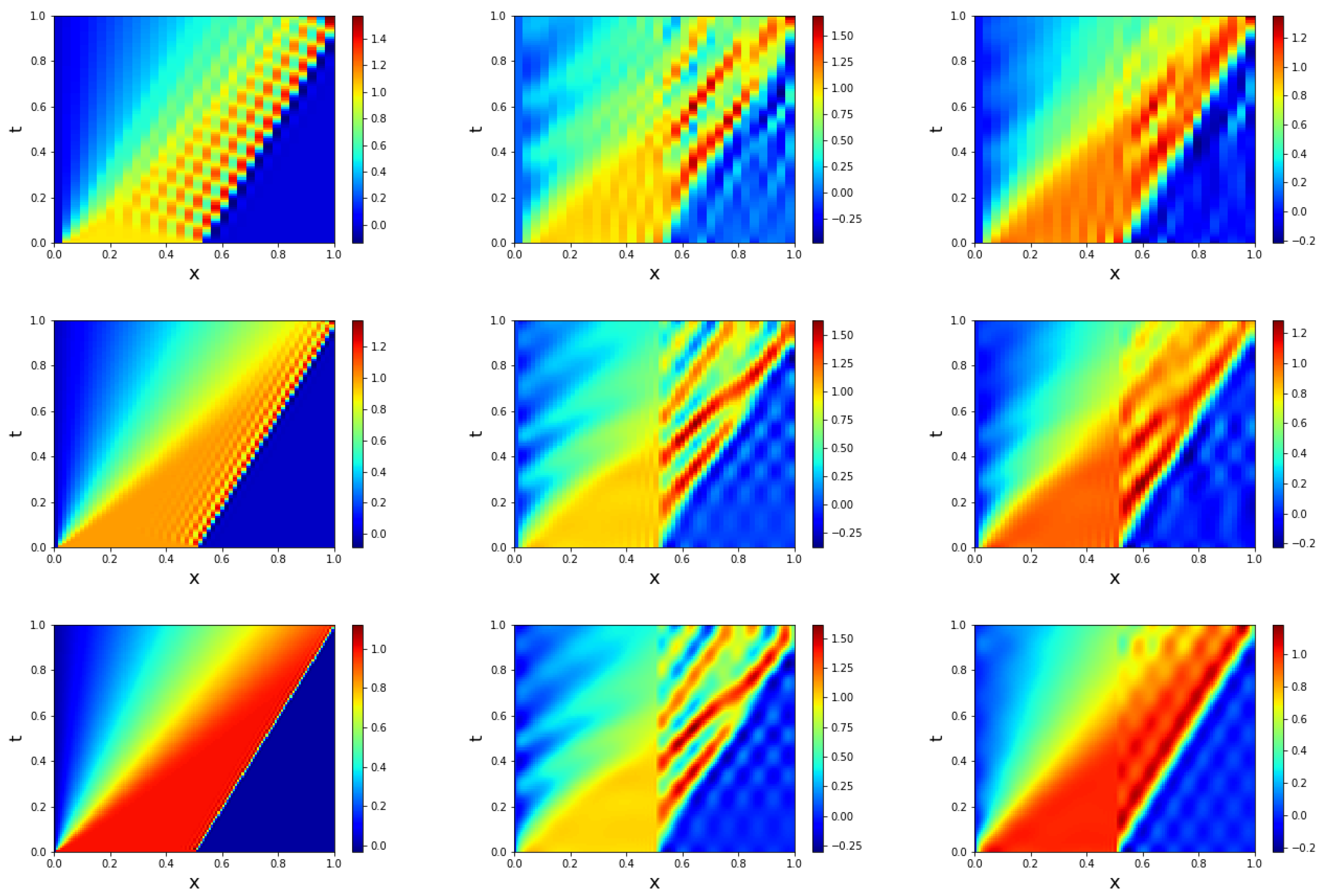
We also perform a sensitivity study for the new ResNet-ROM with respect to the meshsize h. In Figure 8, for the reconstructive regime and , we plot the FOM, GP-ROM, and ResNet-ROM results for three coarse meshsize values. The plots in Figure 8 show that the ResNet-ROM is still significantly more accurate than the GP-ROM. In the predictive regime, however, both the ResNet-ROM and the GP-ROM yield inaccurate results for these three coarse meshes. The relationship between the FOM mesh utilized to generate the snapshots and the ROM accuracy is subject of current research (see, e.g., [56,57]) and should be further investigated for the new ResNet-ROM.
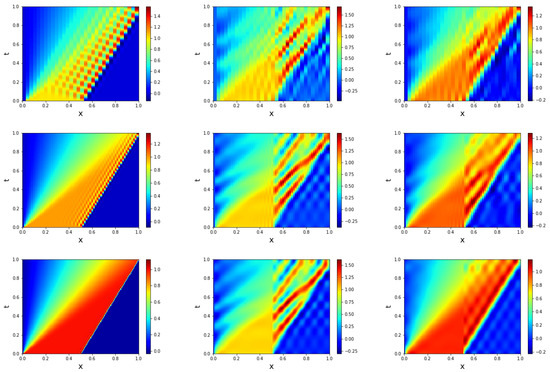
Figure 8.
Reconstructive regime, : FOM (first column), GP-ROM (second column), and ResNet-ROM (third column), for meshsizes (first row), (second row), and (third row). ResNet-ROM yields the most accurate solution.
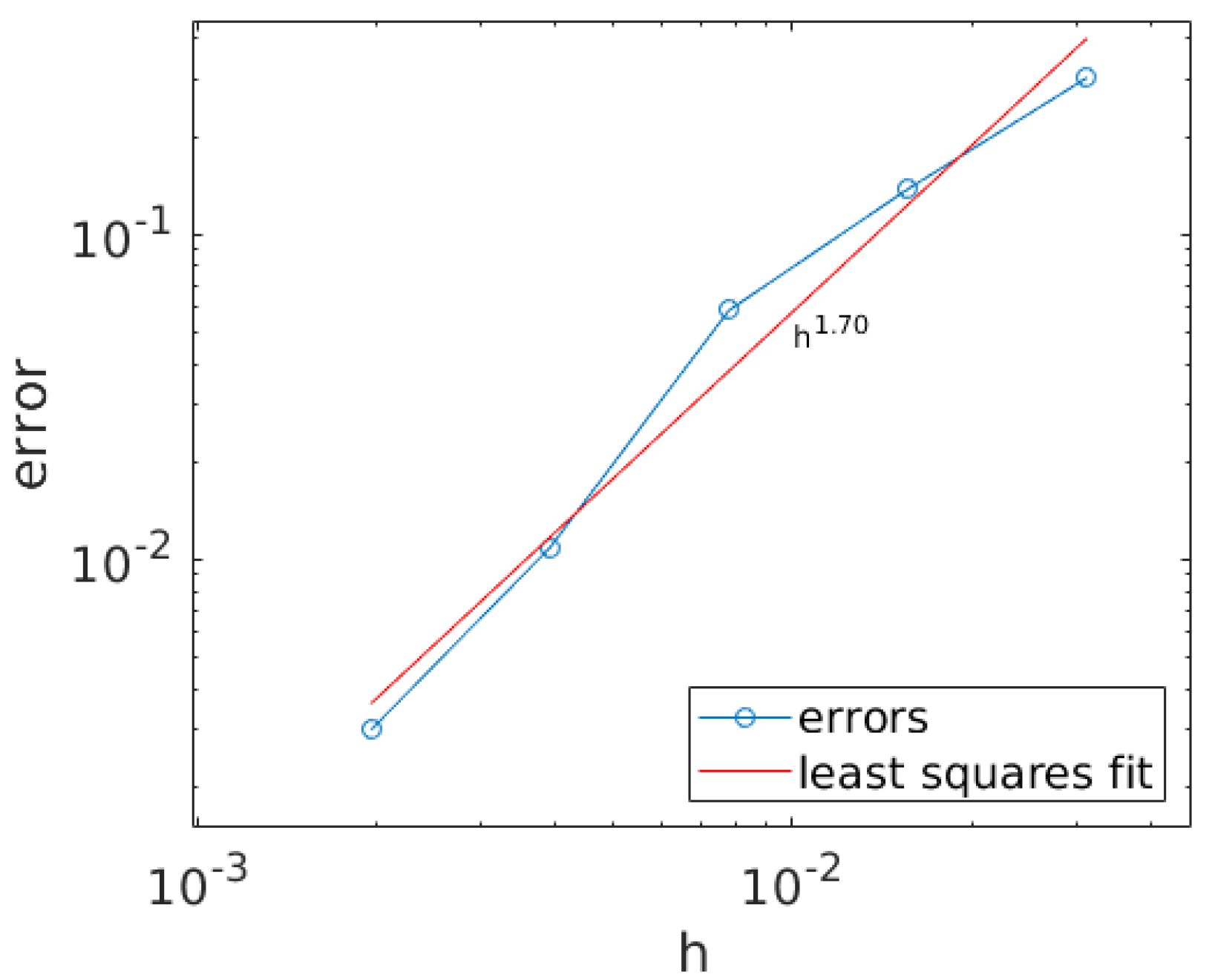
We also investigate the ResNet-ROM rate of convergence with respect to the meshsize h. To this end, we fixed the ResNet-ROM dimension at and the time-step size at . The plot in Figure 9 shows that the rate of convergence (obtained with a least squares fit) is about , which is an acceptable approximation to the theoretical rate of convergence of .
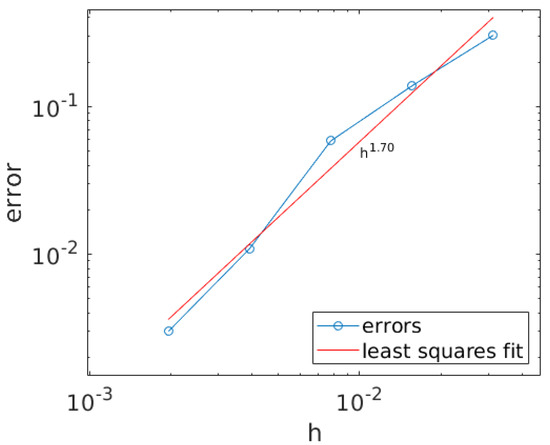
Figure 9.
The ResNet-ROM rate of convergence with respect to the meshsize h.
Finally, we investigate the potential improvement in GP-ROM accuracy when the number of snapshots and the dimension r of the ResNet-ROM are increased.
First, we collect the maximum number of snapshots that are available from the FOM simulations in the training interval. That is, we collect 1001 snapshots, which yield a snapshot matrix whose rank is 251. Comparing the left plot in Figure 10 (for the highest number of snapshots) with the top right plot in Figure 3 (for the lower number of snapshots), we conclude that increasing the number of snapshots does not seem to improve the ResNet-ROM accuracy.
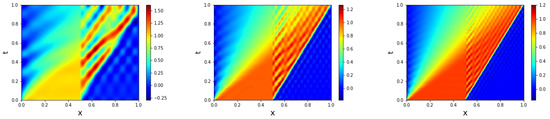
Figure 10.
Reconstructive regime, , GP-ROM results: (left), (middle), and (right).
Next, we increase the GP-ROM dimension. In Figure 10, we plot the GP-ROM results for three r values: , , and . As expected, the GP-ROM accuracy improves as we increase r. We emphasize, however, that the ROM closure models (such as that used in the new ResNet-ROM) are designed to improve the GP-ROM accuracy in under-resolved numerical simulations, i.e., when only a few ROM basis functions can be used, which is often the case in realistic settings [1,2,14,16,17,18,20,21,22,23,25,27,28,29,32,38,40,41,42,46,47,48,50,51,54,58]. As shown earlier, for , the ResNet-ROM is significantly more accurate than the GP-ROM both in the reconstructive and the predictive regimes.
5. Conclusions
In this paper, we used available data and deep residual neural networks (ResNet) to construct a novel reduced order model (ROM) closure for complex nonlinear settings. We emphasize that the ResNet-ROM closure terms are much more general than the phenomenological ansatzes generally used in ROM closure modeling [29]. We tested the novel ResNet-ROM in the numerical simulation of the Burgers equation. For comparison purposes, we investigated the standard Galerkin projection ROM (GP-ROM) and the full order model (FOM). We considered two settings: (i) a reconstructive regime, in which the Reynolds number is the same in the training and testing stages; and (ii) a predictive regime, in which used in the testing regime is different from the used in the training regime. In both regimes, the new ResNet-ROM was consistently more accurate than the standard GP-ROM. Furthermore, the ResNet-ROM was also dramatically more accurate than several other ROM closure models from the literature.
There are several research directions that we plan to pursue: We will test the novel ResNet-ROM on realistic test problems (e.g., 3D turbulent flows) and we will compare it with state of the art closure models. We will also investigate alternative approaches to develop the ROM closure term . Indeed, in this paper we used the ROM projection as a spatial filter in the construction of the ROM closure term . We plan to investigate different ROM spatial filters, such as the ROM differential filter [55]. This alternative ROM filter will yield a different ROM closure term and, therefore, a different ResNet-ROM. Finally, a numerical investigation of alternative machine learning approaches (see, e.g., [22]) could yield improved ROM closure models. Indeed, for the one-dimensional Burgers equation test case considered in this paper, the computational cost of training the ROM closure model with ResNet was acceptable. For more complex settings, however, this computational cost could be much higher. In those cases, neural networks with a lower computational cost could be more effective.
Author Contributions
Conceptualization, X.X., C.W. and T.I.; methodology, X.X., C.W. and T.I.; writing—original draft preparation, X.X.; writing—review and editing, C.W., T.I. All authors have read and agreed to the published version of the manuscript.
Funding
The work of the second author was supported by U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research. The work of the third author was supported by National Science Foundation grant DMS-1821145.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ResNet | Residual Neural Network |
| ROM | Reduced Order Modeling |
| GP-ROM | Galerkin Projection Reduced Order Model |
| POD | Proper Orthogonal Decomposition |
| FOM | Full Order Model |
| LES | Large Eddy Simulation |
| VMS | Variational Multiscale |
| NSE | Navier-Stokes Equations |
References
- Holmes, P.; Lumley, J.L.; Berkooz, G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Noack, B.R.; Morzynski, M.; Tadmor, G. Reduced-Order Modelling for Flow Control; Springer: Berlin/Heidelberg, Germany, 2011; Volume 528. [Google Scholar]
- Hesthaven, J.S.; Rozza, G.; Stamm, B. Certified Reduced Basis Methods for Parametrized Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations: An Introduction; Springer: Berlin/Heidelberg, Germany, 2015; Volume 92. [Google Scholar]
- Mohebujjaman, M.; Rebholz, L.G.; Xie, X.; Iliescu, T. Energy balance and mass conservation in reduced order models of fluid flows. J. Comput. Phys. 2017, 346, 262–277. [Google Scholar] [CrossRef]
- Akkari, N.; Casenave, F.; Moureau, V. Time stable reduced order modeling by an enhanced reduced order basis of the turbulent and incompressible 3D Navier–Stokes equations. Math. Comput. Appl. 2019, 24, 45. [Google Scholar] [CrossRef]
- Cagniart, N.; Maday, Y.; Stamm, B. Model order reduction for problems with large convection effects. In Contributions to Partial Differential Equations and Applications; Springer: Berlin, Germany, 2019; pp. 131–150. [Google Scholar]
- Iollo, A.; Lanteri, S.; Désidéri, J.A. Stability properties of POD–Galerkin approximations for the compressible Navier–Stokes equations. Theoret. Comput. Fluid Dyn. 2000, 13, 377–396. [Google Scholar] [CrossRef]
- Stabile, G.; Hijazi, S.; Mola, A.; Lorenzi, S.; Rozza, G. POD-Galerkin reduced order methods for CFD using finite volume discretisation: Vortex shedding around a circular cylinder. Commun. Appl. Ind. Math. 2017, 8, 210–236. [Google Scholar] [CrossRef]
- Loiseau, J.C.; Brunton, S.L. Constrained sparse Galerkin regression. J. Fluid Mech. 2018, 838, 42–67. [Google Scholar] [CrossRef]
- Noack, B.R.; Stankiewicz, W.; Morzyński, M.; Schmid, P.J. Recursive dynamic mode decomposition of transient and post-transient wake flows. J. Fluid Mech. 2016, 809, 843–872. [Google Scholar] [CrossRef]
- Amsallem, D.; Farhat, C. Stabilization of projection-based reduced-order models. Int. J. Num. Meth. Eng. 2012, 91, 358–377. [Google Scholar] [CrossRef]
- Carlberg, K.; Farhat, C.; Cortial, J.; Amsallem, D. The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 2013, 242, 623–647. [Google Scholar] [CrossRef]
- Baiges, J.; Codina, R.; Idelsohn, S. Reduced-order subscales for POD models. Comput. Methods Appl. Mech. Eng. 2015, 291, 173–196. [Google Scholar] [CrossRef]
- Feppon, F.; Lermusiaux, P.F.J. Dynamically orthogonal numerical schemes for efficient stochastic advection and Lagrangian transport. SIAM Rev. 2018, 60, 595–625. [Google Scholar] [CrossRef]
- Fick, L.; Maday, Y.; Patera, A.T.; Taddei, T. A stabilized POD model for turbulent flows over a range of Reynolds numbers: Optimal parameter sampling and constrained projection. J. Comput. Phys. 2018, 371, 214–243. [Google Scholar] [CrossRef]
- Hijazi, S.; Stabile, G.; Mola, A.; Rozza, G. Data-driven POD-Galerkin reduced order model for turbulent flows. arXiv 2019, arXiv:1907.09909. [Google Scholar]
- Lu, F.; Lin, K.K.; Chorin, A.J. Data-based stochastic model reduction for the Kuramoto–Sivashinsky equation. Phys. D 2017, 340, 46–57. [Google Scholar] [CrossRef]
- Majda, A.J.; Harlim, J. Physics constrained nonlinear regression models for time series. Nonlinearity 2012, 26, 201. [Google Scholar] [CrossRef]
- Rebollo, T.C.; Ávila, E.D.; Mármol, M.G.; Ballarin, F.; Rozza, G. On a certified Smagorinsky reduced basis turbulence model. SIAM J. Numer. Anal. 2017, 55, 3047–3067. [Google Scholar] [CrossRef]
- San, O.; Iliescu, T. A stabilized proper orthogonal decomposition reduced-order model for large scale quasigeostrophic ocean circulation. Adv. Comput. Math. 2015, 41, 1289–1319. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Neural network closures for nonlinear model order reduction. Adv. Comput. Math. 2018, 44, 1–34. [Google Scholar] [CrossRef]
- Stabile, G.; Ballarin, F.; Zuccarino, G.; Rozza, G. A reduced order variational multiscale approach for turbulent flows. Adv. Comput. Math. 2019, 45, 2349–2368. [Google Scholar] [CrossRef]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 237–240, 10–26. [Google Scholar] [CrossRef]
- Bergmann, M.; Bruneau, C.H.; Iollo, A. Enablers for robust POD models. J. Comput. Phys. 2009, 228, 516–538. [Google Scholar] [CrossRef]
- Carlberg, K.; Bou-Mosleh, C.; Farhat, C. Efficient non-linear model reduction via a least-squares Petrov–Galerkin projection and compressive tensor approximations. Int. J. Num. Meth. Eng. 2011, 86, 155–181. [Google Scholar] [CrossRef]
- Parish, E.J.; Wentland, C.; Duraisamy, K. The adjoint Petrov-Galerkin method for non-linear model reduction. arXiv 2018, arXiv:1810.03455. [Google Scholar] [CrossRef]
- Xie, X.; Wells, D.; Wang, Z.; Iliescu, T. Approximate deconvolution reduced order modeling. Comput. Methods Appl. Mech. Eng. 2017, 313, 512–534. [Google Scholar] [CrossRef]
- Xie, X.; Mohebujjaman, M.; Rebholz, L.; Iliescu, T. Data-driven filtered reduced order modeling of fluid flows. SIAM J. Sci. Comput. 2018, 40, B834–B857. [Google Scholar] [CrossRef]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows, 3rd ed.; Scientific Computation; Springer: Berlin, Germany, 2006. [Google Scholar]
- Couplet, M.; Sagaut, P.; Basdevant, C. Intermodal energy transfers in a proper orthogonal decomposition—Galerkin representation of a turbulent separated flow. J. Fluid Mech. 2003, 491, 275–284. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Lu, Y.; Zhong, A.; Li, Q.; Dong, B. Beyond finite layer neural networks: Bridging deep architectures and numerical differential equations. arXiv 2017, arXiv:1710.10121. [Google Scholar]
- Chang, B.; Meng, L.; Haber, E.; Tung, F.; Begert, D. Multi-level residual networks from dynamical systems view. arXiv 2017, arXiv:1710.10348. [Google Scholar]
- Chang, B.; Meng, L.; Haber, E.; Ruthotto, L.; Begert, D.; Holtham, E. Reversible architectures for arbitrarily deep residual neural networks. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2 February 2018. [Google Scholar]
- Maulik, R.; Mohan, A.; Lusch, B.; Madireddy, S.; Balaprakash, P. Time-series learning of latent-space dynamics for reduced-order model closure. arXiv 2019, arXiv:1906.07815. [Google Scholar] [CrossRef]
- Rahman, S.M.; Pawar, S.; San, O.; Rasheed, A.; Iliescu, T. A non-intrusive reduced order modeling framework for quasi-geostrophic turbulence. arXiv 2019, arXiv:11906.11617. [Google Scholar]
- Ahmed, S.E.; San, O.; Rasheed, A.; Iliescu, T. A long short-term memory embedding for hybrid uplifted reduced order models. arXiv 2019, arXiv:1912.06756. [Google Scholar]
- Maulik, R.; Lusch, B.; Balaprakash, P. Reduced-order modeling of advection-dominated systems with recurrent neural networks and convolutional autoencoders. arXiv 2020, arXiv:2002.00470. [Google Scholar]
- San, O.; Maulik, R. Machine learning closures for model order reduction of thermal fluids. Appl. Math. Model. 2018, 60, 681–710. [Google Scholar] [CrossRef]
- Koc, B.; Mohebujjaman, M.; Mou, C.; Iliescu, T. Commutation error in reduced order modeling of fluid flows. Adv. Comput. Math. 2019, 45, 2587–2621. [Google Scholar] [CrossRef]
- Chen, T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural ordinary differential equations. arXiv 2018, arXiv:1806.07366. [Google Scholar]
- Baiges, J.; Codina, R.; Castanar, I.; Castillo, E. A finite element reduced order model based on adaptive mesh refinement and artificial neural networks. Int. J. Numer. Methods Eng. 2019, 121, 588–601. [Google Scholar] [CrossRef]
- Chekroun, M.D.; Liu, H.; McWilliams, J.C. Variational approach to closure of nonlinear dynamical systems: Autonomous case. J. Stat. Phys. 2019, 1–88. [Google Scholar] [CrossRef]
- Lin, K.K.; Lu, F. Data-driven model reduction, Wiener projections, and the Mori-Zwanzig formalism. arXiv 2019, arXiv:1908.07725. [Google Scholar]
- Mohebujjaman, M.; Rebholz, L.G.; Iliescu, T. Physically-constrained data-driven correction for reduced order modeling of fluid flows. Int. J. Num. Methods Fluids 2019, 89, 103–122. [Google Scholar] [CrossRef]
- John, V. Finite Element Methods for Incompressible Flow Problems; Springer: Berlin, Germany, 2016. [Google Scholar]
- Mou, C.; Koc, B.; San, O.; Iliescu, T. Data-driven variational multiscale reduced order models. arXiv 2020, arXiv:2002.06457. [Google Scholar]
- Borggaard, J.; Iliescu, T.; Wang, Z. Artificial viscosity proper orthogonal decomposition. Math. Comput. Model. 2011, 53, 269–279. [Google Scholar] [CrossRef]
- Kunisch, K.; Volkwein, S. Galerkin proper orthogonal decomposition methods for parabolic problems. Numer. Math. 2001, 90, 117–148. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Akhtar, I.; Wang, Z.; Borggaard, J.; Iliescu, T. A new closure strategy for proper orthogonal decomposition reduced-order models. J. Comput. Nonlinear Dyn. 2012, 7, 39–54. [Google Scholar] [CrossRef]
- Wells, D.; Wang, Z.; Xie, X.; Iliescu, T. An evolve-then-filter regularized reduced order model for convection-dominated flows. Int. J. Num. Methods Fluids 2017, 84, 598–615. [Google Scholar] [CrossRef]
- Caiazzo, A.; Iliescu, T.; John, V.; Schyschlowa, S. A numerical investigation of velocity-pressure reduced order models for incompressible flows. J. Comput. Phys. 2014, 259, 598–616. [Google Scholar] [CrossRef]
- Giere, S.; Iliescu, T.; John, V.; Wells, D. SUPG reduced order models for convection-dominated convection-diffusion-reaction equations. Comput. Methods Appl. Mech. Eng. 2015, 289, 454–474. [Google Scholar] [CrossRef]
- Wang, Z. Reduced-Order Modeling of Complex Engineering and Geophysical Flows: Analysis and Computations. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2012. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).