Gravitational Effects in the Collision of Elasto-Viscoplastic Drops on a Vertical Plane

Abstract

The collision of drops in a solid substrate is an interesting problem with several practical applications. When the drop is made of a complex fluid the problem presents numerical challenges due to the interaction of the mechanical properties and the free surface approach. In the present work, we solve the numerical problem of elasto-viscoplastic drops colliding in vertical plane. The free surface evolution is handled by a Marker-And-Cell method combined with a Front-Tracking interface representation. Special emphasis is given to the gravitational effects by means of exploring the Froude number. We were able to find a rich variety of outputs that can be classified as sticking, sliding, bouncing, detaching, and slithering.

1. Introduction

The study of liquid drops on a solid substrate is an important problem due to the number of industrial applications such as spray-cooling of hot surfaces, inkjet printing, agriculture pesticides, spray coating, precision molten drop deposition, fire suppression, internal combustion engines, and others. Depending on the application considered, the focus of the investigation can be very different. While in some studies, the collision of the drop is a relevant part of the analysis, the cases where the drop is deposited on the substrate have also received considerable attention in the literature. From the drop perspective, the analyses can deal with drops made of simple and/or complex fluids, spherical/non-spherical drops, the action of surfactants in the surface tension. With respect to the substrate, variations come also from multiple sources. The surface solid can have different levels of roughness, be more hydrophobic or hydrophilic, be placed with different inclinations with respect to the drop velocity and gravity.

Experimental works of the Newtonian drop impact are mainly focused on the surface tension (e.g., [1,2,3,4]) and dynamic contact angle effects (e.g., [5,6,7,8]). The motion of the triple point, where the liquid, the solid and the air are in contact is one of the main challenges in droplet dynamics. The oblique drop impact was studied by [9,10,11,12] due to the importance of this condition in real applications, mainly establishing conditions where different outputs were obtained. A number of works (e.g., [13,14]) are dedicated to the study of coating treatments and other surface effects that can change the adherence of the solid substrate and hence, the evolution dynamics of the drops that are in contact with this solid

In the cases where the motion of drops on inclined surfaces is induced by gravity and there is no previous drop collision, the main concerns generally encompass the drop shape and the conditions that induce detachment, rolling and breakage of the drop integrity [15]. The pioneering works conducted by Dussan & Chow [16], Dussan [17] established the firsts fundamental aspects of this problem, examining droplets attached to non-horizontal surfaces and determining conditions for these droplets to slide by means of asymptotic methods. Dimitrakopoulos & Higdon [18] considered the influence of the advancing and the receding contact angles of three-dimensional fluid droplets from inclined solid surfaces. They employed a procedure to optimize the shape of drop seeking for the contact line which yields the maximum displacing force for which the droplet can remain attached to the surface. They were able to recover the results obtained by Dussan & Chow [16], Dussan [17] as asymptotic limits. The experimental study presented by Podgorski et al. [19] analyzed the effect of the inclination angle from a horizontal to a vertical configuration and highlighted the influence of the capillary (ratio of viscous to surface tension effects) and Bond (ratio of gravitational to surface tension effects) numbers on the analysis. Since there is no impact velocity, the initial kinetic energy of the system is null and, therefore, surface tension can act to preserve integrity and to restrict deformation. On the other hand, gravity induces non-symmetric shapes where a “belly” can be formed in the lower part of the drop. Some numerical investigations tried to address this competition between gravity and surface tension, such as the studies conducted by Milinazzo & Shinbrot [20] considering a simplified configuration of the problem and Schwartz et al. [21] who were able to find regimes where the drop splits into smaller ones, as well as a long stretching motion on the vertical wall.

The use of pesticide for pest control in crops is an application where these effects can be important, due to the small size of the droplets that are sprayed on the plants (e.g., [22]). Different contact angles for advancing and receding contact line were considered by Glass et al. [23]. Local variations in wettability in the leaves [24] can be challenging for modelling. In inclined leaves the competition between gravity and surface tension translated by the Bond number plays an important role, as analyzed by Veremiev et al. [25], who also considered the air effect on the determination of the final impact velocity.

Applications where there is a temperature difference between the drop and the wall were also the subject of attention of several works. Fire suppression [26] is a challenging problem where temperature effects need to be considered when the drop hits a wall. Fine-tube heat exchangers applied in refrigeration systems can induce surface low temperatures that induce the formation of water drops at tube walls, as analyzed by Zhuang et al. [27]. While Duy & Vu [28] analyzed liquid drop solidifying on a vertical cold wall using numerical simulations, Demidovich et al. [29] investigated the impact of single and multicomponent liquid drops on a heated wall.

There are important experimental works in the literature that have explored the motion of drops made of complex fluids. Few experimental works examined the motion of a non-Newtonian drop on an inclined plane. Xu et al. [30] investigated this problem with viscoelastic Boger fluids (PEG–PEO solutions) and concluded that elasticity did not significantly influence the results when compared to the Newtonian outputs. Yield stress materials were studied by Jalaal et al. [31] who found significant slip of spreading drops made of Carbopol and of Xanthan gum solutions. The drop impact on a thin liquid film was studied in [32,33] where the limits between sticking and splashing were established using a reduced set of dimensionless numbers where the Reynolds number and the aspect ratio between the drop diameter and the thickness of the liquid played a major role.

Some experimental studies of the drop impact of viscoelastic materials were carried out by [34,35,36,37,38]. As a general conclusion, there are elastic effects of the fluid as whole that replace the contribution of the surface tension in purely Newtonian drops. In the case of yield stress materials, the studies performed by Luu & Forterre [39], Nigen [40], German & Bertola [41], Saidi et al. [42] deserve to be highlighted. The main concern of these works was to investigate the influence of the yield stress and surface tension. The exception is the work of Luu & Forterre [39], where an elasto-viscoplastic analysis was made, since they found some influence of elasticity in the presence of the yield stress.

To address the drop dynamics in these problems from a numerical perspective, a technique to deal with the free surface is necessary. There are some challenges to tackle this problem, even in the Newtonian case. In the non-Newtonian scenario different methods and different fluids were employed in the recent years [43,44,45,46,47,48], as described by Oishi et al. [49].

Concerning the mechanical properties of the fluid, a broad study on drop impact was conducted in [49], where elasticity, viscoplasticity, inertia, and thixotropy were investigated for large ranges of the corresponding dimensionless numbers. The main outputs considered in the normal impact were bouncing and non-bouncing. The main conclusions with respect to the normal drop impact on a solid surface are summarized next. In general, high levels of the yield stress inhibit bouncing due to highly plastic deformation induced, which is unable to recover. When elasticity is significant, in most of the times, the retraction does not imply on the detachment of the drop from the substrate. Since in viscoelastic fluids (in contrast to viscoelastic solids) higher elastic effects are accomplished by increasing the flexibility of the fluid, the spreading stage is accompanied by large deformations, leading to flatter configurations that have to face a long dissipative path to return to a more rounded configuration and to abandon the solid substrate. Inertia has also a tendency to inhibit bouncing. The initial kinetic energy is used to spread the drop and is dissipated in the spreading and retraction stages (in the case where elasticity is low and surface tension effects are negligible there is no retraction stage, since the fluid is unable to store energy). The influence of surface tension was analyzed in [50] in a subsequent work where it was found that high yield stress inhibits the role of capillary effects, as already demonstrated by Luu & Forterre [39] in their experiments. Again, some results generally attributed to surface tension in inelastic fluids were obtained by an elastic fluid neglecting surface tension effect.

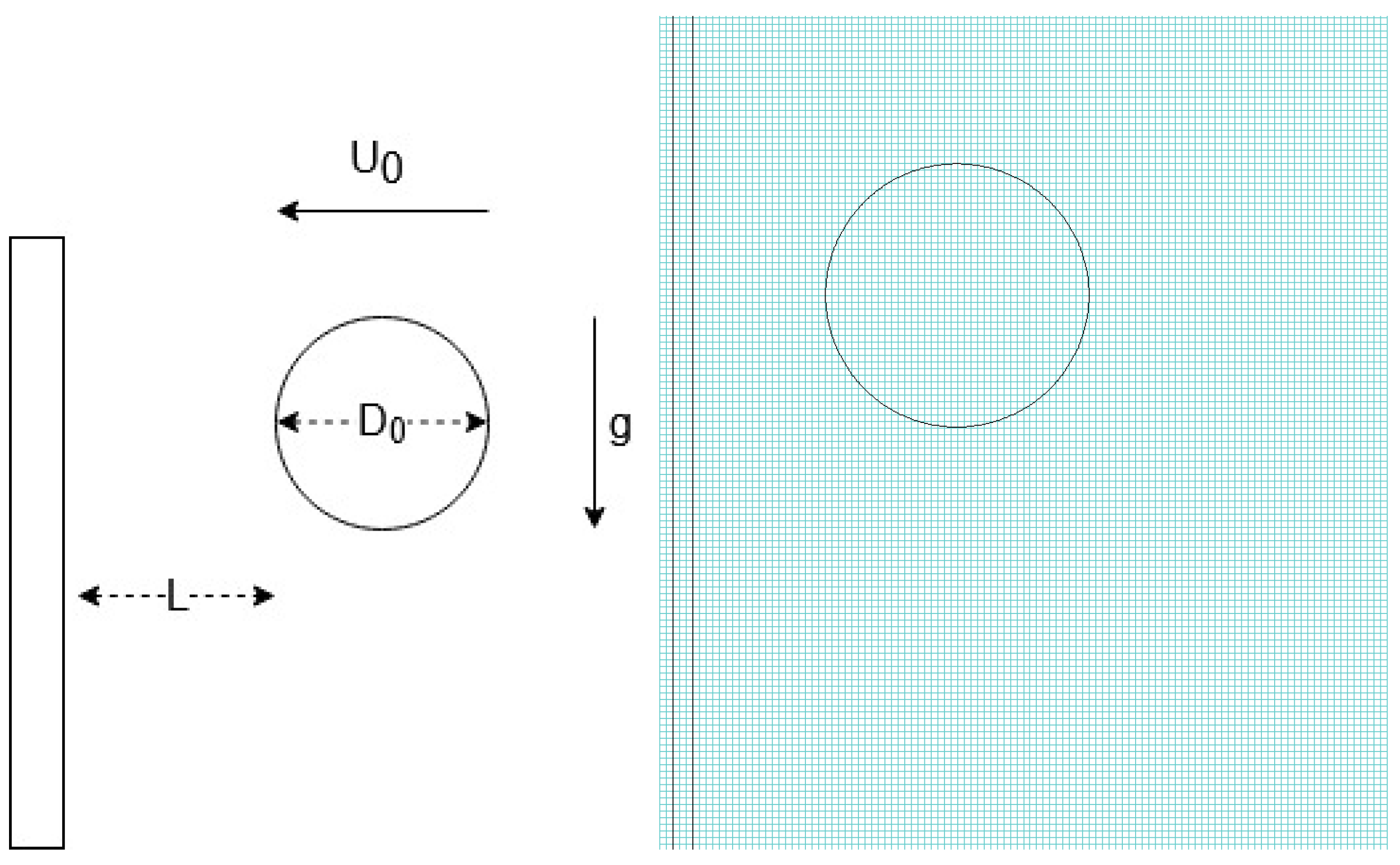
The objective of present work is to investigate the collision of an elasto-viscoplastic drop on a vertical wall. As discussed above, even when the drop is deposited on the wall, gravitational forces lead to an asymmetry in the spreading stage that is worthy of investigation. The impact introduces an addition concern which is the possibility of providing different levels of energy to the system by means of the initial kinetic energy before impact. In addition, sliding is a possible outcome not present in horizontal drop collision. Hence, the study conducted here aims to understand how gravitational effects interact with the mechanical properties of a complex fluid is this problem. In this regard, the role of the Froude number receives special attention and is the main focus of our analysis.

The rest of the text is organized as follows. In Section 2, the governing equations, the model and the numerical scheme are presented. The description of the problem is shown in Section 3. The results are presented in Section 4, where real and parametric mechanical properties are given as input to the problem. Finally, in Section 5, we summarize and draw conclusions with respect to the problem.

2. Governing Equations and Overview of the Numerical Scheme

The mathematical modelling used in this work to describe the complex fluid flows is based on the elasto-viscoplastic framework. Below, we present the motion and constitutive equations in a dimensionless form, following [51,52]:

$$\nabla ·\mathbf{u}=0,$$

(1)

$$\frac{\partial \mathbf{u}}{\partial t}+\nabla ·\left(\mathbf{u}\mathbf{u}\right)=-\nabla p+\frac{1}{Re}\left({\eta }_{\infty }{\nabla }^2\mathbf{u}+\nabla ·{\tau }^M\right)+\frac{1}{{Fr}^2}\mathbf{g},$$

(2)

$$\frac{\partial {\tau }^M}{\partial t}+\nabla ·\left(\mathbf{u}{\tau }^M\right)-\left[\left(\nabla \mathbf{u}\right)·{\tau }^M+{\tau }^M·{\left(\nabla \mathbf{u}\right)}^{\mathbf{T}}\right]=\frac{f\left(\lambda \right)}{Wi}\left[-\frac{1}{\eta \left(\lambda \right)}{\tau }^M+2\mathbf{D}\right].$$

(3)

In these equations, the velocity and pressure fields are represented by $\mathbf{u}$ and p, respectively, while ${\tau }^M$ is the non-Newtonian contribution of the total stress tensor which is given by:

$$\sigma =-p\mathbf{I}+2{\eta }_{\infty }\mathbf{D}+{\tau }^M$$

(4)

with $\mathbf{D}$ being the rate of deformation tensor. The dimensionless parameters of Equations (2) and (3) are the Reynold number $Re$, the viscosity related to the fully unstructured material ${\eta }_{\infty }$, the Froude number $Fr$ and the Weissenberg number $Wi$. These dimensionless numbers related to inertia, gravity, and elasticity of the fluid are defined by

$$Re=\frac{\rho U^2}{{\tau }_c},Fr=\frac{U}{\sqrt{gD}},Wi=\frac{{\tau }_c}{G_0},$$

(5)

where U is the characteristic velocity, chosen to be the impact velocity and D is the characteristic length chosen to be the initial drop diameter. The characteristic stress ${\tau }_c$ is chosen to be the flow curve stress value associated with the characteristic shear rate of the problem which in the present case is ${\dot{\gamma }}_c=U/D$.

In the above equations, the mechanical properties of viscosity and elastic modulus are dependent on a dimensionless structure parameter $\lambda$. In a more general approach, we could introduce a time-dependency aspect to the material, like thixotropy for example, by solving a transport equation for $\lambda$. However, we explore the elasto-viscoplastic nature of the fluid in this work and, therefore, the microstructure is always at equilibrium conditions and no thixotropic effects are present. In other words, although the mechanical properties depend on the structure parameter, abrupt changes in stress are accompanied with instantaneous changes in microstructure, although elasticity still induces memory effects on the fluid. The material properties $f\left(\lambda \right)$ and $\eta \left(\lambda \right)$ are defined by

$$f\left(\lambda \right)=\frac{G\left(\lambda \right)}{G_0}=exp\left[m\left(\frac{1}{\lambda }-1\right)\right],$$

(6)

and

$$\eta \left(\lambda \right)=\left[{\left(\frac{{\eta }_0}{{\eta }_{\infty }}\right)}^{\lambda }-1\right]{\eta }_{\infty },$$

(7)

respectively, where ${\eta }_0$ and $G_0$ are the values of the viscosity and the elastic modulus in the fully structured state, $f\left(\lambda \right)$ is a dimensionless function that represents the ratio between the current and fully structured elastic modulus, and m is a positive constant.

In the present model, the flow curve is an input that is used to compute the viscosity at equilibrium conditions and the corresponding structure level. The viscoplastic nature of the material is captured by the presence of a yield stress in the flow curve which is given by

$$\tau =\zeta \left(\dot{\gamma }\right)\left({\tau }_y+K{\dot{\gamma }}^n\right)+{\eta }_{\infty }\dot{\gamma },$$

(8)

where ${\tau }_y$ is the apparent yield stress of the material; K and n are the consistency and exponent of the power-law term in the flow curve; and $\zeta \left(\dot{\gamma }\right)$ is a regularization factor given by

$$\zeta \left(\dot{\gamma }\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\tau \ge {\tau }_y\hfill \\ \frac{\left({\eta }_0-{\eta }_{\infty }\right)\dot{\gamma }}{{\tau }_y+K{\dot{\gamma }}^n}\hfill & \mathrm{if}\tau <{\tau }_y\hfill \end{array}\right.$$

(9)

The dimensionless parameters associated with the flow curve are obtained by inputting ${\dot{\gamma }}_c$ in Equation (8), discarding the regularization factor, and dividing the resulting equation by the characteristic stress, ${\tau }_c$. This procedure leads to

$$1={\tau }_y^{*}+K^{*}+{\eta }_{\infty }^{*},$$

(10)

where

$${\tau }_y^{*}=\frac{{\tau }_y}{{\tau }_c},K^{*}=\frac{K}{{\tau }_c}{\left(\frac{U}{D}\right)}^n,{\eta }_{\infty }^{*}=\frac{{\eta }_{\infty }}{{\eta }_c}$$

(11)

with the characteristic viscosity defined as ${\eta }_c\equiv {\tau }_{c}D/U$. With this definition, differently from the Bingham number, the plastic number, ${\tau }_y^{*}$, is a normalized quantity.

Assuming $\tau ={\sigma }_{dev}$, where ${\sigma }_{dev}$ is the deviatoric part of the stress tensor, we are able to solve (8) for implicitly computing the deformation rate value, $\dot{\gamma }$, which is used for determining the viscosity through

$$\eta =\frac{{\sigma }_{dev}}{\dot{\gamma }}.$$

(12)

Once the viscosity is obtained, the structure parameter is computed as

$$\lambda =\frac{ln\left(\frac{\eta }{{\eta }_{\infty }}\right)}{ln\left(\frac{{\eta }_0}{{\eta }_{\infty }}\right)}.$$

(13)

It is worth noticing that the mathematical model used in this current work is similar that one proposed by Saramito [53] for dealing with yield-stress materials.

The equations presented in this section are solved in the context of a finite difference scheme. In particular, the continuity and momentum Equations (1) and (2) are solved via the projection method while the constitutive Equation (3) is computed via an explicit time discretization. The non-linear Equation (8) for variable $\dot{\gamma }$ is solved using a hybrid version of the Newton-bissection scheme.

3. Flow Problem Description and Moving Interface Dynamics

The flow problem addressed in this work consists of the impact of a fluid drop with diameter $D_0$ on a vertical wall, as illustrated in Figure 1, where one can also find (in the right) the computational domain filled with the mesh employed after the mesh study presented below.

We have imposed no-slip and no-penetration boundary condition, i.e., $\mathbf{u}=\mathbf{0}$ at the rigid wall. For the drop interface, the boundary conditions for the free surface are given by the following equations:

$$\mathbf{n}·\sigma ·{\mathbf{n}}^T=0,$$

(14)

$$\mathbf{m}·\sigma ·{\mathbf{n}}^T=0,$$

(15)

where $\mathbf{n}$ and $\mathbf{m}$ are the unit normal and tangent vectors, respectively. Equation (14) reflects the assumption of negligible surface tension effects.

To model the moving free surface interface, we have adopted a Front-Tracking method combined with the Marker-And-Cell scheme. In summary, in this framework, the interface is explicitly represented by massless marker particles that are advected by the flow as a passive quantity, i.e., solving the equation

$$\frac{d\mathbf{x}}{dt}=\mathbf{u}.$$

(16)

More details concerning the combination of Marker-And-Cell method and Front-Tracking scheme can be found in the previous works [45,50].

4. Results

This section is divided into two parts. The first one is dedicated to the verification of the code while in the second part of the results we investigate the role of the different dimensionless numbers of the problem, by means of parametric studies.

For the verification part, we performed a mesh refinement study using mechanical properties of real fluids adopting the material data of the Carbopol and Kaolin water solutions obtained from the literature.

In the context of the parametric study, we have disposed the investigation in three groups of cases. In the first group, gravitational effects are captured by analyzing the role of the Froude number for a high and a low value of the Weissenberg number keeping low levels of inertia. The second group analyses the role of elasticity for a high and a low value of the Froude number and large inertial effects. Finally, the third group explores the plastic number in the scenario where the Froude number is high, and inertia is low. In all simulations of the parametric study we have fixed the value of the dimensionless unstructured viscosity as ${\eta }_{\infty }^{*}=0.2$. Drop evolution is presented as a function of the dimensionless time, $t^{*}=tU/D_0$.

From now on, the dimensionless numbers are presented without the * symbol.

4.1. Code Verification

For the mesh refinement study, we have selected three meshes, for instance, M0, with 40 cells in the diameter of the drop ($\delta x^{*}=\delta y^{*}=0.025$), M1, with 80 cells in the diameter of the drop ($\delta x^{*}=\delta y^{*}=0.0125$) and M2, with 160 cells in the diameter of the drop ($\delta x^{*}=\delta y^{*}=0.00625$).

In this Section we have considered two real yield stress fluids commonly used in the literature, e.g., Carbopol and Kaolin. The data of Carbopol and Kaolin fluids were respectively obtained from [54] and [39]. We set the following values for the dimensionless parameters: (i) Carbopol with $Re=19.71$, $Wi=1.21,{\tau }_y=0.41,K=0.58$ and (ii) Kaolin with $Re=6.75,Wi=0.00652,{\tau }_y=0.21,K=0.78$. In the analysis of both fluids, we kept the same Froude number and unstructured viscosity as $Fr=2.26$ and ${\eta }_{\infty }=0.01$.

Results for the evolution of the free surface shape of the drops considering M0, M1 and M2 for the two fluids at different times are shown in Figure 2 (see video0.mp4 for the complete evolution). Additional results for the mesh refinement study are presented in Figure 3. In this figure, we have plotted the maximum spreading length in the y-direction relative to the initial drop diameter as a function of time for Carbopol and Kaolin. From Figure 2 and Figure 3, we can confirm the adequate convergence of the free surface with a mesh refinement. In particular, the results for M1 are slightly different those from M2; therefore, in order to save CPU time, we have adopted M1 for the remaining simulations in this work.

From a physical point-of-view, we can conclude from Figure 3a that the elastic effects in the Carbopol solution are more evident since the drop presents oscillations after the vertical impact. On the other hand, after achieving the maximum size in y-direction, the drop of Kaolin does not retract, but stays stuck on the vertical wall, in a typical plastic deformation. These results are explained by the discrepancy in the Weissenberg number between the solutions

4.2. Group 1

In this first group, we maintained fixed the values of the Reynolds number, $Re=3.0$, and the plastic number, ${\tau }_y=0.4$, while the Froude number values examined were $Fr=\left\{1.69;2.26;4.51;9.03\right\}$. Figure 4, Figure 5, Figure 6 and Figure 7 show the evolution of the collision of elasto-viscoplastic drops on a vertical plane for this group. In order to better illustrate the interface dynamics of these simulations, we have included videos related to these figures as supplementary materials (see video1.mp4). The time values shown in these figures are $t=\left\{2;4;6;34\right\}$. The left column corresponds to a very low Weissenberg number, $Wi=0.01$, which can be considered to be a viscoplastic material since the elastic effects are negligible. In the right column, the value $Wi=1$ corresponds to cases where the elastic nature of the material is significant.

A remarkable result is the connection between elasticity and the detachment of the drop from the solid surface. For $Wi=0.01$ all the drops remained attached to the vertical wall. In these cases, the gravitational effects, which are more pronounced in the lowest $Fr$ case, act to dislocate the drop downwards. We can observe that as the Froude number is decreased the drop goes through a higher dislocation, as expected. For the lowest $Fr$ case, in addition to reaching the lowest position, the induced deformation is acting to inflate its bottom part, as illustrated by the $Fr=1.69$-drop on the left column of Figure 7. This happens because the wall imposes a resistance to the fluid, which is in contact to the solid, while far from the wall, gravity acts more freely. Similar effects were found by Podgorski et al. [19] and Dimitrakopoulos & Higdon [18] when gravitational effects were much higher than surface tension ones. On the other hand, the high elasticity promoted by the $Wi=1$ value of the Weissenberg number was able to induce a detachment from the wall for all the values of Froude number analyzed, including the highest Froude number case, $Fr=9.03$. As expected, lower values of $Fr$ anticipates the detachment of the drop. It is worth noticing that the elasticity of the drop plays the role in this case of the surface tension in Newtonian drops where capillary effects are present, i.e., the stored elastic energy during the spreading stage is able to induce receding and the detachment of the drop.

4.3. Group 2

In this second group of cases, we increased the value of the Reynolds number to $Re=8.0$, and kept the plastic number in the same level, ${\tau }_y=0.4$. The high and low values of the Froude number are $Fr=4.52$ (left columns) and $Fr=1.13$ (right columns). Figure 8, Figure 9, Figure 10 and Figure 11 correspond to dimensionless time values given by $t=\left\{1;3;6;20\right\}$. Videos related to these figures can be found in the supplementary materials (see video3.mp4). The values of the Weissenberg number shown in each frame are $Wi=\left\{0.01;0.1;0.5;1\right\}$, ranging from a viscoplastic behavior to a reasonably elastic one.

The gravitational effects are very highlighted in this group of cases. In the first captured frame, $t=1$, elastic effects did not have time to appear and the drops on the left and on the right are almost coincident. At this time, the only Froude number effect was to dislocate downwards the drops on the right. At the time $t=3$, we notice a significant gravitational effect on the right column where the drop has slithered down the vertical wall. This kind of behavior was already found in [55] for the problem of a material deposited on an inclined plane. It is worth observing an important difference with respect to the previous group which is the highest Reynolds number value in this case. The additional energy that came from the kinetic energy source was able to induce a more stretched deformation that was amplified by gravity. Figure 10 reveals that the less elastic drops ($Wi=0.01$ and $Wi=0.10$) of the higher-Forude-number column (right) exhibited a “pinned tail”, i.e., the top tip remains at fixed position. This condition is in contrast with respect to the drops with higher $Wi$, where an elastic retraction takes place. The left column shows the beginning of a detachment process of the highest $Wi$ case that ends in Figure 11, where this drop begins to fall. For the low values of the Weissenberg number, the weak elastic effects were unable to detach the drops. In all cases, the high initial kinetic energy was mostly dissipated in the impact and spreading. The weak gravitational effects for the low $Fr$ cases showed more symmetric drops as final configurations.

4.4. Group 3

In this third group of cases, inertia and gravitational effects are low, with $Re=2.0$ and $Fr=9.03$. Three columns are shown in Figure 12, Figure 13 and Figure 14, corresponding to different levels of the plastic number (see video2.mp4 in supplementary materials). From left to right, the values of the plastic number are ${\tau }_y=0.1$, ${\tau }_y=0.2$, ${\tau }_y=0.4$. The values of the Weissenberg number shown in each frame are $Wi=\left\{0.01;0.1;0.5;1.0;2.0\right\}$.

After impact, as shown by Figure 12 for $t=1$, there is no significant difference among the three columns. We can notice a tinny variation with respect to the elasticity of the fluid. Higher values of $Wi$ lead to more deformed drops. This is expected because significant elastic effects in the case of viscoelastic fluids are connected with lower rigidity, what in turn favors deformation. As time evolves to $t=4$ we notice a rebound of the more elastic drop in the highest plastic number, Figure 13 right column. We can see that this bouncing occurs in the horizontal direction, revealing that gravity did not play a role until this moment, due to the low Froude number. However, differently from an impact on a horizontal plane, we have no kicking after a first rebound, since the gravitational force does not induce the drop to return to the plane, as in the collision on a floor. In this regard, we see in Figure 14 that the drops of high Weissenberg numbers detached from the vertical wall and have fallen down. The plastic number effects for this set of cases were not significant.

5. Summary and Conclusions

In the present work we investigated the collision of elasto-viscoplastic drops on a vertical plane. Special emphasis is given on the gravitational effects of this problem. The combination of the dimensionless numbers that govern the problem, namely the Reynolds, Weissenberg, plastic, and Froude numbers, were able to induce a rich variety of outputs. Gravitational effects anticipate the detachment of more elastic drops from the wall and induce large deformations in less elastic drops in the cases of low impact velocities. In addition, gravity favors sliding and slithering of the drops that collide with high impact velocities. Differently from horizontal planes, in vertical ones there is no kicking and, therefore, bouncing refrains the drop from being in contact with the solid, what can affect significantly real applications.