2. Governing Equations
The equations governing the flow and heat transfer in rotating porous media are presented in a dimensionless form subject to the assumptions of constant angular velocity of rotation, Boussinesq approximation (Boussinesq [
67]), and local thermal equilibrium (LTE or Lotheq). The latter implies that the difference in the local temperature between the solid and fluid phases in the porous medium is insignificantly small and can be neglected. Boussinesq approximation [
67] applicable to buoyancy flows states that the density id constant in all terms of the governing equations except the buoyancy terms in the momentum equation. The notation being used refers to symbols having an asterisk as dimensional, while symbols without an asterisk represent dimensionless quantities, except symbols carrying the subscript “c” representing characteristic values, or the subscript “o” representing reference values, both being dimensional. The continuity equation is presented in the form
where
is the filtration velocity vector presented in Cartesian coordinates,
are the components of the the filtration velocity vector in the
directions, respectively, and
are unit vectors in the
directions, respectively. The operator
is the divergence operator defined in the form
.
The momentum transport in porous media is governed primarily by the Darcy law, which is presented in the rotating frame of reference of the solid matrix in the following dimensionless form
where four dimensionless groups emerged, i.e., a pressure number
(equivalent to a porous media Euler number where
replaces
), a porous media Froude number
, a centrifugal number
, and a porous media Ekman number
defined in the form
and where
and
are the permeability and the porosity of the porous matrix, respectively,
is the dynamic viscosity,
is a constant reference value of the fluid density used to convert the density into a dimensionless form,
is the kinematic viscosity of the fluid,
is the constant angular velocity of rotation,
and
are the dimensionless pressure and density, respectively,
is a unit vector in the direction of the gravity acceleration,
is a unit vector in the direction of the angular velocity of roation, and
is the position vector measured from the axis of rotation. Also
are constant dimensional characteristic values of length, filtration velocity, and pressure, respectively, used to convert the space variables, the filtration velocity, and the pressure into dimensionless forms. The gradient operator in Equation (2) is defined in the form
.
The third term in the brackets in Equation (2) represents the centrifugal force while the fourth term represents the Coriolis acceleration.
When fast transients or high frequency effects are of interest there is another extension to the Darcy equation that is applicable. Then, the time resolution obtained by assuming a very fast reaction of Darcy flow to changes and therefore the quasi-steady approximation which is inherent in the formulation of the Darcy law is not sufficient and a time derivative of the filtration velocity needs to be incorporated leading to the following dimensionless form of the extended Darcy equation in a rotating frame of reference
where the additional dimensionless groups that emerged are the Darcy number
, and the Reynolds number
and
is a ratio of heat capacities that its the definition will follow later. The corresponding length scale is a macro-level length scale, not the pore-size, despite the fact that it is the porous media filtration velocity that emerged in the definition of the Reynolds number. However the Reynolds number appears in Equation (4) in a product combination with the Darcy number, bringing therefore the pore-scale effects into account too.
Following the definition of the dimensionless temperature in the form
where
is the dimensional temperature,
is a reference value of temperature, and
is a characteristic temperature difference, the dimensionless form of the energy equation subject to local thermal equilibrium (LTE or Lotheq) is presented in the form
where Peclet number emerged as an additional dimensionless group, defined in the form
where the porous media Prandtl number
is defined by
The effective thermal diffusivity of the porous medium appearing in (8) and (9) is defined as
and
is the heat capacity ratio, i.e., the ratio between the effective heat capacity of the fluid phase and the effective heat capacity of the porous medium, where
,
are the effective heat capacity and effective thermal conductivity of the porous medium and subscripts “s” and “f” refer to the solid and fluid phases, respectively. Then the adjusted effective thermal diffusivity is defined as follows
.
To complete the governing equations one needs a relationship between the density, temperature and pressure (and solute concentration when the fluid is a solution of soluble substances, e.g., salt in water, alcohol in water, etc., in which case an additional species equation needs to be added to). A linear approximation for this relationship is usually sufficiently accurate if the temperature and pressure differences are no excessively high. The dimensionless form of the linear approximation of the equation of state can be obtained by using the definition of the dimensionless temperature from Equation (6) and the dimensionless pressure in the form
. Then the equation of state becomes
where
is the dimensionless density, and
,
are the dimensionless thermal expansion and pressure compression coefficients, respectively. For most fluid flows and especially for incompressible flows, i.e., flows of liquids,
. Therefore the common approximation of the dimensionless equation of state is
There are some identities relevant to flows in a rotating frame of reference and in buoyancy flows that are useful in the following derivations. These identities are
Their proof can be found in Vadasz [
3].
Although for a significantly high number of practical instances Darcy’s model (or its extension) for a rotating frame of reference is sufficient for representing the effects of rotation, non-Darcy models have been used as well. Their relevance and limitations are subject to professional discourse (e.g., Nield [
68,
69,
70] and Vafai and Kim [
71]).
4. Natural Convection Due to Centrifugal Buoyancy
Natural convection is the effect of flow and convection heat transfer due to the existence of density gradients in a body force field (such as gravity or centrifugal force field). As density depends on temperature as demonstrated in the derivation of the equation of state, temperature gradients may create natural convective flows when a body force field is present. What characterizes natural convection is the lack of a known value of characteristic filtration velocity that can be applied upfront in a problem. No characteristic velocity can be specified because the latter is dictated by the temperature gradients and their resulting buoyancy rather than being known upfront. Therefore a sensible choice of
would be
. With this choice of
the Froude number
, the pressure number
, and the centrifugal dimensionless group
in Equations (12) and (14) become
,
,
. Without loss of generality for the same reason as for the filtration velocity one can chose the characteristic pressure difference to be such that the pressure number
becomes unity, i.e.,
leading to
. Also the Reynolds number in Equation (5) renders into the reciprocal Prandtl number
and the Peclet number in Equations (7) and (8) becomes equal to one by definition
. One may define the effective Prandtl number in terms of the effective thermal diffusivity
(see the equation and the text following Equation (9))
. Then the coefficient to the time derivative term in Equation (4) becomes
a new dimensionless group that Straughan [
73] named the Vadasz number (
), or the Vadasz coefficient named by Straughan [
73] (see also Sheu [
74] and Govender [
26]). By using Equations (11)–(13) leads to transforming Equations (2) and (4) into the following form
The product of
by
and
produced two new dimensionless groups in the form of the gravity related Rayleigh number and the centrifugal Rayleigh number, respectively in the form
The particular cases when
and
will be considered later. Subject to this orientation of the gravity and angular velocity of rotation Equations (26) and (27) take the form
The vector
in Equations (30) and (31) represents the perpendicular radius vector from the axis of rotation to any point in the flow domain. Three dimensionless groups emerged in Equation (30) when fast transients or high frequencies are not of interest. These dimensionless groups control the significance of the different phenomena. Therefore, the value of Ekman number (
) controls the significance of the Coriolis effect, and the ratio between the gravity related Rayleigh number (
) and centrifugal Rayleigh number (
) controls the significance of gravity with respect to centrifugal forces as far as natural convection is concerned. This ratio is
. When fast transients or high frequencies are of interest Equation (27) is to be considered. In such a case one additional dimensionless group emerged, the
number representing the ratio between two characteristic frequencies, i.e., the fluid flow frequency
and the thermal diffusion frequency
, i.e.,
, or alternatively the ratio between two time scales, i.e., the thermal diffusion time scale
, and the fluid flow time scale
, i.e.,
. In addition to such cases Equation (27) should be used also when the effective Prandtl number is of the order of magnitude of Darcy number, i.e.,
i.e., a very small number (as
in most porous media). Such small values of the Prandtl number are typical for liquid metals. In such cases too the time derivative term in Equation (27) should be retained.
Considering the Darcy regime subject to a centrifugal body force and by neglecting gravity effects (
) Equations (1), (7) and (26) with
and
represent the mathematical model for this case. The objective in the first instance is to establish the convective flow under small rotation rates, then
, and as a first approximation the Coriolis effect can be neglected, i.e.,
. Following these conditions the governing equations become (by using identity (14))
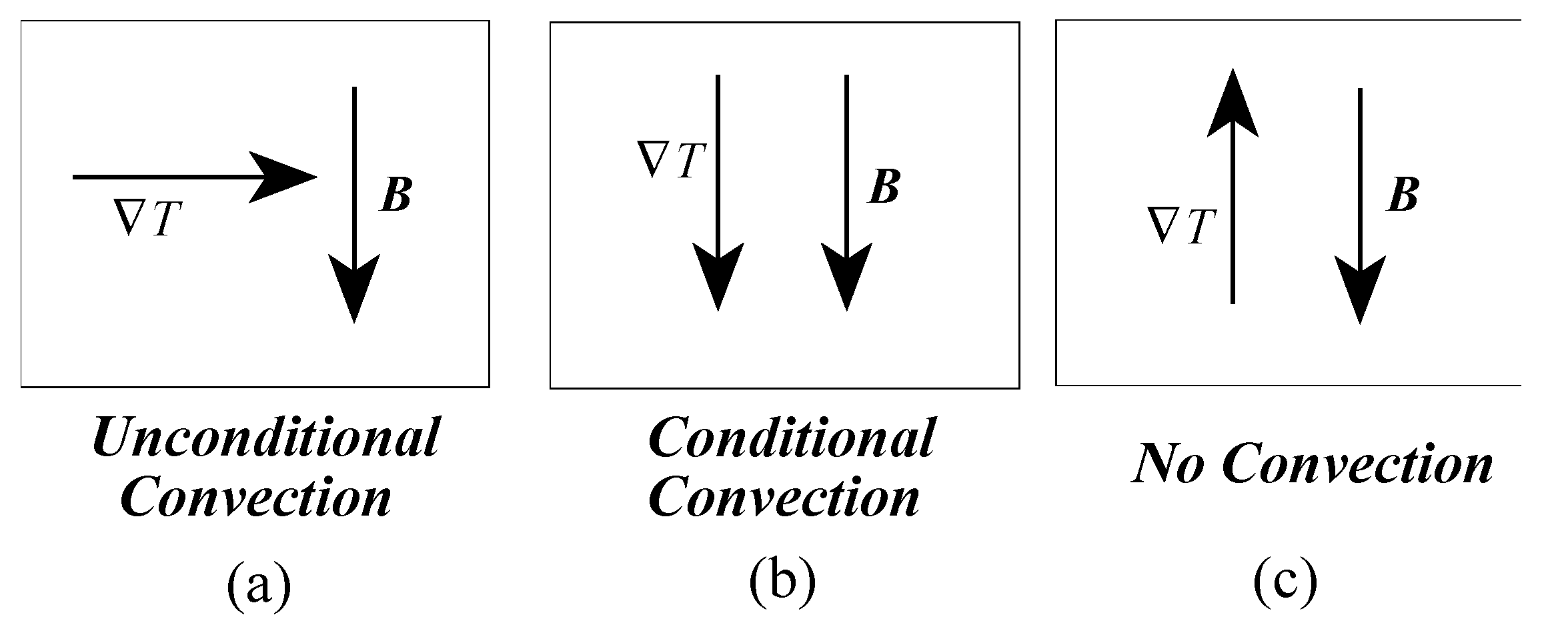
There are three cases corresponding to the relative orientation of the temperature gradient with respect to the centrifugal body force as presented in
Figure 1. Case 1(a) in
Figure 1 corresponds to a temperature gradient, which is perpendicular to the direction of the centrifugal body force and leads to unconditional convection. The solution representing this convection pattern is presented by Vadasz [
3,
4,
34]. Cases 1(b) and 1(c) in
Figure 1 corresponding to temperature gradients collinear with the centrifugal body force represent stability problems and hence our present focus. The objective is then to establish the stability condition as well as the convection pattern when this stability condition is not satisfied.
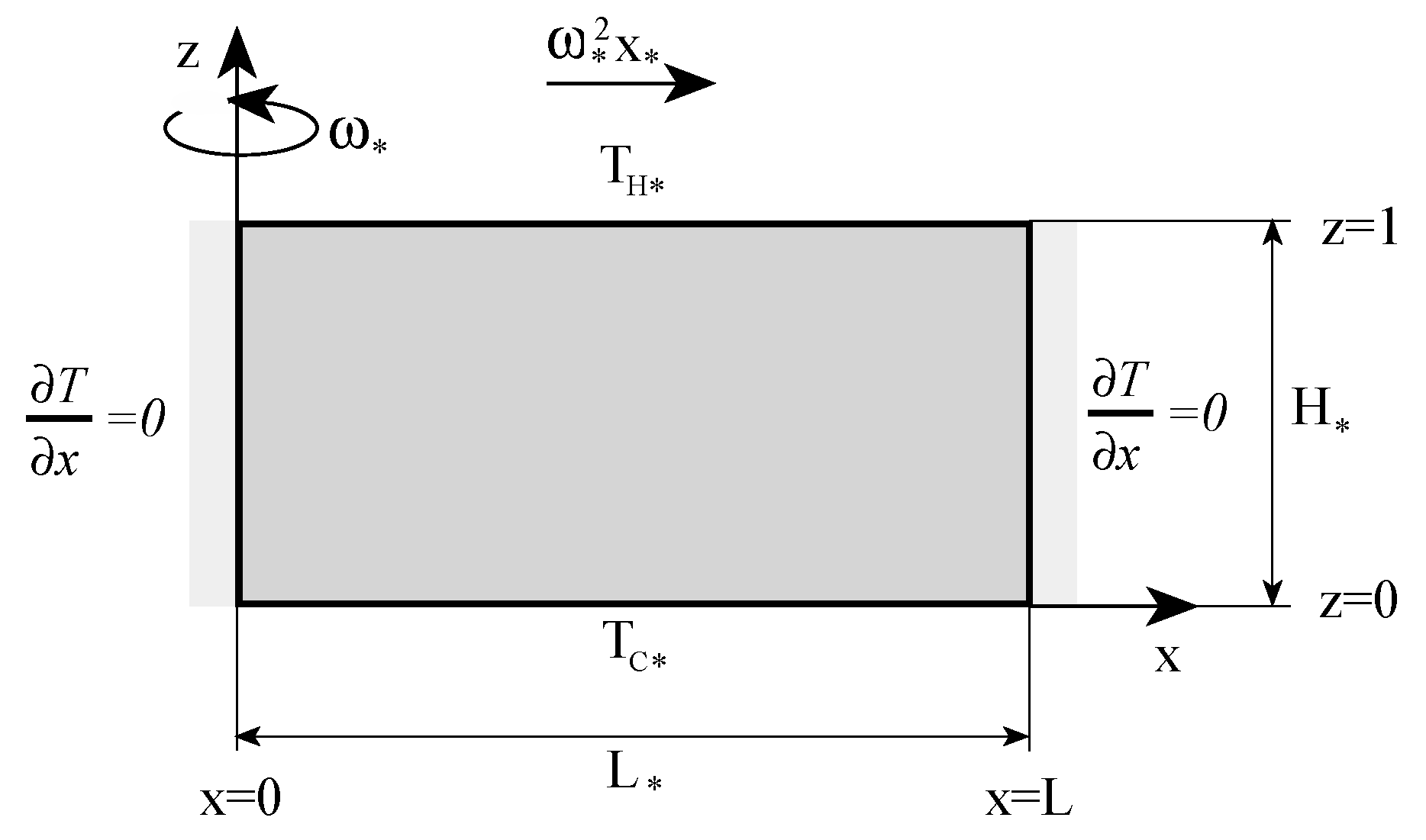
An example of a case when the imposed temperature is perpendicular to the centrifugal body force is a rectangular porous domain rotating about the vertical axis, heated from above and cooled from below. For this case the centrifugal buoyancy term in Equation (33) becomes
leading to
An analytical two-dimensional solution to this problem (see
Figure 2) for a small aspect ratio of the domain was presented by Vadasz [
3,
4,
34]. The solution to the non-linear set of partial differential equations was obtained through an asymptotic expansion of the dependent variables in terms of a small parameter representing the aspect ratio of the domain.
The convection in the core region far from the sidewalls was the objective of the investigation. To first order accuracy, the heat transfer coefficient represented by the Nusselt number was evaluated in the form
where
is the Nusselt number and the length scale used in the definition of
, Equation (54), was
. Vadasz [
37] used a different approach to solve a similar problem without the restriction of a small aspect ratio. A direct extraction and substitution of the dependent variables was found to be useful for de-coupling the non-linear partial differential equations, resulting in a set of independent non-linear ordinary differential equations, which was solved analytically. To obtain an analytical solution to the non-linear convection problem we assume that the vertical component of the filtration velocity,
, and the temperature
are independent of
, i.e.,
, being functions of
only. It is this assumption that will subsequently restrict the validity domain of the results to moderate values of
(practically
). Subject to the assumptions of two-dimensional flow
and
and that
and
are independent of
the governing equations take the form
The method of solution consists of extracting
from Equation (38) and expressing it explicitly in terms of
and
. This expression of
is then introduced into Equation (40) and the derivative
is applied to the result. Then, substituting the continuity Equation (37) in the form
and Equation (39) into the results yields a non-linear ordinary differential equation for
in the form
An interesting observation regarding Equation (41) is the fact that it is identical to the Blasius equation for boundary layer flows of pure fluids (non-porous domains) over a flat plate. To observe this, one simply has to substitute
to obtain
, which is the Blasius equation. Unfortunately, no further analogy to the boundary layer flow in pure fluids exists, predominantly due to the different boundary conditions and because the derivatives [
] and the flow (
) are in the same direction. The solutions for the temperature
and the horizontal component of the filtration velocity
, are related to the solution of the ordinary differential equation
where
stands for
and
where
is a constant defined by
The Relationship (45) is a result of imposing a condition of no net flow through any vertical cross-section in the domain, stating that
.
The following boundary conditions are required to the solution of (41) for
:
representing the impermeability condition at the solid boundaries and
. Since
according to Equation (43), then following the continuity Equation (37)
and the temperature boundary conditions can be converted into conditions in terms of
by using Equation (44), leading to the following complete set of boundary conditions for
:
Equations (46) and (47) represent four boundary conditions, while only three are necessary to solve the third order Equation (41). The reason for the fourth condition comes from the introduction of the constant
, whose value remains to be determined. Hence, the additional two boundary conditions are expressed in terms of the unknown constant
and the solution subject to these four conditions will determine the value of
as well. A method similar to Blasius’s method of solution was applied to solve Equation (41). Therefore,
was expressed as a finite power series and the objective of the solution was to determine the power series coefficients. Once the solution for
and the value of
were obtained,
and
were evaluated by using
and Equations (43) and (44).
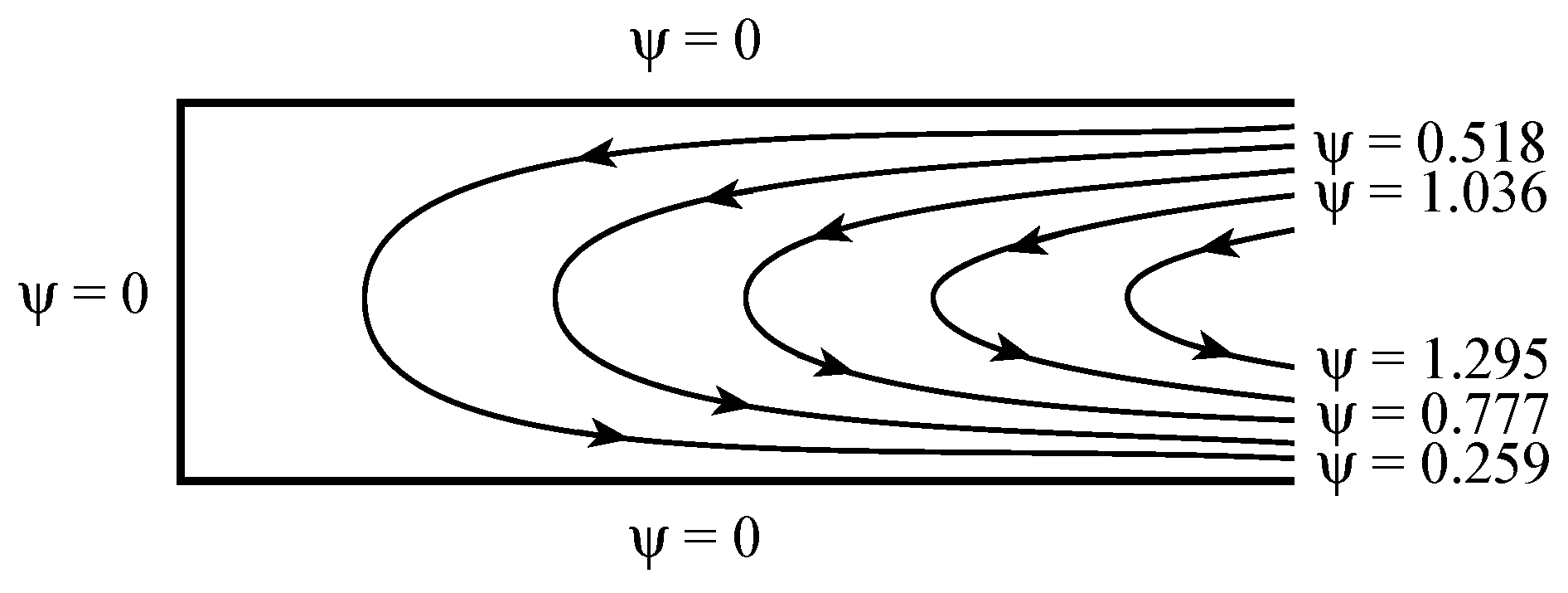
For presentation purposes a stream function
was introduced to plot the results (
,
). An example of the flow field represented by the streamlines is presented in
Figure 3 for
and for an aspect ratio of 3 (excluding a narrow region next to the sidewall at
). Outside this narrow region next to
the streamlines remain open on the right hand side. They are expected to close in the end region. On the left-hand side, however, the streamlines close throughout the domain. The reason for this, is the centrifugal acceleration, which causes
to vary linearly with
, thus creating (due to the continuity equation) a non-vanishing vertical component of the filtration velocity
at all values of
. The local Nusselt number
, representing the local vertical heat flux was evaluated as well by using the definition
and using the solution for
. A comparison between the heat flux results obtained from this solution and the results obtained by Vadasz [
34] using an asymptotic method was presented graphically by Vadasz [
37]. The two results compare well as long as
is very small. However, for increasing values of
the deviation from the linear relationship pertaining to the first order asymptotic solution (
, according to Vadasz [
34]) was evident. The stability of this convection flow was not evaluated, although it is of extreme interest. This would be an interesting though not simple task recommended for future research.
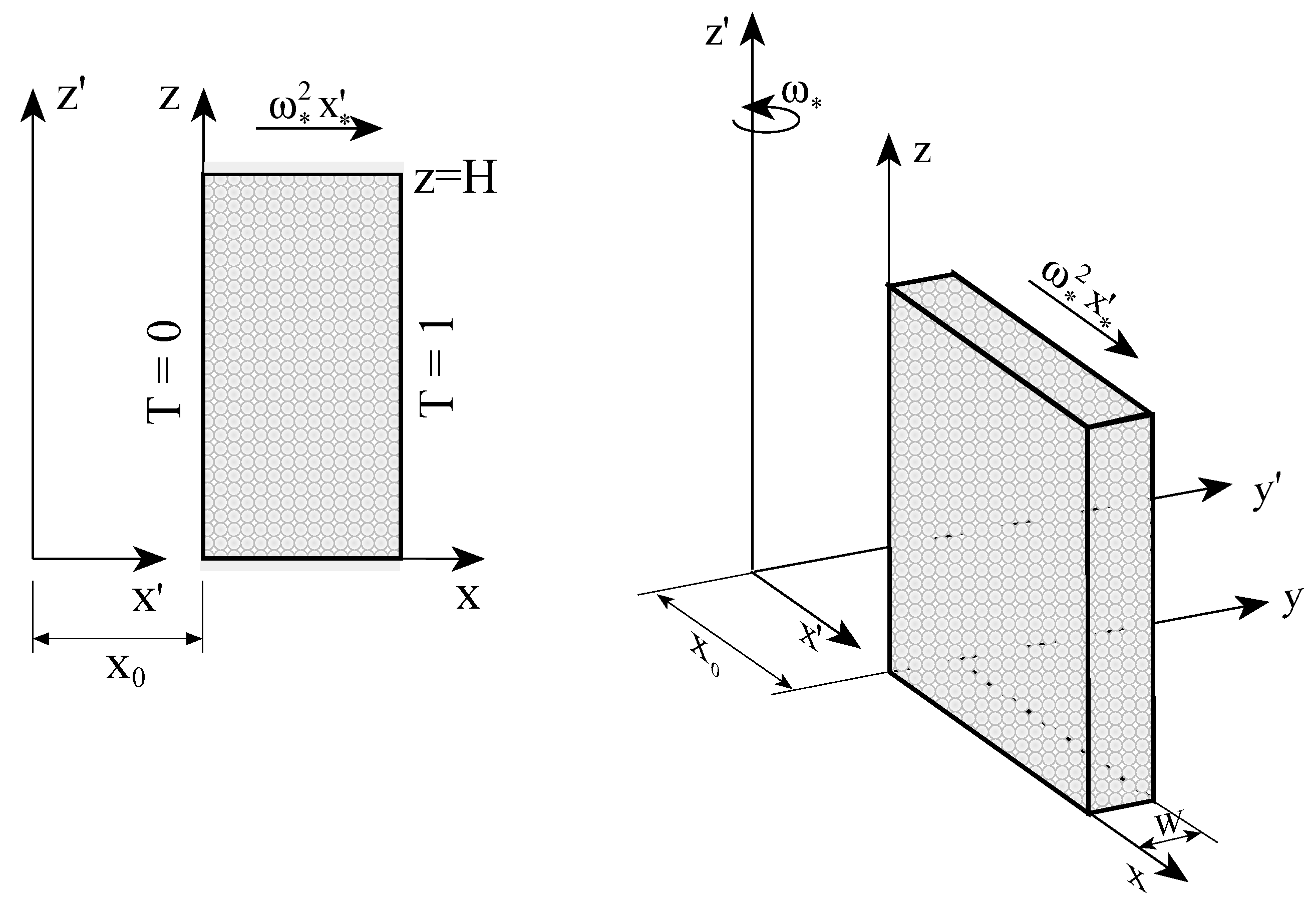
The problem of stability of free convection in a rotating porous layer when the temperature gradient is collinear with the centrifugal body force was treated by Vadasz [
38] and Vadasz [
40] for a narrow layer adjacent to the axis of rotation (Vadasz [
38]) and distant from the axis of rotation (Vadasz [
40]), respectively. The problem formulation corresponding to the latter case is presented in
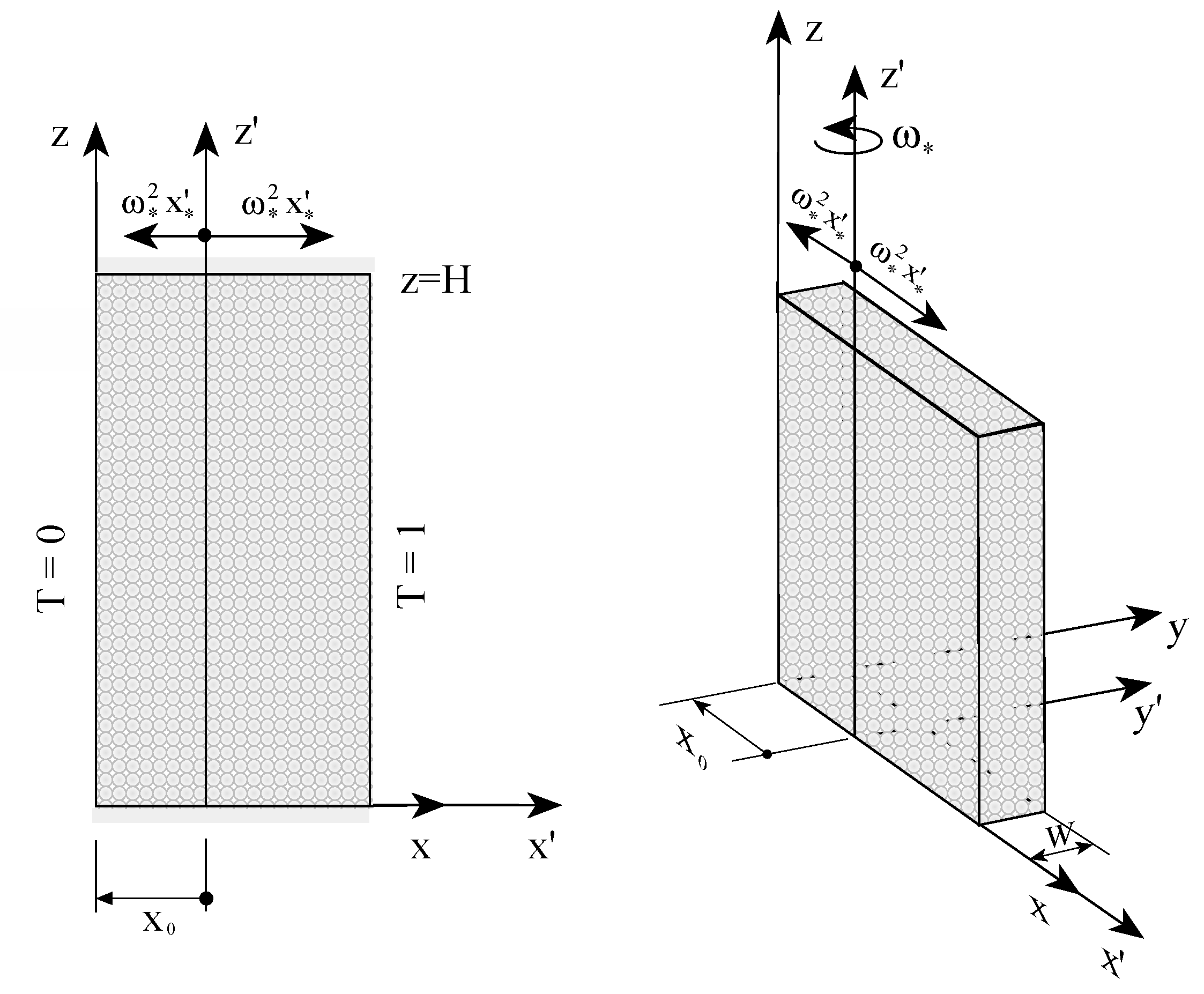
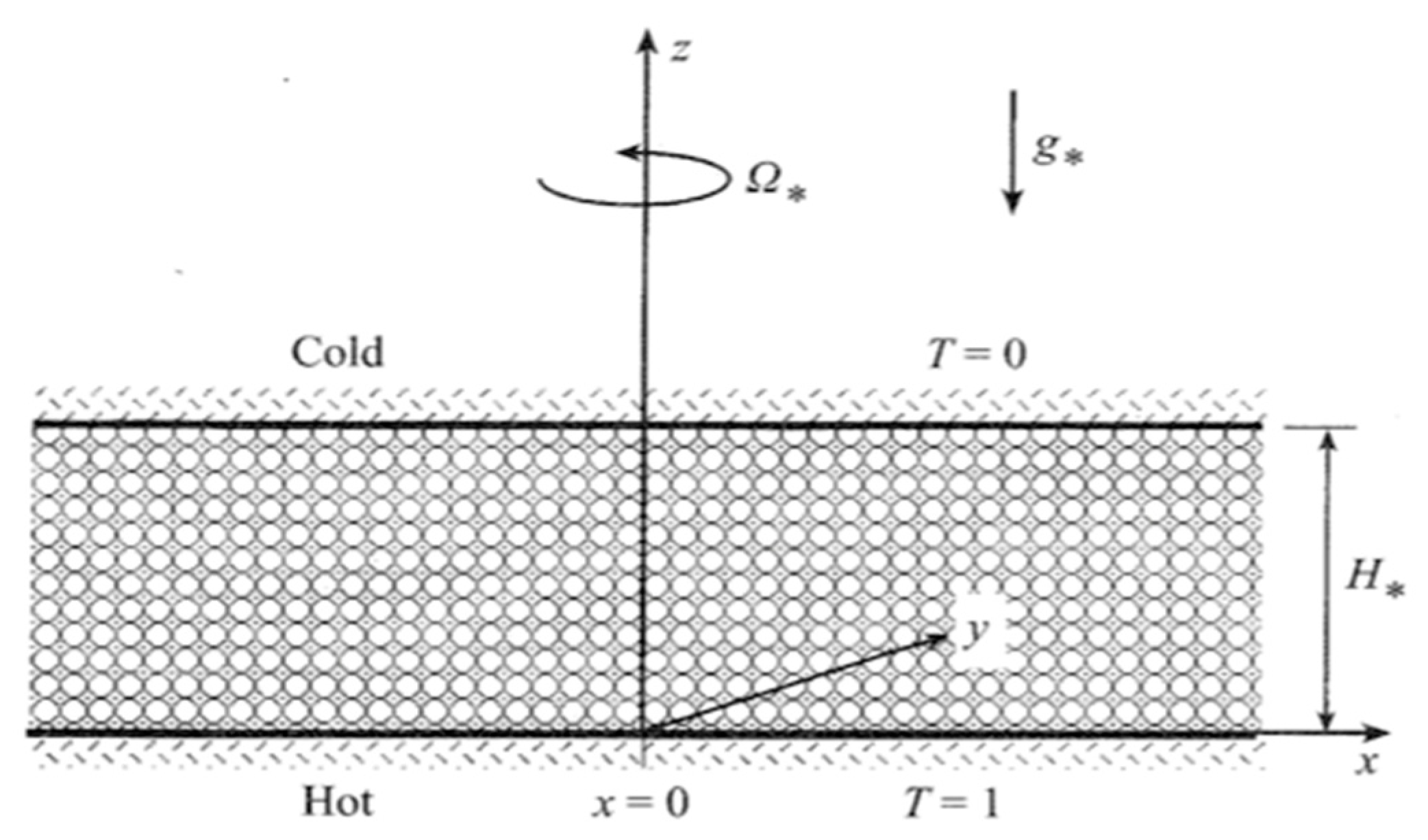
Figure 4. In order to include explicitly the dimensionless offset distance from the axis of rotation
, and to keep the coordinate system linked to the porous layer, Equation (33) was presented in the form
Two centrifugal Rayleigh numbers appear in Equation (48); the first one, representing the contribution of the offset distance from the rotation axis to the centrifugal buoyancy is
, while the second,
, represents the contribution of the horizontal location within the porous layer to the centrifugal buoyancy. The ratio between the two centrifugal Rayleigh numbers is dimensionless reciprocal distance from the axis of rotation
and can be introduced as a parameter in the equations transforming Equation (48) into the form
From Equation (50) it is observed that when the porous layer is far away from the axis of rotation then
(
) and the contribution of the term
is not significant, while for a layer close enough to the rotation axis
(
) and the contribution of the first term becomes insignificant. In the first case the only controlling parameter is
while in the latter case the only controlling parameter is
. The flow boundary conditions are
on the boundaries, where
is a unit vector normal to the boundary. These conditions stipulate that all boundaries are rigid and therefore non-permeable to fluid flow. The thermal boundary conditions are:
at
,
at
and
on all other walls representing the insulation condition on these walls. The governing equations accept a basic motionless conduction solution in the form
The objective of the investigation was to establish the condition when the motionless solution (51) is not stable and consequently a resulting convection pattern appears. Therefore a linear stability analysis was employed, representing the solution as a sum of the basic solution (51) and small perturbations in the form
where
stands for perturbed values. Solving the resulting linearized system for the perturbations by assuming a normal modes expansion in the
and
directions, and
in the
direction, i.e.,
, and using the Galerkin method to solve for
one obtains at marginal stability, i.e., for
, a homogeneous set of linear algebraic equations. This homogeneous linear system accepts a non-zero solution only for particular values of
such that its determinant vanishes. The solution of this system was evaluated up to order 7 for different values of
, representing the offset distance from the axis of rotation. However, useful information was obtained by considering the approximation at order 2. At this order the system reduces to two equations, which lead to the characteristic values of
in the form
where the following notation was used
and
is the wavenumber such that
while the subscript
in Equation (53) represents characteristic (neutral) values (values for which
). A singularity in the solution for
, corresponding to the existence of a single root for
, appears when
. This singularity persists at higher orders as well. Resolving for the value of
when this singularity occurs shows that it corresponds to negative
values implying that the location of the rotation axis falls within the boundaries of the porous domain (or to the right side of the hot wall-a case of little interest due to its inherent unconditional stability). This particular case will be discussed later in this section. The critical values of the centrifugal Rayleigh number as obtained from the solution up to order 7 are presented graphically in
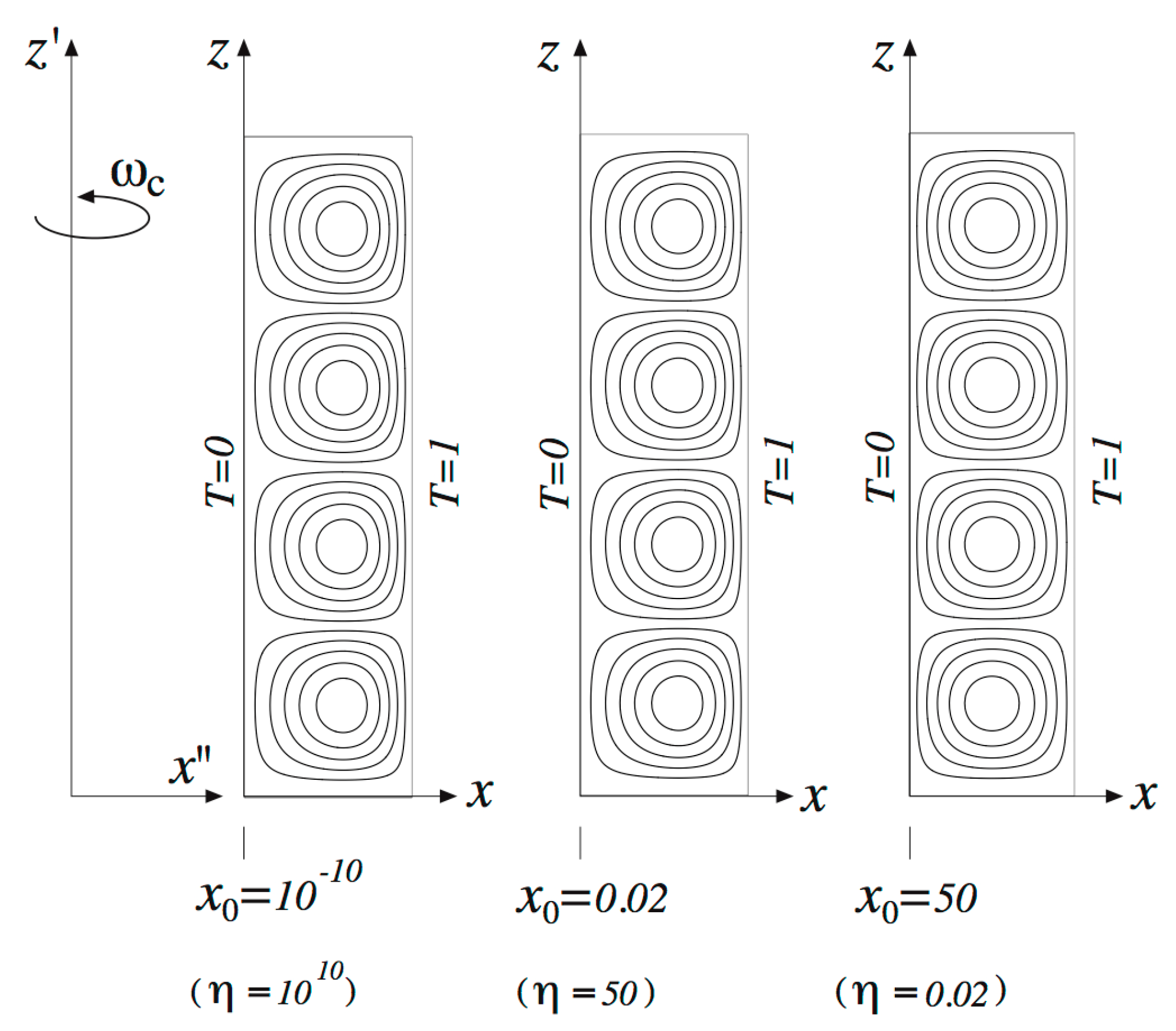
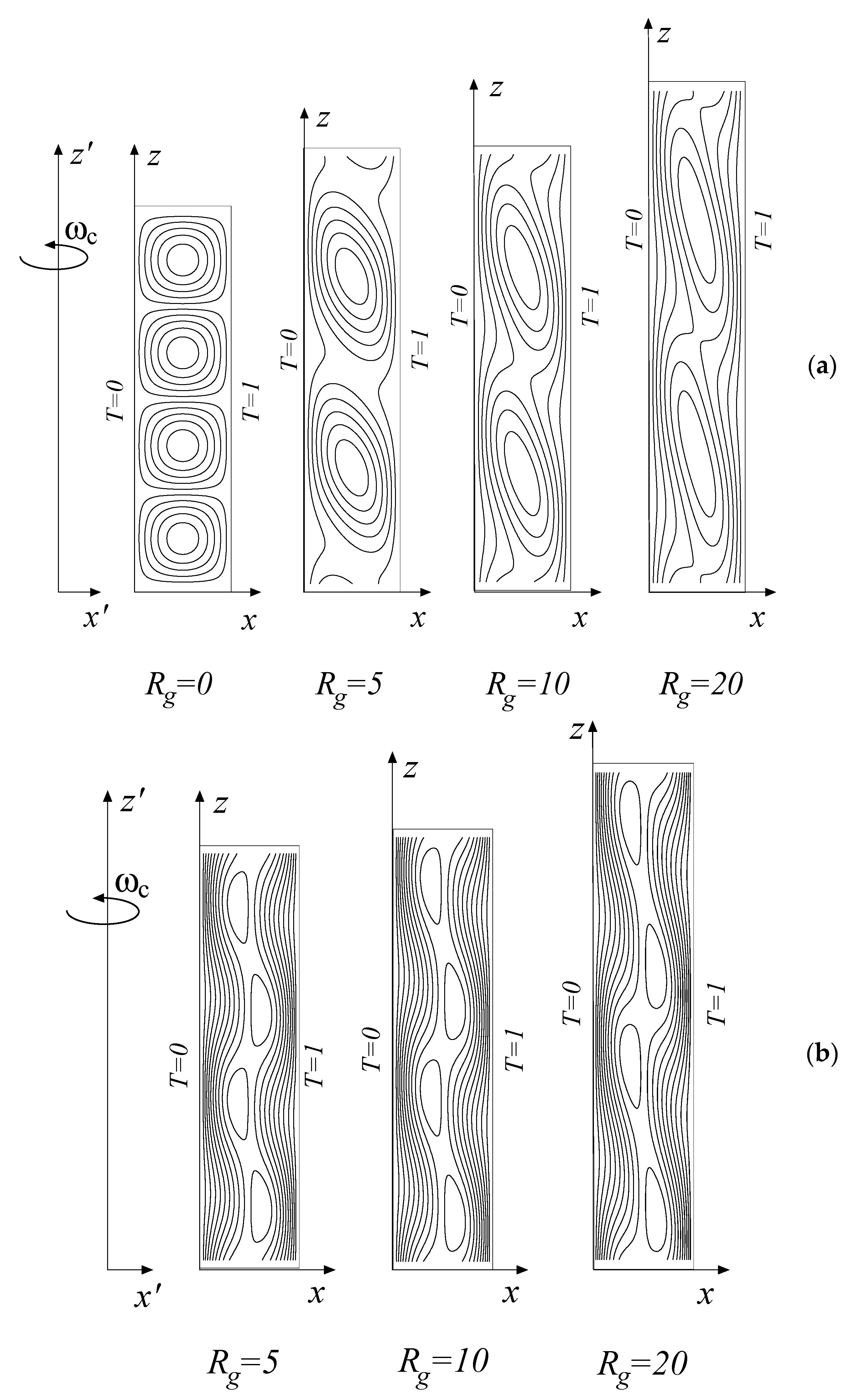
Figure 5a in terms of both
and
as a function of the offset parameter
. The results presented in
Figure 5 are particularly useful in order to indicate the stability criterion for all positive values of
. It can be observed from the figure that as the value of
becomes small, i.e., for a porous layer far away from the axis of rotation, the critical centrifugal Rayleigh number approaches a limit value of
. This corresponds to the critical Rayleigh number in a porous layer subject to gravity and heated from below. For high values of
it is appropriate to use the other centrifugal Rayleigh number
, instead of
, by introducing the relationship
(see Equations (49) and (54)) in order to establish and present the stability criterion. It is observed from
Figure 5a that as the value of
becomes large, i.e., for a porous layer close to the axis of rotation, the critical centrifugal Rayleigh number approaches a limit value of
. This corresponds to the critical Rayleigh number for the problem of a rotating layer adjacent to the axis of rotation as presented by Vadasz [
38]. The stability map on the
plane is presented in
Figure 5b, showing that the plane is divided between the stable and unstable zones by the straight line
.
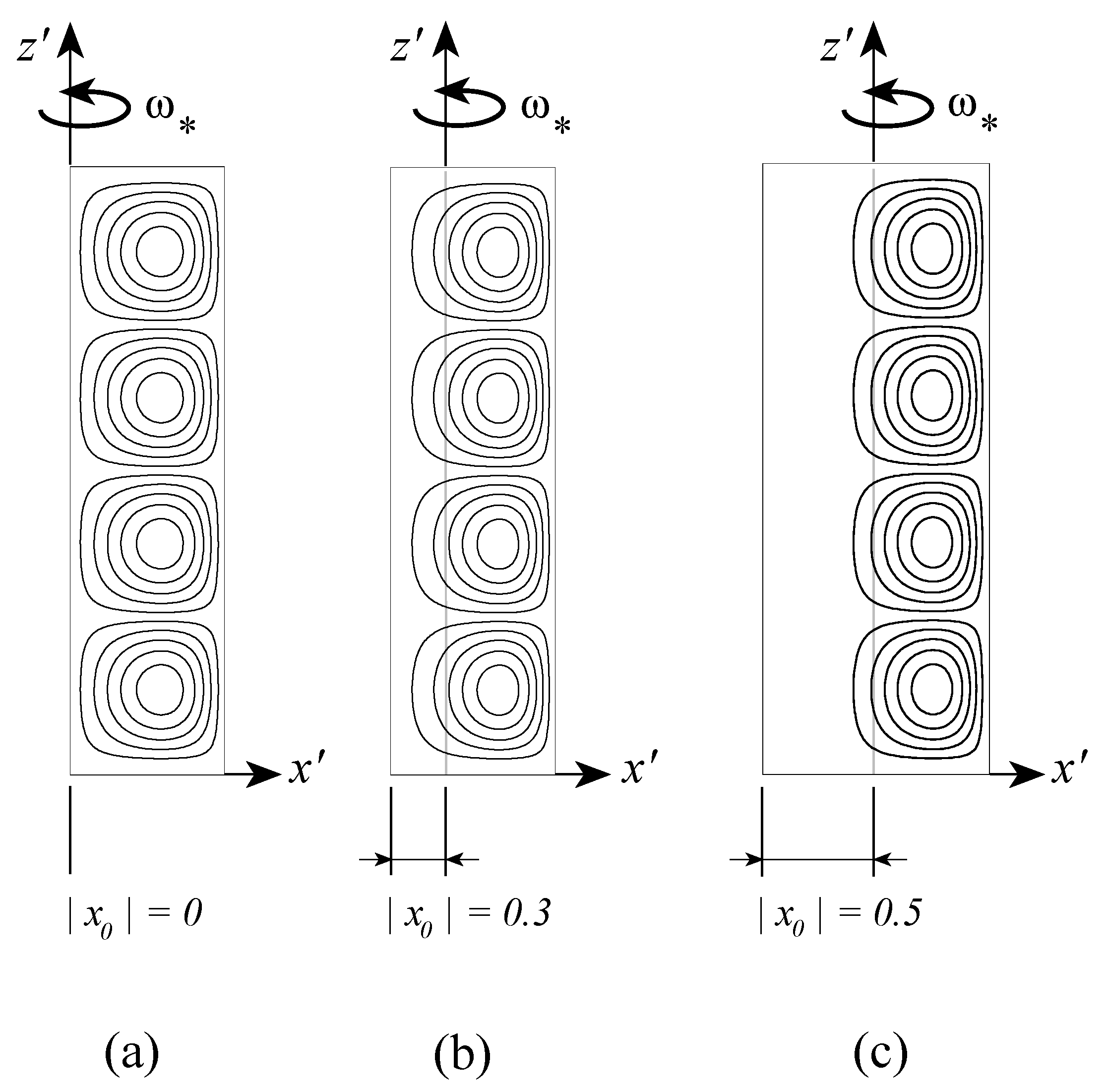
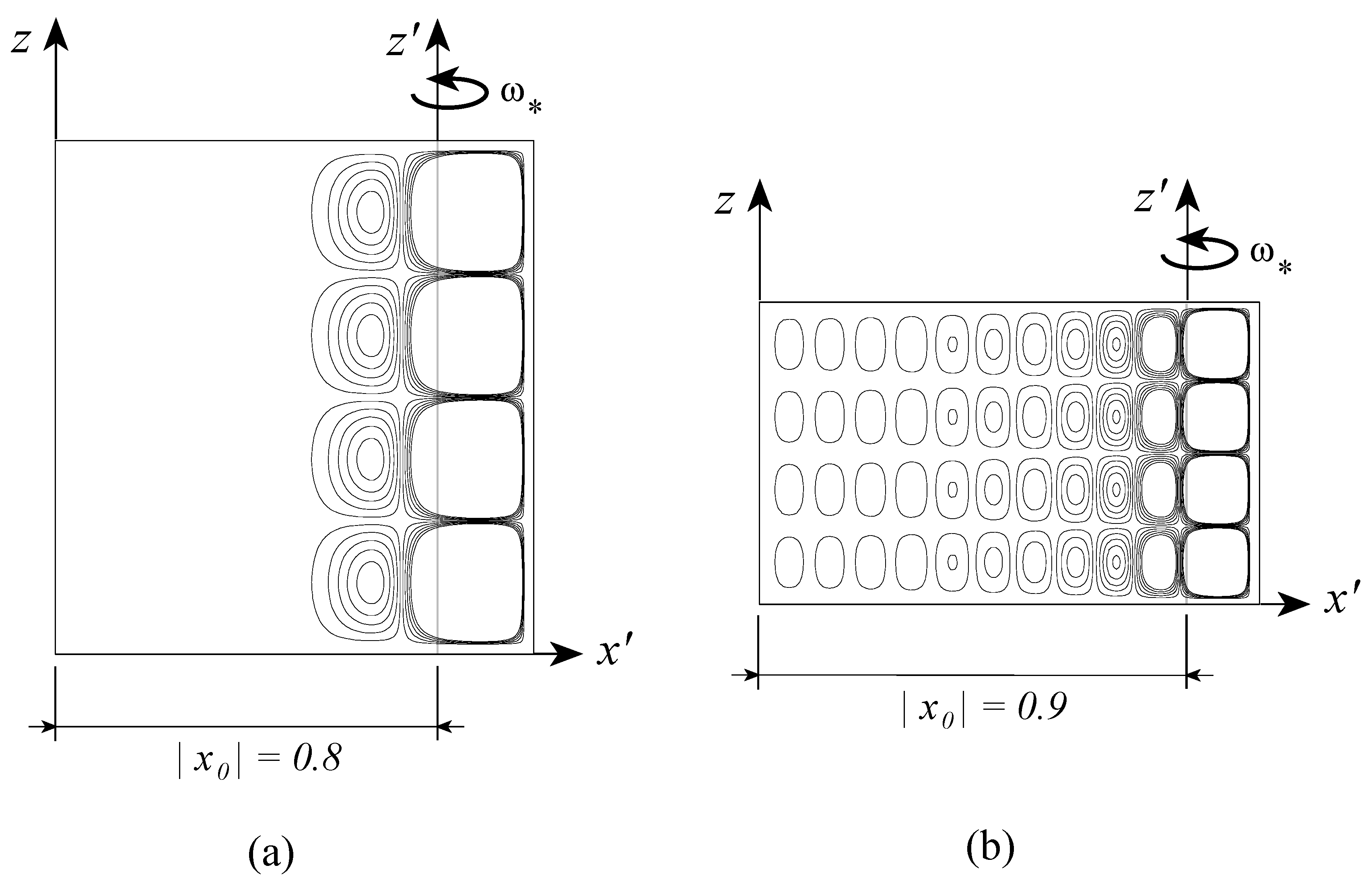
The results for the convective flow field are presented graphically in
Figure 6 following Vadasz [
40], where it was concluded that the effect of the variation of the centrifugal acceleration within the porous layer is definitely felt when the box is close to the axis of rotation, corresponding to an eccentric shift of the convection cells towards the sidewall at
. However, when the layer is located far away from the axis of rotation (e.g.,
) the convection cells are concentric and symmetric with respect to
as expected for a porous layer subject to gravity and heated from below (here “below” means the location where
).
Although the linear stability analysis is sufficient for obtaining the stability condition of the motionless solution and the corresponding eigenfunctions describing qualitatively the convective flow, it cannot provide information regarding the values of the convection amplitudes, nor regarding the average rate of heat transfer. To obtain this additional information, Vadasz and Olek [
46] analyzed and provided a solution to the non-linear equations by using Adomian’s decomposition method to solve a system of ordinary differential equations for the evolution of the amplitudes.
This system of equations was obtained by using the first three relevant Galerkin modes for the stream function and the temperature in the form
where
,
,
being the layer’s aspect ratio,
,
, and
the possibly time dependent amplitudes of convection. In this model it was considered of interest including the time derivative term in Darcy’s equation in the form
, where
, and
are the Darcy and the effective Prandtl numbers, respectively, defined as
and
(see Equation (58) with
and
). The reason for including the time derivative term in the Darcy equation was the fact that one anticipates oscillatory and possibly chaotic solutions for which very high frequencies may occur. Then, the following equations were obtained for the time evolution of the amplitudes
where
, and
is a rescaled Rayleigh number introduced above according to the definitions in the text following Equation (56). The results obtained are presented in
Figure 7 in the form of projection of trajectories data points onto the
and
planes. Different transitions as the value of
varies are presented and they relate to the convective fixed point which is a stable simple node in
Figure 7a, a stable spiral in
Figure 7b,c, and loses stability via an inverse Hopf bifurcation in
Figure 7d, where the trajectory describes a limit cycle, moving towards a chaotic solution presented in
Figure 7e,f. A further transition from chaos to a periodic solution was obtained at a value of
slightly above 100, which persists over a wide range of
values. This periodic solution is presented in
Figure 7g,h for
.
Previously in this section (see Equation (53)) a singularity in the solution was identified and associated with negative values of the offset distance from the axis of rotation. It is this resulting singularity and its consequences, which were investigated by Vadasz [
41] and are the objective of the following presentation. As this occurs at negative values of the offset distance from the axis of rotation it implies that the location of the rotation axis falls within the boundaries of the porous domain, as presented in
Figure 8. This particular axis location causes positive values of the centrifugal acceleration on the right side of the rotation axis and negative values on its left side. The rotation axis location implies that the value of
is not positive. The solution for this case is similar to the previous case leading to the same characteristic equation for
at order 2 as obtained previously in Equation (53) for
, with the only difference appearing in the different definition of
and
as follows
It is therefore convenient to explicitly introduce this fact in the problem formulation specifying explicitly that
. As a result Equation (50) can be expressed in the form
The singularity is obtained when
, corresponding to
or
. Since
is uniquely related to the offset distance
and
is a constant, one can relate the singularity to specific values of
. At order 2 this corresponds to
and
. It was shown by Vadasz [
41] that the second value
is the only one, which has physical consequences. This value corresponds to a transition beyond which, i.e., for
, no positive roots of
exist. It therefore implies an unconditional stability of the basic motionless solution for all values of
if
. The transitional value of
was investigated at higher orders showing
at order 3 and the value increases with increasing the order. The indications are that as the order increases the transition value of
tends towards the limit value of 1. The results for the critical values of the centrifugal Rayleigh number expressed in terms of
vs.
are presented graphically by Vadasz [
41], who concluded that increasing the value of
has a stabilizing effect. The results for the convective flow field as obtained by Vadasz [
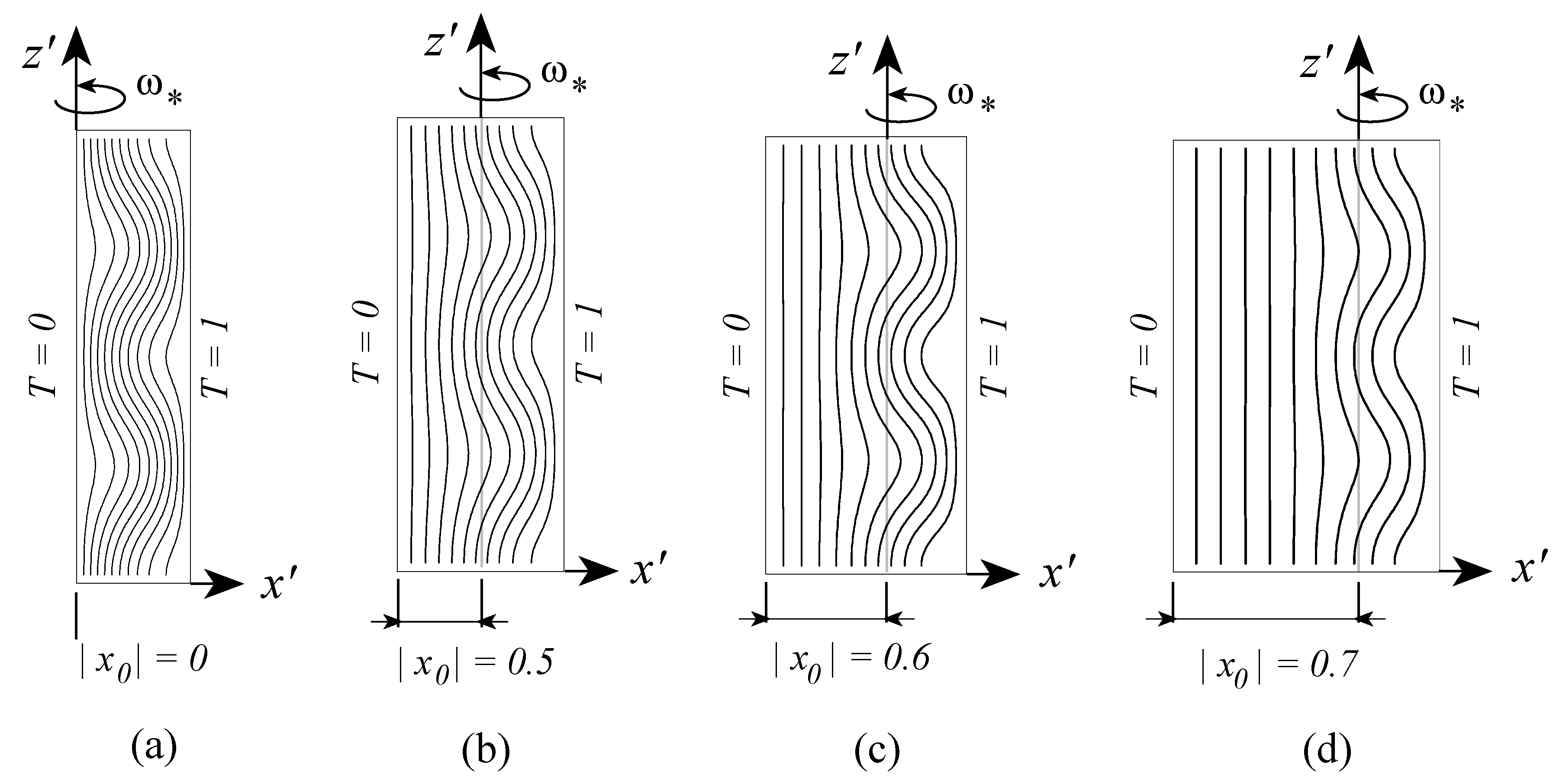
41] are presented in
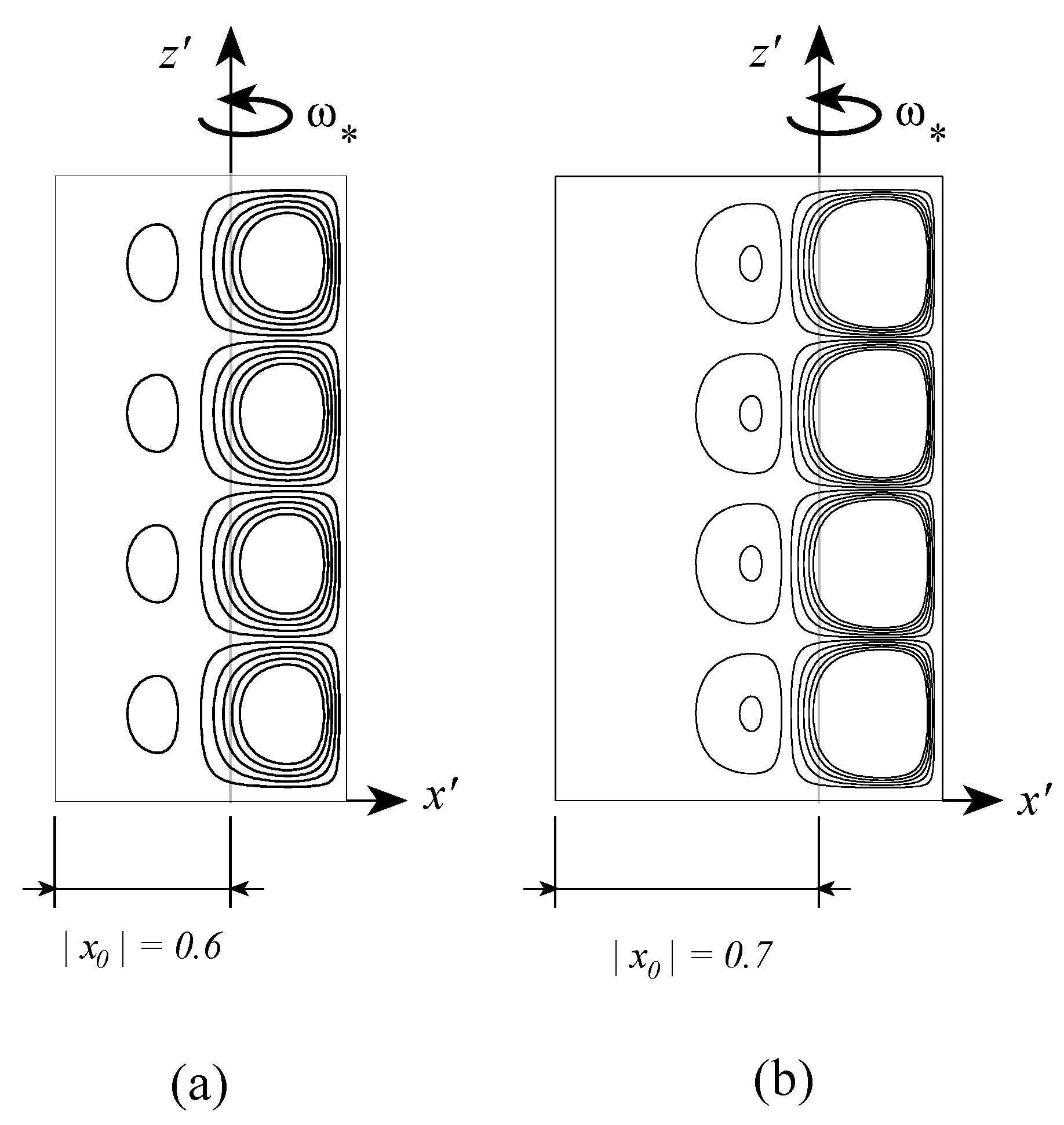
Figure 9,
Figure 10 and
Figure 11 for different values of
. Keeping in mind that to the right of the rotation axis the centrifugal acceleration has a destabilizing effect while to its left a stabilizing effect is expected; the results presented in
Figure 9b,c reaffirm this expectation showing an eccentric shift of the convection cells towards the right side of the rotation axis. When the rotation axis is moved further towards the hot wall, say at
as presented in
Figure 10a, weak convection cells appear even to the left of the rotation axis. This weak convection becomes stronger as
increases, as observed in
Figure 10b for
and formation of boundary layers associated with the primary convection cells is observed to the right of the rotation axis. These boundary layers become more significant for
as represented by sharp streamlines gradients in
Figure 11a. When
Figure 11b shows that the boundary layers of the primary convection are well established and the whole domain is filled with weaker secondary, tertiary and further convection cells. The results for the isotherms corresponding to values of
are presented in
Figure 12 where the effect of moving the axis of rotation within the porous layer, on the temperature is evident.
Previously the discussion focused on centrifugally driven natural convection under conditions of small rotation rates, i.e.,
. Then, as a first approximation the Coriolis effect was neglected. In this section the effect of the Coriolis acceleration on natural convection is presented even when this effect is small, i.e.,
. A long rotating porous box where the temperature gradient was perpendicular to the centrifugal body force was considered by Vadasz [
35]. The possibility of internal heat generation was included but the case without heat generation, i.e., when the box is heated from above and cooled from below was dealt with separately. The leading order basic flow was evaluated analytically. From the solutions it was concluded that the Coriolis effect on natural convection is controlled by the combined dimensionless group
The flow and temperature fields in the plane , perpendicular to the leading order natural convection plane as evaluated through the analytical solution shows single or double vortices secondary flow in this plane, perpendicular to the basic flow.
6. Natural Convection Due to Combined Centrifugal and Gravity Buoyancy
Previous sections dealt with natural convection due to centrifugal buoyancy, when the gravity body force contribution was negligible,
, satisfying the condition:
, or with gravity buoyancy when the centrifugal body force contribution was insignificant,
, satisfying the condition:
. In the present section the focus is on conditions when both centrifugal buoyancy as well as gravity buoyancy effects are significant,
, but at small rotation rates, i.e.,
. Then, as a first approximation the Coriolis effect can be neglected.
Figure 4 still applies to the present problem, subject to a slight modification of drawing the gravity acceleration
in the negative
direction. The notation remains the same and Equation (50) becomes
where
represents the reciprocal of the offset distance from the axis of rotation. The approach being the same as before, the solution is expressed as a sum of a basic solution and small perturbations as presented in Equation (52). However, because of the presence of the gravity component in Equation (65), a motionless conduction solution is not possible any more. Therefore, the basic solution far from the top and bottom walls is obtained in the form
Substituting this basic solution into the governing equations and linearizing the result by neglecting terms that include products of perturbations, which are small, yields a set of partial differential equations for the perturbations. Assuming a normal modes expansion in the
and
directions in the form
where
and
are the wave numbers in
and
directions respectively, i.e.,
, and using the Galerkin method, the following set of linear algebraic equations is obtained at marginal stability (i.e., for
)
for
and
. In Equation (68)
is the Kronecker delta function and the index
can take arbitrary integer values, since it stands only for setting the second index in the Kronecker delta function to be an odd integer. A particular case of interest is the configuration when the layer is placed far away from the axis of rotation, i.e., when the length of the layer
is much smaller than the offset distance from the rotation axis
. Therefore for
or
the contribution of the term
in Equation (65) is not significant. Substitution of this limit into Equation (68) and solving the system at the second order, i.e.,
, yields a quadratic equation for the characteristic values of
. This equation has no real solutions for values of
beyond a transitional value
. This value was evaluated at higher orders too, showing that for
the transitional value varies very little with
, beyond a certain
value around
. The critical values of
were evaluated for different values of
and the corresponding two-dimensional convection solutions in terms of streamlines are presented graphically for the odd modes in
Figure 16a, showing the perturbation solutions in the
plane as skewed convection cells when compared with the case without gravity. The corresponding convection solutions for the even modes are presented in
Figure 16b, where it is evident that the centrifugal effect is felt predominantly in the central region of the layer, while the downwards and upwards basic gravity driven convection persists along the left and right boundaries, respectively, although not in straight lines. Beyond the transition value of
, the basic gravity driven convective flow (Equation (66)) is unconditionally stable. These results were shown to have an analogy with the problem of gravity driven convection in a non-rotating, inclined porous layer (Govender and Vadasz [
29]). Qualitative experimental confirmation of these results was presented by Vadasz and Heerah [
45] by using a thermo-sensitive liquid-crystal tracer in a rotating Hele-Shaw cell. When the layer is placed at an arbitrary finite distance from the axis of rotation no real solutions exist for the characteristic values of
corresponding to any values of
other than
. In the presence of gravity
, and
can be satisfied only if
. Therefore the presence of gravity in this case has no other role but to exclude the vertical modes of convection. The critical centrifugal Rayleigh numbers and the corresponding critical wave numbers are the same as in the corresponding case without gravity as presented in
Section 4. However, the eigenfunctions representing the convection pattern are different as they exclude the vertical modes replacing them with a corresponding horizontal mode in the
direction. Therefore, a cellular convection in the
plane is superimposed to the basic convection in the
plane.
7. Additional Effects on Flow and Natural Convection in Rotating Porous Media
Not much research results are available for thermo-haline convection in porous media subject to rotation. Chakrabarti and Gupta [
78] investigated a non-Darcy model, which includes the Brinkman term as well as a non-linear convective term in the momentum equation (in the form
). Therefore the model’s validity is subject to the limitations pointed out by Nield [
69]. Both linear and non-linear analyses were performed and overstability was particularly investigated. Overstability is affected in this case by both the presence of a salinity gradient and by the Coriolis effect. Apart from the thermal and solutal Rayleigh numbers and the Taylor number, two additional parameters affect the stability. These are the Prandtl number
, and the Darcy number
, where
is the layer’s height. The authors found that, in the range of values of the parameters, which were considered, the linear stability results favor setting-in of convection through a mechanism of overstability. The results for non-linear steady convection show that the system becomes unstable to finite amplitude steady disturbances before it becomes unstable to disturbances of infinitesimal amplitude. Thus the porous layer may exhibit subcritical instability in the presence of rotation. These results are surprising at least in the sense of their absolute generality and the authors mention that further confirmation is needed in order to increase the degree of confidence in these results. A similar problem was investigated by Rudraiah et al. [
16] while focusing on the effect of rotation on linear and non-linear double-diffusive convection in a sparsely packed porous medium. A non-Darcy model identical to the one used by Chakrabarti and Gupta [
78] was adopted by Rudraiah et al. [
16], however the authors spelled out explicitly that the model validity is limited to high porosity and high permeability which makes it closer to the behavior of a pure fluid system (non-porous domain). It is probably for this reason that the authors preferred to use the non-porous medium definitions for Rayleigh and Taylor numbers which differ by a factor of
and
, respectively, from the corresponding definitions for porous media. It is because of these definitions that the authors concluded that for small values of
number the effect of rotation is negligible for values of
. This means that rotation has a significant effect for large rotation rates, i.e.,
. If the porous media Taylor number had been used instead, i.e., the proper porous media scales, then one could have significant effects of rotation at porous media Taylor numbers as small as
. Hence, the results presented by Rudraiah et al. [
16] are useful provided
which is applicable for high permeability (or sparsely packed) porous layers. Marginal stability as well as overstability were investigated and the results show different possibilities of existence of neutral curves by both mechanisms, i.e., monotonic as well as oscillatory instability. In this regard the results appear more comprehensive in the study by Rudraiah et al. [
16] than in Chakrabarti and Gupta [
78]. The finite amplitude analysis was performed by using a severely truncated representation of a Fourier series for the dependent variables. As a result a seventh-order Lorenz model of double diffusive convection in a porous medium in the presence of rotation was obtained. From the study of steady, finite amplitude analysis the authors found that subcritical instabilities are possible, depending on the parameter values. The effect of the parameters on the heat and mass transport was investigated as well, and results presenting this effect are discussed in Rudraiah et al. [
16]. The onset of double-diffusive convection in a rotating porous layer was investigated by Lombardo and Mulone [
60], Malashety, Pop, and Heera [
48], Falsaperla, Giacobbe and Mulone [
63]. Triple-diffusion effects in rotating porous layers were investigated by Capone and De Luca [
64]. They evaluated the ultimate boundedness of the solutions and found a necessary and sufficient condition for the global nonlinear asymptotic
L2-stability of the motionless conduction solution.
Lack of local thermal equilibrium (LaLotheq) or local thermal non-equilibrium (LTNE) means that distinct temperature values exist between the solid and fluid phases within the same Representative Elementary Volume (REV). Malashetty et al. [
53] presented the linear stability and the onset of convection in a porous layer heated from below and subject to rotation, accounting for the Coriolis effect as in Vadasz [
42] but allowing for distinct temperature values between the solid and fluid phases, i.e., lack of local thermal equilibrium (LaLotheq), or local thermal non-equilibrium (LTNE). The nonlinear part of the analysis was undertaken by using a truncated mode spectral system, such as the one used by Vadasz and Olek [
46] but adapted for the LaLotheq conditions. The effect of finite heat transfer between the phases leading to lack of local thermal equilibrium was investigated also by Govender and Vadasz [
32] while investigating also the effect of mechanical and thermal anisotropy on the stability of a rotating porous layer heated from below and subject to gravity. The topic of anisotropic effects is discussed in the next section. Bhadauria [
47] investigated the effect of temperature modulation on the onset of thermal instability in a horizontal fluid-saturated porous layer heated from below and subject to uniform rotation. An extended Darcy model, which includes the time derivative term, has been considered, and a time-dependent periodic temperature field was applied to modulate the surfaces’ temperature. A perturbation procedure based on small amplitude of the imposed temperature modulation was used to study the combined effect of rotation, permeability, and temperature modulation on the stability of the fluid saturated porous layer. The correction of the critical Rayleigh number was calculated as a function of amplitude and frequency of modulation, the porous media Taylor number, and the Vadasz number. It was found that both rotation and permeability suppress the onset of thermal instability. Furthermore, the author concluded that temperature modulation could either promote or retard the onset of convection.
The effect of anisotropy on the stability of convection in a rotating porous layer subject to centrifugal body forces was investigated by Govender [
25]. The Darcy model extended to include anisotropic effects and rotation was used to describe the momentum balance and a modified energy equation that included the effects of thermal anisotropy was used to account for the heat transfer. The linear stability theory was used to evaluate the critical Rayleigh number for the onset of convection in the presence of thermal and mechanical anisotropy. It was found that the convection was stabilized when the thermal anisotropy ratio (which is a function of the thermal and mechanical anisotropy parameters) increased in magnitude. Malashetty and Swamy [
54], and Govender and Vadasz [
32] investigated the Coriolis effect on natural convection in a rotating anisotropic fluid-saturated porous layer heated from below and subject to gravity as the body force. Malashetty and Swamy [
54] assumed local thermal equilibrium while Govender and Vadasz [
32] dealt with lack of local thermal equilibrium (LaLotheq), or local thermal non-equilibrium (LTNE). Malashetty and Swamy [
54] used the linear stability theory as well as a nonlinear spectral method. The linear theory was based on the usual normal mode technique and the nonlinear theory on a truncated Galerkin analysis. The Darcy model extended to include a time derivative and the Coriolis terms with an anisotropic permeability was used to describe the flow through the porous media. A modified energy equation including the thermal anisotropy was used. The effect of rotation, mechanical and thermal anisotropy parameters and the Prandtl number on the stationary and overstable convection was discussed. It was found that the effect of mechanical anisotropy is to prefer the onset of oscillatory convection instead of the stationary one. It was also found, just as in Vadasz [
42], that the existence of overstable motions in case of rotating porous media is not restricted to a particular range of Prandtl number as compared to the pure viscous fluid case. The steady finite amplitude analysis was performed using the truncated Galerkin modes to find the Nusselt number. The effect of various parameters on heat transfer was investigated. Govender and Vadasz [
32] analyzed the stability of a horizontal rotating fluid saturated porous layer exhibiting both thermal and mechanical anisotropy, subject to lack of local thermal equilibrium (LaLotheq), or local thermal non-equilibrium (LTNE). All of the results were presented as a function of the scaled inter-phase heat transfer coefficient. The results of the linear stability theory have revealed that increasing the conductivity ratio and the mechanical anisotropy has a destabilizing effect, whilst increasing the fluid and solid thermal conductivity ratios is stabilizing. In general it was found that rotation has a stabilizing effect in a porous layer exhibiting mechanical or thermal (or both mechanical and thermal) anisotropy. Additional results for the effect of rotation on thermal convection in an anisotropic porous medium were presented by Vanishree and Siddheshwar [
49].
An interesting, more recent, application is related to nanofluids. A nanofluid is a suspension of nanoparticles or nanotubes in a liquid. When the liquid is saturating a porous matrix one deals with nanofluids in porous media. Chand and Rana [
79] analyzed the Coriolis effect on natural convection in a rotating porous layer saturated by a nanofluid. Agarwal an Bhadauria [
52], Rana and Agarwal [
55], investigated the natural convection in a rotating porous layer saturated by a nanofluid and a binary mixture. This implies that the nanoparticles are suspended in a binary mixture, e.g., in a water and salt solution. Therefore double-diffusive convection is anticipated. The model used for the nanofluid incorporates the effects of Brownian motion and thermophoresis, while the Darcy model is used for the porous medium. The neutral and critical Rayleigh numbers for stationary and oscillatory convection have been obtained in terms of various dimensionless parameters. The authors concluded that the principle of exchange of stabilities is applicable in the present problem, while more amount of heat is required in the nanofluid case for convection to set-in. Agarwal et al. [
50] considered the convection in a rotating anisotropic porous layer saturated by a nanofluid. The model used for nanofluid combines the effect of Brownian motion along with thermophoresis, while for a porous medium the Darcy model has been used. Using linear stability analysis the expression for the critical Rayleigh number has been obtained in terms of various dimensionless parameters. Agarwal et al. [
50] indicate that bottom-heavy and top-heavy arrangements of nanoparticles tend to prefer oscillatory and stationary modes of convection, respectively. The onset of double-diffusive nanofluid convection in a rotating porous layer was investigated by Yadav et al. [
56].
During solidification of binary alloys the solidification front between the solid and the liquid phases is not a sharp front but rather a mushy layer combining liquid and solid phases each one being interconnected. It is not surprising therefore that the treatment of this mushy layer follows all the rules applicable to a porous medium. Natural convection due to thermal as well as concentration gradients occurs in the mushy layer resulting in possible creation of freckles that might affect the quality of the cast. When such a process occurs in a system that is subject to rotation, centrifugal buoyancy as well as Coriolis effects are relevant and essential to be included in any model of this process. Govender and Vadasz [
31] investigated such a system via a weak nonlinear analysis for moderate Stefan numbers applicable to stationary convection in a rotating mushy layer. Consequently Govender and Vadasz [
30] investigated a similar system via a weak nonlinear analysis for moderate Stefan numbers applicable to oscillatory convection in a rotating mushy layer. A near-eutectic approximation and large far-field temperature were employed in both papers in order to decouple the mushy layer from the overlying liquid melt. The parameter regimes in terms of Taylor number for example where the bifurcation is subcritical or supercritical were identified. In the case of oscillatory convection increasing the Taylor number lead to a supercritical bifurcation.
Linear stability was the primary method used in previous sections to establish the stability criteria for the onset of natural convection in a rotating porous layer. Straughan [
73] pioneered the introduction of a nonlinear analysis producing a sharp nonlinear stability threshold in rotating porous convection. The application and generalization of this method was presented by Lombardo and Mulone [
60], while deriving necessary and sufficient conditions of global nonlinear stability for double-diffusive convection in rotating porous media. The nonlinear method was expanded and summarized by Straughan [
59]. The application of this nonlinear method to natural convection in non-rotating porous media was expanded showing the coincidence between linear and global nonlinear stability of non-constant through-flows was presented by Capone and De Luca [
66] by using the “Rionero Auxiliary System Method”. Weak nonlinear solutions were presented by Bhadauria et al. [
51]. Investigations into the effects of inertia on rotating porous convection were undertaken by Falsaperla, Mulone, and Straughan [
62], and by Capone and Rionero [
65]. The latter used again the “Rionero Auxiliary System Method” to derive a set of conditions for the significance of inertia in this problem and for global nonlinear stability in terms of the porous media Taylor number as well as Vadasz number.
Other studies considered effects of rotation for a combination of previously presented conditions. For example Capone and Gentile [
80] presented sharp stability results in a rotating anisotropic porous layer subject to lack of local thermal equilibrium (LaLotheq, LTNE). Double diffusive convection in a rotating anisotropic porous layer was presented by Galkwad and Kouser [
81], Malashetty and Heera [
82], and Malashetty and Begum [
83]. Double diffusive convection in a rotating porous medium saturated with a coupled stress fluid was considered by Malashetty et al. [
84], while double diffusive convection in a rotating porous layer saturated by a viscoelastic fluid was investigated by Kumar and Bhadauria [
85]. The effect of rotation on a micropolar ferromagnetic fluid heated from below saturating a porous medium was presented by Sunil et al. [
86]. Rotation effects on convection in a porous layer saturated by nanofluids was further considered by Bhadauria and Agrawal [
87], for a porous medium model including the Brinkman term. A similar model was presented by Yadav and Lee [
88] for the case of lack of local thermal equilibrium (LaLotheq, LTNE), and by Yadav et al. [
89] for a Darcy model Soret driven convection in a rotating porous medium saturated by a nanofluid. Brinkman convection induced by internal heating in a rotating porous medim layer saturated by a nanofluid was investigated by Yadav et al. [
90], while thermal instability in a rotating porous layer saturated by a non-Newtonian nanofluid was considered by Yadav et al. [
91]. Yadav et al. [
92] presented the conditions for the onset of convection in a rotating porous layer due internal heating by using a Brinkman model. The effects of thermal modulation, i.e., top and bottom imposed temperatures are allowed to vary slightly in time, were considered by Malashetty and Swamy [
93] using a Darcy model and Bhadauria [
94] using a Brinkman model. A similar Brinkman model was applied for investigating the effects of centrifugal buoyancy in a rotating porous layer far away from the center of rotation subject to modulation of rotation by Om et al. [
95], i.e., the angular velocity was allowed to slightly vary periodically in time. The same conditions applied to a rotating porous layer distant an arbitrary distance from the center of rotation was presented by Om et al. [
96]. Coriolis effect on thermal convective instability of viscoelastic fluids in a rotating porous cylindrical annulus was investigated by Kang et al. [
97]. Küppers-Lortz instability in rotating Rayleigh-Benard convection in a porous medium was studied by Rameshwar et al. [
98].