Three-Dimensional Interaction of Viscous Fingering and Gravitational Segregation in Porous Media
Abstract
1. Introduction
2. Materials and Methods
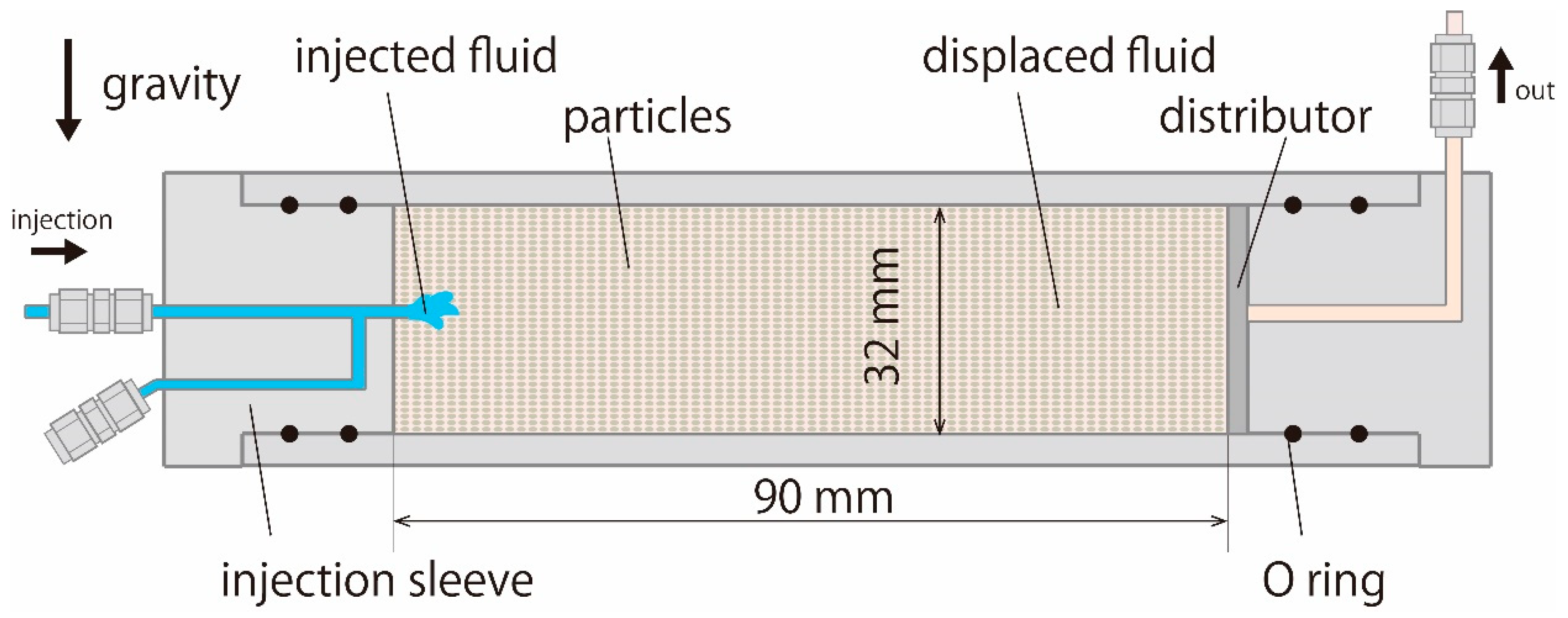
2.1. Experimental Apparatus
2.2. Experimental Procedure
2.3. Experimental Conditions
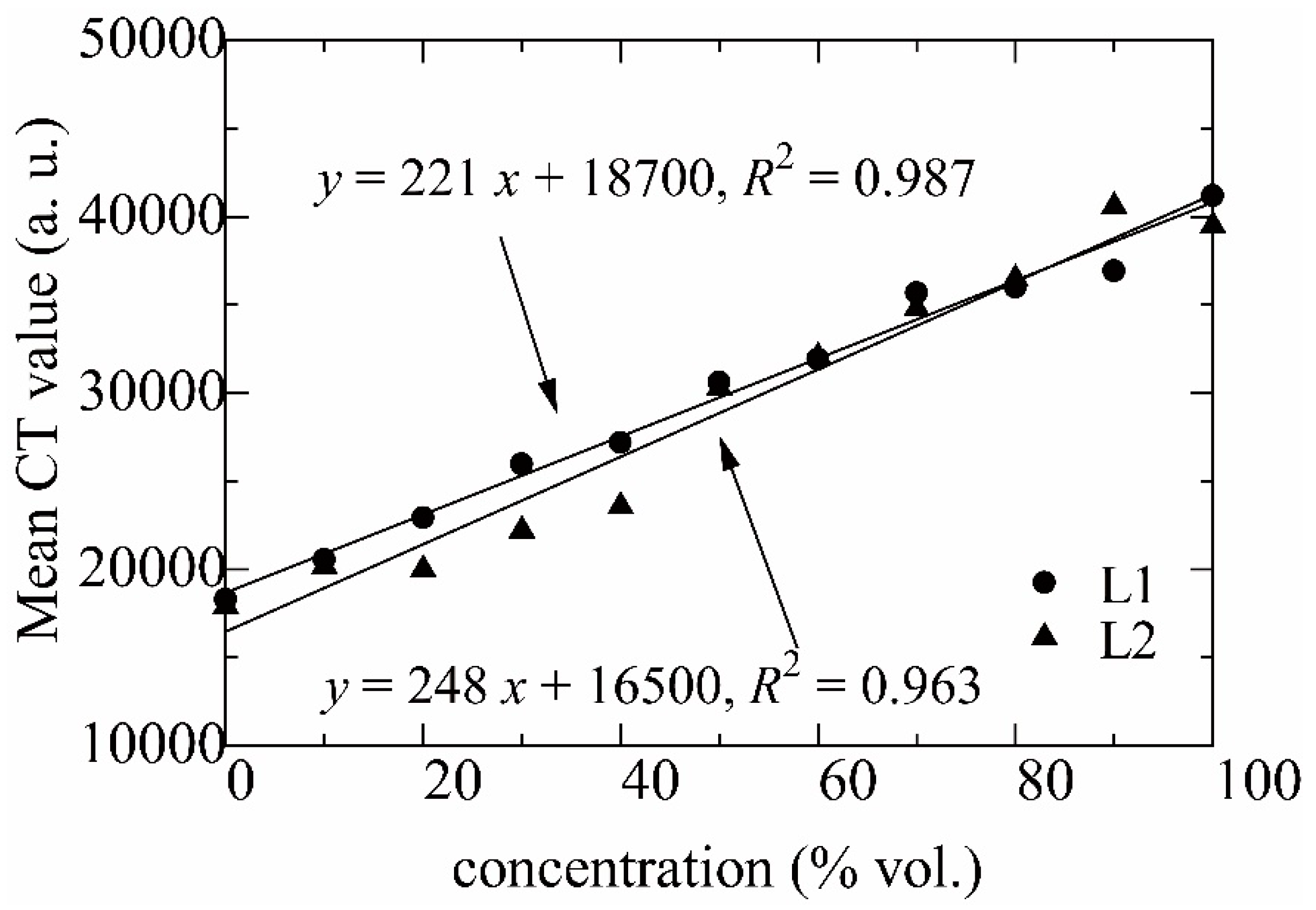
2.4. Image Processing
- Rough-cut: the undesirable black background area around the cylinder was eliminated to allow focus on the porous medium in the next step of image processing.
- Adjustment: to eliminate the drift in brightness of the CT images among the scans; the brightness of the CT images was adjusted to ensure a constant CT value for the cylinder wall.
- Noise Removal: a noise filter was applied to remove local bright noise associated with impurities in the particles.
- Subtract: to enhance the finger structure, the “after” scan image was subtracted from the “before” scan image.
3. Results and Discussion
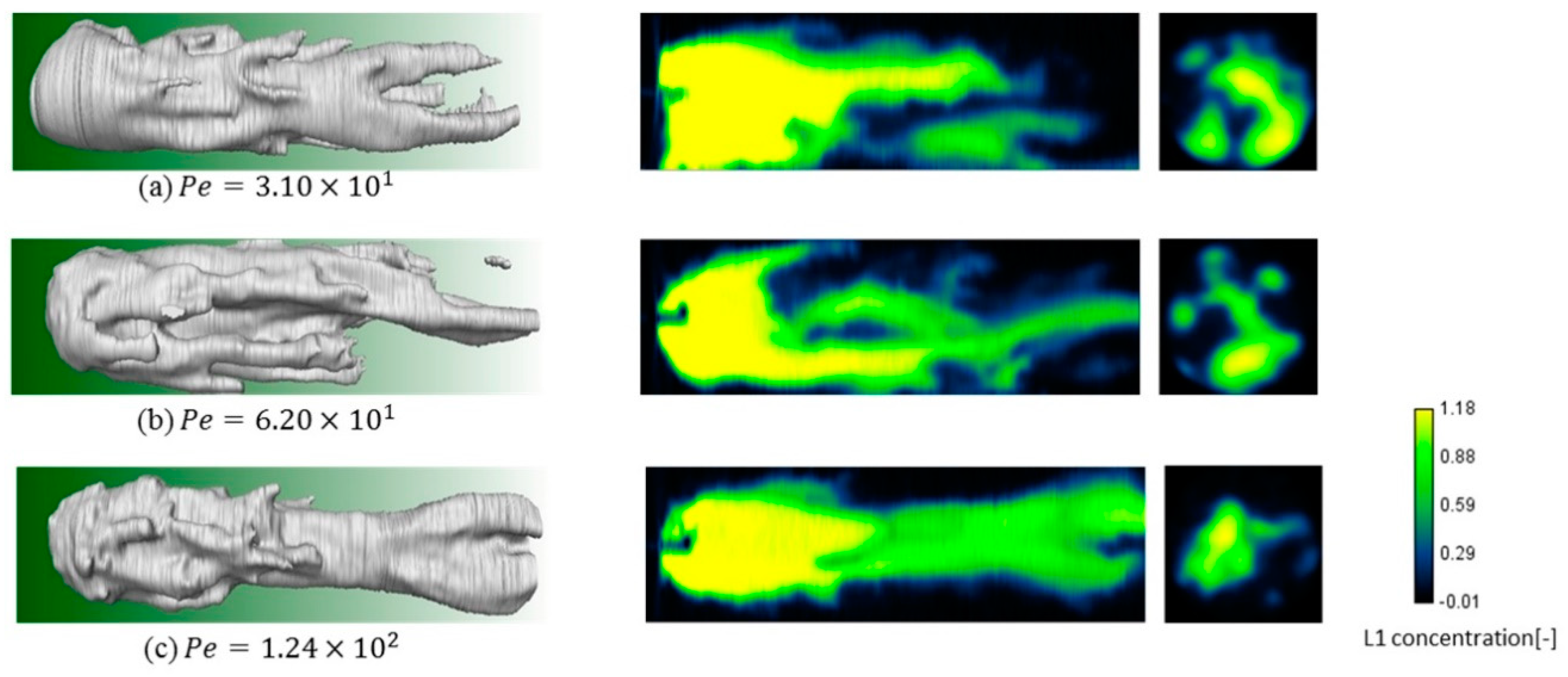
3.1. Three-Dimensional Structure
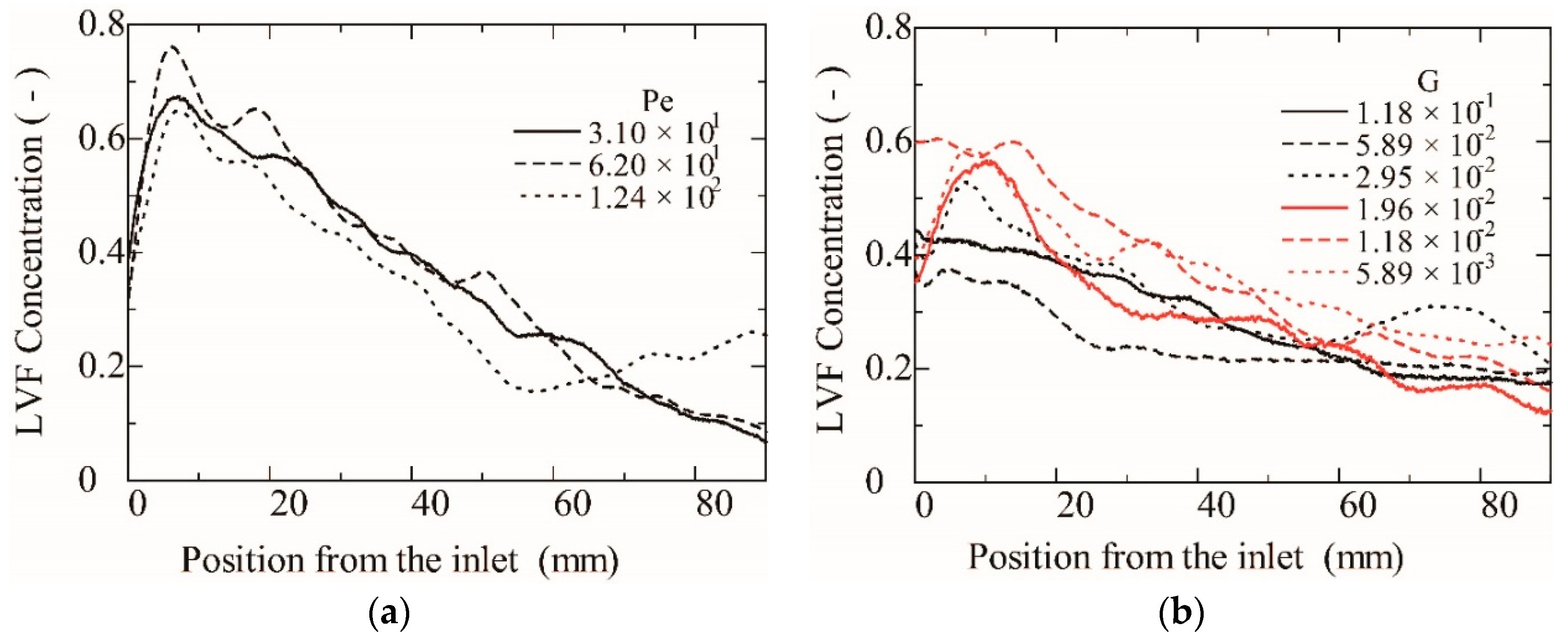
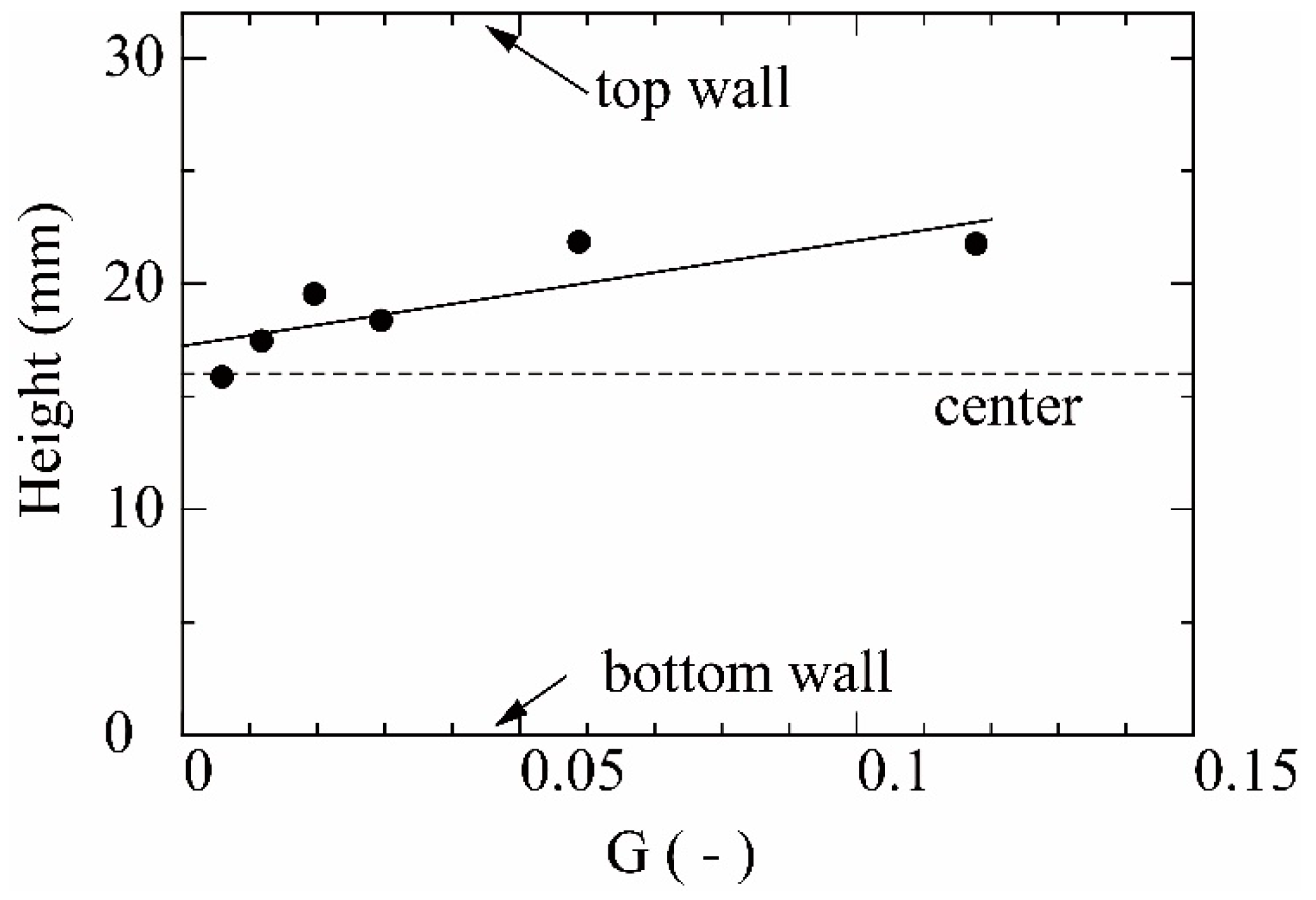
3.2. Concentration Profiles and the Center of Gravity of LVF
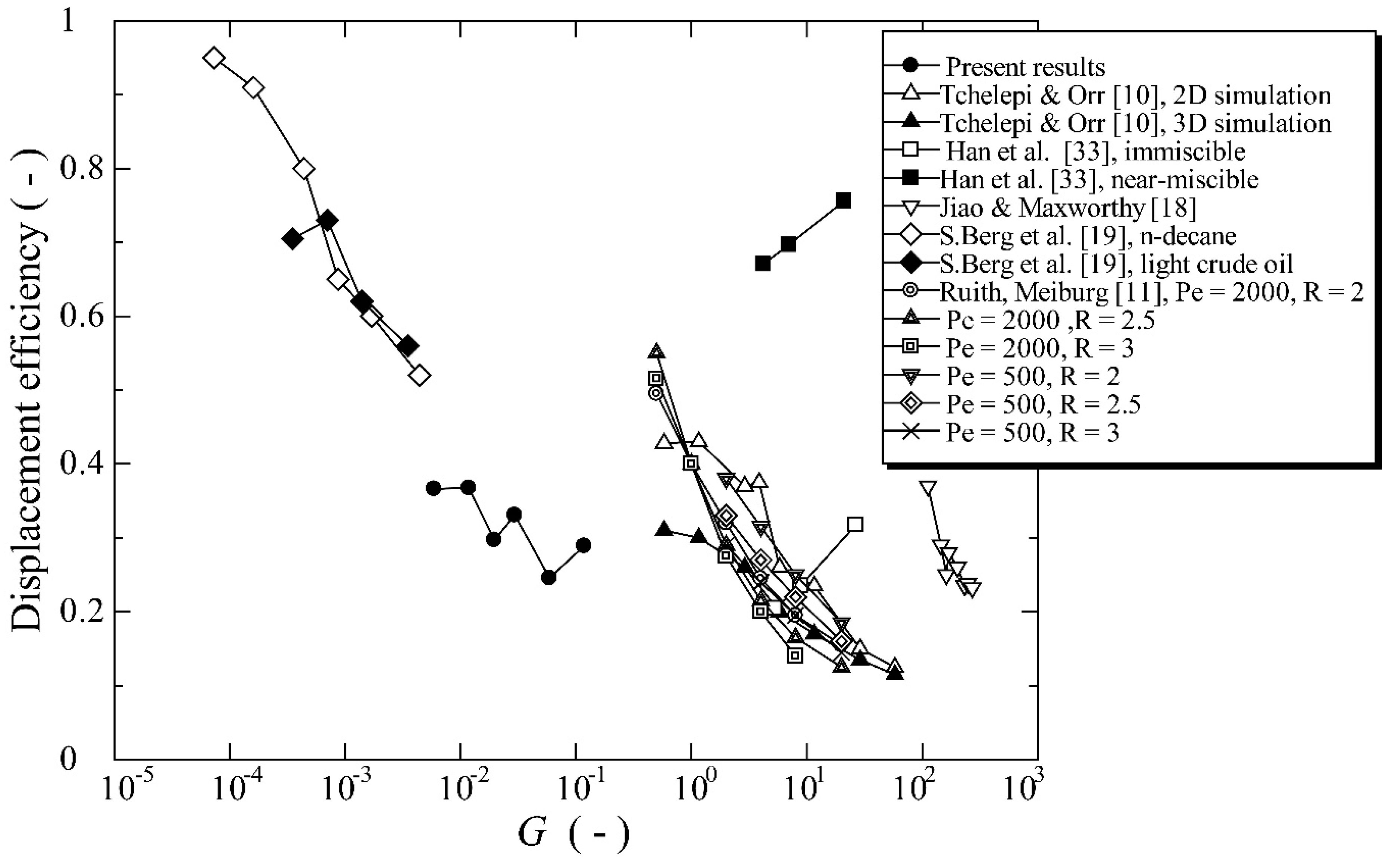
3.3. Displacement Efficiency
4. Conclusions
- At a low gravity number, viscous fingering like that without gravity occurs showing nonlinear interactions like tip-splitting, shielding, and coalescence.
- At a moderate gravity number, the gravitational tongue and viscous fingering appeared simultaneously, and the concentration of LVF in the gravitational tongue was higher than that in the finger.
- At a high gravity number, a clear gravitational tongue penetrated from the inlet to the outlet, whereas viscous fingering was only observed around the inlet. In the gravitational tongue, the concentration of LVF increases as the position gets closer to the top wall in the gravity direction.
- The averaged concentration near the inlet reduces with an increase in the gravity number and is characterized by a flat concentration profile. The average concentration at the gravitational tongue was almost constant at 0.2.
- The displacement efficiency decreases with the gravity number from the highest value achieved without gravity but depends on many factors, including the viscosity ratio and Péclet number.
Author Contributions
Funding
Conflicts of Interest
References
- Homsy, G.M. Viscous Fingering in Porous Media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Kueper, B.H.; Frind, E.O. An overview of immiscible fingering in porous media. J. Contam. Hydrol. 1988, 2, 95–110. [Google Scholar] [CrossRef]
- McCloud, K.; Maher, J. Experimental perturbations to Saffman-Taylor flow. Phys. Rep. 1995, 260, 139–185. [Google Scholar] [CrossRef]
- Hill, S.; Inst, P.F. Channeling in packed columns. Chem. Eng. Sci. 1952, 1, 247–253. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G.I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1958, 245, 312–329. [Google Scholar]
- Blackwell, R.J.; Rayne, J.R.; Terry, W.M. Factors influencing the efficiency of miscible displacement. Petrol. Trans. AIME 1959, 217, 1–8. [Google Scholar]
- Casademunt, J. Viscous fingering as a paradigm of interfacial pattern formation: Recent results and new challenges. Chaos Interdiscip. J. Nonlinear Sci. 2004, 14, 809. [Google Scholar] [CrossRef]
- Sahimi, M. Flow phenomena in rocks: From continuum models to fractals, percolation, cellular automata, and simulated annealing. Rev. Mod. Phys. 1993, 65, 1393–1534. [Google Scholar] [CrossRef]
- Fayers, F.J.; Muggeridge, A.H. Extensions to Dietz Theory and Behavior of Gravity Tongues in Slightly Tilted Reservoirs. SPE Reserv. Eng. 1990, 5, 487–494. [Google Scholar] [CrossRef]
- Tchelepi, H.A.; Orr, F.M., Jr. Interaction of viscous fingering, permeability heterogeneity, and gravity segregation in three dimensions. SPE Reserv. Eng. 1994, 9, 266–271. [Google Scholar] [CrossRef]
- Ruith, M.; Meiburg, E. Miscible rectilinear displacements with gravity override. Part 1. Homogeneous porous medium. J. Fluid Mech. 2000, 420, 225–257. [Google Scholar] [CrossRef]
- Camhi, E.; Meiburg, E.; Ruith, M. Miscible rectilinear displacements with gravity override. Part 2 Heterogeneous porous media. J. Fluid Mech. 2000, 420, 259–276. [Google Scholar] [CrossRef]
- Riaz, A.; Tchelepi, H.A. Numerical simulation of immiscible two-phase flow in porous media. Phys. Fluids 2006, 18, 014104. [Google Scholar] [CrossRef]
- Riaz, A.; Meiburg, E. Three-dimensional miscible displacement simulations in homogeneous porous media with gravity override. J. Fluid Mech. 2003, 494, 95–117. [Google Scholar] [CrossRef]
- Moortgat, J. Viscous and gravitational fingering in multiphase compositional and compressible flow. Adv. Water Resour. 2016, 89, 53–66. [Google Scholar] [CrossRef]
- Muggeridge, A.; Cockin, A.; Webb, K.; Frampton, H.; Collins, I.; Moulds, T.; Salino, P. Recovery rates, enhanced oil recovery and technological limits. Philos. Trans. R. Soc. 2014, 372, 20120320. [Google Scholar] [CrossRef]
- Zhang, H.; Sorbie, K.; Tsibuklis, N.; Sorbie, K. Viscous fingering in five-spot experimental porous media: New experimental results and numerical simulation. Chem. Eng. Sci. 1997, 52, 37–54. [Google Scholar] [CrossRef]
- Jiao, C.; Maxworthy, T. An experimental study of miscible displacement with gravity-override and viscosity-contrast in a Hele Shaw cell. Exp. Fluids 2008, 44, 781–794. [Google Scholar] [CrossRef]
- Berg, S.; Oedai, S.; Landman, A.J.; Brussee, N.; Boele, M.; Valdez, R.; Van Gelder, K. Miscible displacement of oils by carbon disulfide in porous media: Experiments and analysis. Phys. Fluids 2010, 22, 113102. [Google Scholar] [CrossRef]
- Richardson, J.; Sangree, J.; Sneider, R. Oil Recovery by Gravity Segregation. J. Pet. Technol. 1989, 41, 581–582. [Google Scholar] [CrossRef]
- Berg, S.; Ott, H. Stability of CO2 –brine immiscible displacement. Int. J. Greenh. Gas Control 2012, 11, 188–203. [Google Scholar] [CrossRef]
- Kumar, A.; Kimbler, O.K. Effect of Dispersion, Gravitational Segregation, and Formation Stratification on the Recovery of Freshwater Stored in Saline Aquifers. Water Resour. Res. 1970, 6, 1689–1700. [Google Scholar] [CrossRef]
- Suekane, T.; Ono, J.; Hyodo, A.; Nagatsu, Y. Three-dimensional viscous fingering in miscible displacement in porous media. Phys. Rev. Fluids 2017, 2, 103902. [Google Scholar] [CrossRef]
- Nakanishi, Y.; Hyodo, A.; Wang, L.; Suekane, T. Experimental study of 3D Rayleigh–Taylor convection between miscible fluids in a porous medium. Adv. Water Resour. 2016, 97, 224–232. [Google Scholar] [CrossRef]
- Wang, L.; Nakanishi, Y.; Hyodo, A.; Suekane, T. Three-dimensional structure of natural convection in a porous medium: Effect of dispersion on finger structure. Int. J. Greenh. Gas Control 2016, 53, 274–283. [Google Scholar] [CrossRef]
- Sin, S.; Suekane, T.; Nagatsu, Y.; Patmonoaji, A. Three-dimensional visualization of viscous fingering for non-Newtonian fluids with chemical reactions that change viscosity. Phys. Rev. Fluids 2019, 4, 054502. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, Y.; Yang, M.; Zhou, X.; Yu, M.; Zhang, Y.; Song, Y.; Xue, Z.; Suekane, T. Behavior of CO2/water flow in porous media for CO2 geological storage. Magn. Reson. Imaging 2016, 37, 100–106. [Google Scholar] [CrossRef]
- Suekane, T.; Furukawa, N.; Tsushima, S.; Hirai, S.; Kiyota, M. Application of MRI in the Measurement of Two-Phase Flow of Supercritical CO2 and Water in Porous Rocks. J. Porous Media 2009, 12, 143–154. [Google Scholar] [CrossRef]
- Suekane, T.; Soukawa, S.; Iwatani, S.; Tsushima, S.; Hirai, S. Behavior of supercritical CO2 injected into porous media containing water. Energy 2005, 30, 2370–2382. [Google Scholar] [CrossRef]
- Wang, L.; Nakanishi, Y.; Teston, A.D.; Suekane, T. Effect of diffusing layer thickness on the density-driven natural convection of miscible fluids in porous media: Modeling of mass transport. J. Fluid Sci. Technol. 2018, 13, 1–20. [Google Scholar] [CrossRef]
- Rasband, W.S. ImageJ U.S. National Institutes of Health, Bethesda, Maryland, USA. Available online: http://rsb.info.nih.gov/ij/ (accessed on 15 June 2019).
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Han, J.; Lee, M.; Lee, W.; Lee, Y.; Sung, W. Effect of gravity segregation on CO2 sequestration and oil production during CO2 flooding. Appl. Energy 2016, 161, 85–91. [Google Scholar] [CrossRef]

| Fluids | Composition | Density ρ (kg/m3) | Viscosity 1 μ (mPa·s) |
|---|---|---|---|
| M1 | Glycerol solution 85 wt.% glycerol | 1.21 × 103 | 138 |
| L1 | NaI + NaCl solution 7.85 wt.% NaI 21.5 wt.% NaCl | 1.21 × 103 | 2.63 |
| L2 | NaI solution 10 wt.% NaI | 1.07 × 103 | 1.16 |
| Fluids | Pe | Darcy Velocity v (m/s) | Viscosity Ratio M | Density Difference Δρ (kg/m3) | G |
|---|---|---|---|---|---|
| M1-L1 | 52.5 | 0 | 0 | ||
| M1-L2 | 119 | 140 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suekane, T.; Koe, T.; Barbancho, P.M. Three-Dimensional Interaction of Viscous Fingering and Gravitational Segregation in Porous Media. Fluids 2019, 4, 130. https://doi.org/10.3390/fluids4030130
Suekane T, Koe T, Barbancho PM. Three-Dimensional Interaction of Viscous Fingering and Gravitational Segregation in Porous Media. Fluids. 2019; 4(3):130. https://doi.org/10.3390/fluids4030130
Chicago/Turabian StyleSuekane, Tetsuya, Tomotaka Koe, and Pablo Marin Barbancho. 2019. "Three-Dimensional Interaction of Viscous Fingering and Gravitational Segregation in Porous Media" Fluids 4, no. 3: 130. https://doi.org/10.3390/fluids4030130
APA StyleSuekane, T., Koe, T., & Barbancho, P. M. (2019). Three-Dimensional Interaction of Viscous Fingering and Gravitational Segregation in Porous Media. Fluids, 4(3), 130. https://doi.org/10.3390/fluids4030130






