Abstract
A review on instability and consequent natural convection in rotating porous media is presented. Taylor-Proudman columns and geostrophic flows exist in rotating porous media just the same as in pure fluids. The latter leads to a tendency towards two-dimensionality. Natural convection resulting from density gradients in a gravity field as well as natural convection induced by density gradients due to the centripetal acceleration are being considered. The former is the result of gravity-induced buoyancy, the latter is due to centripetally-induced buoyancy. The effect of Coriolis acceleration is also discussed. Linear stability analysis as well as weak nonlinear solutions are being derived and presented.
1. Introduction
The research into the effects of rotation on the flow and transport phenomena in porous media is driven by the fundamental scientific significance as well as by engineering and geophysical applications. To be specific, one refers to flows in porous geological formations subject to earth rotation, to the flow of magma in the earth mantle close to the earth crust (Fowler [1]) as geophysical applications. The food process industry, chemical process industry, centrifugal filtration processes, and rotating machinery are examples of engineering applications.
For example, packed bed mechanically agitated vessels are being used in the food processing and chemical engineering industries in batch processes. The packed bed consists of solid particles or fibers of material, which form the solid matrix while fluid flows through the pores. As the solid matrix rotates, due to the mechanical agitation, a rotating frame of reference is a necessity when investigating these flows. The role of the flow of fluid through these beds can vary from drying processes to extraction of soluble components from the solid particles. Two examples of such processes are the molasses subject to centrifugal crystal separation in the sugar milling industry and the extraction of sodium alginate from kelp. Additional industrial applications are being presented in Vadasz [2,3,4], Nield and Bejan [5,6], and Bejan [7] in comprehensive reviews of the fundamentals of heat convection in porous media.
With the emerging utilization of the porous medium approach in non-traditional fields, including some applications in which the solid matrix is subjected to rotation (like physiological processes in human body subject to rotating trajectories, cooling of electronic equipment in a rotating radar, cooling of turbo-machinery blades, or cooling of rotors of electric machines) a thorough understanding of the flow in a rotating porous medium becomes essential. Its results can then be used in the more established industrial applications like food processing, chemical engineering or centrifugal processes, as well as to the less traditional applications of the porous medium approach.
The fundamental equations and assumptions applicable to single-phase convective heat transfer were presented by Dagan [8], Acharya [9]. A review of the effects of rotation on heat transfer in general was presented by Wiesche [10].
Reviews of the fundamentals of flow and heat transfer in rotating porous media were presented by Vadasz [2,3,4,11,12,13,14,15].
No reported results were found on isothermal flow in rotating porous media prior to 1994. Research of a pioneering nature on natural convection in rotating porous media were reported by Rudraiah et al. [16], Patil and Vaydianathan [17], Jou and Liaw [18,19], and Palm and Tyvand [20]. Nield [21] found that the effect of rotation on convection in a porous medium attracted limited interest in a comprehensive review of the stability of convective flows in porous media.
The fact that isothermal flow in homogeneous porous media following Darcy law is irrotational and hence the effect of rotation on this flow is insignificant contributed to the limited interest for this type of flow. However, for natural convection in a non-isothermal homogeneous porous medium or for a heterogeneous medium with spatially dependent permeability the flow is not irrotational anymore, and therefore the effects of rotation become significant. More recent interest in this type flow, during the past three decades, led to an increased number of publications. For example, Nield [22], Auriault et al. [23,24], Govender [25,26], Havstad and Vadasz [27], Vadasz and Havstad [28], Govender and Vadasz [29,30,31,32], Vadasz [2,3,4,11,12,13,14,15,33,34,35,36,37,38,39,40,41,42], Vadasz and Govender [43,44], Vadasz and Heerah [45], Vadasz and Olek [46], Bhadauria [47], Malashetty, Pop, Heera [48], Vanishree and Siddheshwar [49], Agarwal et al. [50], Bhadauria et al. [51], Agarwall and Bhadauria [52], Malashetty et al. [53], Malashetty and Swamy [54], Rana and Agarwal [55], Yadav et al. [56], Rashidi et al. [57], Makinde et al. [58], Straughan [59], Lombardo and Mulone [60], Falsaperla, Mulone and Straughan [61,62], Falsaperla, Giacobbe and Mulone [63], Capone and De Luca [64], Capone and Rionero [65], Capone and De Luca [66].
2. Governing Equations
The equations governing the flow and heat transfer in rotating porous media are presented in a dimensionless form subject to the assumptions of constant angular velocity of rotation, Boussinesq approximation (Boussinesq [67]), and local thermal equilibrium (LTE or Lotheq). The latter implies that the difference in the local temperature between the solid and fluid phases in the porous medium is insignificantly small and can be neglected. Boussinesq approximation [67] applicable to buoyancy flows states that the density id constant in all terms of the governing equations except the buoyancy terms in the momentum equation. The notation being used refers to symbols having an asterisk as dimensional, while symbols without an asterisk represent dimensionless quantities, except symbols carrying the subscript “c” representing characteristic values, or the subscript “o” representing reference values, both being dimensional. The continuity equation is presented in the form
where is the filtration velocity vector presented in Cartesian coordinates, are the components of the the filtration velocity vector in the directions, respectively, and are unit vectors in the directions, respectively. The operator is the divergence operator defined in the form .
The momentum transport in porous media is governed primarily by the Darcy law, which is presented in the rotating frame of reference of the solid matrix in the following dimensionless form
where four dimensionless groups emerged, i.e., a pressure number (equivalent to a porous media Euler number where replaces ), a porous media Froude number , a centrifugal number , and a porous media Ekman number defined in the form
and where and are the permeability and the porosity of the porous matrix, respectively, is the dynamic viscosity, is a constant reference value of the fluid density used to convert the density into a dimensionless form, is the kinematic viscosity of the fluid, is the constant angular velocity of rotation, and are the dimensionless pressure and density, respectively, is a unit vector in the direction of the gravity acceleration, is a unit vector in the direction of the angular velocity of roation, and is the position vector measured from the axis of rotation. Also are constant dimensional characteristic values of length, filtration velocity, and pressure, respectively, used to convert the space variables, the filtration velocity, and the pressure into dimensionless forms. The gradient operator in Equation (2) is defined in the form .
The third term in the brackets in Equation (2) represents the centrifugal force while the fourth term represents the Coriolis acceleration.
When fast transients or high frequency effects are of interest there is another extension to the Darcy equation that is applicable. Then, the time resolution obtained by assuming a very fast reaction of Darcy flow to changes and therefore the quasi-steady approximation which is inherent in the formulation of the Darcy law is not sufficient and a time derivative of the filtration velocity needs to be incorporated leading to the following dimensionless form of the extended Darcy equation in a rotating frame of reference
where the additional dimensionless groups that emerged are the Darcy number , and the Reynolds number
and is a ratio of heat capacities that its the definition will follow later. The corresponding length scale is a macro-level length scale, not the pore-size, despite the fact that it is the porous media filtration velocity that emerged in the definition of the Reynolds number. However the Reynolds number appears in Equation (4) in a product combination with the Darcy number, bringing therefore the pore-scale effects into account too.
Following the definition of the dimensionless temperature in the form
where is the dimensional temperature, is a reference value of temperature, and is a characteristic temperature difference, the dimensionless form of the energy equation subject to local thermal equilibrium (LTE or Lotheq) is presented in the form
where Peclet number emerged as an additional dimensionless group, defined in the form
where the porous media Prandtl number is defined by
The effective thermal diffusivity of the porous medium appearing in (8) and (9) is defined as and is the heat capacity ratio, i.e., the ratio between the effective heat capacity of the fluid phase and the effective heat capacity of the porous medium, where , are the effective heat capacity and effective thermal conductivity of the porous medium and subscripts “s” and “f” refer to the solid and fluid phases, respectively. Then the adjusted effective thermal diffusivity is defined as follows .
To complete the governing equations one needs a relationship between the density, temperature and pressure (and solute concentration when the fluid is a solution of soluble substances, e.g., salt in water, alcohol in water, etc., in which case an additional species equation needs to be added to). A linear approximation for this relationship is usually sufficiently accurate if the temperature and pressure differences are no excessively high. The dimensionless form of the linear approximation of the equation of state can be obtained by using the definition of the dimensionless temperature from Equation (6) and the dimensionless pressure in the form . Then the equation of state becomes
where is the dimensionless density, and , are the dimensionless thermal expansion and pressure compression coefficients, respectively. For most fluid flows and especially for incompressible flows, i.e., flows of liquids, . Therefore the common approximation of the dimensionless equation of state is
There are some identities relevant to flows in a rotating frame of reference and in buoyancy flows that are useful in the following derivations. These identities are
Their proof can be found in Vadasz [3].
Although for a significantly high number of practical instances Darcy’s model (or its extension) for a rotating frame of reference is sufficient for representing the effects of rotation, non-Darcy models have been used as well. Their relevance and limitations are subject to professional discourse (e.g., Nield [68,69,70] and Vafai and Kim [71]).
3. Taylor-Proudman Columns and Geostrophic Flow in Rotating Porous Media
By using Equations (12) and (13), considering isothermal conditions (no heat transfer) and consequently the density is constant hence , Darcy Equation (2) becomes
The term under the common gradient operator is a reduced pressure , defined as
By using (16) and choosing the direction of the angular velocity of rotation to be aligned with the vertical axis, i.e., , the Darcy Equation (2) can be presented in the following rearranged form
For typical values of viscosity, porosity and permeability the range of variation of Ekman number can be evaluated in some engineering applications. Consequently, the angular velocity may vary from 10 rpm to 10,000 rpm leading to Ekman numbers in the range from to . The latter value is very small, pertaining to the conditions considered here. Therefore, in the limit of , say , Equation (17) takes the simplified form
and the effect of permeability variations disappears. Taking the “curl” of Equation (18) leads to
Evaluating the “curl” operator on the cross product of the left-hand side of Equation (19) leads to
Equation (20) is identical to the Taylor-Proudman theorem for pure fluids (non-porous domains); it thus represents the proof of the Taylor-Proudman theorem in porous media, and can be presented in the following simplified form
The conclusion expressed by Equation (21) is that , i.e., it cannot be a function of , where is the direction of the angular velocity vector. This means that all filtration velocity components can vary only in the plane perpendicular to the angular velocity vector. This result leads to the existence of Taylor-Proudman columns in rotating porous media as presented in detail by Vadasz [3]. The consequence of this result can be demonstrated by considering a particular example that was presented by Vadasz [36] (see Greenspan [72] for the corresponding example in pure fluids).
A further significant consequence of Equation (21) is represented by a geostrophic type of flow. Taking the -component of Equation (21) yields , and the continuity Equation (1) becomes two dimensional
Therefore the flow at high rotation rates has a tendency towards two-dimensionality and a stream function, , can be introduced for the flow in the plane in the form
which satisfies identically the continuity Equation (1). Substituting and with their stream function representation given by Equation (23) into Equation (18) yields
As both the pressure and the stream function can be related to an arbitrary reference value, the conclusion from Equations (24) and (25) is that the stream function and the pressure are the same in the limit of high rotation rates (). This type of geostrophic flow means that isobars represent streamlines at the leading order, for .
4. Natural Convection Due to Centrifugal Buoyancy
Natural convection is the effect of flow and convection heat transfer due to the existence of density gradients in a body force field (such as gravity or centrifugal force field). As density depends on temperature as demonstrated in the derivation of the equation of state, temperature gradients may create natural convective flows when a body force field is present. What characterizes natural convection is the lack of a known value of characteristic filtration velocity that can be applied upfront in a problem. No characteristic velocity can be specified because the latter is dictated by the temperature gradients and their resulting buoyancy rather than being known upfront. Therefore a sensible choice of would be . With this choice of the Froude number , the pressure number , and the centrifugal dimensionless group in Equations (12) and (14) become , , . Without loss of generality for the same reason as for the filtration velocity one can chose the characteristic pressure difference to be such that the pressure number becomes unity, i.e., leading to . Also the Reynolds number in Equation (5) renders into the reciprocal Prandtl number and the Peclet number in Equations (7) and (8) becomes equal to one by definition . One may define the effective Prandtl number in terms of the effective thermal diffusivity (see the equation and the text following Equation (9)) . Then the coefficient to the time derivative term in Equation (4) becomes a new dimensionless group that Straughan [73] named the Vadasz number (), or the Vadasz coefficient named by Straughan [73] (see also Sheu [74] and Govender [26]). By using Equations (11)–(13) leads to transforming Equations (2) and (4) into the following form
The product of by and produced two new dimensionless groups in the form of the gravity related Rayleigh number and the centrifugal Rayleigh number, respectively in the form
The particular cases when and will be considered later. Subject to this orientation of the gravity and angular velocity of rotation Equations (26) and (27) take the form
The vector in Equations (30) and (31) represents the perpendicular radius vector from the axis of rotation to any point in the flow domain. Three dimensionless groups emerged in Equation (30) when fast transients or high frequencies are not of interest. These dimensionless groups control the significance of the different phenomena. Therefore, the value of Ekman number () controls the significance of the Coriolis effect, and the ratio between the gravity related Rayleigh number () and centrifugal Rayleigh number () controls the significance of gravity with respect to centrifugal forces as far as natural convection is concerned. This ratio is . When fast transients or high frequencies are of interest Equation (27) is to be considered. In such a case one additional dimensionless group emerged, the number representing the ratio between two characteristic frequencies, i.e., the fluid flow frequency and the thermal diffusion frequency , i.e., , or alternatively the ratio between two time scales, i.e., the thermal diffusion time scale , and the fluid flow time scale , i.e., . In addition to such cases Equation (27) should be used also when the effective Prandtl number is of the order of magnitude of Darcy number, i.e., i.e., a very small number (as in most porous media). Such small values of the Prandtl number are typical for liquid metals. In such cases too the time derivative term in Equation (27) should be retained.
Considering the Darcy regime subject to a centrifugal body force and by neglecting gravity effects () Equations (1), (7) and (26) with and represent the mathematical model for this case. The objective in the first instance is to establish the convective flow under small rotation rates, then , and as a first approximation the Coriolis effect can be neglected, i.e., . Following these conditions the governing equations become (by using identity (14))
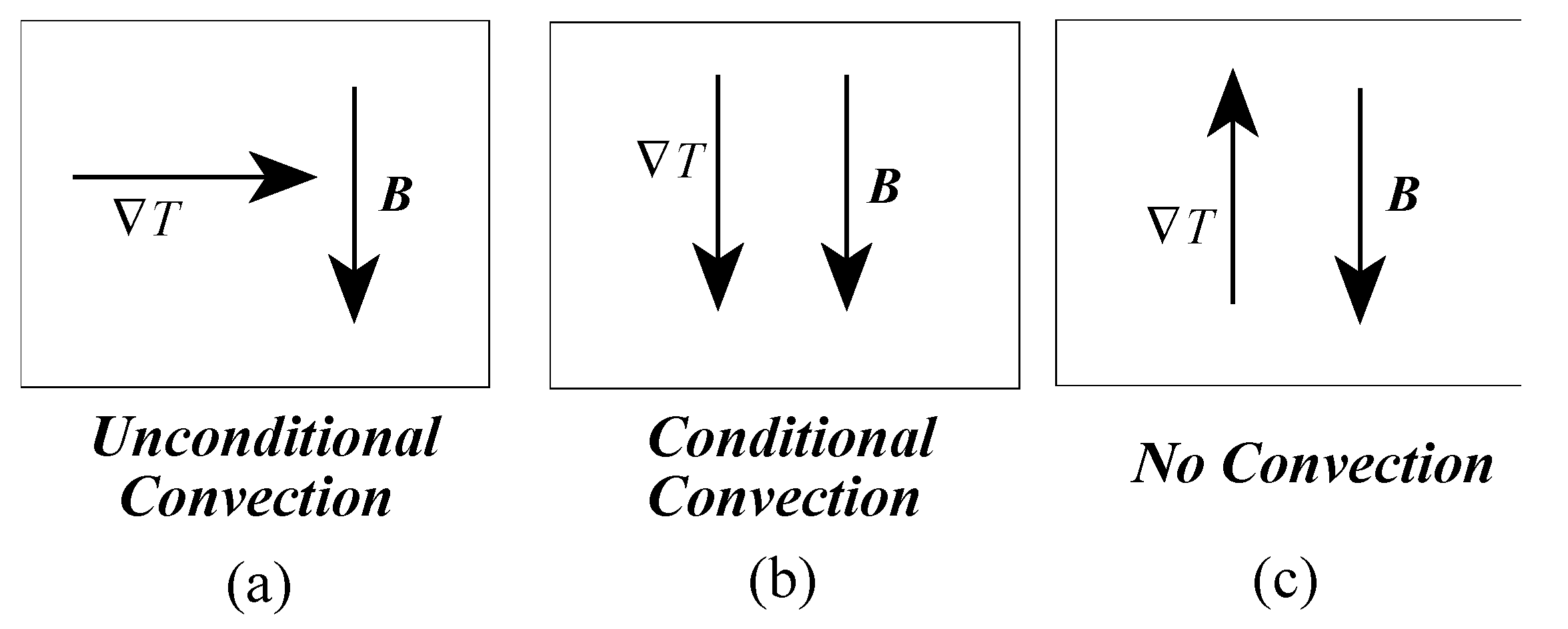
There are three cases corresponding to the relative orientation of the temperature gradient with respect to the centrifugal body force as presented in Figure 1. Case 1(a) in Figure 1 corresponds to a temperature gradient, which is perpendicular to the direction of the centrifugal body force and leads to unconditional convection. The solution representing this convection pattern is presented by Vadasz [3,4,34]. Cases 1(b) and 1(c) in Figure 1 corresponding to temperature gradients collinear with the centrifugal body force represent stability problems and hence our present focus. The objective is then to establish the stability condition as well as the convection pattern when this stability condition is not satisfied.
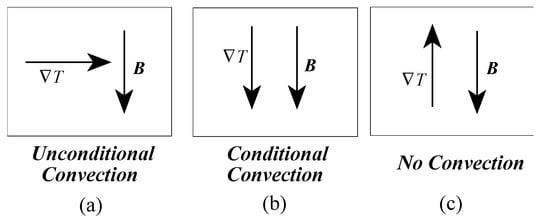
Figure 1.
The effect of the relative orientation of the temperature gradient with respect to the body force on the setup of convection. (a) Unconditional convection; (b) conditional convection; (c) no convection.
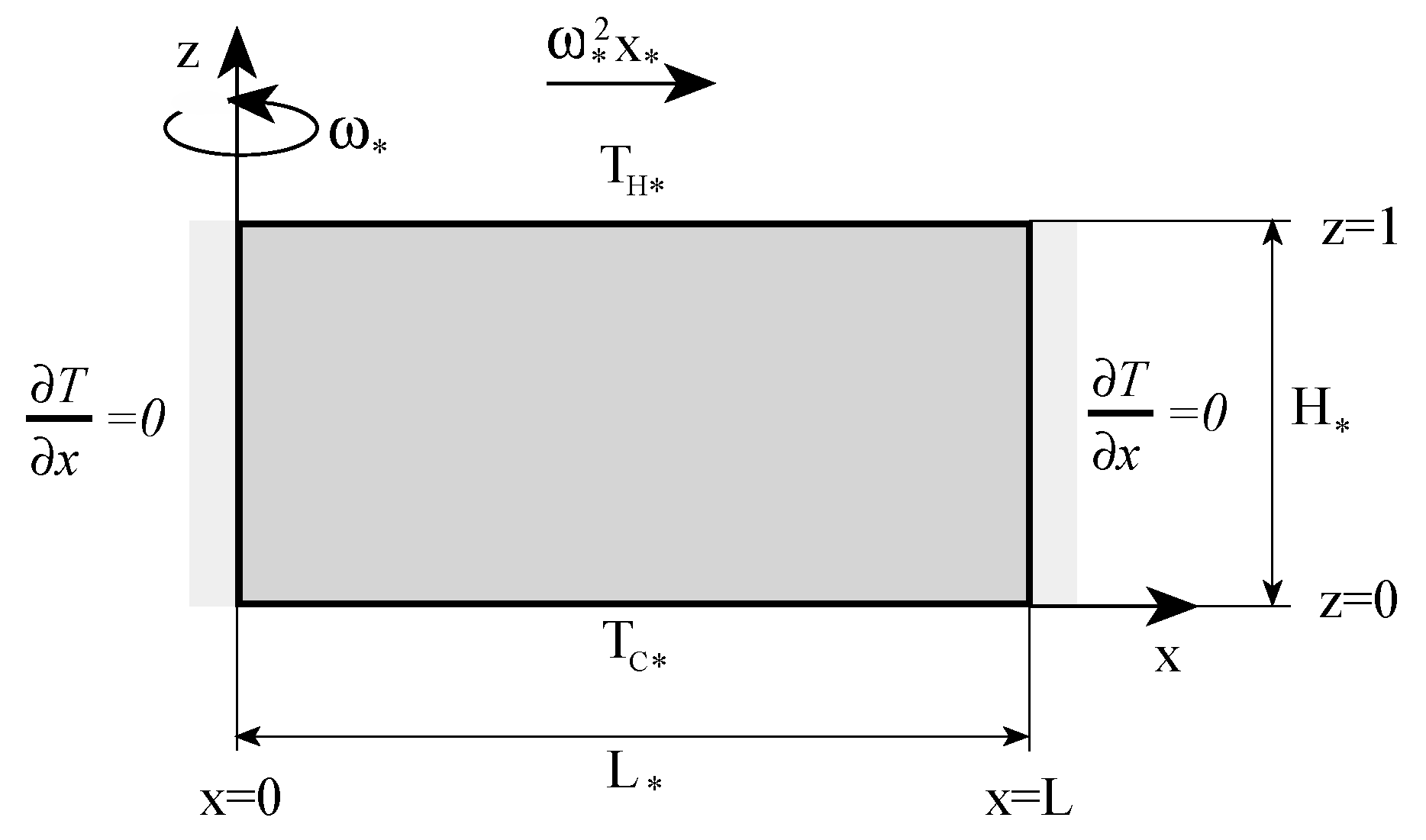
An example of a case when the imposed temperature is perpendicular to the centrifugal body force is a rectangular porous domain rotating about the vertical axis, heated from above and cooled from below. For this case the centrifugal buoyancy term in Equation (33) becomes leading to
An analytical two-dimensional solution to this problem (see Figure 2) for a small aspect ratio of the domain was presented by Vadasz [3,4,34]. The solution to the non-linear set of partial differential equations was obtained through an asymptotic expansion of the dependent variables in terms of a small parameter representing the aspect ratio of the domain.
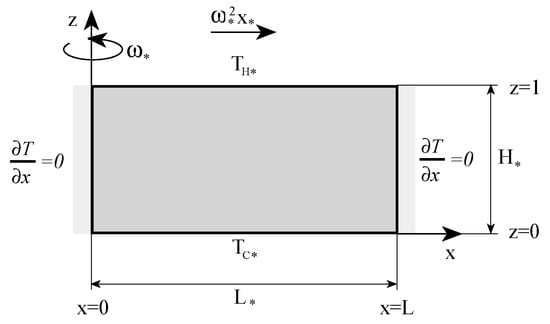
Figure 2.
A rotating rectangular porous domain heated from above, cooled from below, and insulated on its sidewalls. (Reprinted from [37], with permission from Elsevier Science Ltd).
The convection in the core region far from the sidewalls was the objective of the investigation. To first order accuracy, the heat transfer coefficient represented by the Nusselt number was evaluated in the form
where is the Nusselt number and the length scale used in the definition of , Equation (54), was . Vadasz [37] used a different approach to solve a similar problem without the restriction of a small aspect ratio. A direct extraction and substitution of the dependent variables was found to be useful for de-coupling the non-linear partial differential equations, resulting in a set of independent non-linear ordinary differential equations, which was solved analytically. To obtain an analytical solution to the non-linear convection problem we assume that the vertical component of the filtration velocity, , and the temperature are independent of , i.e., , being functions of only. It is this assumption that will subsequently restrict the validity domain of the results to moderate values of (practically ). Subject to the assumptions of two-dimensional flow and and that and are independent of the governing equations take the form
The method of solution consists of extracting from Equation (38) and expressing it explicitly in terms of and . This expression of is then introduced into Equation (40) and the derivative is applied to the result. Then, substituting the continuity Equation (37) in the form and Equation (39) into the results yields a non-linear ordinary differential equation for in the form
An interesting observation regarding Equation (41) is the fact that it is identical to the Blasius equation for boundary layer flows of pure fluids (non-porous domains) over a flat plate. To observe this, one simply has to substitute to obtain , which is the Blasius equation. Unfortunately, no further analogy to the boundary layer flow in pure fluids exists, predominantly due to the different boundary conditions and because the derivatives [] and the flow () are in the same direction. The solutions for the temperature and the horizontal component of the filtration velocity , are related to the solution of the ordinary differential equation
where stands for and
where is a constant defined by
The Relationship (45) is a result of imposing a condition of no net flow through any vertical cross-section in the domain, stating that .
The following boundary conditions are required to the solution of (41) for : representing the impermeability condition at the solid boundaries and . Since according to Equation (43), then following the continuity Equation (37) and the temperature boundary conditions can be converted into conditions in terms of by using Equation (44), leading to the following complete set of boundary conditions for :
Equations (46) and (47) represent four boundary conditions, while only three are necessary to solve the third order Equation (41). The reason for the fourth condition comes from the introduction of the constant , whose value remains to be determined. Hence, the additional two boundary conditions are expressed in terms of the unknown constant and the solution subject to these four conditions will determine the value of as well. A method similar to Blasius’s method of solution was applied to solve Equation (41). Therefore, was expressed as a finite power series and the objective of the solution was to determine the power series coefficients. Once the solution for and the value of were obtained, and were evaluated by using and Equations (43) and (44).
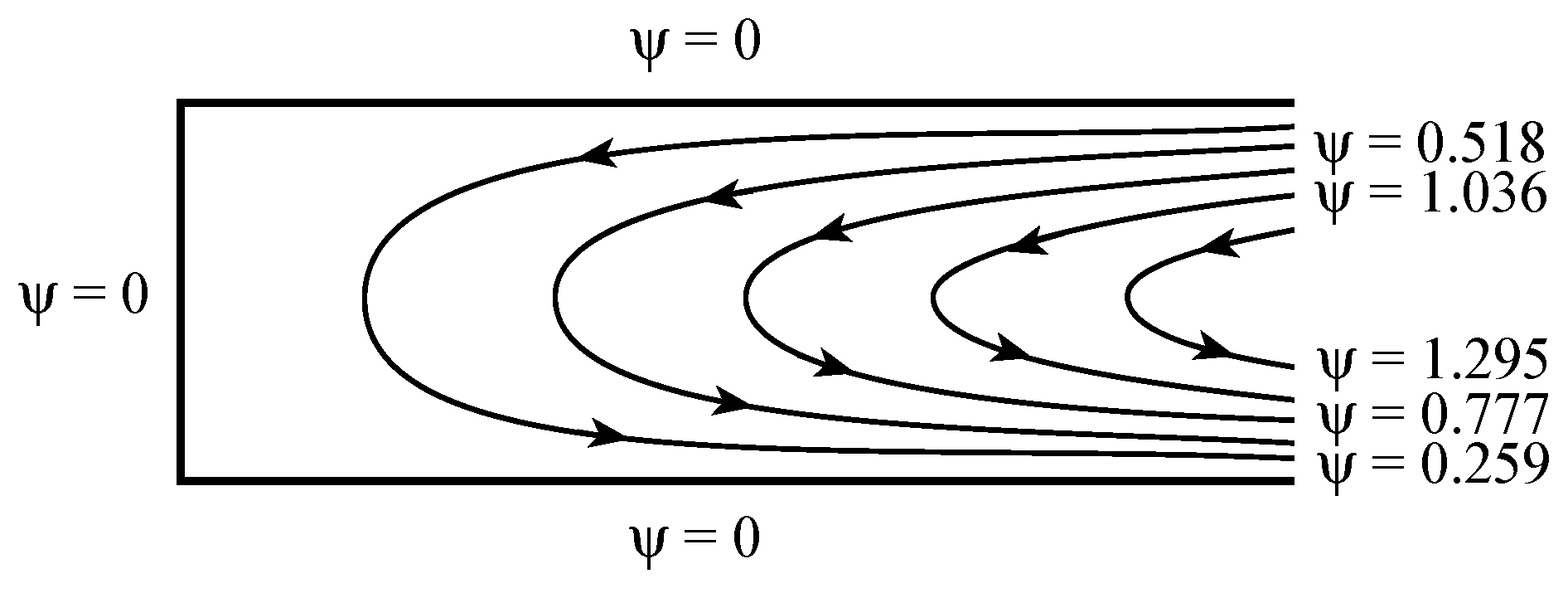
For presentation purposes a stream function was introduced to plot the results (, ). An example of the flow field represented by the streamlines is presented in Figure 3 for and for an aspect ratio of 3 (excluding a narrow region next to the sidewall at ). Outside this narrow region next to the streamlines remain open on the right hand side. They are expected to close in the end region. On the left-hand side, however, the streamlines close throughout the domain. The reason for this, is the centrifugal acceleration, which causes to vary linearly with , thus creating (due to the continuity equation) a non-vanishing vertical component of the filtration velocity at all values of . The local Nusselt number , representing the local vertical heat flux was evaluated as well by using the definition and using the solution for . A comparison between the heat flux results obtained from this solution and the results obtained by Vadasz [34] using an asymptotic method was presented graphically by Vadasz [37]. The two results compare well as long as is very small. However, for increasing values of the deviation from the linear relationship pertaining to the first order asymptotic solution (, according to Vadasz [34]) was evident. The stability of this convection flow was not evaluated, although it is of extreme interest. This would be an interesting though not simple task recommended for future research.
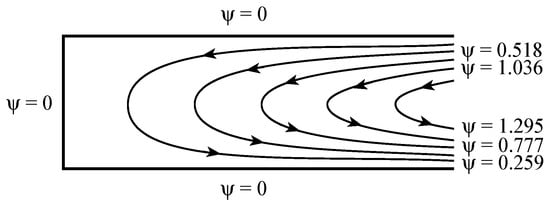
Figure 3.
Graphical description of the resulting flow field; five streamlines equally spaced between their minimum value at the rigid boundaries and their maximum value . The values in the figure correspond to every other streamline. (Reprinted from [37], with permission from Elsevier Science Ltd).
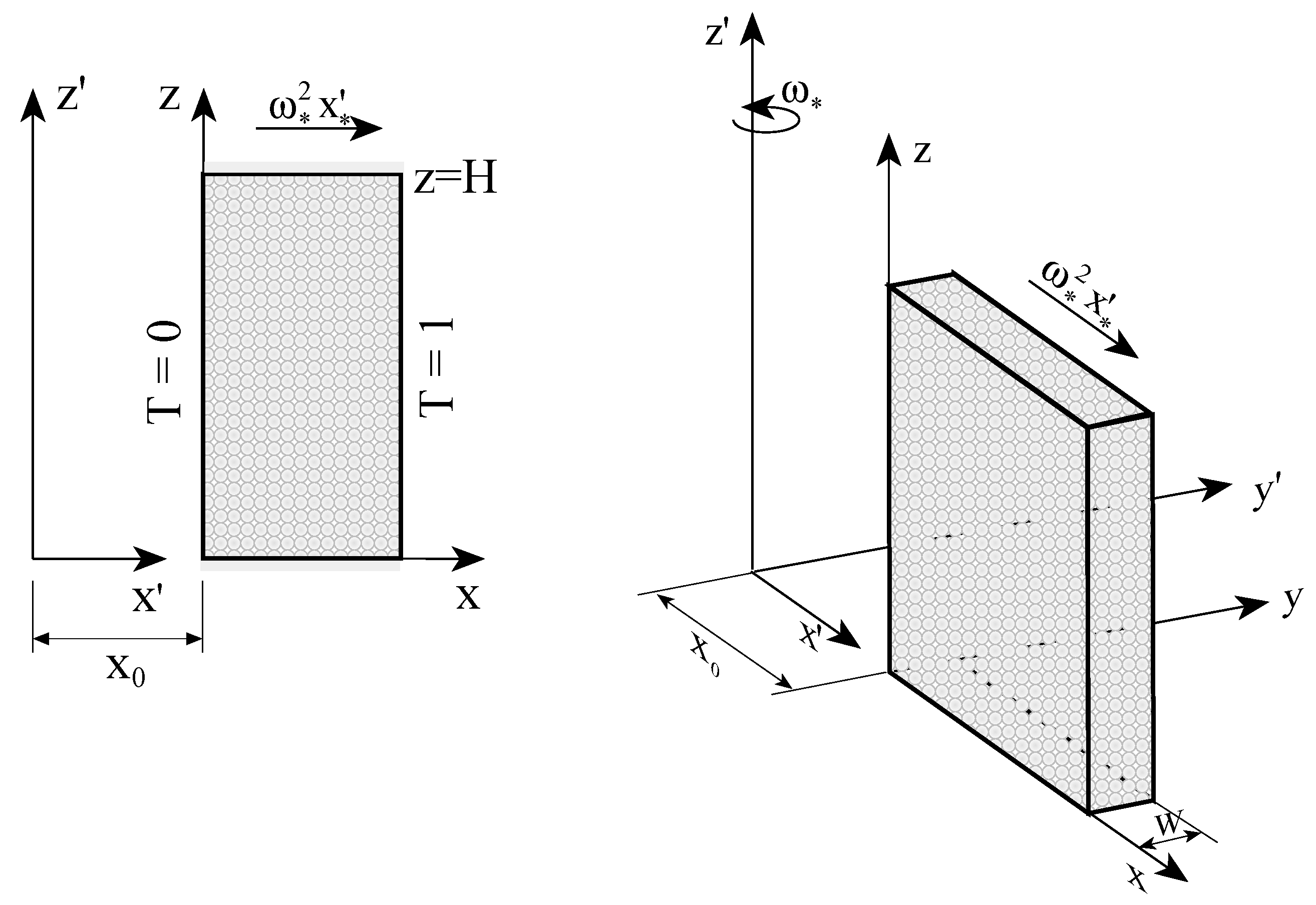
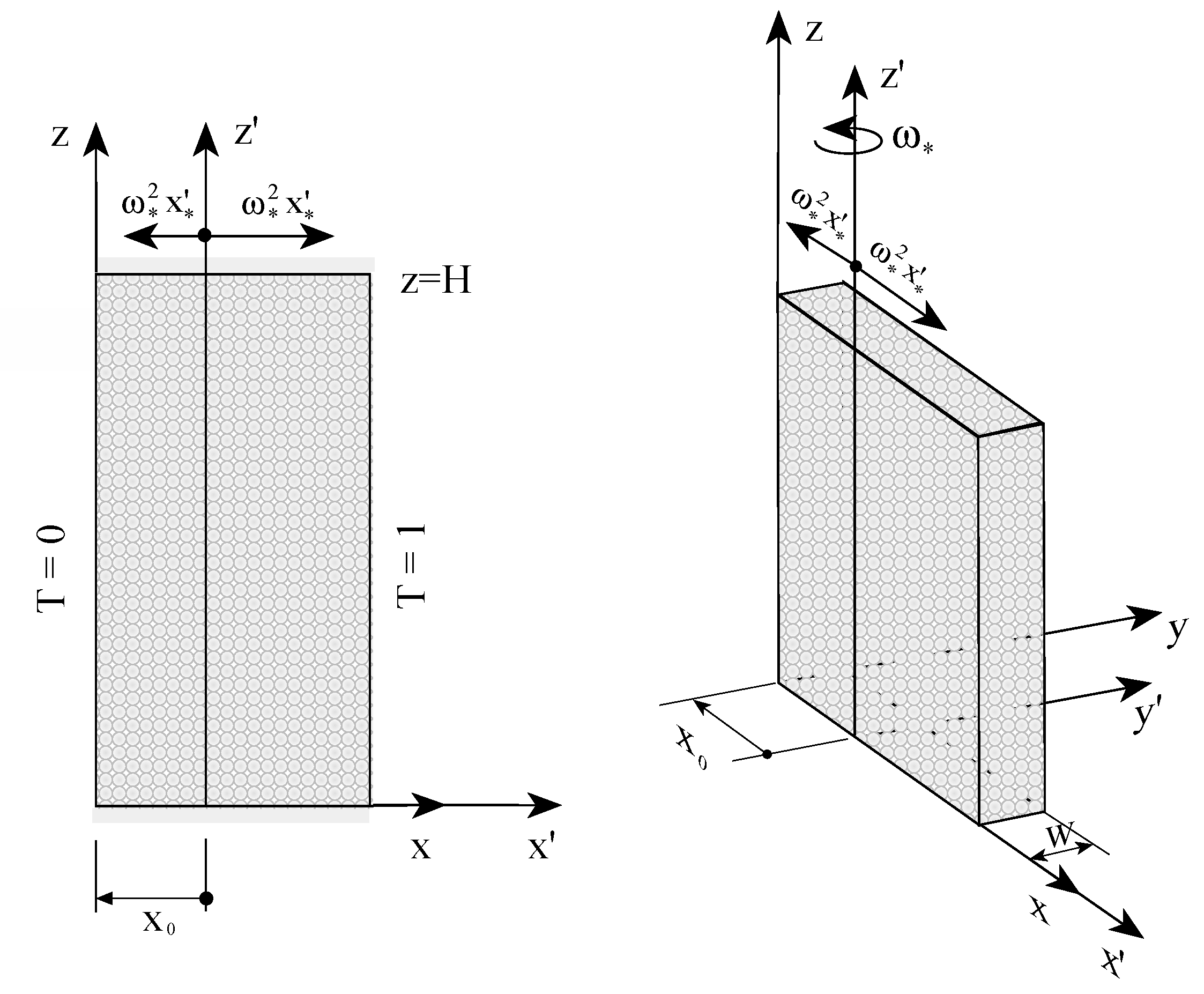
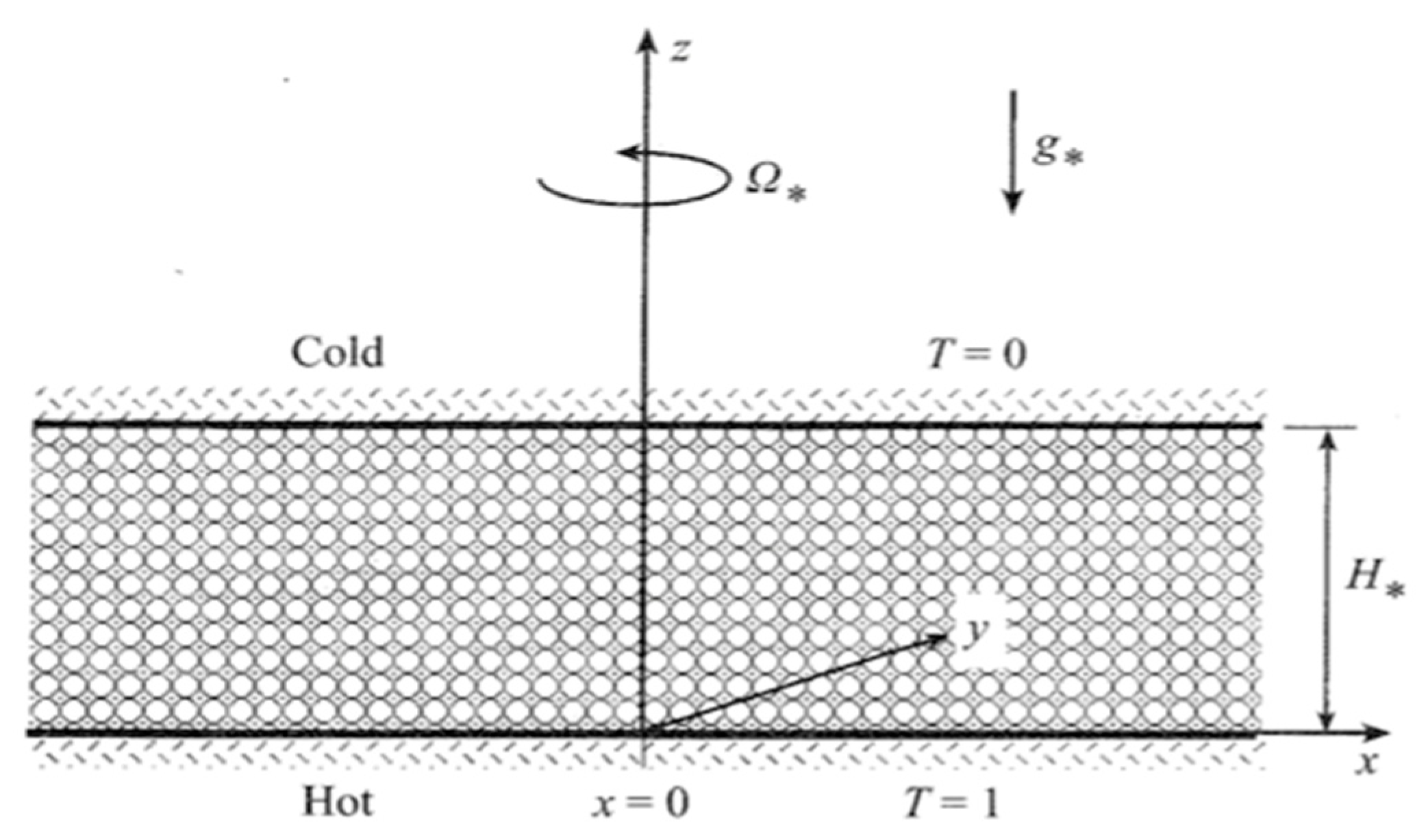
The problem of stability of free convection in a rotating porous layer when the temperature gradient is collinear with the centrifugal body force was treated by Vadasz [38] and Vadasz [40] for a narrow layer adjacent to the axis of rotation (Vadasz [38]) and distant from the axis of rotation (Vadasz [40]), respectively. The problem formulation corresponding to the latter case is presented in Figure 4. In order to include explicitly the dimensionless offset distance from the axis of rotation , and to keep the coordinate system linked to the porous layer, Equation (33) was presented in the form
Two centrifugal Rayleigh numbers appear in Equation (48); the first one, representing the contribution of the offset distance from the rotation axis to the centrifugal buoyancy is , while the second, , represents the contribution of the horizontal location within the porous layer to the centrifugal buoyancy. The ratio between the two centrifugal Rayleigh numbers is dimensionless reciprocal distance from the axis of rotation
and can be introduced as a parameter in the equations transforming Equation (48) into the form
From Equation (50) it is observed that when the porous layer is far away from the axis of rotation then () and the contribution of the term is not significant, while for a layer close enough to the rotation axis () and the contribution of the first term becomes insignificant. In the first case the only controlling parameter is while in the latter case the only controlling parameter is . The flow boundary conditions are on the boundaries, where is a unit vector normal to the boundary. These conditions stipulate that all boundaries are rigid and therefore non-permeable to fluid flow. The thermal boundary conditions are: at , at and on all other walls representing the insulation condition on these walls. The governing equations accept a basic motionless conduction solution in the form
The objective of the investigation was to establish the condition when the motionless solution (51) is not stable and consequently a resulting convection pattern appears. Therefore a linear stability analysis was employed, representing the solution as a sum of the basic solution (51) and small perturbations in the form
where stands for perturbed values. Solving the resulting linearized system for the perturbations by assuming a normal modes expansion in the and directions, and in the direction, i.e., , and using the Galerkin method to solve for one obtains at marginal stability, i.e., for , a homogeneous set of linear algebraic equations. This homogeneous linear system accepts a non-zero solution only for particular values of such that its determinant vanishes. The solution of this system was evaluated up to order 7 for different values of , representing the offset distance from the axis of rotation. However, useful information was obtained by considering the approximation at order 2. At this order the system reduces to two equations, which lead to the characteristic values of in the form
where the following notation was used
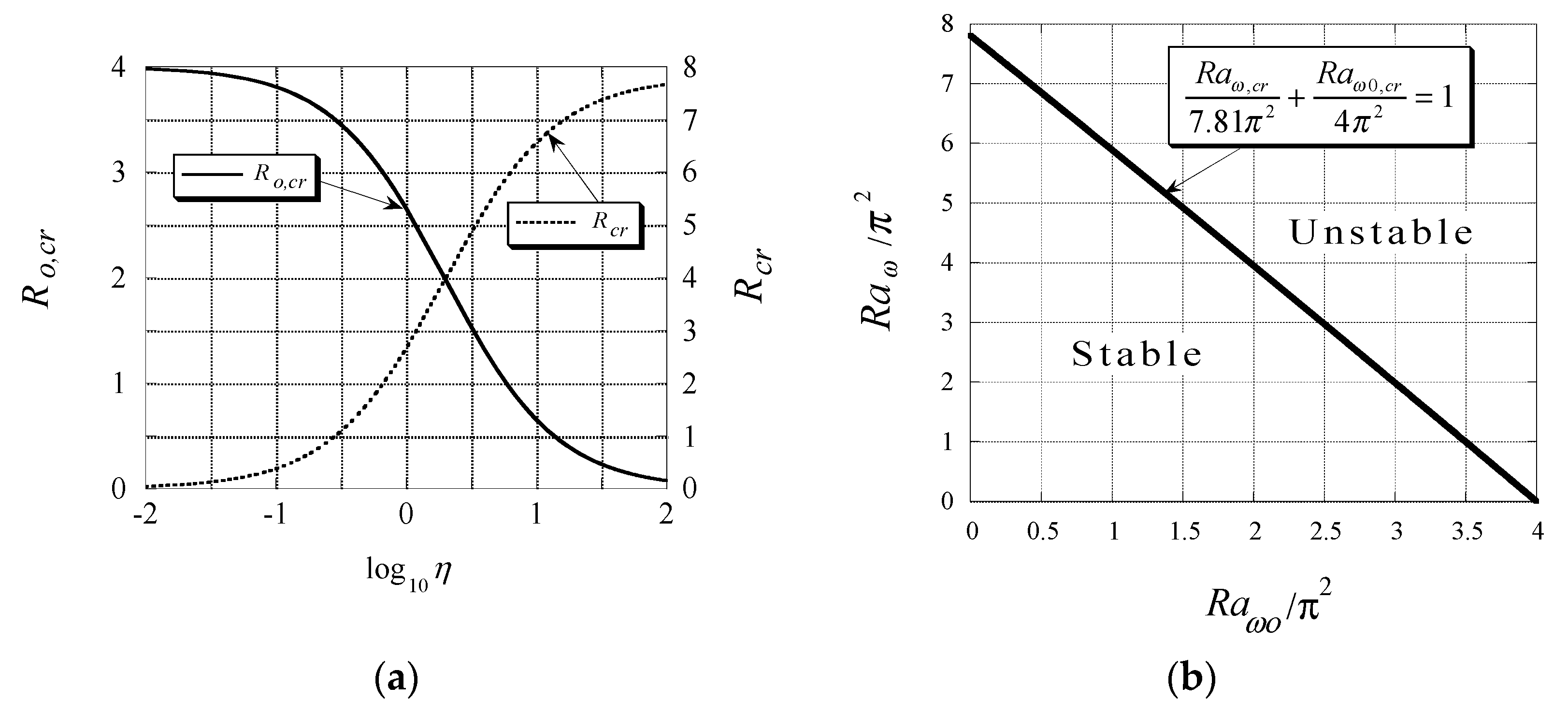
and is the wavenumber such that while the subscript in Equation (53) represents characteristic (neutral) values (values for which ). A singularity in the solution for , corresponding to the existence of a single root for , appears when . This singularity persists at higher orders as well. Resolving for the value of when this singularity occurs shows that it corresponds to negative values implying that the location of the rotation axis falls within the boundaries of the porous domain (or to the right side of the hot wall-a case of little interest due to its inherent unconditional stability). This particular case will be discussed later in this section. The critical values of the centrifugal Rayleigh number as obtained from the solution up to order 7 are presented graphically in Figure 5a in terms of both and as a function of the offset parameter . The results presented in Figure 5 are particularly useful in order to indicate the stability criterion for all positive values of . It can be observed from the figure that as the value of becomes small, i.e., for a porous layer far away from the axis of rotation, the critical centrifugal Rayleigh number approaches a limit value of . This corresponds to the critical Rayleigh number in a porous layer subject to gravity and heated from below. For high values of it is appropriate to use the other centrifugal Rayleigh number , instead of , by introducing the relationship (see Equations (49) and (54)) in order to establish and present the stability criterion. It is observed from Figure 5a that as the value of becomes large, i.e., for a porous layer close to the axis of rotation, the critical centrifugal Rayleigh number approaches a limit value of . This corresponds to the critical Rayleigh number for the problem of a rotating layer adjacent to the axis of rotation as presented by Vadasz [38]. The stability map on the plane is presented in Figure 5b, showing that the plane is divided between the stable and unstable zones by the straight line .
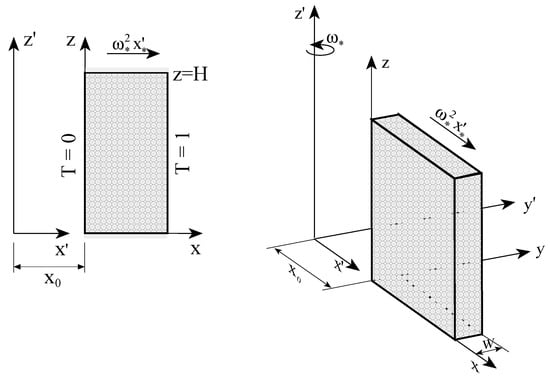
Figure 4.
A rotating fluid saturated porous layer distant from the axis of rotation and subject to different temperatures at the sidewalls. (Reprinted from [40], with permission from Springer).
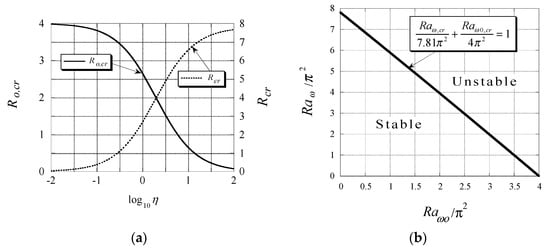
Figure 5.
(a) The variation of the critical values of the centrifugal Rayleigh numbers as a function of ; (b) The stability map on the plane showing the division of the plane. (Reprinted from [40], with permission from Springer).
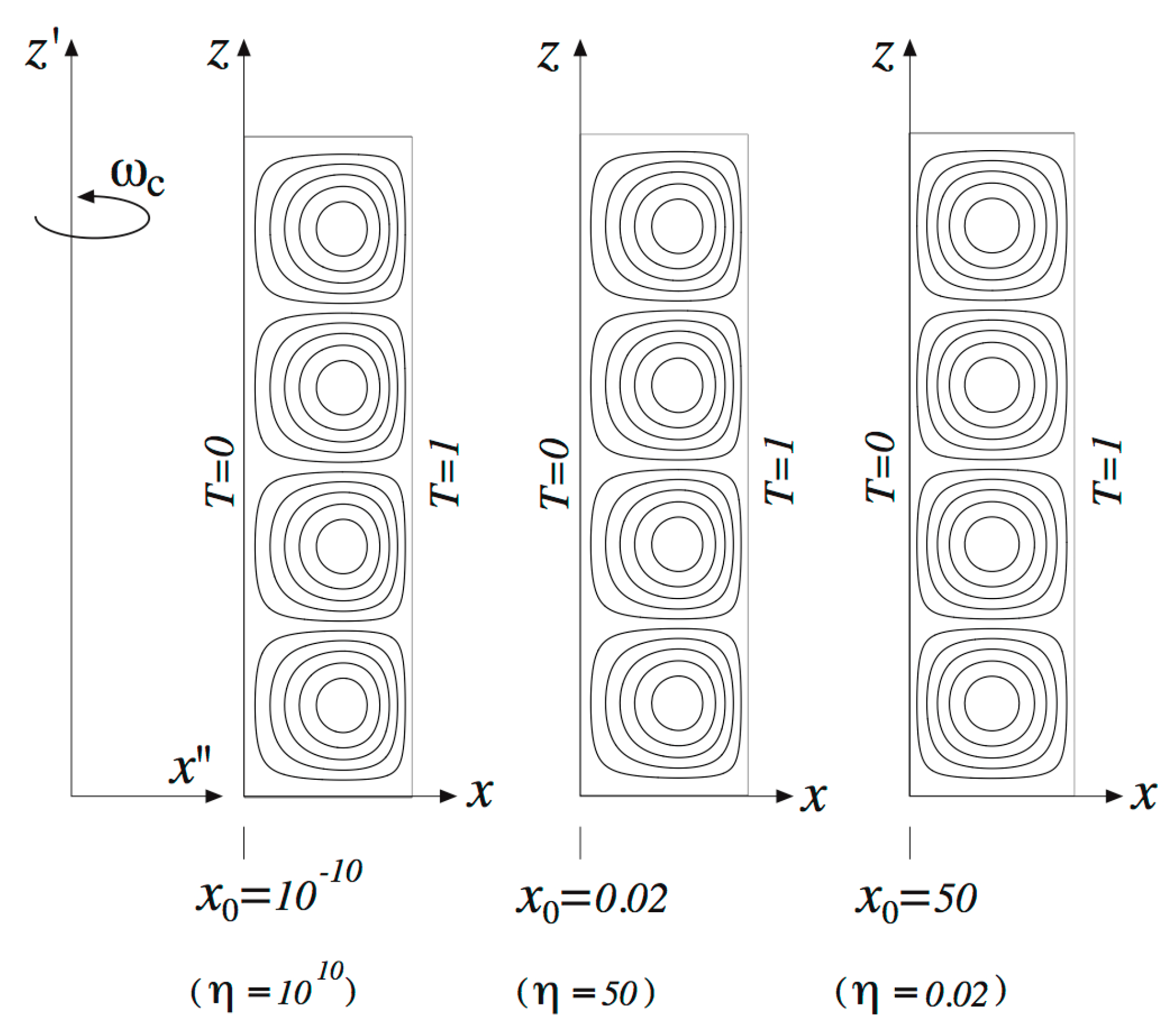
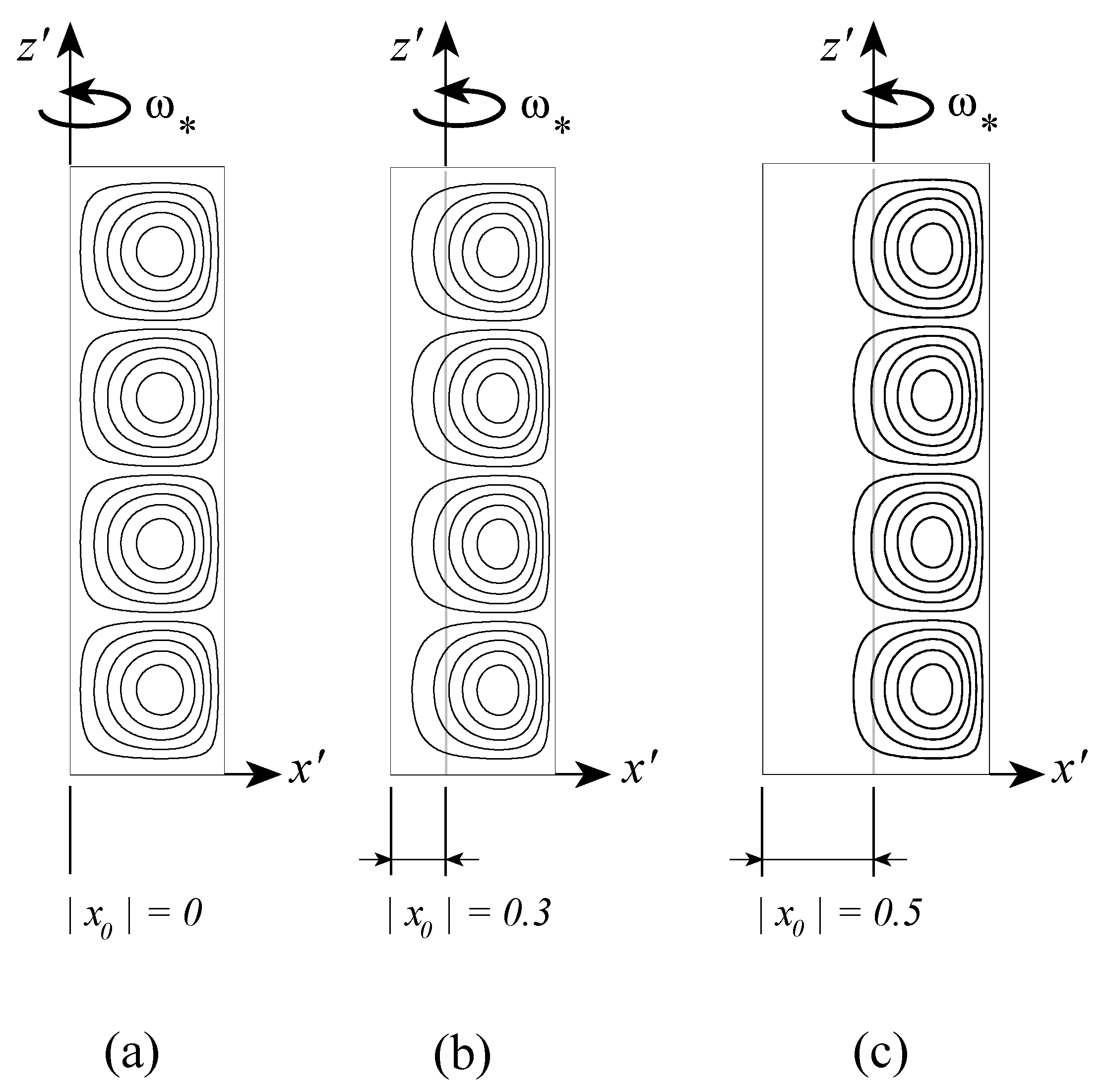
The results for the convective flow field are presented graphically in Figure 6 following Vadasz [40], where it was concluded that the effect of the variation of the centrifugal acceleration within the porous layer is definitely felt when the box is close to the axis of rotation, corresponding to an eccentric shift of the convection cells towards the sidewall at . However, when the layer is located far away from the axis of rotation (e.g., ) the convection cells are concentric and symmetric with respect to as expected for a porous layer subject to gravity and heated from below (here “below” means the location where ).
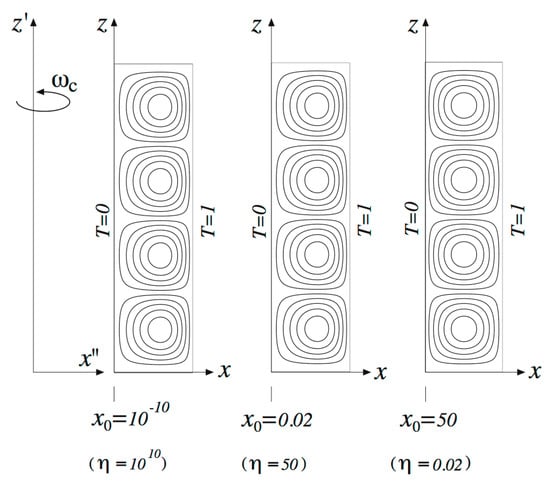
Figure 6.
The convective flow field at marginal stability for three different values of ; 10 stream lines equally divided between and . At , at and at . (Reprinted from [40], with permission from Springer).
Although the linear stability analysis is sufficient for obtaining the stability condition of the motionless solution and the corresponding eigenfunctions describing qualitatively the convective flow, it cannot provide information regarding the values of the convection amplitudes, nor regarding the average rate of heat transfer. To obtain this additional information, Vadasz and Olek [46] analyzed and provided a solution to the non-linear equations by using Adomian’s decomposition method to solve a system of ordinary differential equations for the evolution of the amplitudes.
This system of equations was obtained by using the first three relevant Galerkin modes for the stream function and the temperature in the form
where , , being the layer’s aspect ratio, , , and the possibly time dependent amplitudes of convection. In this model it was considered of interest including the time derivative term in Darcy’s equation in the form , where , and are the Darcy and the effective Prandtl numbers, respectively, defined as and (see Equation (58) with and ). The reason for including the time derivative term in the Darcy equation was the fact that one anticipates oscillatory and possibly chaotic solutions for which very high frequencies may occur. Then, the following equations were obtained for the time evolution of the amplitudes
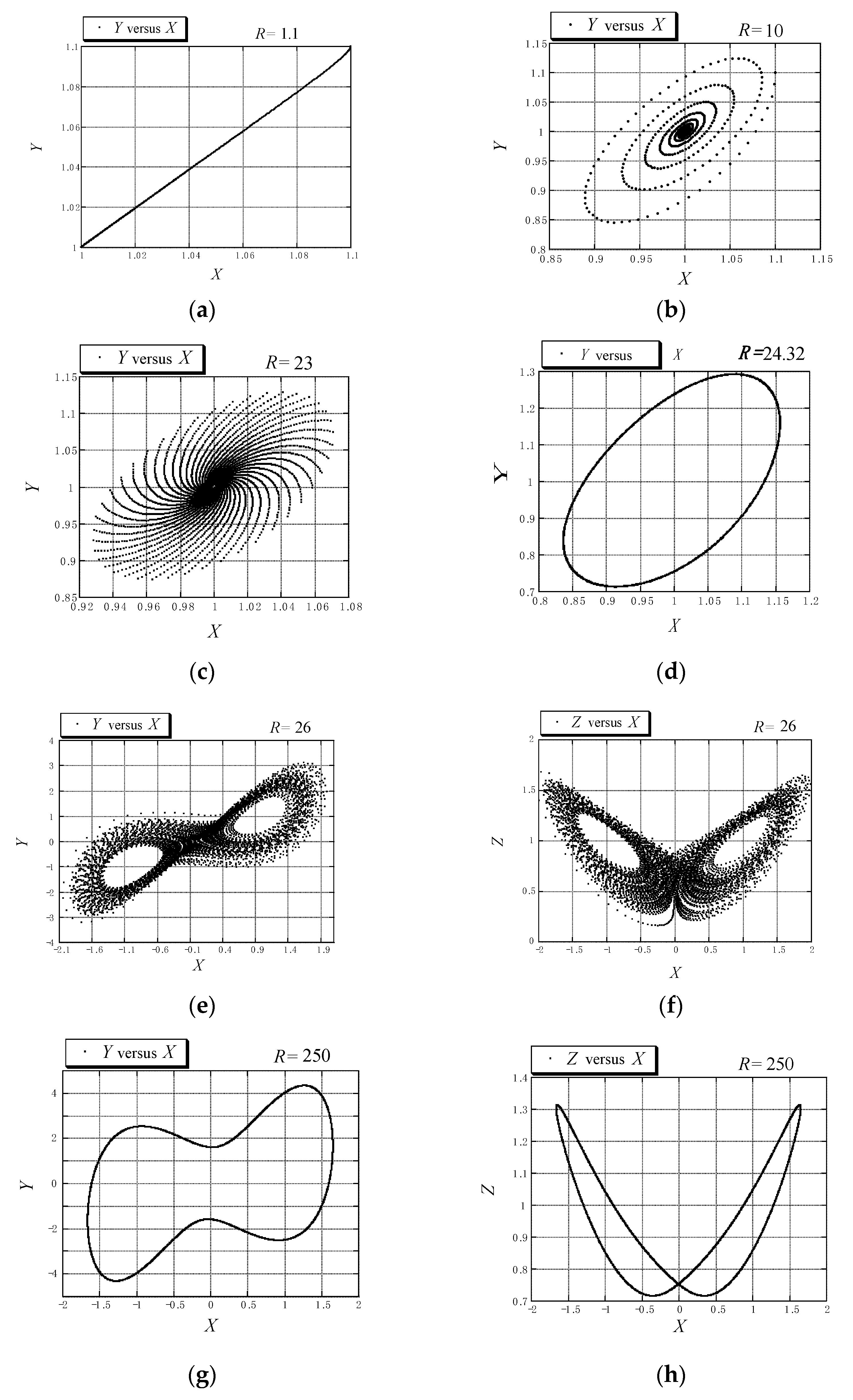
where , and is a rescaled Rayleigh number introduced above according to the definitions in the text following Equation (56). The results obtained are presented in Figure 7 in the form of projection of trajectories data points onto the and planes. Different transitions as the value of varies are presented and they relate to the convective fixed point which is a stable simple node in Figure 7a, a stable spiral in Figure 7b,c, and loses stability via an inverse Hopf bifurcation in Figure 7d, where the trajectory describes a limit cycle, moving towards a chaotic solution presented in Figure 7e,f. A further transition from chaos to a periodic solution was obtained at a value of slightly above 100, which persists over a wide range of values. This periodic solution is presented in Figure 7g,h for .
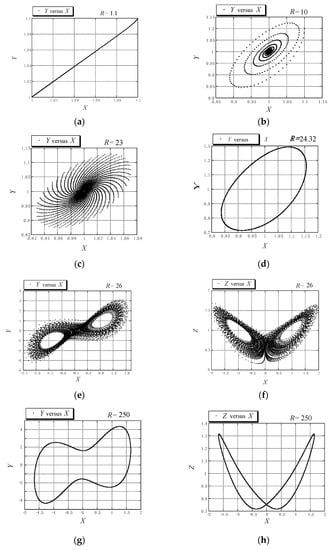
Figure 7.
Different transitions in natural convection in a rotating porous layer. (Reprinted from [46], with permission from Elsevier Science Ltd.) (a) projection on the Y-X plane for R = 1.1; (b) projection on the Y-X plane for R = 10; (c) projection on the Y-X plane for R = 23; (d) projection on the Y-X plane for R = 24.32; (e) projection on the Y-X plane for R = 26; (f) projection on the Z-X plane for R = 26; (g) projection on the Y-X plane for R = 250; (h) projection on the Z-X plane for R = 250.
Previously in this section (see Equation (53)) a singularity in the solution was identified and associated with negative values of the offset distance from the axis of rotation. It is this resulting singularity and its consequences, which were investigated by Vadasz [41] and are the objective of the following presentation. As this occurs at negative values of the offset distance from the axis of rotation it implies that the location of the rotation axis falls within the boundaries of the porous domain, as presented in Figure 8. This particular axis location causes positive values of the centrifugal acceleration on the right side of the rotation axis and negative values on its left side. The rotation axis location implies that the value of is not positive. The solution for this case is similar to the previous case leading to the same characteristic equation for at order 2 as obtained previously in Equation (53) for , with the only difference appearing in the different definition of and as follows
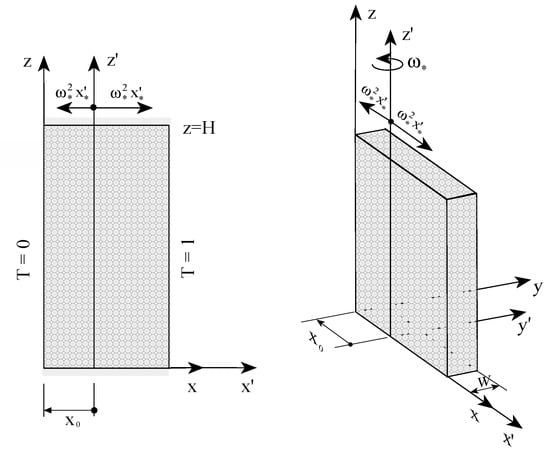
Figure 8.
A rotating porous layer having the rotation axis within its boundaries and subject to different temperatures at the sidewalls (Reprinted from [41], with permission from Elsevier Science Ltd).
It is therefore convenient to explicitly introduce this fact in the problem formulation specifying explicitly that . As a result Equation (50) can be expressed in the form
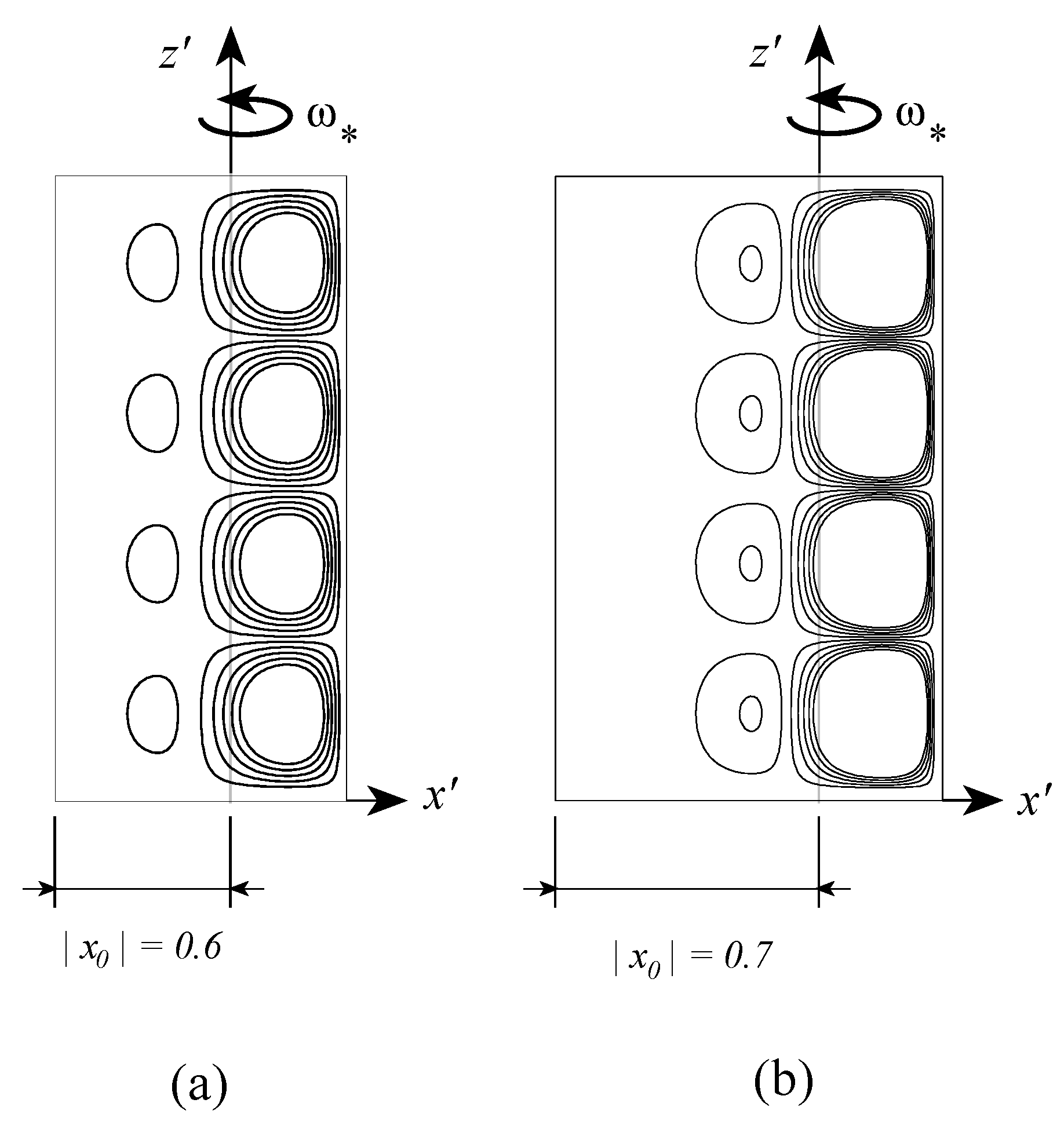
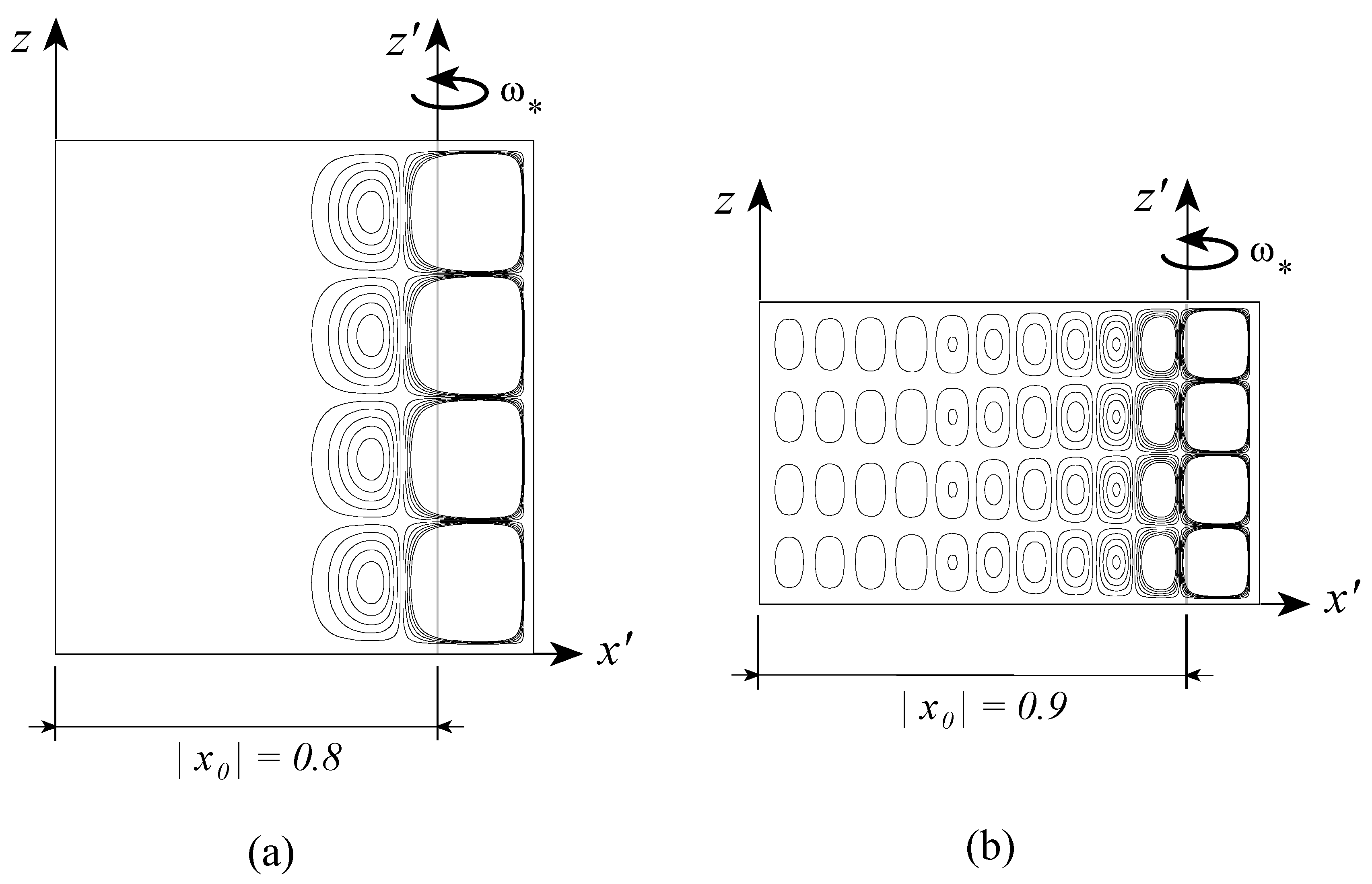
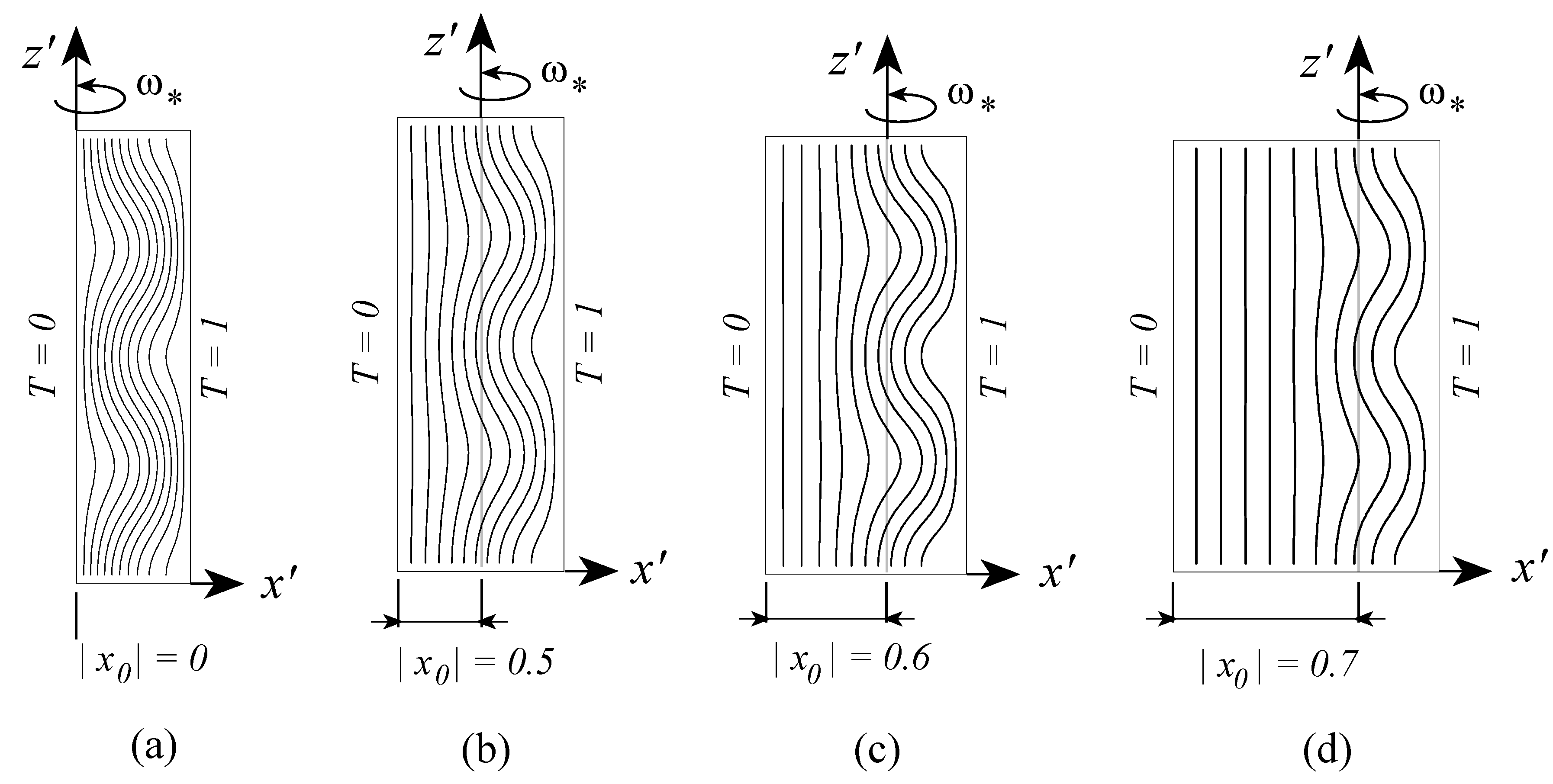
The singularity is obtained when , corresponding to or . Since is uniquely related to the offset distance and is a constant, one can relate the singularity to specific values of . At order 2 this corresponds to and . It was shown by Vadasz [41] that the second value is the only one, which has physical consequences. This value corresponds to a transition beyond which, i.e., for , no positive roots of exist. It therefore implies an unconditional stability of the basic motionless solution for all values of if . The transitional value of was investigated at higher orders showing at order 3 and the value increases with increasing the order. The indications are that as the order increases the transition value of tends towards the limit value of 1. The results for the critical values of the centrifugal Rayleigh number expressed in terms of vs. are presented graphically by Vadasz [41], who concluded that increasing the value of has a stabilizing effect. The results for the convective flow field as obtained by Vadasz [41] are presented in Figure 9, Figure 10 and Figure 11 for different values of . Keeping in mind that to the right of the rotation axis the centrifugal acceleration has a destabilizing effect while to its left a stabilizing effect is expected; the results presented in Figure 9b,c reaffirm this expectation showing an eccentric shift of the convection cells towards the right side of the rotation axis. When the rotation axis is moved further towards the hot wall, say at as presented in Figure 10a, weak convection cells appear even to the left of the rotation axis. This weak convection becomes stronger as increases, as observed in Figure 10b for and formation of boundary layers associated with the primary convection cells is observed to the right of the rotation axis. These boundary layers become more significant for as represented by sharp streamlines gradients in Figure 11a. When Figure 11b shows that the boundary layers of the primary convection are well established and the whole domain is filled with weaker secondary, tertiary and further convection cells. The results for the isotherms corresponding to values of are presented in Figure 12 where the effect of moving the axis of rotation within the porous layer, on the temperature is evident.
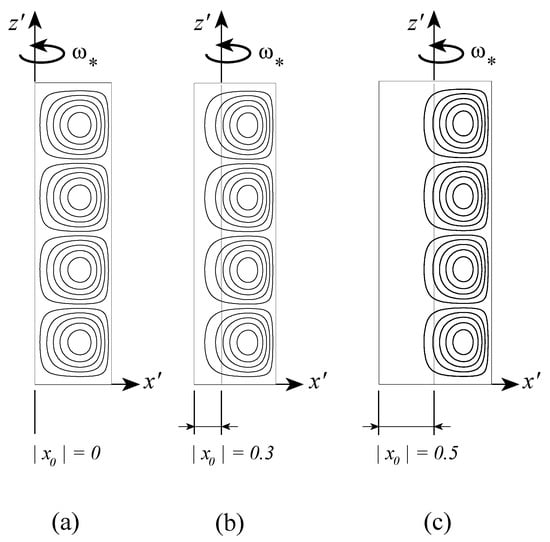
Figure 9.
The convective flow field at marginal stability for three different values of ; 10 streamlines equally divided between and . (a) streamlines for a layer adjacent to the rotation axis ; (b) streamlines for the axis of rotation located at ; (c) streamlines for the axis of rotation located at ; (Reprinted from [41], with permission from Elsevier Science Ltd).
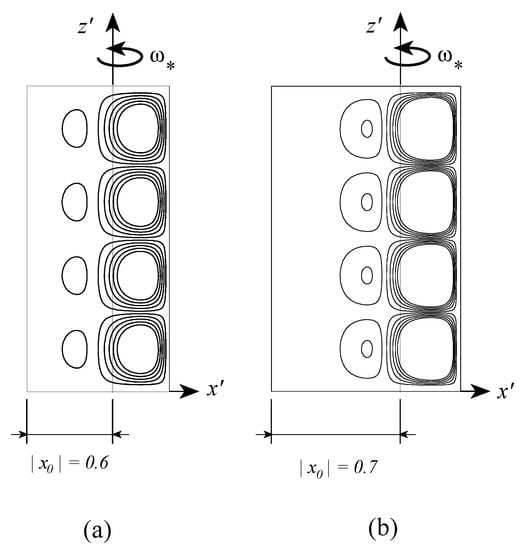
Figure 10.
The convective flow field at marginal stability for two different values of ; 10 streamlines equally divided between and . (a) streamlines for the axis of rotation located at ; (b) streamlines for the axis of rotation located at ; (Reprinted from [41], with permission from Elsevier Science Ltd).
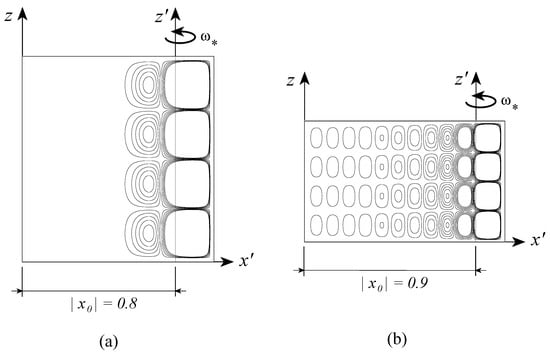
Figure 11.
The convective flow field at marginal stability for two different values of ; 10 streamlines equally divided between and . (a) streamlines for the axis of rotation located at ; (b) streamlines for the axis of rotation located at ; (Reprinted from [41], with permission from Elsevier Science Ltd).
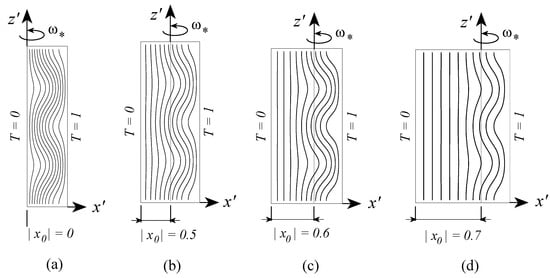
Figure 12.
The convective temperature field at marginal stability for four different values of ; 10 isotherms equally divided between and . Isotherms for the axis of rotation located at (a) ; (b) ; (c) ; (d) ; (Reprinted from [41], with permission from Elsevier Science Ltd).
Previously the discussion focused on centrifugally driven natural convection under conditions of small rotation rates, i.e., . Then, as a first approximation the Coriolis effect was neglected. In this section the effect of the Coriolis acceleration on natural convection is presented even when this effect is small, i.e., . A long rotating porous box where the temperature gradient was perpendicular to the centrifugal body force was considered by Vadasz [35]. The possibility of internal heat generation was included but the case without heat generation, i.e., when the box is heated from above and cooled from below was dealt with separately. The leading order basic flow was evaluated analytically. From the solutions it was concluded that the Coriolis effect on natural convection is controlled by the combined dimensionless group
The flow and temperature fields in the plane , perpendicular to the leading order natural convection plane as evaluated through the analytical solution shows single or double vortices secondary flow in this plane, perpendicular to the basic flow.
5. Coriolis Effect on Natural Convection Due to Gravity Buoyancy
The problem of a rotating porous layer subject to gravity and heated from below (see Figure 13) was originally investigated by Friedrich [75] and by Patil and Vaidyanathan [17]. Both studies considered a non-Darcy model, which is probably subject to the limitations as shown by Nield [68]. Friedrich [74] focused on the effect of Prandtl number on the convective flow resulting from a linear stability analysis as well as a non-linear numerical solution, while Patil and Vaidyanathan [17] dealt with the influence of variable viscosity on the stability condition. The latter concluded that variable viscosity has a destabilizing effect while rotation has a stabilizing effect. Although the non-Darcy model considered included the time derivative in the momentum equation the possibility of convection setting-in as an oscillatory instability was not explicitly investigated by Patil and Vaidyanathan [17]. It should be pointed out that for a pure fluid (non-porous domain) convection sets in as oscillatory instability for a certain range of Prandtl number values (Chandrasekhar [76,77]). This possibility was explored by Friedrich [75], which presents stability curves for both monotonic and oscillatory instability. Jou and Liaw [19] investigated a similar problem of gravity driven thermal convection in a rotating porous layer subject to transient heating from below. By using a non-Darcy model they established the stability conditions for the marginal state without considering the possibility of oscillatory convection.
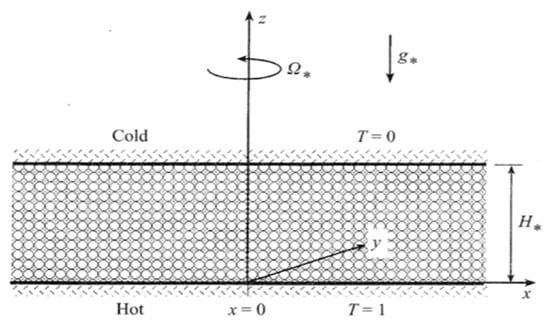
Figure 13.
A rotating fluid saturated porous layer heated from below [42]. (Reproduced with permission from Cambridge University Press).
An important analogy was discovered by Palm and Tyvand [20] who showed, by using a Darcy model, that the onset of gravity driven convection in a rotating porous layer is equivalent to the case of an anisotropic porous medium. The critical Rayleigh number was found to be
where is the Taylor number defined here as
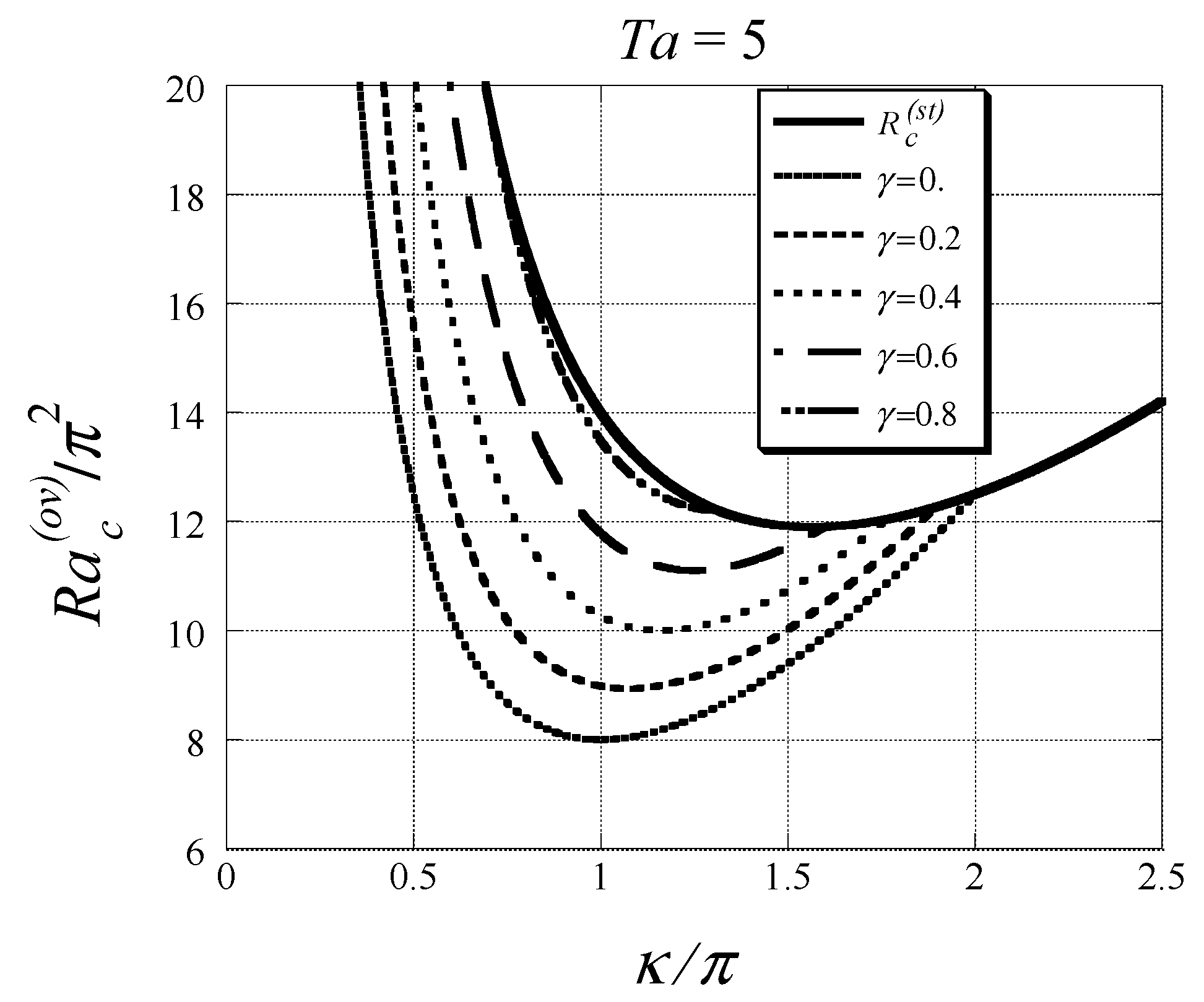
and the corresponding critical wave number is . The porosity is missing in Palm and Tyvand [20] definition of . Nield [21,22] has pointed out that these authors and others have omitted the porosity from the Coriolis term. This result, Equation (63) (amended to include the correct definition of ), was confirmed by Vadasz [41] for a Darcy model extended to include the time derivative term (see Equation (31) with ), while performing linear stability as well as a weak non-linear analyses of the problem to provide differences as well as similarities with the corresponding problem in pure fluids (non-porous domains). As such, Vadasz [42] found that, in contrast to the problem in pure fluids, overstable convection in porous media at marginal stability is not limited to a particular domain of Prandtl number values (in pure fluids the necessary condition is ). Moreover, it was also established by Vadasz [42] that in the porous media problem the critical wave number in the plane containing the streamlines for stationary convection is not identical to the critical wave number associated with convection without rotation, and is therefore not independent of rotation, a result which is quite distinct from the corresponding pure-fluids problem. Nevertheless, it was evident that in porous media, just as in the case of pure fluids subject to rotation and heated from below, the viscosity at high rotation rates has a destabilizing effect on the onset of stationary convection, i.e., the higher the viscosity the less stable is the fluid. An example of stability curves for overstable convection is presented in Figure 14 for , where is the wave number. The upper bound of these stability curves is represented by a stability curve corresponding to stationary convection at the same particular value of the Taylor number, while the lower bound was found to be independent of the value of Taylor number and corresponds to the stability curve for overstable convection associated with .
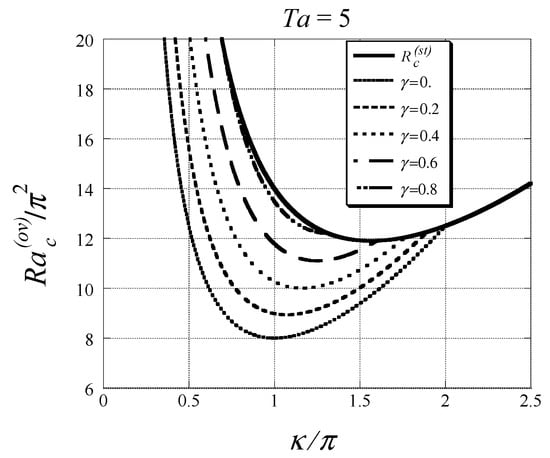
Figure 14.
Stability curves for overstable gravity driven convection in a rotating porous layer heated from below (, ). [42]. (Reproduced with permission from Cambridge University Press).
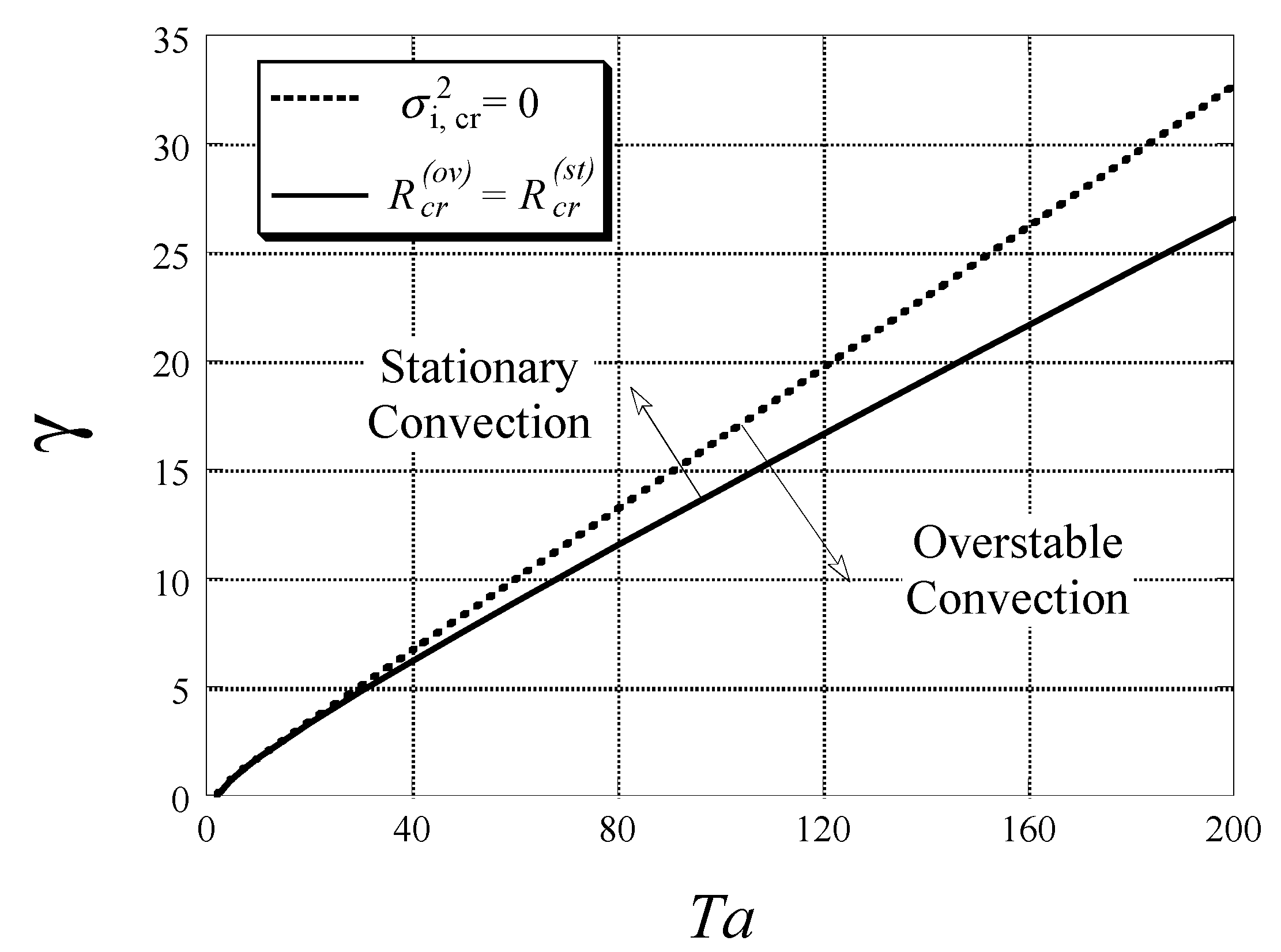
Two conditions have to be fulfilled for overstable convection to set in at marginal stability, i.e., (i) the value of Rayleigh number has to be higher than the critical Rayleigh number associated with overstable convection, and (ii) the critical Rayleigh number associated with overstable convection has to be smaller than the critical Rayleigh number associated with stationary convection. The stability map obtained by Vadasz [42] is presented in Figure 15, which shows that the () plane is divided by a continuous curve (almost a straight line) into two zones, one for which convection sets in as stationary, and the other where overstable convection is preferred. The dotted curve represents the case when the necessary condition (i) above is fulfilled but condition (ii) is not. Weak non-linear stationary as well as oscillatory solutions were derived, identifying the domain of parameter values consistent with supercritical pitchfork (in the stationary case) and Hopf (in the oscillatory case) bifurcations. Unfortunately due to a typo affecting the sign of one of the nonlinear terms in the weak nonlinear analysis the direction of the bifurcations presented seems to be incorrect. The identification of the tricritical point corresponding to the transition from supercritical to subcritical bifurcations was presented on the parameter plane. The possibility of a codimension-2 bifurcation, which is anticipated at the intersection between the stationary and overstable solutions, although identified as being of significant interest for further study, was not investigated by Vadasz [42].
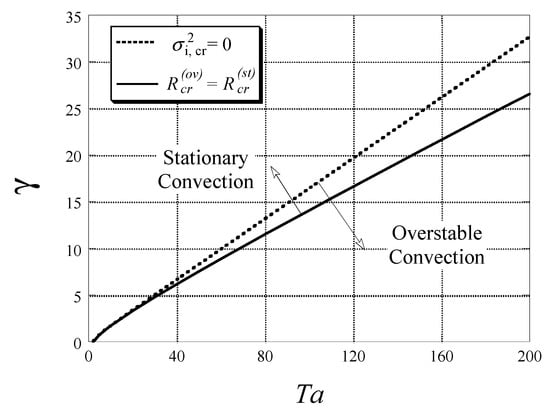
Figure 15.
Stability map for gravity driven convection in a rotating porous layer heated from below (, ) [42]. (Reproduced with permission from Cambridge University Press).
6. Natural Convection Due to Combined Centrifugal and Gravity Buoyancy
Previous sections dealt with natural convection due to centrifugal buoyancy, when the gravity body force contribution was negligible, , satisfying the condition: , or with gravity buoyancy when the centrifugal body force contribution was insignificant, , satisfying the condition: . In the present section the focus is on conditions when both centrifugal buoyancy as well as gravity buoyancy effects are significant, , but at small rotation rates, i.e., . Then, as a first approximation the Coriolis effect can be neglected. Figure 4 still applies to the present problem, subject to a slight modification of drawing the gravity acceleration in the negative direction. The notation remains the same and Equation (50) becomes
where represents the reciprocal of the offset distance from the axis of rotation. The approach being the same as before, the solution is expressed as a sum of a basic solution and small perturbations as presented in Equation (52). However, because of the presence of the gravity component in Equation (65), a motionless conduction solution is not possible any more. Therefore, the basic solution far from the top and bottom walls is obtained in the form
Substituting this basic solution into the governing equations and linearizing the result by neglecting terms that include products of perturbations, which are small, yields a set of partial differential equations for the perturbations. Assuming a normal modes expansion in the and directions in the form
where and are the wave numbers in and directions respectively, i.e., , and using the Galerkin method, the following set of linear algebraic equations is obtained at marginal stability (i.e., for )
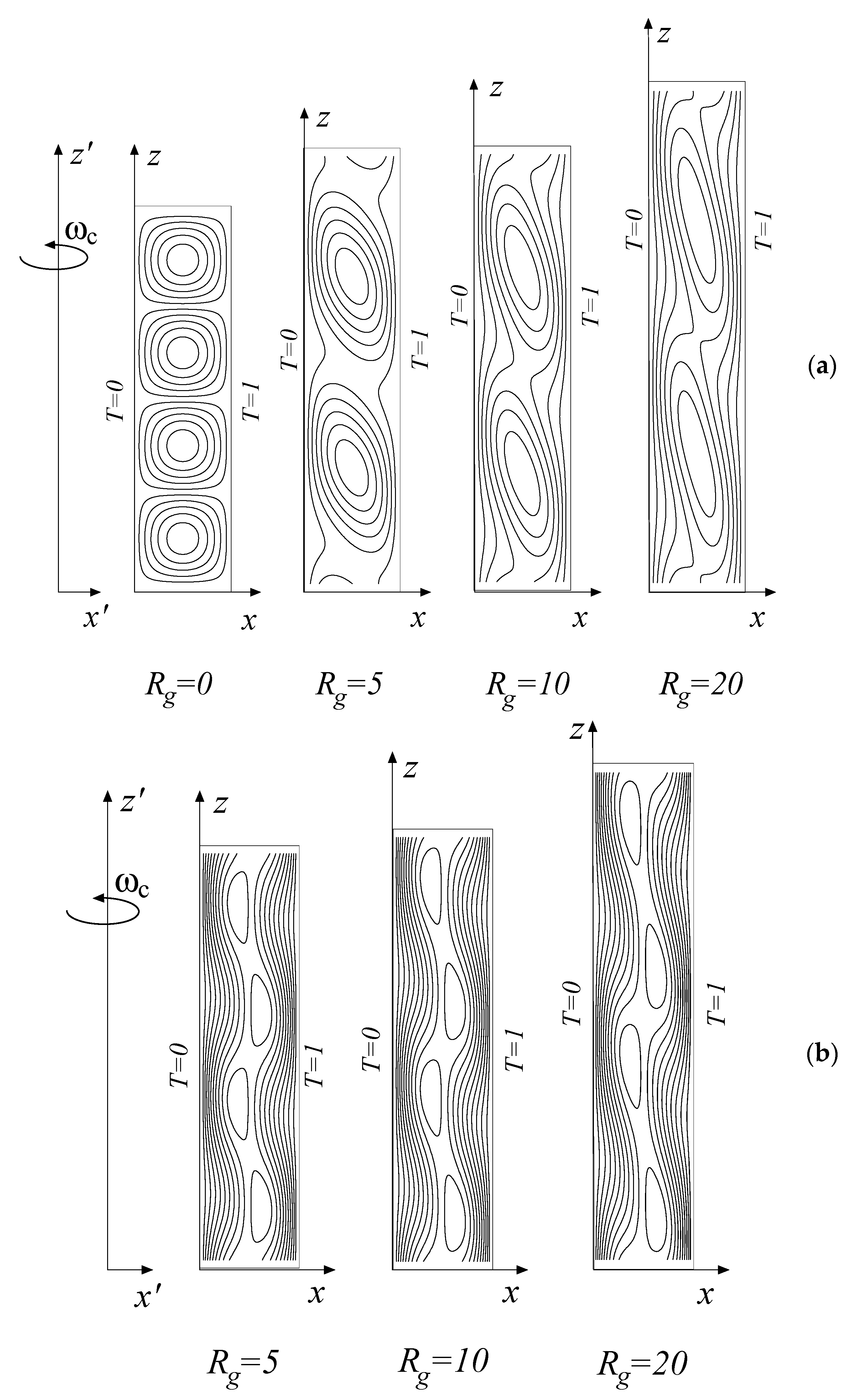
for and . In Equation (68) is the Kronecker delta function and the index can take arbitrary integer values, since it stands only for setting the second index in the Kronecker delta function to be an odd integer. A particular case of interest is the configuration when the layer is placed far away from the axis of rotation, i.e., when the length of the layer is much smaller than the offset distance from the rotation axis . Therefore for or the contribution of the term in Equation (65) is not significant. Substitution of this limit into Equation (68) and solving the system at the second order, i.e., , yields a quadratic equation for the characteristic values of . This equation has no real solutions for values of beyond a transitional value . This value was evaluated at higher orders too, showing that for the transitional value varies very little with , beyond a certain value around . The critical values of were evaluated for different values of and the corresponding two-dimensional convection solutions in terms of streamlines are presented graphically for the odd modes in Figure 16a, showing the perturbation solutions in the plane as skewed convection cells when compared with the case without gravity. The corresponding convection solutions for the even modes are presented in Figure 16b, where it is evident that the centrifugal effect is felt predominantly in the central region of the layer, while the downwards and upwards basic gravity driven convection persists along the left and right boundaries, respectively, although not in straight lines. Beyond the transition value of , the basic gravity driven convective flow (Equation (66)) is unconditionally stable. These results were shown to have an analogy with the problem of gravity driven convection in a non-rotating, inclined porous layer (Govender and Vadasz [29]). Qualitative experimental confirmation of these results was presented by Vadasz and Heerah [45] by using a thermo-sensitive liquid-crystal tracer in a rotating Hele-Shaw cell. When the layer is placed at an arbitrary finite distance from the axis of rotation no real solutions exist for the characteristic values of corresponding to any values of other than . In the presence of gravity , and can be satisfied only if . Therefore the presence of gravity in this case has no other role but to exclude the vertical modes of convection. The critical centrifugal Rayleigh numbers and the corresponding critical wave numbers are the same as in the corresponding case without gravity as presented in Section 4. However, the eigenfunctions representing the convection pattern are different as they exclude the vertical modes replacing them with a corresponding horizontal mode in the direction. Therefore, a cellular convection in the plane is superimposed to the basic convection in the plane.
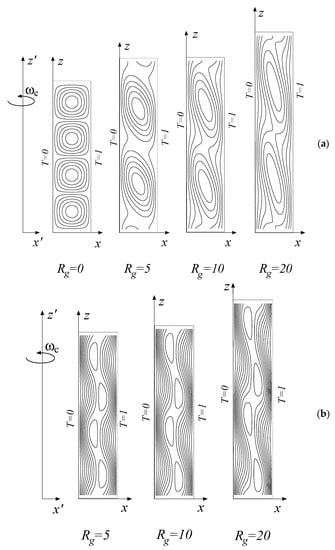
Figure 16.
The convective flow field (streamlines) at marginal stability for different values of (); (a) the odd modes; (b) the even modes. (Reproduced with permission from Hindawi [43]).
7. Additional Effects on Flow and Natural Convection in Rotating Porous Media
Not much research results are available for thermo-haline convection in porous media subject to rotation. Chakrabarti and Gupta [78] investigated a non-Darcy model, which includes the Brinkman term as well as a non-linear convective term in the momentum equation (in the form ). Therefore the model’s validity is subject to the limitations pointed out by Nield [69]. Both linear and non-linear analyses were performed and overstability was particularly investigated. Overstability is affected in this case by both the presence of a salinity gradient and by the Coriolis effect. Apart from the thermal and solutal Rayleigh numbers and the Taylor number, two additional parameters affect the stability. These are the Prandtl number , and the Darcy number , where is the layer’s height. The authors found that, in the range of values of the parameters, which were considered, the linear stability results favor setting-in of convection through a mechanism of overstability. The results for non-linear steady convection show that the system becomes unstable to finite amplitude steady disturbances before it becomes unstable to disturbances of infinitesimal amplitude. Thus the porous layer may exhibit subcritical instability in the presence of rotation. These results are surprising at least in the sense of their absolute generality and the authors mention that further confirmation is needed in order to increase the degree of confidence in these results. A similar problem was investigated by Rudraiah et al. [16] while focusing on the effect of rotation on linear and non-linear double-diffusive convection in a sparsely packed porous medium. A non-Darcy model identical to the one used by Chakrabarti and Gupta [78] was adopted by Rudraiah et al. [16], however the authors spelled out explicitly that the model validity is limited to high porosity and high permeability which makes it closer to the behavior of a pure fluid system (non-porous domain). It is probably for this reason that the authors preferred to use the non-porous medium definitions for Rayleigh and Taylor numbers which differ by a factor of and , respectively, from the corresponding definitions for porous media. It is because of these definitions that the authors concluded that for small values of number the effect of rotation is negligible for values of . This means that rotation has a significant effect for large rotation rates, i.e., . If the porous media Taylor number had been used instead, i.e., the proper porous media scales, then one could have significant effects of rotation at porous media Taylor numbers as small as . Hence, the results presented by Rudraiah et al. [16] are useful provided which is applicable for high permeability (or sparsely packed) porous layers. Marginal stability as well as overstability were investigated and the results show different possibilities of existence of neutral curves by both mechanisms, i.e., monotonic as well as oscillatory instability. In this regard the results appear more comprehensive in the study by Rudraiah et al. [16] than in Chakrabarti and Gupta [78]. The finite amplitude analysis was performed by using a severely truncated representation of a Fourier series for the dependent variables. As a result a seventh-order Lorenz model of double diffusive convection in a porous medium in the presence of rotation was obtained. From the study of steady, finite amplitude analysis the authors found that subcritical instabilities are possible, depending on the parameter values. The effect of the parameters on the heat and mass transport was investigated as well, and results presenting this effect are discussed in Rudraiah et al. [16]. The onset of double-diffusive convection in a rotating porous layer was investigated by Lombardo and Mulone [60], Malashety, Pop, and Heera [48], Falsaperla, Giacobbe and Mulone [63]. Triple-diffusion effects in rotating porous layers were investigated by Capone and De Luca [64]. They evaluated the ultimate boundedness of the solutions and found a necessary and sufficient condition for the global nonlinear asymptotic L2-stability of the motionless conduction solution.
Lack of local thermal equilibrium (LaLotheq) or local thermal non-equilibrium (LTNE) means that distinct temperature values exist between the solid and fluid phases within the same Representative Elementary Volume (REV). Malashetty et al. [53] presented the linear stability and the onset of convection in a porous layer heated from below and subject to rotation, accounting for the Coriolis effect as in Vadasz [42] but allowing for distinct temperature values between the solid and fluid phases, i.e., lack of local thermal equilibrium (LaLotheq), or local thermal non-equilibrium (LTNE). The nonlinear part of the analysis was undertaken by using a truncated mode spectral system, such as the one used by Vadasz and Olek [46] but adapted for the LaLotheq conditions. The effect of finite heat transfer between the phases leading to lack of local thermal equilibrium was investigated also by Govender and Vadasz [32] while investigating also the effect of mechanical and thermal anisotropy on the stability of a rotating porous layer heated from below and subject to gravity. The topic of anisotropic effects is discussed in the next section. Bhadauria [47] investigated the effect of temperature modulation on the onset of thermal instability in a horizontal fluid-saturated porous layer heated from below and subject to uniform rotation. An extended Darcy model, which includes the time derivative term, has been considered, and a time-dependent periodic temperature field was applied to modulate the surfaces’ temperature. A perturbation procedure based on small amplitude of the imposed temperature modulation was used to study the combined effect of rotation, permeability, and temperature modulation on the stability of the fluid saturated porous layer. The correction of the critical Rayleigh number was calculated as a function of amplitude and frequency of modulation, the porous media Taylor number, and the Vadasz number. It was found that both rotation and permeability suppress the onset of thermal instability. Furthermore, the author concluded that temperature modulation could either promote or retard the onset of convection.
The effect of anisotropy on the stability of convection in a rotating porous layer subject to centrifugal body forces was investigated by Govender [25]. The Darcy model extended to include anisotropic effects and rotation was used to describe the momentum balance and a modified energy equation that included the effects of thermal anisotropy was used to account for the heat transfer. The linear stability theory was used to evaluate the critical Rayleigh number for the onset of convection in the presence of thermal and mechanical anisotropy. It was found that the convection was stabilized when the thermal anisotropy ratio (which is a function of the thermal and mechanical anisotropy parameters) increased in magnitude. Malashetty and Swamy [54], and Govender and Vadasz [32] investigated the Coriolis effect on natural convection in a rotating anisotropic fluid-saturated porous layer heated from below and subject to gravity as the body force. Malashetty and Swamy [54] assumed local thermal equilibrium while Govender and Vadasz [32] dealt with lack of local thermal equilibrium (LaLotheq), or local thermal non-equilibrium (LTNE). Malashetty and Swamy [54] used the linear stability theory as well as a nonlinear spectral method. The linear theory was based on the usual normal mode technique and the nonlinear theory on a truncated Galerkin analysis. The Darcy model extended to include a time derivative and the Coriolis terms with an anisotropic permeability was used to describe the flow through the porous media. A modified energy equation including the thermal anisotropy was used. The effect of rotation, mechanical and thermal anisotropy parameters and the Prandtl number on the stationary and overstable convection was discussed. It was found that the effect of mechanical anisotropy is to prefer the onset of oscillatory convection instead of the stationary one. It was also found, just as in Vadasz [42], that the existence of overstable motions in case of rotating porous media is not restricted to a particular range of Prandtl number as compared to the pure viscous fluid case. The steady finite amplitude analysis was performed using the truncated Galerkin modes to find the Nusselt number. The effect of various parameters on heat transfer was investigated. Govender and Vadasz [32] analyzed the stability of a horizontal rotating fluid saturated porous layer exhibiting both thermal and mechanical anisotropy, subject to lack of local thermal equilibrium (LaLotheq), or local thermal non-equilibrium (LTNE). All of the results were presented as a function of the scaled inter-phase heat transfer coefficient. The results of the linear stability theory have revealed that increasing the conductivity ratio and the mechanical anisotropy has a destabilizing effect, whilst increasing the fluid and solid thermal conductivity ratios is stabilizing. In general it was found that rotation has a stabilizing effect in a porous layer exhibiting mechanical or thermal (or both mechanical and thermal) anisotropy. Additional results for the effect of rotation on thermal convection in an anisotropic porous medium were presented by Vanishree and Siddheshwar [49].
An interesting, more recent, application is related to nanofluids. A nanofluid is a suspension of nanoparticles or nanotubes in a liquid. When the liquid is saturating a porous matrix one deals with nanofluids in porous media. Chand and Rana [79] analyzed the Coriolis effect on natural convection in a rotating porous layer saturated by a nanofluid. Agarwal an Bhadauria [52], Rana and Agarwal [55], investigated the natural convection in a rotating porous layer saturated by a nanofluid and a binary mixture. This implies that the nanoparticles are suspended in a binary mixture, e.g., in a water and salt solution. Therefore double-diffusive convection is anticipated. The model used for the nanofluid incorporates the effects of Brownian motion and thermophoresis, while the Darcy model is used for the porous medium. The neutral and critical Rayleigh numbers for stationary and oscillatory convection have been obtained in terms of various dimensionless parameters. The authors concluded that the principle of exchange of stabilities is applicable in the present problem, while more amount of heat is required in the nanofluid case for convection to set-in. Agarwal et al. [50] considered the convection in a rotating anisotropic porous layer saturated by a nanofluid. The model used for nanofluid combines the effect of Brownian motion along with thermophoresis, while for a porous medium the Darcy model has been used. Using linear stability analysis the expression for the critical Rayleigh number has been obtained in terms of various dimensionless parameters. Agarwal et al. [50] indicate that bottom-heavy and top-heavy arrangements of nanoparticles tend to prefer oscillatory and stationary modes of convection, respectively. The onset of double-diffusive nanofluid convection in a rotating porous layer was investigated by Yadav et al. [56].
During solidification of binary alloys the solidification front between the solid and the liquid phases is not a sharp front but rather a mushy layer combining liquid and solid phases each one being interconnected. It is not surprising therefore that the treatment of this mushy layer follows all the rules applicable to a porous medium. Natural convection due to thermal as well as concentration gradients occurs in the mushy layer resulting in possible creation of freckles that might affect the quality of the cast. When such a process occurs in a system that is subject to rotation, centrifugal buoyancy as well as Coriolis effects are relevant and essential to be included in any model of this process. Govender and Vadasz [31] investigated such a system via a weak nonlinear analysis for moderate Stefan numbers applicable to stationary convection in a rotating mushy layer. Consequently Govender and Vadasz [30] investigated a similar system via a weak nonlinear analysis for moderate Stefan numbers applicable to oscillatory convection in a rotating mushy layer. A near-eutectic approximation and large far-field temperature were employed in both papers in order to decouple the mushy layer from the overlying liquid melt. The parameter regimes in terms of Taylor number for example where the bifurcation is subcritical or supercritical were identified. In the case of oscillatory convection increasing the Taylor number lead to a supercritical bifurcation.
Linear stability was the primary method used in previous sections to establish the stability criteria for the onset of natural convection in a rotating porous layer. Straughan [73] pioneered the introduction of a nonlinear analysis producing a sharp nonlinear stability threshold in rotating porous convection. The application and generalization of this method was presented by Lombardo and Mulone [60], while deriving necessary and sufficient conditions of global nonlinear stability for double-diffusive convection in rotating porous media. The nonlinear method was expanded and summarized by Straughan [59]. The application of this nonlinear method to natural convection in non-rotating porous media was expanded showing the coincidence between linear and global nonlinear stability of non-constant through-flows was presented by Capone and De Luca [66] by using the “Rionero Auxiliary System Method”. Weak nonlinear solutions were presented by Bhadauria et al. [51]. Investigations into the effects of inertia on rotating porous convection were undertaken by Falsaperla, Mulone, and Straughan [62], and by Capone and Rionero [65]. The latter used again the “Rionero Auxiliary System Method” to derive a set of conditions for the significance of inertia in this problem and for global nonlinear stability in terms of the porous media Taylor number as well as Vadasz number.
Other studies considered effects of rotation for a combination of previously presented conditions. For example Capone and Gentile [80] presented sharp stability results in a rotating anisotropic porous layer subject to lack of local thermal equilibrium (LaLotheq, LTNE). Double diffusive convection in a rotating anisotropic porous layer was presented by Galkwad and Kouser [81], Malashetty and Heera [82], and Malashetty and Begum [83]. Double diffusive convection in a rotating porous medium saturated with a coupled stress fluid was considered by Malashetty et al. [84], while double diffusive convection in a rotating porous layer saturated by a viscoelastic fluid was investigated by Kumar and Bhadauria [85]. The effect of rotation on a micropolar ferromagnetic fluid heated from below saturating a porous medium was presented by Sunil et al. [86]. Rotation effects on convection in a porous layer saturated by nanofluids was further considered by Bhadauria and Agrawal [87], for a porous medium model including the Brinkman term. A similar model was presented by Yadav and Lee [88] for the case of lack of local thermal equilibrium (LaLotheq, LTNE), and by Yadav et al. [89] for a Darcy model Soret driven convection in a rotating porous medium saturated by a nanofluid. Brinkman convection induced by internal heating in a rotating porous medim layer saturated by a nanofluid was investigated by Yadav et al. [90], while thermal instability in a rotating porous layer saturated by a non-Newtonian nanofluid was considered by Yadav et al. [91]. Yadav et al. [92] presented the conditions for the onset of convection in a rotating porous layer due internal heating by using a Brinkman model. The effects of thermal modulation, i.e., top and bottom imposed temperatures are allowed to vary slightly in time, were considered by Malashetty and Swamy [93] using a Darcy model and Bhadauria [94] using a Brinkman model. A similar Brinkman model was applied for investigating the effects of centrifugal buoyancy in a rotating porous layer far away from the center of rotation subject to modulation of rotation by Om et al. [95], i.e., the angular velocity was allowed to slightly vary periodically in time. The same conditions applied to a rotating porous layer distant an arbitrary distance from the center of rotation was presented by Om et al. [96]. Coriolis effect on thermal convective instability of viscoelastic fluids in a rotating porous cylindrical annulus was investigated by Kang et al. [97]. Küppers-Lortz instability in rotating Rayleigh-Benard convection in a porous medium was studied by Rameshwar et al. [98].
8. Conclusions
A review of the variety of instability problems linked to natural convection in rotating porous media was presented. The effect of centrifugal buoyancy was investigated separately, and later in combination with gravitational buoyancy. The cases when the Coriolis effect is significant were also analyzed and the corresponding results were discussed. The diversity of additional effects linked to natural convection in rotating porous media, such as thermo-solutal and double-diffusive convection, the effect of anisotropy of the porous medium, the inclusion of nanofluids in rotating porous media, solidification of binary alloys, and lack of local thermal equilibrium are examples that were also shortly reviewed. The pioneering studies on global nonlinear analyses and investigations of the effect of inertia on natural convection in rotating porous media concluded the present review.
Funding
This research received no current external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Fowler, A.C. A compaction model for melt transport in the earth asthenosphere Part I: The base model. In Magma Transport and Storage; Raya, M.P., Ed.; John Wiley and Sons Ltd.: Chichester, UK, 1990; pp. 3–14. [Google Scholar]
- Vadasz, P. Fluid Flow and Thermal Convection in Rotating Porous Media. In Handbook of Porous Media; Vadfai, K., Ed.; Marcel Dekker: New York, NY, USA, 2000; pp. 395–439. [Google Scholar]
- Vadasz, P. Fluid Flow and Heat Transfer in Rotating Porous Media; Kulacki, F.A., Ed.; Springer Briefs in applied Science and Engineering; Springer: Cham, Switzerland; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2016. [Google Scholar]
- Vadasz, P. Natural Convection in Rotating Flows. In Handbook of Thermal Science and Engineering; Kulacki, F.A., Ed.; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 691–758. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 4th ed.; Springer: Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2013. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2017. [Google Scholar]
- Bejan, A. Convection Heat Transfer, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Dagan, G. Some aspects of heat and mass transfer in porous media. In Fundamentals of Transport Phenomena in Porous Media; Bear, J., Ed.; Int. Association for Hydraulic Research, Elsevier: New York, NY, USA, 1972; pp. 55–64. [Google Scholar]
- Acharya, S. Single-phase convective heat transfer: Fundamental equations and foundational assumptions. In Handbook of Thermal Science and Engineering; Kulacki, A.F., Ed.; Springer International Publishing AG: Cham, Switzerland, 2017. [Google Scholar]
- Wiesche, S. Heat Transfer in Rotating Flows. In Handbook of Thermal Science and Engineering; Kulacki, A.F., Ed.; Springer International Publishing AG: Cham, Switzerland, 2017. [Google Scholar]
- Vadasz, P. Fundamentals of Flow and Heat Transfer in Rotating Porous Media. In Heat Transfer PA 5; Taylor and Francis: Bristol, UK, 1994; pp. 405–410. [Google Scholar]
- Vadasz, P. Flow in rotating porous media. In Fluid Transp. Porous Media; From the Series Advances in Fluid Mechanics 13; Plessis, P.D., Rahman, M., Eds.; Computational Mechanics Publications: Southampton, UK, 1997; pp. 161–214. [Google Scholar]
- Vadasz, P. Free convection in rotating porous media. In Transport Phenomena in Porous Media; Ingham, D.B., Pop, I., Eds.; Elsevier Science: Oxford, UK, 1998; pp. 285–312. [Google Scholar]
- Vadasz, P. Heat Transfer and Fluid Flow in Rotating Porous Media. In Computational Methods in Water Resources 1; Hassanizadeh, S.M., Schotting, R.J., Gray, W.G., Pinder, G.F., Eds.; Development in Water Science 47; Elsevier: Amsterdam, The Netherlands, 2002; pp. 469–476. [Google Scholar]
- Vadasz, P. Thermal Convection in Rotating Porous Media. In Trends in Heat, Mass & Momentum Transfer 8; Research Trends: Trivandrum, Kerala, India, 2002; pp. 25–58. [Google Scholar]
- Rudraiah, N.; Shivakumara, I.S.; Friedrich, R. The effect of rotation on linear and non-linear double-diffusive convection in a sparsely packed porous medium. Int. J. Heat Mass Transf. 1986, 29, 1301–1317. [Google Scholar] [CrossRef]
- Patil, P.R.; Vaidyanathan, G. On setting up of convection currents in a rotating porous medium under the influence of variable viscosity. Int. J. Eng. Sci. 1983, 21, 123–130. [Google Scholar] [CrossRef]
- Jou, J.J.; Liaw, J.S. Transient thermal convection in a rotating porous medium confined between two rigid boundaries. Int. Comm. Heat Mass Transf. 1987, 14, 147–153. [Google Scholar] [CrossRef]
- Jou, J.J.; Liaw, J.S. Thermal convection in a porous medium subject to transient heating and rotation. Int. J. Heat Mass Transf. 1987, 30, 208–211. [Google Scholar]
- Palm, E.; Tyvand, A. Thermal convection in a rotating porous layer. J. Appl. Math. Physics (ZAMP) 1984, 35, 122–123. [Google Scholar] [CrossRef]
- Nield, D.A. The stability of convective flows in porous media. In Convective Heat and Mass Transfer in Porous Media; Kakaç, S., Kilkis, B., Kulacki, F.A., Arniç, F., Eds.; Kluwer Academic Publ.: Dordrecht, The Netherlands, 1991; pp. 79–122. [Google Scholar]
- Nield, D.A. Modeling the effect of a magnetic field or rotation on flow in a porous medium: Momentum equation and anisotropic permeability analogy. Int. J. Heat Mass Transf. 1999, 42, 3715–3718. [Google Scholar] [CrossRef]
- Auriault, J.L.; Geindreau, C.; Royer, P. Filtration law in rotating porous media. C. R. Acad. Sci. Ser. IIB Mech. 2000, 328, 779–784. [Google Scholar] [CrossRef][Green Version]
- Auriault, J.L.; Geindreau, C.; Royer, P. Coriolis effects on filtration law in rotating porous media. Transp. Porous Media 2002, 48, 315–330. [Google Scholar] [CrossRef]
- Govender, S. On the effect of anisotropy on the stability of convection in rotating porous media. Transp. Porous Media 2006, 64, 413–422. [Google Scholar] [CrossRef]
- Govender, S. Vadasz number influence on vibration in a rotating porous layer placed far away from the axis of rotation. J. Heat Transf. 2010, 132, 112601. [Google Scholar] [CrossRef]
- Havstad, M.A.; Vadasz, P. Numerical Solution of the Three Dimensional Fluid Flow in a Rotating Heterogeneous Porous Channel. Int. J. Numer. Methods Fluids 1999, 31, 411–429. [Google Scholar] [CrossRef]
- Vadasz, P.; Havstad, M.A. The Effect of Permeability Variations on the Flow in a Rotating Porous Channel. ASME J. Fluids Eng. 1999, 121, 568–573. [Google Scholar] [CrossRef]
- Govender, S.; Vadasz, P. Centrifugal and gravity driven convection in rotating porous media—An analogy with the inclined porous layer. ASME-HTD 1995, 309, 93–98. [Google Scholar]
- Govender, S.; Vadasz, P. Weak non-linear analysis of moderate Stefan number oscillatory convection in rotating mushy layers. Transp. Porous Media 2002, 48, 353–372. [Google Scholar] [CrossRef]
- Govender, S.; Vadasz, P. Weak non-linear analysis of moderate Stefan number stationary convection in rotating mushy layers. Transp. Porous Media 2002, 49, 247–263. [Google Scholar] [CrossRef]
- Govender, S.; Vadasz, P. The effect of mechanical and thermal anisotropy on the stability of gravity driven convection in rotating porous media in the presence of thermal non-equilibrium. Transp. Porous Media 2007, 69, 55–66. [Google Scholar] [CrossRef]
- Vadasz, P. On the evaluation of heat transfer and fluid flow by using the porous media approach with application to cooling of electronic equipment. In Proceedings of the 5th Israeli Conference on Packaging of Electronic Equipment, Herzlia, Israel, 8–11 December 1991; pp. D.4.1–D.4.6. [Google Scholar]
- Vadasz, P. Natural convection in rotating porous media induced by the centrifugal body force: The solution for small aspect ratio. ASME J. Energy Resour. Technol. 1992, 114, 250–254. [Google Scholar] [CrossRef]
- Vadasz, P. Three-dimensional free convection in a long rotating porous box. ASME J. Heat Transf. 1993, 115, 639–644. [Google Scholar] [CrossRef]
- Vadasz, P. On Taylor-Proudman columns and geostrophic flow in rotating porous media. R D J. 1994, 10, 53–57. [Google Scholar]
- Vadasz, P. Centrifugally generated free convection in a rotating porous box. Int. J. Heat Mass Transf. 1994, 37, 2399–2404. [Google Scholar] [CrossRef]
- Vadasz, P. Stability of free convection in a narrow porous layer subject to rotation. Int. Comm. Heat Mass Transf. 1994, 21, 881–890. [Google Scholar] [CrossRef]
- Vadasz, P. Coriolis effect on free convection in a rotating porous box subject to uniform heat generation. Int. J. Heat Mass Transf. 1995, 38, 2011–2018. [Google Scholar] [CrossRef]
- Vadasz, P. Stability of free convection in a rotating porous layer distant from the axis of rotation. Transp. Porous Media 1996, 23, 153–173. [Google Scholar] [CrossRef]
- Vadasz, P. Convection and stability in a rotating porous layer with alternating direction of the centrifugal body force. Int. J. Heat Mass Transf. 1996, 39, 1639–1647. [Google Scholar] [CrossRef]
- Vadasz, P. Coriolis effect on gravity-driven convection in a rotating porous layer heated from below. J. Fluid Mech. 1998, 376, 351–375. [Google Scholar] [CrossRef]
- Vadasz, P.; Govender, S. Two-dimensional convection induced by gravity and centrifugal forces in a rotating porous layer far away from the axis of rotation. Int. J. Rotating Mach. 1998, 4, 73–90. [Google Scholar] [CrossRef]
- Vadasz, P.; Govender, S. Stability and stationary convection induced by gravity and centrifugal forces in a rotating porous layer distant from the axis of rotation. Int. J. Eng. Sci. 2001, 39, 715–732. [Google Scholar] [CrossRef]
- Vadasz, P.; Heerah, A. Experimental confirmation and analytical results of centrifugally-driven free convection in rotating porous media. J. Porous Media 1998, 1, 261–272. [Google Scholar]
- Vadasz, P.; Olek, S. Transitions and chaos for free convection in a rotating porous layer. Int. J. Heat Mass Transf. 1998, 41, 1417–1435. [Google Scholar] [CrossRef]
- Bhadauria, B.S. Effect of temperature modulation on the onset of Darcy convection in a rotating porous medium. J. Porous Media 2008, 11, 361–375. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Pop, I.; Heera, R. Linear and nonlinear double diffusive convection in a rotating sparsely packed porous layer using a thermal non-equilibrium model. Contin. Mech. Thermodyn. 2009, 21, 317–339. [Google Scholar] [CrossRef]
- Vanishree, R.K.; Siddheshwar, P.G. Effect of Rotation on Thermal Convection in an Anisotropic Porous Medium with Temperature-dependent Viscosity. Transp. Porous Media 2010, 81, 73–87. [Google Scholar] [CrossRef]
- Agarwal, S.; Bhadauria, B.S.; Siddheshwar, P.G. Thermal instability of a nanofluid saturating a rotating anisotropic porous medium. Spec. Top. Rev. Porous Media Int. J. 2011, 2, 53–64. [Google Scholar]
- Bhadauria, B.S.; Siddheshwar, P.G.; Kumar, J.; Suthar, O.P. Weakly nonlinear stability analysis of temperature/gravity-modulated stationary Rayleigh–Bénard convection in a rotating porous medium. Transp. Porous Media 2012, 92, 633–647. [Google Scholar] [CrossRef]
- Agarwal, S.; Bhadauria, B.S. Flow patterns in linear state if Rayleigh-Benard convection in a rotating nanofluid layer. Appl. Nanosci. 2014, 4, 935–941. [Google Scholar] [CrossRef][Green Version]
- Malashetty, M.S.; Swamy, M.; Kulkarni, S. Thermal convection in a rotating porous layer using a thermal nonequilibrium model. Phys. Fluids 2007, 19, 054102. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Swamy, M. The effect of rotation on the onset of convection in a horizontal anisotropic porous layer. Int. J. Therm. Sci. 2007, 46, 1023–1032. [Google Scholar] [CrossRef]
- Rana, P.; Agarwal, S. Convection in a binary nanofluid saturated rotating porous layer. J. Nanofluids 2015, 4, 1–7. [Google Scholar] [CrossRef]
- Yadav, D.; Lee, D.; Hee Cho, H.; Lee, J. The Onset of Double Diffusive Nanofluid Convection in a Rotating Porous Medium Layer with Thermal Conductivity and Viscosity Variation: A. Revised Model. J. Porous Media 2016, 19, 31–46. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mohimanian Pour, S.A.; Hayat, T.; Obaidat, S. Analytic Approximate Solutions for Steady Flow over a Rotating Disk in Porous Medium with heat Transfer by Homotopy Analysis Method. Comput. Fluids 2012, 54, 1–9. [Google Scholar] [CrossRef]
- Makinde, O.D.; Beg, O.A.; Takhar, H.S. Magnetohydrodynamic Viscous Flow in a Rotating Porous Medium Cylindrical Annulus with a Applied Radial Magnetic Field. Int. J. Appl. Math. Mech. 2009, 5, 68–81. [Google Scholar]
- Straughan, B. Stability and Wave Motion in Porous Media; Applied Mathematical Sciences Series 165; Springer: New York, NY, USA, 2008. [Google Scholar]
- Lombardo, S.; Mulone, G. Necessary and sufficient conditions of global nonlinear stability for rotating double-diffusive convection in a porous medium. Contin. Mech. Thermodyn. 2002, 14, 527–540. [Google Scholar] [CrossRef]
- Falsaperla, P.; Mulone, G.; Straughan, B. Rotating porous convection with Prescribed Heat Flux. Int. J. Eng. Sci. 2010, 48, 685–692. [Google Scholar] [CrossRef]
- Falsaperla, P.; Mulone, G.; Straughan, B. Inertia effects on rotating porous convection. Int. J. Heat Mass Transf. 2011, 54, 1352–1359. [Google Scholar] [CrossRef]
- Falsaperla, P.; Giacobbe, A.; Mulone, G. Double Diffusion in Rotating Porous Media under General Boundary Conditions. Int. J. Heat Mass Transf. 2012, 55, 2412–2419. [Google Scholar] [CrossRef]
- Capone, F.; De Luca, R. Ultimately boundedness and stability of triply diffusive mixtures in rotating porous layers under the action of Brinkman law. Int. J. C Mech. 2012, 47, 799–805. [Google Scholar] [CrossRef]
- Capone, F.; Rionero, S. Inertia effect on the onset of convection in rotating porous layers via the “auxiliary system method”. Int. J. Non-Linear Mech. 2013, 57, 192–200. [Google Scholar] [CrossRef]
- Capone, F.; De Luca, R. Coincidence between linear and global nonlinear stability of non-constant throughflows via the Rionero ‘‘Auxiliary System Method’’. Meccanica 2014, 49, 2025–2036. [Google Scholar] [CrossRef][Green Version]
- Boussinesq, J. Theorie Analitique de la Chaleur [Volume 2]; Gutheir-Villars: Paris, France, 1903; p. 172. [Google Scholar]
- Nield, D.A. The boundary correction for the Rayleigh-Darcy problem: Limitations of the Brinkman equation. J. Fluid Mech. 1983, 128, 37–46. [Google Scholar] [CrossRef]
- Nield, D.A. The limitations of the Brinkman-Forchheimer equation in modeling flow in a saturated porous medium and at an interface. Int. J. Heat Fluid Flow 1991, 12, 269–272. [Google Scholar] [CrossRef]
- Nield, D.A. Discussion on “Analysis of heat transfer regulation and modification employing intermittently emplaced porous cavities”. J. Heat Transf. 1995, 117, 554–555. [Google Scholar] [CrossRef][Green Version]
- Vafai, K.; Kim, S.J. Analysis of surface enhancement by a porous substrate. ASME J. Heat Transf. 1990, 112, 700–706. [Google Scholar] [CrossRef]
- Greenspan, H.P. The Theory of Rotating Fluids; Cambridge Univ. Press: Cambridge, UK, 1980; pp. 5–18. [Google Scholar]
- Straughan, B. A sharp nonlinear stability threshold in rotating porous convection. Proc. R. Soc. Lond. A 2001, 457, 87–93. [Google Scholar] [CrossRef]
- Sheu, L.-J. An autonomous system for chaotic convection in a porous medium using a thermal non-equilibrium model. Chaos Solitons Fractals 2006, 30, 672–689. [Google Scholar] [CrossRef]
- Friedrich, R. The effect of Prandtl number on the cellular convection in a rotating fluid saturated porous medium. ZAMM 1983, 63, 246–249. (In German) [Google Scholar]
- Chandrasekhar, S. The instability of a layer of fluid heated from below and subject to Coriolis forces. Proc. R. Soc. Lond. A 1953, 217, 306–327. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford Univ. Press: Oxford, UK, 1961; reprint by Dover Publications Inc.: New York, NY, USA, 1981. [Google Scholar]
- Chakrabarti, A.; Gupta, A.S. Nonlinear thermohaline convection in a rotating porous medium. Mech. Res. Commun. 1981, 8, 9–22. [Google Scholar] [CrossRef]
- Chand, R.; Rana, G.C. On the onset of thermal convection in rotating nanofluid layer saturating a Darcy-Brinkman porous medium. Int. J. Heat Mass Transf. 2012, 55, 5417–5424. [Google Scholar] [CrossRef]
- Capone, F.; Gentile, M. Sharp stability results in LTNE rotating anisotropic porous layer. Int. J. Therm. Sci. 2018, 134, 661–664. [Google Scholar] [CrossRef]
- Galkwad, S.N.; Kouser, S. Analytical study of linear and nonlinear double diffusive convection in a rotating anisotropic porous layer with Soret effect. J. Porous Media 2012, 12, 745–761. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Heera, R. The effect of rotation on the onset of double diffusive convection in a horizontal anisotropic porous layer. Transp. Porous Media 2008, 74, 105–127. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Begum, I. The effect of rotation on the onset of double diffusive convection in a sparsely packed anisotropic porous layer. Transp. Porous Media 2011, 88, 315–345. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Kollur, P.; Sidram, W. Effect of rotation on the onset of double diffusive convection in a Darcy porous medium saturated with a couple stress fluid. Appl. Math. Model. 2013, 37, 172–186. [Google Scholar] [CrossRef]
- Kumar, A.; Bhadauria, B.S. Non-linear two dimensional double diffusive convection in a rotating porous layer saturated by a viscoelastic fluid. Transp. Porous Media 2011, 87, 229–250. [Google Scholar] [CrossRef]
- Sunil; Sharma, A.; Bharti, P.K.; Shandil, R.G. Effect of rotation on a layer of micropolar ferromagnetic fluid heated from below saturating a porous medium. Int. J. Eng. Sci. 2006, 44, 683–698. [Google Scholar] [CrossRef]
- Bhadauria, B.S.; Agarwal, S. Natural convection in a nanofluid saturated rotating porous layer: A nonlinear study. Transp. Porous Media 2011, 87, 585–602. [Google Scholar] [CrossRef]
- Yadav, D.; Lee, J. The effect of local thermal non-equilibrium on the onset of Brinkman convection in a nanofluid saturated rotating porous layer. J. Nanofluids 2015, 4, 335–342. [Google Scholar] [CrossRef]
- Yadav, D.; Kim, M.C. The effect of rotation on the onset of transient Soret-driven buoyancy convection in a porous layer saturated by a nanofluid. Microfluid. Nanofluidics 2014, 17, 1085–1093. [Google Scholar] [CrossRef]
- Yadav, D.; Lee, J.; Cho, H.H. Brinkman convection induced by purely internal heating in a rotating porous medium layer saturated by a nanofluid. Powder Technol. 2015, 286, 592–601. [Google Scholar] [CrossRef]
- Yadav, D.; Bhargava, R.; Agrawal, G.S.; Yadav, N.; Lee, J.; Kim, M.C. Thermal instability in a rotating porous layer saturated by a non-Newtonian nanofluid with thermal conductivity and viscosity variation. Microfluid. Nanofluidics 2014, 16, 425–440. [Google Scholar] [CrossRef]
- Yadav, D.; Wang, J.; Lee, J. Onset of Darcy-Brinkman convection in a rotating porous layer induced by purely internal heating. J. Porous Media 2017, 20, 691–706. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Swamy, M. Combined effect of thermal modulation and rotation on the onset of stationary convection in a porous layer. Transp. Porous Media 2007, 69, 313–330. [Google Scholar] [CrossRef]
- Bhadauria, B.S. Fluid convection in a rotating porous layer under modulated temperature on the boundaries. Transp. Porous Media 2007, 67, 297–315. [Google Scholar] [CrossRef]
- Bhadauria, B.S.; Khan, A. Modulated centrifugal convection in a vertical rotating porous layer distant from the axis of rotation. Transp. Porous Media 2009, 79, 255–264. [Google Scholar]
- Bhadauria, B.S.; Khan, A. Rotating Brinkman-Lapwood convection with modulation. Transp. Porous Media 2011, 88, 369–383. [Google Scholar]
- Kang, J.; Niu, J.; Fu, C.; Tan, W. Coriolis effect on thermal convective instability of viscoelastic fluids in a rotating porous cylindrical annulus. Transp. Porous Media 2013, 98, 349–362. [Google Scholar] [CrossRef]
- Rameshwar, Y.; Sultana, S.; Tagare, S.G. Küppers-Lortz instability in rotating Rayleigh-Benard convection in a porous medium. Meccanica 2013, 48, 2401–2414. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).