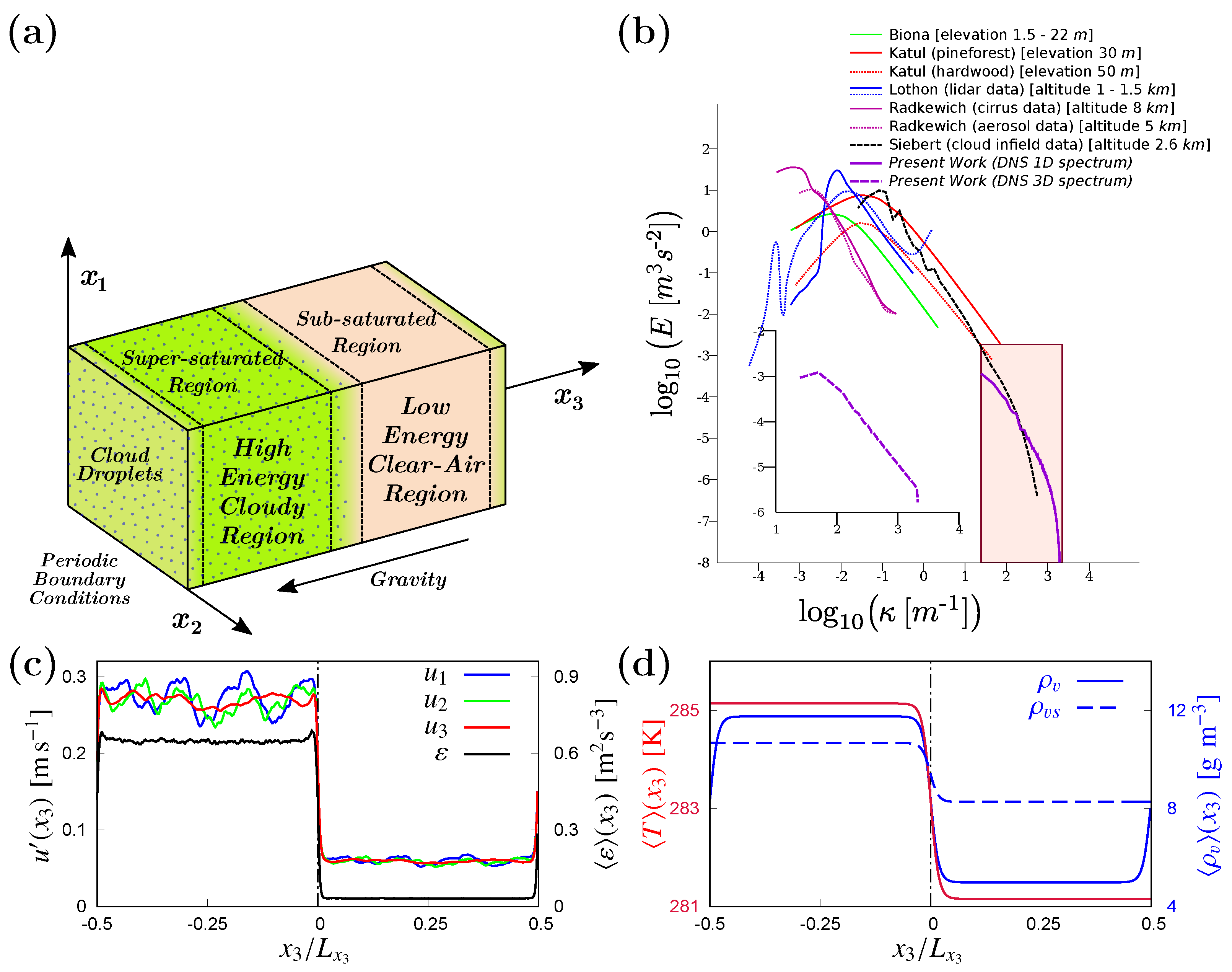
3.1. Time Evolution of the Fluid Flow
Since no external forcing has been introduced, the only force that can amplify the velocity of the fluid flow is the buoyancy force generated by the variations of temperature and water vapour density in the humid air. Transient evolution of the volume averaged quantities, such as TKE
E, its dissipation rate
, Taylor micro-scale Reynold’s number
and integral length scales
L exhibit transient decay or growth with time as shown in
Figure 2. Turbulent fluid statistics along anisotropic
direction is carried out by plane averaging
across homogeneous
horizontal planes. For computation of volume averaged turbulent quantities
, the plane averaged quantities
are averaged over the bulk of the cloudy region [
] and the clear air region [
]. The definitions for
E,
,
,
and
L are given as
where
is the average of rms velocity fluctuations along two homogeneous directions (
) along which flow should remain homogeneous and isotropic, since the only sources of in-homogeneity and anisotropy are gravity and energy/temperature/density of water vapour gradient, which are acting along vertical
direction; and
is the velocity correlation function [
45]. Evolution of
E and
is plotted in
Figure 2a using logarithmic scale in the both axes. More than the half of the initial
E and
inside the cloudy region is lost during the first 0.3 s, after which the evolution of the
E and
follows a power-law scaling with time (with scaling exponent of −1.25 for
E and −2.25 for
).
Figure 2b presents time evolution of
, which shows two phases in its evolution inside the cloudy region. During the first phase till 0.3 s of initial transient, turbulence develops from the initial random conditions. Initially a increase in
is observed due to the rapid increase in spatial scales (such as
) compared to the decrease in
E with time. This is followed by a sharp decrease in
, due to the rapid decrease in
E with time which dominates over the the increase in
. During the second phase,
E decays at
and
grows as
, which results in a gentle decay of
at
. Since decrease in
E inside the clear air region is much slower than the increase in its spatial scales and the detrainment of
E happens from the cloudy to clear air region; the evolution of
in clear air shows increment for longer duration compared to the cloudy region, which is followed by a slow decrease.
For calculation of the integral length scales
L, both longitudinal and transversal integral scales are computed along the two homogeneous directions and averaged. In
Figure 2c, the transversal length scales are not exactly one half of the longitudinal length scales, which is an indication of anisotropic evolution of the flow across the domain with time. The effect of the numerical boundary of the domain also influenced this anisotropic evolution of the integral scale, since the scales can not grow beyond the domain size. The decay in kinetic energy also produces a growth of the Kolmogorov micro-scale
. The resolution of the simulation increases with time, since
varies from 1.0 at the beginning to 3.7 at the end of the simulation inside the cloudy region of the domain (inside clear air region,
always). The growth of the
also produces a transient evolution in the average droplet Stokes number
and the settling parameter
of the different droplet populations in the domain, as shown in
Figure 2d.
is a ratio between the droplet response time
in Equation (
10) and the Kolmogorov time scale
and
is a ratio between
and
, where
is the terminal velocity of a droplet and
is the Kolmogorov velocity. Due to decay in the kinetic energy (and the corresponding growth in
) in the domain, the droplets become gradually less and less sensitive to the turbulence (indicated by the transient growth of the
parameter), whereas, the droplet Stokes number
gradually reduces.
Figure 3 presents the time evolution of air statistics. Time has been re-scaled using the initial eddy turnover time
taken at
0.043 s, which is 0.115 s, in order to reduce the influences of the initial evolution of the flow. Since all the three different simulations were initialized with same initial background fluid flow conditions, similar transient evolutions are observed for various fluid turbulent quantities. In transient evolution of
in
Figure 3a, detrainment of TKE to clear air region of the domain is observed to happen through the interface (dotted line in the middle) and also through the top boundary on top of the clear air region of the domain (due to periodic boundary condition, which generates a secondary inhomogeneous layer). Detrainment of TKE and widening of the TKE interface towards the clear air region of the domain can be recognized by following the positions of the kurtosis peaks of vertical component of fluid velocity
in the
Figure 3b, which moves toward the core of the clear air region. Skewness
and kurtosis
of the fluid quantities are computed using horizontal plane averages
as a function of vertical direction
. After 6 initial eddy turnover time (
), overall TKE and the amplitude of the kurtosis peaks are observed to become lower. During the final stage of the simulation (
), negligible TKE is left inside the fluid motion and the smaller peaks of kurtosis represent a well mixed stage in distribution of rms of velocity fluctuations throughout the domain. Decay in kinetic energy is reduced by the production of buoyancy inside the mixing layer. Unstably stratified temperature profile in the vertical direction amplifies vertical motion (see also Gallana et al. (2014) [
46]) and the fluctuations of
and
T produce buoyancy fluctuations (Equation (
5)), which introduce energy into the vertical motion (Equation (
2)). This cumulative effect becomes visible after
(see the growth of
in the mixing region in
Figure 3a), when the flow lost most of its initial kinetic energy. This source of kinetic energy accelerates the growth of the mixing layer and reduces the extent of the undiluted regions as well. During the later stage of evolution,
, the initial configuration of two different regions is no more distinct and the flow begins to approach a homogenized state.
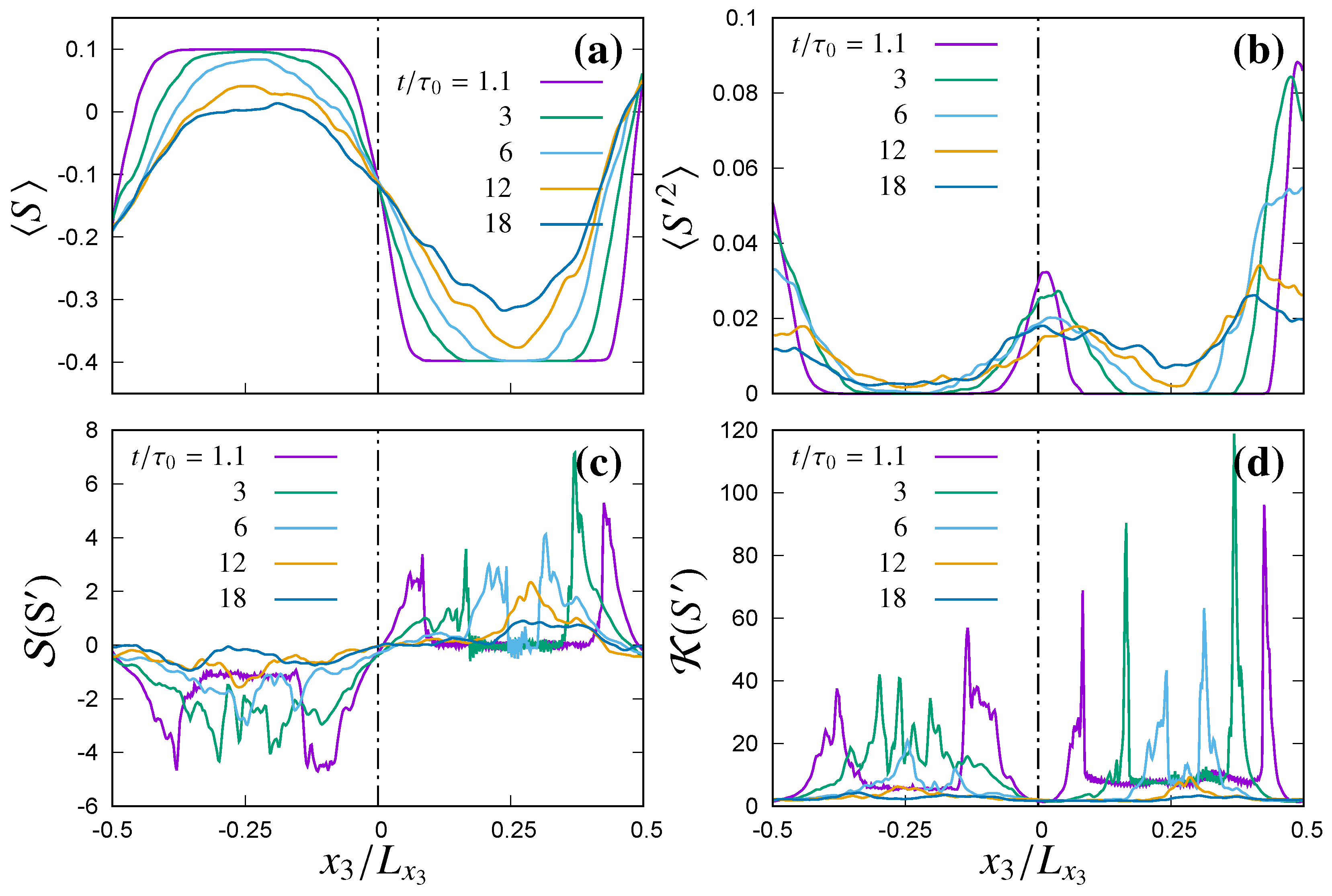
Figure 3c,d presents the time evolution of the mean of water vapour density
and temperature
profiles respectively. Mean of both the density of water vapour and temperature decrease inside the cloudy region of the domain, whereas, it increase inside the clear air region. The resulting profile of mean supersaturation
(which is initialized with a magnitude of 10% inside the cloudy region and −40% inside the clear air region) shows a decrease in its magnitude inside the supersaturated cloudy region and an increase inside subsaturated clear air region (
Figure 4a). The mixing process tends to produce a uniform supersaturation profile, therefore, during the final stage (
), the mean supersaturation value remains positive (
) only in the central part of the cloudy region, whereas, most of the domain is subsaturated (
).
Figure 3e,f present the time evolution of the variance of water vapour fluctuations
and temperature fluctuations
. Resulting variance in plane averaged supersaturation fluctuations
is shown in
Figure 4b. Though no fluctuations are introduced in the initial condition for the temperature and the density of water vapour, fluctuations are generated by the mixing in the interface region and are propagated inside the undiluted core of the cloudy or the clear air region gradually with the spreading of the mixing region. A minor source for the fluctuations in the fluid flow quantities is the droplet feedback term
in Equations (
3) and (
4). However, since the mean condensational time-scale is much larger than the eddy turnover time-scale,
gives an overall small contribution for generating fluctuations. In
Figure 3e and
Figure 4b, two peaks (one in the interface in the middle of the domain and another one near the bottom and the top boundaries) are observed in the fluctuations of the density of water vapour and supersaturation, due to periodicity in the initial density of water vapour condition. However, since the initial temperature is non-periodic in the vertical direction and varies only at the mixing interface in the middle of the domain,
Figure 3f shows only one peak in the variance of the temperature fluctuations. Temporal growth of the scalar (density of water vapour, temperature and supersaturation) mixing layers and widening of the scalar interfaces are evident from the shift in the peaks of the skewness and kurtosis of the scalars towards the undiluted central regions as shown in
Figure 3g,h and
Figure 4c,d, which gradually decrease in magnitude with mixing spreading all across the domain.
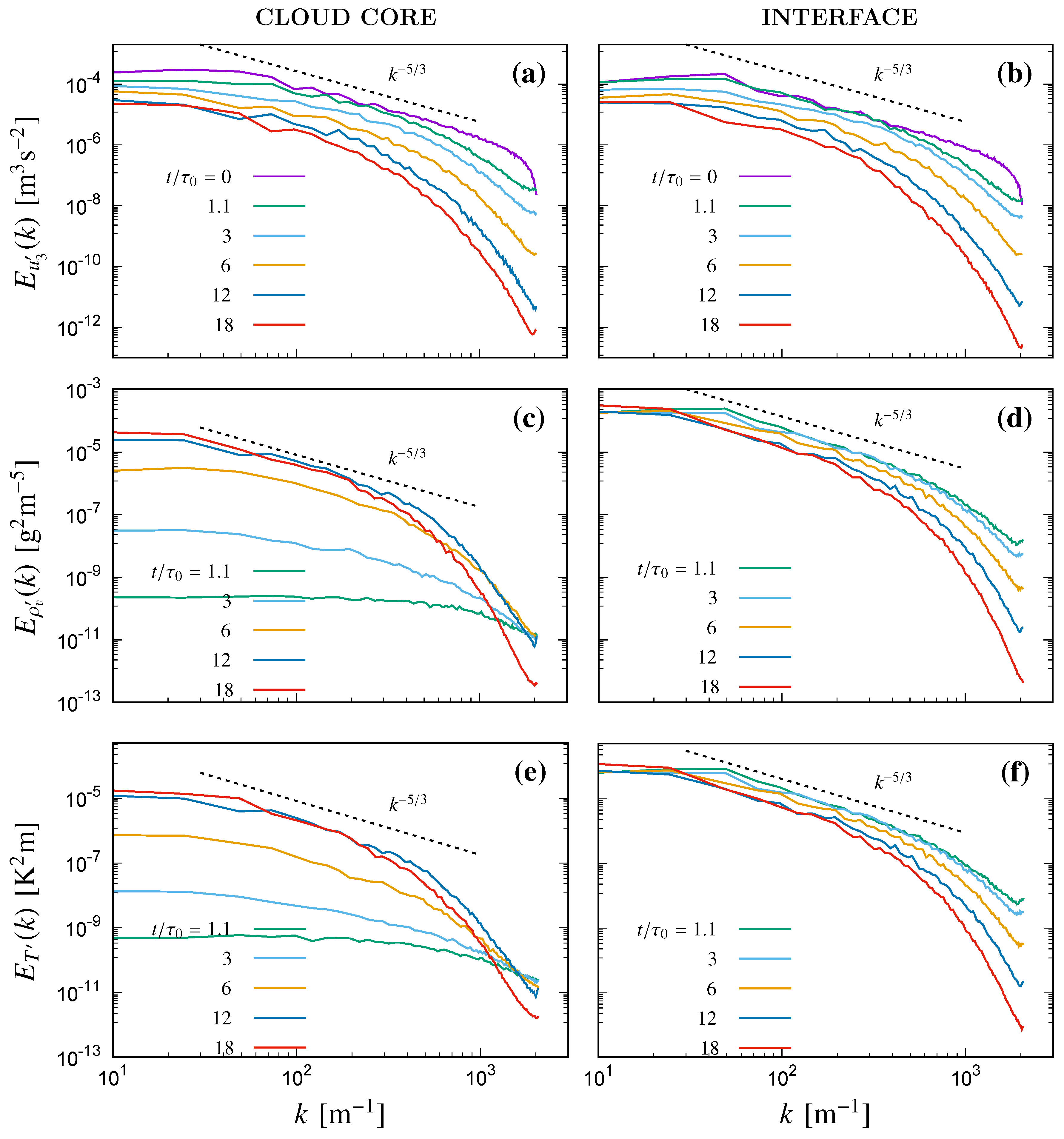
Figure 5a,b presents the time evolution of one dimensional (1D) horizontal spectrum of the vertical component of air velocity
in the wavenumber space
k, sampled at the middle horizontal plane of the initial configuration of the cloudy region and at the middle plane of the initial interface region (with 3 adjacent plane averaging in both cases). The 1D spectra in wavenumber space
distributed in the homogeneous
directions is computed as
where
is the number of grid points in
direction,
is the Fourier transform of quantity
f. Since initially the cloudy and the clear air region were initialized with two homogeneous and isotropic turbulent cubic domains with a TKE ratio of 20 in between the two regions, the initial 1D transversal spectra for all the three components of velocity fluctuations looks almost similar (some differences can be observed in the lowest wavenumbers due to smaller number of samples). The interface region in the initial condition contains lower TKE than that of the cloudy region of the domain (due to linear interpolation in TKE magnitudes in between the cloudy and the clear air region), which can also be observed in the initial TKE spectra of the interface showing vertical shift downwards than that of the cloud core region. With time advancement, the dissipative wavenumber range from the initial condition shows transition towards smaller wavenumbers indicating growth in the Kolmogorov micro-scale
with time, gradually shrinking the inertial sub-range. Moreover, the spectra of different components of velocity fluctuations do not replicate each other during the later instances of the simulation, resembling an anisotropic time evolution of the fluid flow.
In
Figure 5c,d, the transient evolution of the water vapour density fluctuations spectra
and in
Figure 5e,f, temperature fluctuations spectra
in wavenumber space
k is presented, sampled at the cloud core and the interface. Presence of a mean gradient in the initial scalar profiles along the vertical direction creates a large variance of that scalar in the mixing layer (
Figure 3), which is observed to spread towards the undiluted regions with time. Since the mean gradient in the mixing region is large enough to produce sufficient variance in the scalars to counter its dissipation and the turbulent transport, a well mixed region is observed to be created with a scalar spectrum quickly approaching
Kolmogorov inertial range [
23]. Initially the only source of temperature and density of water vapour variance inside the undiluted cloudy region is the droplet condensation/evaporation. Therefore, initially the scalar spectra are not well developed but after
, the growth of the mixing layer gradually destroys the cloudy region, so that similar scalar spectra like the mixing region are replicated inside the cloud core as well.
3.2. Time Evolution of the Cloud Droplet Population
The three simulations of this study are initialized with three different mono-disperse cloud droplet populations as enlisted in
Table 2. The droplet populations go trough distinct transient evolution according to their surrounding fluid flow conditions. In general, droplets in the cloud core experience an average condensational growth due to supersaturated ambient, whereas, the droplets exiting the cloud core region, tend to evaporate due to subsaturation. A visualization of the flow is shown in
Figure 6, where enstrophy (
) of the fluid field across a vertical plane (plane
) is presented with superposition of the cloud droplets around that plane (thickness of droplets containing slice is 0.0025 m) after 6 initial eddy (
) turnover time and along with the supersaturation
S field in contour lines. The line at
marks the extent of the cloudy region, where condensational growth occurs. In the region with
, droplets would instead experience a quick evaporation. Although almost similar, small differences in the local enstrophy can be observed as a consequences of the cloud droplet feedback term
in Equations (
3) and (
4), which determines also the buoyancy term
B in the momentum balance Equation (
2). Since buoyancy is sensitive to the small local fluctuations in the density of the water vapour
and temperature
T, differences in droplet feedback
due to different droplet sizes (Equation (
6)) can result into differences in the local fluid velocity, although the initial fluid flow conditions are identical. Distribution of enstrophy in
Figure 6 gradually decreases with time, as TKE distribution also decreased as shown in
Figure 2a and
Figure 3a. Due to differences in the cloud droplet Stokes number
as shown in
Figure 2d, droplets show different responses to the local enstrophy field. In
Figure 6a, droplets of initial 25
m mono-disperse distribution can be seen to preferentially concentrate away from the regions of higher enstrophy and often forming string like patterns and clustering in the areas of lower enstrophy. However, the gradual reduction of the average Stokes number with time reduces the tendency to cluster, while gravitational settling, droplet size broadening reduce correlation between the droplet concentration and the local strain. A similar but much milder tendency can also be observed in
Figure 6b for the simulation with an initial 18
m mono-disperse droplet population. On the contrary, a higher uniform concentration can be seen in
Figure 6c for the droplet population with initial 6
m radius.
At the same time, droplets undergo gravitational sedimentation which is only partially counterbalanced by turbulence. The relative importance of sedimentation is controlled by the dimensionless settling parameter
[
19]. Since
decays as
in these present simulations, the importance of gravitational sedimentation grows with time (see
Figure 2d). Larger droplets (initial 25
m radius population) begin to gather at the bottom of the domain from the beginning of the simulation and rarely enters the mixing layer (
Figure 6a). Droplets with initial 18
m radii have a comparatively slower rate of sedimentation and are observed to cross the cloudy region border through detrainment process (
Figure 6b). On the contrary, smaller droplets (initial 6
m radius population) do not show significant sedimentation. They are observed to easily diffuse in the clear air zone (
Figure 6c), where, due to their shorter evaporation time-scale (proportional to
) and longer residence time (roughly proportional to
but modified by the droplet settling velocity
), they can completely evaporate. Moreover, for the smaller droplet population, the presence of strong subsaturation near the bottom boundary and at the clear air region of the domain also removed droplets by complete evaporation. This evaporation contributes to cool down the subsaturated layer above the mixing region, increasing the negative buoyancy [
7] and thus enhancing the mixing process. Whereas, for the larger droplets, after a few initial time-scales, this process of detrainment to subsaturated clear air zone and complete evaporation of the droplets is not present.
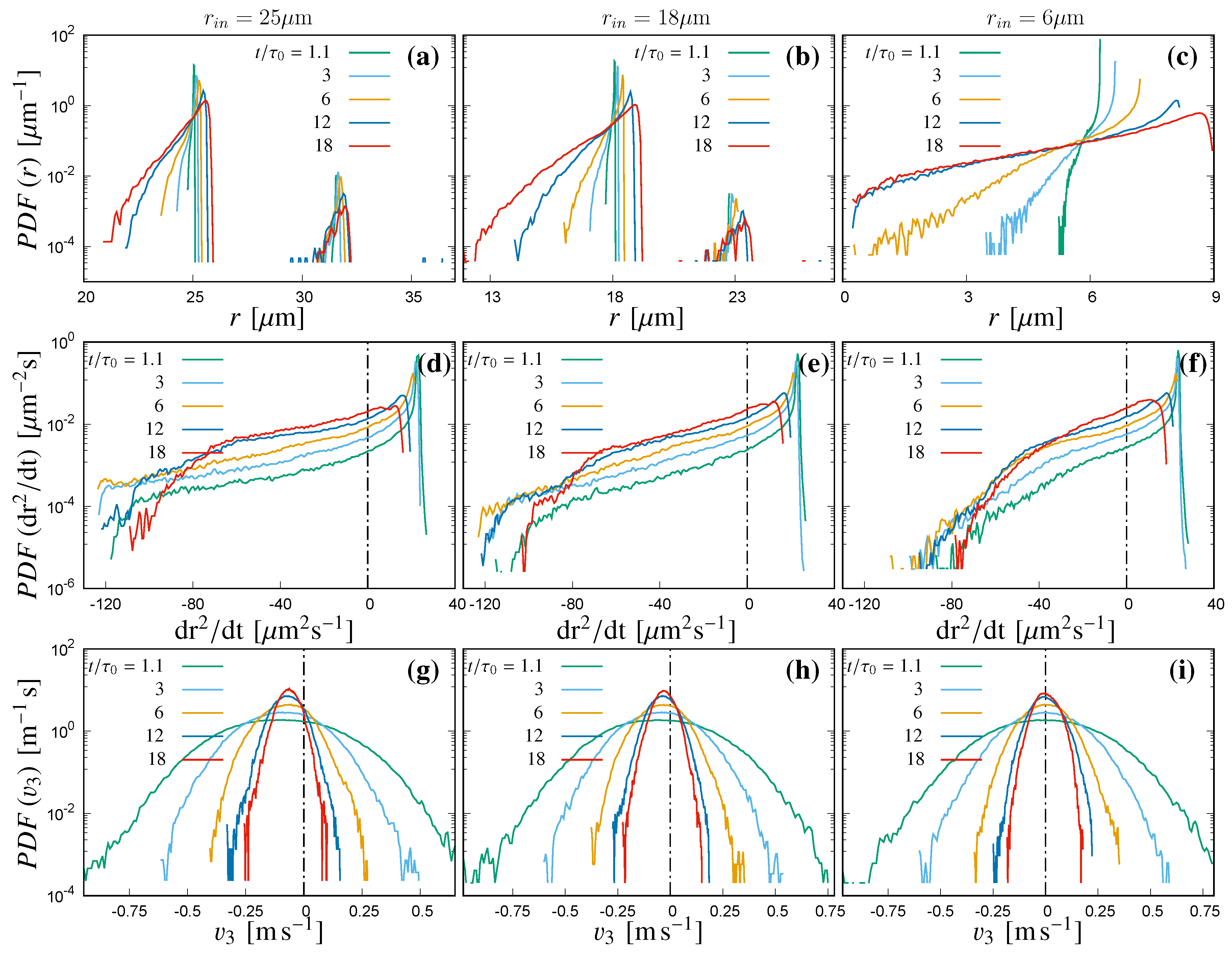
This is reflected in the transient evolution of normalized probability density functions (PDFs) of the droplet size, velocity and growth rate; which are presented in
Figure 7.
Figure 7a–c present the evolution of PDFs of the cloud droplet radius with time. Both the cloud droplet populations with initial 25 and 18
m radius show limited broadening of their sizes due to condensation/evaporation and the presence of two secondary peaks which correspond to the collisions (
Figure 7a,b). However for the droplet population with initial 6
m radius, no collisional growth is observed to happen during the simulation duration. Whereas, the width of the DSD due to both the evaporation and condensation processes is observed to be wider in
Figure 7c and certain number of droplets are observed to evaporate completely. The impact of condensational size growth or evaporative size reduction is more efficient for the smaller droplets (since droplet radius growth rate
is proportional to
, see Equation (
9)). PDFs of
, which indicates the growth rate in the droplet surface area, are presented in
Figure 7d–f. As
from Equation (
9) is proportional to the local supersaturation
, simulations of the three initial mono-disperse cloud population should exhibit similar transient evolution, since the background supersaturation spatial distribution is similar for the three simulations. However, droplets experience different supersaturation conditions due to their different paths, which also depends on their individual sizes and the local air conditions. Smaller droplets of initial 6
m radius do not show the extreme negative tail of
as observed for larger droplets in
Figure 7d,e, because this leads to a complete evaporation of the droplets (
Figure 7f).
Moreover, since subsaturation can result in highly negative
for the sub-micron droplets from the initial 6
m droplet population and since the numerical time-step for the sub-micron droplets needs to be very small and their micro-physics cannot be modelled using Equation (
9); the droplets with sizes below 4% (≤0.24
m) are removed.
Due to gravity, vertical component of the cloud droplet velocity
can exhibit different behaviour compared to the velocity components along the horizontal directions. Transient evolution of PDFs for
is plotted in
Figure 7g–i. During the early stage of evolution, the PDFs of
shows wider distribution due to the presence of TKE inside the domain, influencing the droplet velocity as well. However the decay of TKE narrows the spectrum of
and therefore
with time. The gravitational settling is visible in the shift of the maxima of the PDFs of
toward the negative values for the larger droplets. From
Figure 7g, most of the cloud droplets of initial 25
m population are observed to have higher negative
during the later instances of the simulation. Free fall velocity for a 25
m cloud water droplet is 0.077 m/s and the peak of the PDF of
of this population is observed at 0.063 m/s after the first time-scale, which is implying dominance of gravitational settlement with velocities close to the free fall condition. Simulation with initial 18
m population (
Figure 6b and
Figure 7h) is observed to comparatively settle down slowly than the initial 25
m population. However, the simulation with initial 6
m population shows almost symmetric evolution of
around the zero (
Figure 7i), which indicates negligible effect of gravitational acceleration on this cloud droplet population.
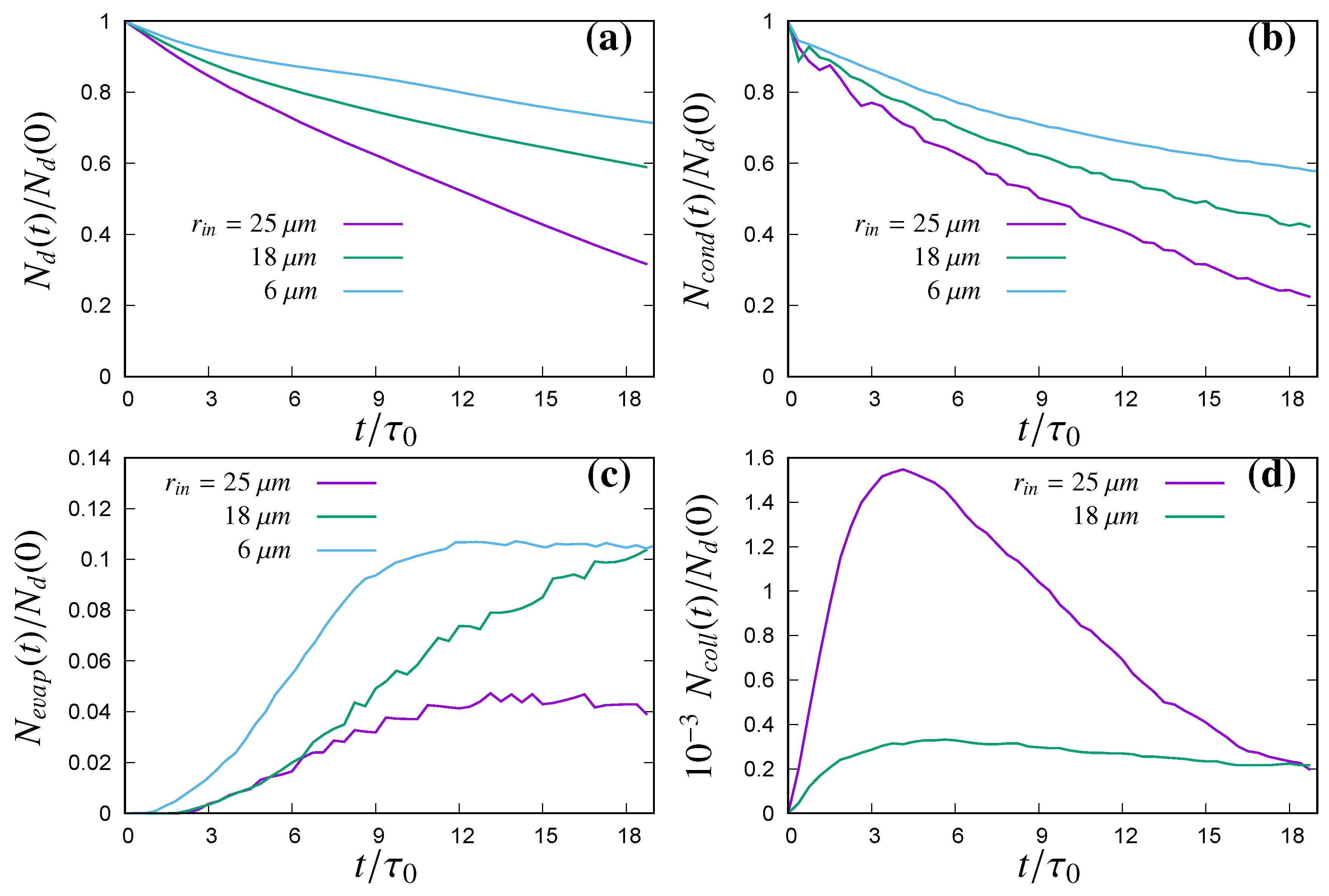
The number density of the droplets inside the simulation domain can change with time due to collisions or complete evaporation of the liquid water or due to gravitational sedimentation of the droplet out of the domain bottom boundary. To quantify the relative importance of condensation, evaporation, collision and gravitational sedimentation; the transient evolution in the number density of droplets is presented in
Figure 8. Evolution in number density of all droplets
(normalized by initial droplet number density
) is presented in
Figure 8a, where most significant reduction in total number of droplets can be observed for the initial 25
m droplet population and comparatively less for the initial 18
m droplet population and much lesser for the initial 6
m droplet population. The most active physical process to result in reduction of the total number of cloud droplets for the initial 25 and 18
m droplet populations is the gravitational settling and subsequent removal of the droplets falling below the bottom boundary of the domain. However, the most active physical process for the initial 6
m droplet population, reducing the total number of droplets is the complete evaporation. In
Figure 8b, time evolution in the normalized number density of the droplet population remaining to its initial radius or exhibiting size growth due to condensational water vapour deposition
is presented (
, where
corrospond to radius of a droplet after first collision with a similar sized droplet). Though, the initial 6
m droplet population did not exhibit any collisional growth but some fraction of the population grew more than
size due to higher degree of condensational growth. Transient evolution in the normalized number density of the cloud droplets experiencing evaporative size reduction
is presented in
Figure 8c. For the initial 25
m droplet population, droplets with a radius smaller or equal to 24.5
m are considered for counting the number density of evaporating droplets (
17.5
m for initial 18
m population and
5.5
m for initial 6
m population). The effect of complete evaporation for the initial 6
m droplet population is evident from
Figure 8b where the number density of the droplets that is equal to, or larger than, the initial 6
m size is observed to decrease with time but in
Figure 8c the number density of evaporating droplets during the later stage of the simulation is almost steady, implying some physical process is resulting in the removal of droplets in the evaporating range. In
Figure 7c, the absence of sub-micron droplets is seen to happen from 12 to 18 initial eddy turnover time, which also confirms the presence of the complete evaporation of sub-micron droplets for initial 6
m droplet population. The initial 25 and 18
m droplet population shows growth in the DSD due to occurrence of collision in different size ranges.
Figure 8d presents normalized number density of the droplets in size ranges corresponding to collision between two similar sized droplets
(secondary peaks in
Figure 7a,b). For this transient evolution of the number density of colliding droplets, the source is the occurrence of collisions but the sink is the gravitational sedimentation of the droplets out of the domain. For both the initial 25 and 18
m droplet population in
Figure 8d, during the initial 4 initial eddy turnover time, occurrence of collision dominates over the gravitational sedimentation but later the droplets with 1 collision for 25
m initial droplet population are removed from the domain very rapidly, whereas for the 18
m initial droplet population, the number of droplets with 1 collision remains almost steady. The occurrence of collision in between larger sized droplets (already with one collision) to the smaller droplets resulting in droplets with two or more collisions was very rare and happened mostly in the case of 25
m initial droplet population.
Time evolution of the one-point correlation between fluid flow and cloud droplet
(where
a and
b are fluid and droplet quantities respectively) is presented in
Figure 9. Since the droplet distribution is not uniform, for the calculation of these correlation parameters, both the fluctuations in the cloud droplets and fluid flow quantities are plane averaged in horizontal directions
, considering only grid cells containing cloud droplets withing its
volume and the droplet quantities are averaged to the corresponding grid points. In the correlation between the fluctuations in the vertical component of fluid velocity
and droplet velocity
in
Figure 9a–c,
and
are very well correlated for initial 6
m droplet population but less correlated for 18
m and lesser for 25
m initial droplet population during the initial instances. Spurious fluctuations in correlation parameters are observed in the interface region, where number of droplet samples are much smaller. Since TKE inside the domain during later instances was much smaller and the Stokes numbers decreases (
Figure 2d), as well for all the populations, the velocity fluctuations for both the fluid
and the droplet
tend to correlate more with time advancement. In
Figure 9d–f, correlation between the supersaturation fluctuations
and fluctuations in liquid water content
is presented. Due to particle clustering and high fluctuations in the size of the statistical samples, bezier smoothing has been applied to the correlation in between
and
. This smoothing significantly modifies the data only in the clear air region of the domain, where number of droplets are very small. Improved statistics could be obtained by considering ensamble averaging between different simulations with independent initial conditions. Since initially inside the undiluted cloudy part of the domain,
was 0 and gradually the fluctuations picked up, the widening of the interface mixing region can be witnessed in these correlation plots. With positive
, positive
is observed, which shows highest positive correlation for initial 6
m droplet population and the correlation is less for 18
m and lesser for the 25
m initial droplet population. In general, almost no correlation is observed in between the fluid enstrophy
and
. However, for the two larger cloud droplet population (initial 25 and 18
m radii), increase in negative correlation was observed to happen with time.
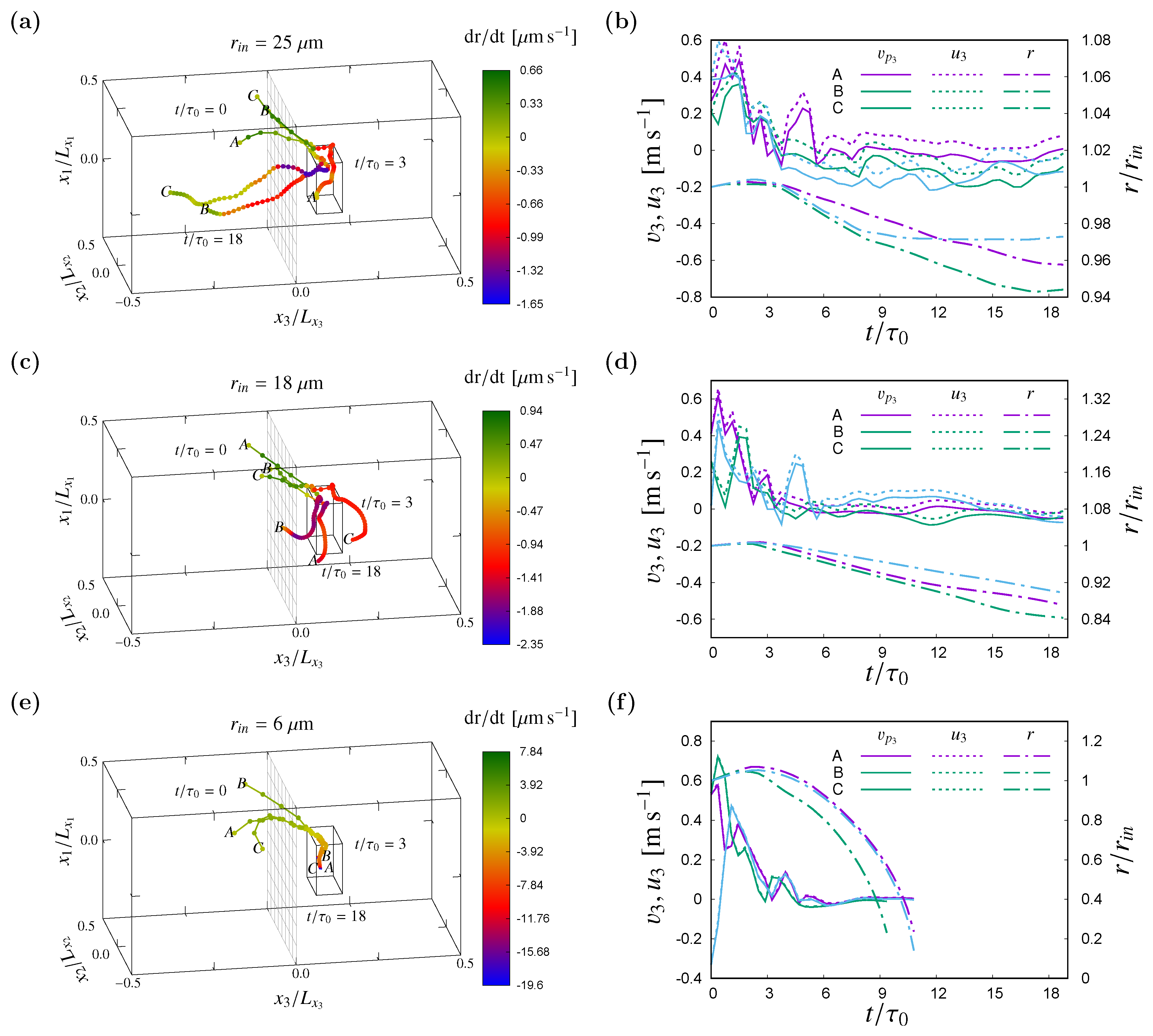
In
Figure 10, time evolution of three sample droplets from the three different simulations reaching a specific region in the initial clear air portion of the domain (see the box in the clear air region of panel (
a), (
c), (
e) of
Figure 10) after 3 initial eddy (
) turnover time is presented. These droplets were transported to the subsaturated clear air region due to detrainment from the near interface region of the cloudy part of the domain. Due to subsaturation, only the droplets from simulations with initial 25 and 18
m droplet populations are observed to survive the entire simulation. The impact of gravitational settlement is observed to be very pronounced for the larger droplet population, leading to a short residence time in the subsaturated area (two out of the three droplets were back to the cloudy supersaturated region of the domain almost immediately, see
Figure 10a). Whereas, the other remaining droplet was trapped in some eddy to follow lateral movement inside the clear air region. In
Figure 10b, these droplets are observed not to follow the fluid velocity exactly but rather show negative
indicating stronger influences of gravitational forces on these droplets. The sample droplets from the simulation with initial 18
m droplet population shows comparatively less influence under gravitational forces and remains entrapped in the eddies inside the clear air region of the domain (
Figure 10c), which produces a continuous size reduction due to local subsaturation (
Figure 10d). Whereas, local subsaturation played most important impact on the samples of the droplets from the simulation with initial 6
m droplet population. After being detrained to the subsaturated clear air region, these droplets cloud not return back to the saturated cloudy part of the domain due to decay in TKE inside the domain (
Figure 10e) and eventually evaporated completely in the middle of the simulation duration (
Figure 10f).