Data-Driven Model Reduction for Coupled Flow and Geomechanics Based on DMD Methods
Abstract
1. Introduction
2. Problem Formulation and Methodology
2.1. Multi-Phase Flow Problem
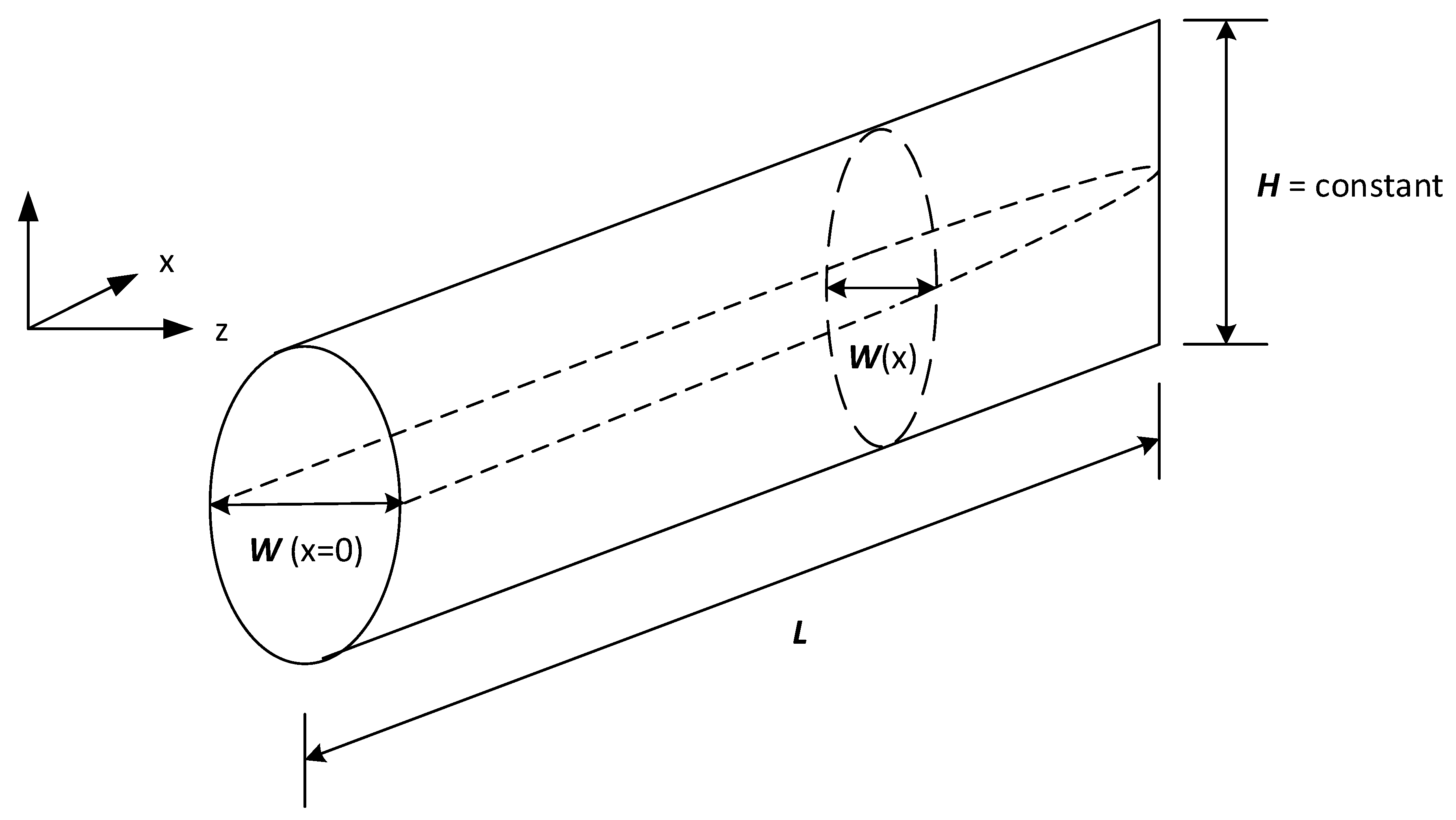
2.2. Hydraulic Fracturing Process
2.3. Model Reduction by Projection
2.4. The POD Method
2.5. Dynamic Mode Decomposition (DMD)
2.6. Local DMDc
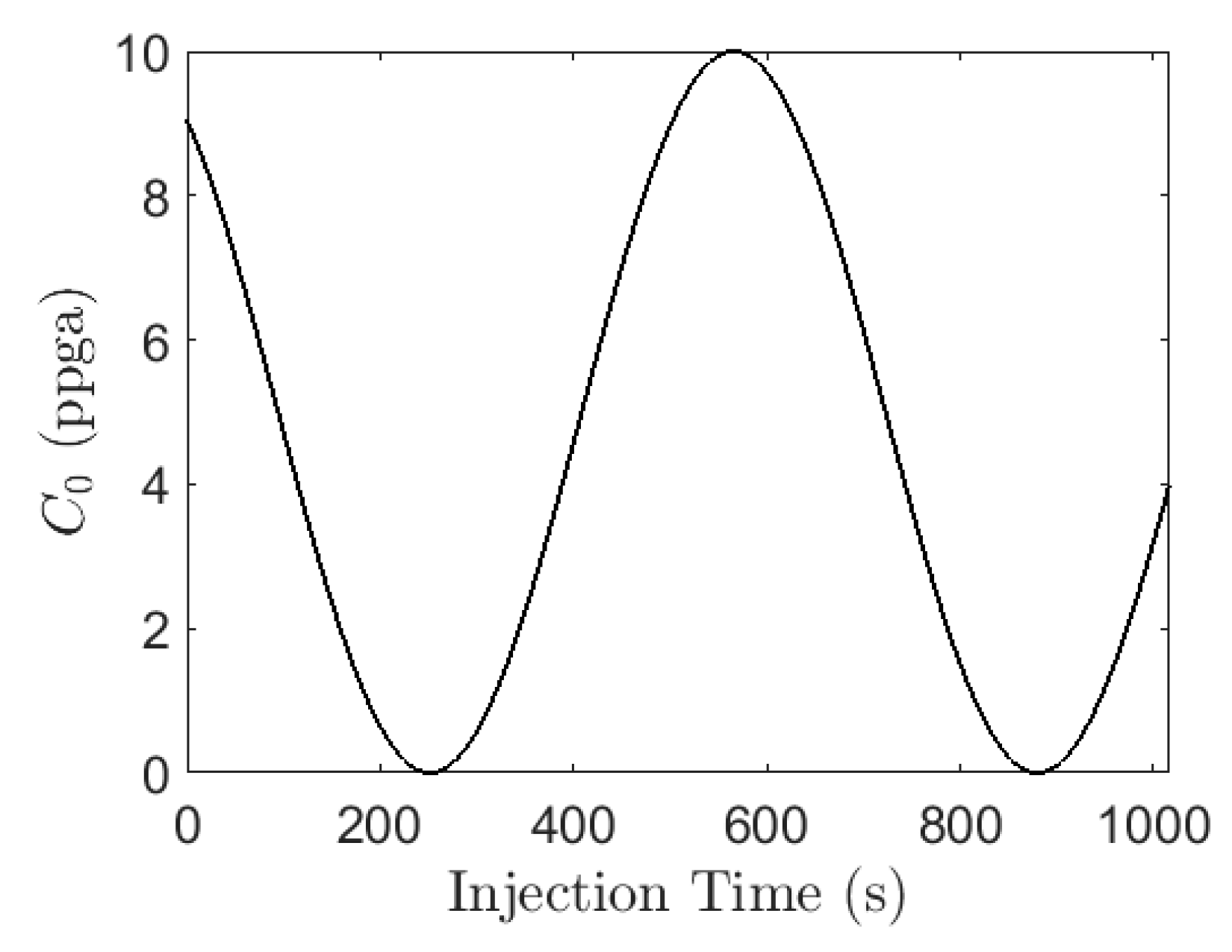
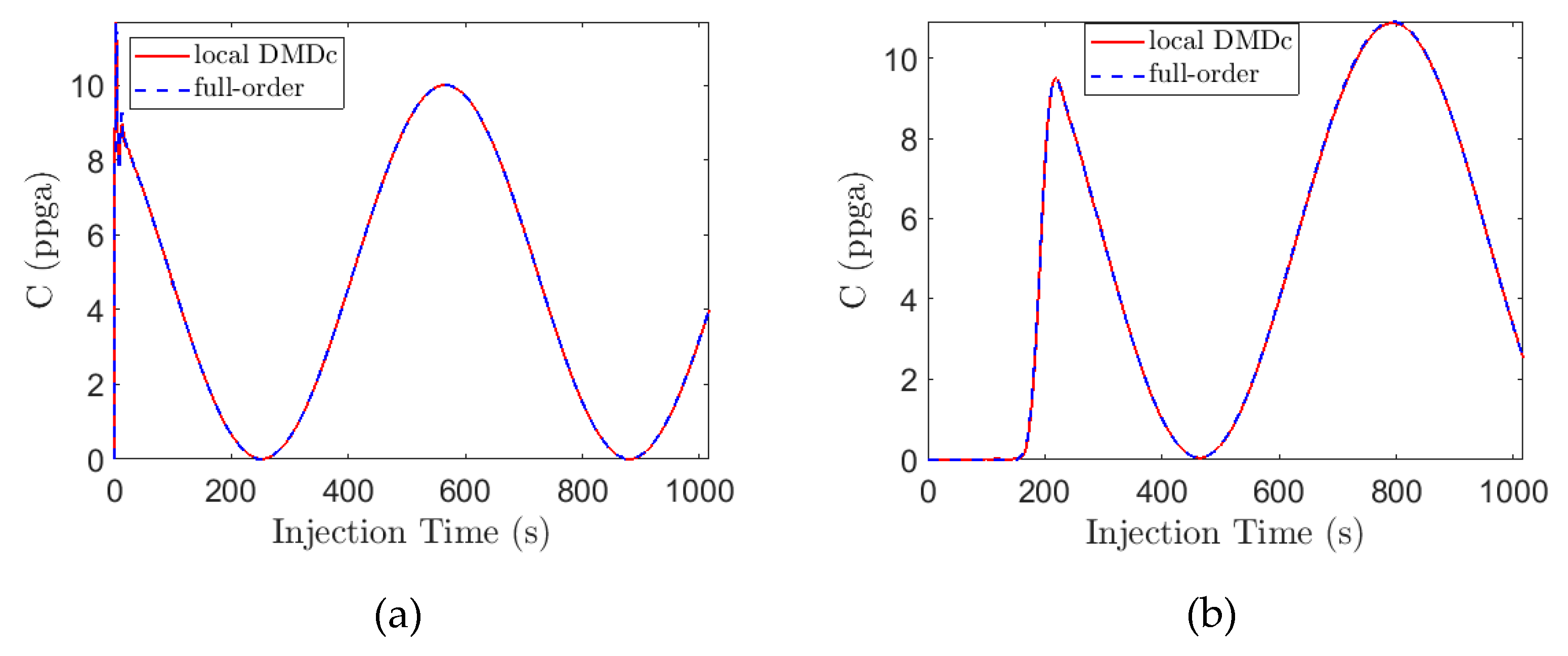
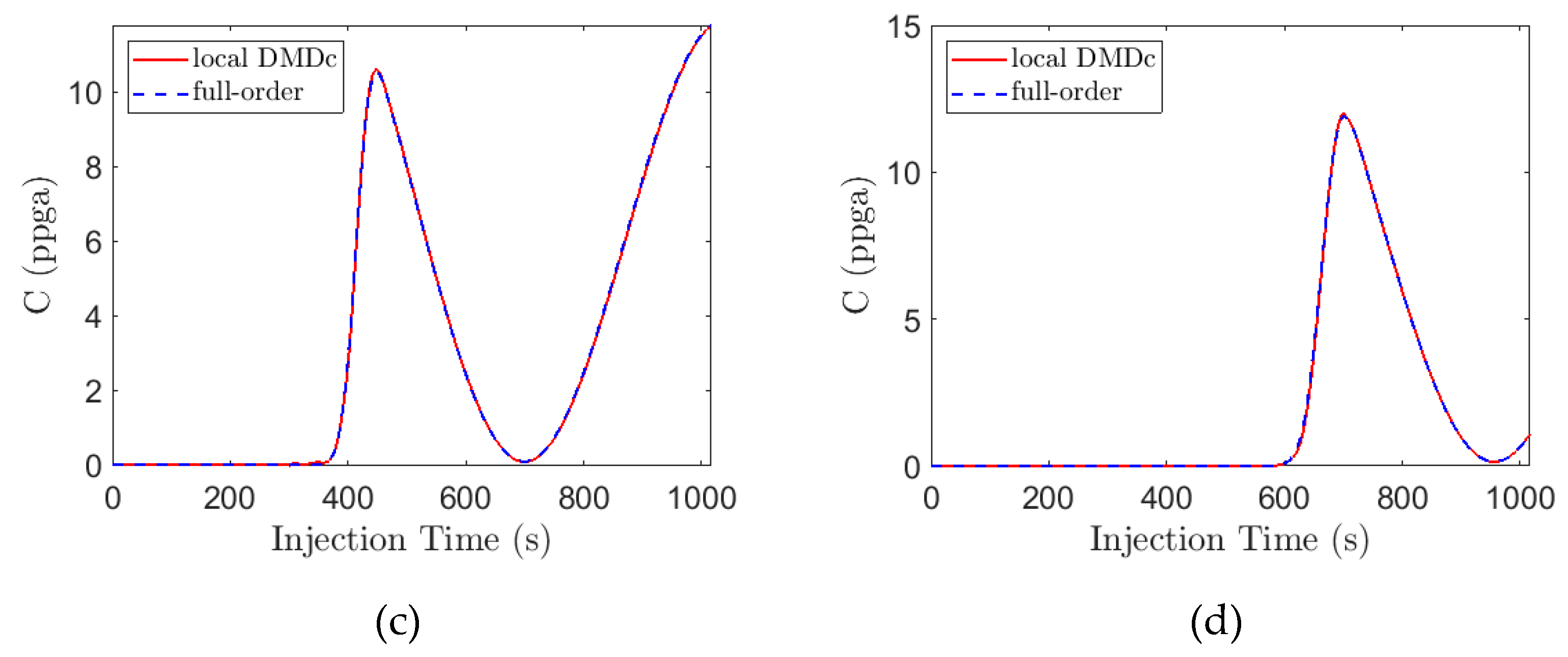
- Similar to DMD, we first collect the snapshot data for the states of the system at time steps. With regards to the hydraulic fracturing process, these can be the time-series proppant concentration or width profiles at different positions. We also collect the input data and construct the state and input snapshot matrices as below:where each is a vector of proppant concentrations with spatial nodes obtained from discretizing the PDEs, so that and the manipulated input for the system is the injected proppant concentration at the wellbore .
- Apply the GOS algorithm to cluster the entire snapshot data, i.e., into optimal clusters such thatwhere denotes the -th cluster configuration and denotes the number of snapshots in the -th cluster. Please note that the following relations will be satisfied.
- For every cluster, form the augmented state matrix, by stacking the state and input matrices as shown below and compute the reduced SVD of along with the shifted snapshot matrixwhere are the matrices comprising the left singular vectors, right singular vectors and singular values of and similarly and are the matrices comprising the left singular vectors, right singular vectors and singular values of .
- Using the above matrices, compute the local reduced-order models as followswhere are obtained by decomposing as such that , and are the reduced-order representations of the system matrices.
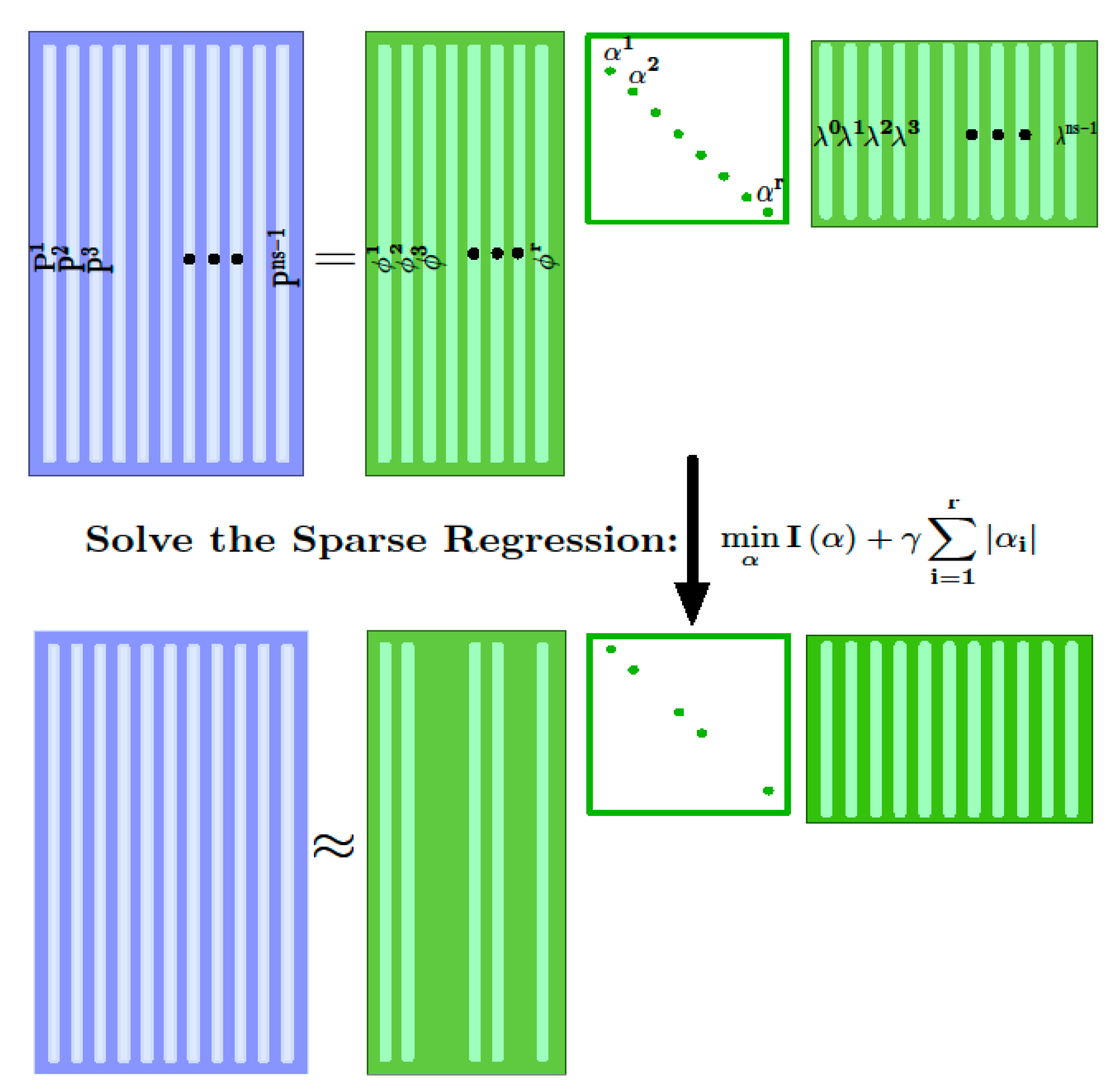
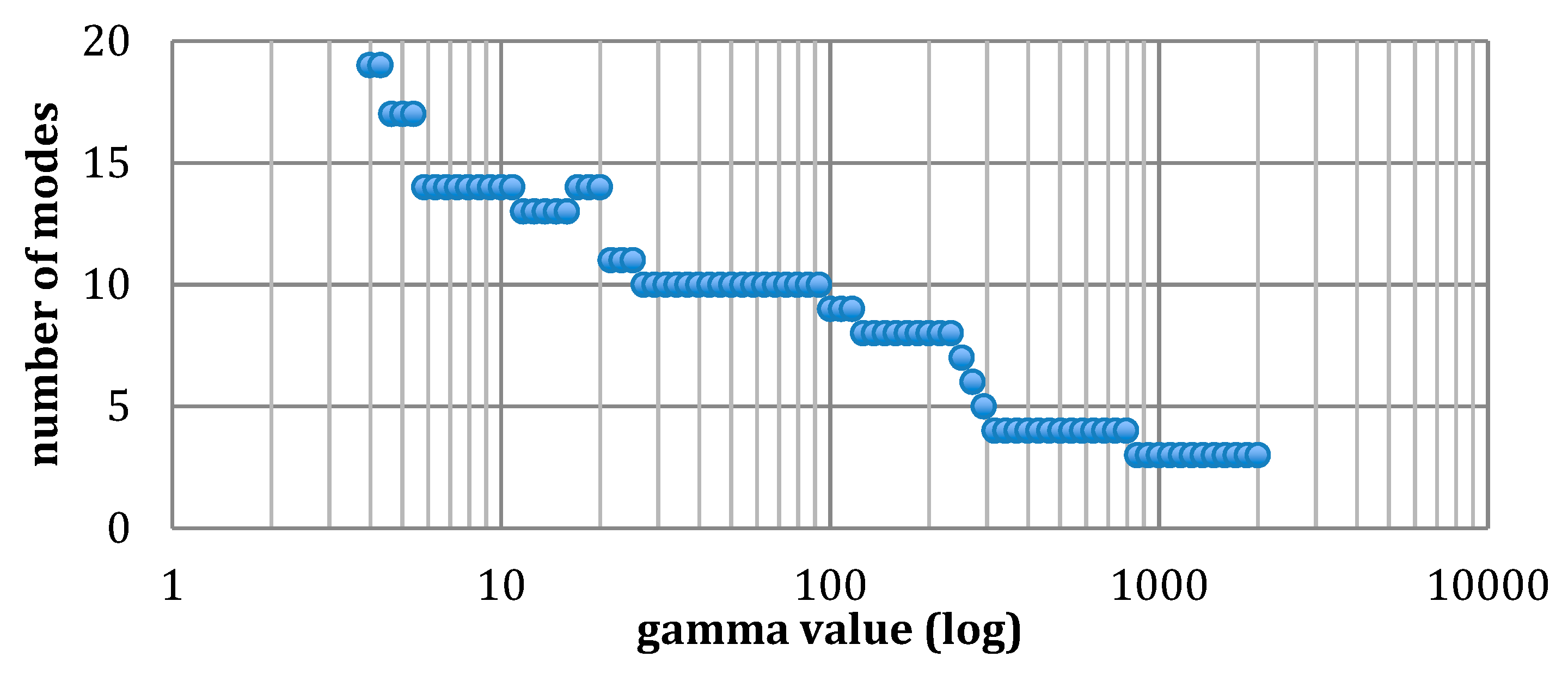
2.7. Sparsity Promoting Dynamic Mode Decomposition
3. Results
3.1. Single Phase Flow Example
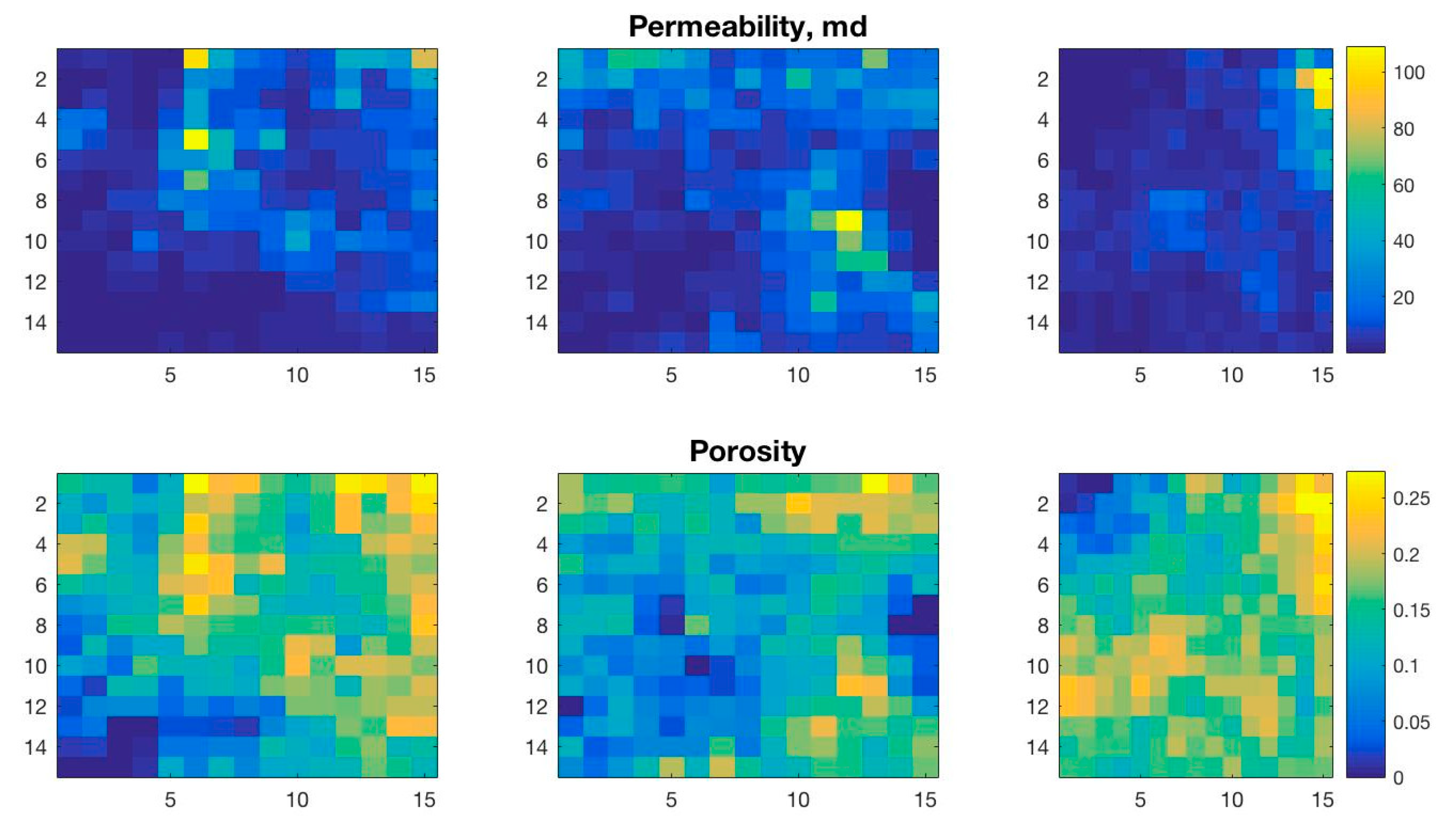
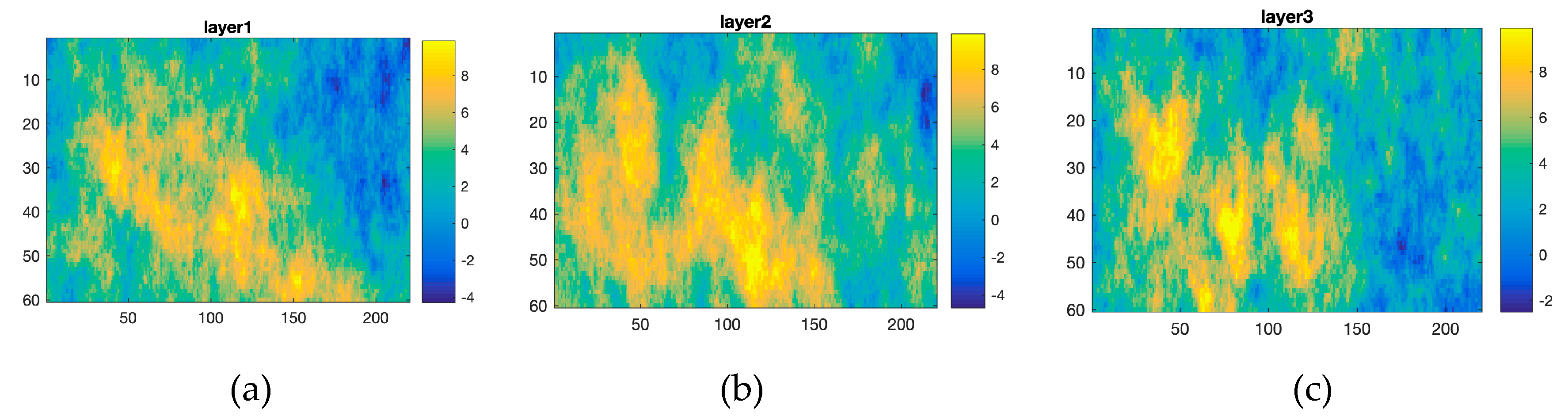
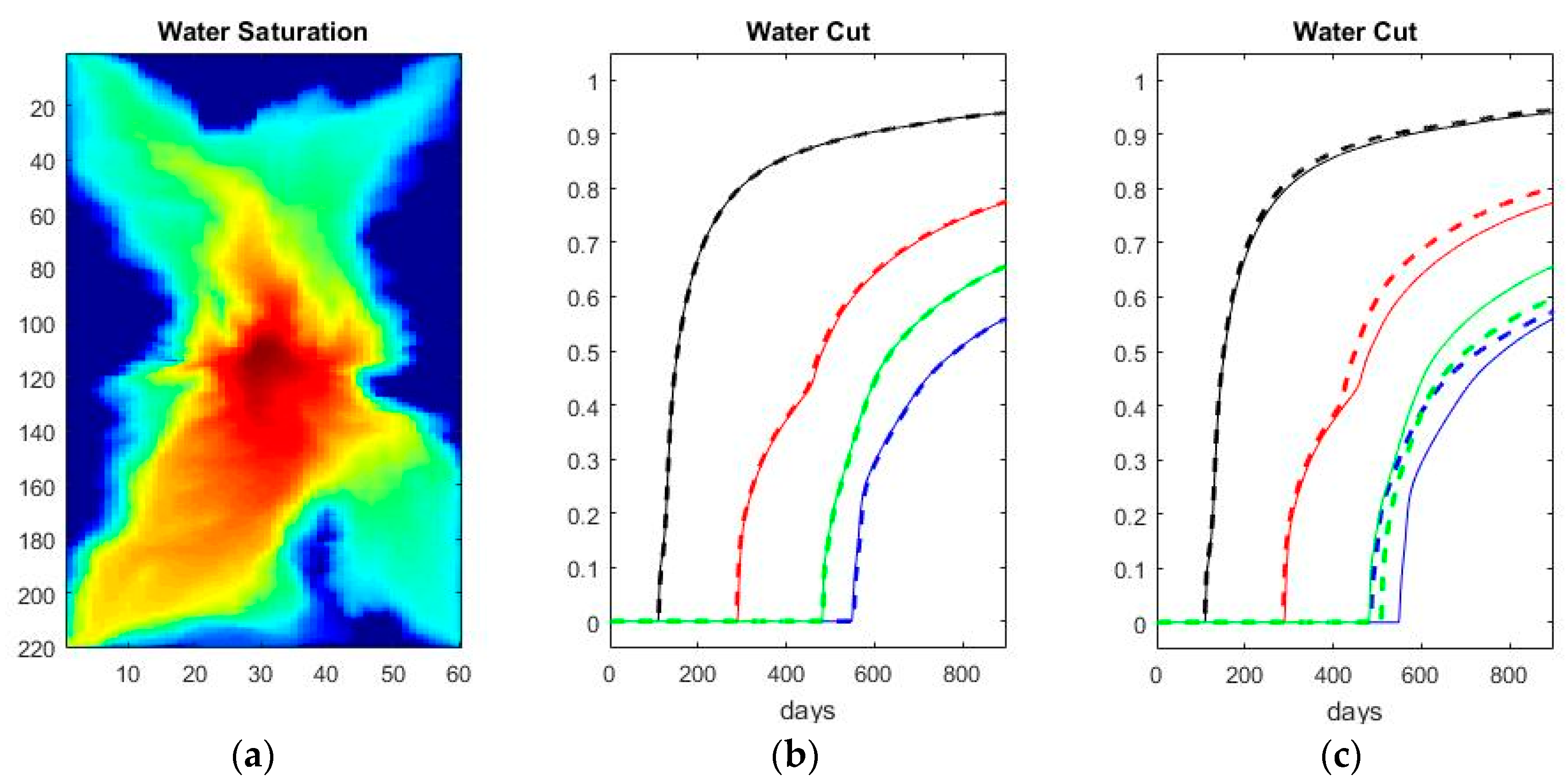
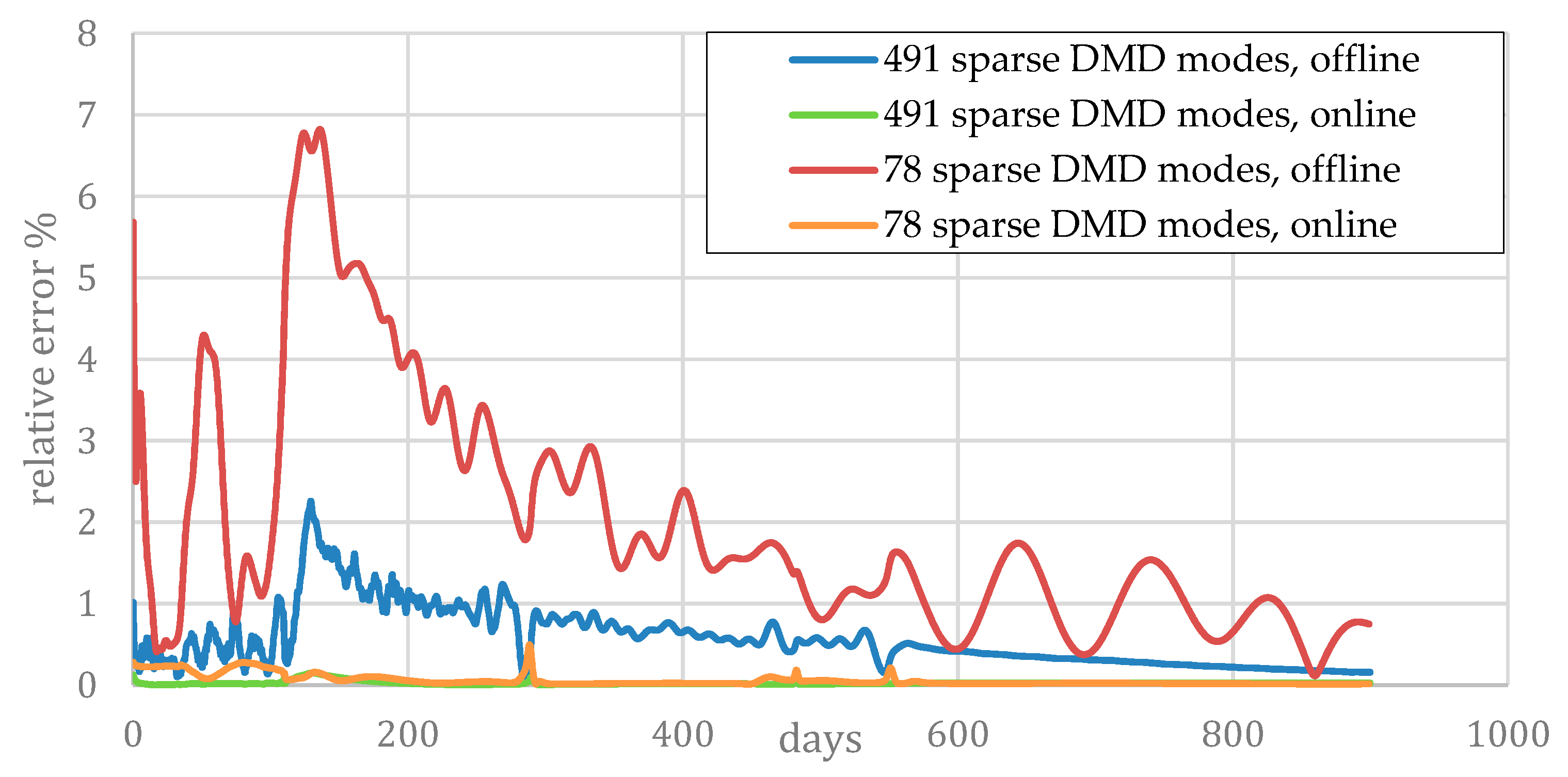
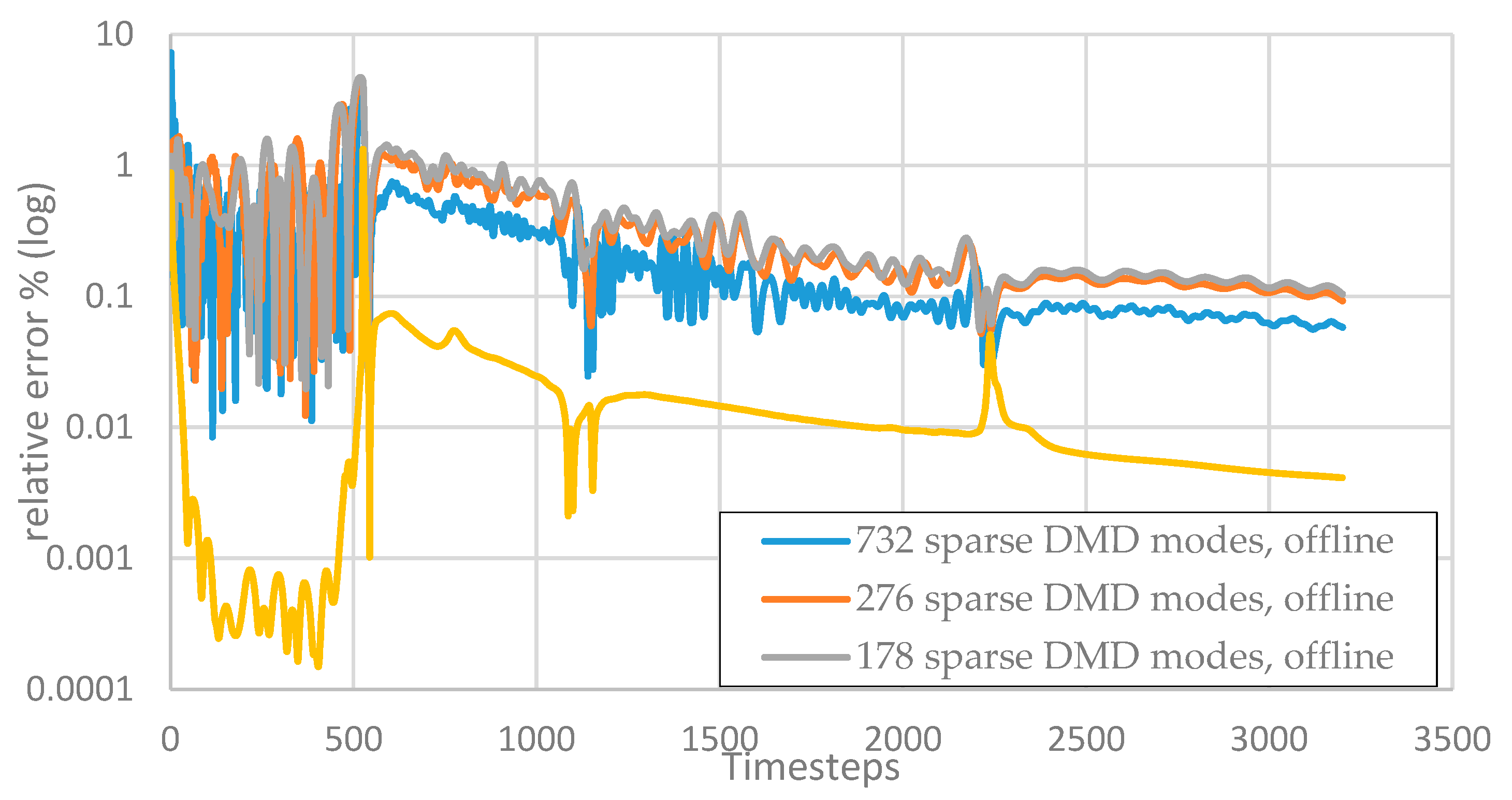
3.2. Two-Phase Flow Example
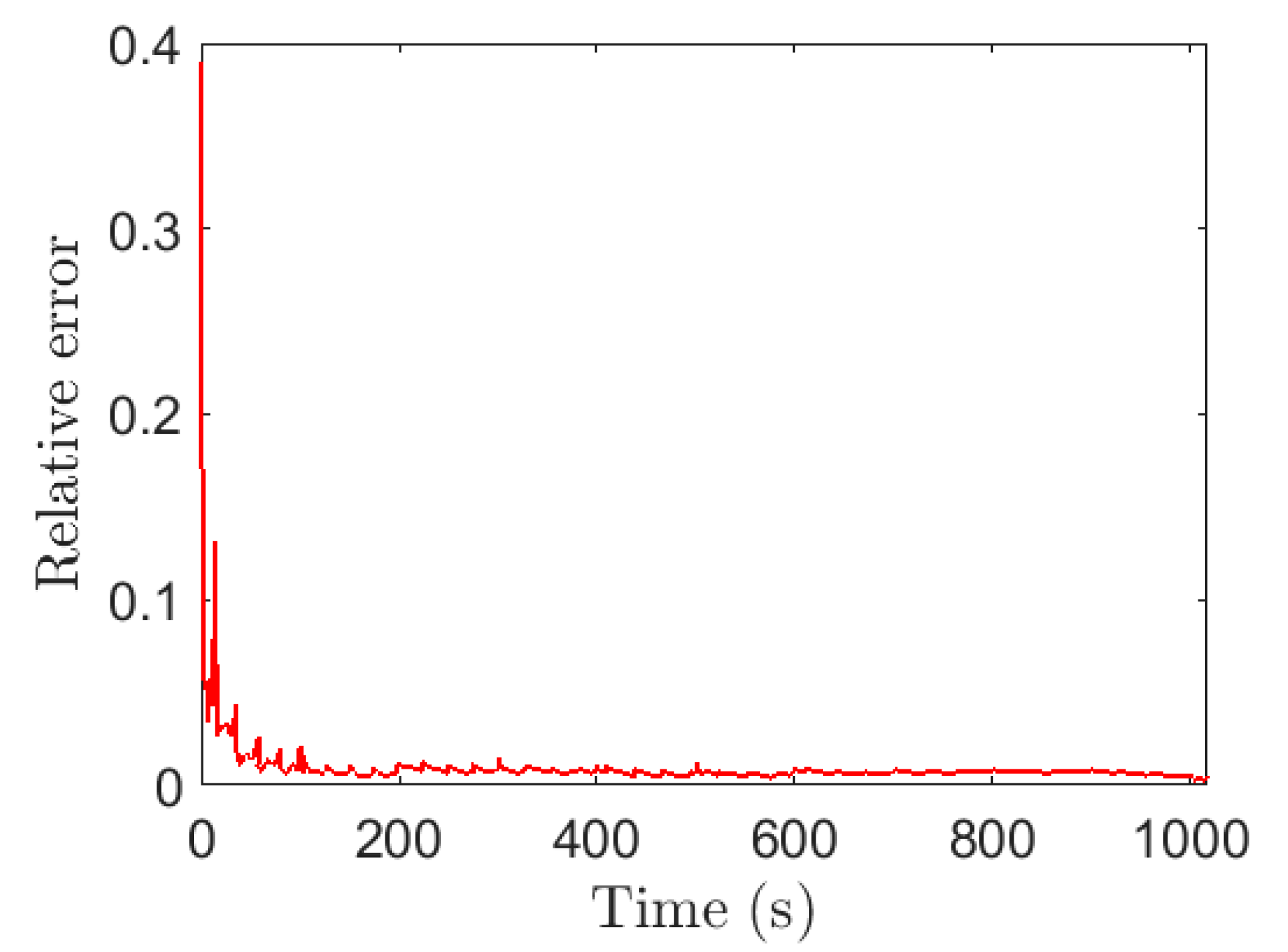
3.3. Hydraulic Fracturing Example
4. Discussion on Data-Driven DMD
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, Z.; Reynolds, A.C.; Zhao, H. A physics-based data-driven model for history matching, prediction, and characterization of waterflooding performance. SPE J. 2018, 23, 367–395. [Google Scholar] [CrossRef]
- Guo, Z.; Reynolds, A.C.; Zhao, H. Waterflooding optimization with the insim-ft data-driven model. Comput. Geosci. 2018, 22, 745–761. [Google Scholar] [CrossRef]
- Lerlertpakdee, P.; Jafarpour, B.; Gildin, E. Efficient production optimization with flow-network models. SPE J. 2014, 19. [Google Scholar] [CrossRef]
- Salehi, A.; Hetz, G.; Olalotiti, F.; Sorek, N.; Darabi, H.; Castineira, D. A Comprehensive Adaptive Forecasting Framework for Optimum Field Development Planning. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 10–11 April 2019; Society of Petroleum Engineers: Galveston, TX, USA, 2019. [Google Scholar] [CrossRef]
- Liu, Z.; Forouzanfar, F.; Zhao, Y. Comparison of sqp and al algorithms for deterministic constrained production optimization of hydrocarbon reservoirs. J. Pet. Sci. Eng. 2018, 171, 542–557. [Google Scholar] [CrossRef]
- Liu, Z.; Reynolds, A.C. An sqp-filter algorithm with an improved stochastic gradient for robust life-cycle optimization problems with nonlinear constraints. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 10–11 April 2019; Society of Petroleum Engineers: Galveston, TX, USA, 2019. [Google Scholar] [CrossRef]
- Klie, H. Physics-based and data-driven surrogates for production forecasting. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 23–25 February 2015; Society of Petroleum Engineers: Houston, TX, USA, 2015; p. 18. [Google Scholar]
- Mohaghegh, S.D. Shale Analytics: Data-Driven Analytics in Unconventional Resources; Springer: Berlin, Germany, 2017. [Google Scholar]
- Klie, H.; Florez, H. Data-driven discovery of unconventional shale reservoir dynamics. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 10–11 April 2019; Society of Petroleum Engineers: Galveston, TX, USA, 2019; p. 24. [Google Scholar]
- Bao, A.; Gildin, E.; Zalavadia, H. Development of proxy models for reservoir simulation by sparsity promoting methods and machine learning techniques. In Proceedings of the ECMOR XVI-16th European Conference on the Mathematics of Oil Recovery, Barcelona, Spain, 3–6 September 2018. [Google Scholar] [CrossRef]
- Narasingam, A.; Sang-Il Kwon, J. Data-driven identification of interpretable reduced-order models using sparse regression. Comput. Chem. Eng. 2018, 119, 101–111. [Google Scholar] [CrossRef]
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems; Siam: Philadelphia, PA, USA, 2005; Volume 6. [Google Scholar]
- Aziz, K. Petroleum Reservoir Simulation; Applied Science Publishers Ltd.: London, UK, 1979; Volume 476. [Google Scholar]
- Aarnes, J.; Krogstad, S.; Lie, K. A hierarchical multiscale method for two-phase flow based upon mixed finite elements and nonuniform coarse grids. Multiscale Model. Simul. 2006, 5, 337–363. [Google Scholar] [CrossRef]
- Chen, Z.; Huan, G.; Ma, Y. Computational Methods for Multiphase Flows in Porous Media; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006. [Google Scholar]
- Ghommem, M.; Gildin, E.; Ghasemi, M. Complexity reduction of multiphase flows in heterogeneous porous media. SPE J. 2016, 21, 144–151. [Google Scholar] [CrossRef]
- Van Doren, J.F.M.; Markovinović, R.; Jansen, J.-D. Reduced-order optimal control of water flooding using proper orthogonal decomposition. Comput. Geosci. 2006, 10, 137–158. [Google Scholar] [CrossRef]
- Gildin, E.; Ghasemi, M.; Romanovskay, A.; Efendiev, Y. Nonlinear complexity reduction for fast simulation of flow in heterogeneous porous media. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 18–20 February 2013; Society of Petroleum Engineers: The Woodlands, TX, USA, 2013; p. 14. [Google Scholar]
- Tan, X.; Gildin, E.; Trehan, S.; Yang, Y.; Hoda, N. Trajectory-based deim tdeim model reduction applied to reservoir simulation. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017; Society of Petroleum Engineers: Montgomery, TX, USA, 2017; p. 19. [Google Scholar]
- Cardoso, M.A.; Durlofsky, L.J. Use of reduced-order modeling procedures for production optimization. SPE J. 2010, 15, 426–435. [Google Scholar] [CrossRef]
- Trehan, S.; Durlofsky, L.J. Trajectory piecewise quadratic reduced-order model for subsurface flow, with application to pde-constrained optimization. J. Comput. Phys. 2016, 326, 446–473. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory—Implementation—Applications; Springer: New York, NY, USA, 1996. [Google Scholar]
- Ghommem, M.; Presho, M.; Calo, V.M.; Efendiev, Y. Mode decomposition methods for flows in high-contrast porous media. Global–local approach. J. Comput. Phys. 2013, 253, 226–238. [Google Scholar] [CrossRef]
- Florez, H.; Gildin, E. Model order reduction applied to coupled flow and geomechanics. In Proceedings of the ECMOR XVI-16th European Conference on the Mathmatics of Oil Recovery, Barcelona, Spain, 3–6 September 2018. [Google Scholar]
- Yang, Y.; Ghasemi, M.; Gildin, E.; Efendiev, Y.; Calo, V. Fast multiscale reservoir simulations with pod-deim model reduction. SPE J. 2016, 21, 2141–2154. [Google Scholar] [CrossRef]
- Jovanović, M.R.; Schmid, P.J.; Nichols, J.W. Sparsity-promoting dynamic mode decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef]
- Rowley, C.W.; Mezic, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef]
- Chen, K.K.; Tu, J.H.; Rowley, C.W. Variants of dynamic mode decomposition: Boundary condition, koopman, and fourier analyses. J. Nonlinear Sci. 2012, 22, 887–915. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Lusch, B.; Kutz, J.N.; Brunton, S.L. Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 2018, 9, 4950. [Google Scholar] [CrossRef]
- Takeishi, N.; Kawahara, Y.; Yairi, T. Learning koopman invariant subspaces for dynamic mode decomposition. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Guangzhou, China, 14–18 November 2017; Curran Associates Inc.: Long Beach, CA, USA, 2017; pp. 1130–1140. [Google Scholar]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data–driven approximation of the koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Narasingam, A.; Kwon, J.S.-I. Development of local dynamic mode decomposition with control: Application to model predictive control of hydraulic fracturing. Comput. Chem. Eng. 2017, 106, 501–511. [Google Scholar] [CrossRef]
- Proctor, J.L.; Brunton, S.L.; Kutz, J.N. Dynamic mode decomposition with control. SIAM J. Appl. Dyn. Syst. 2016, 15, 142–161. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Narasingam, A.; Siddhamshetty, P.; Sang-Il Kwon, J. Temporal clustering for order reduction of nonlinear parabolic pde systems with time-dependent spatial domains: Application to a hydraulic fracturing process. AIChE J. 2017, 63, 3818–3831. [Google Scholar] [CrossRef]
- Christie, M.A.; Blunt, M.J. Tenth spe comparative solution project: A comparison of upscaling techniques. SPE Reserv. Eval. Eng. 2001, 4, 308–317. [Google Scholar] [CrossRef]
- Narasingam, A.; Siddhamshetty, P.; Kwon, J.S.-I. Handling spatial heterogeneity in reservoir parameters using proper orthogonal decomposition based ensemble kalman filter for model-based feedback control of hydraulic fracturing. Ind. Eng. Chem. Res. 2018, 57, 3977–3989. [Google Scholar] [CrossRef]
- Bangi, M.S.F.; Narasingam, A.; Siddhamshetty, P.; Kwon, J.S.-I. Enlarging the domain of attraction of the local dynamic mode decomposition with control technique: Application to hydraulic fracturing. Ind. Eng. Chem. Res. 2019, 58, 5588–5601. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of Well-Block Pressures in Numerical Reservoir Simulation with Nonsquare Grid Blocks and Anisotropic Permeability. Soc. Pet. Eng. J. 1983, 23, 531–543. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Perkins, T.K.; Kern, L.R. Widths of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Yang, S.; Siddhamshetty, P.; Kwon, J.S.-I. Optimal pumping schedule design to achieve a uniform proppant concentration level in hydraulic fracturing. Comput. Chem. Eng. 2017, 101, 138–147. [Google Scholar] [CrossRef]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Daneshy, A.A. Numerical solution of sand transport in hydraulic fracturing. J. Pet. Technol. 1978, 30, 132–140. [Google Scholar] [CrossRef]
- Kunisch, K.; Volkwein, S. Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics. SIAM J. Numer. Anal. 2002, 40, 492–515. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. arXiv 2013, arXiv:1312.0041. [Google Scholar]
- Tan, M.P.; Broach, J.R.; Floudas, C.A. A novel clustering approach and prediction of optimal number of clusters: Global optimum search with enhanced positioning. J. Glob. Optim. 2007, 39, 323–346. [Google Scholar] [CrossRef]
- Bao, A.; Gildin, E. Data-driven model reduction based on sparsity-promoting methods for multiphase flow in porous media. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 17–19 May 2017; Society of Petroleum Engineers: Buenos Aires, Argentina, 2017; p. 16. [Google Scholar]
- Siddhamshetty, P.; Yang, S.; Kwon, J.S.-I. Modeling of hydraulic fracturing and designing of online pumping schedules to achieve uniform proppant concentration in conventional oil reservoirs. Comput. Chem. Eng. 2018, 114, 306–317. [Google Scholar] [CrossRef]
- Gu, Q.; Hoo, K.A. Evaluating the performance of a fracturing treatment design. Ind. Eng. Chem. Res. 2014, 53, 10491–10503. [Google Scholar] [CrossRef]
| Method | Jacobian Size | Computation Time (s) | Relative Error (%) |
|---|---|---|---|
| Fine-scale | 675 × 675 | 9.89 (solver time) | - |
| Standard DMD, online | 50 × 50 | 1.51 (solver time) | 1.77 × 10−4 |
| Sparse DMD, online | 10 × 10 | 0.09 (solver time) | 0.0056 |
| Sparse DMD, online | 5 × 5 | 0.0748 (solver time) | 0.011 |
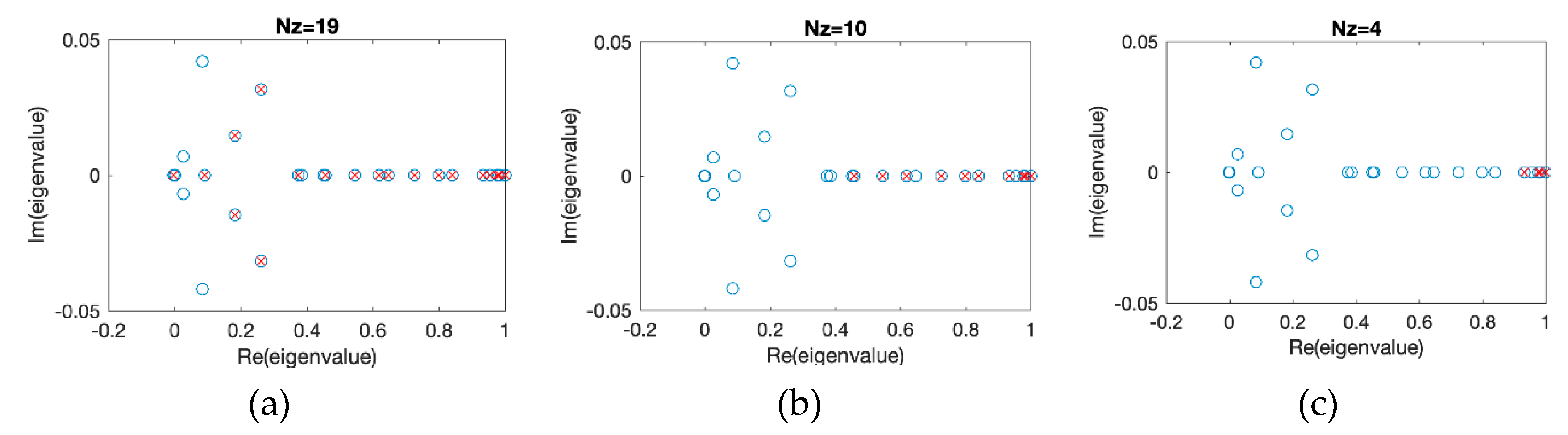
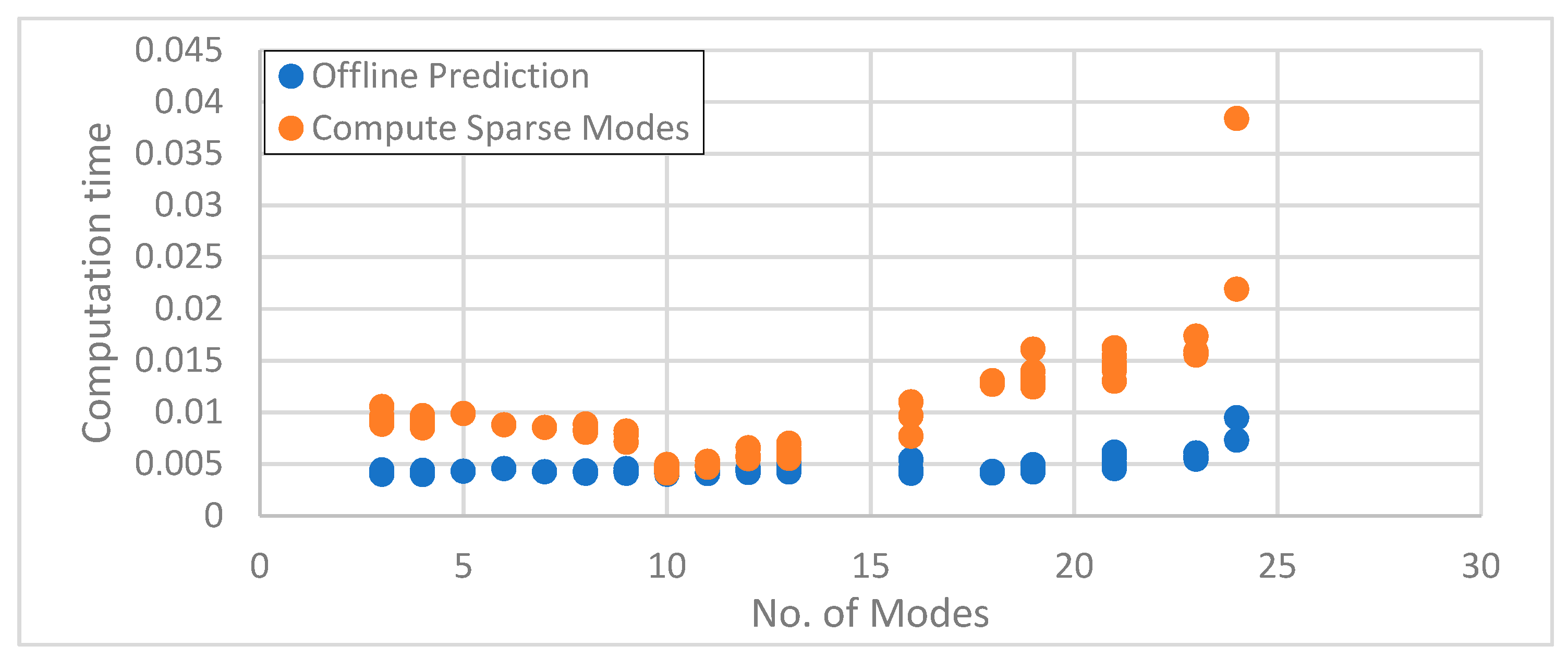
| Sparse DMD, offline | 23 × 23 | 0.042 (total time) | 0.010 |
| Grid Block | Gride Block Size | Porosity | Water Viscosity | Oil Viscosity | Injection Rate |
|---|---|---|---|---|---|
| 220 × 60 × 3 | 10 ft × 20 ft × 2 ft | 0.2 | 0.3 | 3 | 235 stb/day |
| BHP | Total Injection | Initial Sw | Initial Pressure | Time Step Size | Total Time |
| 2500 pisa | 1 Pore volume | 0.25 | 3100 psia | 0.25 days | 1000 days |
| Model | Solver Time (sec) | Relative Online Error% | Relative Offline Error% | Energy Factor for POD |
|---|---|---|---|---|
| 211 Sparse DMD modes, 2D | 9.64 | 0.093 | 2.3112 | - |
| 78 Sparse DMD modes, 2D | 4.01 | 0.1277 | 3.0878 | - |
| 211 POD modes, 2D | 10.14 | 0.1043 | - | 0.9999987 |
| 78 POD modes, 2D | 6.28 | 0.497 | - | 0.9999646 |
| Fine-scale simulator run, 2D | 2013.00 | - | - | - |
| 178 sparse DMD modes, 3D | 5.1364 | 0.0593 | 0.8268 | |
| Fine-scale simulator run, 3D | 1.7047 × 104 | - | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, A.; Gildin, E.; Narasingam, A.; Kwon, J.S. Data-Driven Model Reduction for Coupled Flow and Geomechanics Based on DMD Methods. Fluids 2019, 4, 138. https://doi.org/10.3390/fluids4030138
Bao A, Gildin E, Narasingam A, Kwon JS. Data-Driven Model Reduction for Coupled Flow and Geomechanics Based on DMD Methods. Fluids. 2019; 4(3):138. https://doi.org/10.3390/fluids4030138
Chicago/Turabian StyleBao, Anqi, Eduardo Gildin, Abhinav Narasingam, and Joseph S. Kwon. 2019. "Data-Driven Model Reduction for Coupled Flow and Geomechanics Based on DMD Methods" Fluids 4, no. 3: 138. https://doi.org/10.3390/fluids4030138
APA StyleBao, A., Gildin, E., Narasingam, A., & Kwon, J. S. (2019). Data-Driven Model Reduction for Coupled Flow and Geomechanics Based on DMD Methods. Fluids, 4(3), 138. https://doi.org/10.3390/fluids4030138






