Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media
Abstract
:1. Introduction
1.1. Proxy Modeling
1.2. Application of Neural Networks in Fluid Flow Modeling
2. Materials and Methods
2.1. Numerical Reservoir Model Development
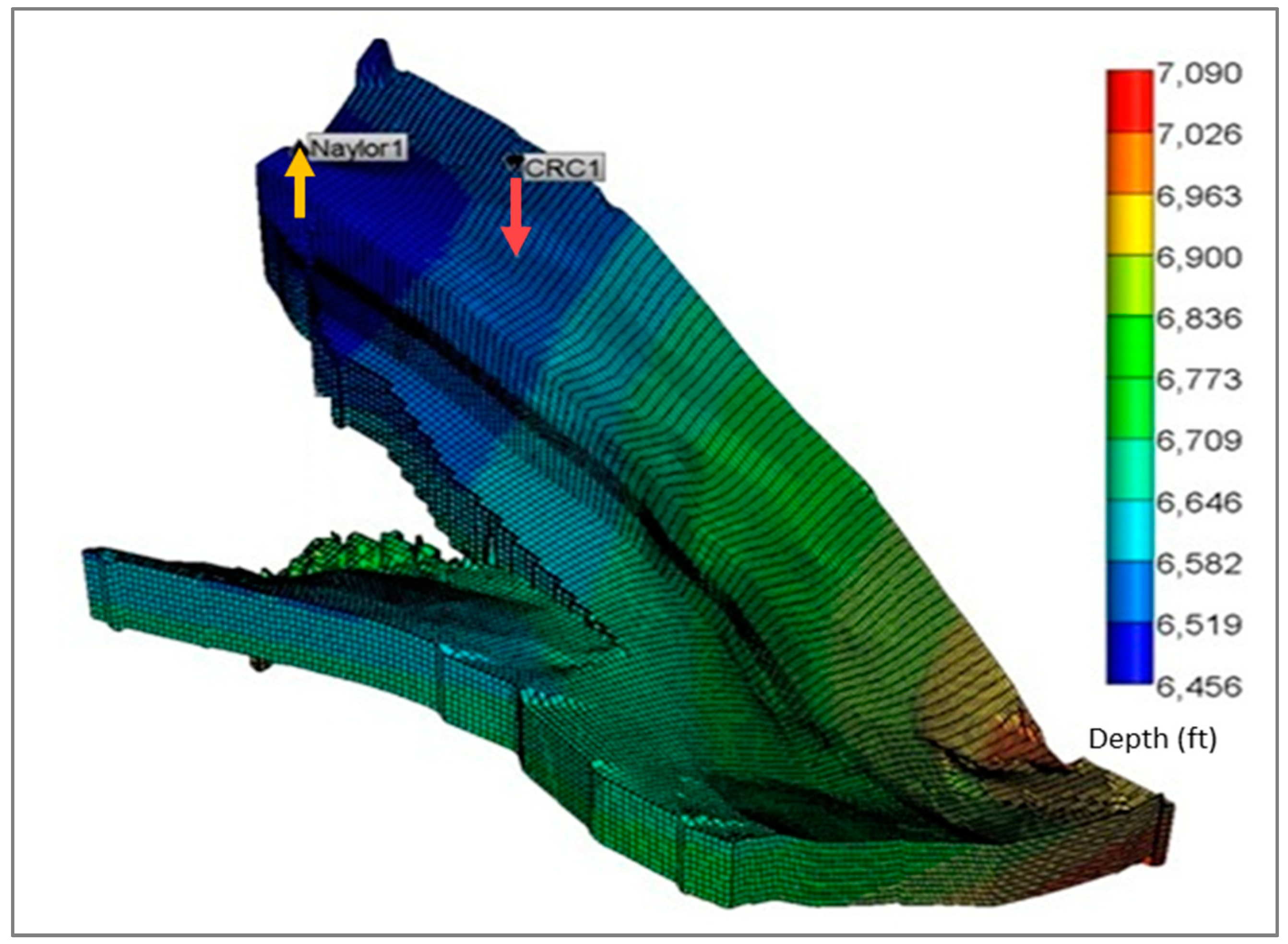
2.1.1. Field Background
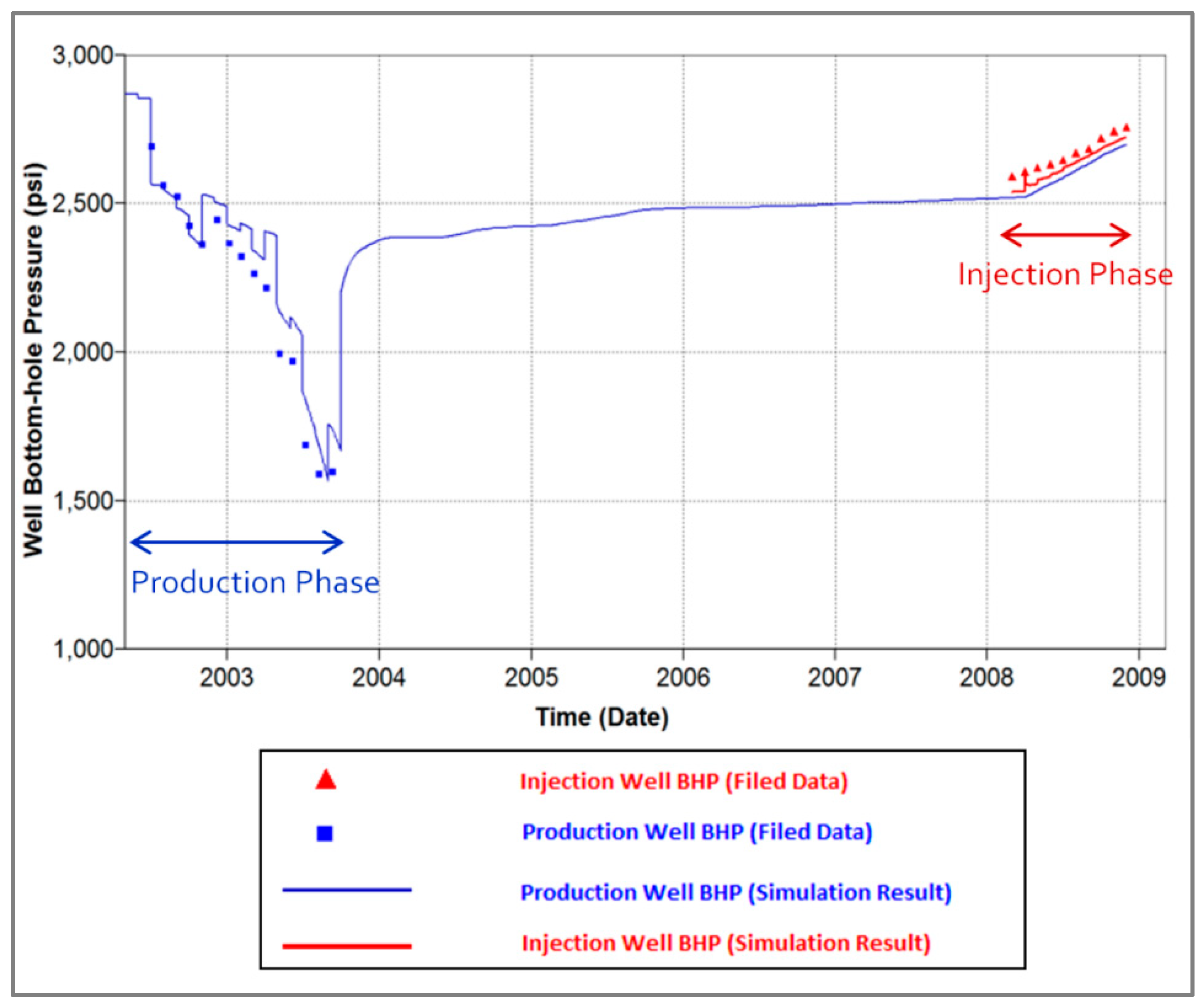
2.1.2. History Matching
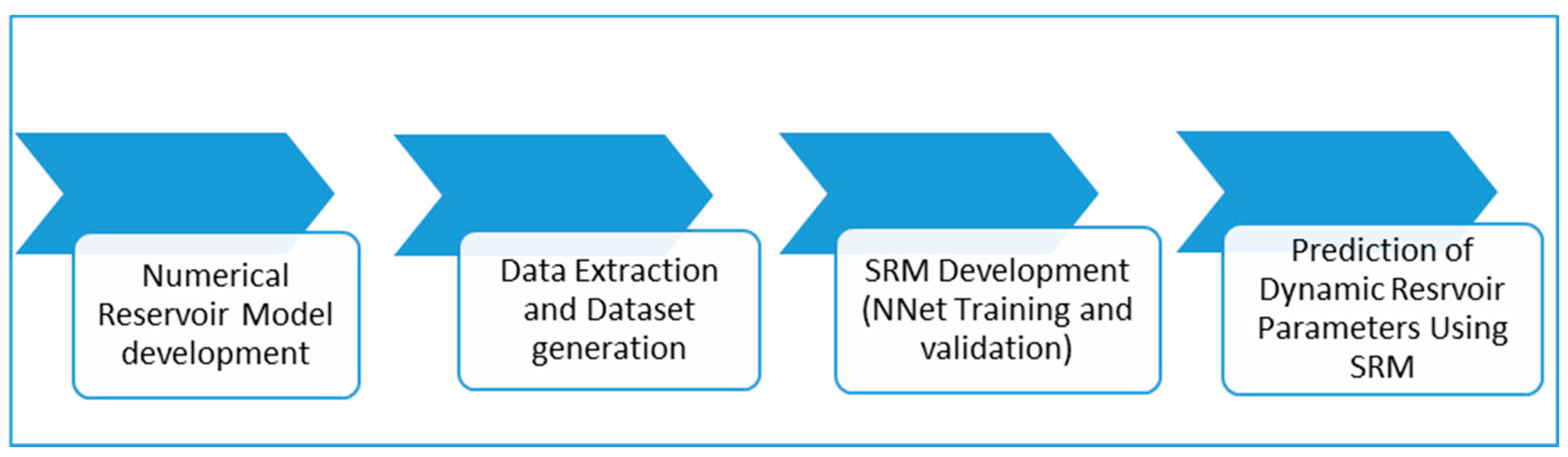
2.2. Proxy Model Development
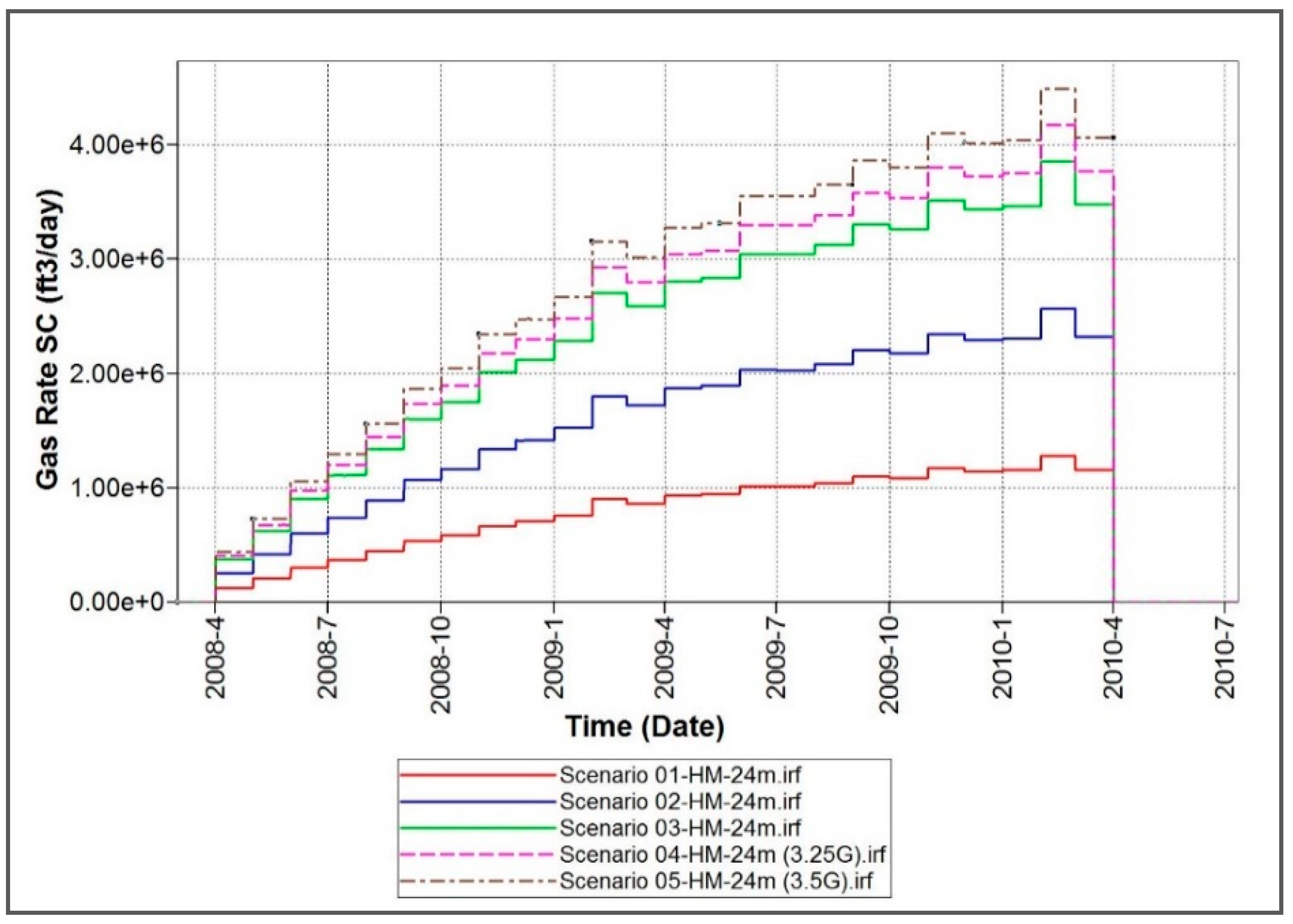
2.2.1. Simulation Scenario Design
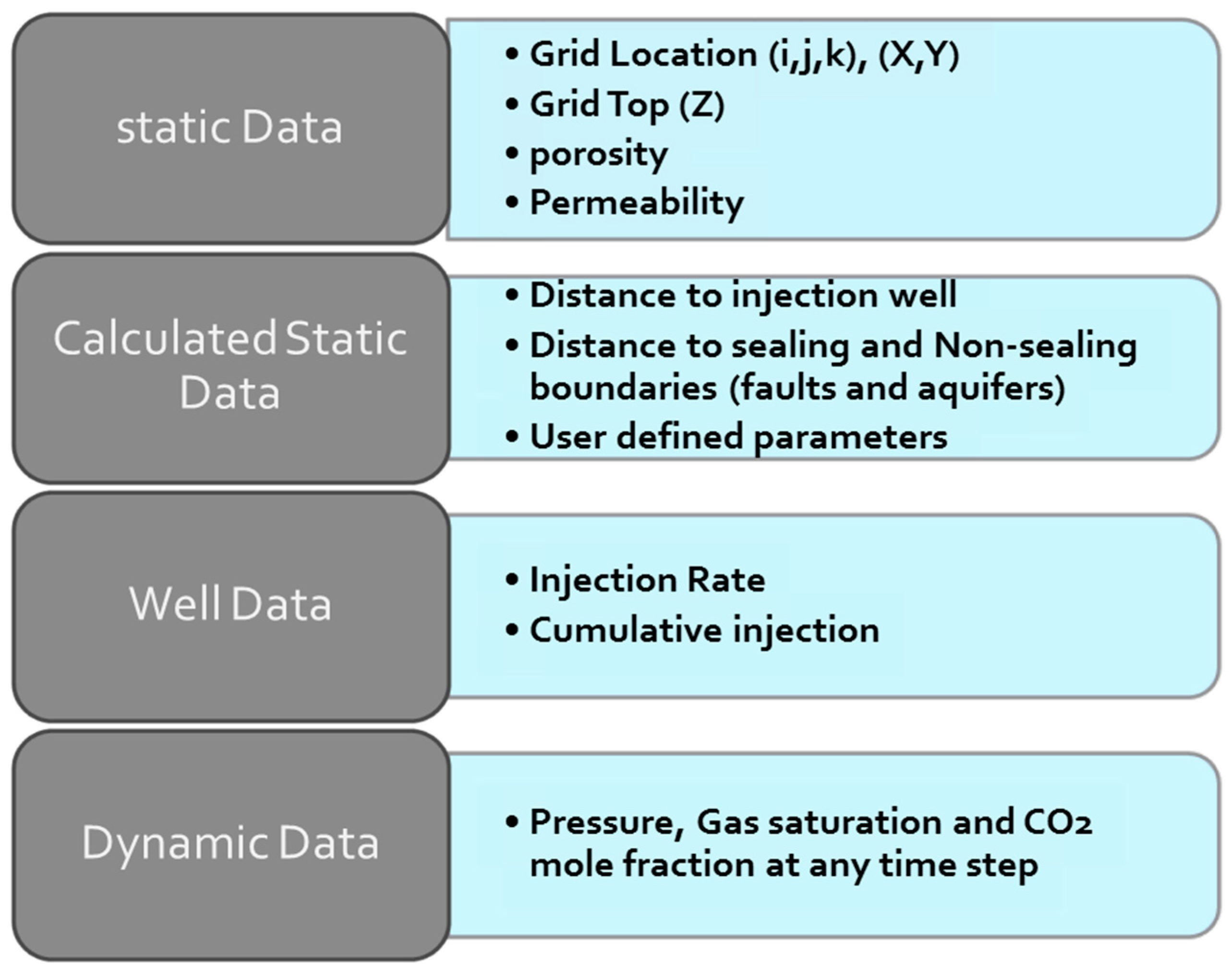
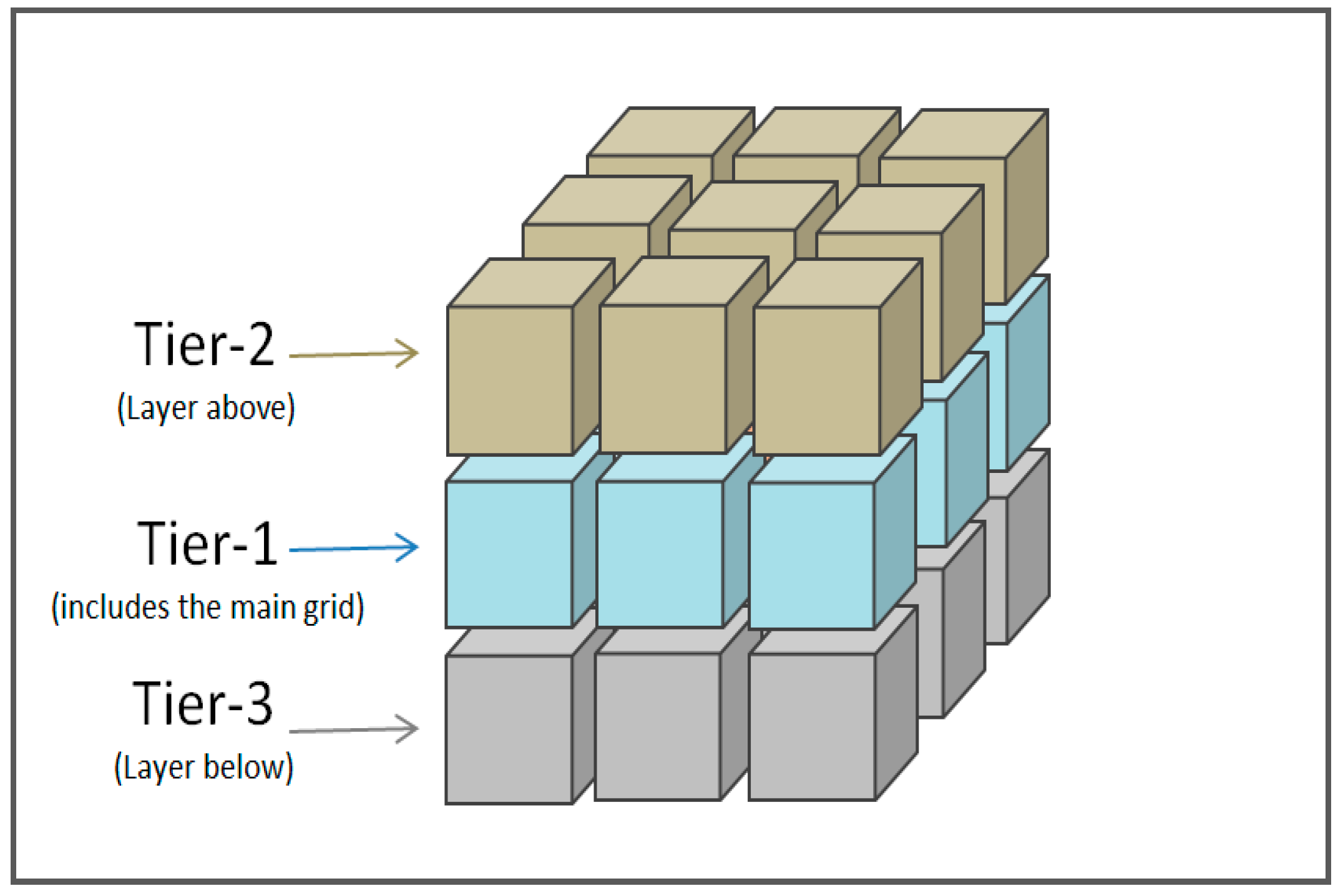
2.2.2. Data Set Generation
2.2.3. Data Sampling
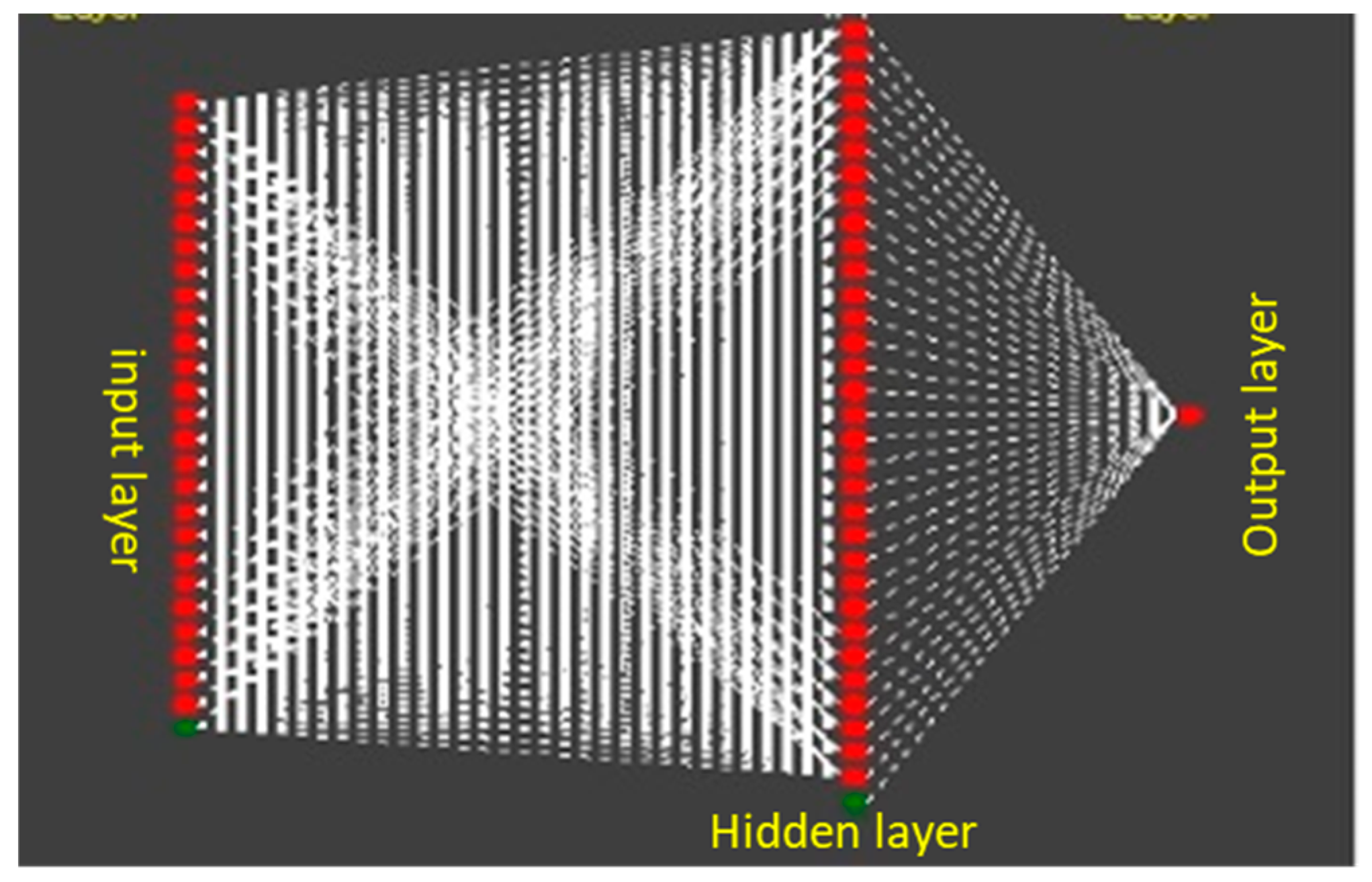
2.2.4. Proxy Flow Model Development
3. Results
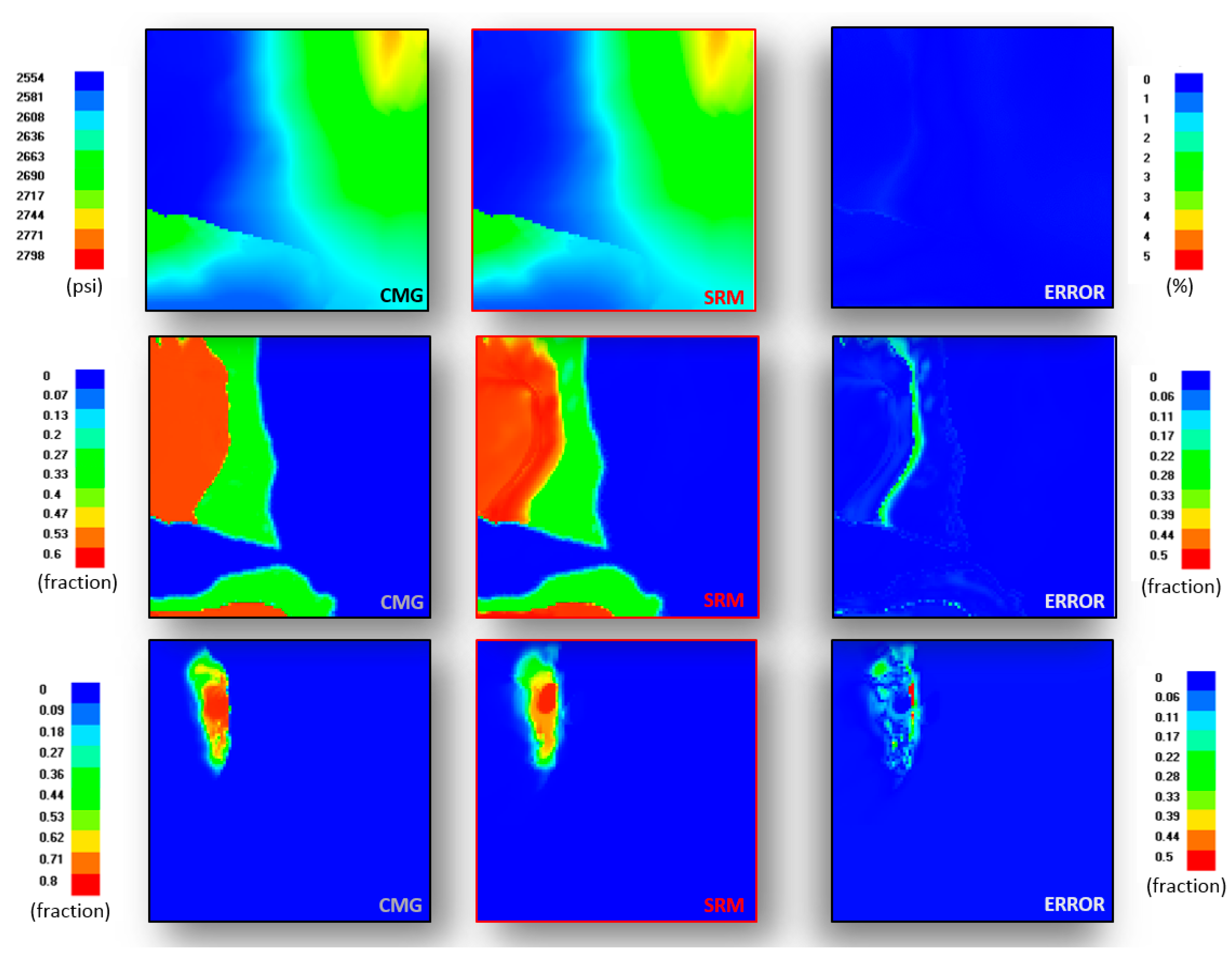
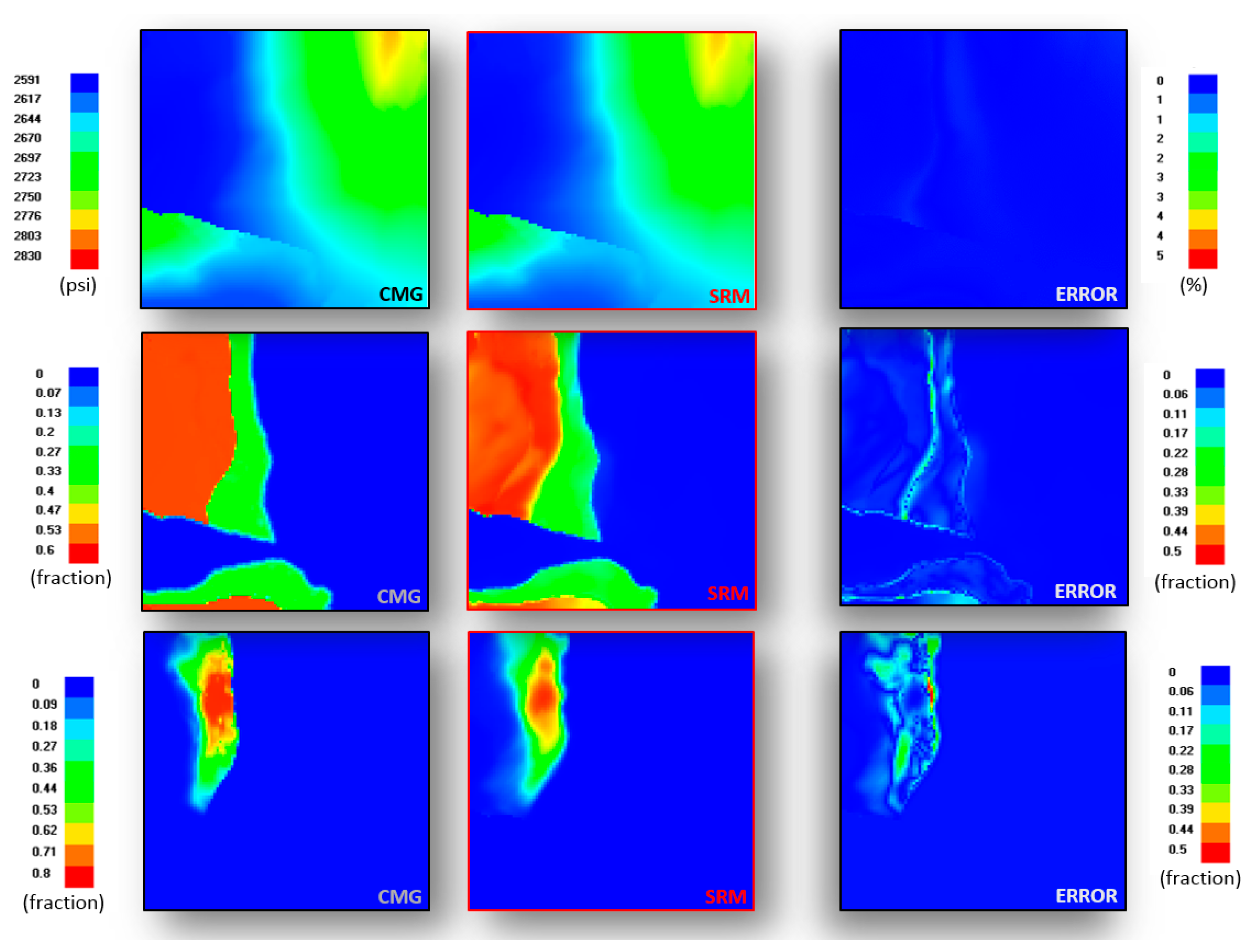
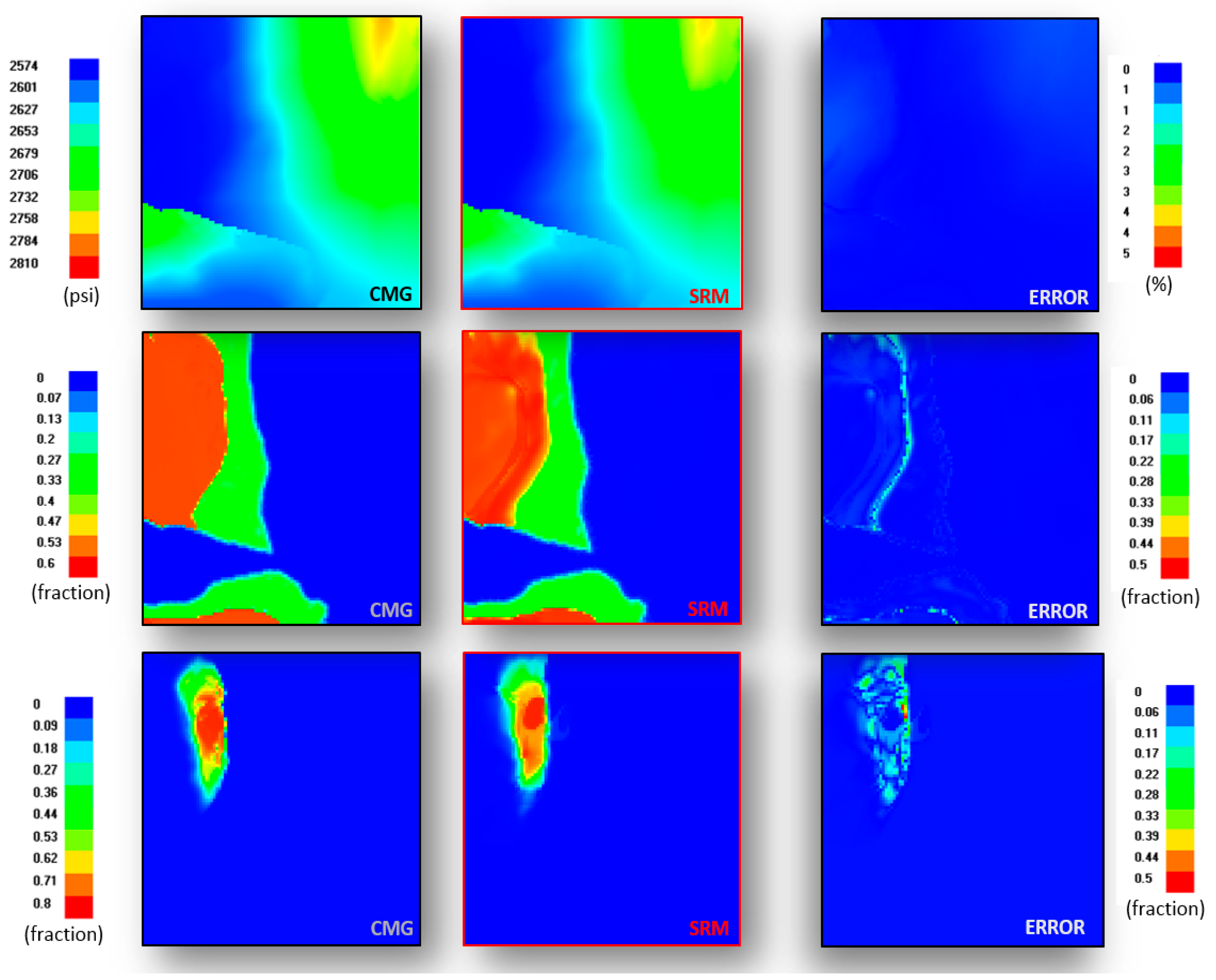
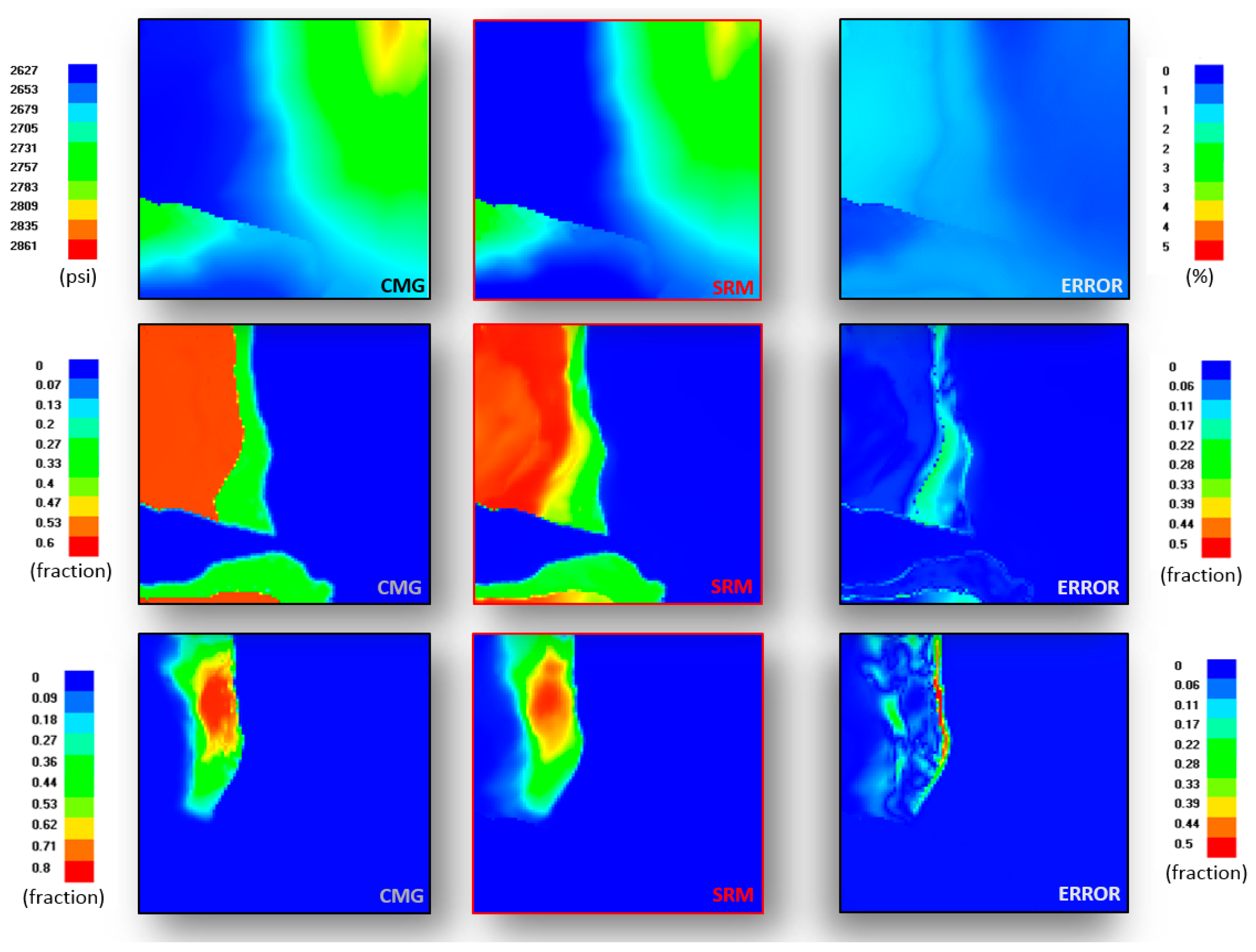
3.1. Proxy Model and Numercial Model Output Comparison
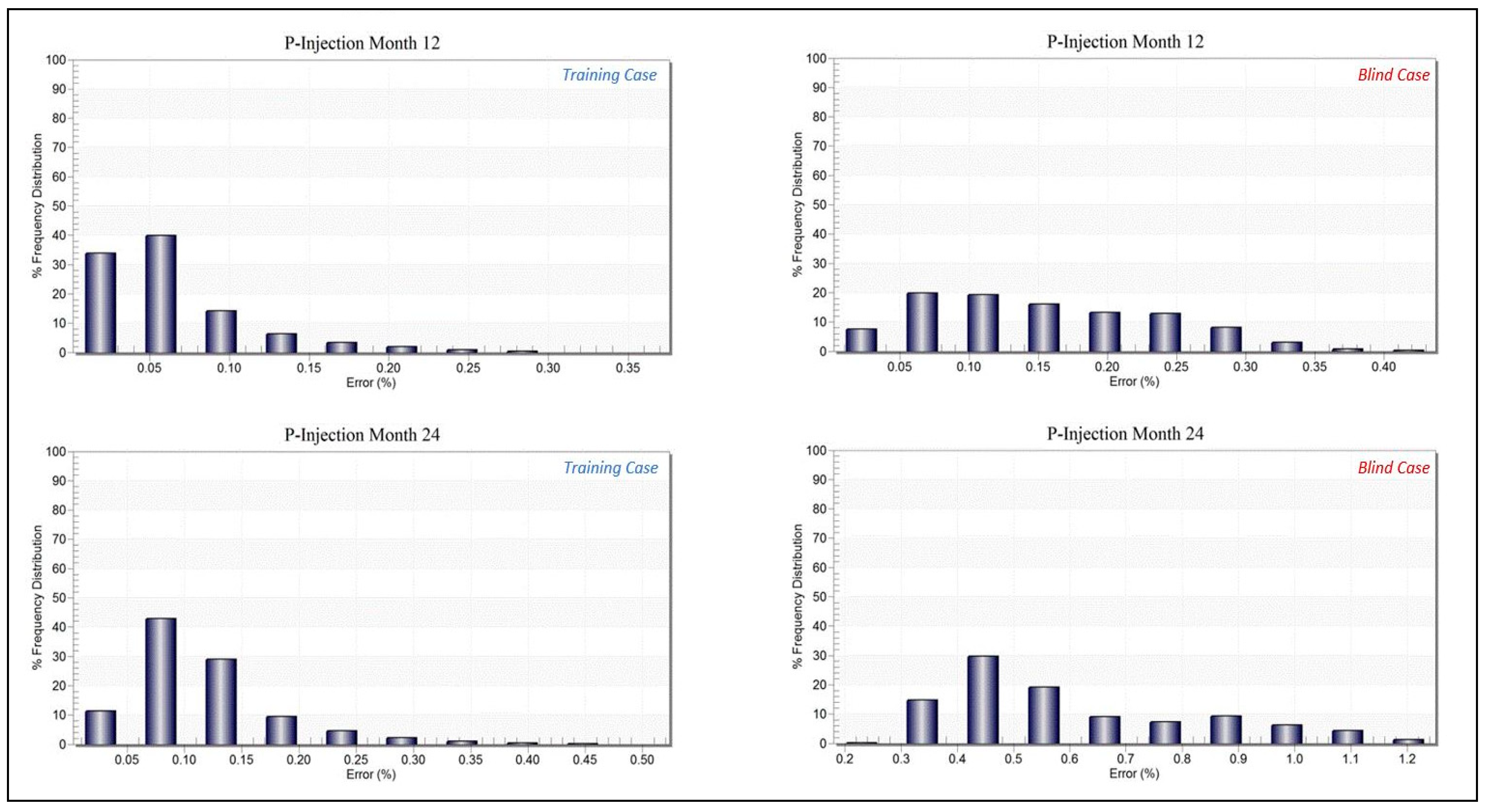
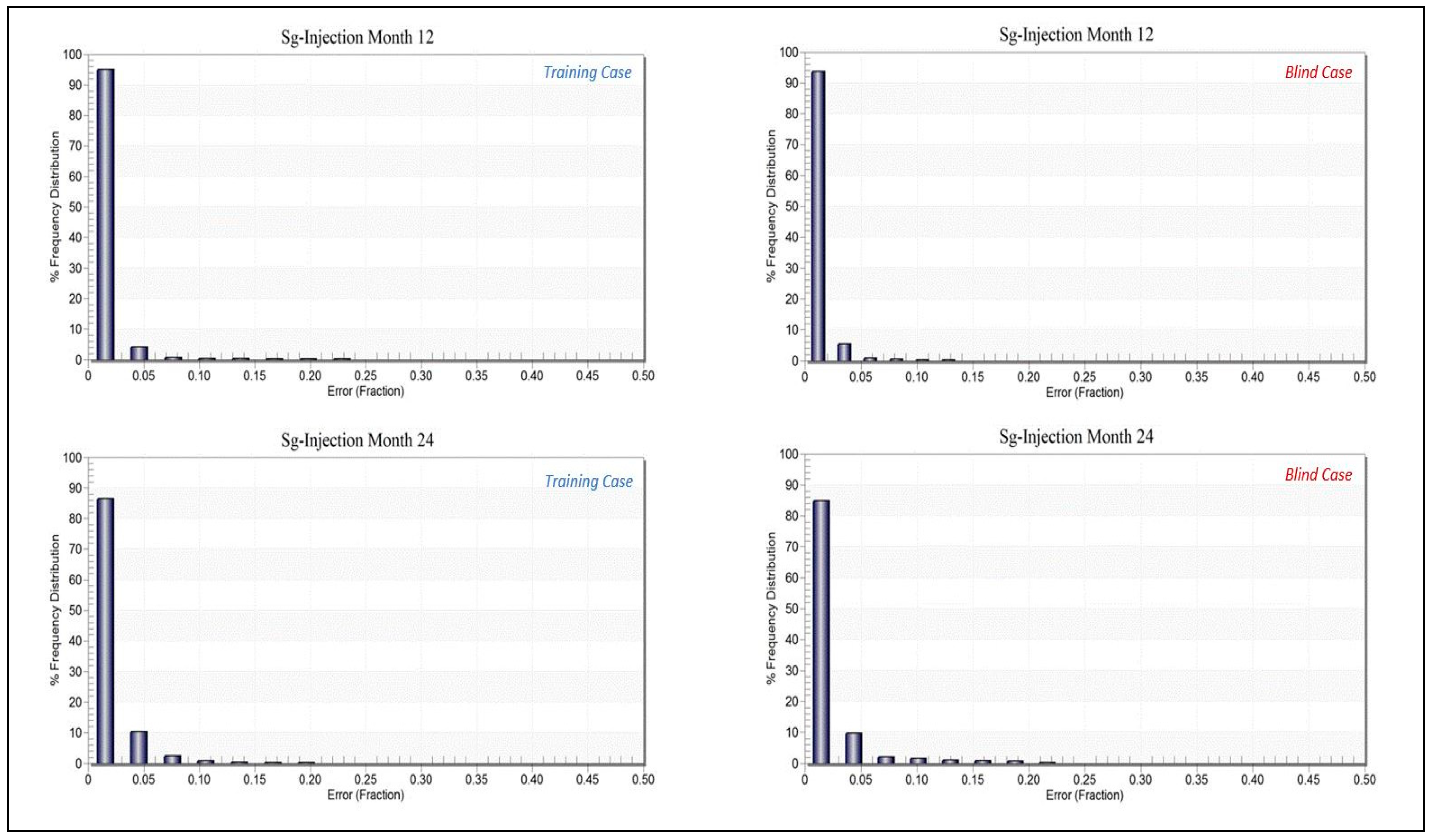
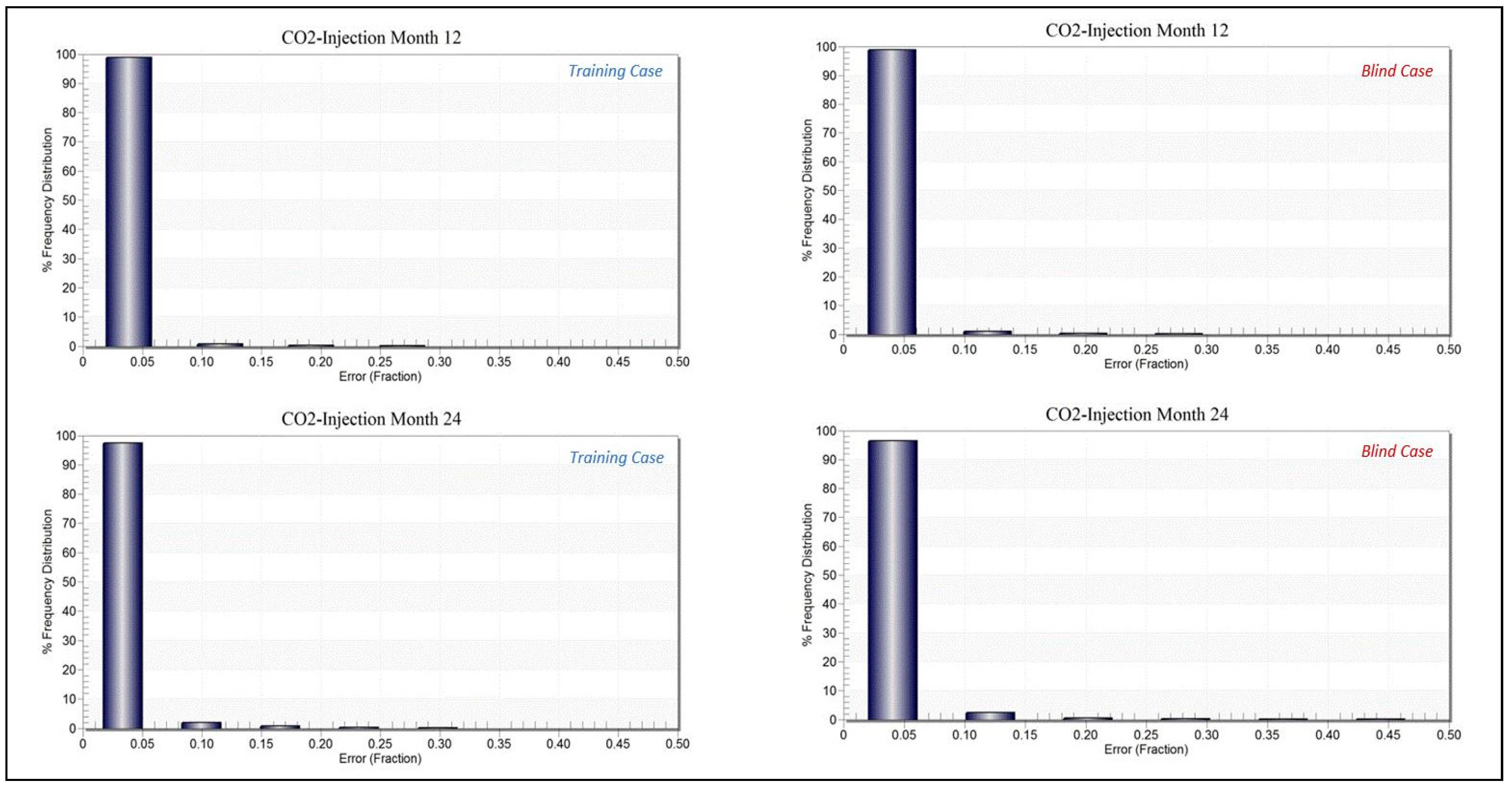
3.2. Proxy Model Error Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Slotte, P.A.; Smorgrav, E. Response Surface Methodology Approach for History Matching and Uncertainty Assessment of Reservoir Simulation Models. In Proceedings of the Europec/EAGE Conference and Exhibition, Rome, Italy, 9–12 June 2008. [Google Scholar]
- Narayanan, K.; White, C.D.; Lake, J.W.; Willis, B.J. Response Surface Methods for Upscaling Heterogeneous Geologic Models. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 14–17 February 1999. [Google Scholar]
- Carreras, P.E.; Turner, S.E.; Wilkinson, G.T. Tahiti: Development Strategy Assessment Using Design of Experiments and Response Surface Methods. In Proceedings of the SPE Western Regional, Anchorage, AK, USA, 26–27 May 2006. [Google Scholar]
- Purwar, S.; Jablonowski, C.J.; Nguyen, Q.P. A Method for Integrating Response Surfaces into Optimization Models with. In Proceedings of the SPE Hydrocarbon Economics and Evaluation Symposium, Dallas, TX, USA, 8–9 March 2010. [Google Scholar]
- Ahmed, S.J.; Recham, R.; Nozari, A.; Bughio, S.; Schulze-Riegert, R.; Ben Salem, R. Uncertainty Quantification Workflow for Mature Oil Fields: Combining Experimental Design Techniques and Different Response Surface Models. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 10–13 March 2013. [Google Scholar]
- Al Salhi, M.S.; Van Rijen, M.F.; Dijk, H.; Wei, L. Structured Uncertainty Assessment for Fahud Field through the Application of Experimental Design and Response Surface Methods. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 12–15 March 2005. [Google Scholar]
- Yeten, B.; Castellini, A.; Guyaguler, B.; Chen, W.H. A Comparison Study on Experimental Design and Response Surface Methodologies. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 31 January–2 February 2005. [Google Scholar]
- Zhang, Y.; Pau, G. Reduced-Order Model Development for CO2 Storage in Brine Reservoirs; Technical Report Series; Earth Sciences Division, Lawrence Berkeley National Lab: Berkeley, CA, USA, 2012. [Google Scholar]
- Azad, A.; Chalaturnyk, R.J.; Movaghati, S. Reservoir Characterization: Application of Extended Kalman Filter and Analytical Physics-Based Proxy Models in Thermal Recovery. In Proceedings of the International Association for Mathematical Geosciences, Houston, TX, USA, 23 May 2011. [Google Scholar]
- Vanegas, W.J.; Deutsch, C.V.; Cunha, L.B. Uncertainty Assessment of SAGD Performance Using a Proxy Model Based on Butler’s Theory. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 23 May 2008. [Google Scholar]
- Butler, R.M. A New Approach to the Modeling of Steam-Assisted Gravity Drainage; Petroleum Society of Canada: Calgary, AB, Canada, 1987. [Google Scholar]
- Cardoso, M.A. Development and Application of Reduced-Order Modeling Procedures for Reservoir Simulation. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 2009. [Google Scholar]
- Cardoso, M.A.; Durlofsky, L.J. Linearized Reduced-Order Models for Subsurface Flow Simulation; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Al-Kaabi, A.A.U.; Lee, J.W. Using Artificial Neural Networks to Identify the Well Test Interpretation Model. SPE Form. Eval. 1993, 8, 233–240. [Google Scholar] [CrossRef]
- Mohaghegh, S.; Arefi, R.; Bilgesu, I.; Ameri, S.; Rose, D. Design and Development of an Artificial Neural Network for Estimation of Formation Permeability. SPE Comput. Appl. 1995, 7, 151–154. [Google Scholar] [CrossRef]
- Mohaghegh, S.; Ameri, S.; Arefi, R. Virtual Measurement of Heterogeneous Formation Premeability Using Geophysical Well Log Responses. Log Anal. 1996, 37, 32–39. [Google Scholar]
- Nikravesh, M.; Kovscek, A.R.; Patzek, T.W. Prediction of Formation Damage During Fluid Injection Into Fractured Low-Permeability Reservoirs via Neural Networks. In Proceedings of the SPE Formation Damage Control Symposium, Lafayette, LA, USA, 14–15 February 1996. [Google Scholar]
- Mohaghegh, S.; Arefi, R.; Ameri, S. Petroleum Reservoir Characterization with the Aid of Artificial Neural Network. J. Pet. Sci. Eng. 1996, 16, 263–274. [Google Scholar] [CrossRef]
- Gorucu, F.; Gorucu, F.B.; Ertekin, T.; Bromhal, G.S.; Smith, D.H.; Sams, W.N.; Jikich, S.A. A Neurosimulation Tool for Predicting Performance in Enhanced Coalbed Methane and CO2 Sequestration Project. In Proceedings of the SPE Annual TEchnical Conference, Dallas, TX, USA, 28–29 November 2005. [Google Scholar]
- Alajmi, M.; Ertekin, T. Development of an Artificial Neural Network as a Pressure Transient Analysis. In Proceedings of the SPE Asia Pacific Oil & Gas Conference, Jakarta, Indonesia, 30 October–1 November 2007. [Google Scholar]
- Wang, S.; Sobecki, N.; Ding, D.; Zhu, L.; Wu, Y.S. Accelerating and stabilizing the vapor-liquid equilibrium (VLE) calculation in compositional simulation of unconventional reservoirs using deep learning based flash calculation. Fuel 2019, 253, 209–219. [Google Scholar] [CrossRef]
- Mohaghegh, S.D.; Modavi, A.; Hafez, H.; Haajizadeh, M.; Guruswamy, S. Development of Surrogate Reservoir Model (SRM) for fast track analysis of a complex reservoir. Int. J. Oil Gas Coal Technol. 2009. [Google Scholar] [CrossRef]
- Shahkarami, A. Assisted History Matching Using Pattern Recognition Technology. Ph.D. Dissertation, West Virginia University, Morgantown, WV, USA, 2014. [Google Scholar]
- Klie, H.; Florez, H. Data-Driven Modeling of Fractured Shale Reservoirs. In Proceedings of the ECMOR XVI-16th European Conference on the Mathematics of Oil Recovery, Barcelona, Spain, 3–6 September 2018. [Google Scholar]
- Klie, H. Unlocking Fast Reservoir Predictions via Non-Intrusive Reduced Order Models. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 18–20 Februray 2013. [Google Scholar]
- Chen, H.; Klie, H.; Wang, Q. A Black-Box Stencil Interpolation Method to Accelerate Reservoir Simulations. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 18–20 Februray 2013. [Google Scholar]
- CSIRO. Carbon Storage Trial Set to Go. Available online: http://www.sciencealert.com.au/features/20081303-17040.html (accessed on 12 December 2009).
- Dancea, T.; Spencera, L.; Xua, J. What a difference a well makes. In Proceedings of the International Conference on Greenhouse Gas Control Technologies (GHGT-9), Washington, DC, USA, 12–16 November 2008. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amini, S.; Mohaghegh, S. Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media. Fluids 2019, 4, 126. https://doi.org/10.3390/fluids4030126
Amini S, Mohaghegh S. Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media. Fluids. 2019; 4(3):126. https://doi.org/10.3390/fluids4030126
Chicago/Turabian StyleAmini, Shohreh, and Shahab Mohaghegh. 2019. "Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media" Fluids 4, no. 3: 126. https://doi.org/10.3390/fluids4030126
APA StyleAmini, S., & Mohaghegh, S. (2019). Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media. Fluids, 4(3), 126. https://doi.org/10.3390/fluids4030126





