Injection of Deformable Capsules in a Reservoir: A Systematic Analysis
Abstract
1. Introduction
2. Computational Method
2.1. Lattice Boltzmann Method
2.2. Immersed Boundary Treatment
2.3. Fluid–Structure Interaction
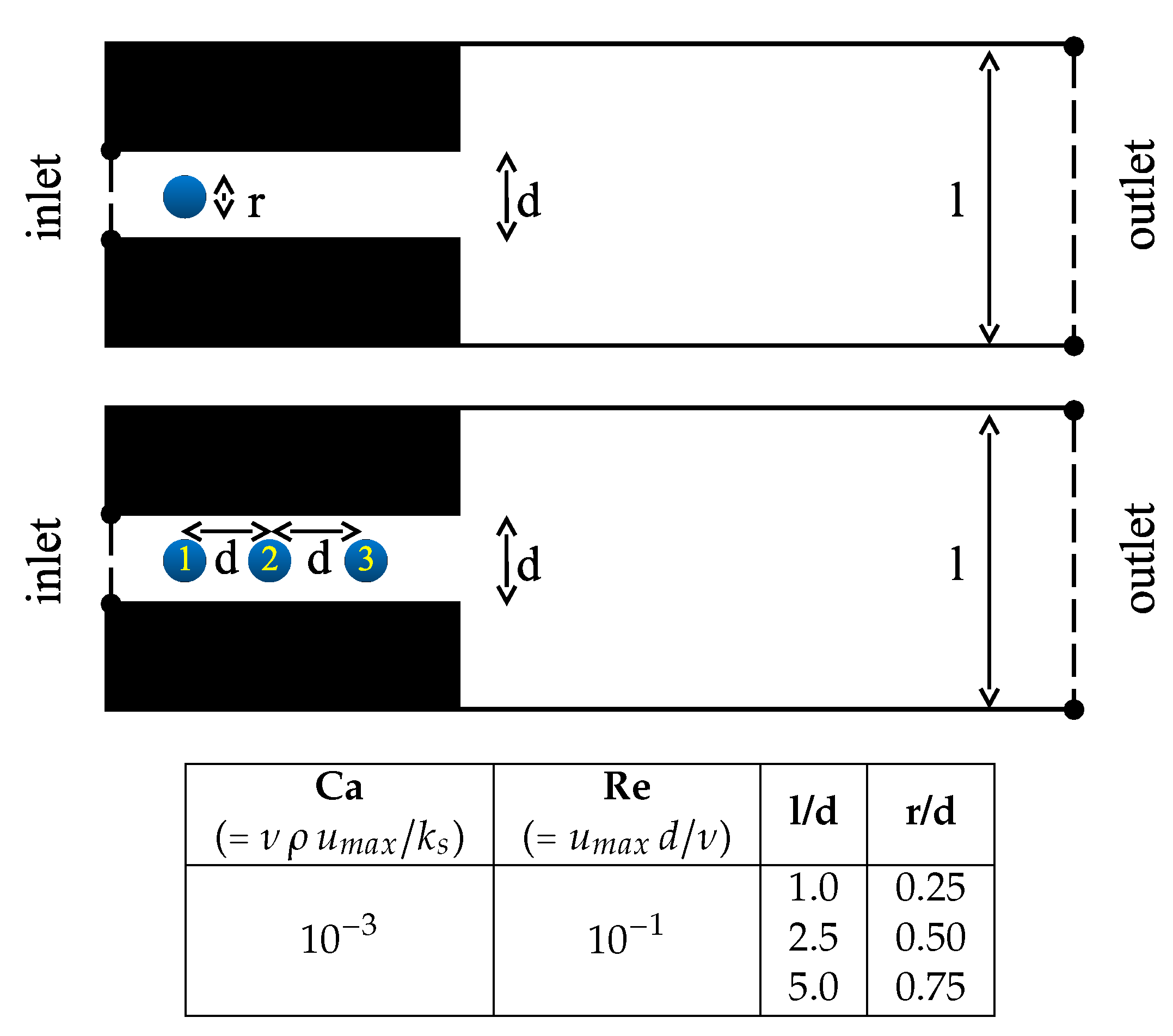
2.4. Set-Up and Boundary Conditions
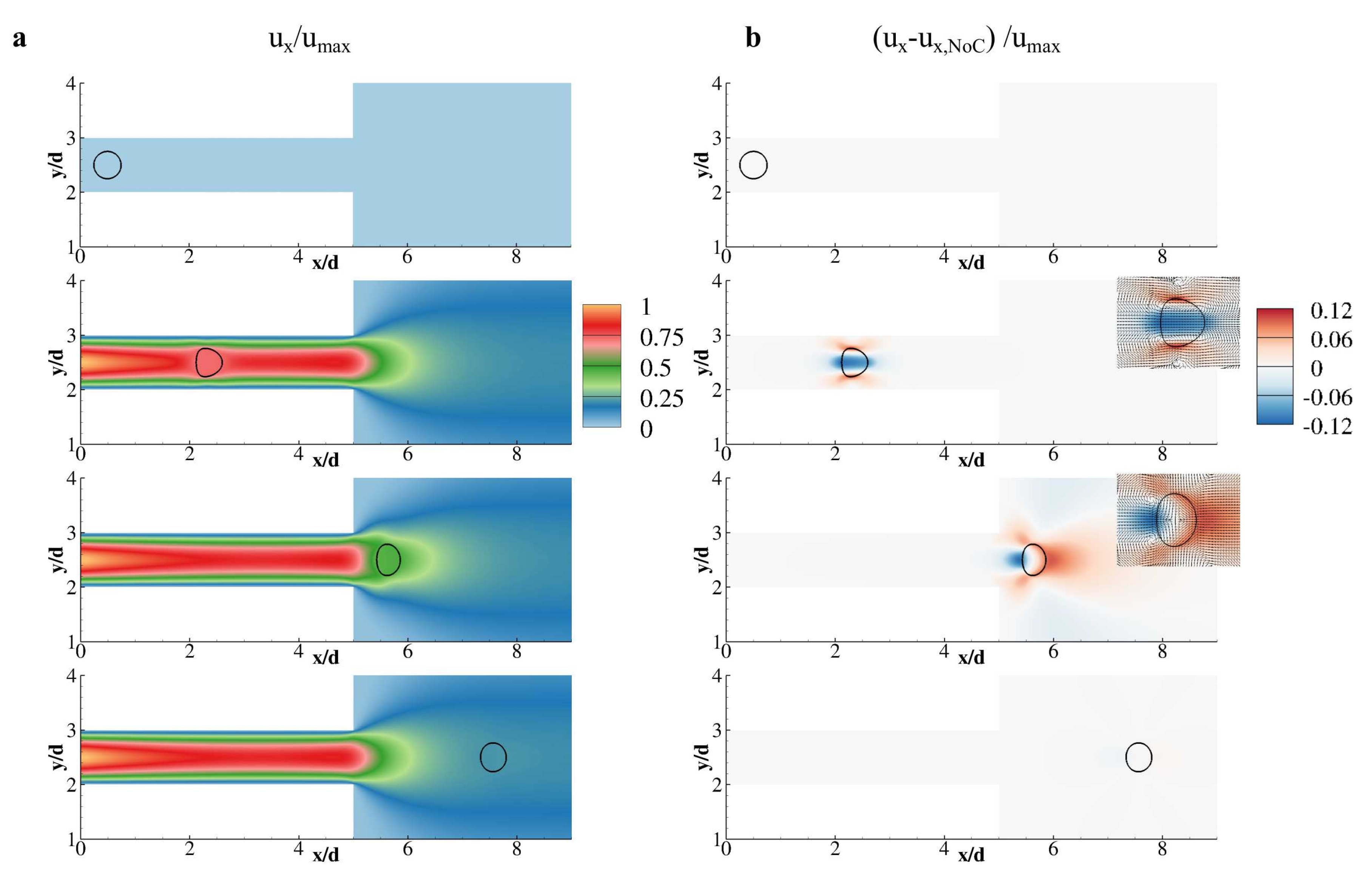
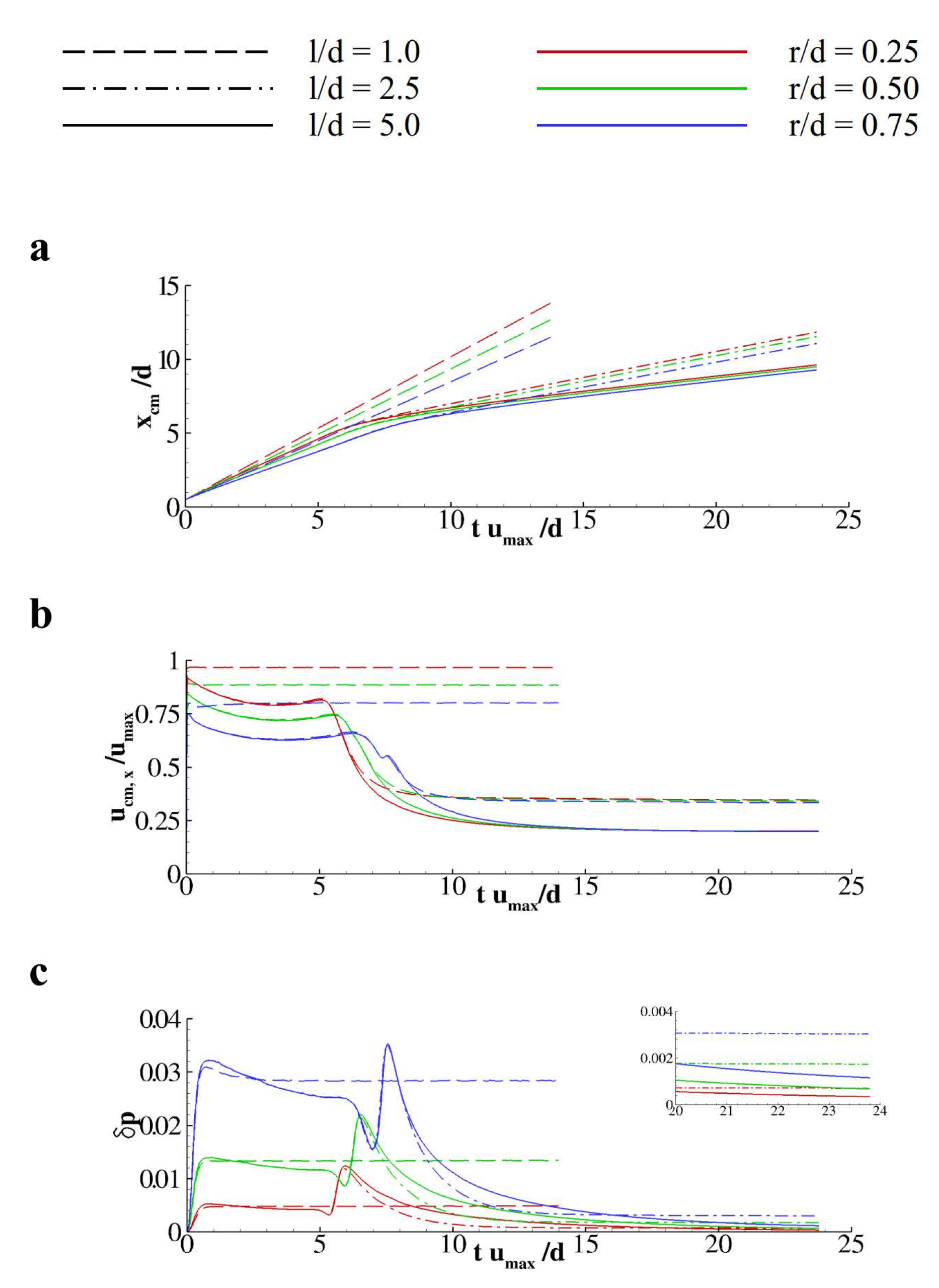
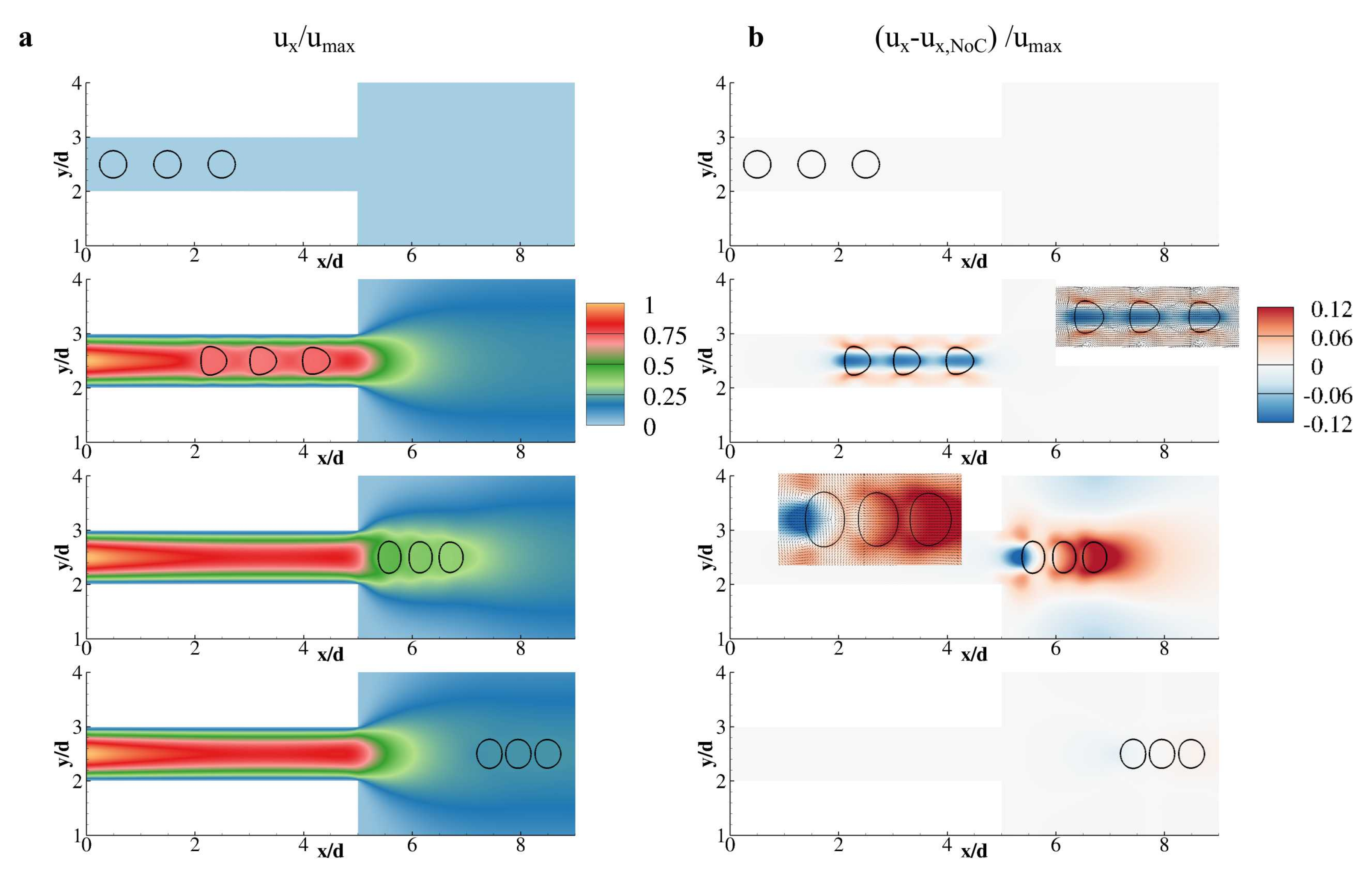
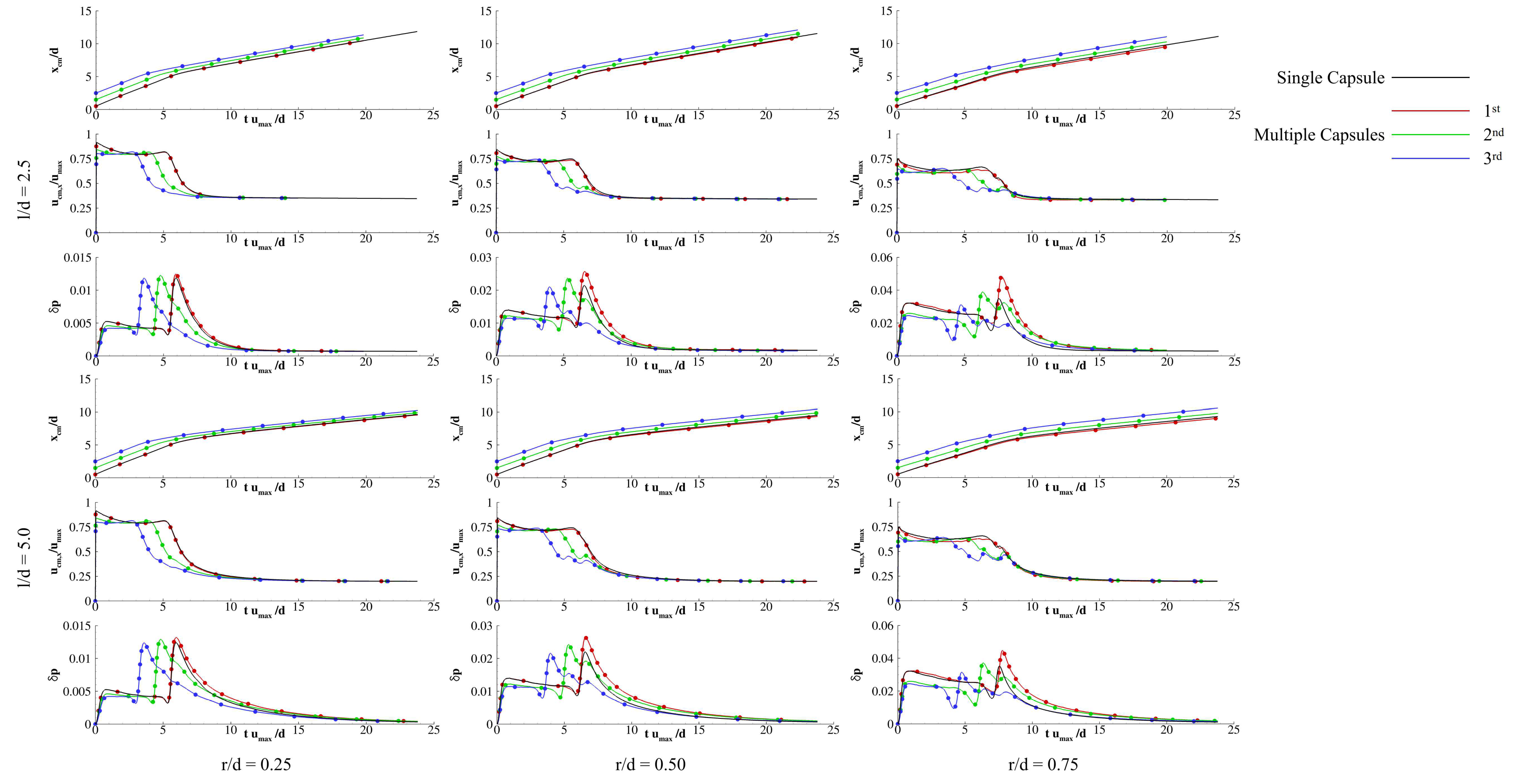
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Robertson, A.M.; Sequeira, A.; Kameneva, M.V. Hemorheology. In Hemodynamical Flows; Springer: Berlin, Germany, 2008; pp. 63–120. [Google Scholar]
- Robertson, A.M.; Sequeira, A.; Owens, R.G. Rheological models for blood. In Cardiovascular Mathematics; Springer: Berlin, Germany, 2009; pp. 211–241. [Google Scholar]
- Goldsmith, H. Red cell motions and wall interactions in tube flow. Fed. Proc. 1971, 30, 1578–1590. [Google Scholar] [PubMed]
- Pozrikidis, C. Finite deformation of liquid capsules enclosed by elastic membranes in simple shear flow. J. Fluid Mech. 1995, 297, 123–152. [Google Scholar] [CrossRef]
- Matsunaga, D.; Imai, Y.; Yamaguchi, T.; Ishikawa, T. Rheology of a dense suspension of spherical capsules under simple shear flow. J. Fluid Mech. 2016, 786, 110–127. [Google Scholar] [CrossRef]
- Tsubota, K.I.; Wada, S. Effect of the natural state of an elastic cellular membrane on tank-treading and tumbling motions of a single red blood cell. Phys. Rev. E 2010, 81, 011910. [Google Scholar] [CrossRef] [PubMed]
- Nix, S.; Imai, Y.; Matsunaga, D.; Yamaguchi, T.; Ishikawa, T. Lateral migration of a spherical capsule near a plane wall in Stokes flow. Phys. Rev. E 2014, 90, 043009. [Google Scholar] [CrossRef]
- Omori, T.; Imai, Y.; Yamaguchi, T.; Ishikawa, T. Reorientation of a nonspherical capsule in creeping shear flow. Phys. Rev. Lett. 2012, 108, 138102. [Google Scholar] [CrossRef]
- Matsunaga, D.; Imai, Y.; Yamaguchi, T.; Ishikawa, T. Deformation of a spherical capsule under oscillating shear flow. J. Fluid Mech. 2015, 762, 288–301. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Lei, H.; Caswell, B.; Suresh, S.; Karniadakis, G.E. Multiscale modeling of red blood cell mechanics and blood flow in malaria. PLoS Comput. Biol. 2011, 7, e1002270. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Noguchi, H.; Gompper, G. Multiscale modeling of blood flow: From single cells to blood rheology. Biomech. Model. Mechanobiol. 2014, 13, 239–258. [Google Scholar] [CrossRef]
- Faivre, M.; Abkarian, M.; Bickraj, K.; Stone, H.A. Geometrical focusing of cells in a microfluidic device: An approach to separate blood plasma. Biorheology 2006, 43, 147–159. [Google Scholar]
- Yaginuma, T.; Oliveira, M.S.; Lima, R.; Ishikawa, T.; Yamaguchi, T. Human red blood cell behavior under homogeneous extensional flow in a hyperbolic-shaped microchannel. Biomicrofluidics 2013, 7, 054110. [Google Scholar] [CrossRef] [PubMed]
- Faustino, V.; Catarino, S.O.; Lima, R.; Minas, G. Biomedical microfluidic devices by using low-cost fabrication techniques: A review. J. Biomech. 2016, 49, 2280–2292. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, R.O.; Lopes, R.; Pinho, D.; Pereira, A.I.; Garcia, V.; Gassmann, S.; Sousa, P.C.; Lima, R. In vitro blood flow and cell-free layer in hyperbolic microchannels: Visualizations and measurements. BioChip J. 2016, 10, 9–15. [Google Scholar] [CrossRef]
- Di Carlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.H.; Di Carlo, D.; Chen, C.; Irimia, D.; Toner, M. Microvortex for focusing, guiding and sorting of particles. Lab Chip 2008, 8, 2128–2134. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Ishikawa, T.; Numayama-Tsuruta, K.; Imai, Y.; Ueno, H.; Matsuki, N.; Yamaguchi, T. Separation of cancer cells from a red blood cell suspension using inertial force. Lab Chip 2012, 12, 4336–4343. [Google Scholar] [CrossRef] [PubMed]
- Omori, T.; Imai, Y.; Kikuchi, K.; Ishikawa, T.; Yamaguchi, T. Hemodynamics in the microcirculation and in microfluidics. Ann. Biomed. Eng. 2015, 43, 238–257. [Google Scholar] [CrossRef] [PubMed]
- Pinho, D.; Yaginuma, T.; Lima, R. A microfluidic device for partial cell separation and deformability assessment. BioChip J. 2013, 7, 367–374. [Google Scholar] [CrossRef]
- Bento, D.; Rodrigues, R.; Faustino, V.; Pinho, D.; Fernandes, C.; Pereira, A.; Garcia, V.; Miranda, J.; Lima, R. Deformation of red blood cells, air bubbles, and droplets in microfluidic devices: Flow visualizations and measurements. Micromachines 2018, 9, 151. [Google Scholar] [CrossRef]
- Yoon, D.H.; Ha, J.B.; Bahk, Y.K.; Arakawa, T.; Shoji, S.; Go, J.S. Size-selective separation of micro beads by utilizing secondary flow in a curved rectangular microchannel. Lab Chip 2009, 9, 87–90. [Google Scholar] [CrossRef]
- Martel, J.M.; Toner, M. Inertial focusing dynamics in spiral microchannels. Phys. Fluids 2012, 24, 032001. [Google Scholar] [CrossRef] [PubMed]
- Losserand, S.; Coupier, G.; Podgorski, T. Migration velocity of red blood cells in microchannels. Microvasc. Res. 2019, 124, 30–36. [Google Scholar] [CrossRef] [PubMed]
- Omori, T.; Ishikawa, T.; Barthès-Biesel, D.; Salsac, A.V.; Imai, Y.; Yamaguchi, T. Tension of red blood cell membrane in simple shear flow. Phys. Rev. E 2012, 86, 056321. [Google Scholar] [CrossRef] [PubMed]
- Sudarsan, A.P.; Ugaz, V.M. Multivortex micromixing. Proc. Natl. Acad. Sci. USA 2006, 103, 7228–7233. [Google Scholar] [CrossRef] [PubMed]
- Coclite, A.; Pascazio, G.; de Tullio, M. D.; Decuzzi, P. Predicting the vascular adhesion of deformable drug carriers in narrow capillaries traversed by blood cells. J. Fluids Struct. 2018, 82, 638–650. [Google Scholar] [CrossRef]
- Coclite, A.; Mollica, H.; Ranaldo, S.; Pascazio, G.; de Tullio, M.D.; Decuzzi, P. Predicting different adhesive regimens of circulating particles at blood capillary walls. Microfluid. Nanofluid. 2017, 21, 168. [Google Scholar] [CrossRef]
- Mollica, H.; Coclite, A.; Miali, M.E.; Pereira, R.C.; Paleari, L.; Manneschi, C.; DeCensi, A.; Decuzzi, P. Deciphering the relative contribution of vascular inflammation and blood rheology in metastatic spreading. Biomicrofluidics 2018. [Google Scholar] [CrossRef]
- Decuzzi, P.; Godin, B.; Tanaka, T.; Lee, S.Y.; Chiappini, C.; Liu, X.; Ferrari, M. Size and shape effects in the biodistribution of intravascularly injected particles. J. Control. Release 2010, 141, 320–327. [Google Scholar] [CrossRef]
- Gambaruto, A.M. Flow structures and red blood cell dynamics in arteriole of dilated or constricted cross section. J. Biomech. 2016, 49, 2229–2240. [Google Scholar] [CrossRef][Green Version]
- Gong, X.; Sugiyama, K.; Takagi, S.; Matsumoto, Y. The deformation behavior of multiple red blood cells in a capillary vessel. J. Biomech. Eng. 2009, 131, 074504. [Google Scholar] [CrossRef]
- Bessonov, N.; Babushkina, E.; Golovashchenko, S.; Tosenberger, A.; Ataullakhanov, F.; Panteleev, M.; Tokarev, A.; Volpert, V. Numerical modelling of cell distribution in blood flow. Math. Model. Nat. Phenom. 2014, 9, 69–84. [Google Scholar] [CrossRef]
- Vahidkhah, K.; Balogh, P.; Bagchi, P. Flow of red blood cells in stenosed microvessels. Sci. Rep. 2016, 6, 28194. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Munn, L.L. Influence of erythrocyte aggregation on leukocyte margination in postcapillary expansions: A lattice Boltzmann analysis. Phys. A Stat. Mech. Its Appl. 2006, 362, 191–196. [Google Scholar] [CrossRef]
- Xiong, W.; Zhang, J. Shear stress variation induced by red blood cell motion in microvessel. Ann. Biomed. Eng. 2010, 38, 2649–2659. [Google Scholar] [CrossRef] [PubMed]
- Freund, J.B.; Vermot, J. The wall-stress footprint of blood cells flowing in microvessels. Biophys. J. 2014, 106, 752–762. [Google Scholar] [CrossRef] [PubMed]
- Takeishi, N.; Imai, Y.; Ishida, S.; Omori, T.; Kamm, R.D.; Ishikawa, T. Cell adhesion during bullet motion in capillaries. Am. J. Physiol. Heart Circ. Physiol. 2016, 311, H395–H403. [Google Scholar] [CrossRef]
- Takeishi, N.; Imai, Y.; Nakaaki, K.; Yamaguchi, T.; Ishikawa, T. Leukocyte margination at arteriole shear rate. Physiol. Rep. 2014, 2. [Google Scholar] [CrossRef]
- Muller, K.; Fedosov, D.; Gompper, G. Margination of micro- and nano-particles in blood flow and its effect on drug delivery. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef]
- Takeishi, N.; Imai, Y. Capture of microparticles by bolus flow of red blood cells in capillaries. Sci. Rep. 2017, 7, 5381. [Google Scholar] [CrossRef]
- Gambaruto, A.M. Computational haemodynamics of small vessels using the moving particle semi-implicit (MPS) method. J. Comput. Phys. 2015, 302, 68–96. [Google Scholar] [CrossRef]
- Alizadehrad, D.; Imai, Y.; Nakaaki, K.; Ishikawa, T.; Yamaguchi, T. Quantification of red blood cell deformation at high-hematocrit blood flow in microvessels. J. Biomech. 2012, 45, 2684–2689. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, N.; Takano, T. Microscopic-scale simulation of blood flow using SPH method. Int. J. Comput. Methods 2005, 2, 555–568. [Google Scholar] [CrossRef]
- Noguchi, H.; Gompper, G. Swinging and tumbling of fluid vesicles in shear flow. Phys. Rev. Lett. 2007, 98, 128103. [Google Scholar] [CrossRef] [PubMed]
- Bakhshian, S.; Sahimi, M. Computer simulation of the effect of deformation on the morphology and flow properties of porous media. Phys. Rev. E 2016, 94, 042903. [Google Scholar] [CrossRef] [PubMed]
- Bakhshian, S.; Hosseini, S.A.; Shokri, N. Pore-scale characteristics of multiphase flow in heterogeneous porous media using the lattice Boltzmann method. Sci. Rep. 2019, 9, 3377. [Google Scholar] [CrossRef] [PubMed]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier–Stokes equation. EPL Europhys. Lett. 1992, 17, 479. [Google Scholar] [CrossRef]
- Shan, X.; Yuan, X.F.; Chen, H. Kinetic theory representation of hydrodynamics: A way beyond the Navier–Stokes equation. J. Fluid Mech. 2006, 550, 413–441. [Google Scholar] [CrossRef]
- Pozrikidis, C. Effect of membrane bending stiffness on the deformation of capsules in simple shear flow. J. Fluid Mech. 2001, 440, 269–291. [Google Scholar] [CrossRef]
- Skalak, R.; Tozeren, A.; Zarda, R.; Chien, S. Strain energy function of red blood cell membranes. Biophys. J. 1973, 13, 245–264. [Google Scholar] [CrossRef]
- Krüger, H. Computer Simulation Study of Collective Phenomena in Dense Suspensions of Red Blood Cells under Shear; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Dao, M.; Li, J.; Suresh, S. Molecularly based analysis of deformation of spectrin network and human erythrocyte. Mater. Sci. Eng. C 2006, 26, 1232–1244. [Google Scholar] [CrossRef]
- Nakamura, M.; Bessho, S.; Wada, S. Spring-network-based model of a red blood cell for simulating mesoscopic blood flow. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 114–128. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.S.; Ng, Y.C.; Tan, J.; Leo, H.L.; Kim, S. Two-dimensional strain-hardening membrane model for large deformation behavior of multiple red blood cells in high shear conditions. Theor. Biol. Med Model. 2014, 11, 19. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Zheng, C.; Shi, B. Force imbalance in lattice Boltzmann equation for two-phase flows. Phys. Rev. E 2011, 83, 036707. [Google Scholar] [CrossRef] [PubMed]
- De Rosis, A.; Ubertini, S.; Ubertini, F. A Comparison Between the Interpolated Bounce-Back Scheme and the Immersed Boundary Method to Treat Solid Boundary Conditions for Laminar Flows in the Lattice Boltzmann Framework. J. Sci. Comput. 2014, 61, 477–489. [Google Scholar] [CrossRef]
- Ubertini, A.D.R.S.U.F. A partitioned approach for two-dimensional fluid-structure interaction problems by a coupled lattice Boltzmann-finite element method with immersed boundary. J. Fluids Struct. 2014, 45, 202–215. [Google Scholar] [CrossRef]
- Suzuki, K.; Minami, K.; Inamuro, T. Lift and thrust generation by a butterfly-like flapping wing-body model: Immersed boundary-lattice Boltzmann simulations. J. Fluid Mech. 2015, 767, 659–695. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, C.; Teo, C. J.; Wu, J. An immersed boundary-lattice Boltzmann flux solver and its applications to fluid-structure interaction problems. J. Fluids Struct. 2015, 54, 440–465. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Coclite, A.; de Tullio, M.D.; Pascazio, G.; Decuzzi, P. A combined Lattice Boltzmann and Immersed boundary approach for predicting the vascular transport of differently shaped particles. Comput. Fluids 2016, 136, 260–271. [Google Scholar] [CrossRef]
- Coclite, A.; Ranaldo, S.; de Tullio, M.; Decuzzi, P.; Pascazio, G. Kinematic and Dynamic Forcing Strategies for Predicting the Transport of Inertial Capsules Via A Combined Lattice Boltzmann Immersed Boundary Method. Comput. Fluids 2019, 180, 41–53. [Google Scholar] [CrossRef]
- Balaras, M.V.E. A moving-least-squares reconstruction for embedded-boundary formulations. J. Comput. Phys. 2009, 6617–6628. [Google Scholar] [CrossRef]
- Favier, J.; Revell, A.; Pinelli, A. A Lattice Boltzmann-Immersed Boundary method to simulate the fluid interaction with moving and slender flexible objects. J. Comput. Phys. 2014, 261, 145–161. [Google Scholar] [CrossRef]
- de Tullio, M.D.; Pascazio, G. A moving-least-squares immersed boundary method for simulating the fluid–structure interaction of elastic bodies with arbitrary thickness. J. Comput. Phys. 2016, 325, 201–225. [Google Scholar] [CrossRef]
- Yang, Z. Lattice Boltzmann outflow treatments: Convective conditions and others. Comput. Math. Appl. 2013, 65, 160–171. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coclite, A.; Gambaruto, A.M. Injection of Deformable Capsules in a Reservoir: A Systematic Analysis. Fluids 2019, 4, 122. https://doi.org/10.3390/fluids4030122
Coclite A, Gambaruto AM. Injection of Deformable Capsules in a Reservoir: A Systematic Analysis. Fluids. 2019; 4(3):122. https://doi.org/10.3390/fluids4030122
Chicago/Turabian StyleCoclite, Alessandro, and Alberto M. Gambaruto. 2019. "Injection of Deformable Capsules in a Reservoir: A Systematic Analysis" Fluids 4, no. 3: 122. https://doi.org/10.3390/fluids4030122
APA StyleCoclite, A., & Gambaruto, A. M. (2019). Injection of Deformable Capsules in a Reservoir: A Systematic Analysis. Fluids, 4(3), 122. https://doi.org/10.3390/fluids4030122




