Reynolds Stress Perturbation for Epistemic Uncertainty Quantification of RANS Models Implemented in OpenFOAM
Abstract
1. Introduction
2. Methodology
2.1. Epistemic Uncertainty
2.2. Decomposition of the Reynolds Stress Tensor
- is a diagonal tensor containing the eigenvalues of the anisotropy tensor in an order such that ,
- is a tensor containing the eigenvectors of the anisotropy tensor in the same order as the eigenvalues.
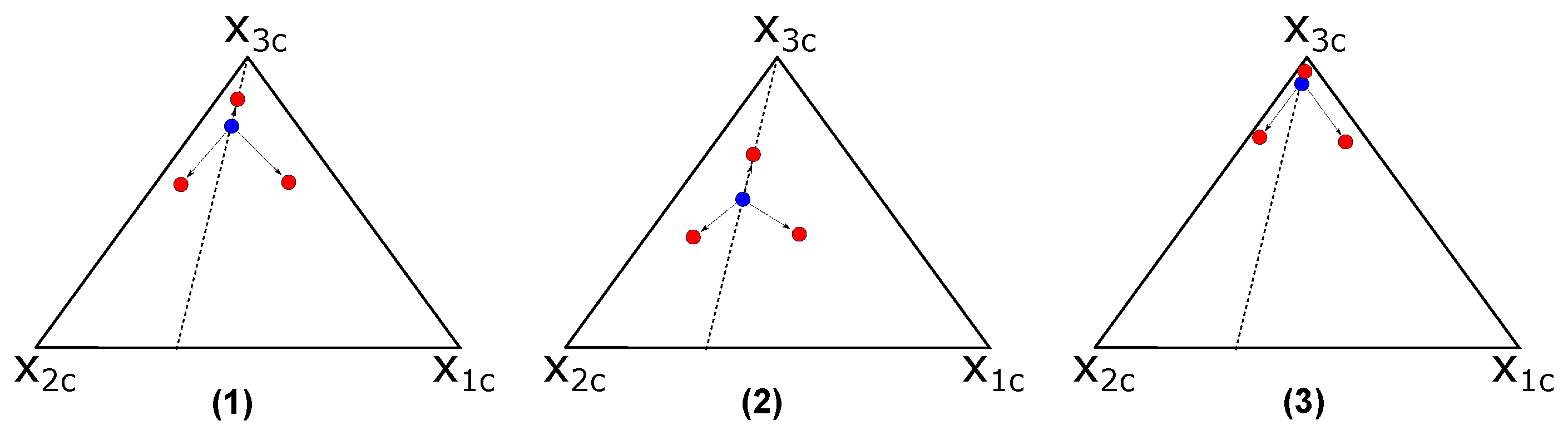
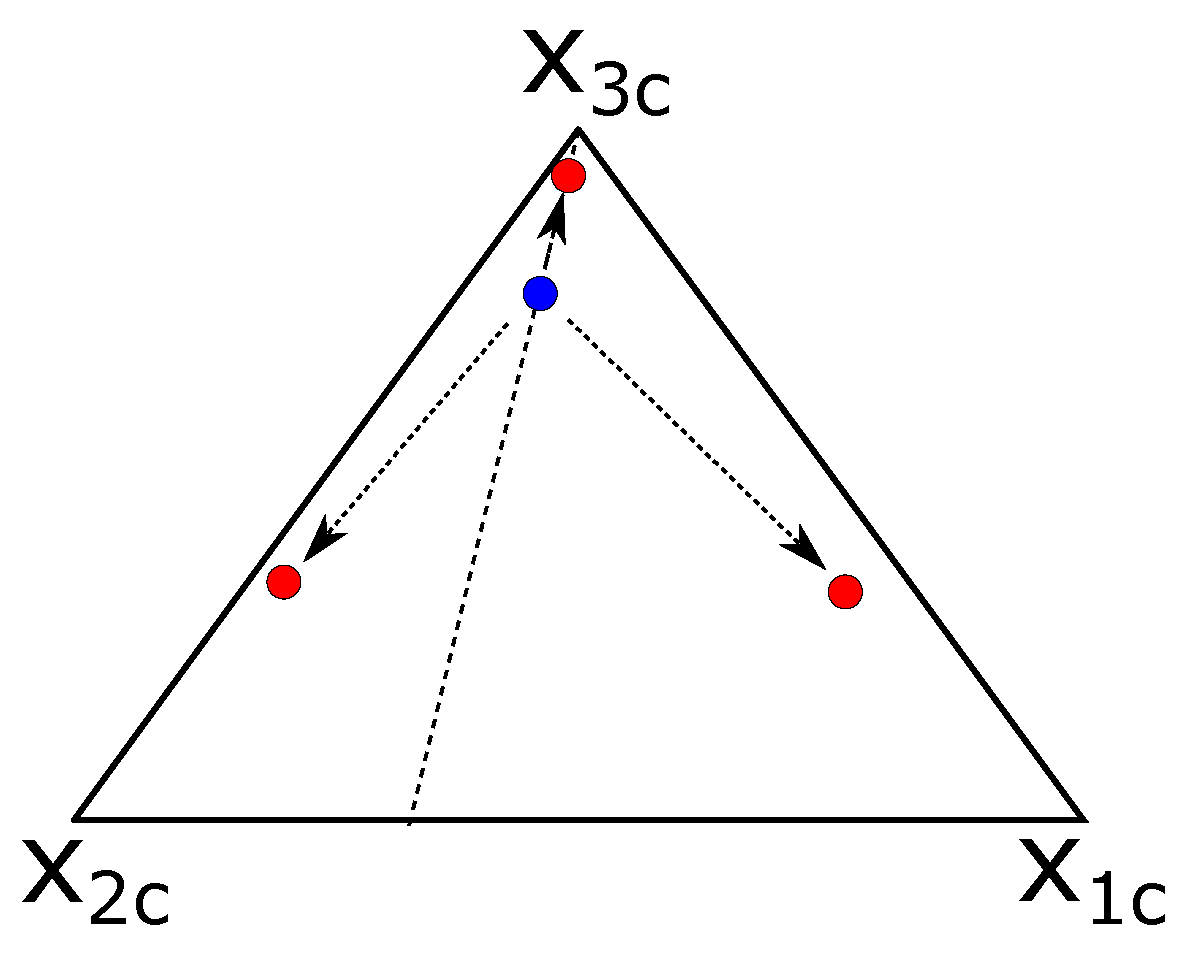
2.3. Perturbation of the Reynolds Stress Tensor
- is the perturbation on the orientation of the Reynolds stresses,
- is the perturbation on the anisotropy of the Reynolds stresses,
- and , is the amplitude of the perturbation of the turbulent kinetic energy. It is established as a range with a minimum and a maximum .
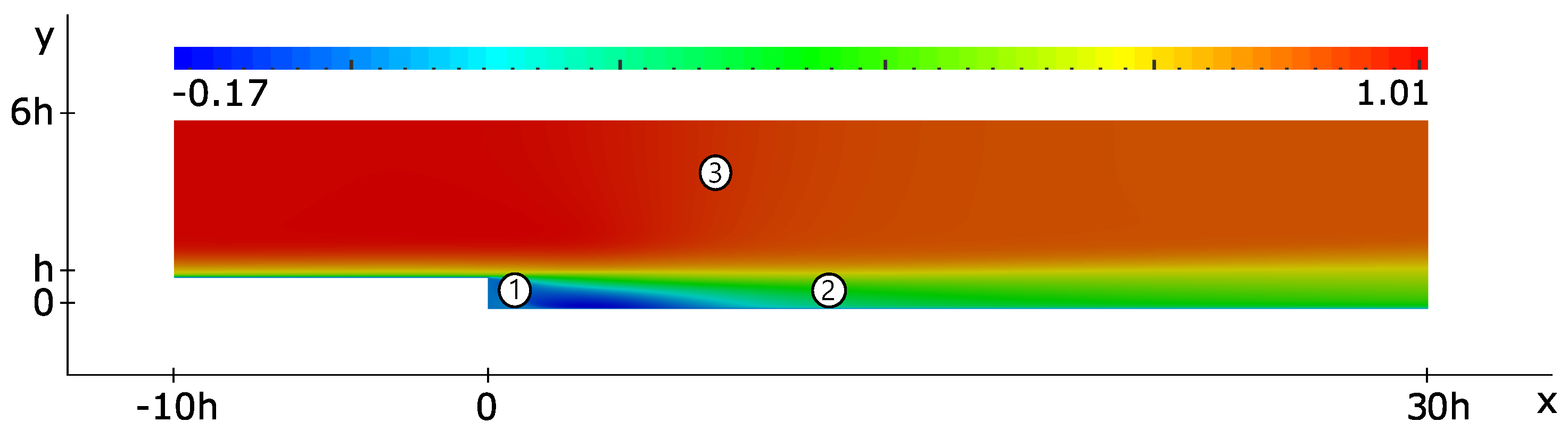
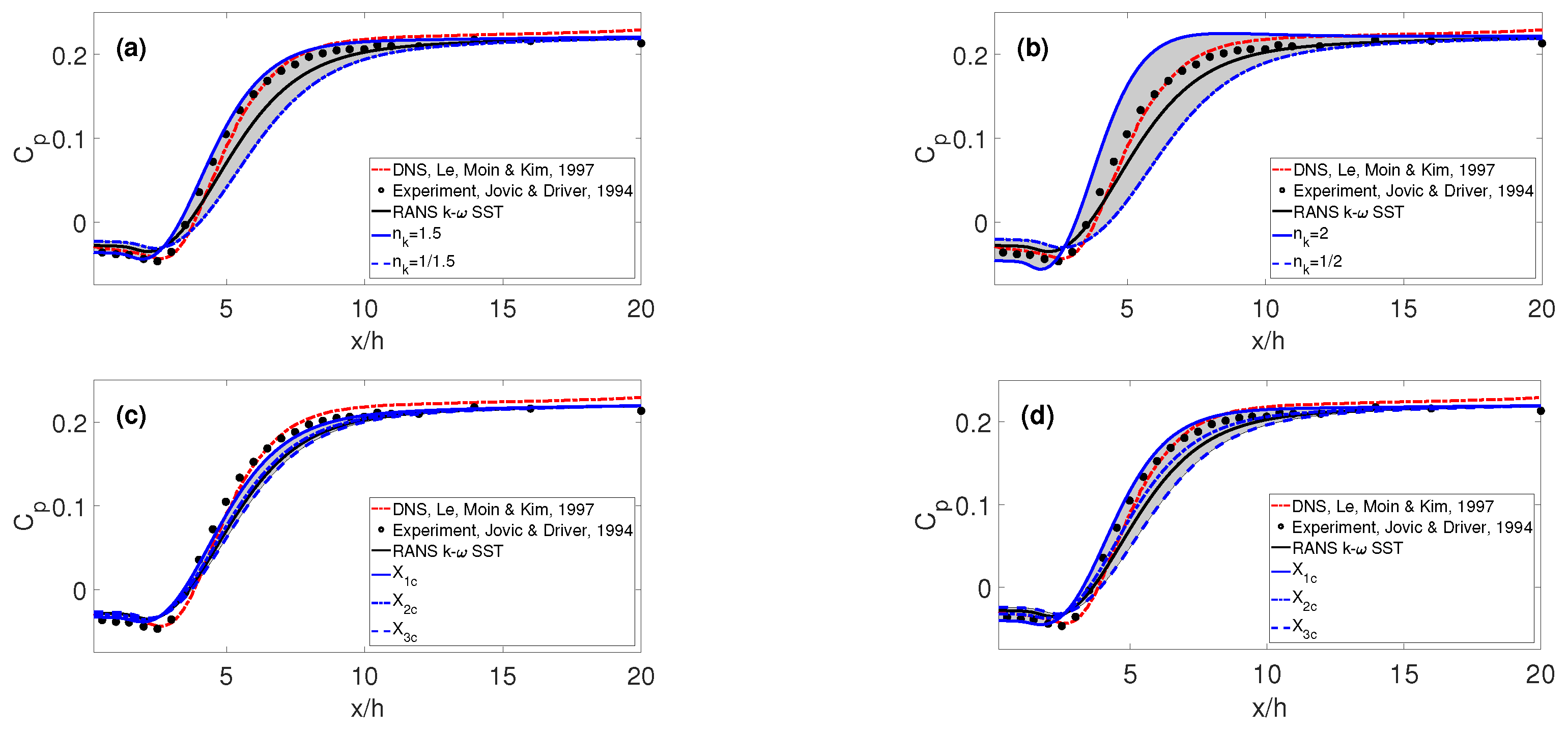
3. Results and Analysis
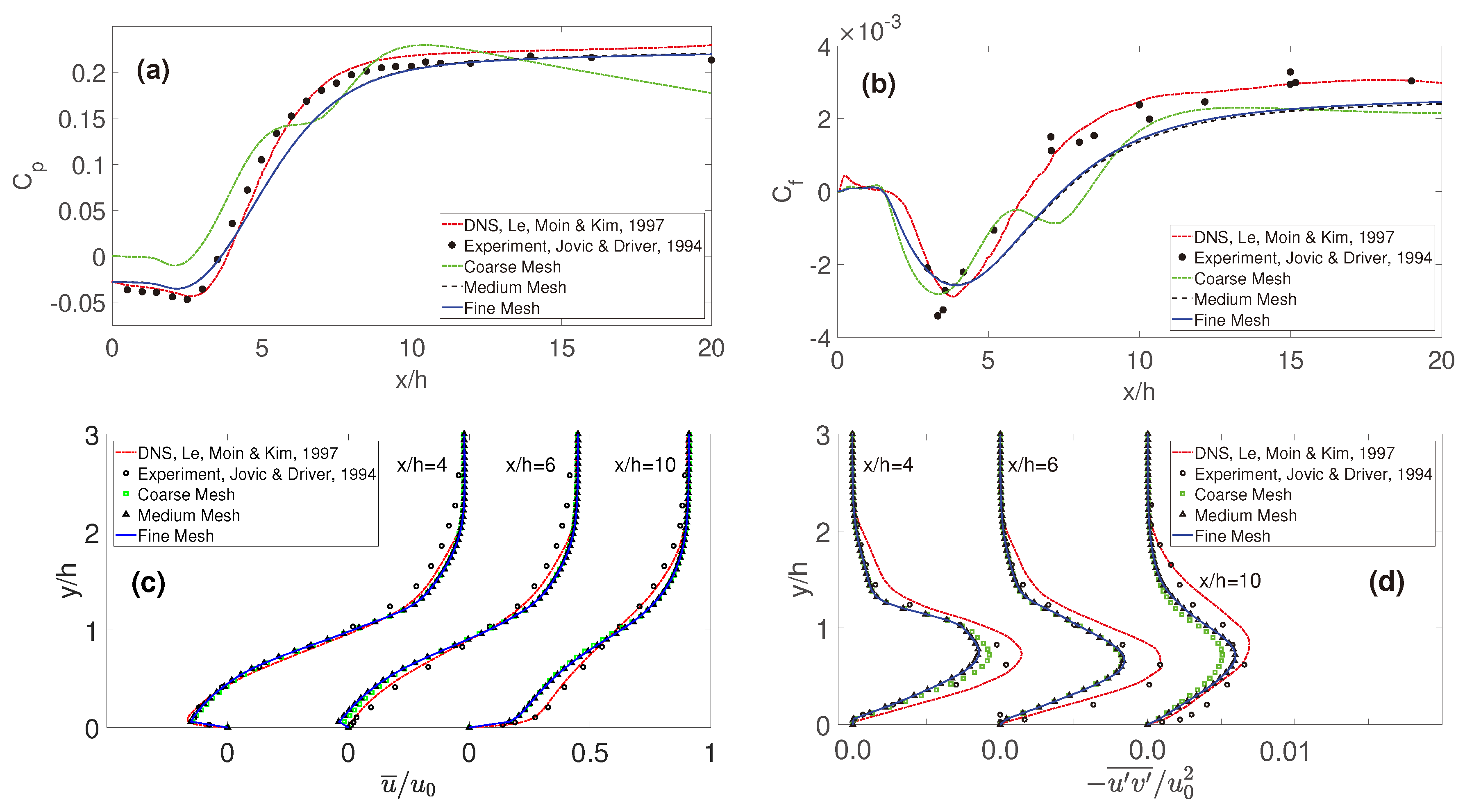
3.1. Pressure Coefficient
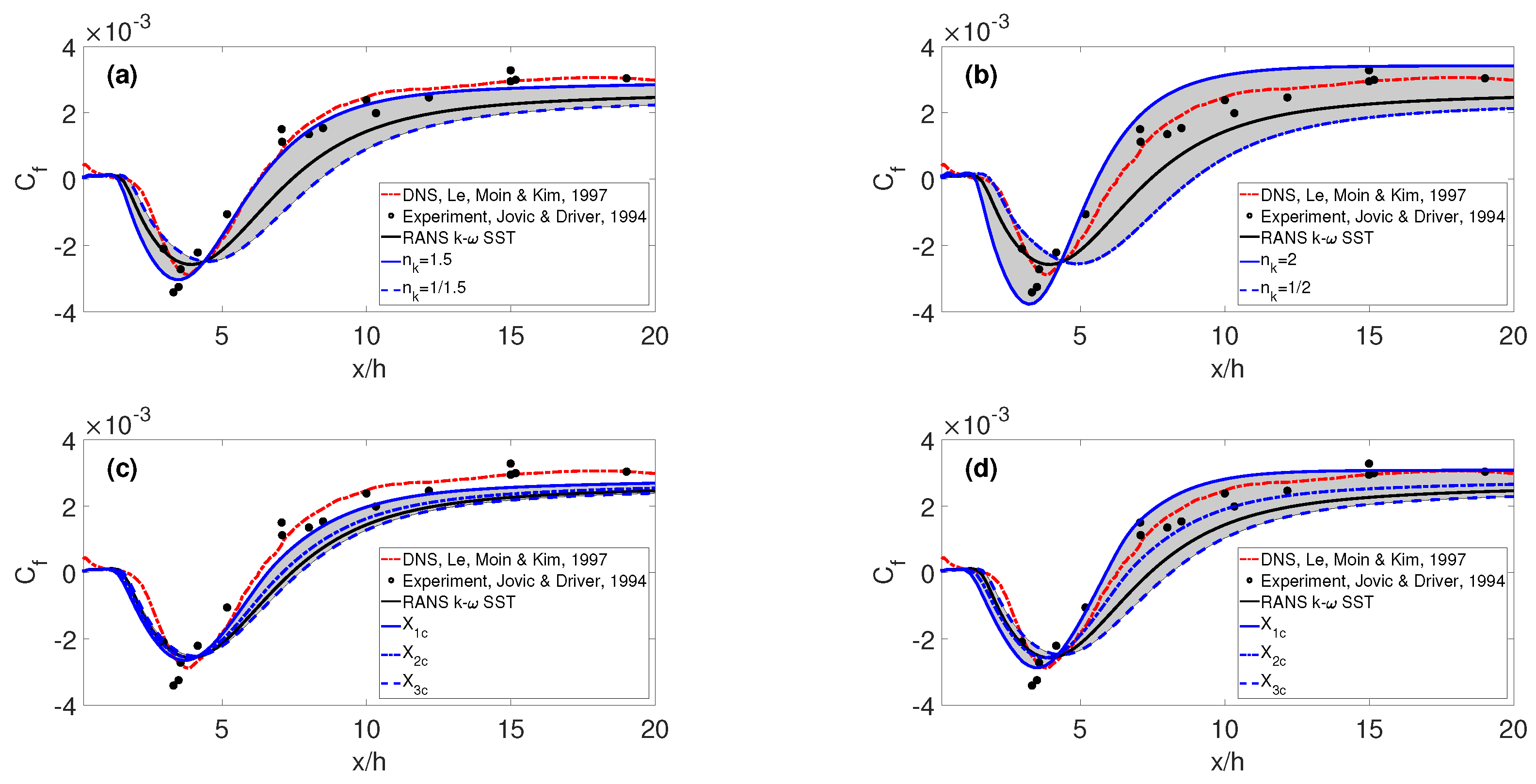
3.2. Friction Coefficient
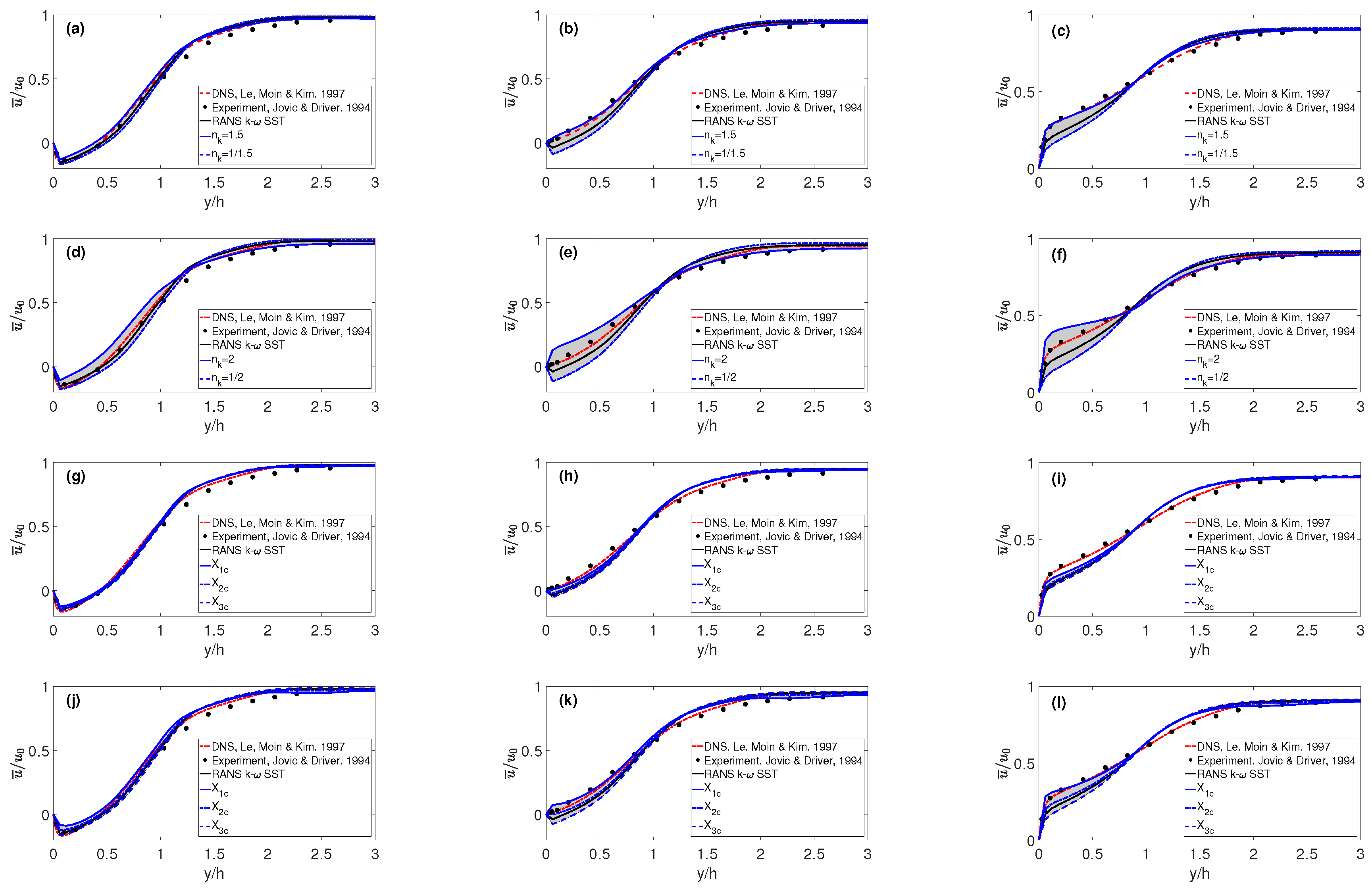
3.3. Mean Velocity in the x-Direction
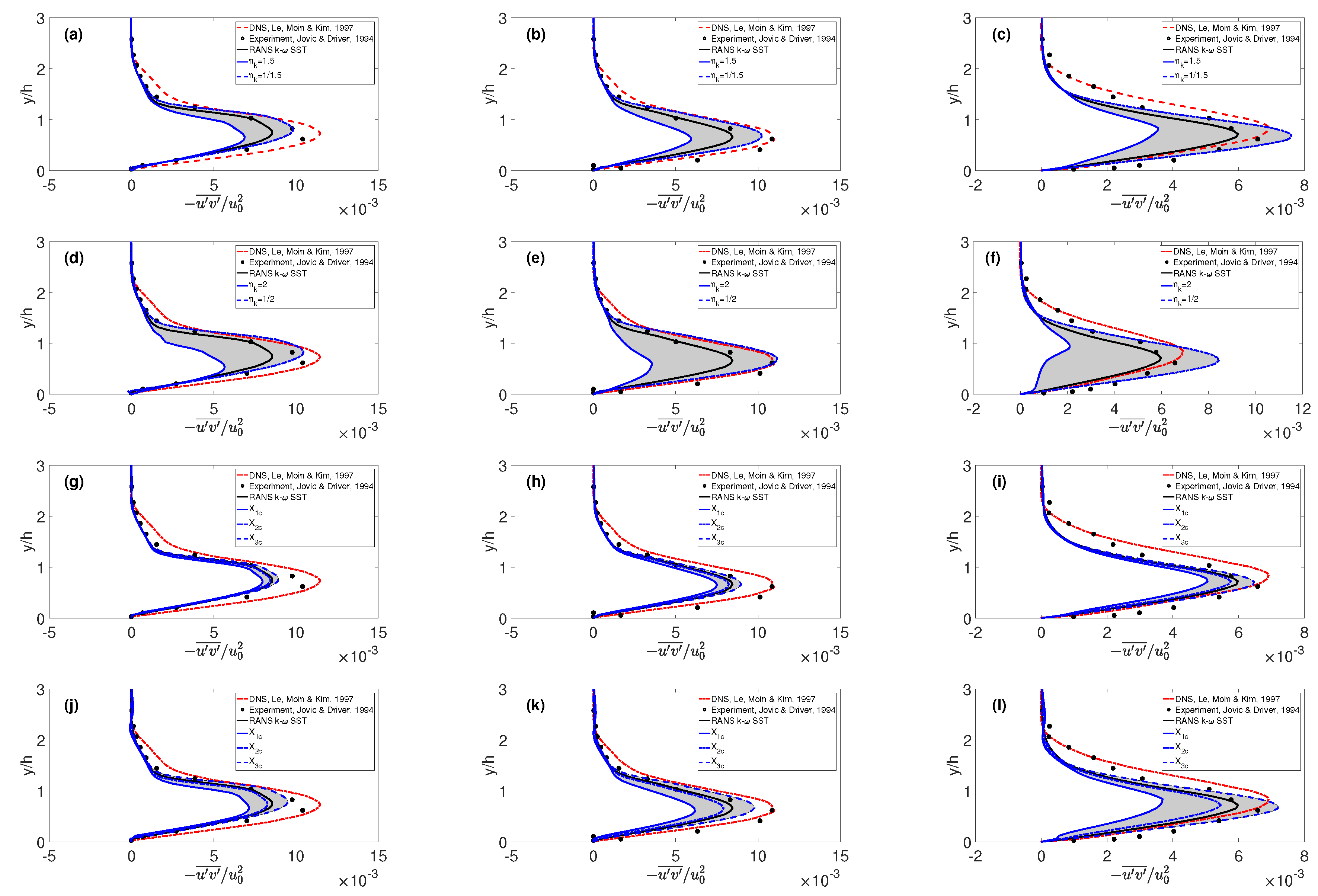
3.4. Reynolds Shear Stress
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
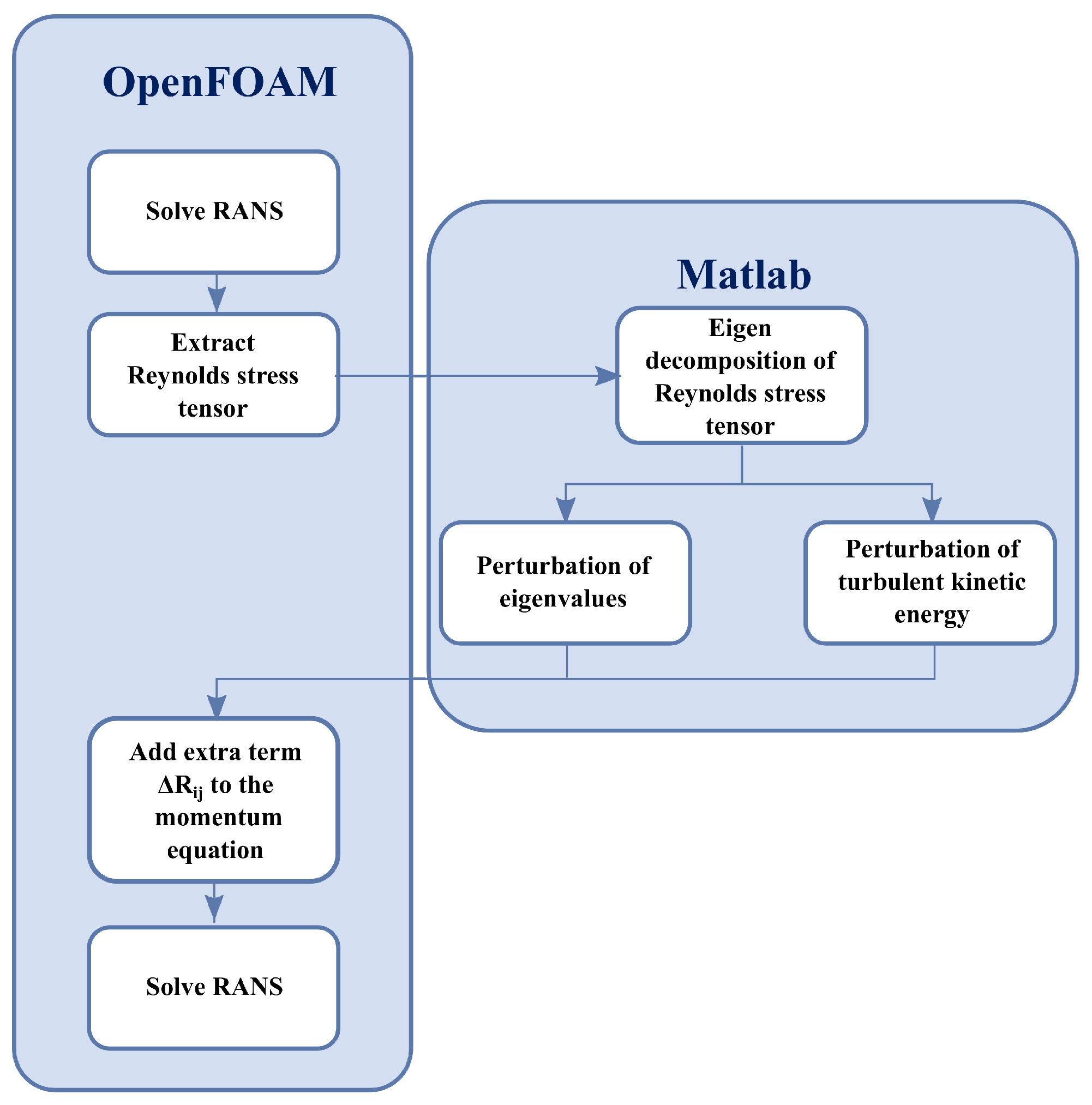
Appendix A. Implementation of the Reynolds Stress Perturbation in OpenFOAM

References
- Emory, J.; Pecnik, R.; Iaccarino, G. Modeling Structural Uncertainties in Reynolds-Averaged Computations of Shock/Boundary Layer Interactions. In Proceedings of the AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 4–7 January 2011; p. 0479. [Google Scholar]
- Banerjee, S.; Krahl, R.; Zenger, C.H. Presentation of anisotropy properties of turbulence, invariants versus eigenvalue approaches. J. Fluid Mech. 2007, 8, N32. [Google Scholar] [CrossRef]
- Gorle, C.; Emory, J.; Iaccarino, G. Epistemic uncertainty quantification of RANS modeling for an underexpanded jet in a supersonic cross flow. In Center for Turbulence Research Annual Research Briefs; Center for Turbulence Research, Stanford University: Stanford, CA, USA, 2011; pp. 147–159. [Google Scholar]
- Gorle, C.; Iaccarino, G. A framework for epistemic uncertainty quantification of turbulent scalar flux models for Reynolds-averaged Navier-Stokes simulations. Phys. Fluids 2013, 25, 055105. [Google Scholar] [CrossRef]
- Gorle, C.; Emory, J.; Larsson, J.; Iaccarino, G. Epistemic uncertainty quantification for RANS modeling of the flow over a wavy wall. In Center for Turbulence Research Annual Research Briefs; Center for Turbulence Research, Stanford University: Stanford, CA, USA, 2012; pp. 81–91. [Google Scholar]
- Emory, J.; Larsson, J.; Iaccarino, G. Modeling of structural uncertainties in Reynolds-averaged Navier-Stokes closures. Phys. Fluids 2013, 25, 110822. [Google Scholar] [CrossRef]
- Iaccarino, G.; Mishra, A.A.; Ghili, S. Eigenspace perturbations for uncertainty estimation of single point turbulence closures. Phys. Rev. Fluids 2017, 2, 024605. [Google Scholar] [CrossRef]
- Le, H.; Moin, P.; Kim, J. Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 1997, 330, 349–374. [Google Scholar] [CrossRef]
- Jovic, S.; Driver, D.M. Backward-facing step measurements at low Reynolds number, Reh = 5000. In NASA Technical Memorandum; Technical Report; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1994; p. 108807. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow, 1st ed.; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Pope, S.B. Turbulent Flows, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 1st ed.; DCW Industries: La Canada, CA, USA, 1993. [Google Scholar]
- Speziale, C.; Abid, R.; Durbin, P. On the realizability of Reynolds stress turbulence closures. J. Sci. Comput. 1994, 9, 369–403. [Google Scholar] [CrossRef]
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Le, H.; Moin, P. Direct numerical simulation of turbulent flow over a backward-facing’ step. In Center for Turbulence Research Annual Research Briefs; Center for Turbulence Research, Stanford University: Stanford, CA, USA, 1992; pp. 161–173. [Google Scholar]
- Spalart, P.R. Direct simulation of a turbulent boundary layer up to ReΘ = 1410. In NASA Technical Memorandum; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1986; p. 89407. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Rumsey, C. Turbulence Modeling Resource. Available online: https://turbmodels.larc.nasa.gov (accessed on 3 May 2019).
- The American Society of Mechanical Engineers (ASME). Standard for Verification and Validation in Computational Fluid Dynamics and Heat Transfer; ASME: New York, NY, USA, 2009. [Google Scholar]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Wu, J.L.; Xiao, H.; Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys. Rev. Fluids 2018, 3, 074602. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Cremades Rey, L.F. Epistemic Uncertainty Quantification of RANS Models. Master’s Thesis, Aarhus University, Aarhus, Denmark, 2018. [Google Scholar]
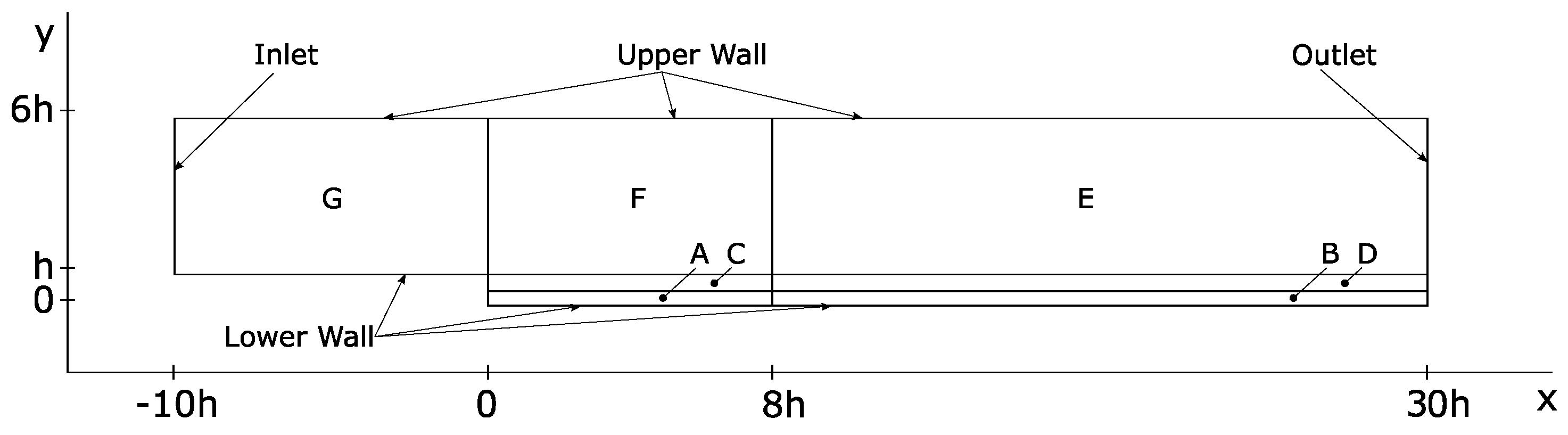

| Boundary | Velocity | Pressure |
|---|---|---|
| Upper Wall | No-stress wall | Zero gradient |
| Lower Wall | No-slip condition | Zero gradient |
| Inlet | Non-uniform inlet | Zero gradient |
| Outlet | Zero gradient | Uniform, |
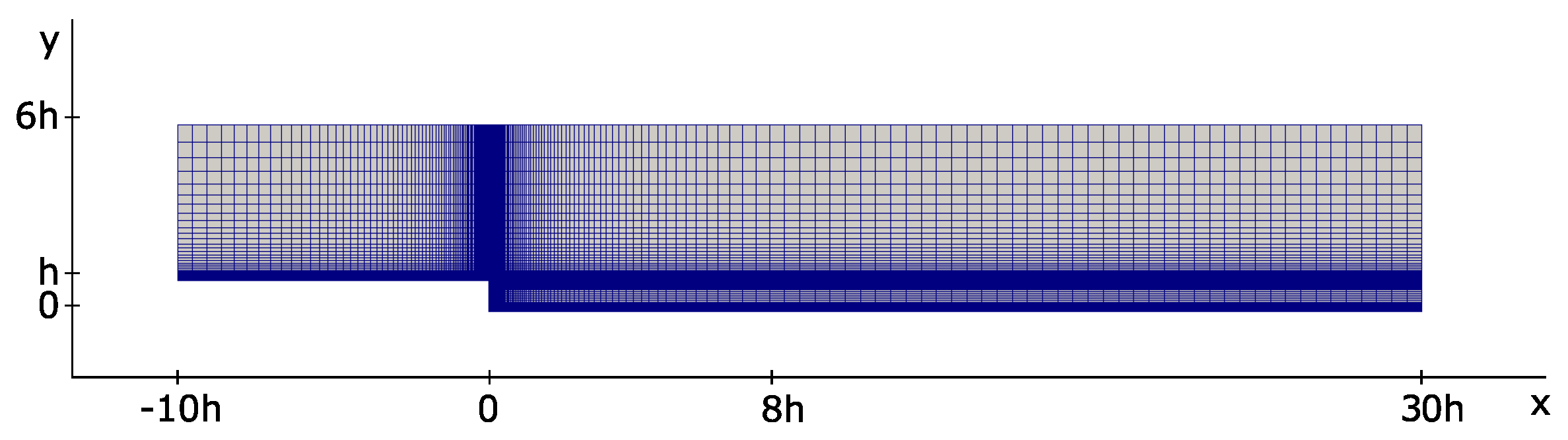
| Coarse Mesh | Intermediate Mesh | Fine Mesh | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cells | Grading | Cells | Grading | Cells | Grading | |||||||
| Block | x | y | x | y | x | y | x | y | x | y | x | y |
| A | 40 | 11 | 50 | 11.29 | 80 | 21 | 50 | 10.61 | 160 | 42 | 50 | 10.91 |
| B | 21 | 11 | 1 | 11.29 | 41 | 21 | 1 | 10.61 | 81 | 42 | 1 | 10.91 |
| C | 40 | 11 | 50 | 0.09 | 80 | 21 | 50 | 0.09 | 160 | 42 | 50 | 0.09 |
| D | 21 | 11 | 1 | 0.09 | 41 | 21 | 1 | 0.09 | 81 | 42 | 1 | 0.09 |
| E | 21 | 20 | 1 | 100 | 41 | 40 | 1 | 100 | 81 | 80 | 1 | 100 |
| F | 40 | 20 | 50 | 100 | 80 | 40 | 50 | 100 | 160 | 80 | 50 | 100 |
| G | 40 | 20 | 0.02 | 100 | 80 | 40 | 0.02 | 100 | 160 | 80 | 0.02 | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cremades Rey, L.F.; Hinz, D.F.; Abkar, M. Reynolds Stress Perturbation for Epistemic Uncertainty Quantification of RANS Models Implemented in OpenFOAM. Fluids 2019, 4, 113. https://doi.org/10.3390/fluids4020113
Cremades Rey LF, Hinz DF, Abkar M. Reynolds Stress Perturbation for Epistemic Uncertainty Quantification of RANS Models Implemented in OpenFOAM. Fluids. 2019; 4(2):113. https://doi.org/10.3390/fluids4020113
Chicago/Turabian StyleCremades Rey, Luis F., Denis F. Hinz, and Mahdi Abkar. 2019. "Reynolds Stress Perturbation for Epistemic Uncertainty Quantification of RANS Models Implemented in OpenFOAM" Fluids 4, no. 2: 113. https://doi.org/10.3390/fluids4020113
APA StyleCremades Rey, L. F., Hinz, D. F., & Abkar, M. (2019). Reynolds Stress Perturbation for Epistemic Uncertainty Quantification of RANS Models Implemented in OpenFOAM. Fluids, 4(2), 113. https://doi.org/10.3390/fluids4020113





