What Can Students Learn While Solving Colebrook’s Flow Friction Equation?
Abstract
1. Introduction
2. Tasks for Students
2.1. Iterative Methods
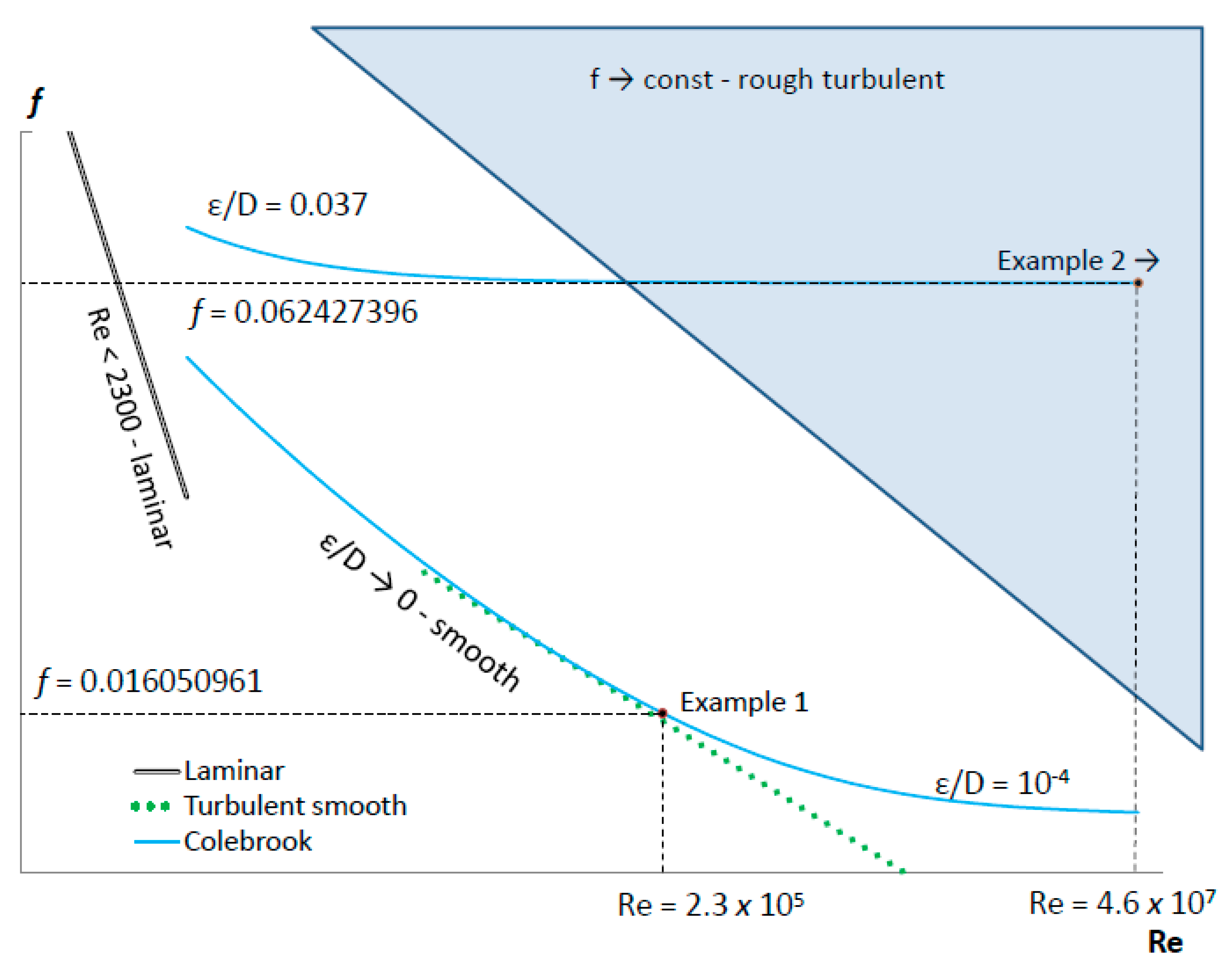
2.1.1. Trial/Error Method
2.1.2. Fixed-Point Iterative Procedure
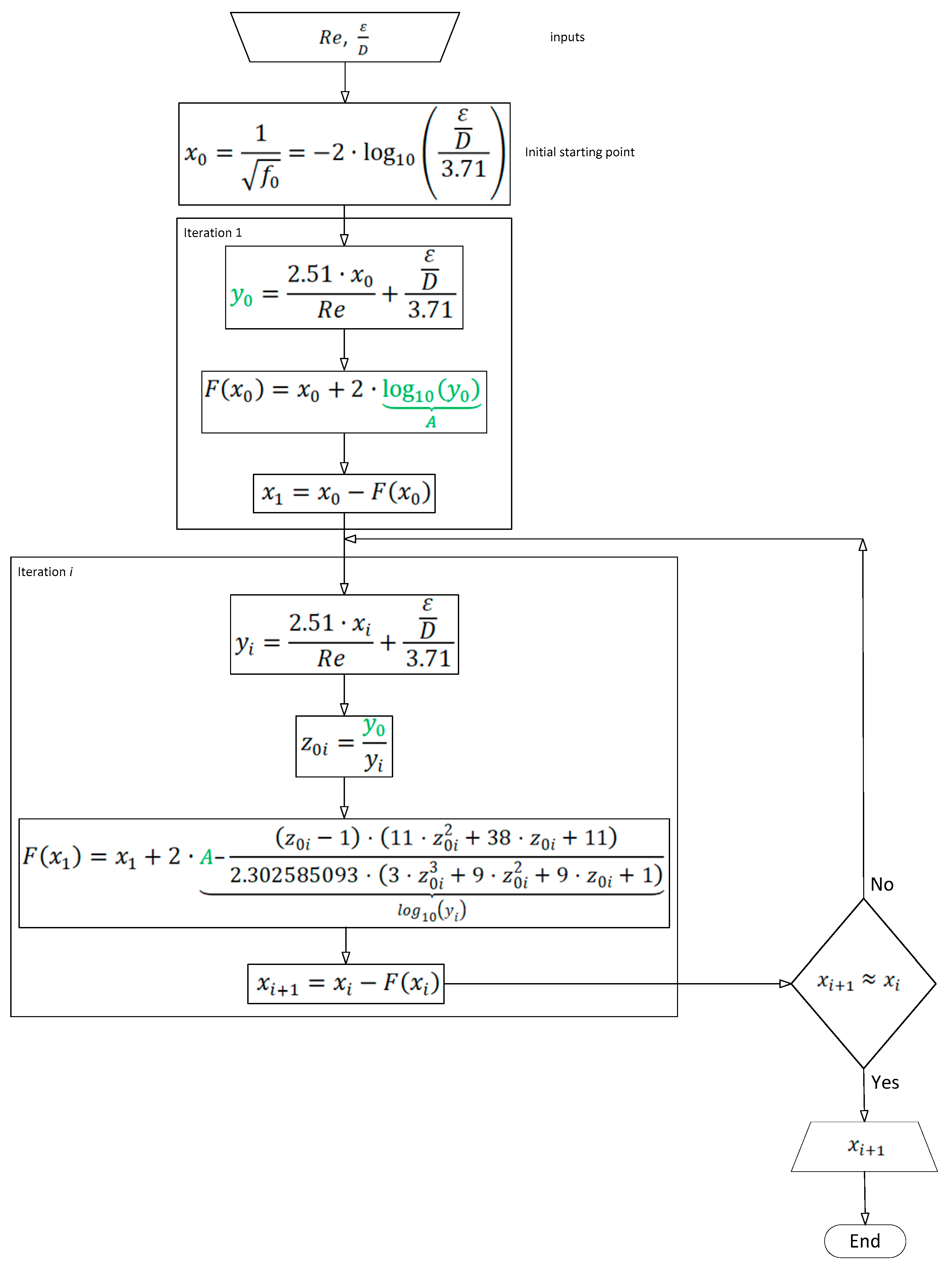
2.1.3. Newton–Raphson Iterative Procedure
2.1.4. Multi-Point Iterative Procedures
2.2. Special Iterative Methods
2.2.1. Padé Approximant
2.2.2. Approximations by Multi-Point Methods with Internal Cycles
2.3. Special Functions
2.3.1. Lambert W Function
2.3.2. Wright ω Function and Related Approximations
2.3.3. Tania Function and Related Approximations
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Colebrook, C.F.; White, C.M. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Hager, W.H. Cedric Masey White and his solution to the pipe flow problem. Proc. Inst. Civ. Eng. Water Manag. 2010, 163, 529–537. [Google Scholar] [CrossRef]
- Keady, G. Colebrook-White formula for pipe flows. J. Hydraul. Eng. 1998, 124, 96–97. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the LambertW function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Hayes, B. Why W? On the Lambert W function, a candidate for a new elementary function in mathematics. Am. Sci. 2005, 93, 104–108. [Google Scholar] [CrossRef]
- More, A.A. Analytical solutions for the Colebrook and White equation and for pressure drop in ideal gas flow in pipes. Chem. Eng. Sci. 2006, 61, 5515–5519. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Choosing the optimal multi-point iterative method for the Colebrook flow friction equation. Processes 2018, 6, 130. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Advanced iterative procedures for solving the implicit Colebrook equation for fluid flow friction. Adv. Civ. Eng. 2018, 2018, 5451034. [Google Scholar] [CrossRef]
- Brkić, D. Determining friction factors in turbulent pipe flow. Chem. Eng. N. Y. 2012, 119, 34–39. [Google Scholar]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Evolutionary optimization of Colebrook’s turbulent flow friction approximations. Fluids 2017, 2, 15. [Google Scholar] [CrossRef]
- Brkić, D. New explicit correlations for turbulent flow friction factor. Nucl. Eng. Des. 2011, 241, 4055–4059. [Google Scholar] [CrossRef]
- Brkić, D. An explicit approximation of Colebrook’s equation for fluid flow friction factor. Pet. Sci. Technol. 2011, 29, 1596–1602. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Improved method of determining friction factor in pipes. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 941–949. [Google Scholar] [CrossRef]
- Pimenta, B.D.; Robaina, A.D.; Peiter, M.X.; Mezzomo, W.; Kirchner, J.H.; Ben, L.H. Performance of explicit approximations of the coefficient of head loss for pressurized conduits. Rev. Bras. Eng. Agrícola Ambient. 2018, 22, 301–307. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Approximate analytical solutions for the Colebrook equation. J. Hydraul. Eng. 2018, 144, 06018007. [Google Scholar] [CrossRef]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar]
- Brkić, D.; Praks, P. Unified friction formulation from laminar to fully rough turbulent flow. Appl. Sci. 2018, 8, 2036. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the implicit Colebrook equation for flow friction using Excel. Spreadsheets Educ. 2017, 10, 2. [Google Scholar]
- Santos-Ruiz, I.; Bermúdez, J.R.; López-Estrada, F.R.; Puig, V.; Torres, L. Estimación experimental de la rugosidad y del factor de fricción en una tubería. In Proceedings of the Memorias del Congreso Nacional de Control Automático, San Luis Potosí, Mexico, 10–12 October 2018; Available online: https://www.researchgate.net/publication/328332798 (accessed on 19 April 2019). (In Spanish).
- Olivares, A.; Guerra, R.; Alfaro, M.; Notte-Cuello, E.; Puentes, L. Experimental evaluation of correlations used to calculate friction factor for turbulent flow in cylindrical pipes. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2019, 35, 15. (In Spanish) [Google Scholar] [CrossRef]
- Olivares Gallardo, A.P.; Guerra Rojas, R.A.; Alfaro Guerra, M.A. Evaluación experimental de la solución analítica exacta de la ecuación de Colebrook-White. Ing. Investig. Tecnol. 2019, 20, 1–11. (In Spanish) [Google Scholar] [CrossRef]
- Zigrang, D.J.; Sylvester, N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J. 1982, 28, 514–515. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Clamond, D. Efficient resolution of the Colebrook equation. Ind. Eng. Chem. Res. 2009, 48, 3665–3671. [Google Scholar] [CrossRef]
- Biberg, D. Fast and accurate approximations for the Colebrook equation. J. Fluids Eng. 2017, 139, 031401. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function. Mathematics 2019, 7, 34. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function: Reply to discussion. Mathematics 2019, 7, 410. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. One-log call iterative solution of the Colebrook equation for flow friction based on Padé polynomials. Energies 2018, 11, 1825. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. An efficient iterative method for looped pipe network hydraulics free of flow-corrections. Fluids 2019, 4, 73. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Short overview of early developments of the Hardy Cross type methods for computation of flow distribution in pipe networks. Appl. Sci. 2019, 9, 2019. [Google Scholar] [CrossRef]
- Brkić, D. Spreadsheet-based pipe networks analysis for teaching and learning purpose. Spreadsheets Educ. 2016, 9, 4. [Google Scholar]
- Brkić, D. A gas distribution network hydraulic problem from practice. Pet. Sci.Technol. 2011, 29, 366–377. [Google Scholar] [CrossRef]
- Brkić, D. Iterative methods for looped network pipeline calculation. Water Resour. Manag. 2011, 25, 2951–2987. [Google Scholar] [CrossRef]
- Brkić, D. An improvement of Hardy Cross method applied on looped spatial natural gas distribution networks. Appl. Energy 2009, 86, 1290–1300. [Google Scholar] [CrossRef]
- Sonnad, J.R.; Goudar, C.T. Constraints for using Lambert W function-based explicit Colebrook–White equation. J. Hydraul. Eng. 2004, 130, 929–931. [Google Scholar] [CrossRef]
- Brkić, D. Comparison of the Lambert W-function based solutions to the Colebrook equation. Eng. Comput. 2012, 29, 617–630. [Google Scholar] [CrossRef]
- Belkić, D. The Euler T and Lambert W functions in mechanistic radiobiological models with chemical kinetics for repair of irradiated cells. J. Math. Chem. 2018, 56, 2133–2193. [Google Scholar] [CrossRef]
- Brkić, D. Lambert W function in hydraulic problems. Math. Balk. 2012, 26, 285–292. [Google Scholar]
- Brkić, D. W solutions of the CW equation for flow friction. Appl. Math. Lett. 2011, 24, 1379–1383. [Google Scholar] [CrossRef]
- Ćojbašić, Ž.; Brkić, D. Very accurate explicit approximations for calculation of the Colebrook friction factor. Int. J. Mech. Sci. 2013, 67, 10–13. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Intelligent flow friction estimation. Comput. Intell. Neurosci. 2016, 2016, 5242596. [Google Scholar] [CrossRef] [PubMed]
- Brkić, D. Discussion of “Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation” by Saeed Samadianfard [J. Pet. Sci. Eng. 92–93 (2012) 48–55]. J. Pet. Sci. Eng. 2014, 124, 399–401. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Symbolic regression-based genetic approximations of the Colebrook equation for flow friction. Water 2018, 10, 1175. [Google Scholar] [CrossRef]
- Ettema, R. Hunter Rouse—His work in retrospect. J. Hydraul. Eng. 2006, 132, 1248–1258. [Google Scholar] [CrossRef]
- Brkić, D. Can pipes be actually really that smooth? Int. J. Refrig. 2012, 35, 209–215. [Google Scholar] [CrossRef]
- Brkić, D. A note on explicit approximations to Colebrook’s friction factor in rough pipes under highly turbulent cases. Int. J. Heat Mass Transf. 2016, 93, 513–515. [Google Scholar] [CrossRef]
- Eaton, J.W. GNU Octave Manual, U.K., Bristol: Network Theory Ltd. 1997. Available online: Ftp://ftp.eeng.dcu.ie/pub/ee454/cygwin/usr/share/doc/octave-2.1.73/pdf/Octave-FAQ.pdf (accessed on 13 June 2019).
- Horchler, A.D. WrightOmegaq: Complex Double-Precision Evaluation of the Wright Omega Function, a Solution of W + LOG (W) = Z. Version 1.0, 3-12-13. Available online: https://github.com/horchler/wrightOmegaq (accessed on 13 June 2019).
- Serghides, T.K. Estimate friction factor accurately. Chem. Eng. N. Y. 1984, 91, 63–64. [Google Scholar]
- Khdhr, F.W.; Saeed, R.K.; Soleymani, F. Improving the computational efficiency of a variant of Steffensen’s method for nonlinear equations. Mathematics 2019, 7, 306. [Google Scholar] [CrossRef]
- Behl, R.; Salimi, M.; Ferrara, M.; Sharifi, S.; Alharbi, S.K. Some real-life applications of a newly constructed derivative free iterative scheme. Symmetry 2019, 11, 239. [Google Scholar] [CrossRef]
- Shacham, M. Comments on: “An explicit equation for friction factor in pipe”. Ind. Eng. Chem. Fundam. 1980, 19, 228–229. [Google Scholar] [CrossRef]
- Romeo, E.; Royo, C.; Monzón, A. Improved explicit equations for estimation of the friction factor in rough and smooth pipes. Chem. Eng. J. 2002, 86, 369–374. [Google Scholar] [CrossRef]
- Offor, U.H.; Alabi, S.B. An accurate and computationally efficient explicit friction factor model. Adv. Chem. Eng. Sci. 2016, 6, 66711. [Google Scholar] [CrossRef]
- Barry, D.A.; Parlange, J.Y.; Li, L.; Prommer, H.; Cunningham, C.J.; Stagnitti, F. Analytical approximations for real values of the Lambert W-function. Math. Comput. Simul. 2000, 53, 95–103. [Google Scholar] [CrossRef]
- Boyd, J.P. Global approximations to the principal real-valued branch of the Lambert W-function. Appl. Math. Lett. 1998, 11, 27–31. [Google Scholar] [CrossRef]
- Demir, S.; Duman, S.; Demir, N.M.; Karadeniz, A. An MS Excel add-in for calculating Darcy friction factor. Spreadsheets Educ. 2018, 10, 2. Available online: https://sie.scholasticahq.com/article/4669 (accessed on 12 May 2019).
- Fukushima, T. Precise and fast computation of Lambert W-functions without transcendental function evaluations. J. Comput. Appl. Math. 2013, 244, 77–89. [Google Scholar] [CrossRef]
- Kouznetsov, D. Doya Function and Tania Function. Available online: http://www.ils.uec.ac.jp/~dima/PAPERS/2013taniadoya.pdf (accessed on 12 May 2019).
- Stewart, S. A new elementary function for our curricula? Aust. Sr. Math. J. 2005, 19, 8–26. Available online: https://files.eric.ed.gov/fulltext/EJ720055.pdf (accessed on 12 May 2019).
- Pal, R. Teaching Fluid Mechanics and Thermodynamics Simultaneously through Pipeline Flow Experiments. Fluids 2019, 4, 103. [Google Scholar] [CrossRef]
- Barreras, F.; López, A.M.; Lozano, A.; Barranco, J.E. Experimental study of the pressure drop in the cathode side of air-forced open-cathode proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2011, 36, 7612–7620. [Google Scholar] [CrossRef]
- Brkić, D. Comments on “Experimental study of the pressure drop in the cathode side of air-forced open-cathode proton exchange membrane fuel cells” by Barreras et al. Int. J. Hydrog. Energy 2012, 37, 10963–10964. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brkić, D.; Praks, P. What Can Students Learn While Solving Colebrook’s Flow Friction Equation? Fluids 2019, 4, 114. https://doi.org/10.3390/fluids4030114
Brkić D, Praks P. What Can Students Learn While Solving Colebrook’s Flow Friction Equation? Fluids. 2019; 4(3):114. https://doi.org/10.3390/fluids4030114
Chicago/Turabian StyleBrkić, Dejan, and Pavel Praks. 2019. "What Can Students Learn While Solving Colebrook’s Flow Friction Equation?" Fluids 4, no. 3: 114. https://doi.org/10.3390/fluids4030114
APA StyleBrkić, D., & Praks, P. (2019). What Can Students Learn While Solving Colebrook’s Flow Friction Equation? Fluids, 4(3), 114. https://doi.org/10.3390/fluids4030114





