Abstract
A method for shock capturing by adaptive filtering for use with high-resolution, high-order schemes for Large Eddy Simulations (LES) is presented. The LES method used in all the examples here employs the Explicit Filtering approach and the spatial derivatives are obtained with sixth-order, compact, finite differences. The adaptation is to drop the order of the explicit filter to two at gridpoints where a shock is detected, and to then increase the order from 2 to 10 in steps at successive gridpoints away from the shock. The method is found to be effective in a series of tests of common inviscid 1D and 2D problems of shock propagation and propagation of waves through shocks. As a prelude to LES, the 3D Taylor–Green problem for the inviscid and a finite viscosity case were simulated. An assessment of the overall performance of the method for LES was carried out by simulating an underexpanded round jet at a Reynolds number of 6.09 million, based in centerline velocity and diameter at nozzle exit plane. Very close quantitative agreement was found for the development of centerline mean pressure when compared to experiment. Simulations on several increasingly finer grids showed a monotonic extension of the computed part of the inertial range, with little change to low frequency content. Amplitudes and locations of large changes in pressure through several cells were captured accurately. A similar performance was observed for LES of an impinging jet containing normal and curved shocks.
1. Introduction
Large eddy simulation (LES) has now become a widely-used technique. The greater expense in computing resources and time is justified when it provides accurate solutions, especially when the more common RANS (Reynolds-averaged Navier–Stokes) methods yield qualitatively incorrect solutions. From this general experience, practitioners have come to rely on their own set of procedures—combinations of numerical method and sub-grid-scale (SGS) model—that they have found to be reliable and accurate. Thus, several models co-exist, including the explicit filtering method. This paper concerns a proposal to extend explicit filtering to compressible flows with shocks by filter adaptation. Our results, from a sequence of elementary problems leading to a general turbulent flow of an underexpanded jet, reveals its excellent potential.
A recent review of methods for direct numerical simulation (DNS) and LES of compressible flows with shocks was provided by Pirozzoli [1]. There have been many efforts to devise methods that could handle shocks in inviscid flows—to incorporate procedures or terms to obtain correctly the jumps across shocks, and suppress oscillations at these jumps to avoid instability. The successes have carried over to RANS computations as well. However, specific assessments of shock-capturing methods for DNS/LES are far fewer, even though methods found to be successful for inviscid flows have been employed for DNS/LES. Pirozzoli [1] noted that such methods “exhibit excessive numerical viscosity” when combined with high-order methods designed for DNS/LES of smooth flows, and suggests that an optimal hybrid is needed for DNS/LES of flows with shocks. Typical hybrid schemes switch to a shock-capturing scheme where indicated by a shock sensor, and over a small set of neighboring gridpoints. Some examples are studies that employed a sixth-order compact scheme switching to sixth-order essentially non-oscillatory (ENO) near the shock [2], compact upwind with fifth-order ENO [3], and a fifth-order compact upwind with seventh-order weighted essentially non-oscillatory (WENO) [4]. An alternative to discontinuous switching is to apply the same discretization scheme with a continuously variable coefficient that adds artificial dissipation near shocks and nearly vanishes in smooth regions [5]. Cook and Cabot [6,7] proposed an artificial stress tensor with both shear and bulk viscosity. The generalization is to use artificial thermal conductivity and species diffusivity as well [8]. It was observed that artificial bulk viscosity provided shock capturing without affecting the vorticity field, but artificial shear viscosity damped vortical fluctuations. These artificial properties were scaled with high-order derivatives of the flow field and are therefore continuous, but rapidly changing, functions. Artificial diffusivity may also be suitable for dealing with other types of large derivatives (e.g., mixing of fluids with large density differences) [9].
A recent examination of these several approaches by Johnsen et al. [10] did not find any of the methods to be completely satisfactory: WENO provides sharp shocks but overwhelms physical dissipation; artificial viscosity works well when shocks are not too close to each other, but can be excessive when there are multiple shocks in the turbulent flow; and all methods exhibit post-shock oscillations. It would thus appear that there is still a need to study variants and other strategies that may yield reliable and accurate solutions. In this paper, we present studies with adaptive filtering. It is a natural extension for the explicit filtering approach of Mathew et al. [11] because spatial, low-pass filtering of transported fields after every time-step is an indispensable part of this LES method. The extension is to change the filter-order alone in the vicinity of shocks. An advantage is that there is no discontinuity due to switching numerical schemes since the same scheme is used. Visbal and Gaitonde [12] examined this strategy. They compared results of two proposals against a standard. In one, a 10th-order filter was applied at gridpoints away from shocks, while at the shock and at adjacent (buffer) points the filter formula was dropped to second order, but with a very high filter cutoff. At successive gridpoints away from the shock, filter order increased in steps to 10th order. In the second method, the Roe scheme was applied at cells spanning the shock and adjacent ones. Test cases included 1D and 2D inviscid flows and shock reflection from a laminar boundary layer. They found that their adaptive filter method provided a significant improvement—oscillation-free solution—over their baseline filter-stabilized compact scheme, but shocks were smeared over a few cells; the hybrid compact-Roe scheme gave sharper shocks.
To the best of our knowledge, no further studies or applications of this technique have appeared. However, the method is appealing for its simplicity and minimal overhead, thus seemed worth re-visiting. Although the study reported here also employed filter-order adaptation, the adaptation stencil is different. Here, as explained in Section 2.2, the lowest order filter was applied at only one adjacent buffer point; adaptation in a direction was selected only when the angle between the coordinate direction and the normal to the shock was not too large. Results from tests with usual problems for shock capturing, and LES of two turbulent jets with multiple shock cells show much promise. A possible criticism of this method is that the filtering seems to be ad hoc—none of filter type, shape, or filter cut-off was obtained by some kind of optimization. We argue below that optimization to arrive at the best filter is possible, but perhaps not essential.
Filter adaptation was tested in Bogey and Bailly [13] as well. Near shocks, they applied an optimized, explicit second-order filter whose filter response function lies between those of standard second- and fourth-order explicit filters. They varied the extent of the region where the lower-order filter was applied. Test cases of 1D and 2D inviscid flows were presented.
In the following, first, we discuss the basic numerical method (sixth-order, Hixon–Turkel split compact scheme for spatial derivatives, and fourth-order Runge–Kutta for time-stepping) and the proposal for filter adaptation. Then, results of a sequence of 1D and 2D inviscid test cases are presented, followed by those for the Taylor–Green problem, and LES of underexpanded, free and impinging, round jets. The five inviscid test cases reveal accurate evolution of the flow and crisp shock-capturing. Quantitative errors are at least as small as other recent strategies. The Taylor–Green problem is included to record the correctness of the code for viscous flows that develop a wide range of scales, as well as the effectiveness as LES for the inviscid case. With these elements of flows completed, we turned to LES of supersonic jets at Reynolds numbers of (based on jet diameter and jet velocity at the nozzle exit). These are representative of applications where LES is needed since DNS is prohibitive. With the free underexpanded jet, which develops a series of shock cells, we observed close quantitative agreement with measured centerline pressure on a grid of about nine million points. By simulating on successively larger grids, up to 200 million points, we observed the extension of the computed part of the inertial range, with little change to low frequency content. The present proposal for shock capturing by adaptive filtering showed no discernible adverse effects on the development over several shock cells. The second LES of an impinging jet provides further support for the method as a suitable approach for applications.
2. Numerical Method
The governing equations for compressible flow were cast in the strong conservation form
in a curvilinear coordinate system . Here, , and is the vector of conserved variables with density , Cartesian velocity components , and energy ; p is the pressure; and is the specific heat ratio. is the Jacobian of the transformation between Cartesian and curvilinear coordinate systems. ,, and include inviscid and viscous fluxes (see, for example, Tannehill et al. [14]). The fluid is Newtonian, with viscosity as per Sutherland’s law, Fourier’s law for conduction applies, the Prandtl number is 0.7, , and specific heat .
LES Model
The explicit filtering approach of Mathew et al. [11] was used for the LES presented here. The essential requirements of this approach are that the numerical method used should consist of high-resolution spatial approximations, and that a spatial, high-resolution, low-pass filter be applied to transported fields after every time step. The high-resolution numerical method should ensure that the evolution of a range of low wavenumber content is obtained accurately, while the high-resolution filter removes only a small range of the smallest computed scales. Examples of high resolution numerical methods are those that use spectral, implicit difference, or high-order explicit difference methods for derivative evaluations. Typically, implicit difference formulas, also known as compact difference formulas, have better resolution properties compared to explicit differences of the same order [15]. If explicit formulas are used instead of compact differences, they should be of higher order, and would require large stencils [16]. Here, a procedure that is approximately equivalent to a sixth-order compact scheme was used for first derivatives. Its resolution characteristics can be noted from its modified wavenumber curve (6/2 curve) plotted in Figure 1a. Filter response functions of several implicit filters of different orders and values of filter parameter are shown in Figure 3a. Either high values of the filter parameter, or high order, results in a flat response (negligible filtering) over a range of low wavenumbers. The arguments for the correctness of this approach have been given before [11,17]. LES of many different kinds of flows, by at least two other groups [18,19] who applied essentially this approach, are available. Although originally devised for high accuracy by using compact schemes [18], or unusually high-order explicit differences [16], with high wavenumber filtering for stability, the authors then demonstrated that these methods were suitable for LES. The performance of computations with our method for incompressible, variable density and compressible flows has also been documented [20,21,22].
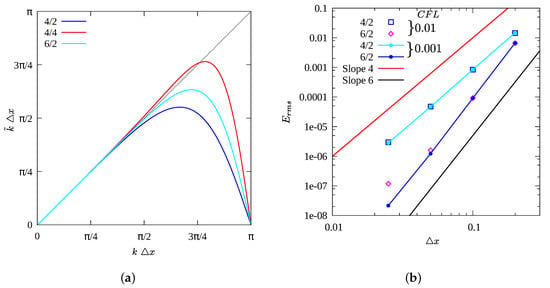
Figure 1.
(a) Modified wavenumber characteristics of Hixon–Turkel split derivative formulas. (b) Effective orders of truncation error. (a) Modified wavenumber, (b) Order behavior.
2.1. Spatial Discretization
As noted above, an essential requirement of the LES approach adopted here is the use of high-resolution numerical schemes. While resolution quality of difference formulas increases with order, implicit difference formulas have smaller resolution error for a given order. Here, we use an extension to sixth order of the splitting proposed by Hixon and Turkel [23]. A sixth-order compact difference formula is
where is the first derivative of the function . A MacCormack-like splitting
leads to the two relations
When
, , but . In their terminology, this would be a 6/2 scheme [23]. Equation (2) leads to a tridiagonal system, whereas Equations (4) and (5) form bidiagonal systems. Instead of finding derivatives as the mean of and , we use either alone as the estimate of the derivative in successive evaluations. Tests showed that the higher-order truncation error was obtained when the time discretization error was small enough. The great advantage in splitting is that the number of operations per derivative, per time step is roughly halved, which is a tremendous saving for an LES or DNS.
Figure 1 shows the modified wavenumber of the 6/2 scheme. The fourth-order schemes 4/2 and 4/4 that Hixon and Turkel [23] studied are also shown. The 4/2 scheme has a first-order truncation error for each split part, while 4/4 was designed for this error to be third order. To demonstrate that higher-order behavior can be realized, we show the fall in error in solutions of the linear wave equation with unit phase speed after unit time over the region [0,5]. The initial condition was the Gaussian . Solutions were obtained on grids with spacing 1/5, 1/10, 1/20 and 1/40, and fourth-order Runge–Kutta time integration with CFL numbers 0.01 and 0.001. The fall in rms of the difference between numerical solutions and the exact solution is shown in Figure 1b. Solutions with the fourth-order (4/2) and sixth-order (6/2) schemes and lines with Slopes 4 and 6 are shown for reference. Clearly, the order behavior of the equivalent symmetric compact scheme has been recovered. Due to time-stepping error, the decay rate reduces at the higher CFL for the sixth-order scheme.
2.2. Treatment of Regions with Shocks
An essential requirement of shock capturing methods is that the growth of oscillations in the vicinity of the shock must be prevented. Visbal and Gaitonde [12] proposed an adaptive filtering strategy, but do not seem to have pursued it further. It is an attractive strategy because it requires but a simple modification of coefficients of a filter that is anyway applied for the LES. A 2Nth-order implicit filter (denoted filter F2N) is represented by the relation
connecting filtered and unfiltered vectors, and f, respectively. As filter order increases, the response function becomes flatter at low wavenumbers. As filter parameter is increased the spectral content of the function that is filtered out is over a smaller range of high wavenumbers.
The explicit filtering LES sub-grid-scale (SGS) model prescribes that transported variables be filtered with a high-resolution, low-pass, spatial filter after every time-step [11]. Accordingly, filter F10 was applied to all transported fields in all three directions, after every timestep, for LES of flows without shocks. When there are shocks, filters of different orders were applied in the vicinity of the shock. The effectiveness of the adaptive filter is dependent on the shock sensor. In fact, both a review [1] and an assessment of methods [10] emphasize its importance in achieving good results. Pirozzoli [1] examined the effectiveness of four types of sensors. The Ducros sensor [24] selected only the shock, whereas other sensors selected parts of regions without shocks as well. Here, the sensor proposed by Bhagatwala and Lele [25] was used. A shock was considered to be near a gridpoint if
From our numerical experiments, was found to work well for various flows containing Mach waves to strong normal shocks. After a gridpoint was detected as being “in” a shock, the inclination of the shock was determined to ensure filter adaptation was in required directions only. The filter was adapted along a coordinate direction i if or at that point, where is the unit vector along the ith coordinate direction. The second-order filter F2 was applied at that point and at the two neighboring points. Filter order was increased progressively from 2 to 10, from shock to the smooth region, as shown in Figure 2a for a single shock and Figure 2b for multiple nearby shocks. Then, all filter stencils (F4–F10) include the point detected by the shock sensor, but do not straddle that point.
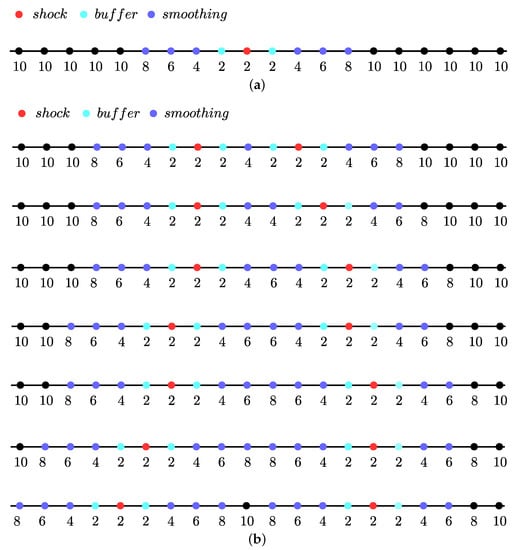
Figure 2.
Scheme for changing filter order near isolated and proximate shocks: (a) isolated shock; and (b) proximate shocks.
By testing with a normal shock, Visbal and Gaitonde [12] determined that filter order had to be reduced to 2 to prevent the appearance of wiggles. However, the filter parameter could be set to a high value . From a large number of our own tests, we found the following parameter-order combinations to provide wiggle-free shocks in several different simulations: filter parameter for filter F2; 0.48 for F4; and 0.498 for F6, F8 and F10. Filter response functions of filters of various orders are shown in Figure 3a. Higher-order filters, F6–F10, remove very little of the solution over a small range of the largest represented wavenumbers. A larger value of filter parameter for F2 may improve solutions in some cases as discussed in Section 3.1. Another comparison of filter characteristics that accentuates low wavenumber differences is obtained by plotting damping functions (Figure 3b).
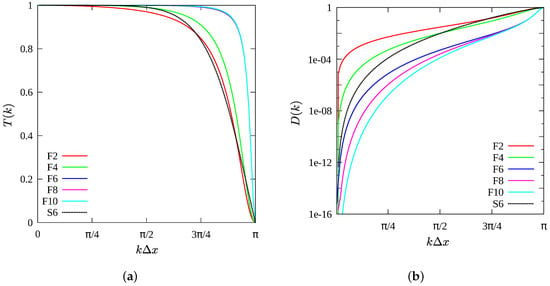
Figure 3.
Response and damping functions of filters and scheme. F2–F10 are filters of various orders, and S6 is the sixth-order difference scheme. Filter parameters: and . (a) Filter response functions; and (b) filter damping functions.
The resolution error of a derivative formula is . To compare with filter characteristics, the function of the 6/2 derivative scheme has been included in Figure 3a, and in Figure 3b. Even when filter F2 is applied, its significant effects are over a high wavenumber range comparable to that of the sixth-order derivative formula. A formal optimization to obtain filter parameters was not carried out. It has been our practice to use the values listed above for new problems as long as stable solutions are obtained. Solution accuracy improves readily with grid refinement, thus it has not seemed worthwhile to implement formal optimization procedures, which may be problem dependent, especially when multiple interacting shocks are present.
The second-order explicit Runge–Kutta scheme was used for the time integration. For simplicity, let us write the 1D version of Equation (1) in the form , where and are the inviscid and viscous fluxes, respectively. Then, the field at time-step is obtained from the field at as follows:
with,
The superscripts F and B signify the use of forward and backward relations (Equations (4) and (5)), respectively. The expressions above can be denoted an FBBF rule. During integration, the sequence is alternated after every time step, i.e., if FBBF is used at a time step, then at the following time step the relations are BFFB.
3. Basic Tests
Several tests were conducted to understand effects of adapting filtering in flows with shocks and simple fluctuations. The first three are Riemann problems and the following two are of shocks interacting with 1D and 2D waves sinusoidal incident waves.
3.1. Riemann Problems
Sod’s conditions for a 1D Riemann problem is a common example. The initial pressure ratio is 10 and density ratio is 8 across the initial discontinuity. The fluid is air. In the simulations, viscosity , and conduction terms also vanish. Grid spacing . The numerical solution at is displayed as the density distribution in Figure 4a, with the analytical solution for comparison. The filter order at the same gridpoints are also shown. Figure 4b shows the solution to Lax’s shock problem. The initial conditions were , and for , and , and for . The solution is everywhere very close to the exact solution. For both problems, grid spacing and times at which their solutions have been presented are the same as those in Kawai and Lele [26] for direct comparison against their artificial diffusivity solutions. They found that artificial viscosity was enhanced at the shock and at the ends of the expansion, and artificial conductivity was enhanced at the shock and contact surface. Here, filter order changes are near the shock only. Small oscillations and a slight smearing at the shock are evident in the solution of the Lax problem.
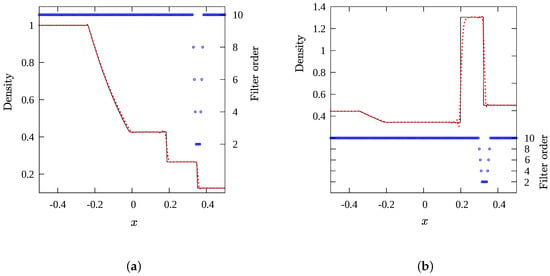
Figure 4.
Solution of shock tube problems. exact (——), numerical (– – –), filter order (•); and . (a) Sod’s problem at t = 0.2; and (b) Lax’s problem at t = 0.13.
The third basic test is with a 2D Riemann problem listed as Case 13 by Lax and Liu [27]. Initial conditions in the four quadrants are listed in Table 1. These conditions imply that there are shocks along the line which move to but at different speeds, and a slip line along . This case was used by Pirozzoli [1] to illustrate the relative performance of standard and hybrid WENO schemes. Figure 5a shows the density distribution at time on a grid with . Gridpoints where filter order has been lowered for treatment of shocks are marked in Figure 5b; where shocks are nearly perpendicular to the y-axis, adaptation is along y only. The shocks are crisp. The vortex sheet is unstable to perturbations of any wavelength. Here, the rolled-up vortices seen along the slip line are selected by the grid spacing, which selects the smallest wavelength. Owing to the high-resolution derivative formula and restriction of low-order filtering to the vicinity of shocks, there is no discernible smearing of the vortices along the slip line. Flow features, especially shock locations, agree closely with the solution given in Lax and Liu [27] using their scheme. Shocks are sharper in the present solution. In their solution, the slip line is thicker and, understandably for an inviscid scheme, does not have any of the vortices shown here.

Table 1.
Initial condition for 2D Riemann problem—Case 13 by Lax and Liu [27].
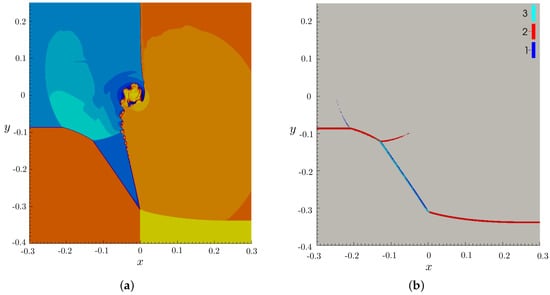
Figure 5.
Solution at for Case 13 by Lax and Liu [27], and filter adaptation: (a) Density; and (b) Filter adaptation ((3) (cyan) adapted along x and y; (2) (red) along y only; and (1) (blue) along x only).
3.2. Interaction of Plane Waves with Shocks
In view of the intended application of the proposed method to LES, it is useful to examine its performance on flows in which fluctuations pass through a shock wave. The Shu–Osher problem [28] is initialized with a Mach 3 shock wave travelling into a quiescent region with sinusoidal density variations. The initial conditions are
A solution on a grid with spacing at is shown in Figure 6. The reference solution is that on a finer grid with spacing . These are the spacings used in Johnsen et al. [10]. The solutions are identical on the finer grid. At this time, acoustic waves have traveled farther into the post-shock region than the entropy waves, and have themselves steepened into weak shocks (in ). The most noticeable differences between solutions on the two grids are in density and entropy immediately downstream of the shock. Entropy fluctuations are damped at the shock only, visible as a drop in amplitude at the peak adjacent to the one at the shock (Figure 6c). There is no further loss to this wave as it propagates away from the shock. The present solution is comparable to that with the Hybrid scheme (sixth-order central switching to fifth-order WENO over discontinuous regions) in Johnsen et al. [10]. It is slightly worse than the artificial diffusivity methods, but better than WENO methods; entropy continues to decay along the wave for WENO methods.
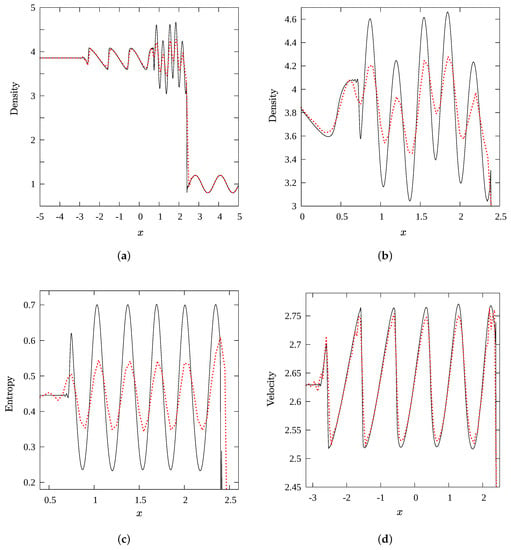
Figure 6.
Shu–Osher problem at t = 1.8 (red dotted curve: ; black curve: ).
A 2D version of the Shu–Osher problem can be posed as the interaction between a plane shock and an inclined plane wave with sinusoidal vorticity and entropy variations. Johnsen et al. [10] examined the performance of several schemes on this problem (considered earlier by Mahesh [29]). The region of interest is and . The solution is periodic in y with period . There is a supersonic inflow at , and a subsonic outflow. A buffer region over ensured that there were no reflections. An initial field was setup, representing steady flow separated by a plane shock at Mach 1.5, given by left and right states
To this, fluctuations
representing a plane wave incident at angle were added. This wave enters at from the unsteady boundary conditions
Grid spacings of , are identical to those of Johnsen et al. [10]. The change due to refinement along x alone (, ) and two levels of refinement in both directions are presented below. Taking small values for amplitudes () allow quantitative comparisons against linear theory (linearization of Rankine–Hugoniot jump conditions) as in [29].
Contours of vorticity for a wave train incident at angle are shown in Figure 7a. The wave refracts and its amplitude changes. The solution along a line () is found to be free of oscillations. On halving alone, a sharper jump is obtained at the shock. Oscillations appear in the vicinity of the shock when the wave is incident at a higher angle (Figure 7c), and are carried into the post-shock region. The grid refinement has confined significant oscillations to a smaller region, and made the post-shock solution smoother. The differences in solution structure arise because the post-shock wave is evanescent at [29].
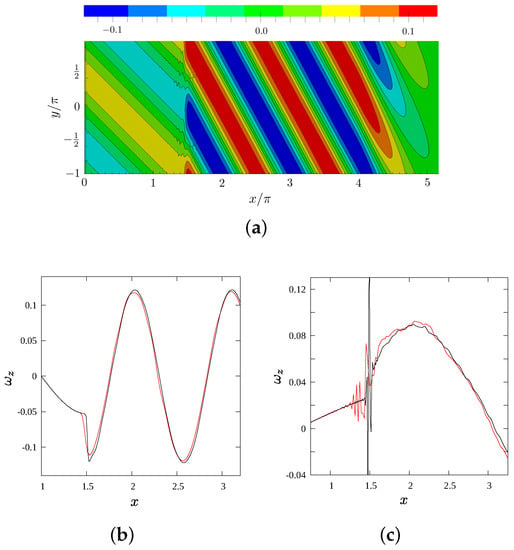
Figure 7.
Shock-vorticity/entropy wave interaction. ; Red curve: ; black curve (finer grid): . (a) Vorticity contours at t = 25 for = 45°, = 1; (b) along for = 45°, = 1 at t = 25; and (c) along for = 75°, = 1 at t = 32.
Quantitative comparisons against linear theory are shown in Figure 8. The amplification of the mean enstrophy across the shock is shown for , and . Averaging is over the time period . The amplification factor obtained in the simulation is slightly smaller than that of linear analysis at , and slightly larger for . The differences increase as wavenumber is increased. On halving grid spacing, in every case, there is a significant improvement as solution comes closer to that of linear theory. In addition, the amplitude of the post-shock oscillations and the extent of the region where these occur decrease significantly. With further refinement, the numerical solution is essentially the same as that of linear theory for . When , there is further improvement for although not significantly for .
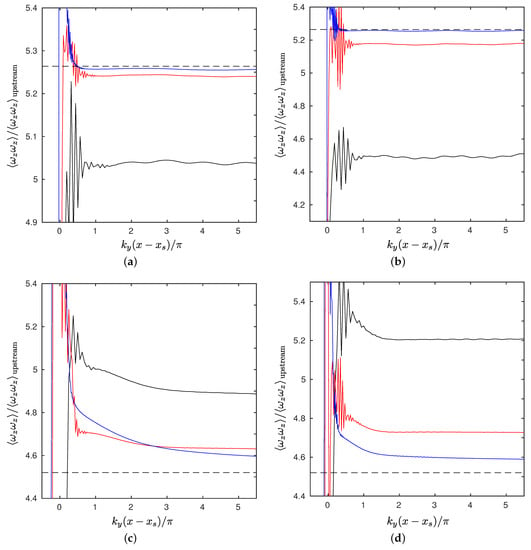
Figure 8.
Shock-vorticity/entropy wave interaction. Black dotted line: linear solution; black: grid as in Johnsen et al. [10]; red: medium grid, halved; blue: fine grid halved again. (a) = 45°, = 1; (b) = 45°, = 2; (c) = 75°, = 1; and (d) = 75°, = 2.
The solutions can be compared with the results of Johnsen et al. [10]. On the same grid as theirs, the amplification factor in the present solutions differ more from the linear analysis solution than some other methods (Hybrid WENO/central differences, WENO and ADPDIS3D). However, when the grid was refined, the differences fell in all cases, and post shock oscillations also reduced in amplitude and occurred over a smaller region. They supposed (Section 4.2.1 in Johnsen et al. [10]) that these are post-shock oscillations owing to, generally, slowly moving shocks in shock-capturing schemes; these oscillations would “not disappear under grid or time step refinement” [10]. In the present simulations, the differences between numerical solutions and linear theory generally diminish with grid refinement.
In all the tests reported above, the same adaptation of filter order as in Figure 2, and same set of filter parameters as in Figure 3 was used. For a given problem, it is always possible to find a set of filter parameters that result in a “better” solution on a given grid. Not only would the solutions look more attractive because of reduced oscillation amplitudes, even accuracy can improve. For example, in the 2D extension of the Shu–Osher problem, with slightly less filtering, the amplification factor comes closer to that of linear theory. However, our proposal is not to seek a new, optimal set of filter parameters for every problem, but to use, e.g., the set given here. Since the computations remained stable for all the problems reported here with this set of parameters, and solutions tend to the reference one (or DNS/experiment), this appears to be a reliable method for obtaining accurate solutions.
3.3. 3D Evolution
The Taylor–Green vortex problem evolves from a periodic initial field and develops smaller scales due to nonlinearity. We consider both inviscid and viscous solutions. No shocks form in this problem. It is included to demonstrate accuracy of the numerical scheme, and convergence with grid refinement by comparisons with reference solutions.
For the inviscid case, there is no lower limit on the scale. An LES model and/or numerical method must stabilize the computation beyond the time at which structures of the order of the grid spacing appear. Excessive damping can be revealed by this test problem. The initial condition is
Simulations were carried out in a cube of edge length on uniformly-spaced grids of , and points. The growth of enstrophy in the box is shown in Figure 9a. A semi-analytical solution is included for comparison [30]. All simulations remained stable but departed from each other when , approximately. As the grid is refined, the numerical solution agrees with enstrophy of the reference solution to later times. The kinetic energy in the box should be preserved because there is no viscous dissipation. Figure 9b shows the kinetic energy to begin to fall at on the grid, and later on the finer grids. Comparisons at two times are shown in Table 2. The monotonic convergence with grid refinement is evident. Owing to the flat filter characteristics, dissipation is active only after small scales have grown.
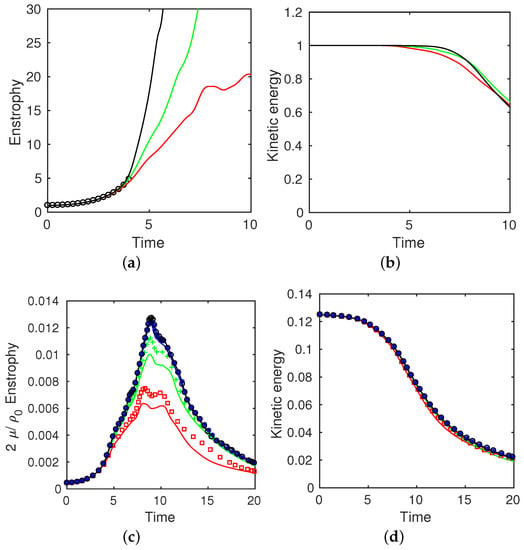
Figure 9.
Evolution of Taylor–Green vortex. Curves are from simulations on grids of (black), (blue), (green), and (red) points. (a,b) Inviscid case with symbols from [30]; and (c,d) viscous case with solid line, present LES and symbols from [31].

Table 2.
Measures of Taylor–Green vortex solution.
The viscous Taylor–Green solution was found for based on the initial length scale (length of cube edge, ), and maximum velocity. The reference data for comparison are from DeBonis [31] (available at https://eprints.soton.ac.uk/401892/1/512.dat). The simulation was carried out for . Differences are evident on coarse grids, but diminishes with refinement.
4. Jet LES
Now that the performance of the proposed method has been evaluated carefully in canonical problems of isolated shocks, wave refraction by a shock, and the evolution of a turbulent flow at a moderate Reynolds number accessible to DNS, we turn to simulations of high Reynolds number, turbulent, supersonic jets. Imperfectly expanded jets exhibit a train of shocks. As turbulent fluctuations travelling through these shocks are distorted, turbulent dissipation and production can get affected. Excessive numerical dissipation can then alter the jet’s development. The following two test cases are model turbulent flows with stationary shocks that can indicate the accuracy that can be expected from LES for compressible flow applications. Comparisons with experiments, and another LES for the impinging case are shown. The Reynolds numbers are quite large, . The intent is to examine the usefulness of this method for practical applications. It is shown that, as the grid is refined, the energy spectrum broadens by extending the computed part of the inertial range.
4.1. Free, Underexpanded Round Jet
Large eddy simulations were performed on the supersonic round jet experiments of Norum and Seiner [32]. A contoured C-D nozzle designed for exit plane Mach number was used. The nozzle pressure ratio (NPR), which is the ratio of reservoir pressure to nozzle exit pressure, was 9.187. Because the jet was slightly underexpanded, the fully expanded Mach number would be . The Reynolds number based on these nozzle exit plane conditions, centerline velocity , and nozzle inner diameter d, was . The simulation was set up in a rectangular domain that was along jet axis, and in cross stream directions. Simulations were performed on a sequence of grids. Each was distinguished by the number of uniformly spaced gridpoints across the jet diameter. Outside the jet, the grid was stretched—spacing increased in geometric progression at 1% in cross stream directions. A much milder stretching of 0.1% was used in the streamwise direction. Buffer zones, with twenty points at the lateral and thirty points at the outflow boundaries, were added with a stretching of 10%. On the coarsest grid there were 20 points across the jet diameter leading to gridpoints in total. A refined grid had 40 points across the jet and points in total (medium grid). Finer grids had 23 million (fine), 43 million (finer), and 200 million (finest) points.
Boundary conditions at the inflow plane () were obtained from radial profiles
Here, is the mean jet radius and the momentum thickness of the jet (taken to be ). Subscripts j and ∞ denote jet centerline and ambient conditions, respectively. To anchor the inflow profile, the following procedure proposed by Bogey and Bailly [19] was employed at every time step. Flow variables at the inflow plane, obtained after applying non-reflecting conditions, were corrected to . Here, is the prescribed inflow profile (Equation (9)), and for and for . Within the jet shear layer alone, small perturbations,
were added to the inflow axial velocity to represent inflow turbulence of the nozzle boundary. Strouhal numbers Sti and phase varied from 0.1 to 0.6 and 0 to , respectively. The quantity within square brackets ensures that fluctuations are added within the shear layer only.
Figure 10a is a visualization of the jet in terms of the mean pressure on a plane containing the jet axis, showing the expected cell structures. Static pressure along the centerline in the experiment was reported (page 27 [32]). Figure 10b shows solutions from the coarse, medium and finest grids along with data from the experiment. There is little change in mean pressure between the medium (9 million points) and the finest grid (200 million points). We can observe that both the locations and strengths of the pressure variations through the cells have been captured accurately. On refining from coarse to medium, pressure variations occur at the same places, but peaks are slightly sharper. The pressure distribution at an instant is also shown. Significant fluctuations on the centerline appear only beyond . Where such fluctuations are significant, we can observe that gradients at an instant are slightly larger than in the mean (see pressure rise near and 6). Contours of pressure on a longitudinal plane also show that significant unsteadiness sets in the 3rd shock cell.
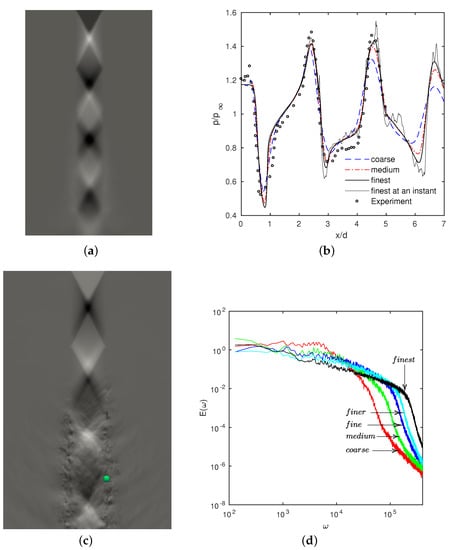
Figure 10.
LES of underexpanded jet for , . Experiment by Norum and Seiner [32] (case on page 27 of their report). (a) Mean pressure on longitudinal plane. (b) Pressure along jet axis. Curves for simulation data, symbol for experiment. (c) Instantaneous pressure on longitudinal plane (Medium grid). (d) Energy spectra (at green dot in the left figure).
The effect of grids finer than the medium one can be seen in energy spectra. Figure 10b shows spectra from the five simulations, calculated from time series at a point near the jet boundary at . As the grid spacing is reduced, a clear inertial range develops, and extends to smaller scales. The magnitude of low frequency content changes little. At the Reynolds number of the flow, the dynamically significant range of scales is still larger, but quantities such as the centerline mean pressure can be obtained accurately in an LES, on a grid of moderate size. Especially, shock positions and strengths change little with refinement. This serves as strong support for the adaptive filtering method for shock capturing used in these simulations. The quality of the simulation was similar for an overexpanded jet [33].
4.2. Impinging Round Jet
The second case, representative of flows of interest in applications, is the impinging jet experiment of Henderson et al. [34]. Velocity data from PIV were reported. This is a sonic jet with NPR = 4.03 impinging on a flat wall placed at a distance of from the nozzle exit. Dauptain et al. [35] reported an LES of this problem. They used 7.5, 16 and 22 million tetrahedral volumes including a region within the nozzle as well. Here, two grids with 30 and 60 points across the jet at the inflow plane were taken, with 5% stretching in the lateral direction. Only lateral buffer zones were used in the current simulation. The total number of points were then for the coarse grid and for the fine grid. The Reynolds number was . A comparison of the mean streamwise velocity with the experiment along the jet axis is shown in Figure 11a. The simulations are consistent among themselves: on the finer grid, the gradients are sharper everywhere. Surprisingly, Dauptain et al. [35] found their coarsest grid to be closest to the experiment. Especially in the vicinity of , the velocity dropped to about 150 m/s whereas in the experiment it is about 300 m/s. Smaller but significant differences were found where flow decelerates again (). They supposed that, in these strongly decelerating regions, the measurement could be in error. Our simulations do not show such large differences with experiment. Figure 11b compares present simulations with data from Dauptain et al. [35] of the pressure along the centerline (experimental data of pressure were not available). Pressure data agree quite closely with the other simulation. Since the pressure jump near is about the same, it is surprising that the velocity jump could be different.
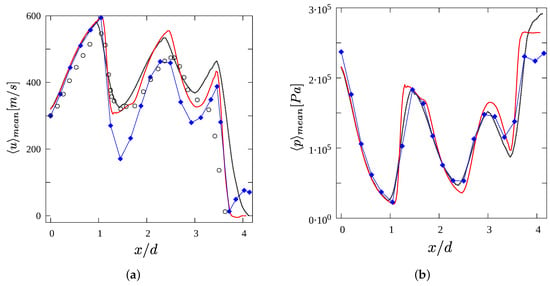
Figure 11.
Mean axial velocity and pressure along centerline of impinging jet. Coarse grid (black curve); fine grid (red), experiment of Henderson et al. [34] (black circles), and simulation of Dauptain et al. [35] (blue curve with filled symbol). (a) Velocity; and (b) Pressure.
Since the objective of this test was to determine the usefulness of the proposed shock-capturing scheme, and not the other implications of this flow, such as impingement acoustics, the simulation domain did not include the flow within the nozzle. There has not been any adverse effect on the quantities that we could compare with experiment and another LES, such as any shift in locations of Mach disk or extent of the cells. Indeed, the very close agreement between our simulations and the one which included the nozzle flow [35] in the initial region () affirms this.
5. Conclusions
An explicit filtering approach to LES of flows has been extended to flows with shocks by filter order adaptation. Although the usual treatment of flows with shock capturing is to reduce the order of the spatial discretization in the vicinity of shocks, here, the discretization remains the same everywhere, and was sixth-order. Instead, the order of the spatial filter was reduced from 10 in smooth regions to 2 at gridpoints where a shock was detected. Filter order was increased in steps at neighboring gridpoints. However, filtering is an essential part of this method for LES. Thus, the adaptation is a convenience. Adaptive filtering had been proposed by Visbal and Gaitonde [12] earlier, but does not appear to have been taken forward either in method assessment or in applications. They lowered filter order to 2 at a band of seven points spanning shocks. Here, it sufficed to use a band of three points. It is not surprising that Bogey and Bailly [13], who also performed LES with an explicit filter, examined filter adaptation briefly. We can expect that the studies presented here may invite its further use.
Although, generally, the results of adaptive filtering are very encouraging, quantitative comparisons with the results in Johnsen et al. [10], for the 2D Shu–Osher problem (Section 3.2), revealed that, on the same grid, some other methods have better performance. Nevertheless, close quantitative agreement with the reference solution was readily obtained on grid refinement. Indeed, it is a common experience in the problems considered here that solutions tend to the reference ones as the grid is refined (explicitly included above for the 2D Shu–Osher, Taylor–Green and free jet problems). For the 2D Shu–Osher problem, not only does the amplification factor approach the linear analysis result, the post-shock oscillations diminish in amplitude and extent. Since computations were stable for all these problems with the same set of parameters, and tend monotonically to reference or exact solutions, we find this to be a reliable method. No search for an optimal set of parameters was considered, since such an optimal set may offer small improvements in computation economy but may be problem-dependent.
Although filter adaptation is but a small change in the LES method used in the examples presented here, because there is always a filtering step, the adaptation strategy can also be used with any other LES code. For example, it can be an alternative to other strategies for shock capturing such as adding artificial diffusion in the vicinity of shocks.
Author Contributions
Software, S.K.P.; all other aspects S.K.P. and J.M.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pirozzoli, S. Numerical Methods for High-Speed Flows. Annu. Rev. Fluid Mech. 2011, 43, 163–194. [Google Scholar] [CrossRef]
- Sangsan Lee, S.K.L.; Moin, P. Interaction of isotropic turbulence with shock waves: Effect of shock strength. J. Fluid Mech. 1997, 340, 225–247. [Google Scholar]
- Adams, N.; Shariff, K. A High-Resolution Hybrid Compact-ENO Scheme for Shock-Turbulence Interaction Problems. J. Comput. Phys. 1996, 127, 27–51. [Google Scholar] [CrossRef]
- Pirozzoli, S. Conservative Hybrid Compact-WENO Schemes for Shock-Turbulence Interaction. J. Comput. Phys. 2002, 178, 81–117. [Google Scholar] [CrossRef]
- Yee, H.C.; Sandham, N.D.; Djomehri, M.J. Low-Dissipative High-Order Shock-Capturing Methods Using Characteristic-Based Filters 1. J. Comput. Phys. 1999, 238, 199–238. [Google Scholar] [CrossRef]
- Cook, A.W.; Cabot, W.H. A high-wavenumber viscosity for high-resolution numerical methods. J. Comput. Phys. 2004, 195, 594–601. [Google Scholar] [CrossRef]
- Cook, A.W.; Cabot, W.H. Hyperviscosity for shock-turbulence interactions. J. Comput. Phys. 2005, 203, 379–385. [Google Scholar] [CrossRef]
- Cook, A.W. Artificial fluid properties for large-eddy simulation of compressible turbulent mixing. Phys. Fluids 2007, 19, 055103. [Google Scholar] [CrossRef]
- Bonelli, F.; Viggiano, A.; Magi, V. How does a high density ratio affect the near-and intermediate-field of high-Re hydrogen jets? Int. J. Hydrog. Energy 2016, 41, 15007–15025. [Google Scholar] [CrossRef]
- Johnsen, E.; Larsson, J.; Bhagatwala, A.V.; Cabot, W.H.; Moin, P.; Olson, B.J.; Rawat, P.S.; Shankar, S.K.; Sjögreen, B.; Yee, H.; et al. Assessment of high-resolution methods for numerical simulations of compressible turbulence with shock waves. J. Comput. Phys. 2010, 229, 1213–1237. [Google Scholar] [CrossRef]
- Mathew, J.; Foysi, H.; Sesterhenn, J.; Friedrich, R. An explicit filtering method for large eddy simulation of compressible flows. Phys. Fluids 2003, 15, 2279–2289. [Google Scholar] [CrossRef]
- Visbal, M.R.; Gaitonde, D.V. Shock capturing using compact-differencing-based methods. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 10–13 January 2005. AIAA 2005-1265. [Google Scholar]
- Bogey, C.; de Cacqueray, N.; Bailly, C. A shock-capturing methodology based on adaptative spatial filtering for high-order non-linear computations. J. Comput. Phys. 2009, 228, 1447–1465. [Google Scholar] [CrossRef]
- Tannehill, J.C.; Anderson, D.A.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer, 2nd ed.; Taylor & Francis: Abingdon, UK, 1984. [Google Scholar]
- Lele, S.K. Compact Finite Difference Schemes with Spectral-like. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 2004, 194, 194–214. [Google Scholar] [CrossRef]
- Mathew, J.; Foysi, H.; Friedrich, R. A new approach to LES based on explicit filtering. Int. J. Heat Fluid Flow 2006, 27, 594–602. [Google Scholar] [CrossRef]
- Visbal, M.R.; Rizzetta, D.P. Large-Eddy Simulation on Curvilinear Grids Using Compact Differencing and Filtering Schemes. ASME J. Fluids Eng. 2014, 124, 836–847. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Computation of a high Reynolds number jet and its radiated noise using large eddy simulation based on explicit filtering. Comput. Fluids 2006, 35, 1344–1358. [Google Scholar] [CrossRef]
- Chakravorty, S.; Mathew, J. A high-resolution scheme for low Mach number flows. Int. J. Numer. Methods Fluids 2004, 46, 245–261. [Google Scholar] [CrossRef]
- Chakravorty, S. On Large Eddy Simulation of Reacting Flows Using the Explicit Filtering Method with a Filtered Mass Density. Ph.D. Thesis, Indian Institute of Science, Bengaluru, India, 2010. [Google Scholar]
- Ganesh, S. Flow and Sound Field of Free and Impinging Jets from LES Using Explicit Filtering Method. Ph.D. Thesis, Indian Institute of Science, Bengaluru, India, 2013. [Google Scholar]
- Hixon, R.; Turkel, E. Compact Implicit MacCormack-Type Schemes with High Accuracy. J. Comput. Phys. 2000, 158, 51–70. [Google Scholar] [CrossRef]
- Ducros, F.; Ferrand, V.; Nicoud, F.; Weber, C.; Darracq, D.; Gacherieu, C.; Poinsot, T. Large-Eddy Simulation of the Shock/Turbulence Interaction. J. Comput. Phys. 1999, 152, 517–549. [Google Scholar] [CrossRef]
- Bhagatwala, A.; Lele, S.K. A modified artificial viscosity approach for compressible turbulence simulations. J. Comput. Phys. 2009, 228, 4965–4969. [Google Scholar] [CrossRef]
- Kawai, S.; Lele, S. Localized artificial diffusivity scheme for discontinuity capturing on curvilinear meshes. J. Comput. Phys. 2008, 227, 9498–9526. [Google Scholar] [CrossRef]
- Lax, P.D.; Liu, X.D. Solution of two-dimensional Riemann problems of gas dynamics by positive schemes. SIAM J. Sci. Comput. 1998, 19, 319–340. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Mahesh, K. The Interaction of a Shock Wave with a Turbulent Shear Flow. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1996. [Google Scholar]
- Brachet, M.E.; Meiron, D.I.; Orszag, S.A.; Nickel, B.G.; Morf, R.H.; Frisch, U. Small-scale structure of the Taylor–Green vortex. J. Fluid Mech. 1983, 130, 411–452. [Google Scholar] [CrossRef]
- DeBonis, J. Solutions of the Taylor-Green vortex problem using high-resolution explicit finite difference methods. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. AIAA 2013-0382. [Google Scholar] [CrossRef]
- Norum, T.D.; Seiner, J.M. Measurements of Mean Static Pressure and Far-Field Acoustics of Shock-Containing Supersonic Jets; NASA Technical Memorandum 84521; NASA: Washington, DC, USA, 1982.
- Patel, S.K.; Mathew, J. Large Eddy Simulation of Supersonic Impinging Jets by adaptive, explicit filtering. In Proceedings of the 22nd AIAA Computational Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015. Paper No. AIAA-2015-2298. [Google Scholar]
- Henderson, A. An experimental study of the oscillatory flow structure of tone-producing supersonic impinging jets. J. Fluid Mech. 2005, 542, 115–137. [Google Scholar] [CrossRef]
- Dauptain, A.; Cuenot, B.; Gicquel, L.Y.M. Large Eddy Simulation of Stable Supersonic Jet Impinging on Flat Plate. AIAA J. 2010, 48, 2325–2338. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).