Abstract
The non-linear Schrödinger (NLS) equation has often been used as a model equation in the study of quantum states of physical systems. Numerical solution of NLS equation is obtained using cubic B-spline Galerkin method. We have applied the Crank–Nicolson scheme for time discretization and the cubic B-spline basis function for space discretization. Three numerical problems, including single soliton, interaction of two solitons and birth of standing soliton, are demonstrated to evaluate to the performance and accuracy of the method. The error norms and conservation laws are determined and found to be in good agreement with the published results. The obtained results show that the approach is feasible and accurate. The proposed method has almost second order convergence. The linear stability of the method is performed using the Von Neumann method.
1. Introduction
The non-linear Schrödinger (NLS) equation describes how the behavior of quantum states of a physical system changes in time and space. The NLS equation can be used to describe the propagation of optical pulses and waves in water and plasmas, among other things. Due to the presence of nonlinearity and the complex nature of the problem, it is still a challenge for researchers to determine the most suitable method. Many theoretical and numerical studies have been carried out to overcome this difficulty. The B-spline Galerkin method is quite advanced and has been used by researchers to solve other complex problems.
Dag [1] presented the quadratic and cubic B-spline Galerkin finite element method for solving the Burger’s equation. This method was found to give satisfactory results for the Burger’s equation, particularly when continuity of the solutions was essential. Dag et al. [2] also proposed a cubic B-splines collocation method for solving the one-dimensional Burger’s equation. The proposed scheme was easy to implement and did not require any inner iteration to deal with the nonlinear term of the Burger’s equation. Gorgulu et al. [3] presented exponential B-splines Galerkin finite element method for the numerical solution of the advection-diffusion equation. In this study, a new algorithm was developed for the numerical solution of differential equations. This algorithm was obtained by utilizing exponential B-spline functions for the Galerkin finite element method. It was reported that the proposed method gave satisfactory results. The exponential B-splines Galerkin method for the numerical solution of the Burger’s equation was also applied by Gorgulu et al. [4].
Saka et al. [5] proposed a quartic B-splines Galerkin finite element method for solving the regularized long wave equation. The performance and accuracy of the method were observed. The method has a weakness because of its large number of matrix operations. The quartic B-spline method was found to be very useful for finding the numerical solutions of the differential equation when higher continuity of solutions occurs. Aksan [6] presented the quadratic B-spline finite element method for finding the approximate solution of the nonlinear Burger’s equation. The high accuracy of the proposed method was thoroughly examined. Gardner et al. [7] also applied a cubic B-spline finite element method for the numerical solution of the Burger’s equation. They noticed that the proposed finite element method gave more accurate results than other approaches.
Sheng et al. [8] solved the NLS equation using a finite difference method based on quartic spline approximation and semidiscretization. The NLS equation was approximated using a finite element method by Zlotnik and Zlotnik [9]. Ersoy et al. [10] studied the numerical solution of the NLS equation using an exponential B-spline with collocation method. In that paper, they used the Crank Nicolson formulation for time integration and exponential cubic B-spline functions for space integration. Mokhtari et al. [11] solved the NLS equation using delta-shaped basis functions. Saka [12] solved the NLS using the collocation method with quintic B-spline functions. The generating function of the Hermite polynomial and the orthogonal Hermite function were introduced with ordinary Hermite polynomials by Cesarano et al. [13]. The nature of Hermite polynomials is described in the Schrödinger Equation. Analytical solutions of the NLS equation for certain initial and boundary conditions were presented by Zakharov and Shabat [14]. The numerical solution of the NLS equation was obtained by Lin [15] using a septic spline function method with the collocation method. The Galerkin finite element method for the NLS equation was applied by Dag, with quadratic B-spline functions as the weight and trial functions over finite elements [16]. The numerical solution of the NLS equation was also obtained by using the collocation method based on cubic B-spline by Gardner et al. [17]. Hu [18] presented a conservative two-grid finite element method for the numerical solution of the NLS equation and applied one Newton iteration for the linearization of the problem by using the coarse-grid solution as the initial guess. The Galerkin B-spline method is not often used for the numerical solution of the NLS equation. A review of some numerical methods for solving the NLS equation indicates that most methods use the collocation finite element method.
In this paper, we study the use of the Galerkin method with cubic B-spline function as the weight and trial functions over finite elements to solve the NLS equation. This paper is organized as follows. In Section 2, we discussed the governing equation and fundamentals of Cubic B-spline Galerkin method. In Section 3, the stability analysis of the numerical scheme is analyzed using the Von Neumann method. The numerical results and test problems are discussed in Section 4. In the last section, the conclusions are given.
2. Governing Equation and Cubic B-Spline Galerkin Method
The NLS equation is
The equation in (1) is called a self-focusing NLS equation when and a defocusing NLS equation when . The subscripts and denote the spatial variable and time variable respectively; is a positive real parameter, and = . is a complex-valued function and defined over the whole real line. The initial condition is
and the boundary conditions are as follows:
The solution is decomposed into its real and imaginary parts as
Substituting Equation (4) into Equation (1), the following coupled partial differential equations are obtained:
The solution domain is divided equally into N finite elements by the nodes such that and . In this paper, we choose cubic B-spline function as the weight and trial function. The cubic B-splines are defined over the interval as follows [1]:
The approximate solution to the analytical solution for Equation (1) is written in terms of the cubic B-spline function as
where
The coefficients and are unknown time-dependent parameters that will be determined from the boundary and weighted residual conditions. Since each cubic B-spline covers 4 elements, each element is covered by 4 splines. Using the local coordinate’s transformation for , the cubic B-spline function over the element can be written as
Here, all other cubic B-spline functions are zero over the finite element . The approximation function (Equation (8)) over the finite element can be defined in terms of the basis functions (Equation (9)) as
Using the B-splines basis defined in Equation (6) and the trial function stated in Equation (8), the nodal values of , and at the knots are determined in terms of time-dependent element parameters and as:
where the prime denotes differentiation with respect to .
Applying the Galerkin approach to Equation (5) with the weight function , the weak form of Equation (5) over the finite element is
where
Using the weight function as the cubic B-spline and substituting Equations (10) into (12) with some manipulations, the following differential equations are obtained:
Equation (14) can be written in matrix form as
where and are the element parameters and dot represents differentiation with respect to . The element matrix , and are given by
where . The element matrix (16) is calculated as
values are calculated by writing and in Equation (13). Using the values of and at the points we obtain
Assembling the contributions from all of the elements, Equation (15) becomes
where and are global element parameters and the matrices , which are global matrices with a generalized kth row, have the following form:
where
Discretization by the Crank-Nicolson method gives us and . Similarly, the time discretization by finite difference scheme gives us and . Substituting these discretizations into Equation (18), we obtain the following system:
Using the boundary conditions in Equation (21) yields a septadiagonal matrix. This system is solved by an appropriate method in MATLAB.
First, the initial vectors of parameters and are calculated to solve System (21) with the use of the initial condition using the relations
where all parameters and are determined. and require the following relations to be satisfied at points :
The initial vectors and can be calculated using the initial and boundary conditions from the following matrix equations:
and
This system is solved using a suitable method in MATLAB. The approximate numerical solution of and is obtained from the and using Equation (21).
3. Stability Analysis
Stability analysis of the numerical scheme is carried out using the von Neumann method. The coupled system of Equation (5) is written as
where and
To perform linear stability analysis, we further linearize the nonlinear term in Equation (24) by taking Here Therefore, the linearized form of Equation (24) is as follows:
The discretization of linear Equation (24) by the proposed scheme is given by
where
We use the following Fourier modes analysis for Scheme (25)
Here is the amplification matrix. Equation (26) is substituted into Equation (25) to obtain the value of the amplification G. After tedious algebra, we obtain the value of G as follows
Matrix is a skew symmetric matrix, and therefore both the matrices and have the same eigen values. Thus, the maximum value of . Hence, the linearized Scheme (25) is unconditionally stable.
4. Numerical Results and Test Problems
Three test problems, including the single soliton, interaction of two solitons and birth of standing soliton, are presented to evaluate the effectiveness and performance of the proposed method. The accuracy of the proposed method is examined using the error norms and conservation laws defined as
Moreover, Equation (1) must satisfy the two conservation laws
4.1. Single Soliton Solution to the NLS Equation
The analytical single soliton solution to the NLS equation is given as [2]:
where is the speed of the soliton solution whose magnitude depends on the parameter .
The numerical solution is computed using the following parameters: . The conservative quantities and and error norms and are calculated. Numerical simulations were carried out at different space steps and time steps for comparison with the published results of the previous methods. The results are documented in Table 1 and Table 2. The numerical simulations and the absolute numerical error are shown at different times in Figure 1.

Table 1.
Error norms and conservation laws for single soliton: with .

Table 2.
Comparisons of the present results with those of Taha et al. [20]., amplitude = 1 at time = 1.
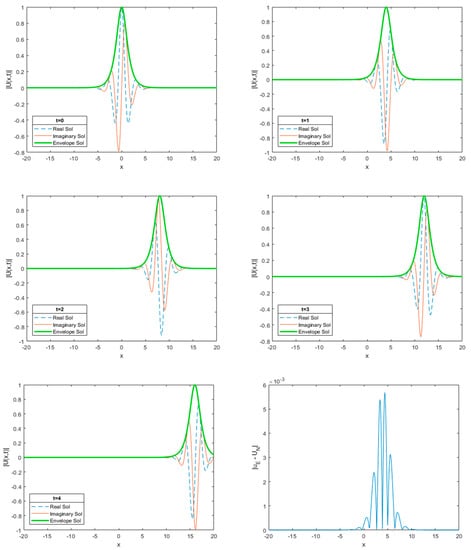
Figure 1.
Single soliton solution and errors |Numerical – Analytical|.
Table 2 displays a comparison between the results obtained by the proposed method and published results. The results of the proposed method are in agreement with analytical solutions within very satisfactory limits, and the proposed method exhibits the same results as the quintic B-spline collocation method and quadratic B-spline method, as can be seen from the comparison in Table 2. We found good results even for large step sizes. It is noted that the error norms of the Galerkin cubic B-spline are lower than Explicit method [3], Implicit/explicit [3], and Split-step Fourier method [3] when we compare the results of the proposed method with those referenced in [1,4,19].
The rate of convergence for spatial and temporal directions is calculated using the formula [21]:
where is the error norms in spatial and temporal directions. The error norms and order of convergence rate at time are shown in Table 3.

Table 3.
Rate of convergence in spatial and temporal directions at
In Table 4, the results are documented for when the soliton amplitude is equal to 2. It was found that the results of the error norms at different times increase very slightly, as shown in Table 4. One soliton solution with is calculated, and simulations are shown in Figure 2.

Table 4.
Error norms and conservation laws for single soliton with .
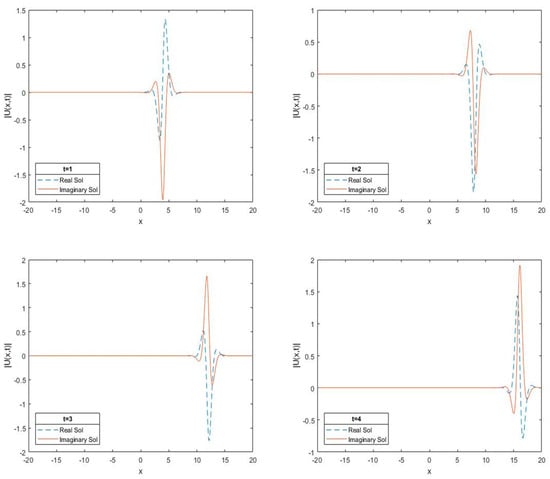
Figure 2.
Single soliton solution with amplitude 2.
Table 5 displays the approximate results obtained using the proposed method compared with the published methods listed in the reference for single soliton when the amplitude is 2. These results are in good agreement with the analytical solution.

Table 5.
Comparisons of single soliton with those of Taha et al. [20], amplitude = 2 at time = 1.
4.2. The Interaction of Two Solitons for the NLS Equation
In the second problem, we discuss the interaction of two solitons moving in opposite directions, have the same amplitude of magnitude 1 with initial conditions as follows [16,17,20]
where and are constants.
The numerical solution is computed by using the following parameters The first soliton is placed at and is moving to the left with speed 4, and the second soliton is placed on the other side at , traveling to the right with speed 4. Both solitons are moving in opposite directions, and they collide and separate. The interactions of these two solitons are visualized in Figure 3. The error norms and are computed at different times and at different space steps and time steps. The calculated results are tabulated in Table 6.
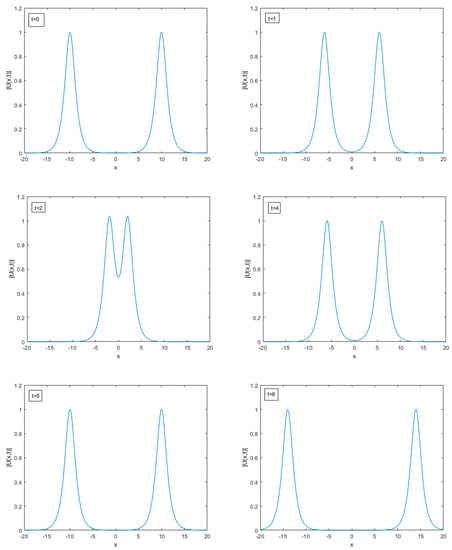
Figure 3.
Interaction of two solitons, amplitude = 1 at different space and time steps.

Table 6.
Two-solitons, amplitude = 1 at different space and time steps.
The error norms and are very small compared with those of Taha et al. [20], as shown in Table 7. It can be clearly seen that the error norms and obtained by the present method are smaller than those of previous methods [20], as shown in Table 7.

Table 7.
Comparisons of two solitons with Taha et al. [20], amplitude = 1.
4.3. Birth of Standing Soliton with the Maxwellian Initial Condition
If
a soliton should appear over time with initial values greater than , otherwise the soliton will decay away [22].
Consider the birth of soliton with the Maxwellian initial condition given by [16]:
The values of all parameters are chosen to be for the domain to exhibit the birth of a soliton. The numerical simulations are shown at different times for the values of over the domain [−45,45] in Figure 4. With , the soliton decays away as expected.
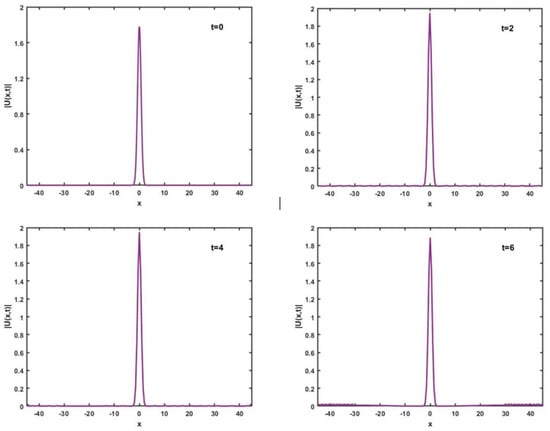
Figure 4.
Birth of a standing soliton for .
The conserved quantities and are computed using the Maxwellian initial condition (34). Analytical conserved quantities can be computed as:
The conserved quantities and are tabulated in Table 8. The numerical results obtained are compared with the published results of Mokhtari et al. [11] and the exact solution, as shown in Table 8. The proposed method conserves to 7 decimal places and to 3 decimal places.

Table 8.
Comparison of conserved quantities of the birth of a standing soliton with Mokhtari et al. [11], .
5. Conclusions
The approximate solution of the NLS equation was investigated using the Galerkin finite element method with a cubic B-spline shape function. Three numerical problems, including single soliton, interaction of two solitons, and birth of a standing soliton with the Maxwellian initial condition, were demonstrated to evaluate to the performance and accuracy of the method. Furthermore, we simulated the numerical solution by choosing different parameters for motion of the single soliton, the interaction of two solitons and the birth of the standing soliton. The error norms and and conservation laws and were determined and compared with published results [11,16,17,20]. It was seen that all of our results for the problems were computed to be reasonably low, and were found to be in good agreement with the analytical solution. The present method was shown to be unconditionally stable. The method has almost a second-order convergence. In conclusion, the proposed scheme with cubic B-spline presents an acceptable result for the NLS equation.
Author Contributions
Formal analysis, A.I. and N.N.A.H.; Investigation, A.I., N.N.A.H. and A.I.M.I.; Methodology, A.I.; Supervision, N.N.A.H. and Ahmad A.I.M.I.; Writing – original draft, A.I.; Writing – review & editing, N.N.A.H. and A.I.M.I.
Funding
This work was supported by USM Short Term Grant of account number 304.PMATHS.6315077.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dag, I.; Saka, B.; Boz, A. B-spline Galerkin methods for numerical solutions of the Burgers equation. Appl. Math. Comput. 2005, 166, 506–522. [Google Scholar]
- Dag, I.; Irk, D.; Saka, B. A numerical solution of the Burger’s equation using cubic B-splines. Appl. Math. Comput. 2005, 163, 199–211. [Google Scholar]
- Gorgulu, M.Z.; Dag, I. Galerkin method for the numerical solution of the advection-diffusion equation by using exponential B-splines. arXiv 2016, arXiv:1604.04267v1. [Google Scholar]
- Gorgulu, M.Z.; Dag, I.; Irk, D. Wave propogation by way of exponential B-spline Galerkin method. J. Phys. 2016, 766, 012031. [Google Scholar]
- Saka, B.; Dag, I. A numerical solution of the RLW equation by Galerkin method using quartic B-splines. Commun. Numer. Meth. Engng. 2008, 24, 1339–1361. [Google Scholar] [CrossRef]
- Aksan, E. Quadratic B-spline finite element method for numerical. Appl. Math. Comput. 2006, 174, 884–896. [Google Scholar]
- Ali, A.; Gardner, G.; Gardner, L. A collocation solution for Burgers using cubic B-spline finite elements. Comput. Meth. Appl. 1992, 100, 325–337. [Google Scholar] [CrossRef]
- Sheng, Q.; Khaliq, A.Q.M.; Al-Said, E.A. Solving the generalized nonlinear Schrödinger equation via quartic spline approximation. J. Comput. Phys. 2001, 166, 400–417. [Google Scholar] [CrossRef]
- Zlotnik, A.A.; Zlotnik, I.A. Finite element method with discrete transparent boundary conditions for the time-dependent 1D schrödinger equation. Kinet. Relat. Models 2012, 5, 639–663. [Google Scholar] [CrossRef]
- Ersoy, O.; Dag, I.; Sahin, A. Numerical investigation of the solution of Schrödinger equation with exponential cubic B-spline finite element method. arXiv 2016, arXiv:1607.00166v1. [Google Scholar]
- Mokhtari, R.; Isvand, D.; Chegini, N.G.; Salaripanah, A. Numerical solution of the Schrödinger equations. Nonlin. Dyn. 2013, 74, 77–93. [Google Scholar] [CrossRef]
- Saka, B. A quintic B-spline finite-element method for solving the nonlinear Schrödinger equation. Phys. Wave Phenom. 2012, 20, 107–117. [Google Scholar] [CrossRef]
- Cesarano, C.; Fornaro, C.; Fornaro, C.; Vazquez, L. Operational results in bi-orthogonal Hermite functions. Acta Mathemat. Univ. Comenian. 2016, 85, 43–68. [Google Scholar]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. J. Exp. Theor. Phys. 1972, 34, 62–68. [Google Scholar]
- Lin, B. Septic spline function method for nonlinear Schrödinger equations. Appl. Analys. 2015, 94, 279–293. [Google Scholar] [CrossRef]
- Dag, I. A quadratic B-spline finite element method for solving nonlinear Schrödinger equation. Comput. Meth. Appl. Mech. Eng. 1999, 174, 247–258. [Google Scholar]
- Gardner, L.R.T.; Gardner, G.A.; Zaki, S.I.; El Sahrawi, Z. B-spline finite element studies of the non-linear Schrödinger equation. Comput. Methods Appl. Mech. Eng. 1993, 108, 303–318. [Google Scholar] [CrossRef]
- Hu, H. Two-grid method for two-dimensional nonlinear Schrödinger equation by finite element method. Numeric. Methods Part. Differ. Eqs. 2018, 75, 900–917. [Google Scholar]
- Prenter, P. Splines and Variational Methods; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Taha, T.R.; Ablowitz, M.J. Analytical and numerical aspects of certain nonlinear evolution equations II: Numerical nonlinear Schrödinger equations. J. Comput. Phys. 1984, 55, 203–230. [Google Scholar] [CrossRef]
- Qu, W.; Liang, Y. Stability and convergence of the Crank-Nicolson scheme for a class of variable-coefficient tempered fractional diffusion equations. Advc. Differ. Eqs. 2017, 2017, 108. [Google Scholar] [CrossRef]
- Delfour, M.; Fortin, M.; Payne, G. Finite-difference solutions of non-linear Schrödinger equation. J. Comput. Phys. 1981, 44, 277–288. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).