On the Kutta Condition in Compressible Flow over Isolated Airfoils
Abstract
:1. Introduction
2. Governing Equations
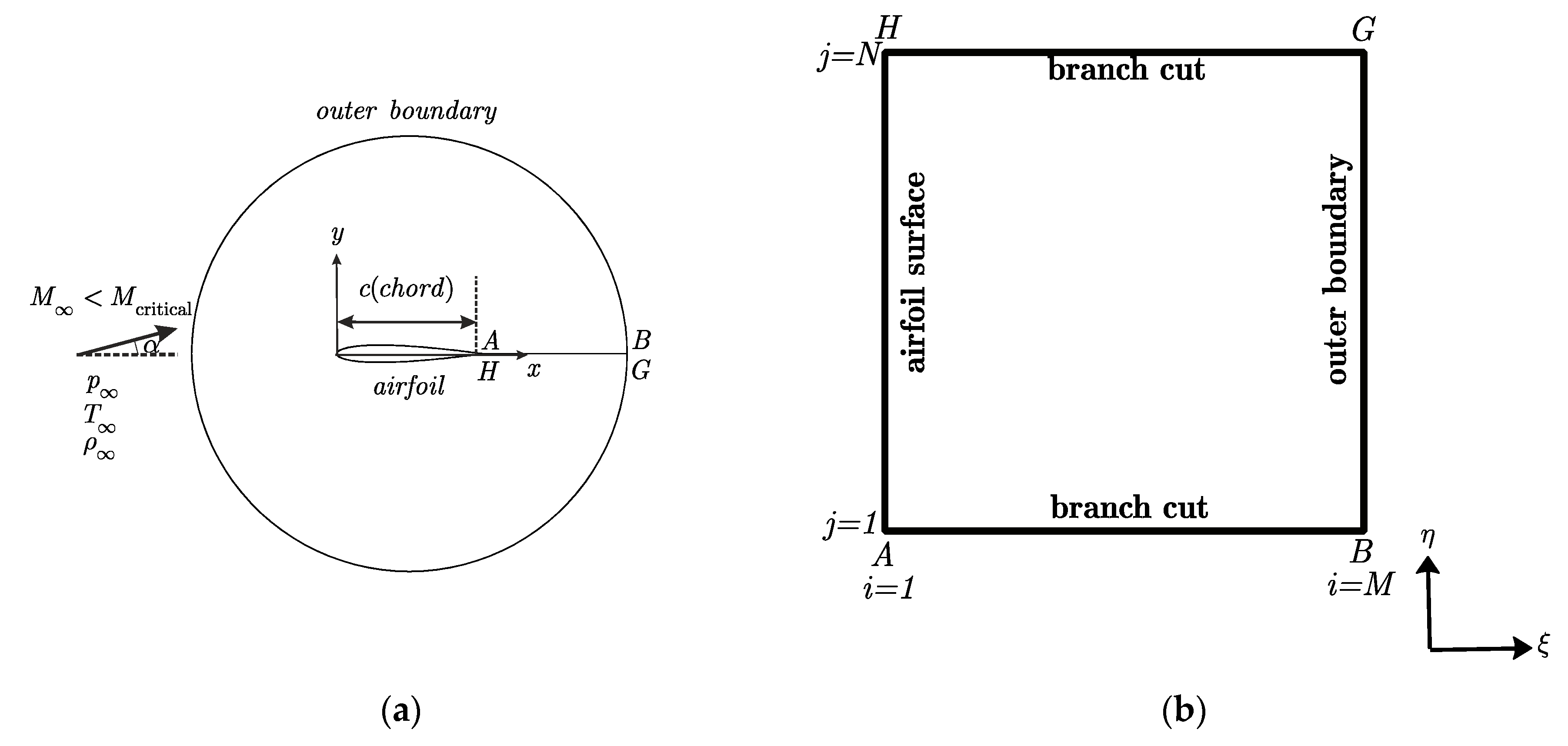
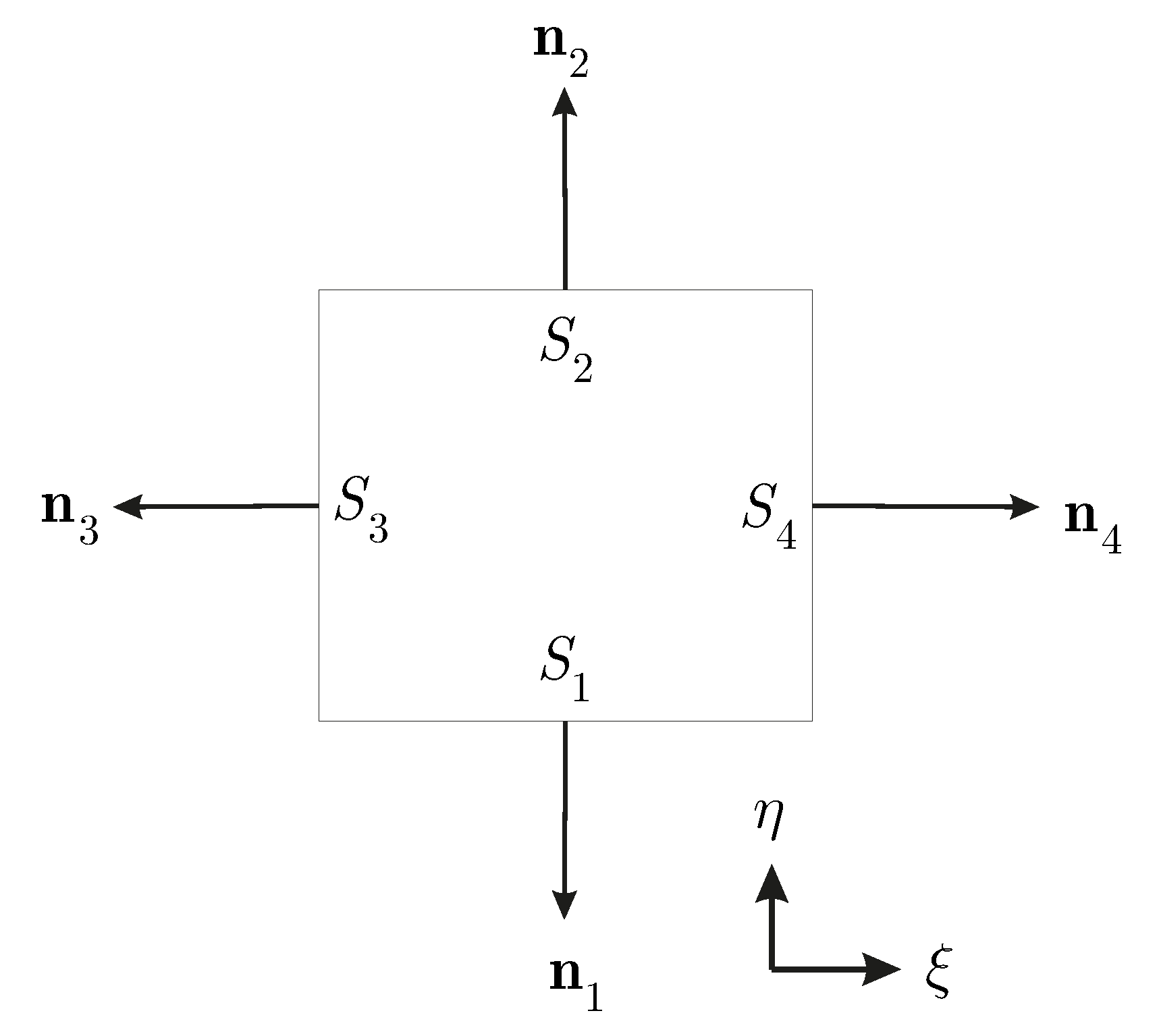
2.1. Transformation
2.2. Boundary Conditions
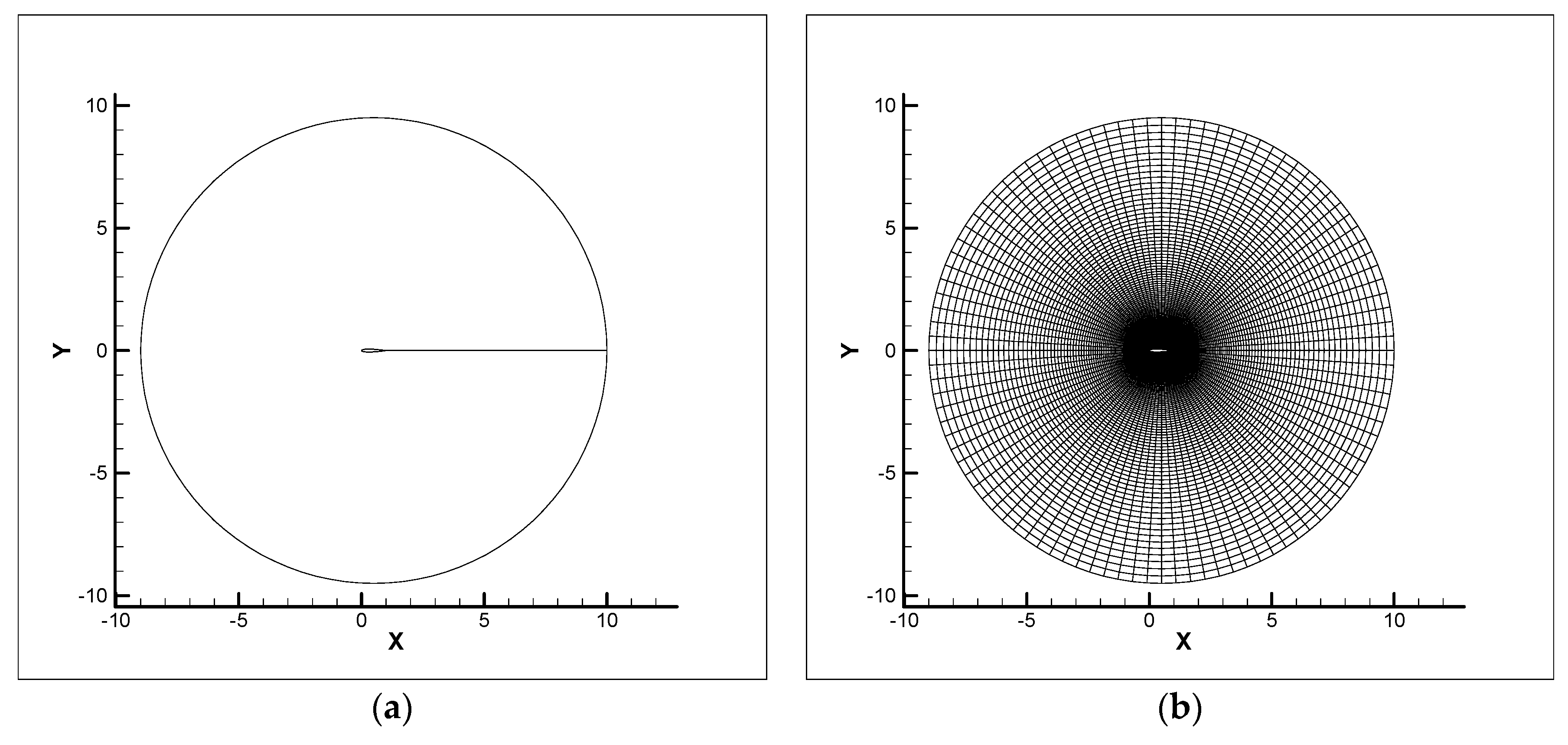
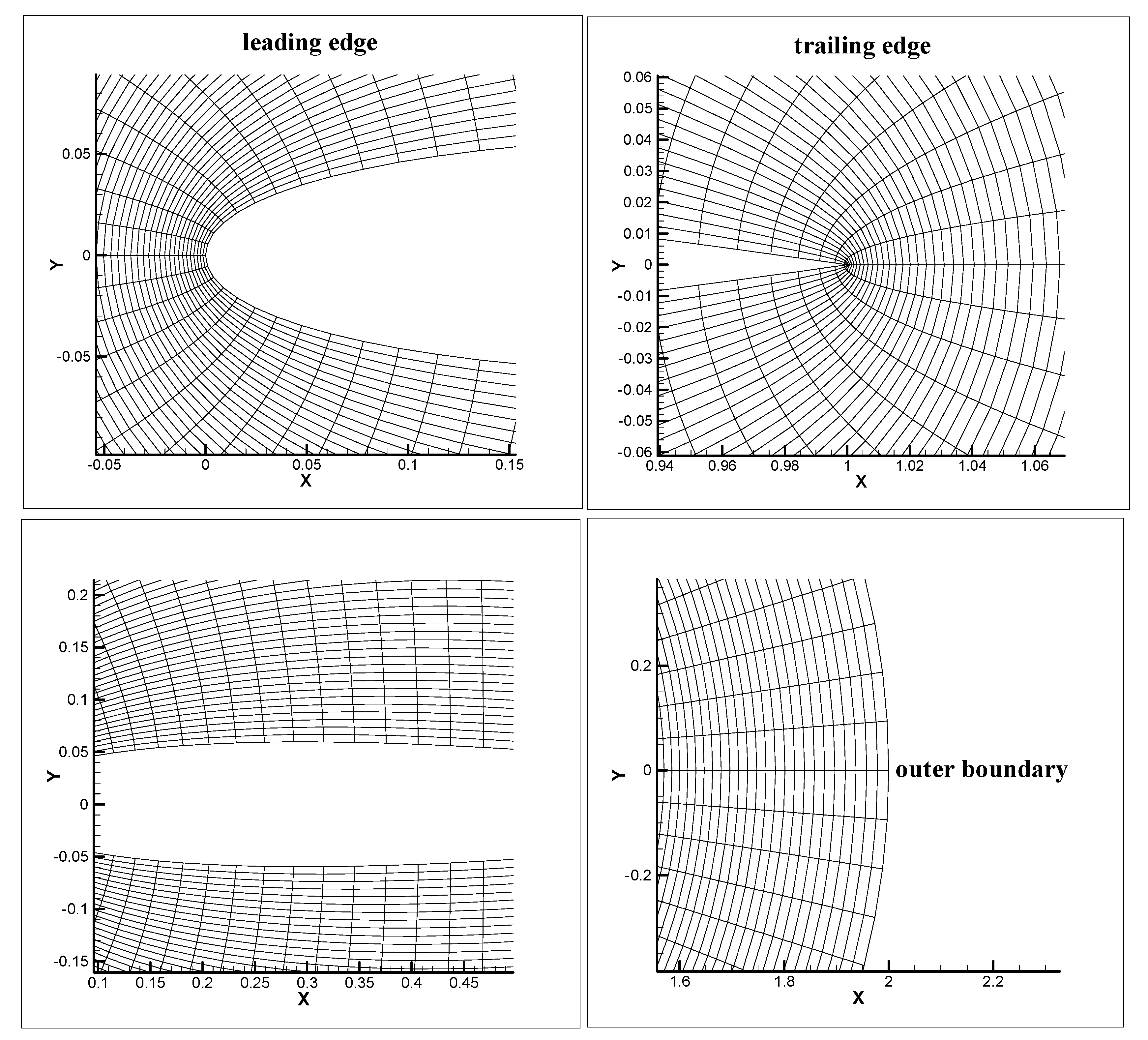
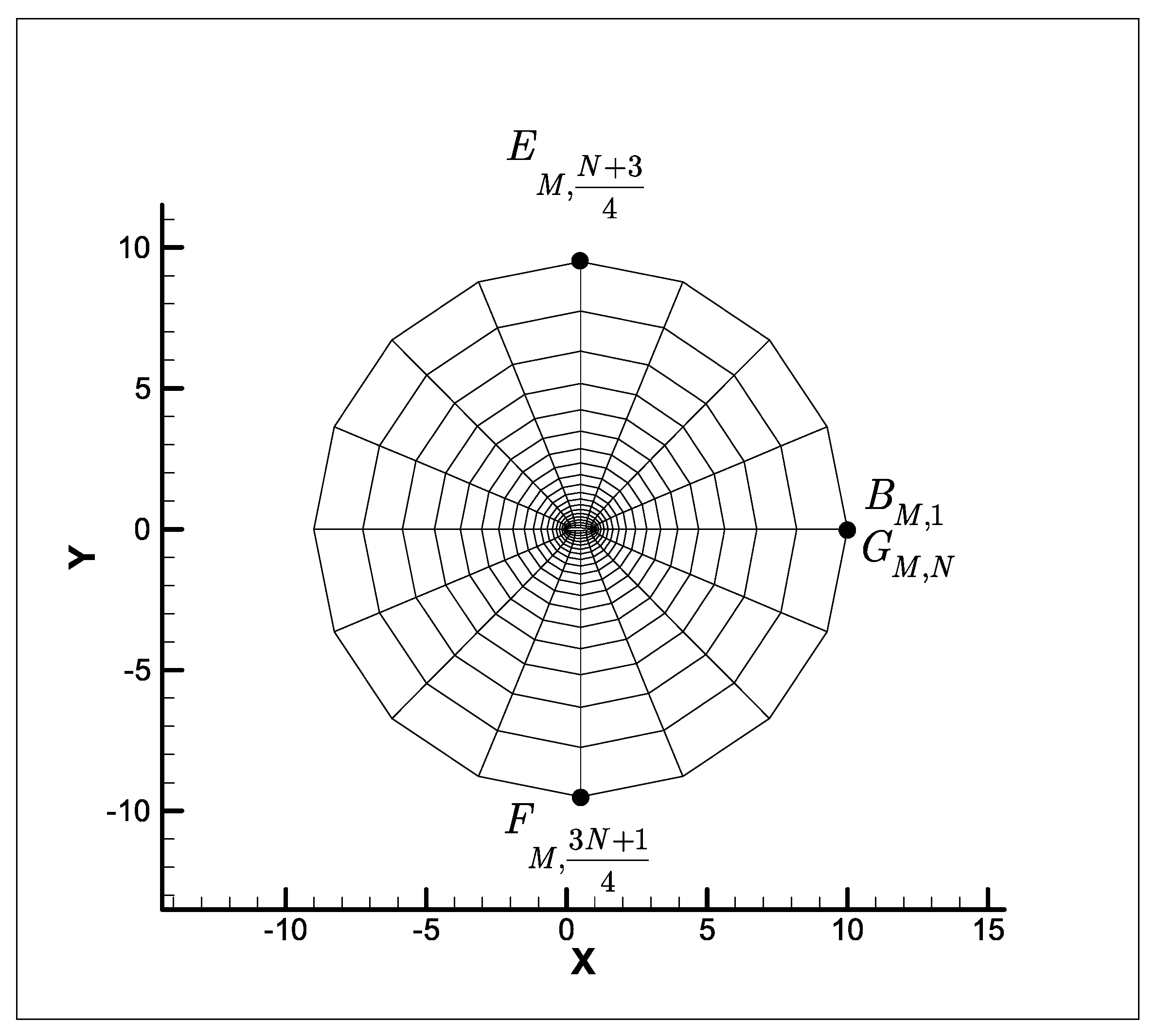
2.3. Grid Generation
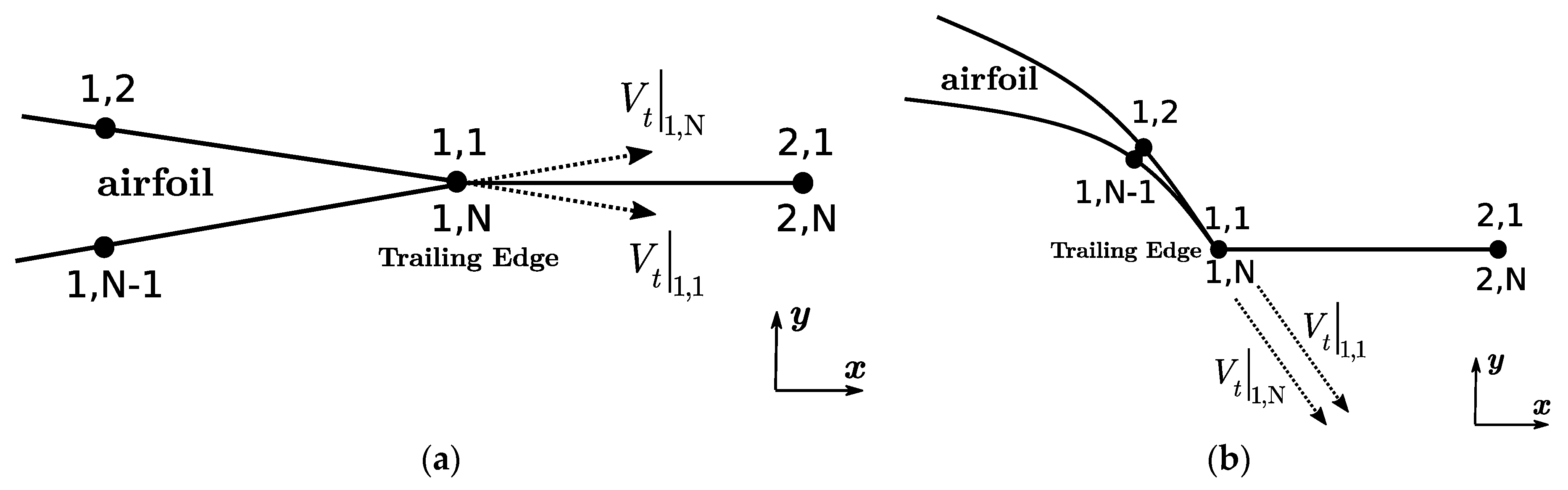
2.4. Kutta Condition
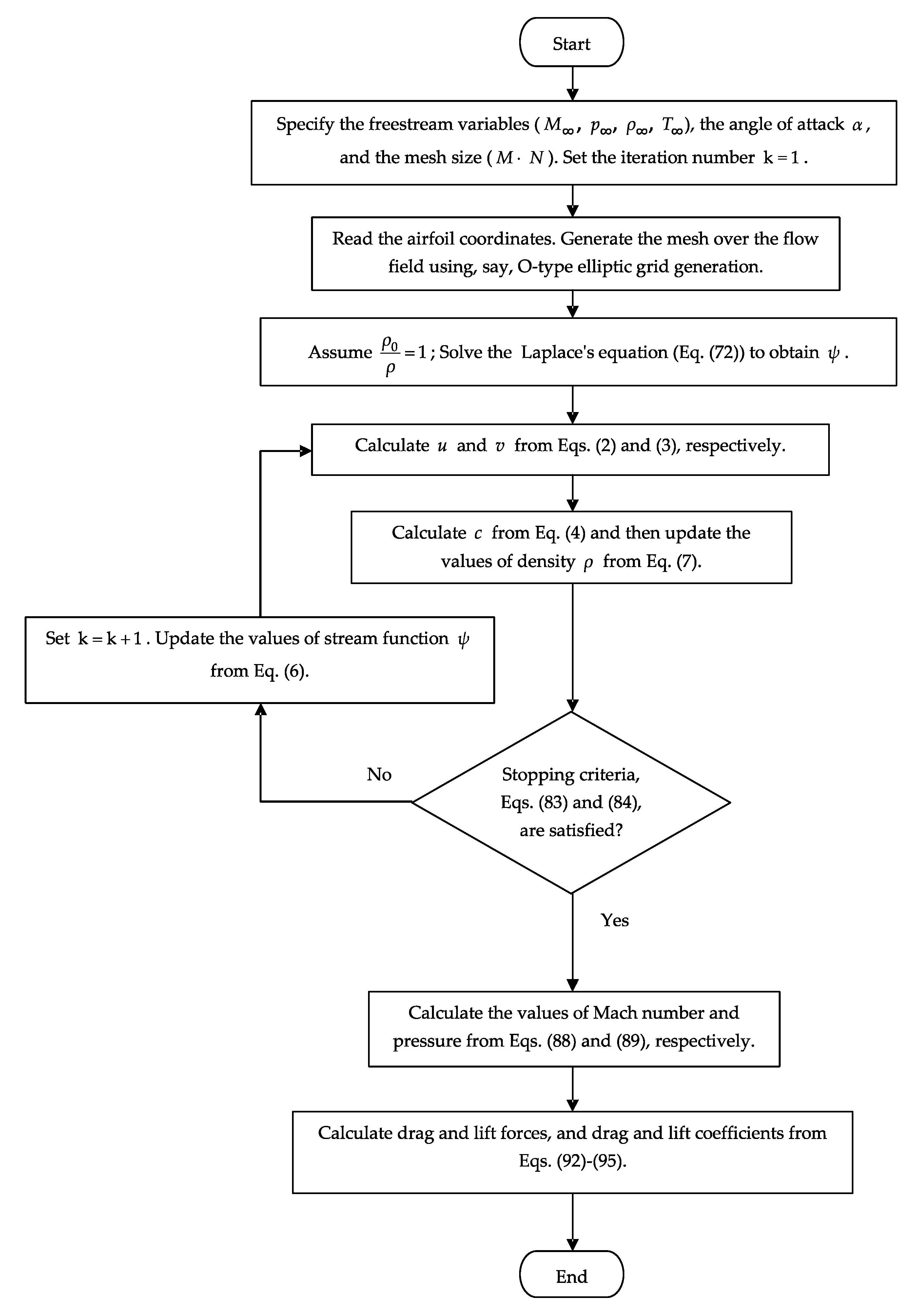
2.5. Computation Procedure
- Inside the domain to calculate the variables (, ).
- On the airfoil surface to calculate the variables ().
- At the outer boundary (far-field) to calculate the variables ().
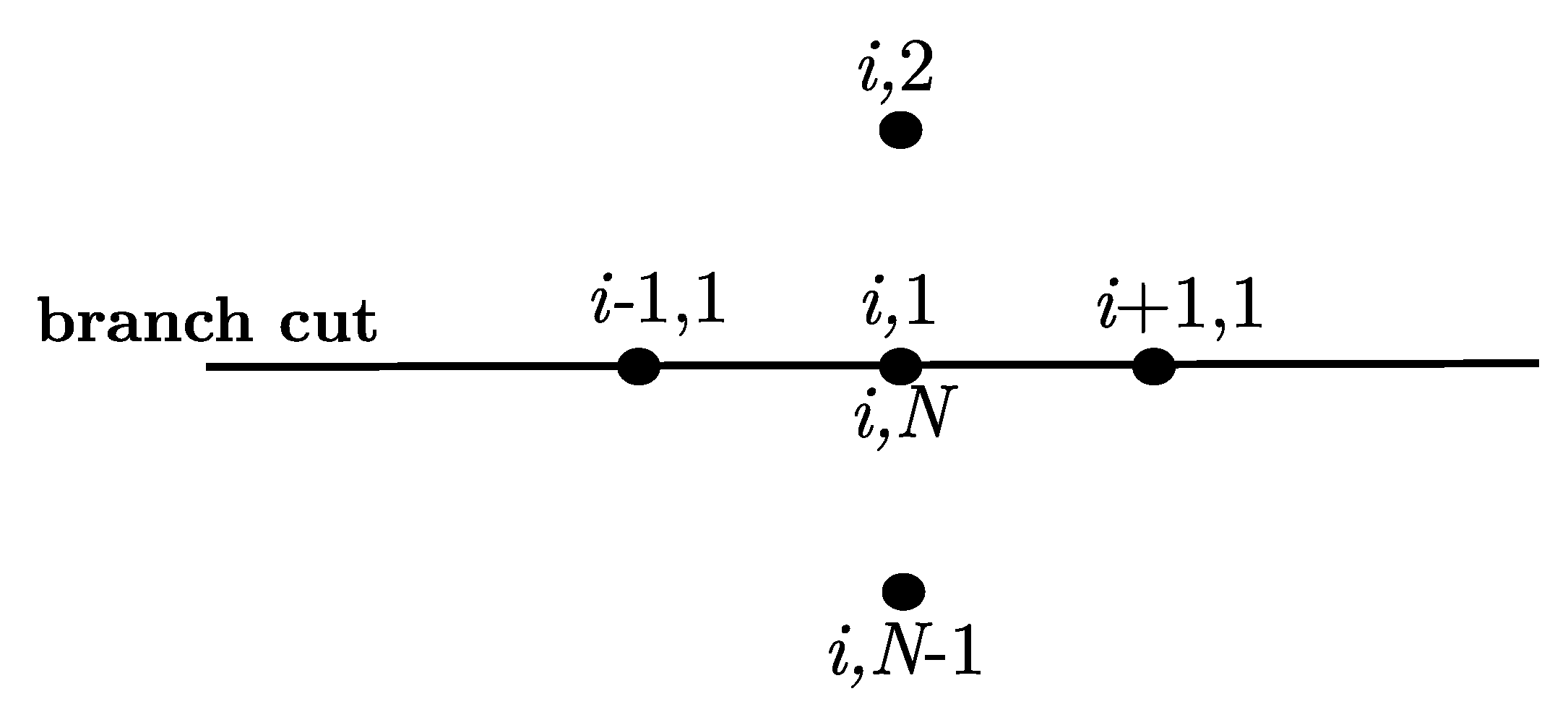
- On the branch cut to calculate the variables (). We know that .
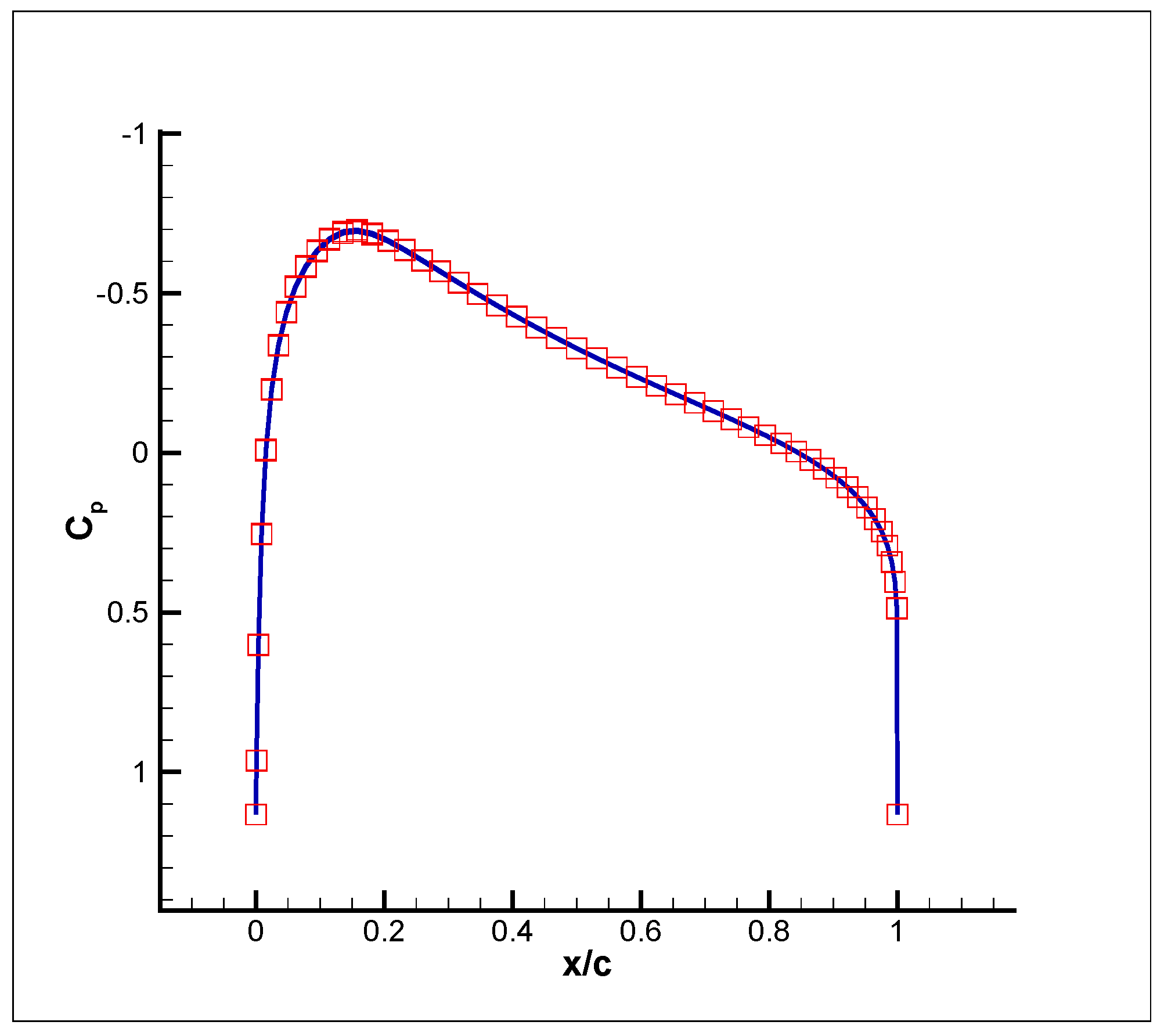
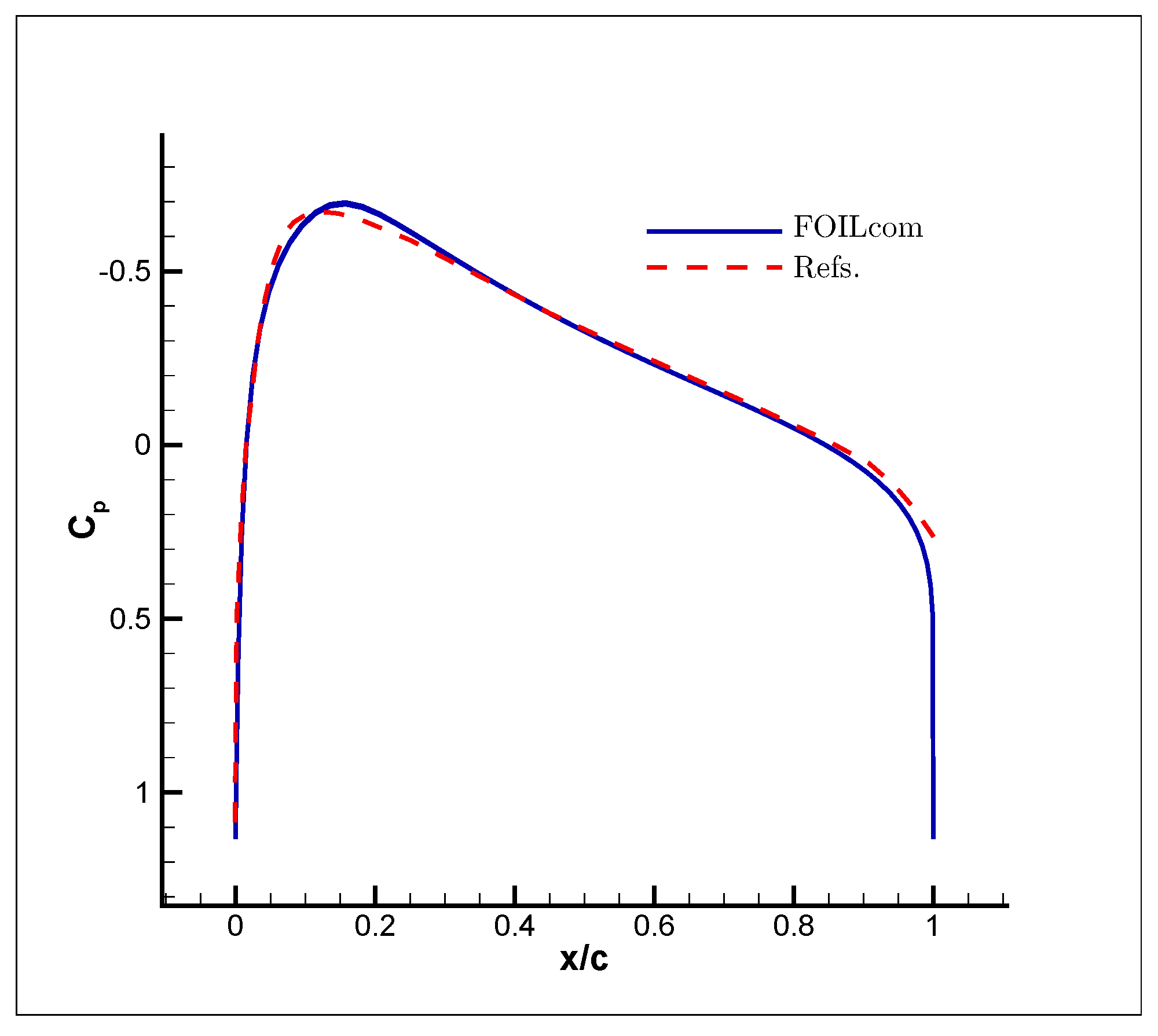
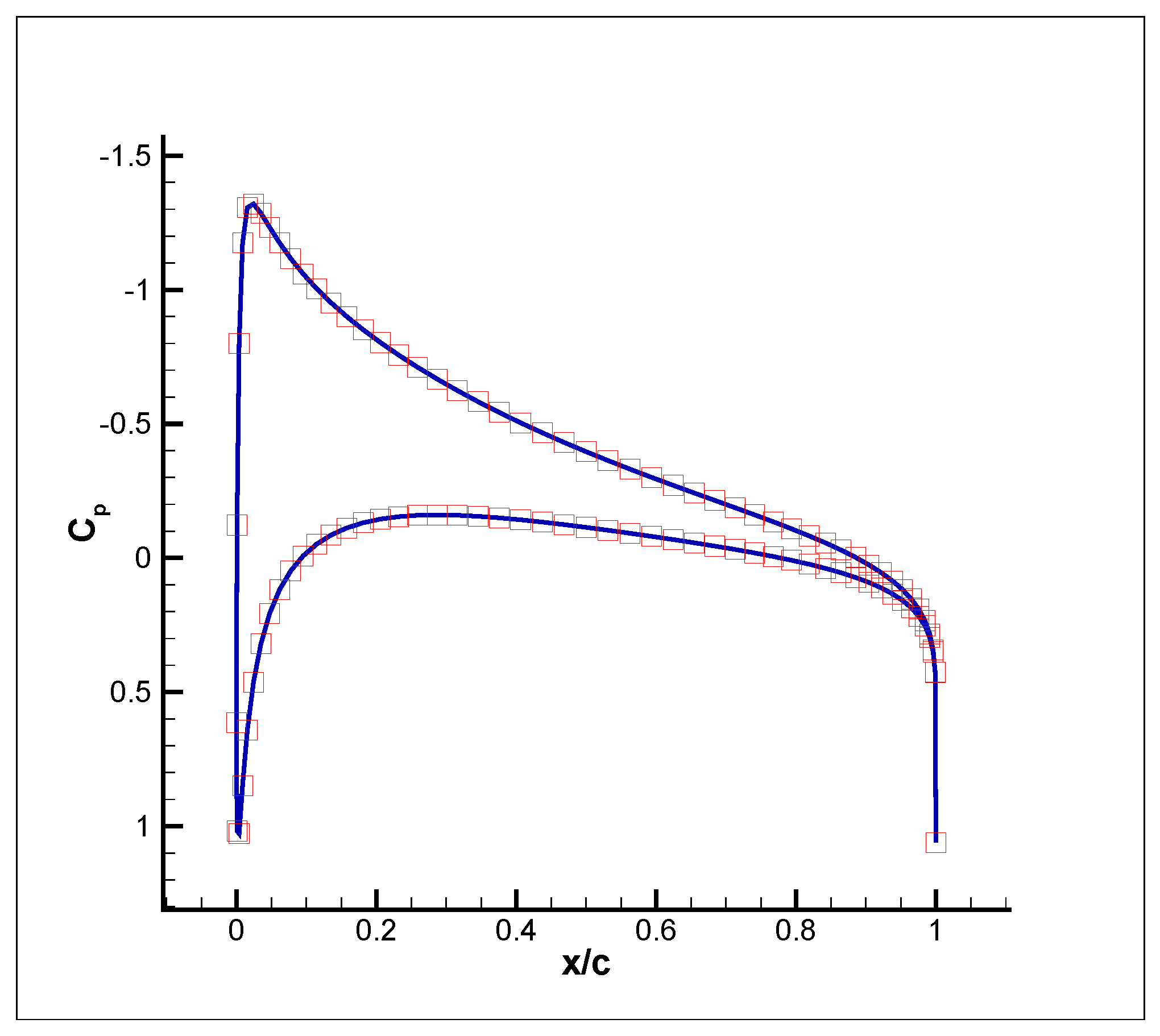
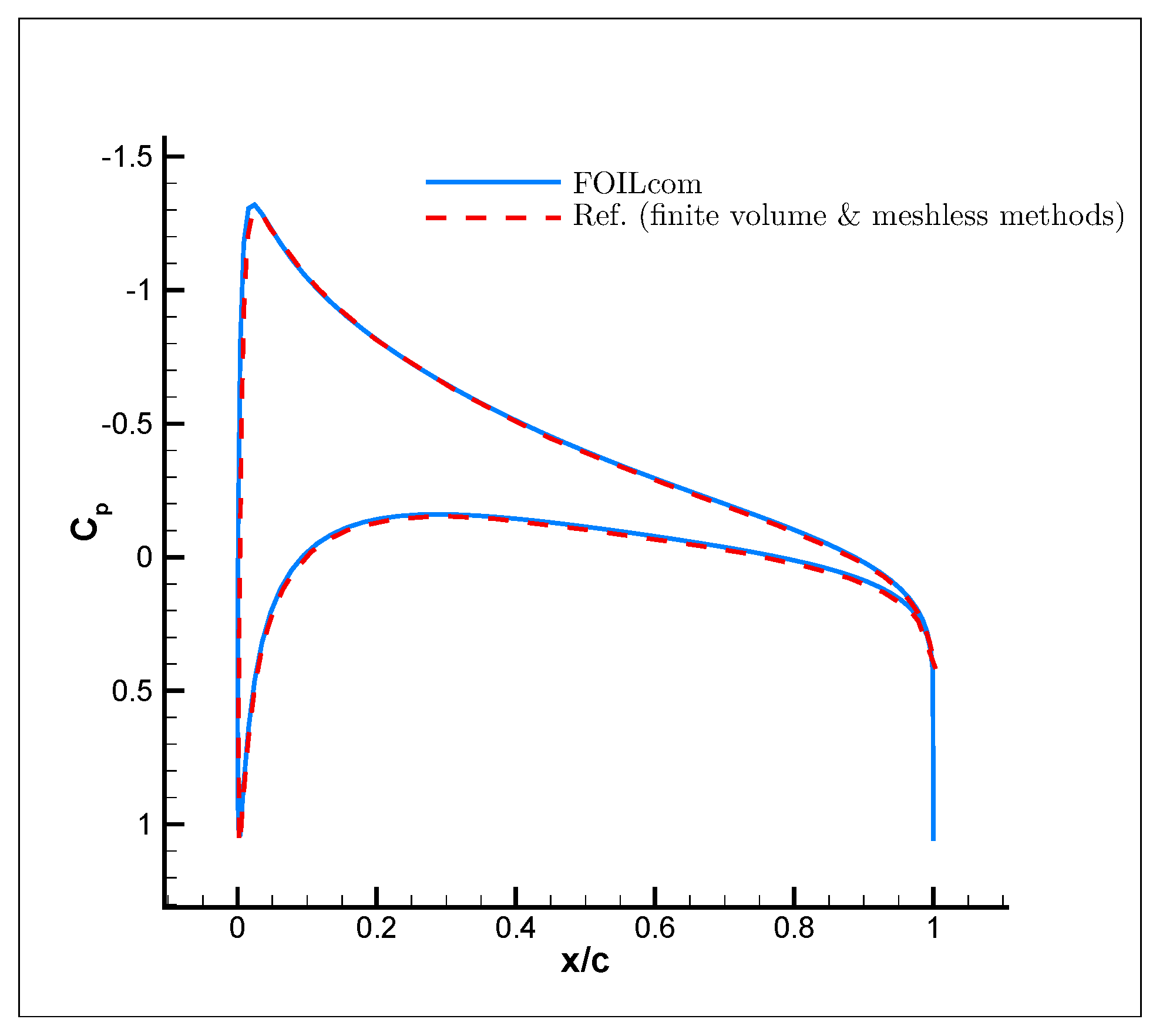
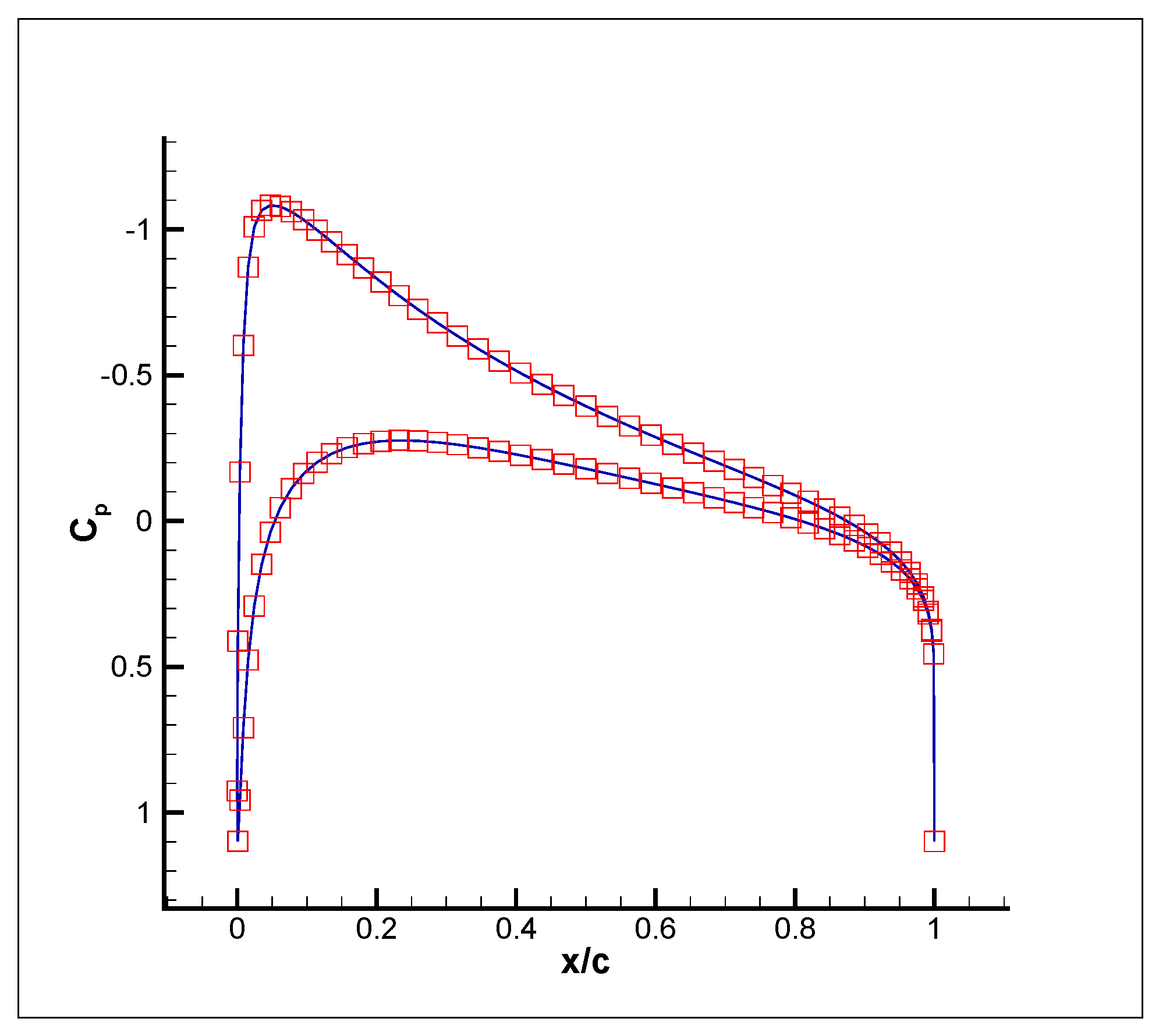
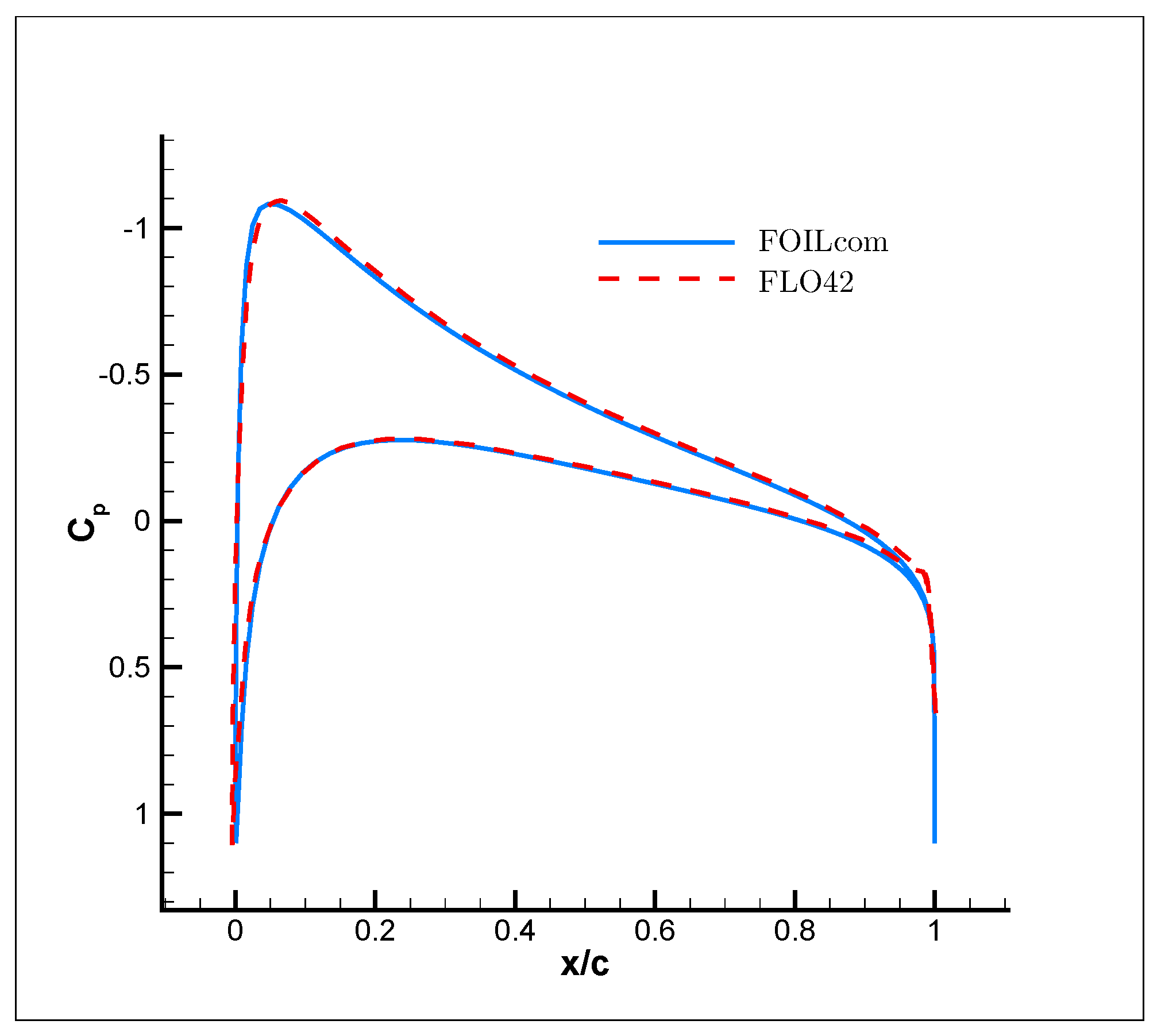
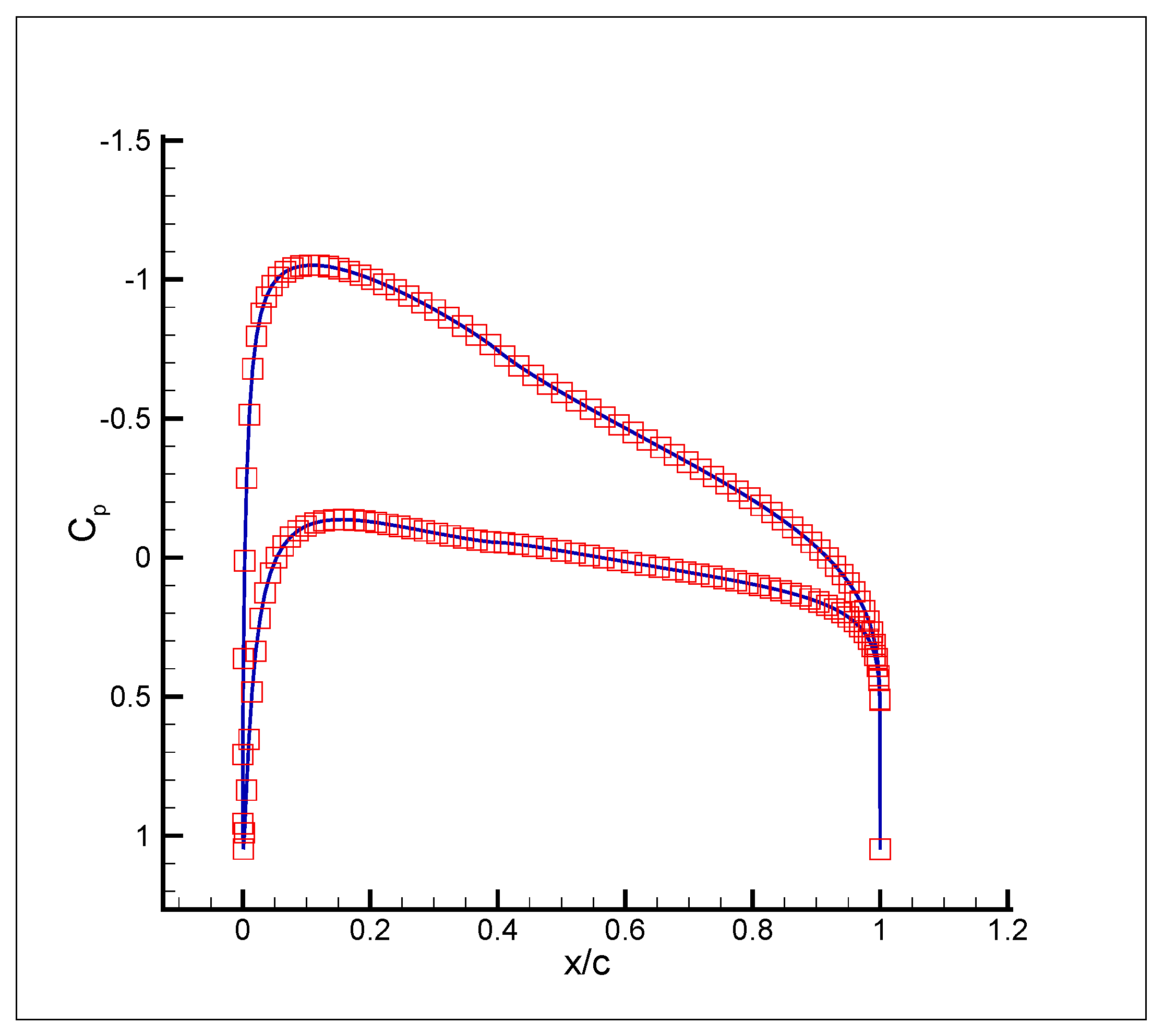
3. Results
- (a)
- (b)
- (c)
- (d)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| axial force | |
| speed of sound | |
| drag coefficient | |
| lift coefficient | |
| drag force | |
| Jacobian of transformation | |
| lift force | |
| Mach number | |
| normal force | |
| pressure | |
| temperature | |
| velocity components | |
| velocity | |
| Cartesian coordinates in the physical domain |
Greek symbols
| angle of attack, metric coefficient in 2-D elliptic grid generation | |
| ratio of specific heats | |
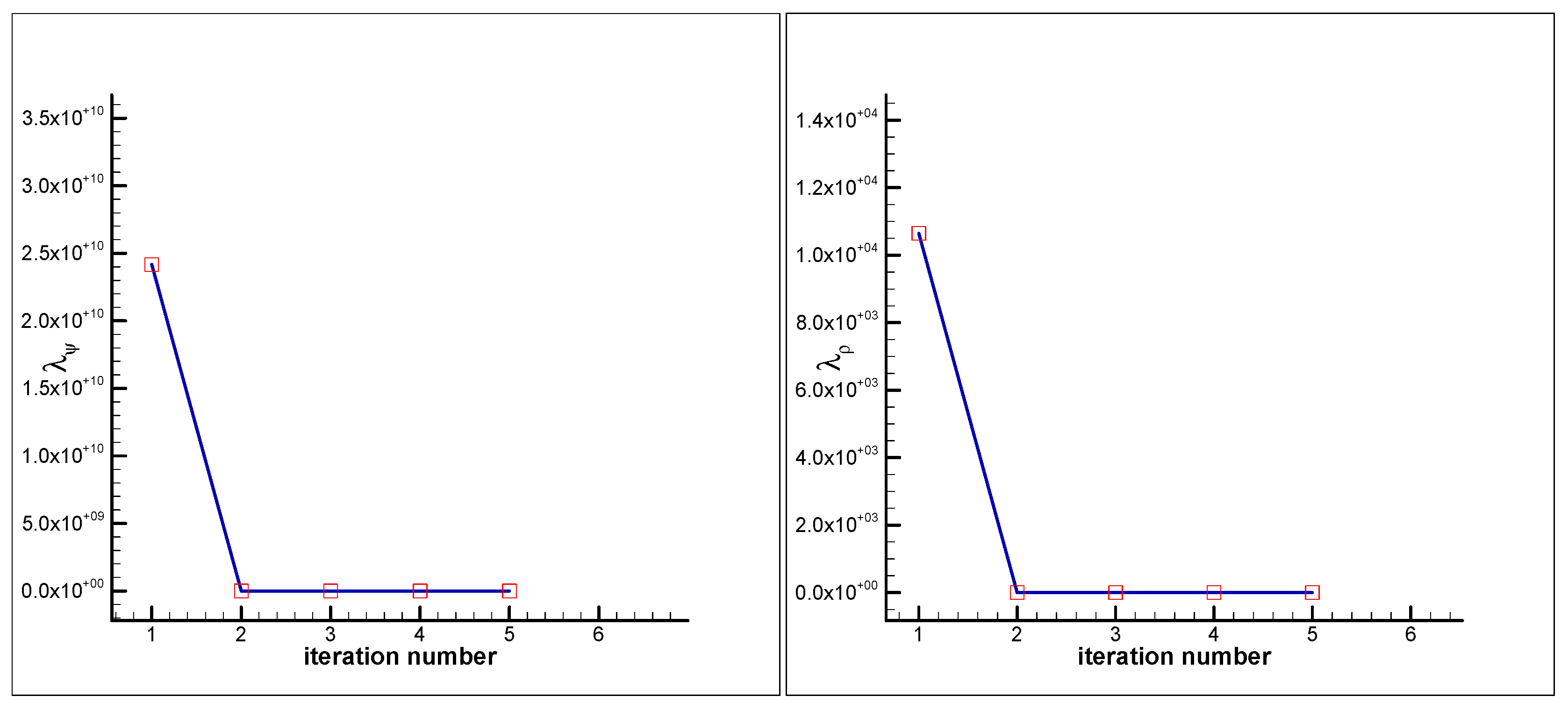
| stopping criterion | |
| density | |
| relaxation factor | |
| Cartesian coordinates in the computational domain | |
| stream function |
Subscripts
| stagnation condition | |
| free stream condition | |
| grid index in -direction | |
| grid index in -direction | |
| number of grid points in -direction | |
| number of grid points in -direction |
Superscript
| iteration number |
Abbreviations
| PDE | Partial Differential Equation |
| FDM | Finite Difference Method |
| SOR | Successive Over Relaxation |
References
- Hess, J.L.; Smith, A.M.O. Calculation of potential flow about arbitrary bodies. Prog. Aerosp. Sci. 1967, 8, 1–138. [Google Scholar] [CrossRef]
- Hess, J. Panel methods in computational fluid dynamics. Annu. Rev. Fluid Mech. 1990, 22, 255–274. [Google Scholar] [CrossRef]
- Erickson, L.L. Panel Methods: An Introduction; NASA Ames Research Center: Moffett Field, CA, USA, 1990. [Google Scholar]
- Anderson, J.D. Fundamentals of Aerodynamics; McGraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Drela, M. Flight Vehicle Aerodynamics; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Kutta, W.M. Lifting Forces in Flowing Fluids; G. Braunbeck & Gutenberg: Berlin, Germany, 1902. [Google Scholar]
- Lewis, R.I. Vortex Element Methods for Fluid Dynamic Analysis of Engineering Systems; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Xu, C. Kutta Condition for sharp edge flows. Mech. Res. Commun. 1998, 25, 415–420. [Google Scholar] [CrossRef]
- Jacob, K.; Riegels, F. The calculation of the pressure distribution over aerofoil sections of finite thickness with and without flaps and slats. Z. Flugwiss 1963, 11, 357–367. [Google Scholar]
- Drela, M. XFOIL: An analysis and design system for low Reynolds number airfoils. InLow Reynolds Number Aerodynamics; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Cummings, R.M.; Mason, W.H.; Morton, S.A.; McDaniel, D.R. Applied Computational Aerodynamics: A Modern Engineering Approach; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External Flows, Computational Methods for Inviscid and Viscous Flows; Wiley: Chichester, UK, 1991. [Google Scholar]
- Shapiro, A.H. The Dynamics and Thermodynamics of Compressible Fluid Flow; John Wiley & Sons: New York, NY, USA, 1953. [Google Scholar]
- Yahya, S.M. Fundamentals of Compressible Flow: SI Units with Aircraft and Rocket Propulsion; New Age International: Delhi, India, 2003. [Google Scholar]
- Johnson, R.W. Handbook of Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Mohebbi, F. Optimal Shape Design based on Body-Fitted Grid Generation; University of Canterbury: Christchurch, New Zealand, 2014. [Google Scholar]
- Thompson, J.; Warsi, Z.; Mastin, C. Numerical Grid Generation: Foundations and Applications. 1997. Available online: https://www.hpc.msstate.edu/publications/gridbook/PDFS/NumericalGridGenerationComplete.pdf (accessed on 25 June 2019).
- Özişik, M.N.; Orlande, H.R.B.; Colaço, M.J.; Cotta, R.M. Finite Difference Methods in Heat Transfer; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Thames, F.C.; Thompson, J.F.; Mastin, C.W. Numerical Solution of the Navier-Stokes Equations for Arbitrary Two-Dimensional Airfoils; Mississippi State Univiversity: Mississippi State, MS, USA, 1975. [Google Scholar]
- Mohebbi, F.; Sellier, M. On the Kutta condition in potential flow over airfoil. J. Aerodyn. 2014, 2014, 676912. [Google Scholar] [CrossRef]
- Freuler, R.; Gregorek, G. An Evaluation of Four Single Element Airfoil Analytic Methods; Ohio State University, General Aviation Airfoil Design and Analysis Center: Columbus, OH, USA, 1979. [Google Scholar]
- Katz, A.; Jameson, A. Meshless scheme based on alignment constraints. AIAA J. 2010, 48, 2501–2511. [Google Scholar] [CrossRef]
- Jameson, A.; Caughey, D.; Jou, W.; Steinhoff, J.; Pelz, R. Accelerated finite-volume calculation of transonic potential flows. In Numerical Methods for the Computation of Inviscid Transonic Flows with Shock Waves; Springer: Braunschweig, Germany, 1981; pp. 11–27. [Google Scholar]
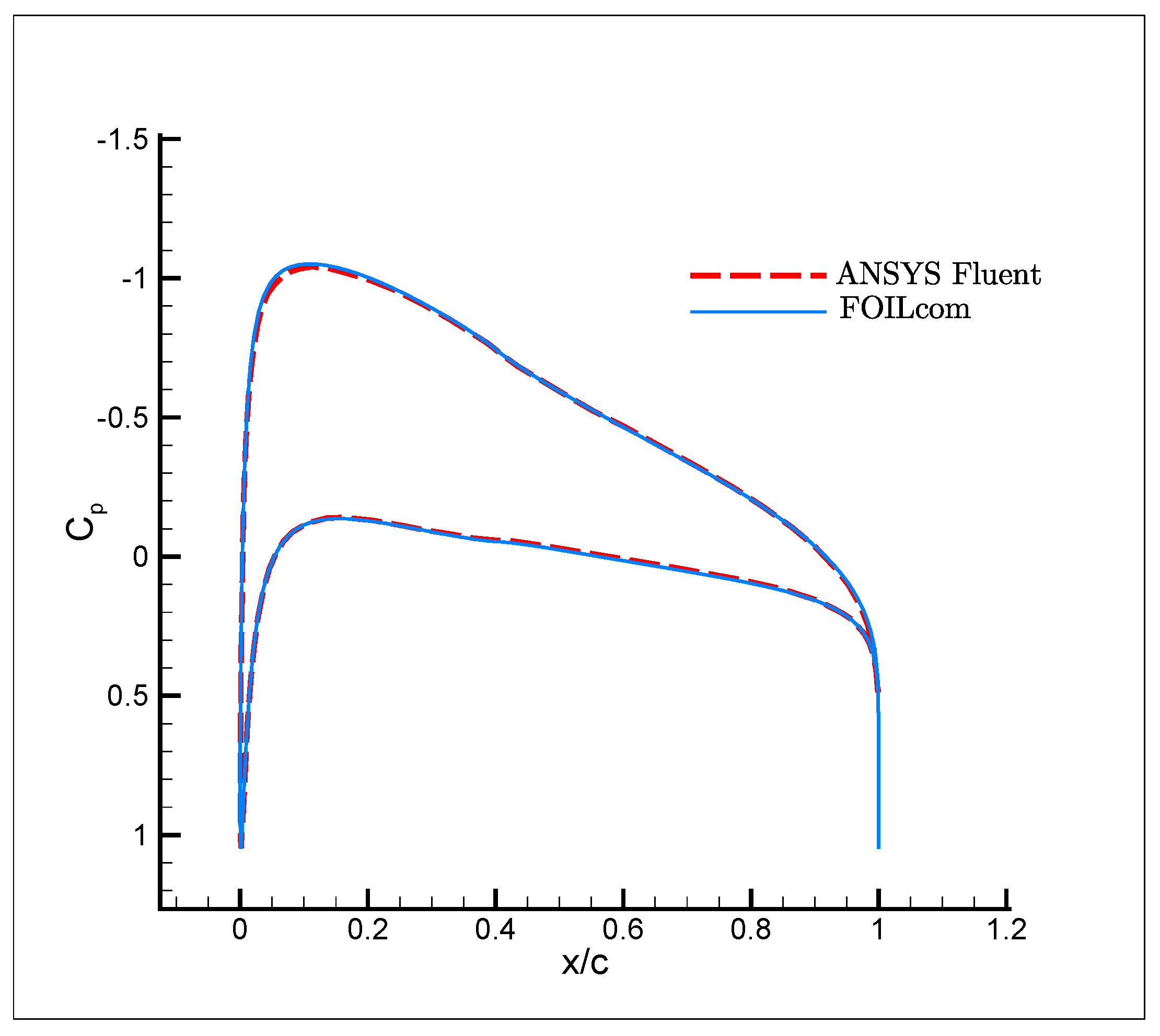

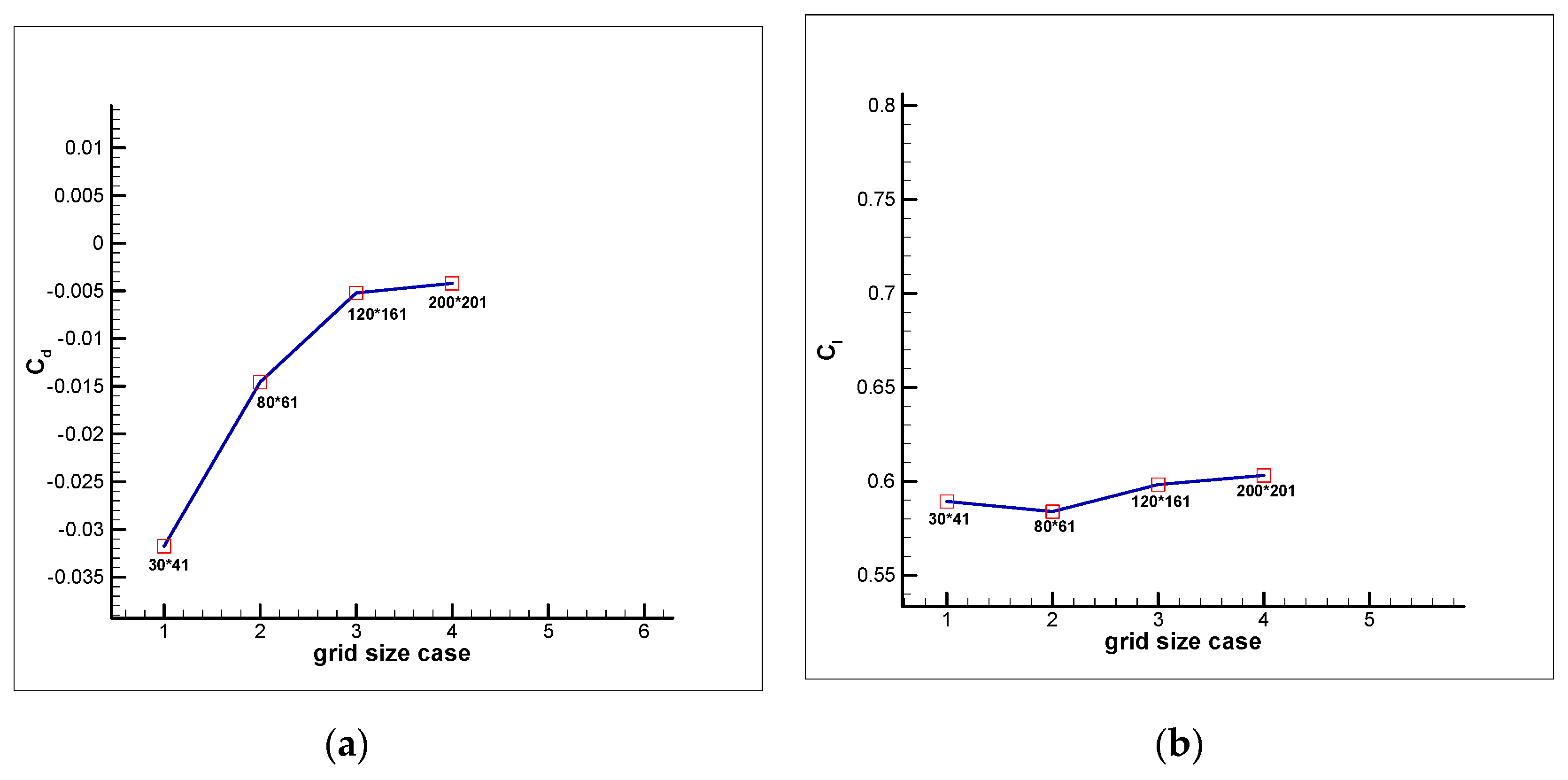
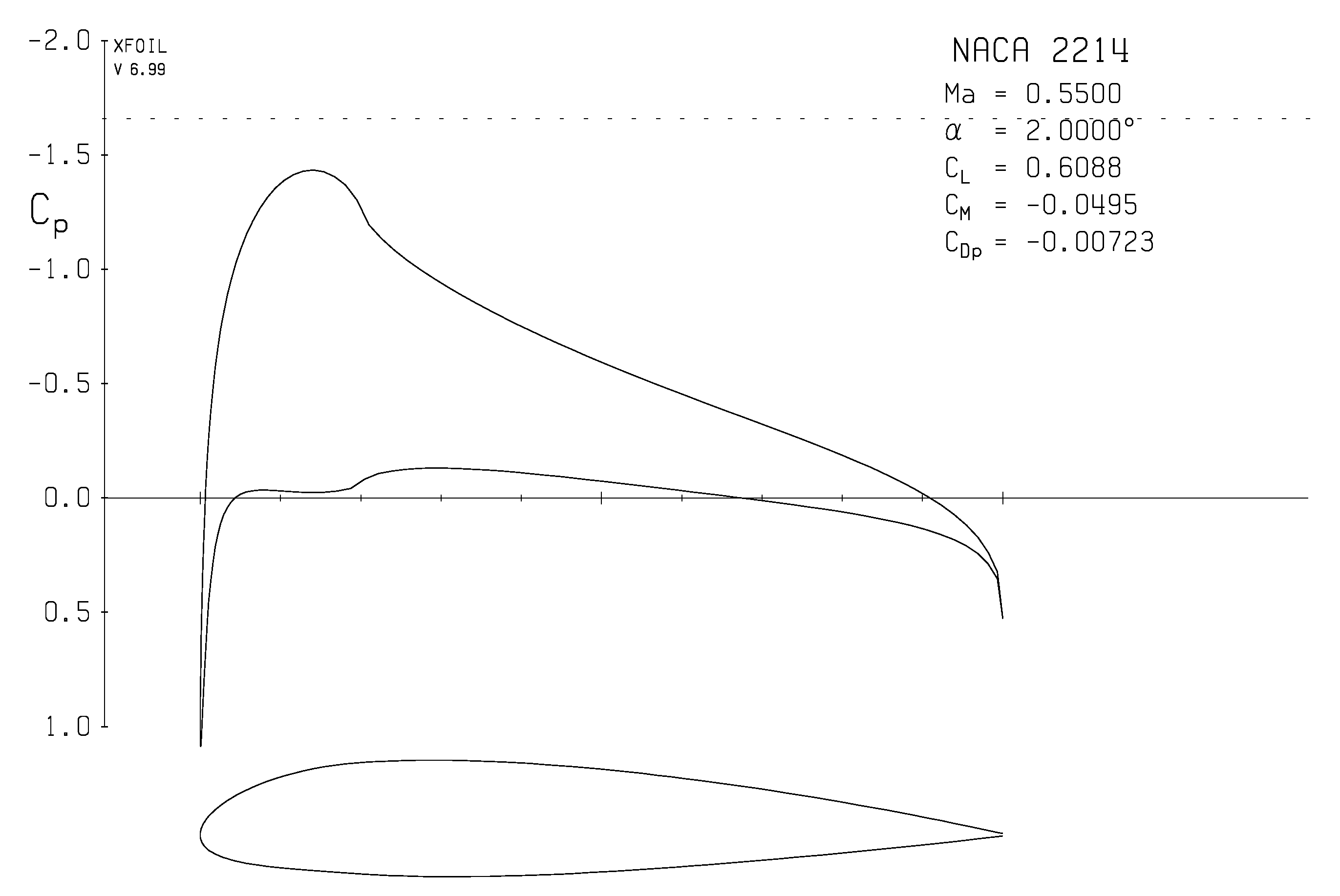
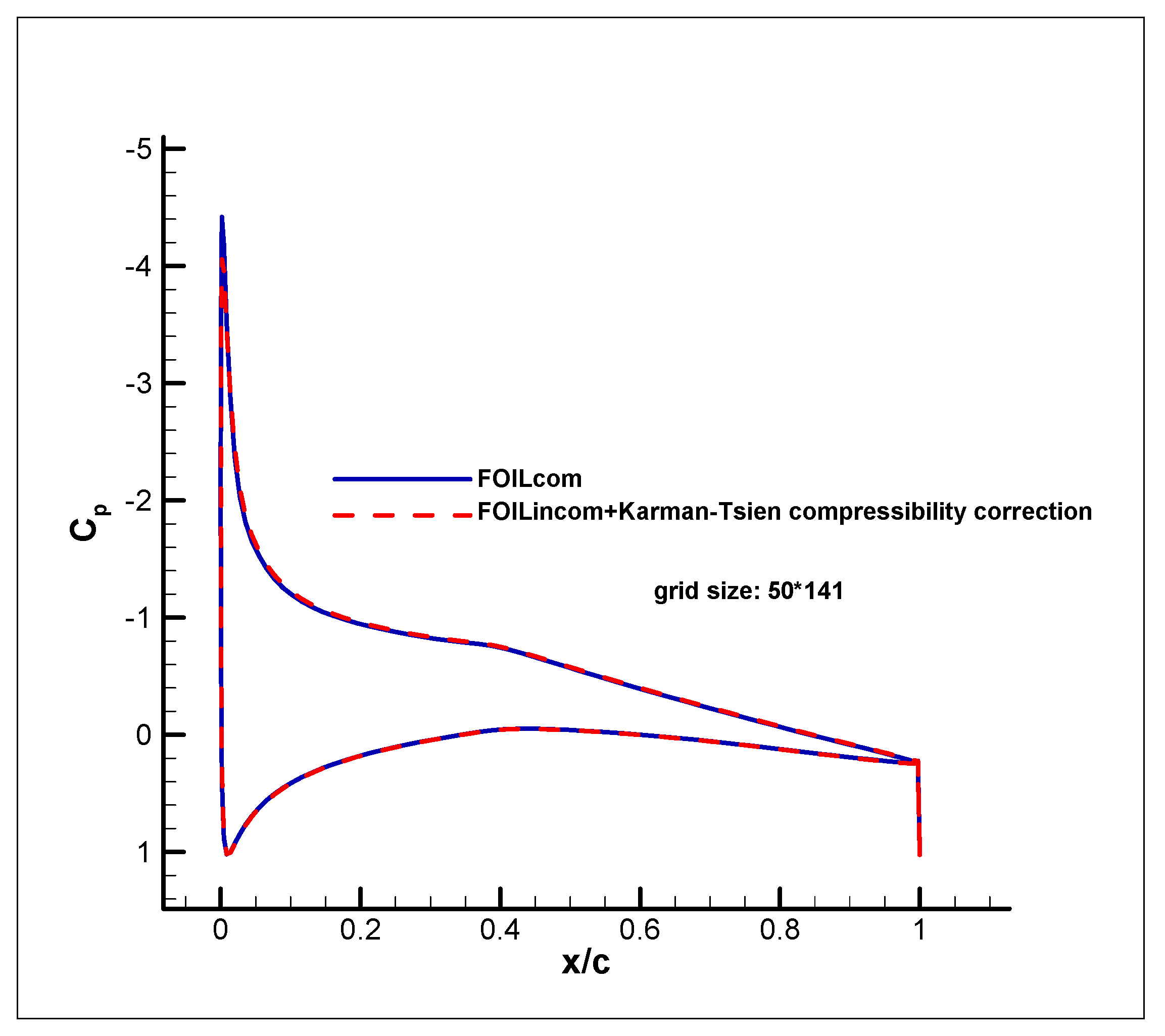



| Code and Grid Size | ||
|---|---|---|
| FOILcom: 30 × 41 | −3.1764 × 10−2 | 0.5893 |
| FOILcom: 80 × 61 | −1.4563 × 10−2 | 0.5839 |
| FOILcom: 120 × 161 | −5.2130 × 10−3 | 0.5983 |
| FOILcom: 200 × 201 | −4.2097 × 10−3 | 0.6032 |
| XFOIL | −7.23 × 10−3 | 0.6088 |
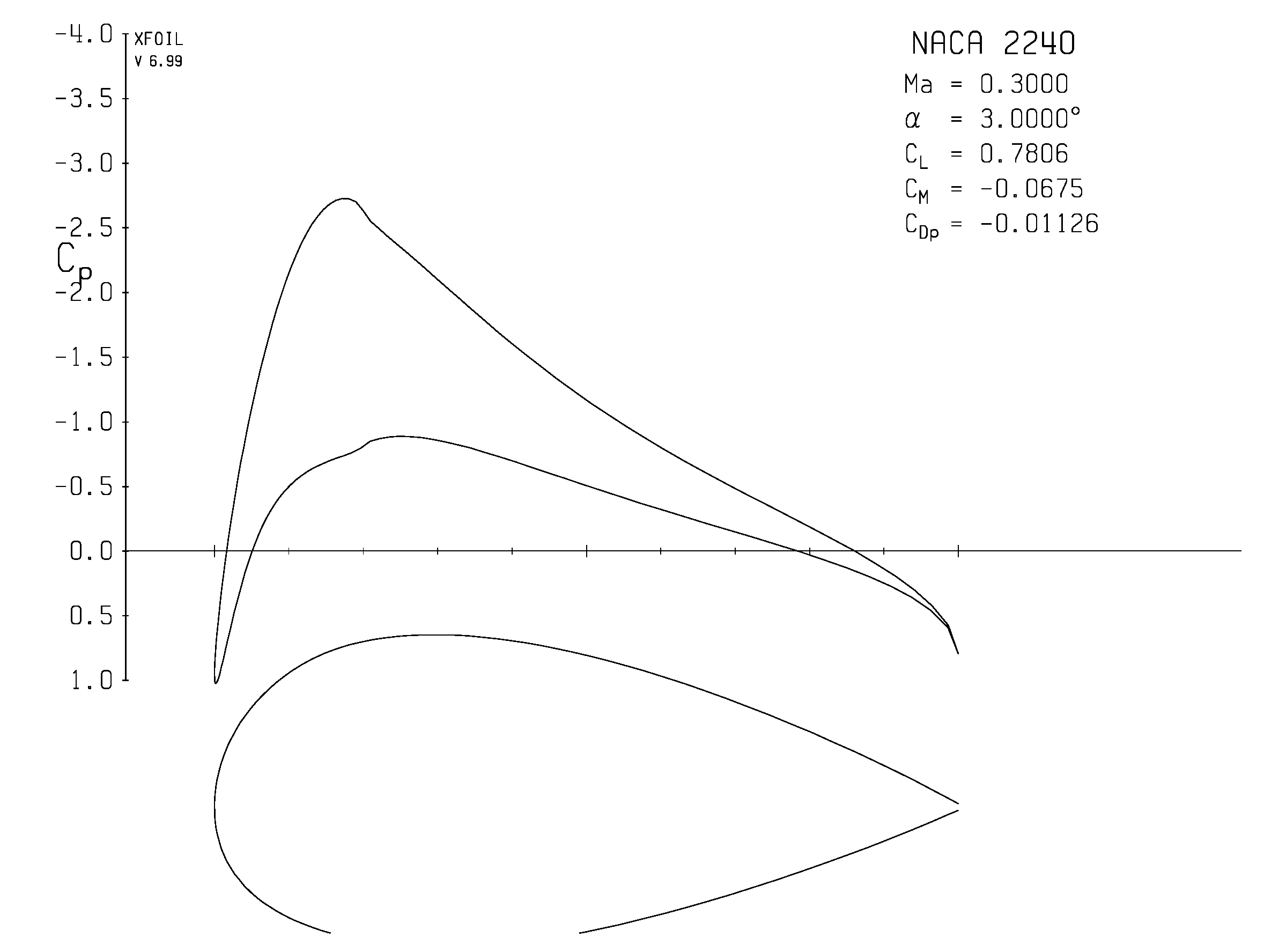
| NACA 2240 Airfoil | ||
|---|---|---|
| , | FOILcom: −0.01668 XFOIL: −0.01126 | FOILcom: 0.7977 XFOIL: 0.7806 |
| , | FOILcom: −0.02684 XFOIL: −0.01418 | FOILcom: 1.2714 XFOIL: 1.2718 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohebbi, F.; Evans, B.; Sellier, M. On the Kutta Condition in Compressible Flow over Isolated Airfoils. Fluids 2019, 4, 102. https://doi.org/10.3390/fluids4020102
Mohebbi F, Evans B, Sellier M. On the Kutta Condition in Compressible Flow over Isolated Airfoils. Fluids. 2019; 4(2):102. https://doi.org/10.3390/fluids4020102
Chicago/Turabian StyleMohebbi, Farzad, Ben Evans, and Mathieu Sellier. 2019. "On the Kutta Condition in Compressible Flow over Isolated Airfoils" Fluids 4, no. 2: 102. https://doi.org/10.3390/fluids4020102
APA StyleMohebbi, F., Evans, B., & Sellier, M. (2019). On the Kutta Condition in Compressible Flow over Isolated Airfoils. Fluids, 4(2), 102. https://doi.org/10.3390/fluids4020102






