Jovian Vortices and Jets
Abstract
1. Introduction
2. Model and Technique
2.1. Layer Model Review
2.2. Hamiltonian Structure of -Layer Model
2.3. Dirac Constraints and Steady States
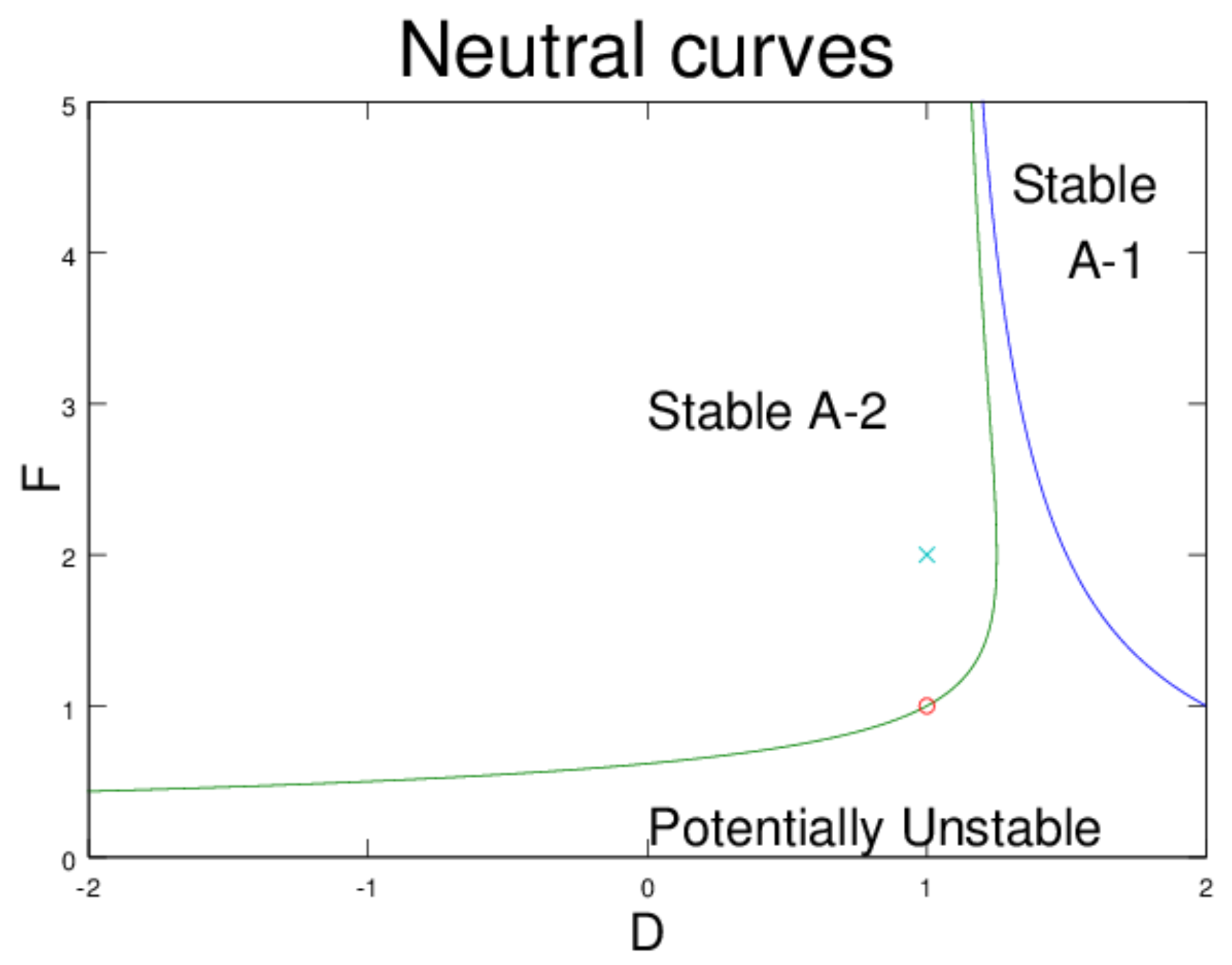
3. Deep and Shallow Jets: Stability
3.1. General Form
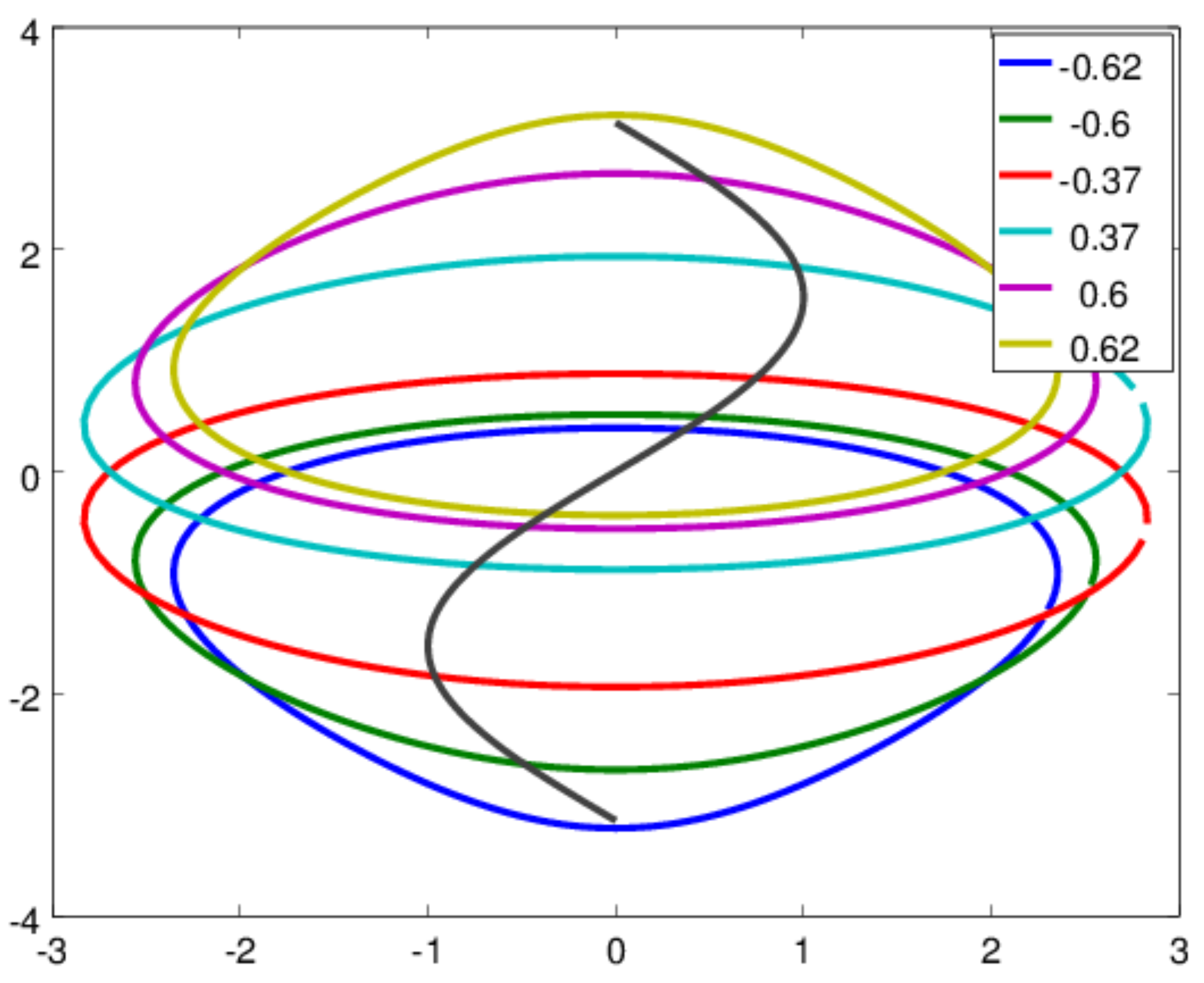
3.2. Localized Vortex in Jets
3.3. Vortices and Jets with a Linear PV–Streamfunction Relationship
4. Steady State Vortices
4.1. Localized Vortex in Jets—Linear Structures
4.2. Integral Conditions
4.3. Linear Jets
4.4. Modified Dynamics
5. Hamiltonian Contour Dynamics and Synthetic Annealing
5.1. Hamiltonian Structure of Contour Dynamics
5.2. Dirac Brackets and Simulated Annealing
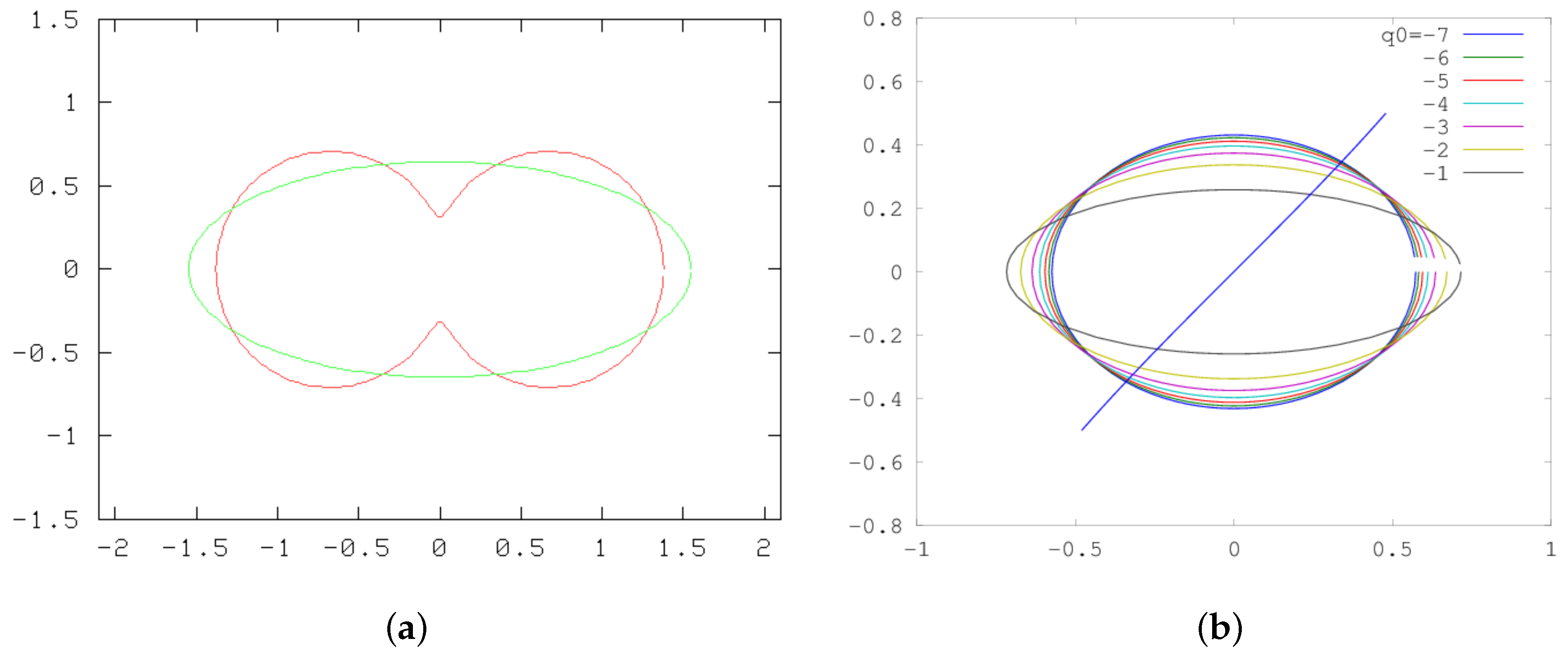
5.3. The Kirchhoff Ellipse with Shear
5.4. Application to Jovian Vortices
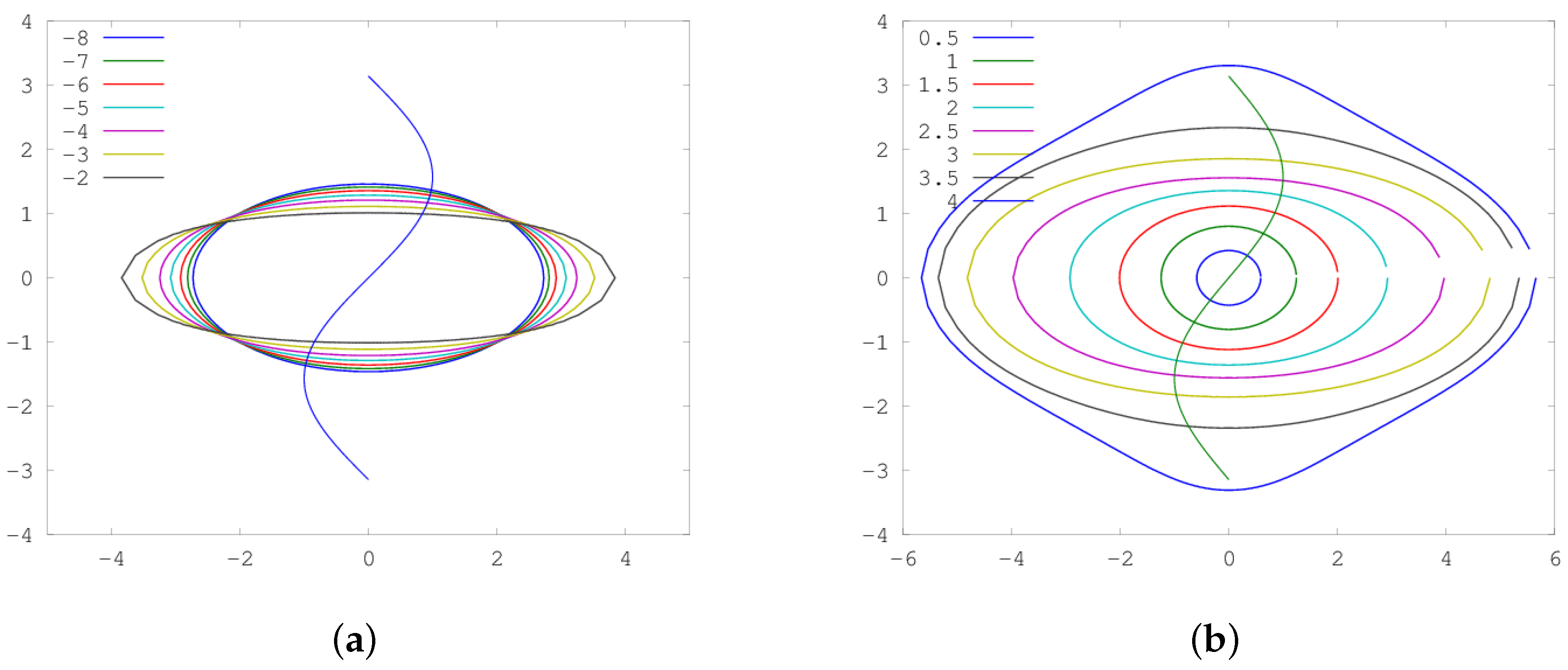
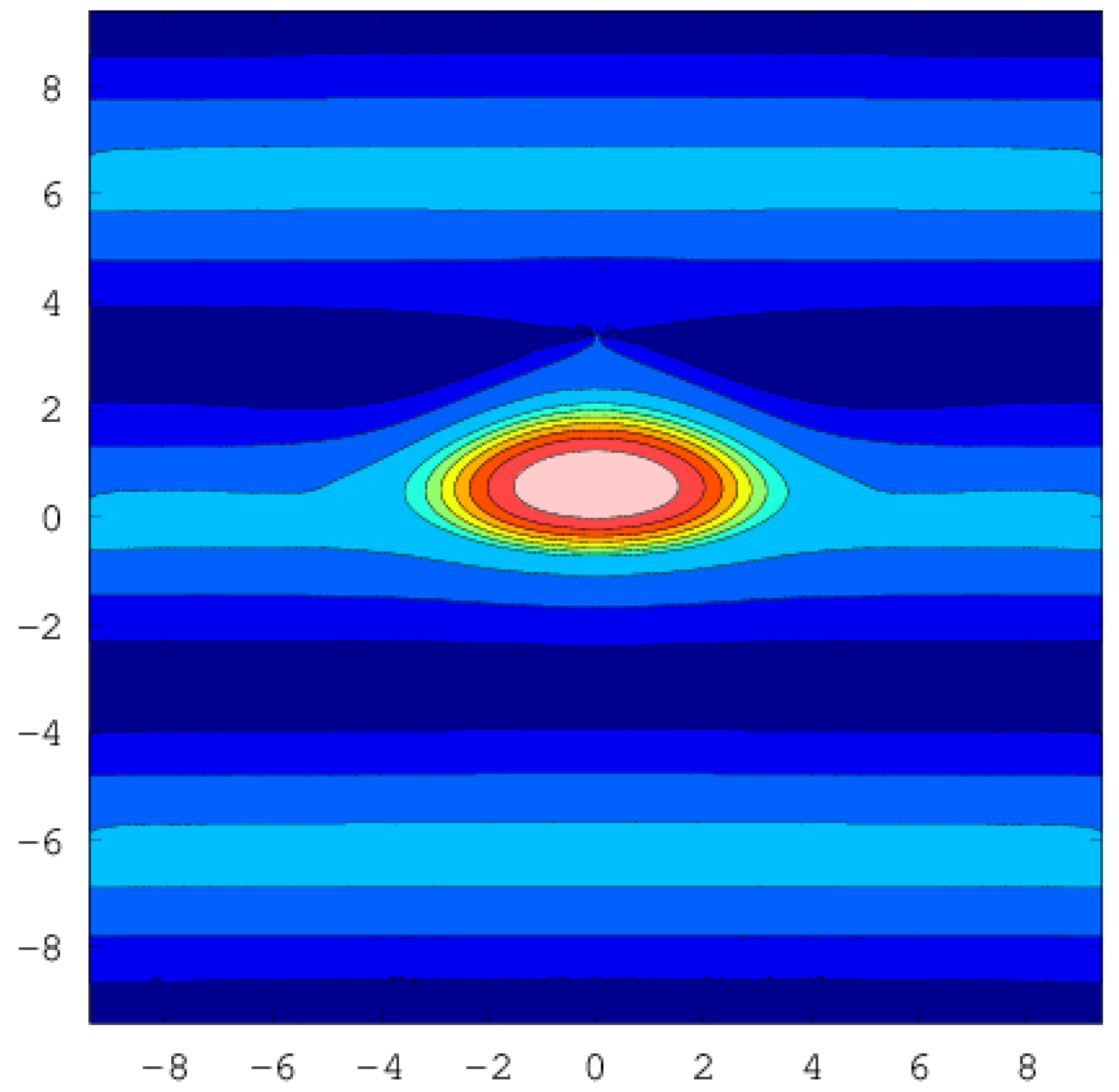
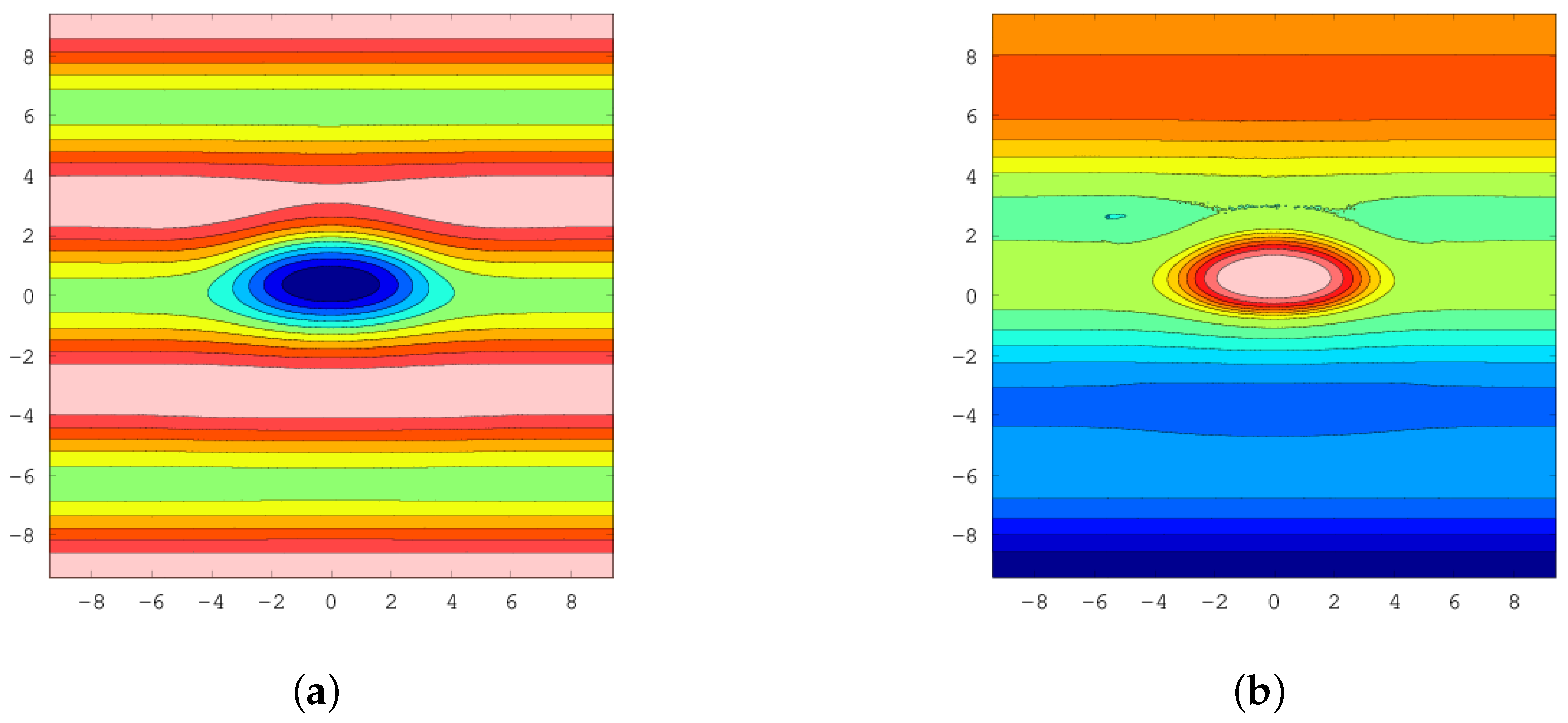
6. Results
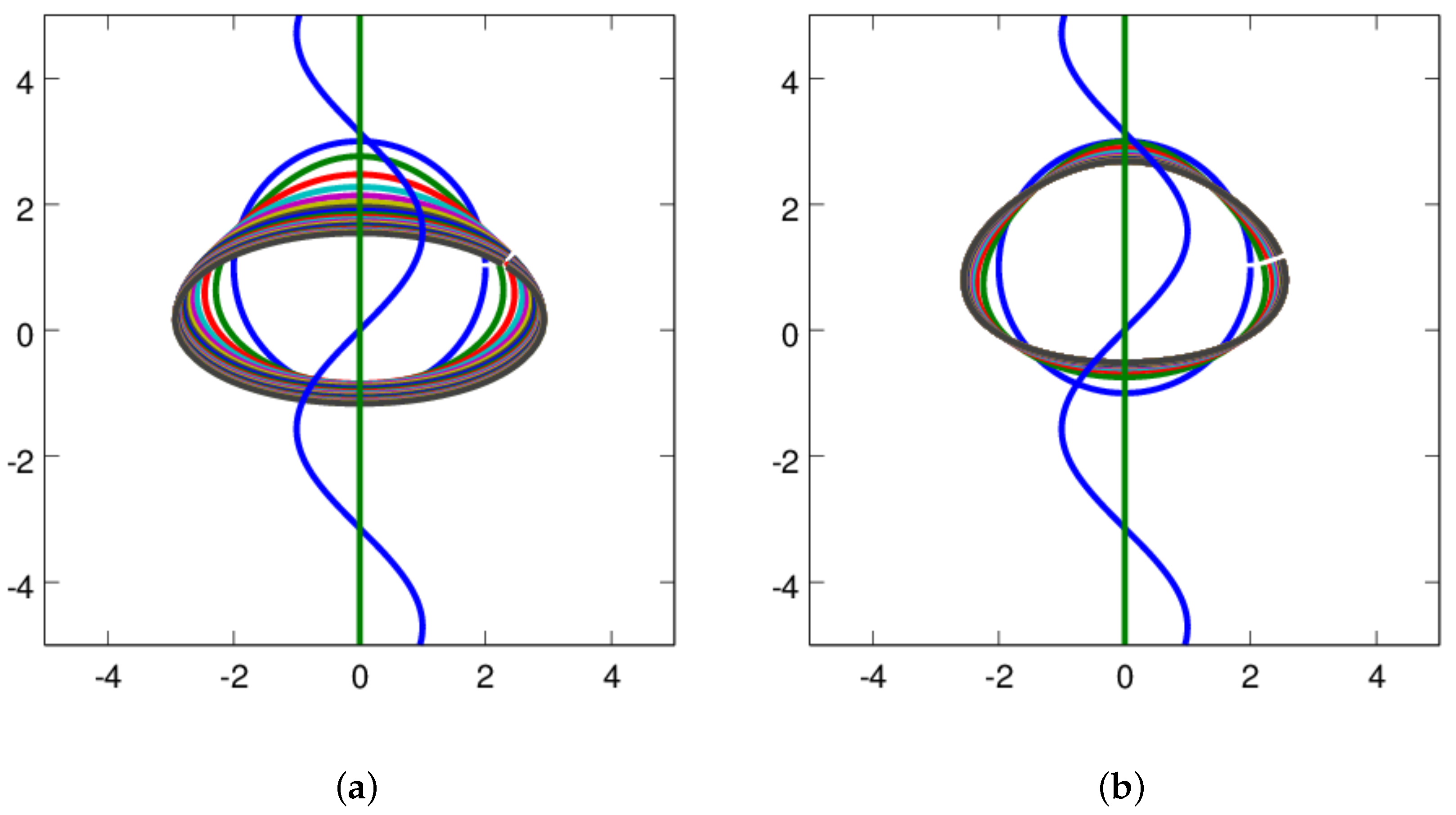
6.1. CD–DBSA
6.2. Comparison with Continuous Case
7. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maxworthy, T.; Redekopp, L.G. A solitary wave theory of the great red spot and other observed features in the Jovian atmosphere. Icarus 1976, 29, 261–271. [Google Scholar] [CrossRef]
- Marcus, P.S. Numerical simulation of Jupiter’s Great Red Spot. Nature 1988, 331, 693–696. [Google Scholar] [CrossRef]
- Dowling, T.E.; Ingersoll, A.P. Jupiter’s Great Red Spot as a shallow water system. J. Atmos. Sci. 1989, 46, 3256–3278. [Google Scholar] [CrossRef]
- Williams, G.P. Jovian Dynamics. Part 1: Vortex Stability, Structure, and Genesis. J. Atmos. Sci. 1996, 53, 2685–2734. [Google Scholar] [CrossRef][Green Version]
- Morrison, P.J. Poisson Brackets for Fluids and Plasmas. AIP Conf. Proc. 1982, 88, 13–46. [Google Scholar]
- Morrison, P.J. Hamiltonian Description of the Ideal Fluid. Rev. Mod. Phys. 1998, 70, 467–521. [Google Scholar] [CrossRef]
- Morrison, P.J. Hamiltonian and Action Principle Formulations of Plasma Physics. Phys. Plasmas 2005, 12, 058102. [Google Scholar] [CrossRef]
- Vallis, G.K.; Carnevale, G.; Young, W.R. Extremal Energy Properties and Construction of Stable Solutions of the Euler Equations. J. Fluid Mech. 1989, 207, 133–152. [Google Scholar] [CrossRef]
- Flierl, G.R.; Morrison, P.J. Hamiltonian-Dirac Simulated Annealing: Application to the Calculation of Vortex States. Physica D 2011, 240, 212–232. [Google Scholar] [CrossRef]
- Stamp, A.P.; Dowling, T.E. Jupiter’s Winds and Arnol’d’s Second Stability Theorem: Slowly Moving Waves and Neutral Stability. J. Geophys. Res. 1993, 98, 18847–18855. [Google Scholar] [CrossRef]
- Kaspi, Y.; Flierl, G.R. Formation of Jets by Baroclinic Instability on Gas Planet Atmospheres. J. Atmos. Sci. 2007, 64, 3177–3194. [Google Scholar] [CrossRef]
- Yano, J.I.; Flierl, G.R. Jupiter’s Great Red Spot: Compactness Condition and Stability. Annales Geophysicae 1994, 12, 1–18. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer: New York, NY, USA, 1987. [Google Scholar]
- Dirac, P. Generalized Hamiltonian dynamics. Can. J. Math. 1950, 2, 129–148. [Google Scholar] [CrossRef]
- Morrison, P.J.; Lebovitz, N.R.; Biello, J. The Hamiltonian Description of Incompressible Fluid ellipsoids. Ann. Phys. 2009, 324, 1747–1762. [Google Scholar] [CrossRef]
- Chandre, C.; Morrison, P.J.; Tassi, E. On the Hamiltonian formulation of incompressible ideal fluids and magnetohydrodynamics via Dirac’s theory of constraints. Phys. Lett. A 2012, 376, 737–743. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Morrison, P.J. Hamiltonian Description of Shear Flow. In Large-Scale Atmosphere-Ocean Dynamics 2: Geometric Methods and Models; Norbury, J., Roulstone, I., Eds.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Hirota, M.; Morrison, P.J.; Hattori, Y. Variational Necessary and Sufficient Stability Conditions for Inviscid Shear Flow. Proc. R. Soc. A 2014, 470, 20140322. [Google Scholar] [CrossRef]
- Hagstrom, G.; Morrison, P.J. Continuum Hamiltonian Hopf Bifurcation II. In Nonlinear Physical Systems—Spectral Analysis, Stability and Bifurcations; Kirillov, O., Pelinovsky, D., Eds.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Roberts, K.V.; Christiansen, J.P. Topics in computational fluid mechanics. Comput. Phys. Commun. 1972, 3, 14–32. [Google Scholar] [CrossRef]
- Zabusky, N.J.; Hughes, M.H.; Roberts, K.V. Contour dynamics for the Euler equations in two dimension. J. Comput. Phys. 1979, 30, 96–106. [Google Scholar] [CrossRef]
- Noether, E. Invariante Varlationsprobleme. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1918, 2, 235–257. [Google Scholar]
- Deem, D.S.; Zabusky, N.J. Vortex Waves: Stationary “V States”, Interactions, Recurrence, and Breaking. Phys. Rev. Lett. 1978, 40, 859–862. [Google Scholar] [CrossRef]
- Meacham, S.P.; Morrison, P.J.; Flierl, G.R. Hamiltonian moment reduction for describing vortices in shear. Phys. Fluids 1997, 9, 2310–2328. [Google Scholar] [CrossRef][Green Version]
- Moore, D.W.; Saffman, P.G. Structure of a line vortex in an imposed strain. In Aircraft Wake Turbulence and Its Detection; Olsen, J.A., Goldburg, A., Rogers, M., Eds.; Plenum: New York, NY, USA, 1971; pp. 339–354. [Google Scholar]
- Kida, S. Motion of an elliptic vortex in a uniform shear flow. J. Phys. Soc. Jpn. 1981, 50, 3517. [Google Scholar] [CrossRef]
- Kirchhoff, G. Vorlesungen über Mathematische Physik, Mechanik c.XX; Teubner: Leipzig, Germany, 1867. [Google Scholar]
- Swaminathan, R.V. Vortices in Sinusoidal Shear, with Applications to Jupiter. Master’s Thesis, MIT, Cambridge, MA, USA, 2016. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flierl, G.R.; Morrison, P.J.; Vilasur Swaminathan, R. Jovian Vortices and Jets. Fluids 2019, 4, 104. https://doi.org/10.3390/fluids4020104
Flierl GR, Morrison PJ, Vilasur Swaminathan R. Jovian Vortices and Jets. Fluids. 2019; 4(2):104. https://doi.org/10.3390/fluids4020104
Chicago/Turabian StyleFlierl, Glenn R., Philip J. Morrison, and Rohith Vilasur Swaminathan. 2019. "Jovian Vortices and Jets" Fluids 4, no. 2: 104. https://doi.org/10.3390/fluids4020104
APA StyleFlierl, G. R., Morrison, P. J., & Vilasur Swaminathan, R. (2019). Jovian Vortices and Jets. Fluids, 4(2), 104. https://doi.org/10.3390/fluids4020104




