Approximating Isoneutral Ocean Transport via the Temporal Residual Mean
Abstract
1. Introduction
2. Approximating Volume Fluxes within Neutral Density Surfaces
2.1. The Temporal Residual Mean (TRM) Streamfunction
2.2. The Neutral Density Temporal Residual Mean (NDTRM)
3. Approximating Volume Fluxes within Local Neutral Surfaces
3.1. Vertical Fluctuations of Local Neutral Surfaces
3.2. Connection to the Neutral Density Temporal Residual Mean (NDTRM)
3.3. Equivalence to Fluctuations of Locally-Referenced Potential Density Surfaces
4. Comparison and Assessment Using an Idealized Numerical Model
4.1. Model Configuration
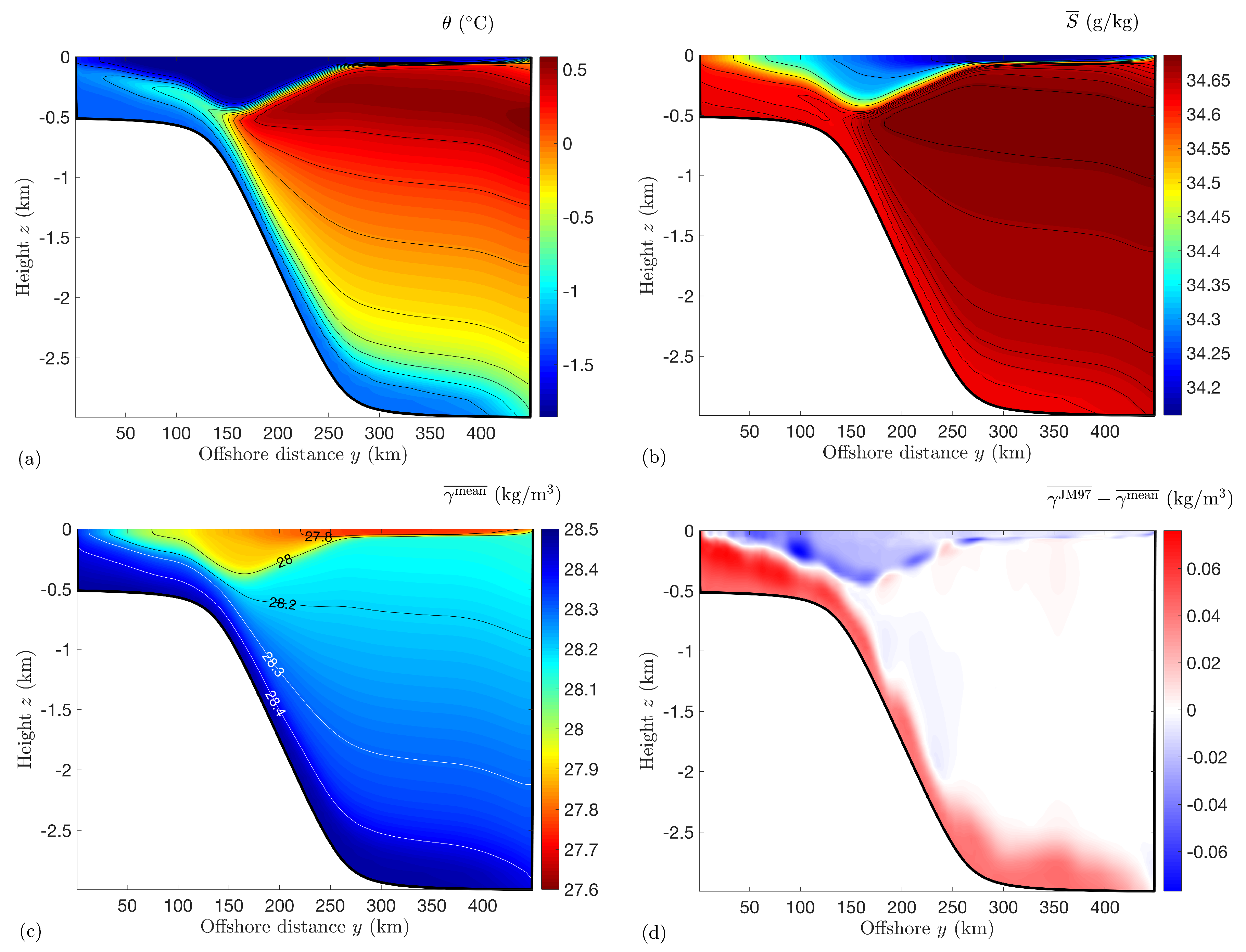
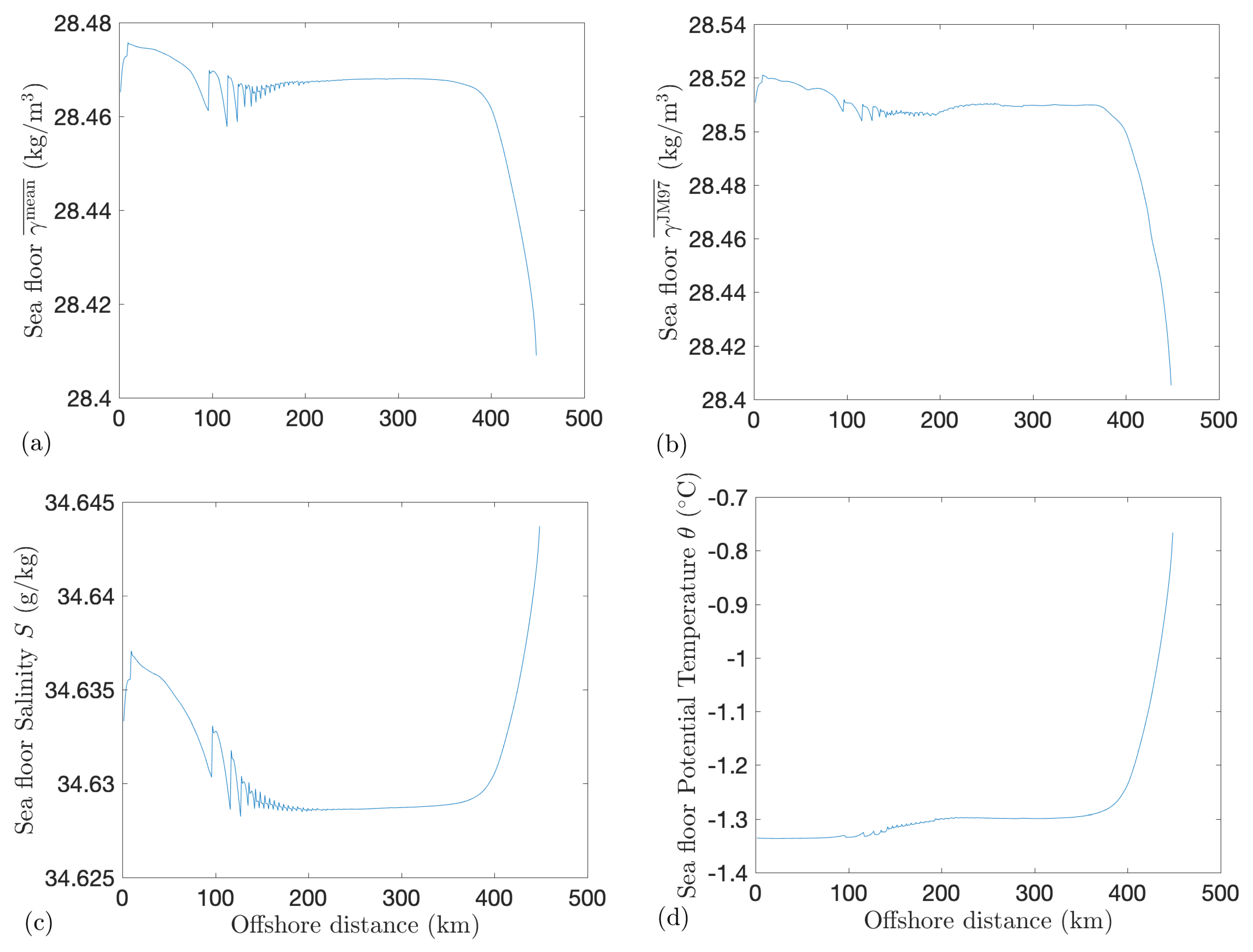
4.2. Constructing Neutral Density from the Model’s Mean State
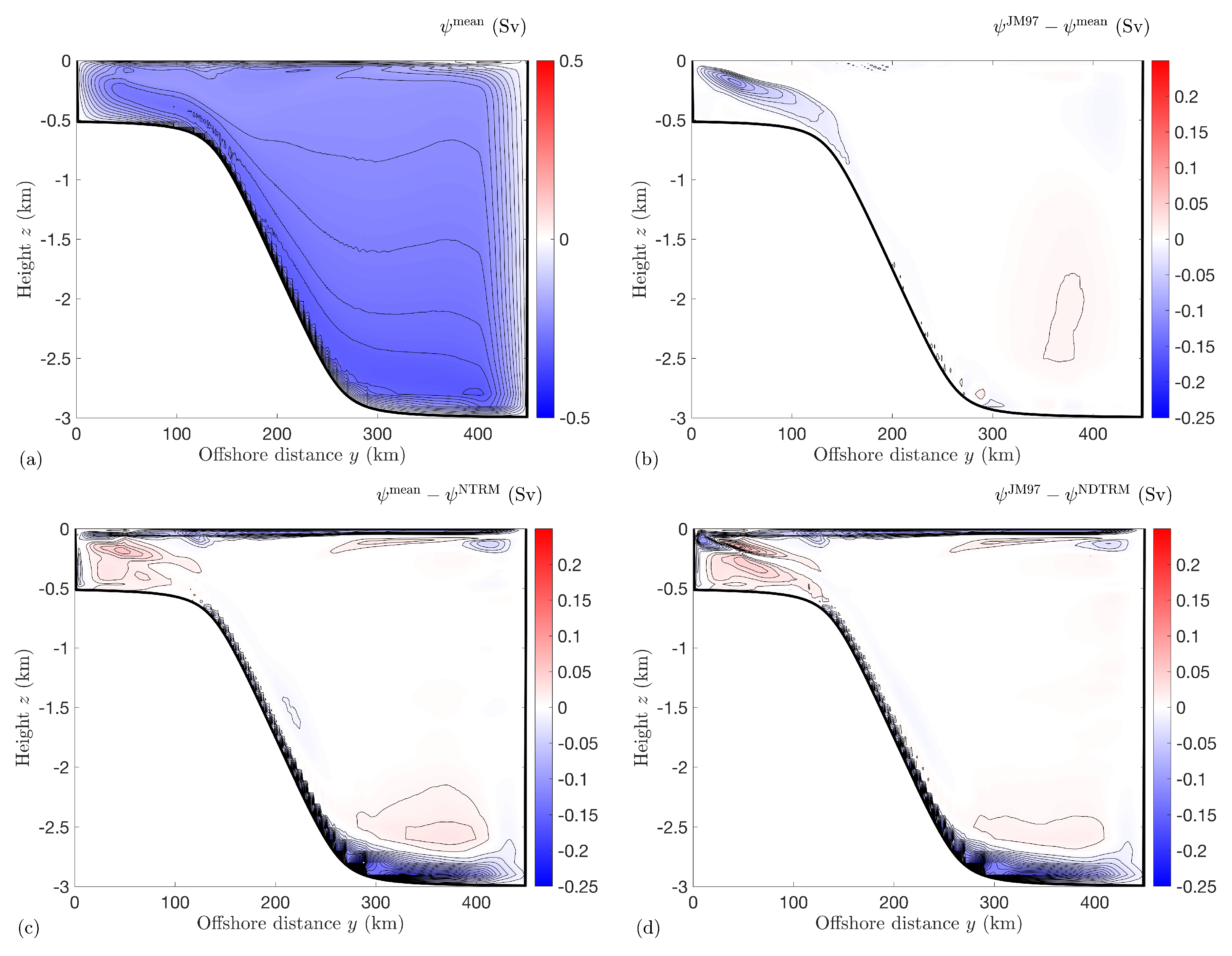
4.3. Comparing Diagnosed and TRM Transports
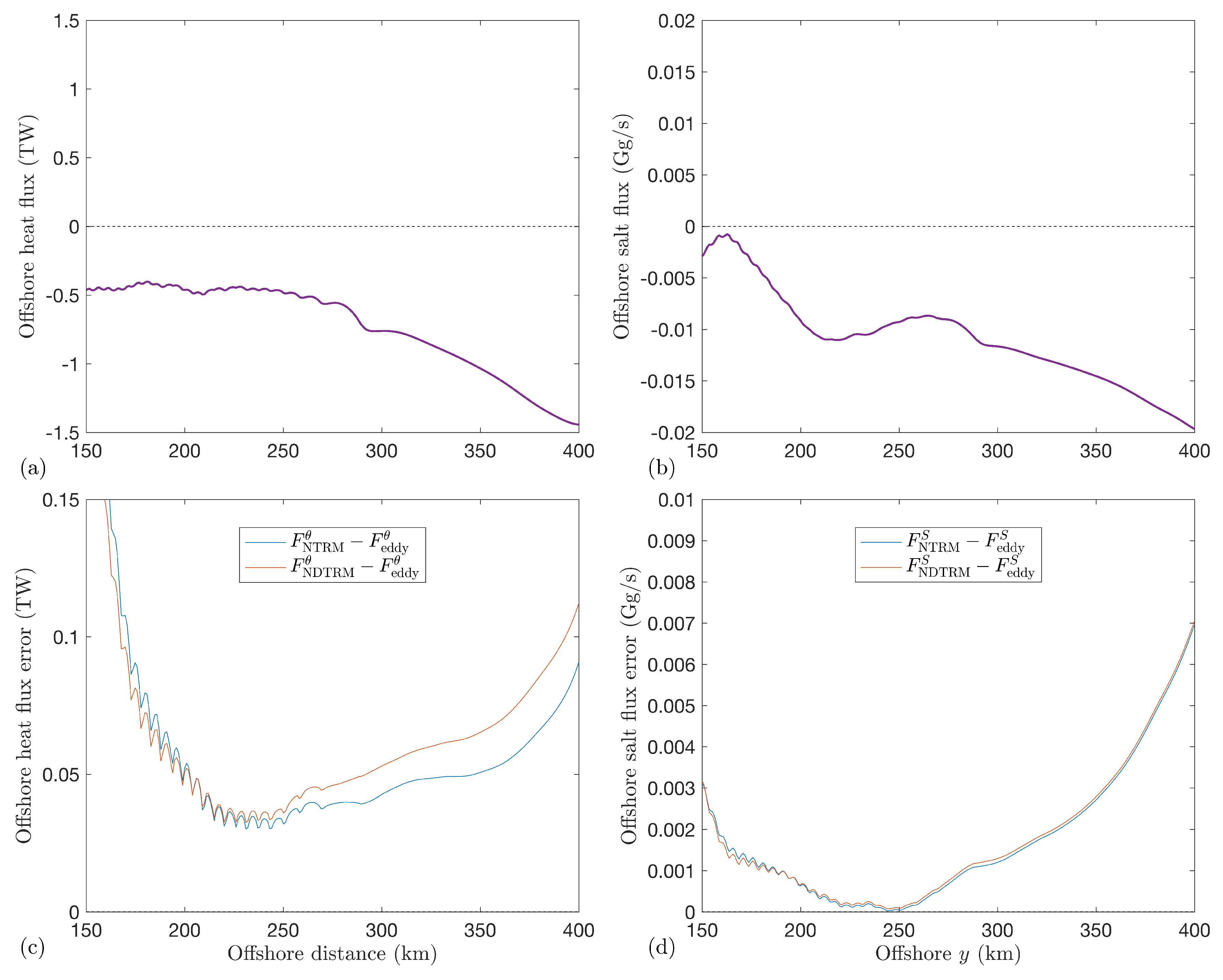
4.4. Advective Tracer Transport
5. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Srokosz, M.; Baringer, M.; Bryden, H.; Cunningham, S.; Delworth, T.; Lozier, S.; Marotzke, J.; Sutton, R. Past, present, and future changes in the Atlantic meridional overturning circulation. Bull. Am. Meteorol. Soc. 2012, 93, 1663–1676. [Google Scholar] [CrossRef]
- Marshall, J.; Speer, K. Closure of the meridional overturning circulation through Southern Ocean upwelling. Nat. Geosci. 2012, 5, 171–180. [Google Scholar] [CrossRef]
- Döös, K.; Webb, D.J. The Deacon cell and the other meridional cells of the Southern Ocean. J. Phys. Oceanogr. 1994, 24, 429–442. [Google Scholar] [CrossRef]
- Hirst, A.C.; McDougall, T.J. Deep-water properties and surface buoyancy flux as simulated by a z-coordinate model including eddy-induced advection. J. Phys. Oceanogr. 1996, 26, 1320–1343. [Google Scholar] [CrossRef]
- Lumpkin, R.; Speer, K. Global ocean meridional overturning. J. Phys. Oceanogr. 2007, 37, 2550–2562. [Google Scholar] [CrossRef]
- Wolfe, C.L.; Cessi, P. Overturning circulation in an eddy-resolving model: The effect of the pole-to-pole temperature gradient. J. Phys. Oceanogr. 2009, 39, 125–142. [Google Scholar] [CrossRef]
- Sun, S.; Eisenman, I.; Stewart, A.L. The influence of Southern Ocean surface buoyancy forcing on glacial-interglacial changes in the global deep ocean stratification. Geophys. Res. Lett. 2016, 43, 8124–8132. [Google Scholar] [CrossRef]
- Sun, S.; Eisenman, I.; Stewart, A.L. Does Southern Ocean surface forcing shape the global ocean overturning circulation? Geophys. Res. Lett. 2018, 45, 2413–2423. [Google Scholar] [CrossRef]
- Eden, C. Relating Lagrangian, residual, and isopycnal means. J. Phys. Oceanogr. 2012, 42, 1057–1064. [Google Scholar] [CrossRef]
- Plumb, R.A. Eddy fluxes of conserved quantities by small-amplitude waves. J. Atmos. Sci. 1979, 36, 1699–1704. [Google Scholar] [CrossRef]
- Marshall, J.; Radko, T. Residual-mean solutions for the Antarctic Circumpolar Current and its associated overturning circulation. J. Phys. Oceanogr. 2003, 33, 2341–2354. [Google Scholar] [CrossRef]
- Abernathey, R.; Marshall, J.; Ferreira, D. The dependence of Southern Ocean meridional overturning on wind stress. J. Phys. Oceanogr. 2011, 41, 2261–2278. [Google Scholar] [CrossRef]
- Stewart, A.L.; Hogg, A.M. Reshaping the Antarctic Circumpolar Current via Antarctic Bottom Water Export. J. Phys. Oceanogr. 2017, 47, 2577–2601. [Google Scholar] [CrossRef]
- Nikurashin, M.; Vallis, G. A theory of deep stratification and overturning circulation in the ocean. J. Phys. Oceanogr. 2011, 41, 485–502. [Google Scholar] [CrossRef]
- Nikurashin, M.; Vallis, G. A theory of the interhemispheric meridional overturning circulation and associated stratification. J. Phys. Oceanogr. 2012, 42, 1652–1667. [Google Scholar] [CrossRef]
- Stewart, A.L.; Ferrari, R.; Thompson, A.F. On the importance of surface forcing in conceptual models of the deep ocean. J. Phys. Oceanogr. 2014, 44, 891–899. [Google Scholar] [CrossRef]
- Burke, A.; Stewart, A.L.; Adkins, J.F.; Ferrari, R.; Jansen, M.F.; Thompson, A.F. The glacial mid-depth radiocarbon bulge and its implications for the overturning circulation. Paleoceanography 2015, 30, 1021–1039. [Google Scholar] [CrossRef]
- Watson, A.J.; Vallis, G.K.; Nikurashin, M. Southern Ocean buoyancy forcing of ocean ventilation and glacial atmospheric CO2. Nat. Geosci. 2015, 8, 861–864. [Google Scholar] [CrossRef]
- Thompson, A.F.; Stewart, A.L.; Bischoff, T. A multibasin residual-mean model for the global overturning circulation. J. Phys. Oceanogr. 2016, 46, 2583–2604. [Google Scholar] [CrossRef]
- McDougall, T.J.; McIntosh, P.C. The temporal-residual-mean velocity. Part I: Derivation and the scalar conservation equations. J. Phys. Oceanogr. 1996, 26, 2653–2665. [Google Scholar] [CrossRef]
- McDougall, T.J.; McIntosh, P.C. The temporal-residual-mean velocity. Part II: Isopycnal interpretation and the tracer and momentum equations. J. Phys. Oceanogr. 2001, 31, 1222–1246. [Google Scholar] [CrossRef]
- Wolfe, C.L. Approximations to the ocean’s residual circulation in arbitrary tracer coordinates. Ocean Model. 2014, 75, 20–35. [Google Scholar] [CrossRef]
- Stewart, A.L.; Thompson, A.F. The Neutral Density Temporal Residual Mean overturning circulation. Ocean Model. 2015, 90, 44–56. [Google Scholar] [CrossRef][Green Version]
- Jackett, D.R.; McDougall, T.J. A neutral density variable for the world’s oceans. J. Phys. Oceanogr. 1997, 27, 237–263. [Google Scholar] [CrossRef]
- Talley, L.D. Closure of the global overturning circulation through the Indian, Pacific, and Southern Oceans: Schematics and transports. Oceanography 2013, 26, 80–97. [Google Scholar] [CrossRef]
- McDougall, T.J. Neutral surfaces. J. Phys. Oceanogr. 1987, 17, 1950–1964. [Google Scholar] [CrossRef]
- Iselin, C.O. The influence of vertical and lateral turbulence on the characteristics of the waters at mid-depths. Eos Trans. Am. Geophys. Union 1939, 20, 414–417. [Google Scholar] [CrossRef]
- McDougall, T.J.; Groeskamp, S.; Griffies, S.M. On geometrical aspects of interior ocean mixing. J. Phys. Oceanogr. 2014, 44, 2164–2175. [Google Scholar] [CrossRef]
- McDougall, T.J.; Jackett, D.R. On the helical nature of neutral trajectories in the ocean. Prog. Oceanogr. 1988, 20, 153–183. [Google Scholar] [CrossRef]
- Eden, C.; Willebrand, J. Neutral density revisited. Deep Sea Res. Part II Top. Stud. Oceanogr. 1999, 46, 33–54. [Google Scholar] [CrossRef]
- Groeskamp, S.; Griffies, S.M.; Iudicone, D.; Marsh, R.; Nurser, A.J.G.; Zika, J.D. The water mass transformation framework for ocean physics and biogeochemistry. Ann. Rev. Mar. Sci. 2019, 11, 271–305. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.G.; McIntyre, M.E. An exact theory of nonlinear waves on a Lagrangian-mean flow. J. Fluid Mech. 1978, 89, 609–646. [Google Scholar] [CrossRef]
- Young, W.R. An exact thickness-weighted average formulation of the Boussinesq equations. J. Phys. Oceanogr. 2012, 42, 692–707. [Google Scholar] [CrossRef]
- Groeskamp, S.; Barker, P.M.; McDougall, T.J.; Abernathey, R.P.; Griffies, S.M. VENM: An Algorithm to Accurately Calculate Neutral Slopes and Gradients. J. Adv. Model. Earth Syst. 2019, 11, 1917–1939. [Google Scholar] [CrossRef]
- Groeskamp, S.; Iudicone, D. The Effect of Air-Sea Flux Products, Shortwave Radiation Depth Penetration, and Albedo on the Upper Ocean Overturning Circulation. Geophys. Res. Lett. 2018, 45, 9087–9097. [Google Scholar] [CrossRef]
- McIntosh, P.C.; McDougall, T.J. Isopycnal averaging and the residual mean circulation. J. Phys. Oceanogr. 1996, 26, 1655–1660. [Google Scholar] [CrossRef]
- Gill, A.E. Circulation and bottom water production in the Weddell Sea. Deep Sea Res. Oceanogr. 1973, 20, 111–140. [Google Scholar] [CrossRef]
- Thompson, A.F.; Stewart, A.L.; Spence, P.; Heywood, K.J. The Antarctic slope current in a changing climate. Rev. Geophys. 2018, 56, 741–770. [Google Scholar] [CrossRef]
- Stewart, A.L.; Thompson, A.F. Sensitivity of the ocean’s deep overturning circulation to easterly Antarctic winds. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Stewart, A.L.; Thompson, A.F. Connecting Antarctic cross-slope exchange with Southern Ocean overturning. J. Phys. Oceanogr. 2013, 43, 1453–1471. [Google Scholar] [CrossRef]
- Stewart, A.L.; Thompson, A.F. Eddy-mediated transport of warm Circumpolar Deep Water across the Antarctic shelf break. Geophys. Res. Lett. 2015, 42, 432–440. [Google Scholar] [CrossRef]
- Stewart, A.L.; Thompson, A.F. Eddy generation and jet formation via dense water outflows across the Antarctic continental slope. J. Phys. Oceanogr. 2016, 46, 3729–3750. [Google Scholar] [CrossRef]
- Marshall, J.; Hill, C.; Perelman, L.; Adcroft, A. Hydrostatic, quasi-hydrostatic, and nonhydrostatic ocean modeling. J. Geophys. Res. Oceans 1997, 102, 5733–5752. [Google Scholar] [CrossRef]
- Marshall, J.; Adcroft, A.; Hill, C.; Perelman, L.; Heisey, C. A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. Oceans 1997, 102, 5753–5766. [Google Scholar] [CrossRef]
- Levitus, S. Climatological atlas of the world ocean. Eos Trans. Am. Geophys. Union 1983, 64, 962–963. [Google Scholar] [CrossRef]
- Stanley, G.J. Neutral surface topology. Ocean Model. 2019, 138, 88–106. [Google Scholar] [CrossRef]
- Held, I.M.; Schneider, T. The surface branch of the zonally averaged mass transport circulation in the troposphere. J. Atmos. Sci. 1999, 56, 1688–1697. [Google Scholar] [CrossRef]
- Colas, F.; Capet, X.; McWilliams, J.C.; Li, Z. Mesoscale eddy buoyancy flux and eddy-induced circulation in Eastern Boundary Currents. J. Phys. Oceanogr. 2013, 43, 1073–1095. [Google Scholar] [CrossRef]
- De Szoeke, R.A.; Springer, S.R.; Oxilia, D.M. Orthobaric density: A thermodynamic variable for ocean circulation studies. J. Phys. Oceanogr. 2000, 30, 2830–2852. [Google Scholar] [CrossRef]
- Tailleux, R. Generalized patched potential density and thermodynamic neutral density: Two new physically based quasi-neutral density variables for ocean water masses analyses and circulation studies. J. Phys. Oceanogr. 2016, 46, 3571–3584. [Google Scholar] [CrossRef]
- Klocker, A.; McDougall, T.; Jackett, D. A new method for forming approximately neutral surfaces. Ocean Sci. 2009, 5, 155–172. [Google Scholar] [CrossRef]
- Tailleux, R. Neutrality versus materiality: A thermodynamic theory of neutral surfaces. Fluids 2016, 1, 32. [Google Scholar] [CrossRef]
- Van Sebille, E.; Baringer, M.O.; Johns, W.E.; Meinen, C.S.; Beal, L.M.; De Jong, M.F.; Van Aken, H.M. Propagation pathways of classical Labrador Sea water from its source region to 26 °N. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Tailleux, R. On the validity of single-parcel energetics to assess the importance of internal energy and compressibility effects in stratified fluids. J. Fluid Mech. 2015, 767. [Google Scholar] [CrossRef]
- McDougall, T.; Groeskamp, S.; Griffies, S. Comment on Tailleux, R. Neutrality versus Materiality: A Thermodynamic Theory of Neutral Surfaces. Fluids 2016, 1, 32. [Google Scholar] [CrossRef]
- Tailleux, R. Reply to “Comment on Tailleux, R. Neutrality Versus Materiality: A Thermodynamic Theory of Neutral Surfaces. Fluids 2016, 1, 32.”. Fluids 2017, 2, 20. [Google Scholar] [CrossRef]
- Stewart, A.L.; Klocker, A.; Menemenlis, D. Circum-Antarctic Shoreward Heat Transport Derived From an Eddy-and Tide-Resolving Simulation. Geophys. Res. Lett. 2018, 45, 834–845. [Google Scholar] [CrossRef]
- Palóczy, A.; Gille, S.T.; McClean, J.L. Oceanic heat delivery to the Antarctic continental shelf: Large-scale, low-frequency variability. J. Geophys. Res. Oceans 2018, 123, 7678–7701. [Google Scholar] [CrossRef]
- Stewart, A.L.; Klocker, A.; Menemenlis, D. Acceleration and overturning of the Antarctic Slope Current by winds, eddies, and tides. J. Phys. Oceanogr. 2019, 49, 2043–2074. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stewart, A.L. Approximating Isoneutral Ocean Transport via the Temporal Residual Mean. Fluids 2019, 4, 179. https://doi.org/10.3390/fluids4040179
Stewart AL. Approximating Isoneutral Ocean Transport via the Temporal Residual Mean. Fluids. 2019; 4(4):179. https://doi.org/10.3390/fluids4040179
Chicago/Turabian StyleStewart, Andrew L. 2019. "Approximating Isoneutral Ocean Transport via the Temporal Residual Mean" Fluids 4, no. 4: 179. https://doi.org/10.3390/fluids4040179
APA StyleStewart, A. L. (2019). Approximating Isoneutral Ocean Transport via the Temporal Residual Mean. Fluids, 4(4), 179. https://doi.org/10.3390/fluids4040179




