On Moderate-Rayleigh-Number Convection in an Inclined Porous Layer
Abstract
1. Introduction
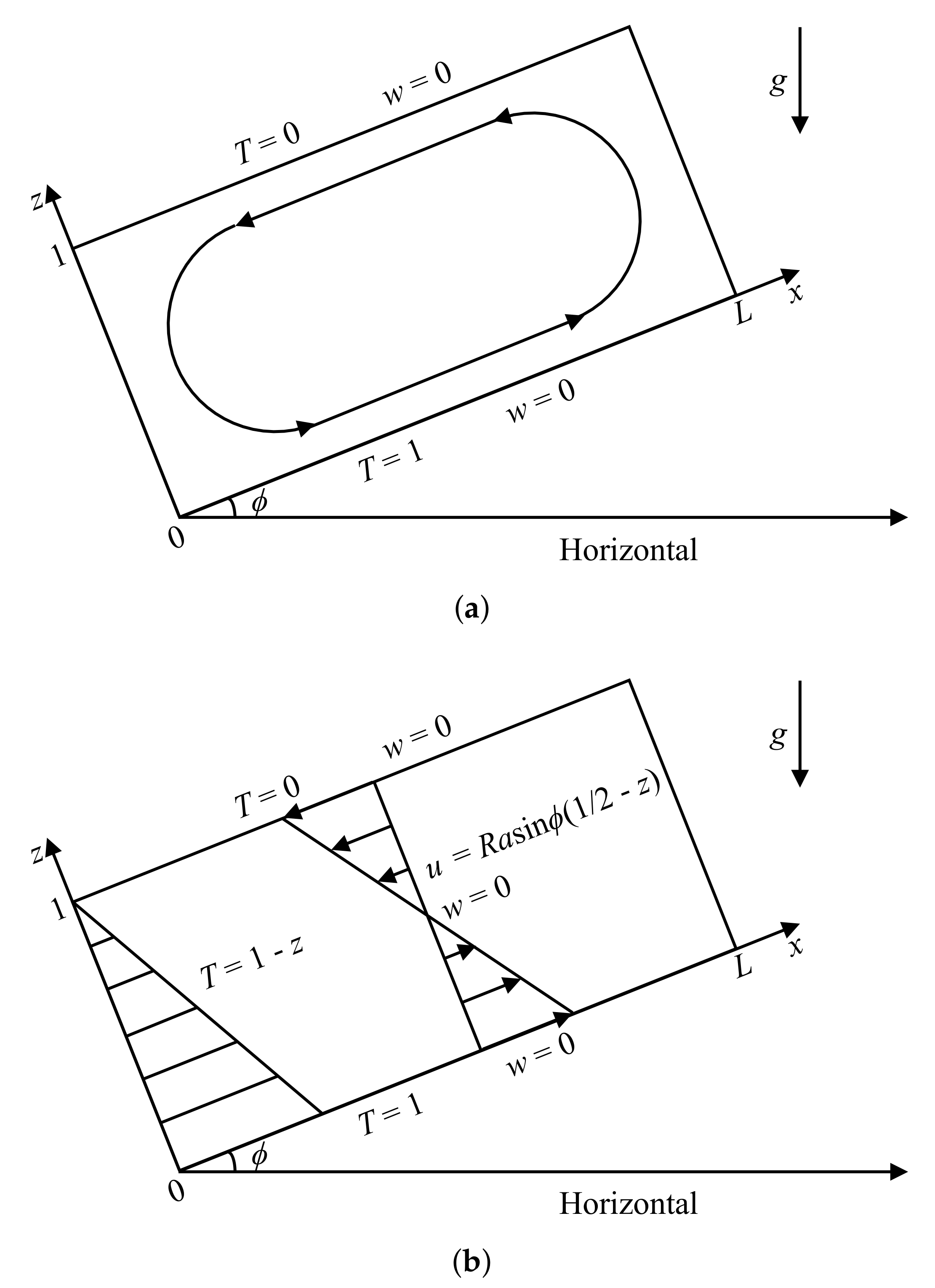
2. Governing Equations
3. Dynamics at Moderate Ra
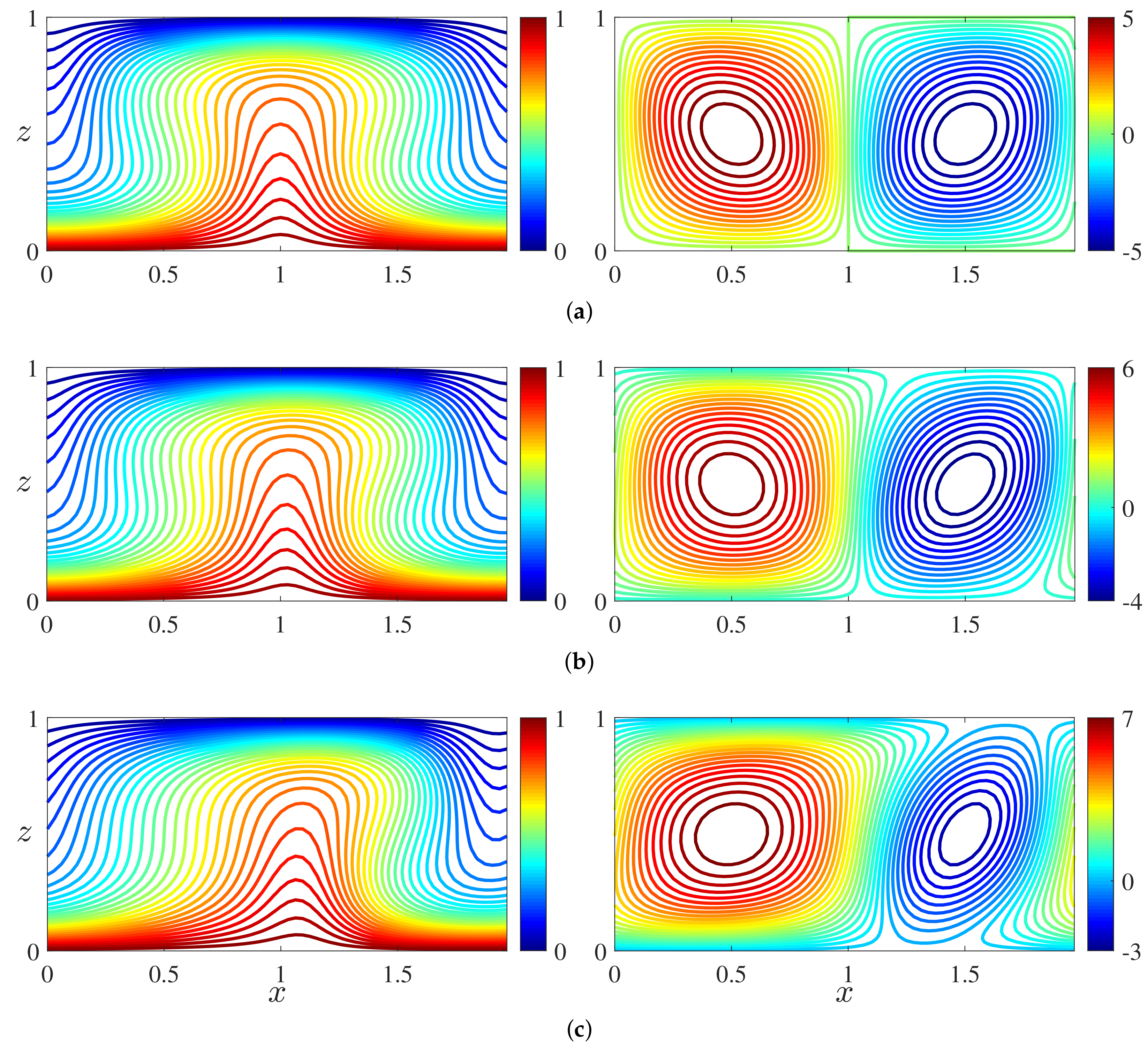
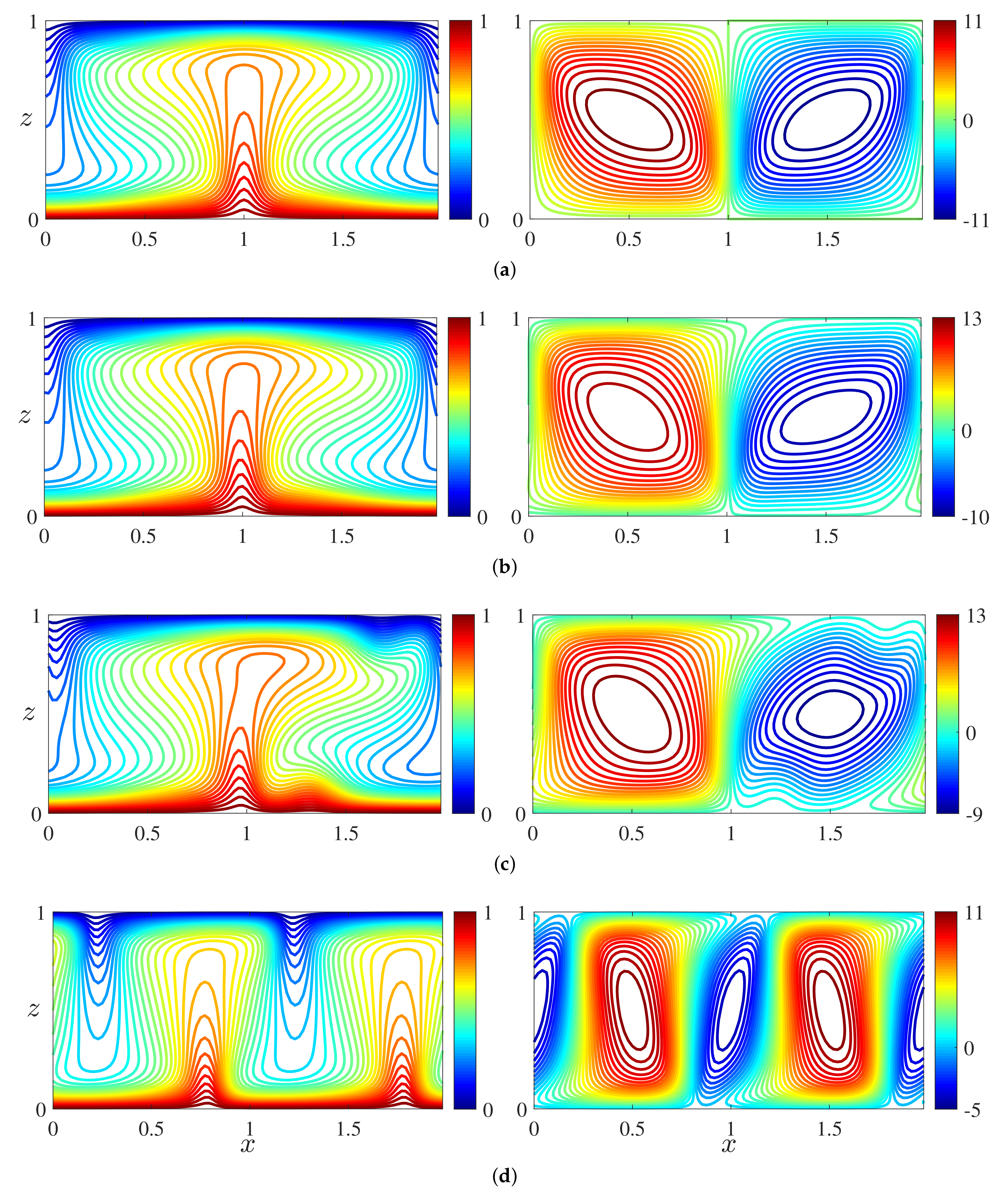
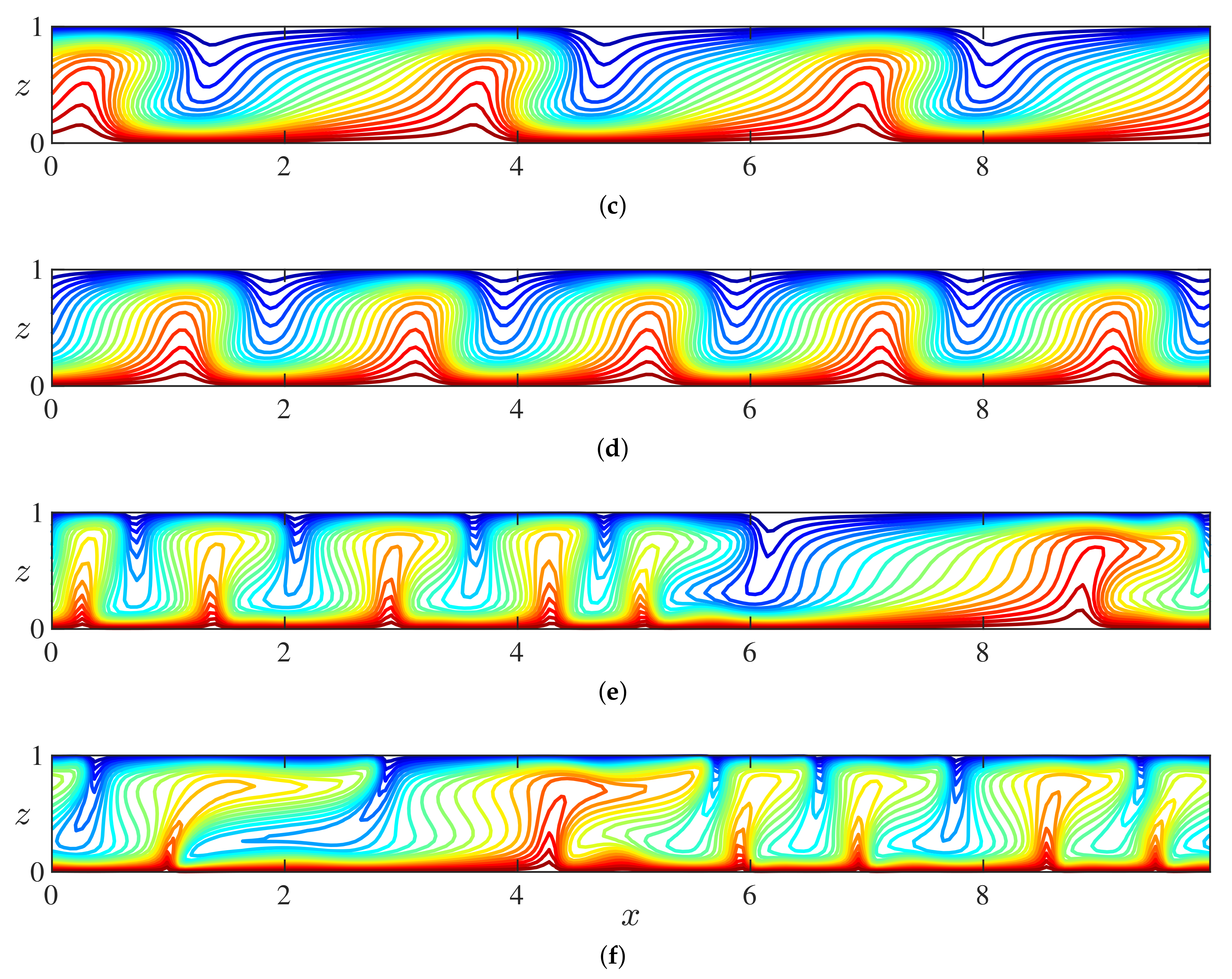
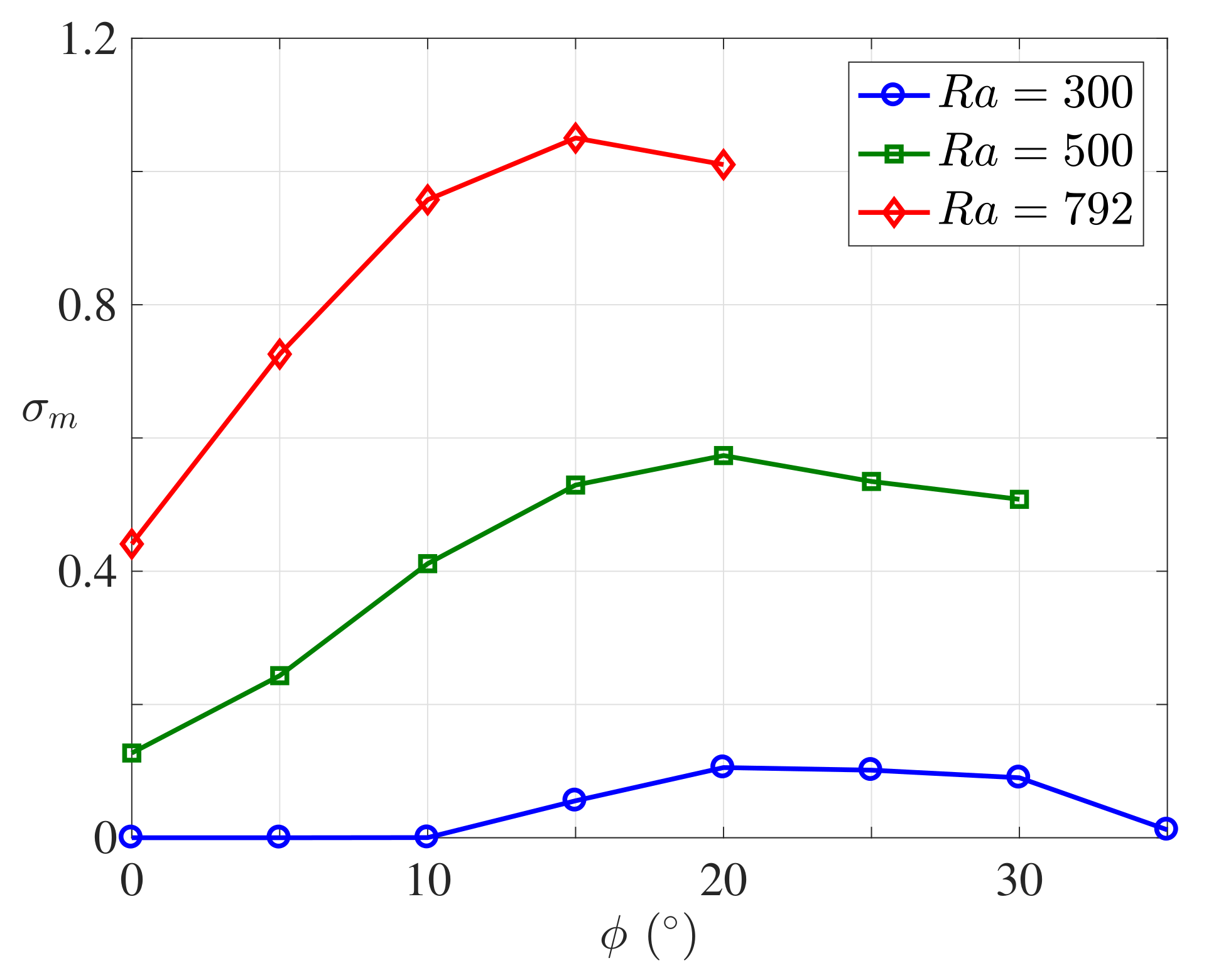
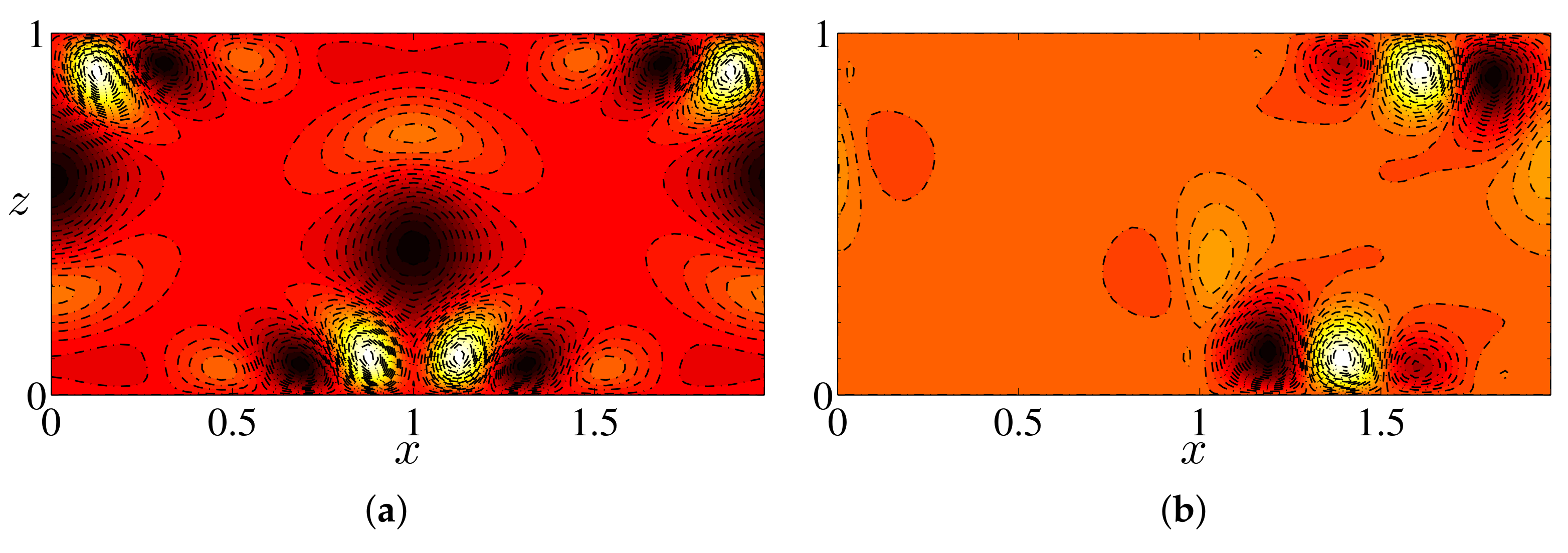
3.1. Numerical Simulation Results
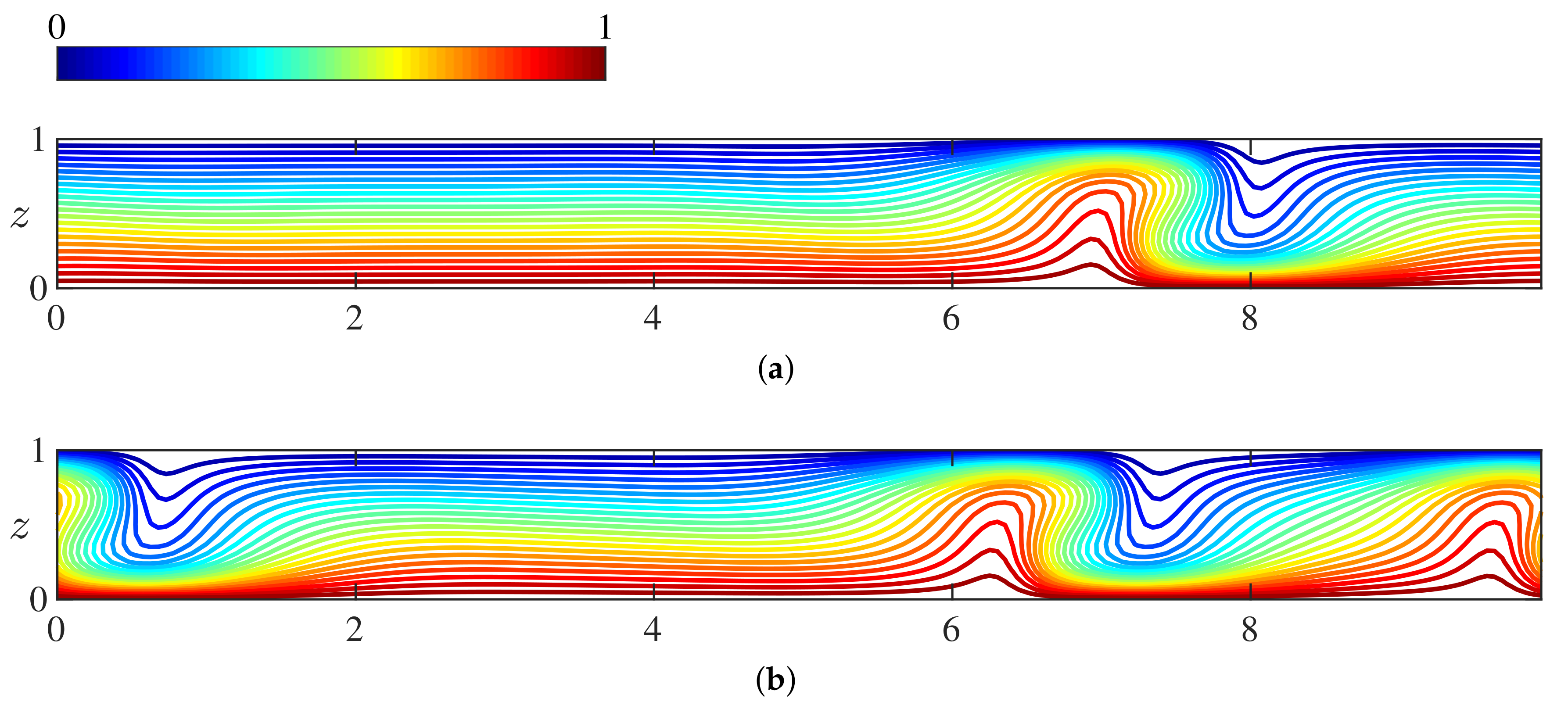
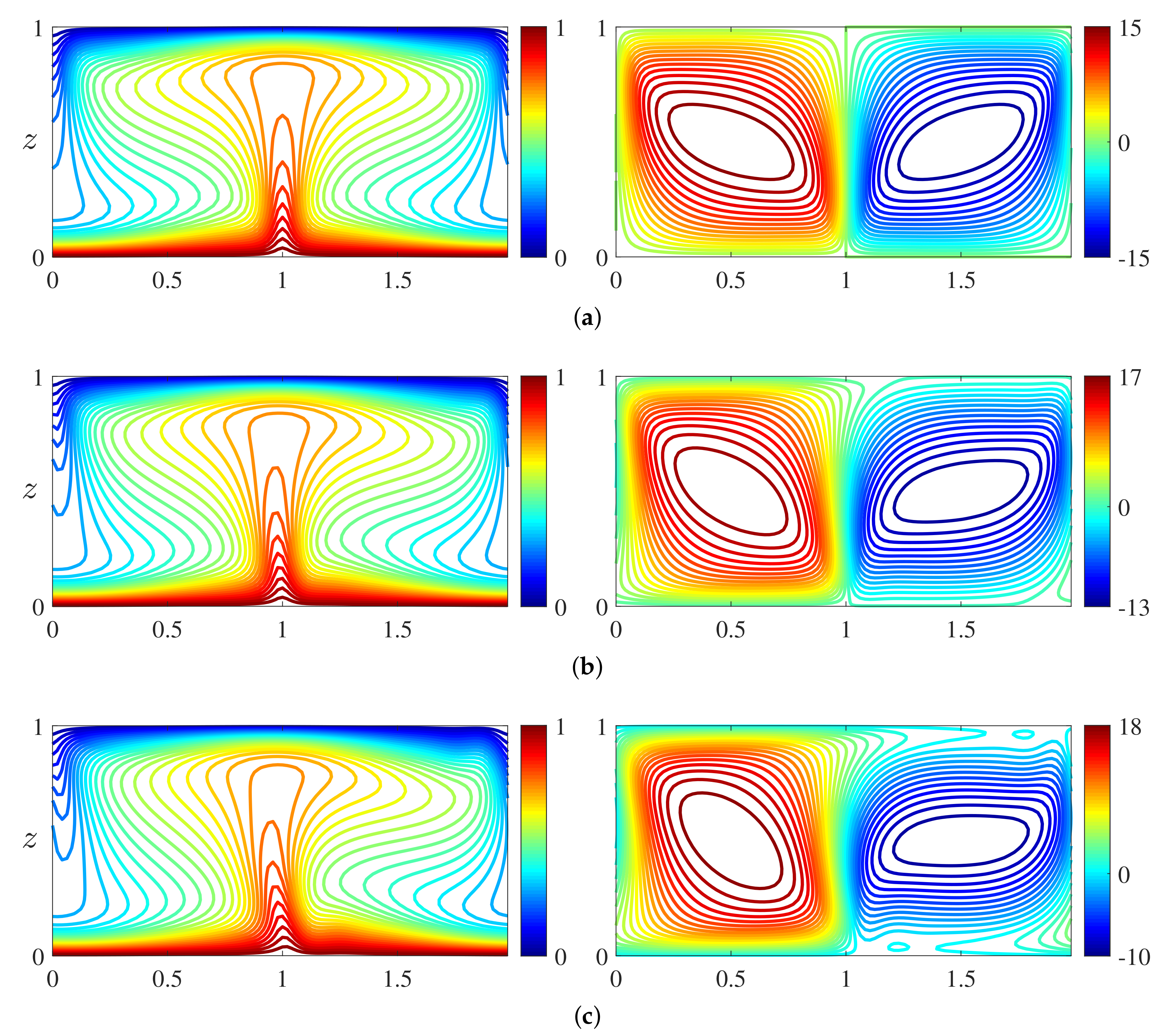
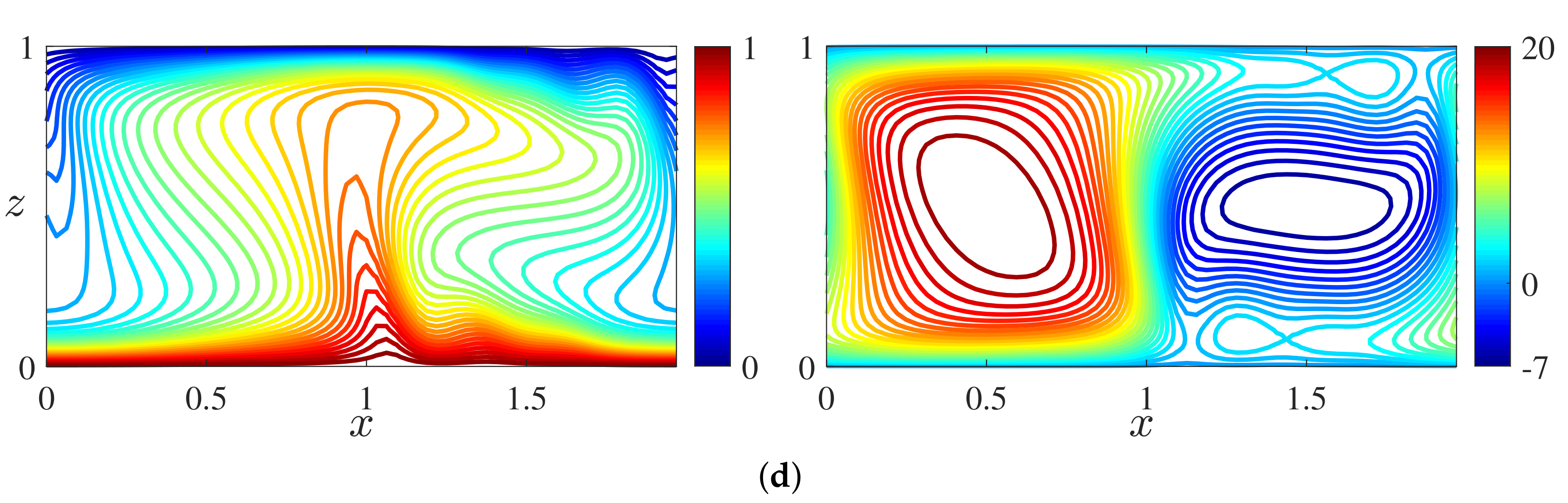
3.2. Steady Convective States
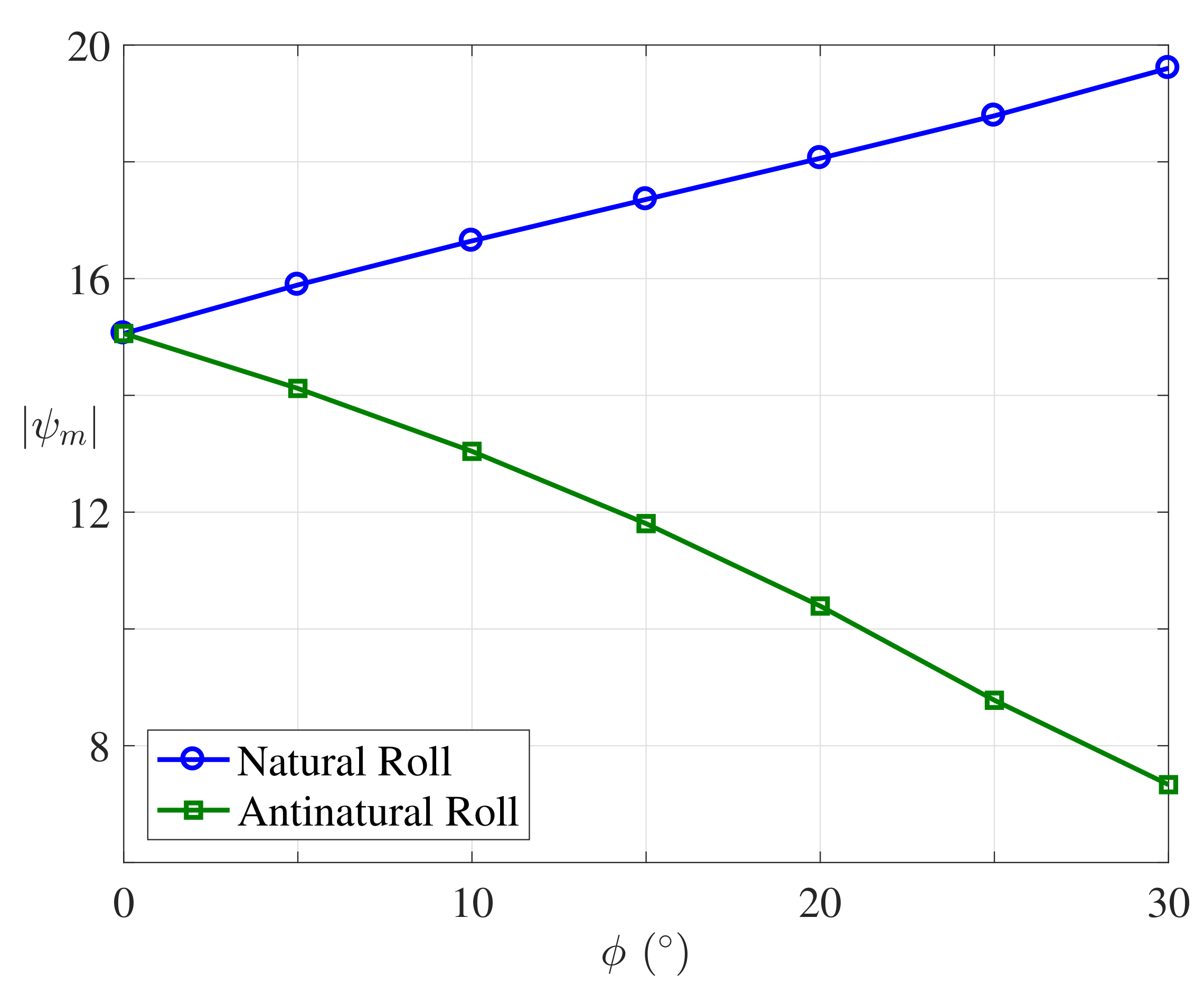
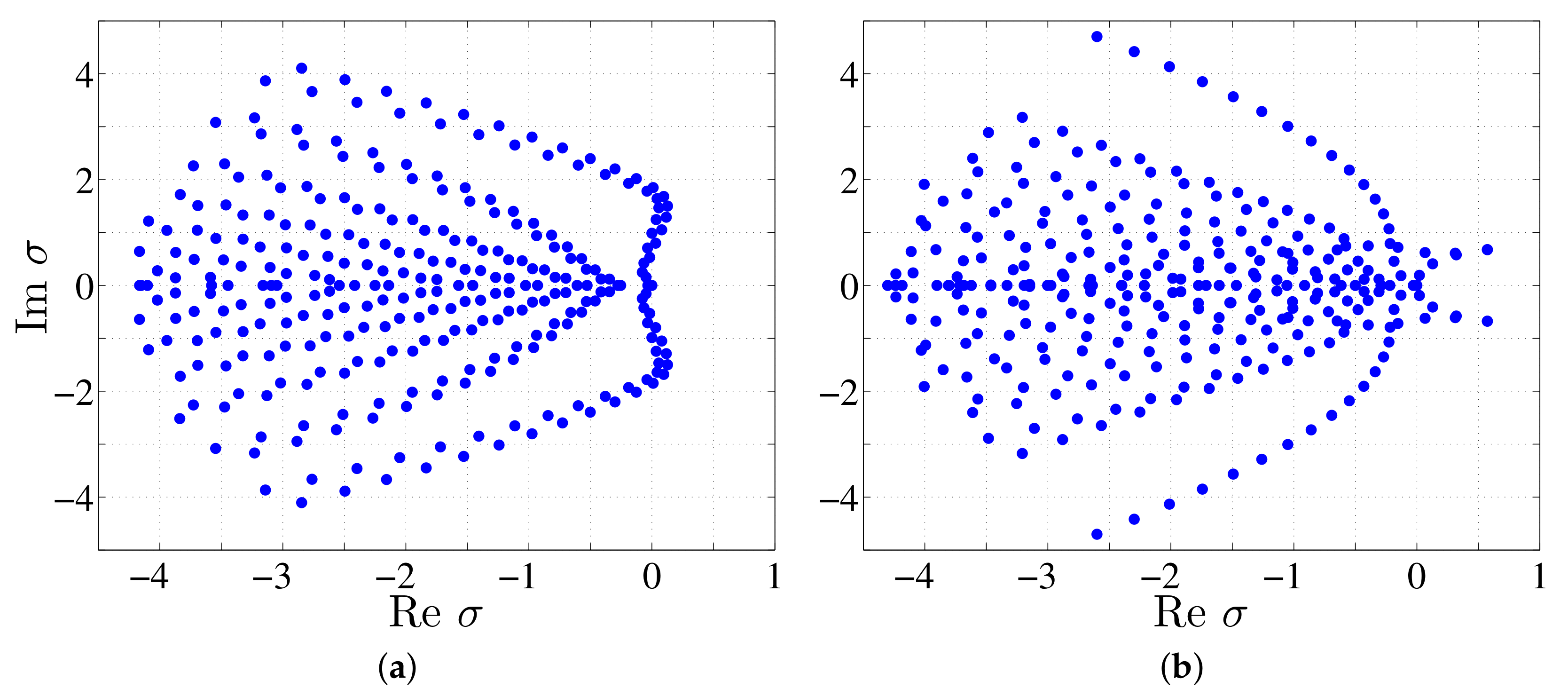
3.3. Secondary Stability Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horton, C.W.; Rogers, F.T. Convection currents in a porous medium. J. Appl. Phys. 1945, 16, 367–370. [Google Scholar] [CrossRef]
- Lapwood, E.R. Convection of a fluid in a porous medium. Proc. Camb. Phil. Soc. 1948, 44, 508–521. [Google Scholar] [CrossRef]
- Graham, M.D.; Steen, P.H. Strongly interacting traveling waves and quasiperiodic dynamics in porous medium convection. Phys. D 1992, 54, 331–350. [Google Scholar] [CrossRef]
- Otero, J.; Dontcheva, L.A.; Johnston, H.; Worthing, R.A.; Kurganov, A.; Petrova, G.; Doering, C.R. High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 2004, 500, 263–281. [Google Scholar] [CrossRef]
- Hewitt, D.R.; Neufeld, J.A.; Lister, J.R. Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 2012, 108, 224503. [Google Scholar] [CrossRef] [PubMed]
- Wen, B.; Corson, L.T.; Chini, G.P. Structure and stability of steady porous medium convection at large Rayleigh number. J. Fluid Mech. 2015, 772, 197–224. [Google Scholar] [CrossRef]
- Liang, Y.; Wen, B.; Hesse, M.; DiCarlo, D. Effect of dispersion on solutal convection in porous media. Geophys. Res. Lett. 2018, 45, 9690–9698. [Google Scholar] [CrossRef]
- Metz, B.; Davidson, O.; de Coninck, H.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture and Storage; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Riaz, A.; Hesse, M.; Tchelepi, H.A.; Orr, F.M. Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 2006, 548, 87–111. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 4th ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Phillips, O.M. Geological Fluid Dynamics: Sub-Surface Flow and Reactions; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Schubert, G.; Straus, J.M. Transitions in time-dependent thermal convection in fluid-saturated porous media. J. Fluid Mech. 1982, 121, 301–313. [Google Scholar] [CrossRef]
- Kimura, S.; Schubert, G.; Straus, J.M. Route to chaos in porous-medium thermal convection. J. Fluid Mech. 1986, 166, 305–324. [Google Scholar] [CrossRef]
- Kimura, S.; Schubert, G.; Straus, J.M. Instabilities of steady, periodic, and quasi-periodic modes of convection in porous media. J. Heat Transf. 1987, 109, 350–355. [Google Scholar] [CrossRef]
- Aidun, C.K.; Steen, P.H. Transition to oscillatory convective heat transfer in a fluid-saturated porous medium. J. Thermophys. Heat Transf. 1987, 1, 268–273. [Google Scholar]
- Graham, M.D.; Steen, P.H. Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 1994, 272, 67–90. [Google Scholar] [CrossRef]
- Wen, B.; Chini, G.P.; Dianati, N.; Doering, C.R. Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A 2013, 377, 2931–2938. [Google Scholar] [CrossRef]
- MacMinn, C.W.; Juanes, R. Buoyant currents arrested by convective dissolution. Geophys. Res. Lett. 2013, 40, 2017–2022. [Google Scholar] [CrossRef]
- Tsai, P.A.; Riesing, K.; Stone, H.A. Density-driven convection enhanced by an inclined boundary: Implications for geological CO2 storage. Phys. Rev. E 2013, 87, 011003. [Google Scholar] [CrossRef]
- Sathaye, K.; Hesse, M.; Cassidy, M.; Stockli, D. Constraints on the magnitude and rate of CO2 dissolution at Bravo Dome natural gas field. Proc. Nat. Acad. Sci. USA 2014, 111, 15332–15337. [Google Scholar] [CrossRef]
- Akhbari, D.; Hesse, M.A. Causes of underpressure in natural CO2 reservoirs and implications for geological storage. Geology 2017, 45, 47–50. [Google Scholar] [CrossRef]
- Bories, S.A.; Combarnous, M.A.; Jaffrenou, J. Observations des différentes formes d’écoulements thermoconvectifs dans une couche poreuse inclinée. CR Acad. Sci. Paris A 1972, 275, 857–860. [Google Scholar]
- Bories, S.A.; Monferran, L. Condition de stabilité et échange thermique par convection naturelle dans une couche poreuse inclinée de grande extension. CR Acad. Sci. Paris B 1972, 274, 4–7. [Google Scholar]
- Bories, S.A.; Combarnous, M.A. Natural convection in a sloping porous layer. J. Fluid Mech. 1973, 57, 63–79. [Google Scholar] [CrossRef]
- Caltagirone, J.P.; Cloupeau, M.; Combarnous, M. Convection naturelle fluctuante dans une couche poreuse horizontale. CR Acad. Sci. Paris B 1971, 273, 833–836. [Google Scholar]
- Kaneko, T. An Experimental Investigation of Natural Convection in Porous Media. Master’s Thesis, University of Calgary, Calgary, AB, Canada, 1972. [Google Scholar]
- Kaneko, T.; Mohtadi, M.F.; Aziz, K. An experimental study of natural convection in inclined porous media. Int. J. Heat Mass Transf. 1974, 17, 485–496. [Google Scholar] [CrossRef]
- Caltagirone, J.P.; Bories, S. Solutions and stability criteria of natural convective flow in an inclined porous layer. J. Fluid Mech. 1985, 155, 267–287. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Bassom, A.P. The onset of Darcy–Bénard convection in an inclined layer heated from below. Acta Mech. 2000, 144, 103–118. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Postelnicu, A. The onset of convection in an inclined anisotropic porous layer. Int. J. Heat Mass Transf. 2001, 44, 4127–4138. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Storesletten, L.; Postelnicu, A. The onset of convection in an inclined anisotropic porous layer with oblique principle axes. Transp. Porous Med. 2006, 62, 139–156. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Barletta, A. Linear instability of the isoflux Darcy–Bénard problem in an inclined porous layer. Transp. Porous Med. 2011, 87, 665–678. [Google Scholar] [CrossRef]
- Barletta, A.; Storesletten, L. Thermoconvective instabilities in an inclined porous channel heated from below. Int. J. Heat Mass Transf. 2011, 54, 2724–2733. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.A.S. Local thermal non-equilibrium analysis of the thermoconvective instability in an inclined porous layer. Int. J. Heat Mass Transf. 2015, 83, 327–336. [Google Scholar] [CrossRef]
- Celli, M.; Barletta, A. Onset of buoyancy driven convection in an inclined porous layer with an isobaric boundary. Int. J. Heat Mass Transf. 2019, 132, 782–788. [Google Scholar] [CrossRef]
- Wen, B.; Chini, G.P. Inclined porous medium convection at large Rayleigh number. J. Fluid Mech. 2018, 837, 670–702. [Google Scholar] [CrossRef]
- Walch, J.; Dulieu, B. Convection de Rayleigh–Béenard dans une cavité poreuse faiblement inclinée. J. Phys. Lett. 1982, 43, 103–107. [Google Scholar] [CrossRef]
- Moya, S.L.; Ramos, E.; Sen, M. Numerical study of natural convection in a tilted rectangular porous material. Int. J. Heat Mass Transfer 1987, 30, 741–756. [Google Scholar] [CrossRef]
- Sen, M.; Vasseur, P.; Robillard, L. Multiple steady states for unicellular natural convection in an inclined porous layer. Int. J. Heat Mass Transf. 1987, 30, 2097–2113. [Google Scholar] [CrossRef]
- Shi, Z.; Wen, B.; Hesse, M.; Tsotsis, T.; Jessen, K. Measurement and modeling of CO2 mass transfer in brine at reservoir conditions. Adv. Water Resour. 2018, 113, 100–111. [Google Scholar] [CrossRef]
- Wen, B.; Akhbari, D.; Zhang, L.; Hesse, M.A. Convective carbon dioxide dissolution in a closed porous medium at low pressure. J. Fluid Mech. 2018, 854, 56–87. [Google Scholar] [CrossRef]
- Wen, B.; Chang, K.W.; Hesse, M.A. Rayleigh-Darcy convection with hydrodynamic dispersion. Phys. Rev. Fluids 2018, 3, 123801. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover: New York, NY, USA, 2000. [Google Scholar]
- Nikitin, N. Third-order-accurate semi-implicit Runge–Kutta scheme for incompressible Navier–Stokes equations. Int. J. Numer. Meth. Fluids 2006, 51, 221–233. [Google Scholar] [CrossRef]
- Peyret, R. Spectral Methods for Incompressible Viscous Flow; Springer: New York, NY, USA, 2002. [Google Scholar]
- Lo Jacono, D.; Bergeon, A.; Knobloch, E. Spatially localized binary fluid convection in a porous medium. Phys. Fluids 2010, 22, 909. [Google Scholar] [CrossRef]
- Lo Jacono, D.; Bergeon, A.; Knobloch, E. Three-dimensional spatially localized binary-fluid convection in a porous medium. J. Fluid Mech. 2013, 730, R2. [Google Scholar] [CrossRef]

| 300 | 500 | 792 | 998 | |
|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, B.; Chini, G.P. On Moderate-Rayleigh-Number Convection in an Inclined Porous Layer. Fluids 2019, 4, 101. https://doi.org/10.3390/fluids4020101
Wen B, Chini GP. On Moderate-Rayleigh-Number Convection in an Inclined Porous Layer. Fluids. 2019; 4(2):101. https://doi.org/10.3390/fluids4020101
Chicago/Turabian StyleWen, Baole, and Gregory P. Chini. 2019. "On Moderate-Rayleigh-Number Convection in an Inclined Porous Layer" Fluids 4, no. 2: 101. https://doi.org/10.3390/fluids4020101
APA StyleWen, B., & Chini, G. P. (2019). On Moderate-Rayleigh-Number Convection in an Inclined Porous Layer. Fluids, 4(2), 101. https://doi.org/10.3390/fluids4020101





