Inertial Effects on Dynamics of Immiscible Viscous Fingering in Homogenous Porous Media
Abstract
:1. Introduction
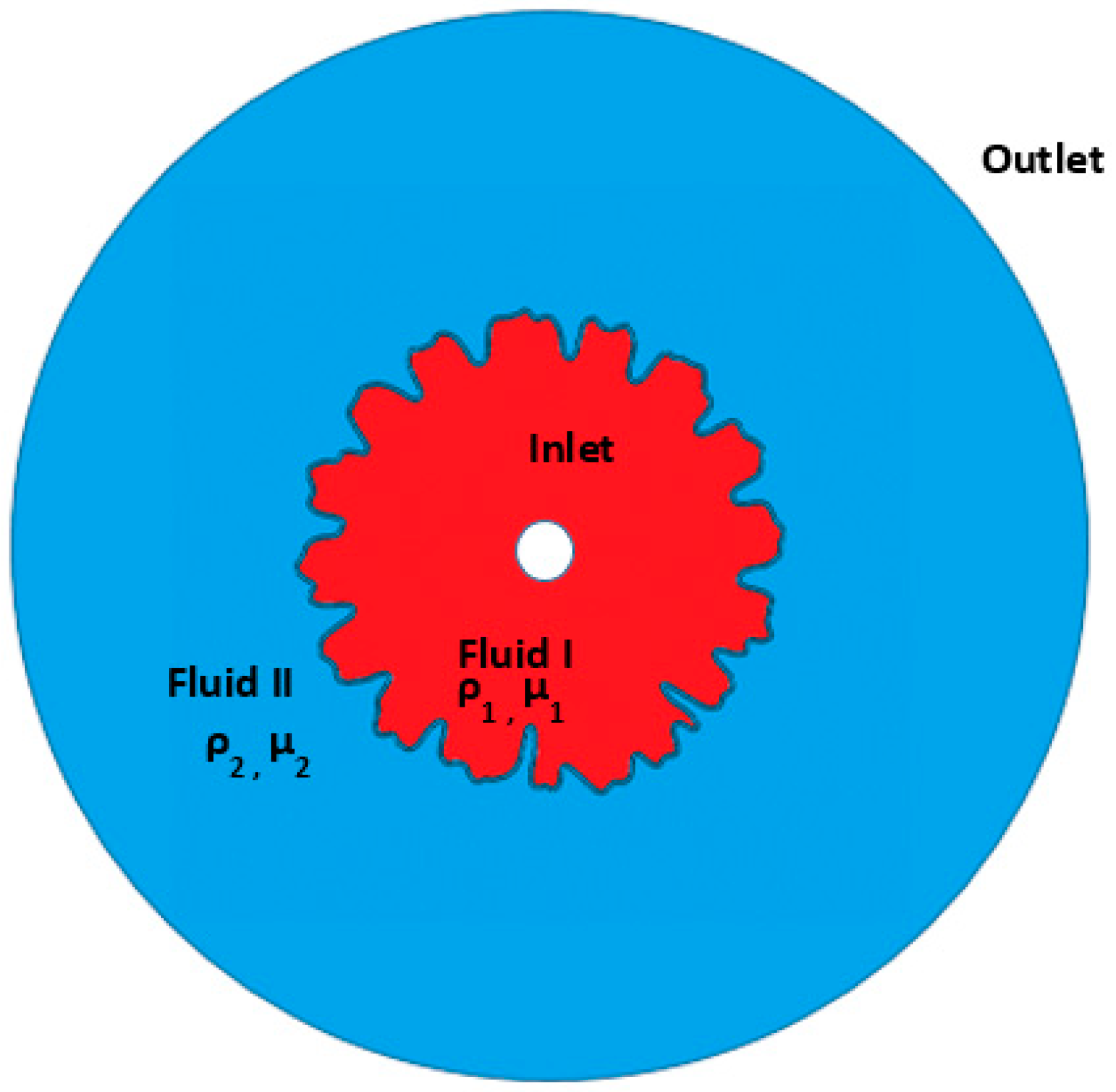
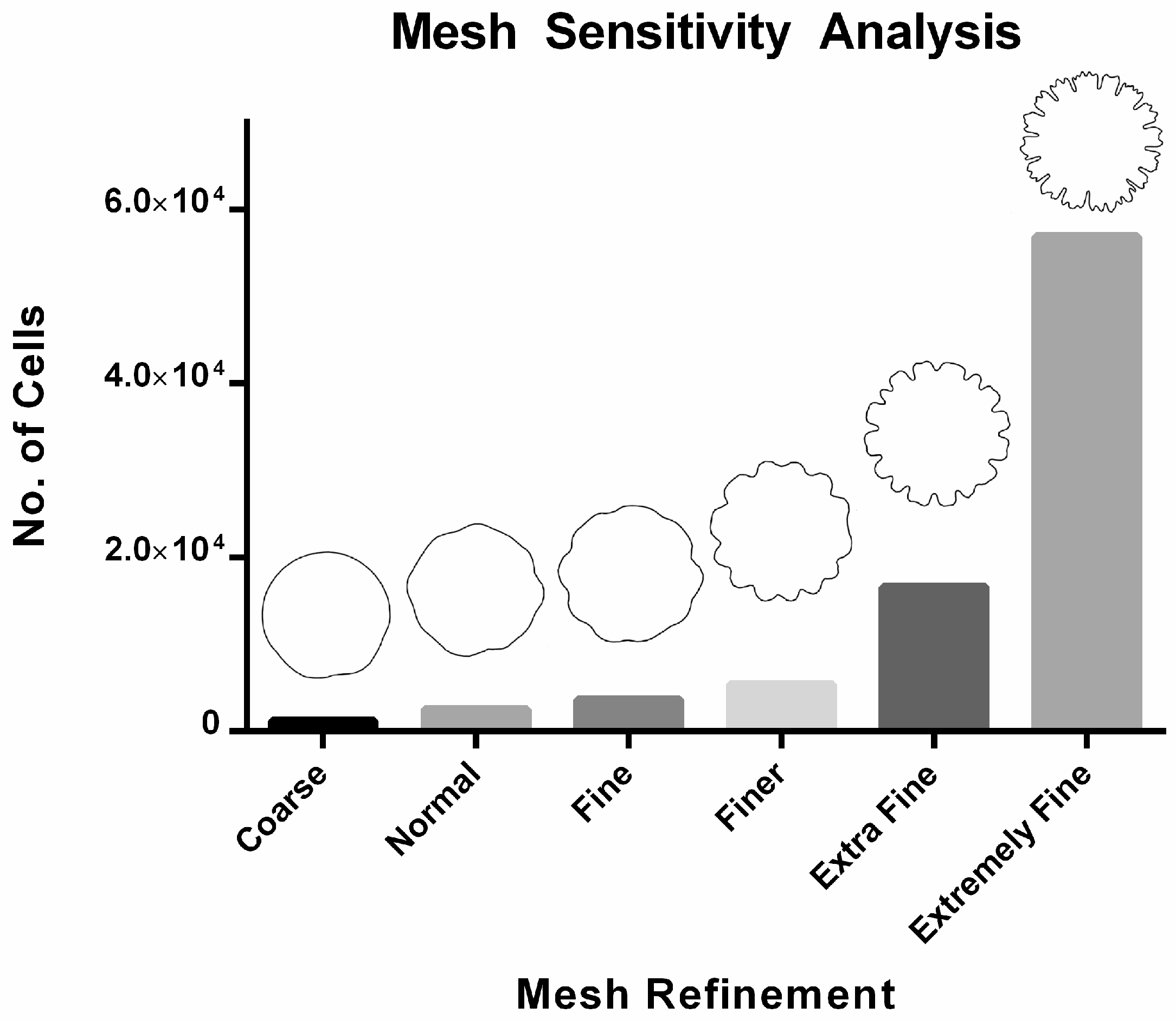
2. Mathematical Modelling
3. Results and Discussion
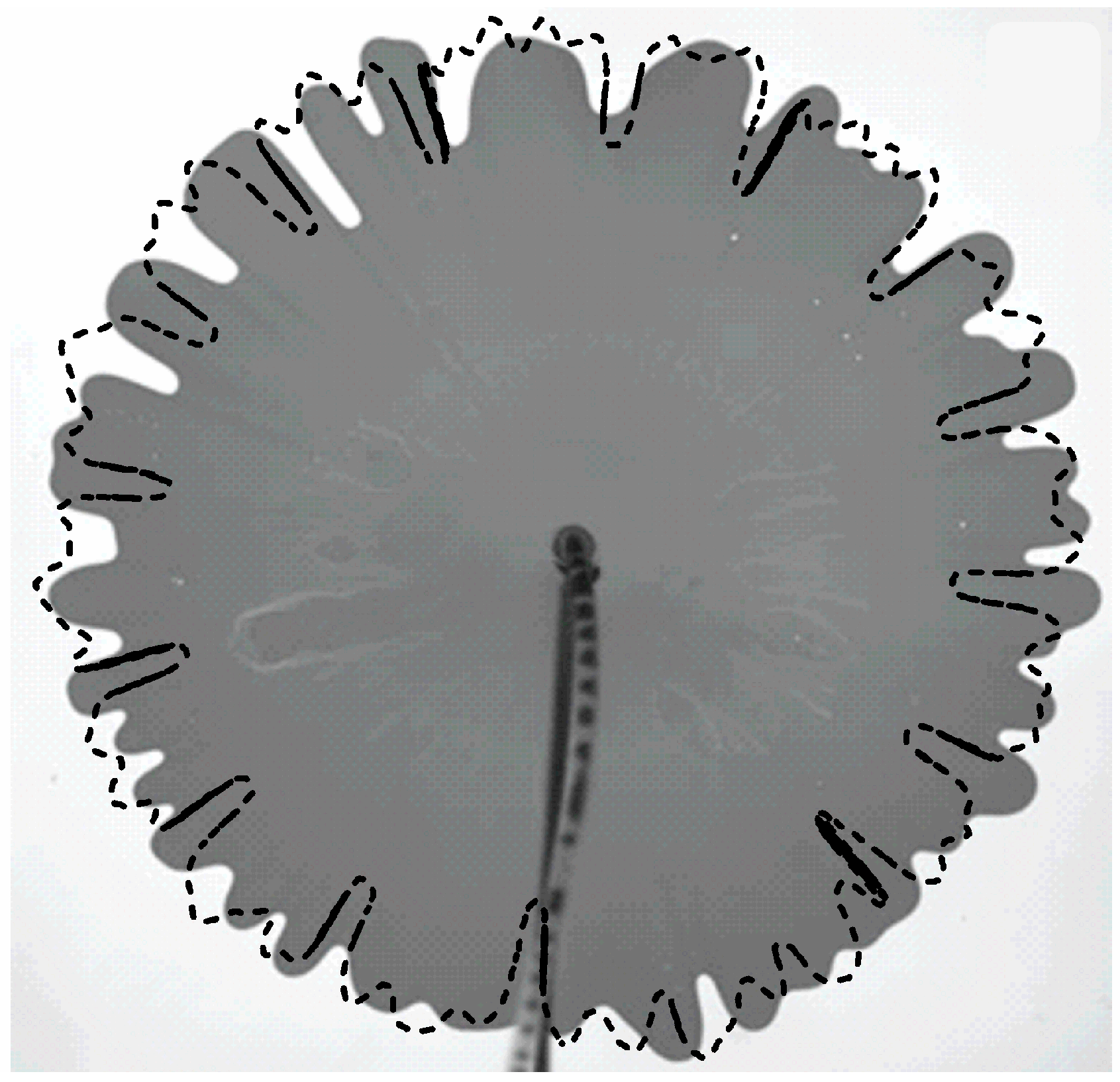
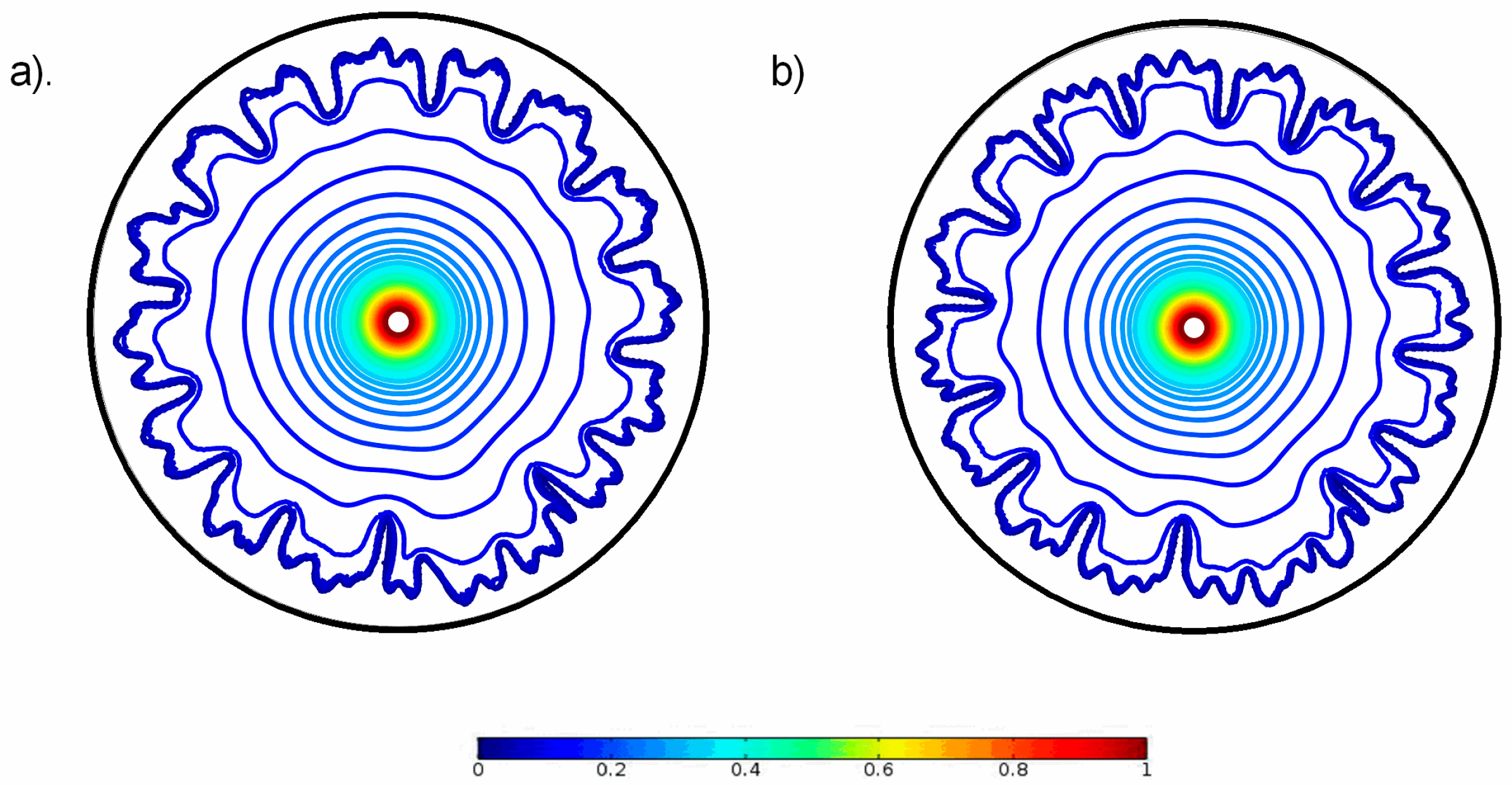
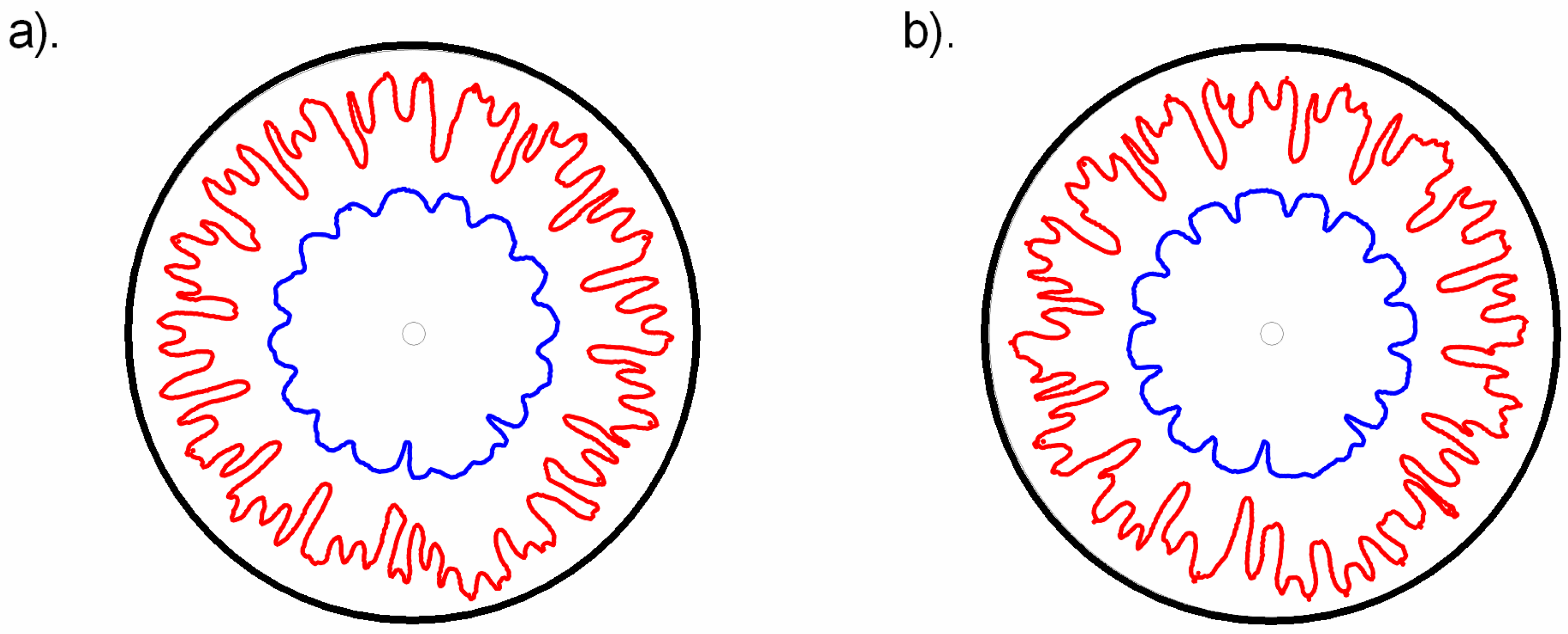
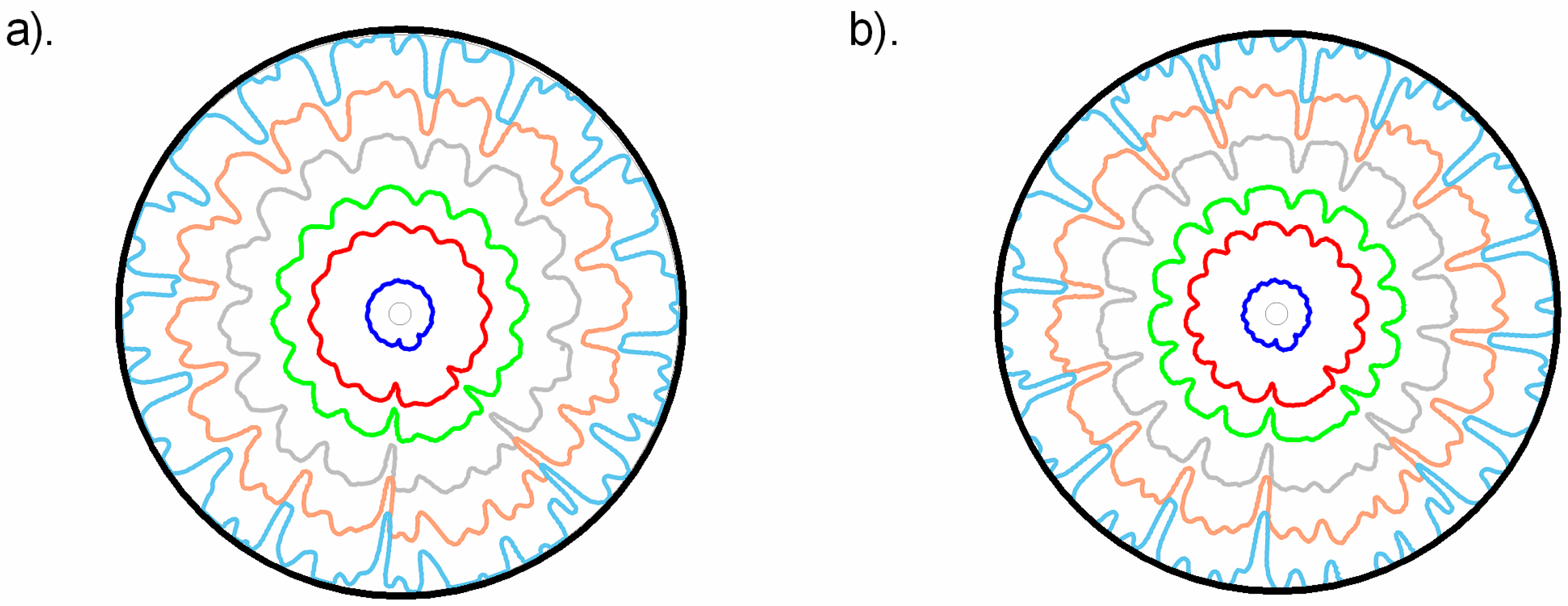
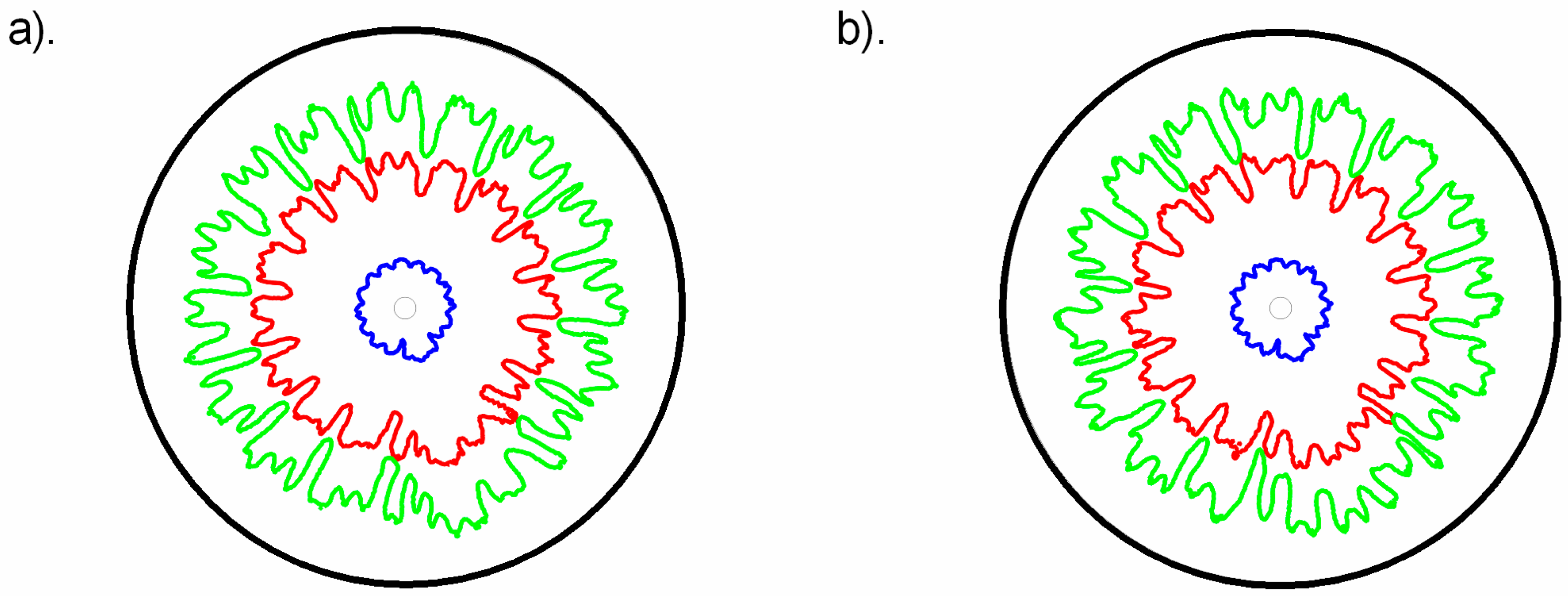
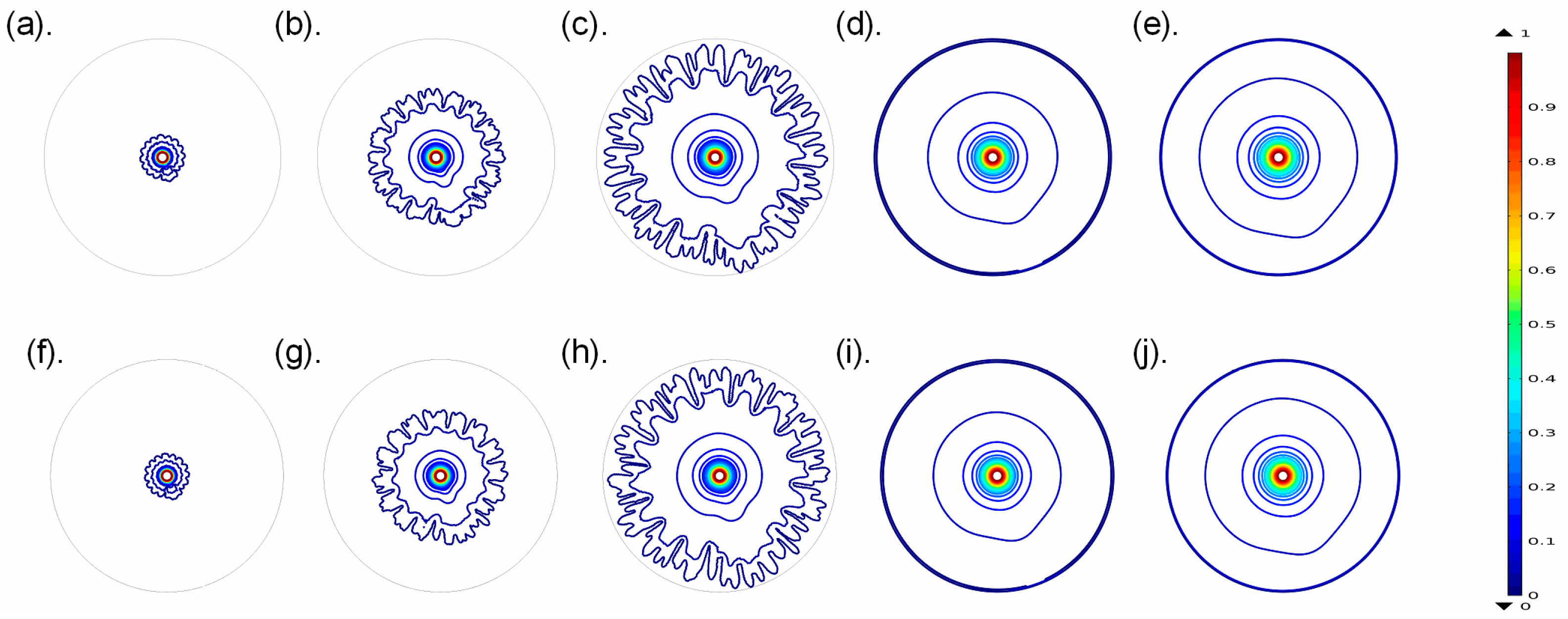
3.1. Qualitative Analysis
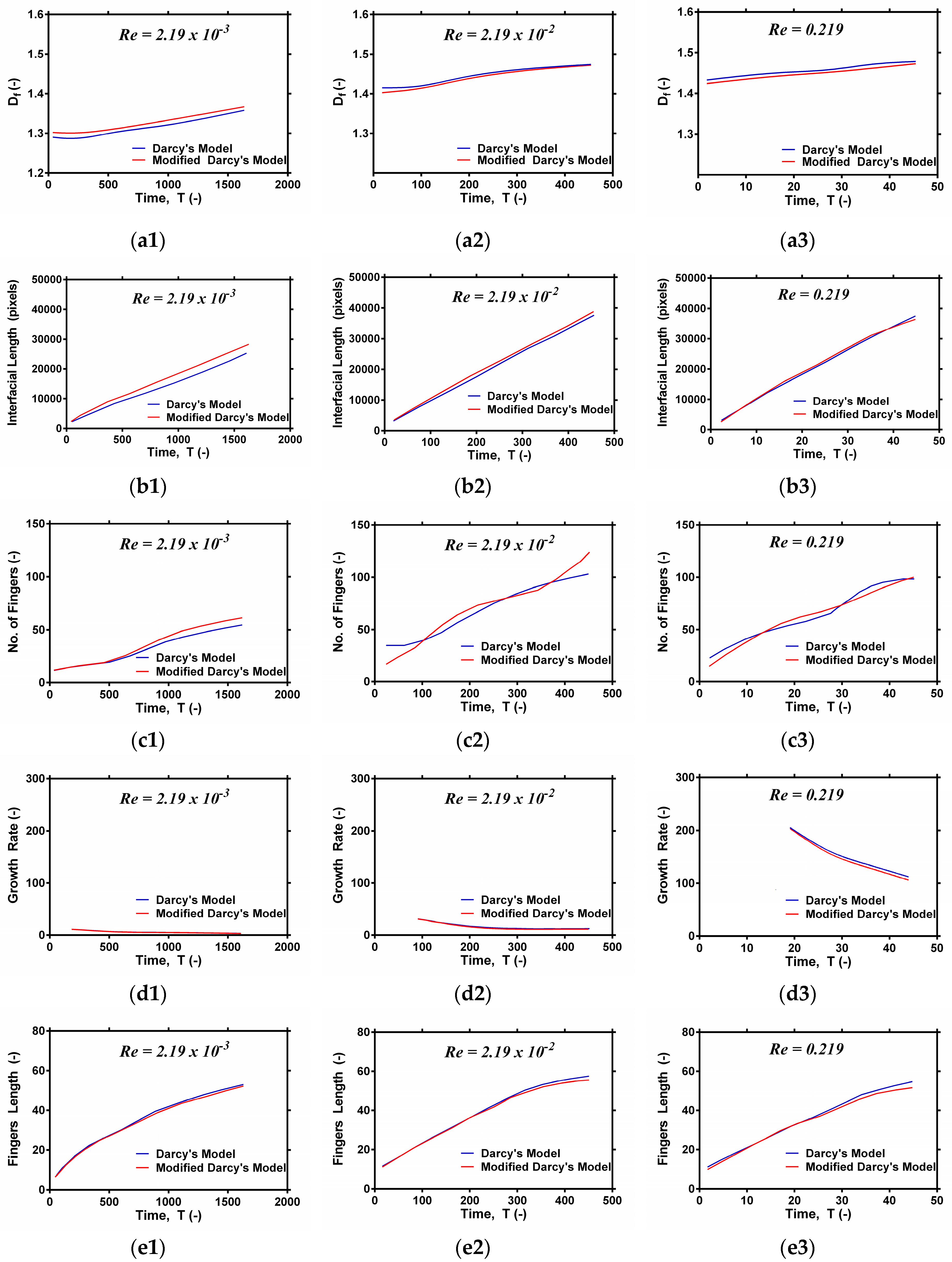
3.2. Quantitative Analysis
4. Conclusions
- The trend of saturation distribution remains the same, both for Darcy’s and the modified Darcy’s law with inertial corrections and convective acceleration. High saturation levels of invading fluid stay near the inlet while levels with low saturation travel far from the inlet.
- While considering the modification in Darcy’s law, the fractal number is found to decrease as the Reynolds number increases.
- The interfacial area is observed to be underestimated by Darcy’s law, especially at low Reynold’s numbers.
- Modification in Darcy’s law affects fingers morphology. At low viscosity ratios, fingers tend to widen while this effect is relatively small at high viscosity ratios.
- Length and growth of fingers are affected mostly at later stages of the fingers evolution, while the growth rate of fingers decreases with an increase in inertial effects and convective acceleration.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saffman, P.G.; Taylor, G. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1958, 245, 312–329. [Google Scholar]
- Chevalier, S.; Faisal, T.F.; Bernabe, Y.; Juanes, R.; Sassi, M. Numerical sensitivity analysis of density driven CO2 convection with respect to different modeling and boundary conditions. Heat Mass Transf. 2015, 51, 941–952. [Google Scholar] [CrossRef]
- Fakhari, A.; Li, Y.; Bolster, D.; Christensen, K.T. A phase-field lattice Boltzmann model for simulating multiphase flows in porous media: Application and comparison to experiments of CO2 sequestration at pore scale. Adv. Water Resour. 2018, 114, 119–134. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Eftekhari, A.; Hajibeygi, H.; van der Meer, J.; Vincent-Bonnieu, S.; Rossen, W. Simulation of Instabilities and Fingering in Surfactant Alternating Gas (SAG) Foam Enhanced Oil Recovery. J. Nat. Gas Sci. Eng. 2016, 34, 1191–1204. [Google Scholar] [CrossRef]
- Kadioglu, S.Y.; Sussman, M. Adaptive solution techniques for simulating underwater explosions and implosions. J. Comput. Phys. 2008, 227, 2083–2104. [Google Scholar] [CrossRef]
- Pramanik, S.; De Wit, A.; Mishra, M. Viscous fingering and deformation of a miscible circular blob in a rectilinear displacement in porous media. J. Fluid Mech. 2015, 782, R2. [Google Scholar] [CrossRef]
- Sharma, V.; Pramanik, S.; Mishra, M. Dynamics of a Highly Viscous Circular Blob in Homogeneous Porous Media. Fluids 2017, 2, 32. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Forchheimer, P. Wasserbewegung durch boden. Z. Ver. Dtsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48. [Google Scholar]
- Du Plessis, J.P.; Masliyah, J.H. Mathematical modelling of flow through consolidated isotropic porous media. Transp. Porous Media 1988, 3, 145–161. [Google Scholar] [CrossRef]
- Zeng, Z.; Grigg, R. A criterion for non-Darcy flow in porous media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Barree, R.; Conway, M. Beyond beta factors: A complete model for Darcy, Forchheimer, and trans-Forchheimer flow in porous media. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar]
- Sutera, S.P.; Skalak, R. The history of Poiseuille’s law. Annu. Rev. Fluid Mech. 1993, 25, 1–20. [Google Scholar] [CrossRef]
- Burke, S.; Plummer, W. Gas Flow through Packed Columns1. Ind. Eng. Chem. 1928, 20, 1196–1200. [Google Scholar] [CrossRef]
- Xie, Y.; Simmons, C.T.; Werner, A.D. Speed of free convective fingering in porous media. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Gondret, P.; Rabaud, M. Shear instability of two-fluid parallel flow in a Hele–Shaw cell. Phys. Fluids 1997, 9, 3267–3274. [Google Scholar] [CrossRef]
- Ruyer-Quil, C. Inertial corrections to the Darcy law in a Hele–Shaw cell. C. R. De L’académie Des Sci.-Ser. IIB-Mech. 2001, 329, 337–342. [Google Scholar] [CrossRef]
- Dias, E.O.; Miranda, J.A. Influence of inertia on viscous fingering patterns: Rectangular and radial flows. Phys. Rev. E 2011, 83, 066312. [Google Scholar] [CrossRef] [PubMed]
- Dias, E.O.; Miranda, J.A. Inertial effects on rotating Hele-Shaw flows. Phys. Rev. E 2011, 83, 046311. [Google Scholar] [CrossRef] [PubMed]
- Homsy, G.M. Viscous fingering in porous media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Nase, J.; Derks, D.; Lindner, A. Dynamic evolution of fingering patterns in a lifted Hele–Shaw cell. Phys. Fluids 2011, 23, 123101. [Google Scholar] [CrossRef]
- Pihler-Puzović, D.; Illien, P.; Heil, M.; Juel, A. Suppression of complex fingerlike patterns at the interface between air and a viscous fluid by elastic membranes. Phys. Rev. Lett. 2012, 108, 074502. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Kamrava, S. A pore-scale mathematical modeling of fluid-particle interactions: Thermo-hydro-mechanical coupling. Int. J. Greenh. Gas Control 2019, 83, 245–255. [Google Scholar] [CrossRef]
- Fagbemi, S.; Tahmasebi, P.; Piri, M. Interaction Between Fluid and Porous Media with Complex Geometries: A Direct Pore-Scale Study. Water Resour. Res. 2018, 54, 6336–6356. [Google Scholar] [CrossRef]
- Fagbemi, S.; Tahmasebi, P.; Piri, M. Pore-scale modeling of multiphase flow through porous media under triaxial stress. Adv. Water Resour. 2018, 122, 206–216. [Google Scholar] [CrossRef]
- Al-Housseiny, T.T.; Stone, H.A. Controlling viscous fingering in tapered Hele-Shaw cells. Phys. Fluids 2013, 25, 092102. [Google Scholar] [CrossRef]
- Zheng, Z.; Kim, H.; Stone, H.A. Controlling Viscous Fingering Using Time-Dependent Strategies. Phys. Rev. Lett. 2015, 115, 174501. [Google Scholar] [CrossRef]
- Zhao, B.; MacMinn, C.W.; Juanes, R. Wettability control on multiphase flow in patterned microfluidics. Proc. Natl. Acad. Sci. USA 2016, 113, 10251–10256. [Google Scholar] [CrossRef]
- Trojer, M.; Szulczewski, M.L.; Juanes, R. Stabilizing fluid-fluid displacements in porous media through wettability alteration. Phys. Rev. Appl. 2015, 3, 054008. [Google Scholar] [CrossRef]
- Wu, Y.-S. Numerical simulation of single-phase and multiphase non-Darcy flow in porous and fractured reservoirs. Transp. Porous Media 2002, 49, 209–240. [Google Scholar] [CrossRef]
- Saez, A.; Carbonell, R. hydrodynamic parameters for gas-liquid cocurrent flow in packed beds. Aiche J. 1985, 31, 52–62. [Google Scholar] [CrossRef]
- Raju, M.P. Parallel computation of finite element Navier-Stokes codes using MUMPS solver. arXiv, 2009; arXiv:0910.1845. [Google Scholar]
- Ramachandran, R. Stability and onset of two-dimensional viscous fingering in immiscible fluids. arXiv, 2017; arXiv:1704.02674. [Google Scholar]
- Mostaghimi, P.; Kamali, F.; Jackson, M.D.; Muggeridge, A.H.; Pain, C.C. Adaptive mesh optimization for simulation of immiscible viscous fingering. SPE J. 2016, 21. [Google Scholar] [CrossRef]
- Adam, A.; Pavlidis, D.; Percival, J.; Salinas, P.; Loubens, R.D.; Pain, C.; Muggeridge, A.; Jackson, M. Dynamic Mesh Adaptivity for Immiscible Viscous Fingering. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017. [Google Scholar]
- Chen, J.-D. Radial viscous fingering patterns in Hele-Shaw cells. Exp. Fluids 1987, 5, 363–371. [Google Scholar] [CrossRef]
- Pons, M.-N.; Weisser, E.; Vivier, H.; Boger, D. Characterization of viscous fingering in a radial Hele-Shaw cell by image analysis. Exp. Fluids 1999, 26, 153–160. [Google Scholar] [CrossRef]
- Thrasher, M.E. Geometry and Dynamics of Fluid-Fluid Interfaces. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, December 2007. [Google Scholar]
- Fraclac. Available online: https://imagej.nih.gov/ij/plugins/fraclac/FLHelp/Introduction.htm (accessed on 2 December 2018).
- Anjos, P.H.; Dias, E.O.; Miranda, J.A. Radial fingering under arbitrary viscosity and density ratios. Phys. Rev. Fluids 2017, 2, 084004. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabbani, S.; Abderrahmane, H.; Sassi, M. Inertial Effects on Dynamics of Immiscible Viscous Fingering in Homogenous Porous Media. Fluids 2019, 4, 79. https://doi.org/10.3390/fluids4020079
Rabbani S, Abderrahmane H, Sassi M. Inertial Effects on Dynamics of Immiscible Viscous Fingering in Homogenous Porous Media. Fluids. 2019; 4(2):79. https://doi.org/10.3390/fluids4020079
Chicago/Turabian StyleRabbani, Shahid, Hamid Abderrahmane, and Mohamed Sassi. 2019. "Inertial Effects on Dynamics of Immiscible Viscous Fingering in Homogenous Porous Media" Fluids 4, no. 2: 79. https://doi.org/10.3390/fluids4020079
APA StyleRabbani, S., Abderrahmane, H., & Sassi, M. (2019). Inertial Effects on Dynamics of Immiscible Viscous Fingering in Homogenous Porous Media. Fluids, 4(2), 79. https://doi.org/10.3390/fluids4020079



