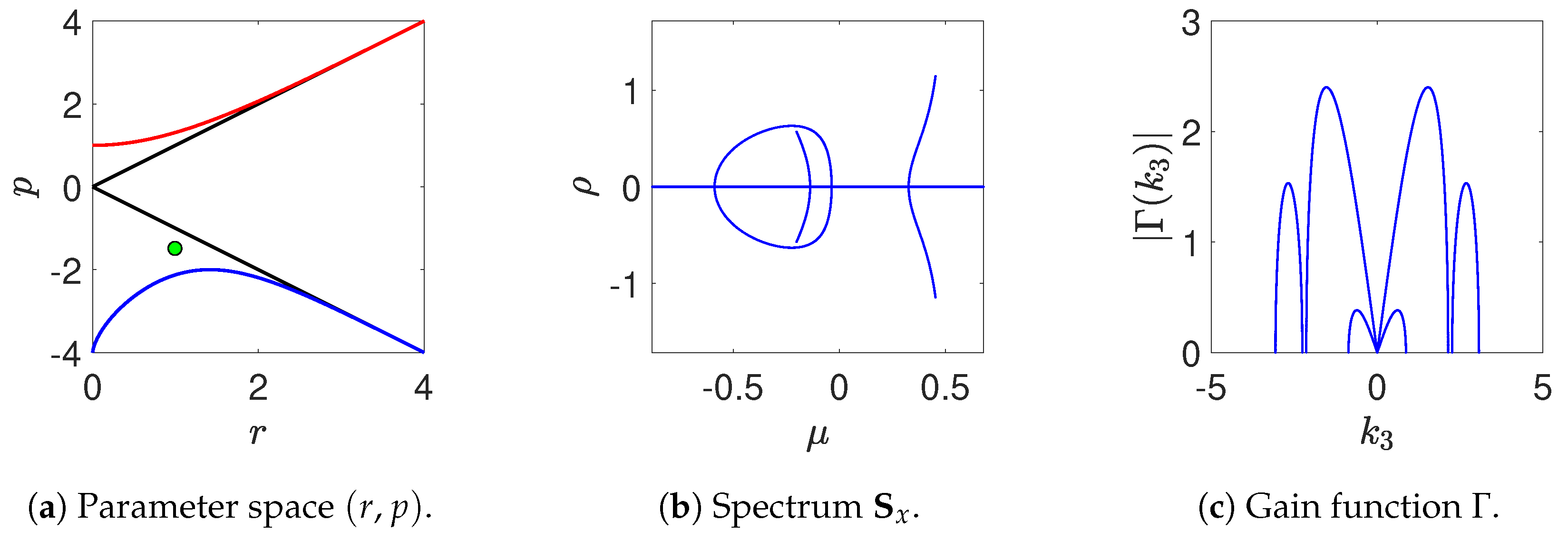Rogue Wave Type Solutions and Spectra of Coupled Nonlinear Schrödinger Equations

Abstract

The formation of rogue oceanic waves may be the result of different causes. Various factors (winds, currents, dispersive focussing, depth, nonlinear focussing and instability) make this subject intriguing, and yet its understanding is quite relevant to practical issues. Here, we deal only with the nonlinear character of this dynamics, which has been recognised as the main ingredient to rogue wave formation. In this perspective, the formation of rogue waves requires a non-vanishing and unstable background such as a nonlinear regular wave train with attractive self-interaction. The simplest, best known model of such dynamics is the universal nonlinear Schrödinger equation. This has proven to serve as a good approximation in various contexts and over a broad range of experimental settings. This model aims to give the slow evolution of the envelope of one monochromatic wave due to nonlinearity. Here, we naturally consider the same problem for the envelopes of two weakly resonant monochromatic waves. As for the nonlinear Schrödinger equation, which is integrable, we adopt an integrable model to describe the interaction of two waves. This is the system of two coupled nonlinear Schrödinger equations (Manakov model) with self- and cross-interactions that may be both defocussing and focussing. We first discuss the linear stability properties of the background by computing the spectrum for all values of the parameters such as coupling constants and amplitudes. In particular, we relate the instability bands to properties of the spectrum and compute the gain function (or growth rate). We also relate to the stability spectrum the value of the spectral variable, which corresponds to a rogue wave solution. In contrast with the nonlinear Schrödinger equation, different types of single rogue wave exist that correspond to different values of the spectral variable even in the same spectrum. For these critical values, which are completely classified, we give the corresponding explicit expression of the rogue wave solution that follows from the well known Darboux–Dressing transformation method. Although not all systems of two coupled nonlinear Schrödinger equations that have been derived in water wave dynamics are integrable, our investigation contributes to the understanding of new effects due to wave coupling, at least for model equations that, even if not integrable, are close enough to the model considered here. For instance, our findings lead to investigate rogue waves generated by instabilities due to self- and cross-interactions of defocusing type. An illustrative selection of two coupled rogue waves solutions is displayed.

1. Introduction

Oceanic rogue waves have attracted significant attention in recent years, becoming a well established subject of studies in the last two decades after a long period in which they were rather regarded as part of the maritime folklore and sailors’ legends. Reminiscence of their legendary past is evident in the many names they have: rogue waves are also called freak, giant, anomalous, extreme, killing or monster waves. These are exceptionally high waves, substantially higher and steeper than those expected for a given sea state. Their existence has been now confirmed by a variety of observations. Their appearance in scientific literature probably dates back to 1964 when Draper presented a first description of the phenomenon in [1]. While in [2] one finds an initial discussion of rogues waves off the southeast African coast, in the Agulhas current, it is essentially in the last decades, thanks also to more reliable wave recordings as wave measurements from oil platforms, that they received wider attention from the scientific community as well as from the shipping and offshore industry [3,4,5,6]. Probably the best known reliable recording of a rogue wave is the so-called New Year wave, or Draupner wave [7,8], recorded at the Draupner platform in the North Sea off the coast of Norway on 1 January 1995. The Draupner wave was confirmed by damage to equipment on the platform deck, so it could not be classed as a measurement error, as it happened often with previous recordings. Even though the existence of rogue waves has been confirmed by various observations, their origin remains a debated subject (see, e.g., [8,9,10]). In this respect, contributions came also from lab experiments as rogue waves have been observed in tank to test the NLS equation as model of rogue wave generation by modulation instability of a long regular wave train [11,12,13,14]. Rogue waves have also been observed in tanks under controlled wind generation [15,16]. It should also be mentioned that it has been recently recognised that, in the near future, the significance of severe sea state conditions may even grow in some ocean regions because of the expected increase in the frequency and severity of extreme weather events associated with global warming [17].

The initial stage of instability of a quasi-monochromatic plane wave is characterised by the exponential growth of a small localised bump of the monochromatic envelope. The short time evolution of this initial perturbation depends on the eigenmodes of the linearised NLS equation around this monochromatic wave. Our purpose here is to infer from these eigenmodes the instability bands and the corresponding rate of growth of a small perturbation. The important question of the long time nonlinear stage of the evolution is out of the scope of the present work (see, e.g., [18,19]). In the past decades, the main focus has been directed on the generation of rogue waves and on the conditions under which such waves are more likely to occur. This work has revealed the existence of similar extreme phenomena in other physical contexts, such as nonlinear optics and lasers [20], atmosphere [21], plasma physics [22], and matter waves (Bose–Einstein condensate) [23,24]. These investigations have given further impulse, and the interest in rogue waves is today a well motivated multidisciplinary research area on its own (see also [25,26]).

Because of the common acceptance of the crucial role that nonlinearity plays in ocean wave dynamics, especially so in rogue wave formation, and because of the computational burden of solving the full nonlinear equations describing the sea state numerically, much of the work done on rogue waves has been carried out using approximate models. An important class of such models, which has been widely used in rogue wave research, is that of Nonlinear Schrödinger (NLS) equations. In oceanography, NLS-type equations can be derived from the full Euler equations by assuming that waves are weakly nonlinear, with small wave steepness, and narrow banded. The simplest NLS equation $i{u}_t+u_{xx}-2s{|u|}^{2}u=0$ accounts for quadratic dispersion and cubic nonlinearity of the slowly varying amplitude of just one quasi-monochromatic wave (for a simple derivation by multi-scale perturbation method, see, for instance, [27]). Indeed, this equation plays the role of a universal model [28] as it emerges by wisely approximating almost any conservative wave dynamics. This accounts for its ubiquity in physical applications, wherever the conditions of weak dispersion and nonlinearity, and of narrow band, are met. By the same token, the  way the NLS equation is derived also explains its integrable character since it also approximates known wave equations such as the Korteweg–de Vries equation for shallow water waves, which is well-known to be integrable [29]. Thus, whenever the wave motion can be considered in a one-dimensional space, the NLS equation is a universal and integrable model with powerful implications for both its physical relevance and mathematical properties. In this respect, the NLS equation has deserved further special interest as it proves to yield, for focusing interaction, a simple description of the instability of a regular wave train, a phenomenon first observed by Talanov [30] in optics and by Benjamin and Feir [31] in a water tank. Such instability is responsible for breaking a plane wave into irregular motion and eventually for generation of novel wave patterns such as rogue waves [19,25] (see also, e.g., [32]). Today, for the scalar NLS equation, the focusing nonlinear regime is well recognised to be a prerequisite for the emergence of rogue waves. On the contrary, the defocusing regime of the NLS equation does not allow for rogue wave solutions, even of dark nature. In fact, the linear stability analysis of the background continuous wave solution in focusing and defocusing regimes is sufficient to make such distinction [33]. In addition to its proven validity, laboratory observations show that the accuracy of the NLS equation is even higher than expected [11,34].

The research area on rogue waves goes well beyond water waves dynamics and extends itself to quite a number of different fields. We deem it worth mentioning that some of them, although not quite ocean physics, have recently received a new impulse from the novel extension of soliton theory to nonlocal equations, namely to models with parity-time symmetry, and time symmetry. In particular, these extended models are, among many others, the nonlocal NLS, coupled NLS and Davey–Stewartson equations [35,36,37].

Since numerous physical phenomena require modelling waves with two or more components to account for different modes, frequencies, or polarisations, coupled-wave systems have recently attracted the interest of the research community. In such systems, however, the situation is much richer, and it has been shown in [38,39] that rogue wave solutions can exist also in the defocussing and mixed regimes [38]. Again, by applying the perturbation method of multiple scale, as in the derivation of the NLS equation, to the envelopes of two quasi-monochromatic waves, and by adding an appropriate weak resonance condition, one arrives at a system of two coupled NLS equations (for such derivation in the description of crossing sea waves, see [40,41,42]). The difference with respect to the single NLS equation is that such system, although it still features quadratic dispersion and cubic nonlinearity, is less universal as it has a larger number of coupling constants, and it is generically non-integrable, although with few important exceptions. In this paper, we take advantage of the existence of integrable versions [43] of a system of two coupled NLS equations to explore the connection between the instability properties of the plane wave solution and the existence and features of rogue wave solutions. Thus, in Section 2, we first introduce the definition of the stability spectrum via the construction of the eigenmodes of the linearised wave equations, and then we give a complete classification of such spectra in the parameter space, namely for different values of coupling constants and amplitudes. Relating then the geometrical properties of the spectrum to rogue waves, in Section 3, we classify also the set of rogue wave solutions, and give their expression via the standard Darboux–Dressing technique [38,44,45]. By numerical computations, we look into few properties of these wave solutions, such as their amplitude height for the sake of comparing them with the analogue Peregrine solution of the NLS equation. According to their relation to spectra, examples of each type of rogue wave solutions are graphically shown. Section 4 is devoted to conclusions.

2. CNLS: Spectra and Stability

Since a main ingredient in the occurrence of rogue waves has been recognised [38,39] to be the instability of their background state, our main focus here is on the linear stability of continuous waves (CW). Moreover, it has been also realised [46] that the stability of two CWs, which are weakly at resonance, features a richer phenomenology with respect to that associated to just one plane wave [47]. Thus, we devote this section to collect and emphasise such novel features by discussing the stability of CW solutions of the following two coupled nonlinear Schrödinger (CNLS) equations

$$\left\{\begin{array}{ccc}i{u}_{1t}+u_{1xx}-2(s_1|u_1{|}^2+s_2|u_2{|}^2)u_1\hfill & =\hfill & 0\hfill \\ i{u}_{2t}+u_{2xx}-2(s_1|u_1{|}^2+s_2|u_2{|}^2)u_2\hfill & =\hfill & 0.\hfill \end{array}\right.$$

(1)

Here, and in the following, a subscripted continuous variable, such as x and t, which are the slow space-time coordinates, stands for partial differentiation with respect to that variable. The two dependent variables $u_j(x,t)$, $j=1,2$, are the (rescaled) complex envelope amplitudes of two quasi-monochromatic waves that are weakly resonant and propagate with self- and cross-interactions. The interactions are modelled by cubic terms with real coupling constants $s_1$ and $s_2$. Coupled equations of this kind, perhaps with different interaction terms and dispersion coefficients, may be derived by multi-scale analysis in several contexts, mainly in optical fibres [48] but also in multi-component Bose–Einstein condensates [23], and in few instances of surface gravity waves in deep water [41]. A limitation to their applicability to water wave propagation comes from the weak resonance condition which requires that the two carrier waves have nearly the same group velocity, which, in turn, is a condition on the carrier waves linear dispersion relation. Our preference for the system in Equation (1) is motivated by its peculiar, and exceptional, property of being integrable for any choice of $s_1$ and $s_2$ [43]. In fact, as shown below, the integrability property does allow one to use powerful, and rather direct, both analytical and numerical, methods to investigate the linear stability of a given solution $u_1$, $u_2$ of the CNLS equations in Equation (1). Moreover, even if the model in Equation (1) is not exactly the one of interest, it is sufficiently close to it that we believe investigating this integrable model is worth doing as the resulting dynamics may serve as reference guide to deal with similar, but non-integrable, equations.

With no loss of generality, we give the coupling constants the rescaled values $s_1=\pm 1$, $s_2=\pm 1$. Thus, the system in Equation (1) describes three different physical settings: the defocusing Manakov model for $s_1=s_2=1$, the focusing Manakov model for $s_1=s_2=-1$ and the mixed case $s_1=-s_2$. This system is therefore a natural integrable vector generalisation of the NLS scalar equation which is obtained from Equation (1) by merely setting $u_2=0$. In our present setting, its integrality stems from the existence of its associated Lax pair of matrix linear ordinary differential equations

$${\mathsf{\Psi }}_x=X\mathsf{\Psi },{\mathsf{\Psi }}_t=T\mathsf{\Psi },$$

(2)

which are compatible with each other if the following equation

$$X_t-T_x+[X,T]=0$$

(3)

is satisfied. Both matrix coefficients $X(x,t,\lambda )$ and $T(x,t,\lambda )$ are $3\times 3$, and have the simple polynomial dependence on the complex spectral variable $\lambda$

$$X(\lambda )=i\lambda \mathsf{\Sigma }+Q,T(\lambda )=2i{\lambda }^2\mathsf{\Sigma }+2\lambda Q+i\mathsf{\Sigma }(Q^2-Q_x),$$

(4)

where

$$\mathsf{\Sigma }=\mathrm{diag}\{1,-1,-1\}$$

(5)

and

$$Q=\left(\begin{array}{ccc}0& s_1{u}_1^{*}& s_2{u}_2^{*}\\ u_1& 0& 0\\ u_2& 0& 0\end{array}\right).$$

(6)

Hereafter, the upper scripted asterisk means complex conjugation and the squared bracket $[X,T]$ is the usual commutator $XT-TX$. The choice in Equation (4) of the matrices $X(\lambda )$ and $T(\lambda )$ implies that the compatibility condition in Equation (3) is equivalent to the CNLS system in Equation (1). As is well known (see, e.g., [49]), the $\lambda$-dependence of the Lax pair in Equation (2), together with the assumption that the wave fields $u_1$ and $u_2$ vanish sufficiently fast as $x\to \pm \infty$, is the departure point of the spectral (alias inverse scattering) transform method, which is the nonlinear analogue of the Fourier transform (see [50] and the introductory lecture [51]). The mathematical setting required by the application of the spectral transform is rather cumbersome, and becomes even more so if the boundary values of the solution $u_1$, $u_2$ do not vanish as $x\to \pm \infty$, as ideally happens when dealing with CW solutions. However, since our aim here is confined to establishing only the linear stability of a given solution of the CNLS system, we take a simpler route. As is standard, the investigation of the linear stability of any known solution $u_1$, $u_2$ of the CNLS equations in Equation (1) starts with the linear equations

$$\begin{array}{c}\delta u_{1t}=i\{\delta u_{1xx}-2[(2s_1|u_1{|}^2+s_2|u_2{|}^2)\delta u_1+s_1{u}_1^2\delta u_1^{*}+s_2{u}_1{u}_2^{*}\delta u_2+s_2{u}_1{u}_2\delta u_2^{*}]\}\hfill \\ \delta u_{2t}=i\{\delta u_{2xx}-2[(s_1|u_1{|}^2+2s_2|u_2{|}^2)\delta u_2+s_2{u}_2^2\delta u_2^{*}+s_1{u}_2{u}_1^{*}\delta u_1+s_1{u}_2{u}_1\delta u_1^{*}]\}\hfill \end{array}$$

(7)

for the unknown functions $\delta u_1$ and $\delta u_2$. This system originates from the assumption that $u_1(x,t)+\delta u_1(x,t)$, $u_2(x,t)+\delta u_2(x,t)$ is an approximate solution of the CNLS system in Equation  (1), provided $\delta u_1(x,t)$, $\delta u_2(x,t)$ is a sufficiently small solution of Equation (7). Hereafter, we consider only perturbations $\delta u_1(x,t)$, $\delta u_2(x,t)$ whose initial data are assumed to be localised (and bounded) in x. Proving that the solution $u_1(x,t)$, $u_2(x,t)$ be linearly stable requires showing that the initially small data $\delta u_1(x,t_0)$, $\delta u_2(x,t_0)$ remain small at any time t. A standard way to face this problem is to construct a (complete) set of solutions $F_1(x,t,\lambda )$, $F_2(x,t,\lambda )$ of the linear Equation (7),

$$\begin{array}{c}{F}_{1t}=i\{F_{1xx}-2[(2s_1|u_1{|}^2+s_2|u_2{|}^2)F_1+s_1{u}_1^2{F}_1^{*}+s_2{u}_1{u}_2^{*}{F}_2+s_2{u}_1{u}_2{F}_2^{*}]\}\hfill \\ F_{2t}=i\{F_{2xx}-2[(s_1|u_1{|}^2+2s_2|u_2{|}^2)F_2+s_2{u}_2^2{F}_2^{*}+s_1{u}_2{u}_1^{*}{F}_1+s_1{u}_2{u}_1{F}_1^{*}]\}.\hfill \end{array}$$

(8)

These solutions, the eigenmodes, depend on the spectral parameter $\lambda$ with the implication that the solution of Equation (7) can be formally represented as the linear combination

$$\delta u_j(x,t)={\int }_{{\mathbf{S}}_x}\mathrm{d}\lambda F_j(x,t,\lambda ),j=1,2.$$

(9)

As shown below in the case of CWs, the expression of these eigenfunctions is sufficient to prove stability while there is no need to actually compute the integral in Equation (9). Indeed, the knowledge of such set of solutions, i.e., the eigenmodes, allows one to compute: (i) the stability spectrum ${\mathbf{S}}_x$, which is the appropriate subset of the complex $\lambda$-plane over which the integral (9) runs; (ii) the dispersion relation associated to the linearised Equation (7); and, quite importantly, (iii) the gain, namely the function of $\lambda$ that characterises the temporal growth of each unstable eigenmode (see below).

The construction of eigenmodes is made rather simple and direct by the following procedure. Suppose $u_1$, $u_2$ is a known given solution of the CNLS equations, then the first step is to compute a corresponding fundamental $3\times 3$ matrix solution $\mathsf{\Psi }(x,t,\lambda )$, $det\mathsf{\Psi }\ne 0$, of the Lax pair in Equation (2). The second step merely requires computing the matrix $\mathsf{\Psi }M(\lambda ){\mathsf{\Psi }}^{-1}$. A solution $F_1(\lambda )$, $F_2(\lambda )$ of the linearised Equation (8) takes the explicit expression of the $F_{21}$ and $F_{31}$ entries of the following matrix F

$$F(\lambda )=[\mathsf{\Sigma },\mathsf{\Psi }(\lambda )M(\lambda ){\mathsf{\Psi }}^{-1}(\lambda )]=\left(\begin{array}{ccc}0& s_1{F}_1^{*}({\lambda }^{*})& s_2{F}_2^{*}({\lambda }^{*})\\ F_1(\lambda )& 0& 0\\ F_2(\lambda )& 0& 0\end{array}\right).$$

(10)

Here, the matrix $M(\lambda )$, apart from some algebraic condition, is arbitrary and x- and t-independent. We omit detailing its explicit expression since it is not relevant to our present purposes. We note however that this computational way to construct eigenmodes is quite general, as it remains valid for a very large class of integrable systems. It has been used in several contexts and in different formulations, in particular in soliton perturbation theory, where these eigenmodes have been termed squared eigenfunctions [52,53]. A general derivation of Equation (10) from the Lax pair is given in [46], with no need to cope with the burden of the direct and inverse spectral problem techniques.

We now follow the way outlined above to investigate the linear stability of the continuous wave solution

$$u_1(x,t)=a_1{e}^{i(qx-\nu t)},u_2(x,t)=a_2{e}^{-i(qx+\nu t)},\nu =q^2+2p$$

(11)

of the CNLS equations in Equation (1). Here, the real parameter p,

$$p=s_1{a}_1^2+s_2{a}_2^2,$$

(12)

is given in terms of the coupling constants and of the amplitudes $a_1$ and $a_2$ that, with no loss of generality, are real and non-negative. The parameter q, which has a relevant role in the following analysis, measures the half-difference of the wave numbers of the two continuous wave components in Equation (11). In this respect, one should keep this parameter in mind, as it makes the stability properties of the continuous wave solution in Equation (11) of the CNLS system considerably different from those due to Benjamin–Feir instability described by the single NLS equation. With no loss of generality, we have chosen to consider here the two CW components in Equation (11) as counter-propagating. According to the general scheme, the first step requires constructing the matrix solution $\mathsf{\Psi }(x,t,\lambda )$ of the Lax pair in Equation (2). This is given by the expression

$$\begin{array}{c}\hfill \mathsf{\Psi }(x,t,\lambda )=R(x,t)e^{i(xW(\lambda )-tZ(\lambda ))},R(x,t)=\mathrm{diag}\{e^{ipt},e^{i(qx-q^{2}t-pt)},e^{-i(qx+q^{2}t+pt)}\},\end{array}$$

(13)

where the x- and t-independent matrices W and Z are found to be

$$W(\lambda )=\left(\begin{array}{ccc}\lambda & -i{s}_1{a}_1& -i{s}_2{a}_2\\ -i{a}_1& -\lambda -q& 0\\ -i{a}_2& 0& -\lambda +q\end{array}\right),$$

(14)

$$Z(\lambda )={\lambda }^2-2\lambda W(\lambda )-W^2(\lambda )-p,$$

(15)

with the property that they commute, $[W,Z]=0$, consistently with the compatibility condition in Equation (3). We consider here the eigenvalues $w_j(\lambda )$ and $z_j(\lambda )$, $j=1,2,3$, of $W(\lambda )$ and $Z(\lambda )$, respectively, as simple, as indeed they are for generic values of $\lambda$. Next, we construct the matrix $F(x,t,\lambda )$ via its definition in Equation (10), which, because of the explicit expression in Equation (13), reads

$$F(x,t,\lambda )=R(x,t)\left[\mathsf{\Sigma },e^{i(xW(\lambda )-tZ(\lambda ))}M(\lambda )e^{-i(xW(\lambda )-tZ(\lambda ))}\right]R^{-1}(x,t).$$

(16)

After some algebraic manipulation of this matrix expression in Equation (16), and by taking into account Equation (10), one ends up with the following equivalent way to express the eigenmode components $F_1$, $F_2$

$$\left(\begin{array}{c}{F}_1\hfill \\ F_2\hfill \end{array}\right)=\sum _{j,m=1}^3{\mu }_{jm}(\lambda )e^{i[(x(w_j-w_m)-t(z_j-z_m)]}{e}^{-it(2p+q^2)}\left(\begin{array}{c}{e}^{iqx}{A}_1^{jm}(\lambda )\hfill \\ e^{-iqx}{A}_2^{jm}(\lambda )\hfill \end{array}\right),$$

(17)

where we have introduced the x- and t-independent coefficients $A_1^{jm}$ and $A_2^{jm}$ that depend only on $\lambda$. In addition, the coefficients ${\mu }_{jm}$ are x- and t-independent and are related to the matrix $M(\lambda )$ which appears in Equation (16). The advantage of Equation (17) is to explicitly show the x- and t-dependence of the eigenfunctions $F_1$ and $F_2$, see Equation (10), through the six exponentials $e^{i[(x(w_j-w_m)-t(z_j-z_m)]}$. Moreover, $F_1$ and $F_2$ are solutions of linearised Equation (8) for any choice of the functions ${\mu }_{jm}(\lambda )$ of the spectral variable. On the other hand, the requirement that the solution of Equation (9) be localised in the variable x implies few necessary conditions on the functions ${\mu }_{jm}(\lambda )$. The further condition that the solution $\delta u_j(x,t)$ be bounded in x at any fixed time t imposes integrating with respect to the variable $\lambda$, see Equation (9), over the spectrum ${\mathbf{S}}_x$, that is an appropriate piece-wise continuous curve of the complex $\lambda$-plane:

$$\delta u_j(x,t)={\int }_{{\mathbf{S}}_x}\mathrm{d}\lambda F_j(x,t,\lambda ).$$

(18)

To define this spectrum ${\mathbf{S}}_x$, we have to first introduce the three “wave-numbers”, see Equation (17),

$$k_1(\lambda )=w_2(\lambda )-w_3(\lambda ),k_2(\lambda )=w_3(\lambda )-w_1(\lambda ),k_3(\lambda )=w_1(\lambda )-w_2(\lambda ),$$

(19)

through the eigenvalues $w_j(\lambda )$ of the matrix in Equation (14) as complex functions of the spectral variable $\lambda$. These are the differences of the three eigenvalues of the matrix $W(\lambda )$ in Equation (14). They appear in the eigenmodes in Equation (17) with both signs and evidently satisfy the condition $k_1+k_2+k_3=0$. It should be also noted that the labelling by the index j of the eigenvalues $w_j$, and therefore of the $k_j$s, is arbitrary and it does not imply any order. Then, ${\mathbf{S}}_x$, namely the spectrum which is relevant to our present analysis, can be defined as follows:

Definition 1.

The stability spectrum ${\mathbf{S}}_x$ is the subset of values of the spectral variable λ such that at least one of the three wave-numbers $k_j(\lambda )$, $j=1,2,3$, see Equation (19), be real.

The computation of the spectrum, as a piecewise algebraic curve in the complex $\lambda$-plane, starts with this definition and requires a lengthy analysis which is detailed in [54]. Two general features of ${\mathbf{S}}_x$ are the following: (1) The real axis of the $\lambda$-plane always belongs to ${\mathbf{S}}_x$, possibly with gaps, namely with finite forbidden intervals. This is the real part of the spectrum where the eigenmodes are stable. (2) A non-real component of the spectrum, which is symmetric with respect to the real axis, may occur for $\lambda \ne {\lambda }^{*}$. When $\lambda$ belongs to this part, the corresponding eigenmodes are unstable.

These features are present also in the well known spectrum associated to the scalar NLS equation to which our present formulation reduces as one of the two waves is not present, e.g., $u_2=0$. In this case, the spectrum is extremely simple and can be calculated explicitly. In our present notation, with $a_2=0$, $q=0$, one finds [47] two types of spectra. One for $s_1=1$ (defocusing case): the spectrum has only the real part, $\lambda ={\lambda }^{*}$, which is the real axis with one gap, $-a_1<\lambda <a_1$, where the wave numbers are $k_1=\lambda (1-\sqrt{1-a_1^2/{\lambda }^2})$, $k_2=-\lambda (1+\sqrt{1-a_1^2/{\lambda }^2})$, $k_3=2\lambda \sqrt{1-a_1^2/{\lambda }^2}$. As for the second type for $s_1=-1$ (focusing case), the real part of the spectrum is the entire real axis, $-\infty <\lambda <+\infty$, while its complex part, with $\lambda =i\rho$, presents itself as a branch, i.e., the finite interval $-a_1<\rho <a_1$ on the imaginary axis. Importantly, on this complex component of the spectrum, only the wave number $k_3=2\lambda \sqrt{1+a_1^2/{\lambda }^2}$ is real, and the other two wave numbers $k_1$, $k_2$ are not real. On this part of the spectrum, eigenmodes are unstable since their amplitude grows exponentially with time. Although the modulational stability/instability, as modelled by the NLS equation in the defocusing/focusing regime, is very much known, our sketch of it given above is meant to emphasise the many differences between the NLS case and the stability/instability properties of the CNLS. In particular, we compare their spectra together with their physical implications.

Let us discuss now the spectra associated to the coupled CW solutions in Equation (11). Now, it obviously happens that, with respect to the scalar NLS equation, more parameters come into play. In addition to the wavenumber mismatch q between the two background waves in Equation (11), the two parameters $p=s_1{a}_1^2+s_2{a}_2^2$ in Equation (12), and

$$r=s_1{a}_1^2-s_2{a}_2^2,$$

(20)

are conveniently replacing the coupling constants $s_1$ and $s_2$ and the amplitudes $a_1$ and $a_2$. As for the parameter q, it is worth observing that the case $q=0$ can be explicitly treated [46], and it leads to defocusing and focusing effects, which are similar to those associated to the NLS equation. Thus, we consider only non-vanishing values of q, say $q\ne 0$, which could also be rescaled to the value $q=1$. We also observe that one may consider, with no loss of generality (see [46]), only non-negative values of r and positive values of q. Thus, the parameter space we explore in the following analysis is the half $(r,p)$ plane with $r\ge 0$. To each point of this parameter space there corresponds a spectrum ${\mathbf{S}}_x$, and our goal is to classify all types of spectra in this space.

We start with few observations of general validity, whose proof is given in [54]. In addition to the two reality properties of the stability spectrum mentioned above, we note that the three wave numbers $k_j$ can all be real if and only if $\lambda$ is real. If $\lambda$ is not real, only one of the wave numbers $k_1$, $k_2$, or $k_3$ can be real. Moreover, our analysis shows that spectra are specifically classified according to whether they possess the following geometrical features: gaps on the real axis, and, in the non-real part, algebraic curves which may be open, termed branches, or closed, termed loops. Regarding gaps and branches, the following result holds true [46]: if G is the number of gaps and B is the number of branches, then, for any generic value of the parameters $r\mathrm{and}p$ the spectrum satisfies the condition

$$G+B=2.$$

(21)

As for loops L, we note that for any generic value of the parameters $r\mathrm{and}p$ the spectrum ${\mathbf{S}}_x$ may have either one loop or none. Our geometric classification of spectra can be summarised by the following statement: if all spectra are characterised by their number of gaps, branches and loops, then, for any generic value of the parameters $r\mathrm{and}p$, the spectrum can be only one out of the following five different types of spectra:

$$1G1B0L,2G0B1L,1G1B1L,0G2B1L,0G2B0L,$$

(22)

where the notation $nX$ stands for n components of type X, with X being G, B, or L [46].

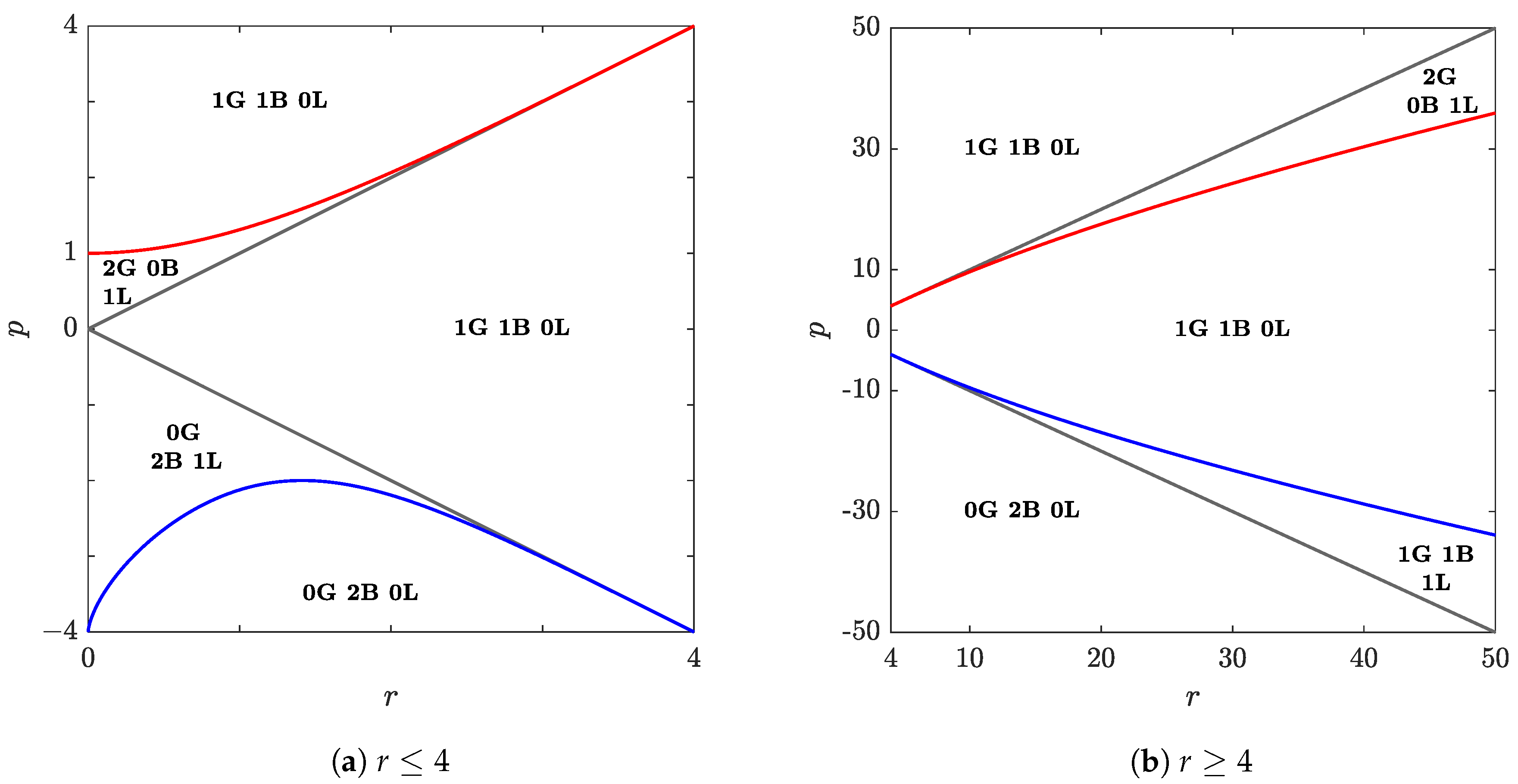
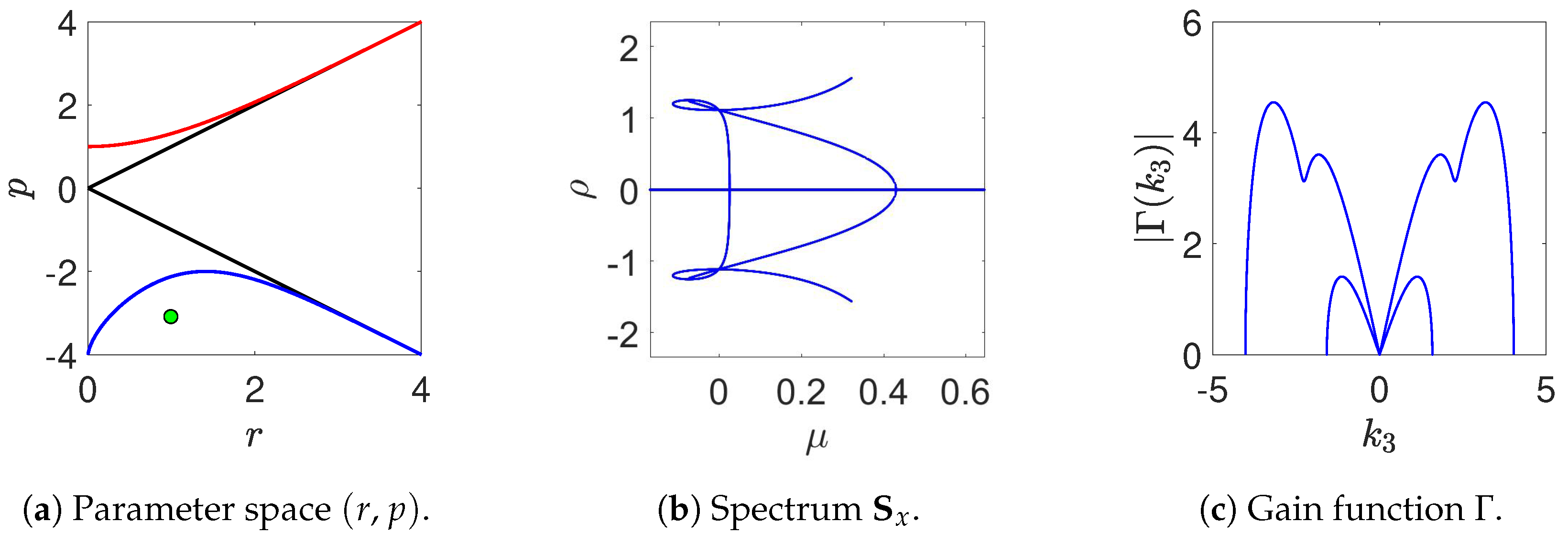
The parameter space is thus divided into regions, in each of which the spectrum remains of the same type by varying the parameters $r\mathrm{and}p$. The spectrum changes by crossing the region boundary curves. These boundaries are explicitly known threshold curves (details can be found in [46,54]). This classification, viewed as regions of the $(r,p)$ half-plane, together with their boundary curves, is shown in Figure 1. In this figure, the defocusing case $s_1=s_2=1$ corresponds to $p>r$, the focusing one $s_1=s_2=-1$ to $p<-r$ and the mixed case $s_1=-s_2=1$ to $-r<p<r$.

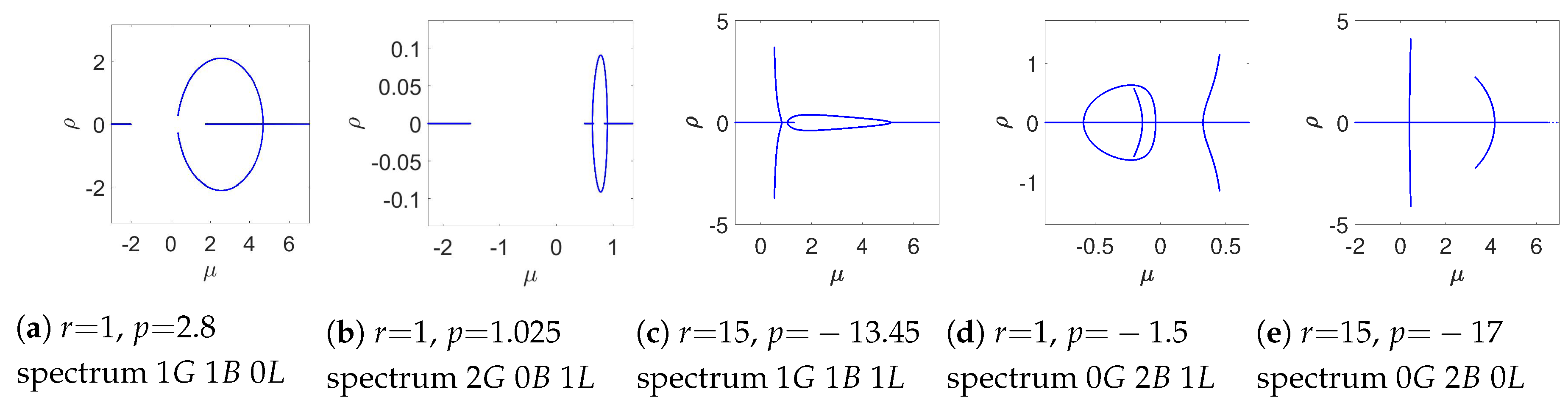
In Figure 2, we plot examples of the five types of spectra ${\mathbf{S}}_x$ as in Equation (22). These are shown in the plane $(\mu ,\rho )$ where the real variables $\mu$ and $\rho$ are the real and imaginary parts, respectively, of the complex spectral variable $\lambda =\mu +i\rho$.

The limit case $r=0$ is discussed and displayed in [54].

As already noticed, to the purpose of establishing the stability properties of the continuous wave solution of Equation (11), we do not need to compute the integral representation in Equation (18) of the solutions $\delta u_j$ of Equation (7). Indeed, it is sufficient to compute the “eigenfrequecies”, whose definition

$${\omega }_1(\lambda )=z_2(\lambda )-z_3(\lambda ),{\omega }_2(\lambda )=z_3(\lambda )-z_1(\lambda ),{\omega }_3(\lambda )=z_1(\lambda )-z_2(\lambda ),$$

(23)

is suggested by the exponentials which appear in Equation (17). They are real on the real part of the spectrum, e.g., for any $\lambda ={\lambda }^{*}$. On the contrary, if $\lambda$ belongs to the non-real component of the spectrum, only one wavenumber, e.g., $k_3$, is real while its corresponding frequency is complex

$${\omega }_3(\lambda )=\Omega (\lambda )+i\mathrm{\Gamma }(\lambda ),\lambda \ne {\lambda }^{*}.$$

(24)

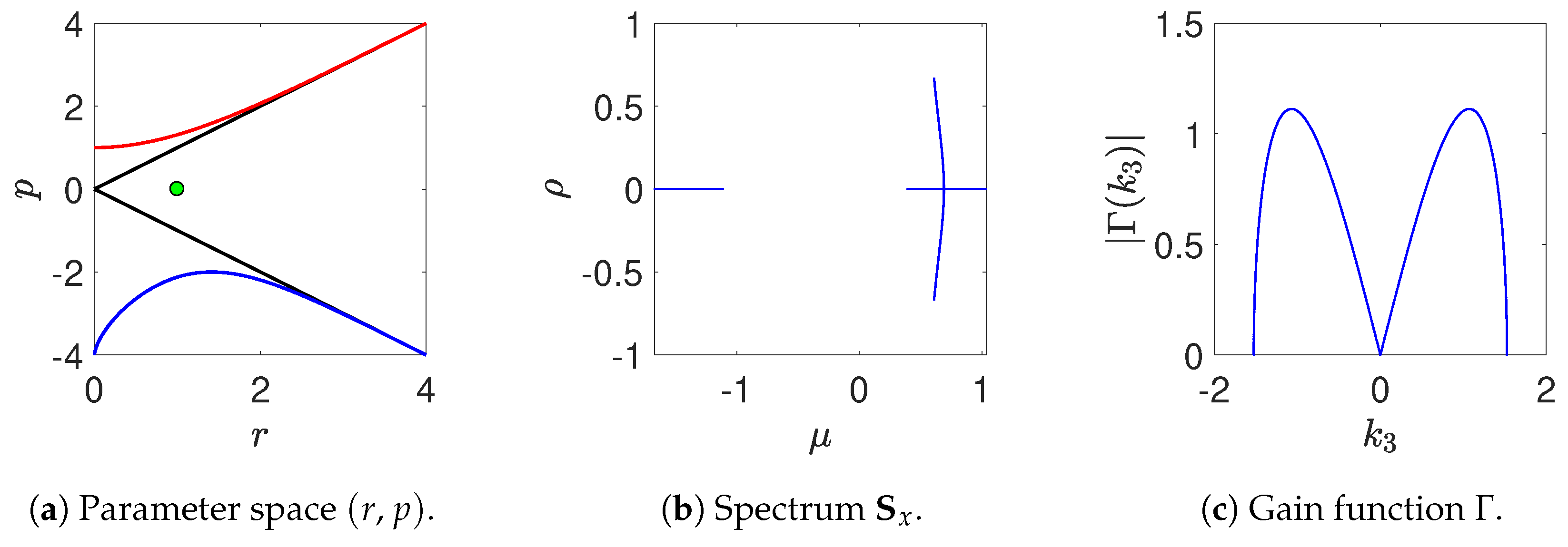
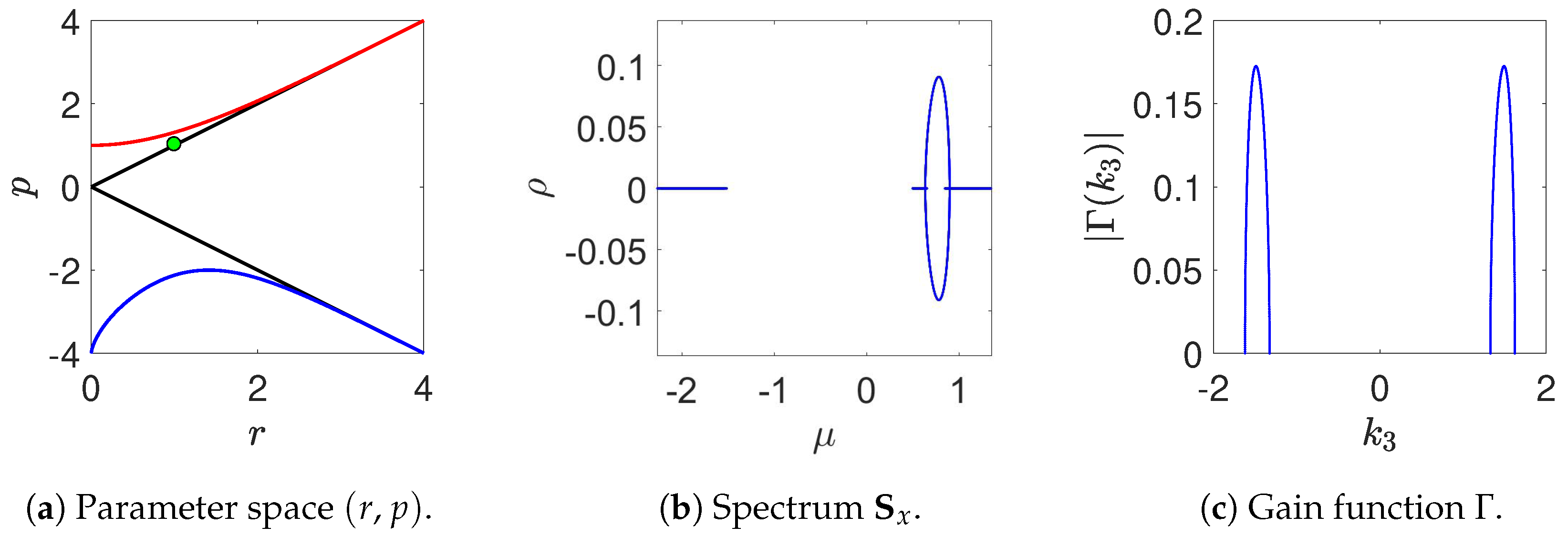
This happens if $\lambda$ lies on a branch or on a loop. The imaginary part $\mathrm{\Gamma }(\lambda )$ of ${\omega }_3$ is the gain (or growth) function, which is different from zero only on branches and loops, namely on a finite instability band of wave numbers. In this respect, we note that the instability band that is associated to a branch differs from that associated to a loop. This difference is of practical interest since in the first case (branch) the band is around $k_3=0$—this instability being commonly known as baseband instability (see, e.g., Figure 3) as it involves very long wavelengths. This is similar to the Benjamin–Feir instability described by the (focussing) NLS equation. The one associated instead to a loop is known as passband instability (see, e.g., Figure 4), which does not include vanishingly small wave numbers [55,56]. This kind of instability does not occur for one single plane wave. Indeed, as predicted by the NLS equation, loops are not present in the single CW instability spectrum. Moreover, for two resonating CWs, branches and loops may be both present in the spectrum (see Equation (22)), and therefore two different instability bands may partially overlap and lead to a rather complicate overall gain function (see, e.g., Figure 5 and Figure 6).

3. CNLS: Rogue Waves and Spectra

In the previous section, we construct and display the stability spectrum ${\mathbf{S}}_x$ of two weakly resonant plane waves. This is definitely more complicated than the one associated to just one plane wave. Moreover, the spectrum depends on parameters that cannot be got rid of by rescaling, such as the ratio $a_1/a_2$ of the CW amplitudes, or which cannot be set to vanish by changing the frame of reference, such as the mismatch q of the wave numbers of the background waves. This richness is evident in a number of predictions of new phenomena associated to the CNLS model. For instance, as already observed [38,39] and in contrast with the instability predicted by NLS equation, new kinds of instabilities occur in defocusing regimes. As pointed out in the extensive literature [57], instabilities lead to generation of nonlinear wave patterns. Although the generation mechanism is out of the scope of the present work, we aim here to investigate the existence, construction and properties of rogue wave (RW) solutions by taking advantage of our spectral approach to linear stability. In particular, by taking into account the stability spectra described in the previous section, we provide an exhaustive classification of RW solutions of the CNLS equations in Equation (1) together with their identification in the complex $\lambda$-plane of the spectral variable.

Motivated by their well established relevance to several observations in oceans and in fibre optics, rogue waves have been investigated mainly as solutions of integrable models. The prototype wave profile pointed out by Peregrine [58] attracted the attention of physicists since, among other reasons, it is not periodic and its amplitude is three times higher than that of the background. On their side, mathematicians found this bounded solution of interest for its rational, rather than exponential, dependence on the space-time variables [38]. These special features of rogue wave profiles proved to be useful to searching for RWs in integrable model equations (see below and [38]). Combining this requirement on the space-time dependence with the distribution over the spectrum ${\mathbf{S}}_x$ of wave numbers $k_j(\lambda )$ of the eigenmodes of the linearised equation (see Equation (7)), leads to a definite rule to find RW solutions. Indeed, the RW discrete eigenvalues, referred to hereafter as the critical values ${\lambda }_c$ in the complex plane of the spectral variable $\lambda$, turn out to be the (strictly) complex solutions $\lambda$ of the equation $k_3(\lambda )=0$. This rule is the consequence of the following arguments. As follows from our analysis reported in the previous section, and better detailed in [46,54], only one of the three wave numbers $k_j(\lambda )$, e.g., $k_3$, is real if $\lambda$ is complex (i.e., on branches and loops) or, if $\lambda$ is real, it lies at the end points of gaps. Moreover, the equation $k_3(\lambda )=0$ has four solutions. They may come as pairs of real values that lie at the end points of gaps of the spectrum, or pairs of complex conjugate values at the extremes of branches. However, soliton solutions of the CNLS equations, whose corresponding discrete eigenvalue solve the equation $k_3(\lambda )=0$ at the endpoints of a gap, are singular in x; consequently, the acceptable solutions ${\lambda }_c$ have to be strictly off the real axis, ${\lambda }_c\ne {\lambda }_c^{*}$, and thus located at the complex conjugate extremes of branches of the spectrum. On the other hand, if $k_3(\lambda )$ were non-vanishing, then the eigenmodes would be periodic (see Equations (17) and (19)) against the condition that the rogue wave solutions have rational (or semi-rational) dependence on x. This establishes a one-to-one correspondence between branches and RWs. A very simple example of this rule is shown by the stability spectrum of the NLS equation: for this equation, there exist only two types of spectrum. If the interaction is defocusing, the spectrum is $1G0B$ type with no RW solution, while in the focusing case the spectrum is $0G1B$ type with the Peregrine soliton critical values ${\lambda }_c$ and ${\lambda }_c^{*}$ at the two extremes of the branch. Similarly, but in a far richer scenario, RW solutions of the coupled NLS equations correspond to eigenvalues ${\lambda }_c$ that lie at the two extreme points of each branch.

In the previous section, we point out that, for $q\ne 0$, the spectrum ${\mathbf{S}}_x$ of the linearised equation around the CW solution of Equation (11) changes in the plane of the parameters $(r,p)$ in such a way that this plane gets divided in five regions (see Figure 1). Within each region the spectrum is one of the five different types (Equation (22)) with the consequence that also RW solutions can be divided into different types according to the fixed $(r,p)$ point in the parameter space. The construction of the RW solution may go via the Darboux–Dressing technique [38] which requires fixing the seed solution, namely the CW (Equation (11)), and the particular ${\lambda }_c$. The correspondence branch-RW discussed above readily implies that there cannot be any RW solution if the point $(r,p)$ lie in the region where the spectrum is $2G0B1L$. As shown in Figure 1, this region is partly in the defocusing section $s_1=s_2=1$, $p>r$ for $r<4q^2$, and in the mixed section $s_1=-s_2=1$, $-r<p<r$ if $r>4q^2$. Note that all threshold curves have an explicit analytic expression; we refer the interested reader to [46,54] for details.

As for the remaining four type of spectra, two of them have one branch, while the other two have two branches. The computation of the critical value ${\lambda }_c$, at a generic point $(r,p)$ in the appropriate spectral region (see Figure 1) is obtained numerically as root of the following fourth-degree polynomial [54]:

$$\Delta (\lambda )=64q^2{\lambda }^4-32qr{\lambda }^3+4(p^2-20q^{2}p-8q^4){\lambda }^2+36qr(p+2q^2)\lambda -4{(p-q^2)}^3-27q^2{r}^2$$

(25)

which has two real and two complex conjugated roots if the spectrum is of type $1G1B0L$ or $1G1B1L$, and has two pairs of two complex conjugated roots if the spectrum is instead $0G2B0L$ or $0G2B1L$. Non-generic limit values of ${\lambda }_c$, which have an explicit expression, are mentioned below. Once the critical value ${\lambda }_c$ is known either numerically or analytically, the computation of the corresponding RW solution may proceed via the standard Darboux–Dressing method (or by other equivalent ways). Omitting details (which can be found in [38]), the final expression of such solution takes the explicit form

$$\begin{array}{ccc}{u}_1^{RW}(x,t)\hfill & =\hfill & e^{i[qx-(q^2+2p)t]}\left[a_1+\frac{2i({\lambda }_c^{*}-{\lambda }_c)V^{*}{V}_1}{{|V|}^2-s_1|V_1{|}^2-s_2{|V_2|}^2}\right],\hfill \\ u_2^{RW}(x,t)\hfill & =\hfill & e^{-i[qx+(q^2+2p)t]}\left[a_2+\frac{2i({\lambda }_c^{*}-{\lambda }_c)V^{*}{V}_2}{{|V|}^2-s_1|V_1{|}^2-s_2{|V_2|}^2}\right].\hfill \end{array}$$

(26)

The parameters $a_1$, $a_2$, $s_1$, $s_2$, q, and p, which appear in this expression, are defined in Section 2. The functions V, $V_1$, and $V_2$ are the components of the vector

$$\left(\begin{array}{c}V\hfill \\ V_1\hfill \\ V_2\hfill \end{array}\right)=U\left(\begin{array}{c}(c+c_1\xi )\hfill \\ c_1\hfill \\ c_2{e}^{-i(k_{1}x-{\omega }_{1}t)}\hfill \end{array}\right),\xi =im(x-gt)$$

(27)

where the constants c, $c_1$, $c_2$ and m are arbitrary complex parameters. Here, the $3\times 3$ matrix U is x- and t-independent and reads

$$U=\left(\begin{array}{ccc}{(w_1+{\lambda }_c)}^2-q^2\hfill & 0& {(w_3+{\lambda }_c)}^2-q^2\hfill \\ -i{a}_1(w_1+{\lambda }_c-q)\hfill & im{a}_1\frac{(w_1+{\lambda }_c-q)}{(w_1+{\lambda }_c+q)}& -i{a}_1(w_3+{\lambda }_c-q)\hfill \\ -i{a}_2(w_1+{\lambda }_c+q)\hfill & im{a}_2\frac{(w_1+{\lambda }_c+q)}{(w_1+{\lambda }_c-q)}& -i{a}_2(w_3+{\lambda }_c+q)\hfill \end{array}\right),$$

(28)

while the velocity g in Equation (27) turns out to be

$$g=-2{\lambda }_c+\frac{s_{1}q{a}_1^2}{{(w_1+{\lambda }_c+q)}^2}-\frac{s_{2}q{a}_2^2}{{(w_1+{\lambda }_c-q)}^2}.$$

(29)

We note that the x- and t-dependence of the three-vector in Equation (27) is both polynomial and exponential so that the RW profile turns out to be a mixture of rational and exponential functions for a generic choice of the free parameters. To complete the construction of the RW solution by Equation (26), it remains to obtain the expression of the simple eigenvalue $w_3$ and of the double eigenvalue $w_1$ of the matrix in Equation (14). However, since they are linked to each other by the trace relation $w_3+2w_1=-{\lambda }_c$, we need to give only the expression

$$w_3={\lambda }_c+\frac{2(8q^2+p){\lambda }_c-9qr}{3(p-q^2)-4{\lambda }_c^2}.$$

(30)

Moreover, the wave number $k_1$ and frequency ${\omega }_1$, which appear in the expression of the vector in Equation (27), are defined by Equations (19) and (23) and read

$$k_1={\lambda }_c+3w_1,{\omega }_1=q^2-p-4{\lambda }_c{w}_1,$$

(31)

where we have made use of the matrix relation in Equation (15).

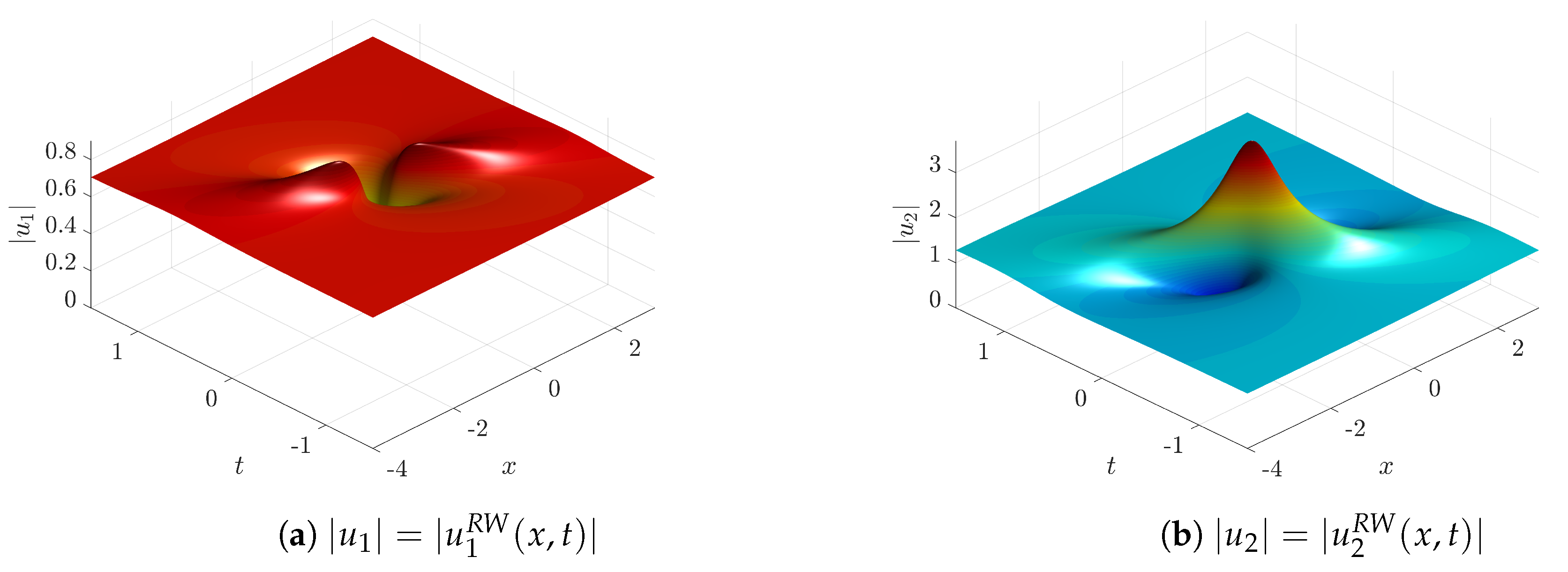
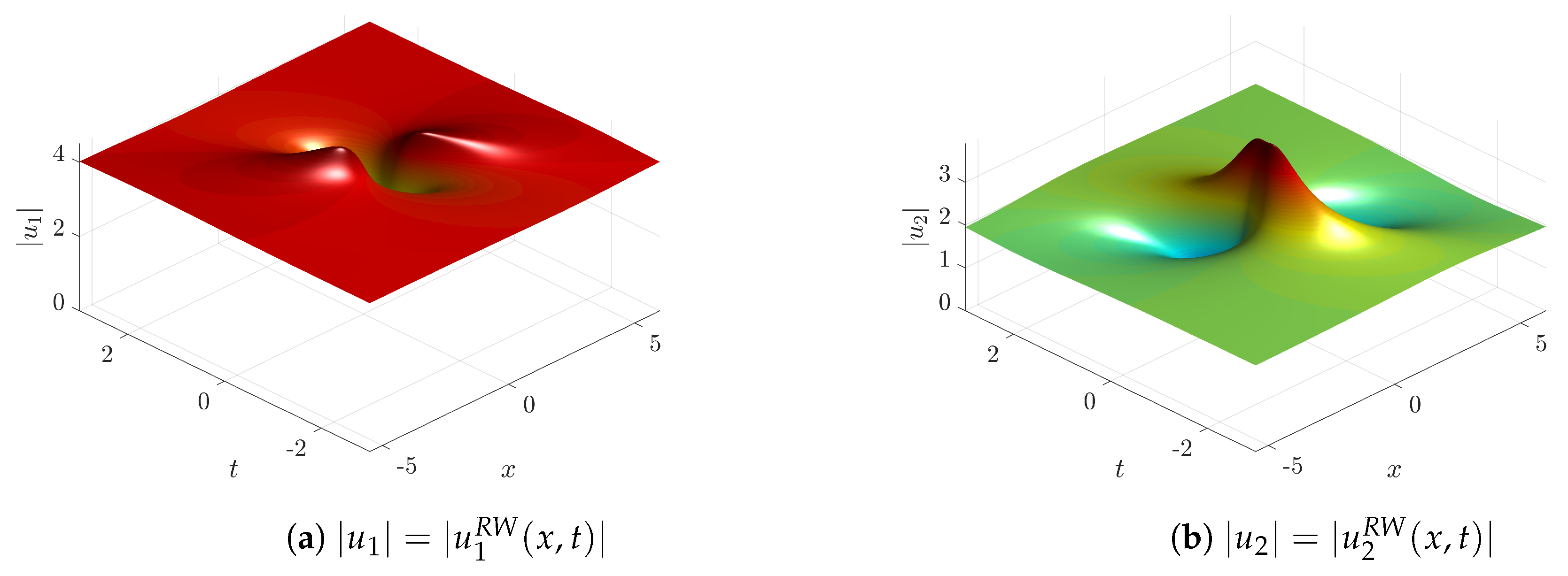
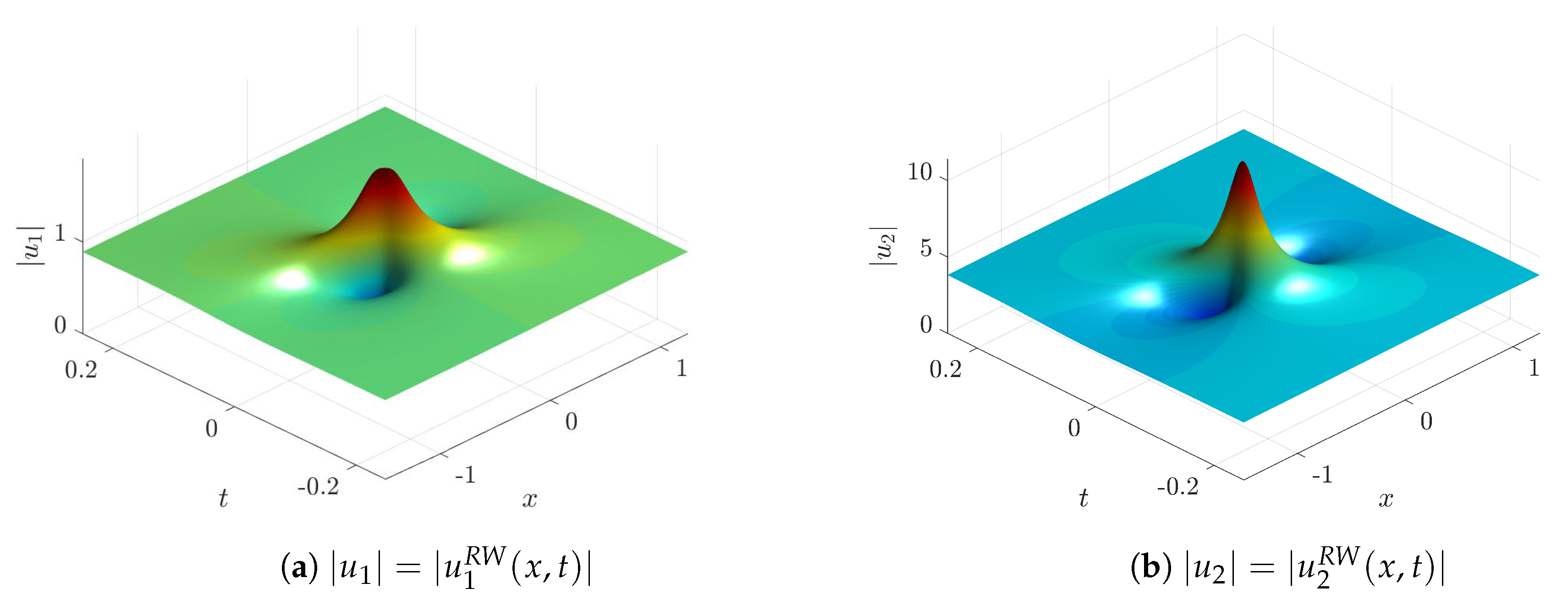
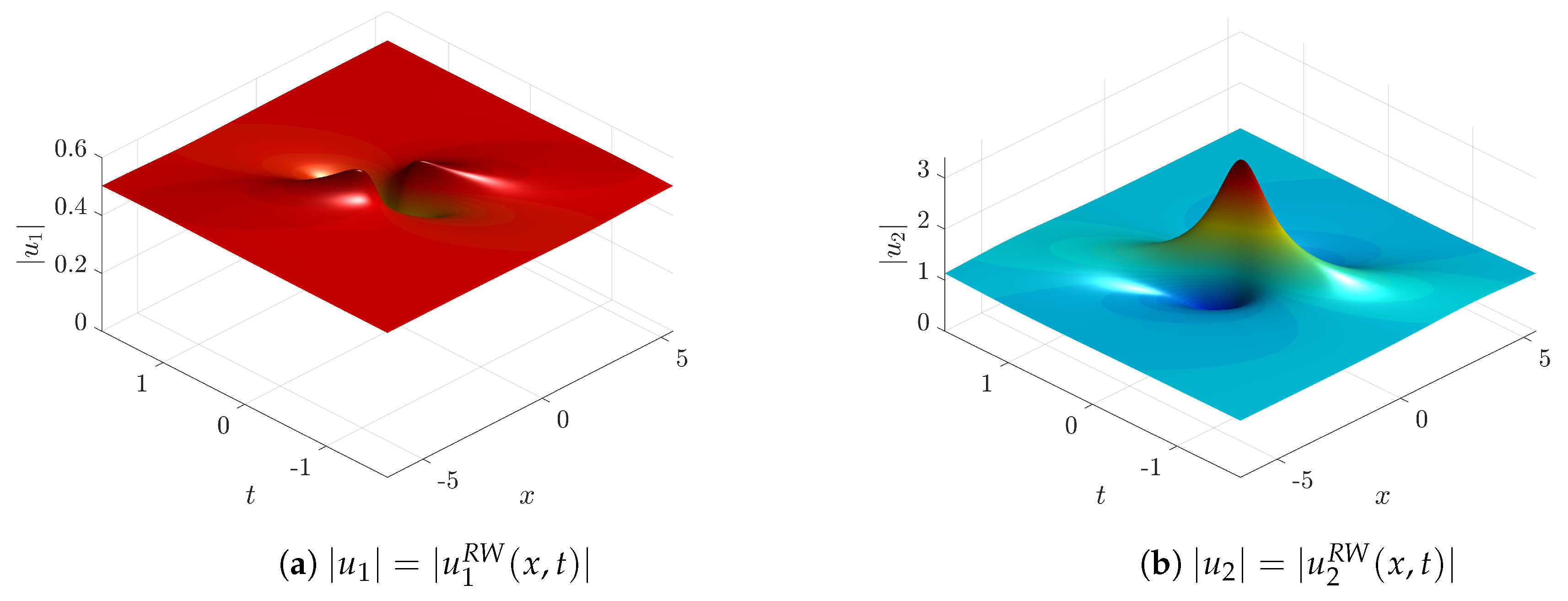
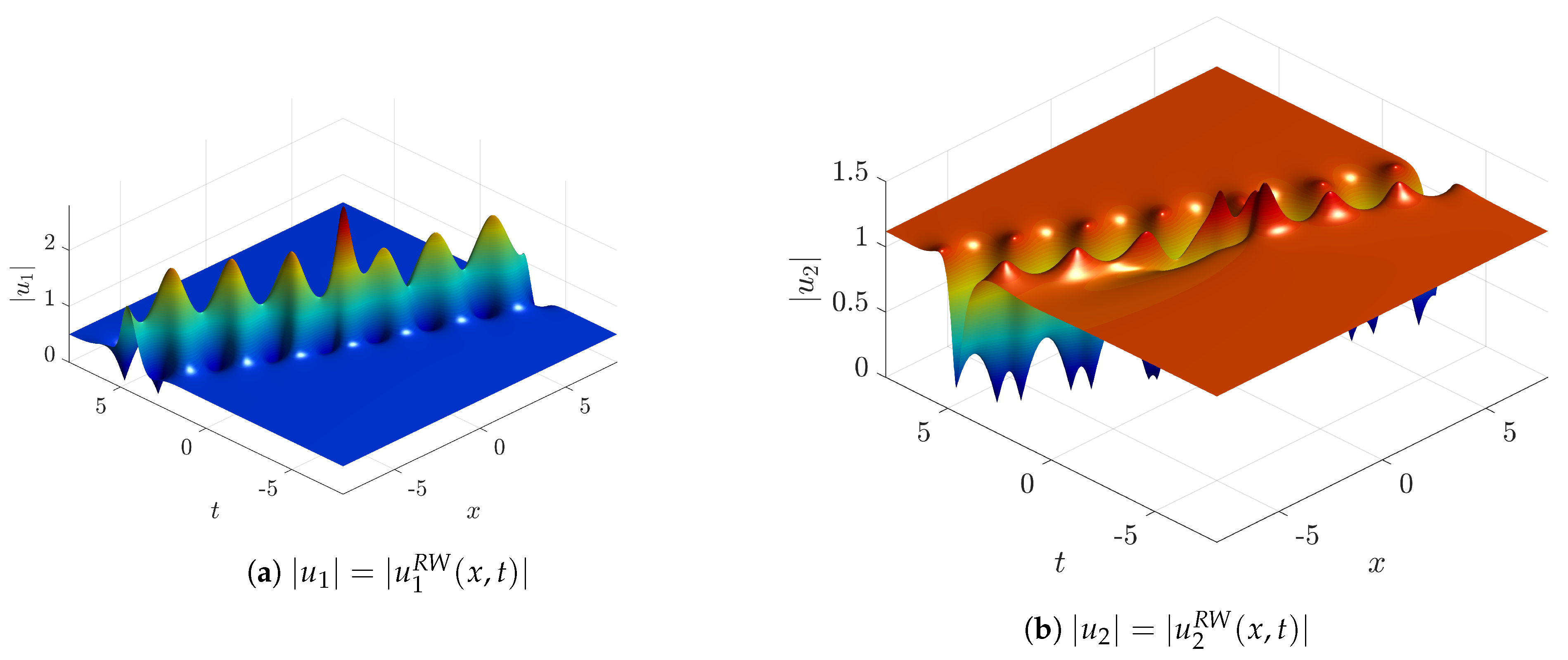
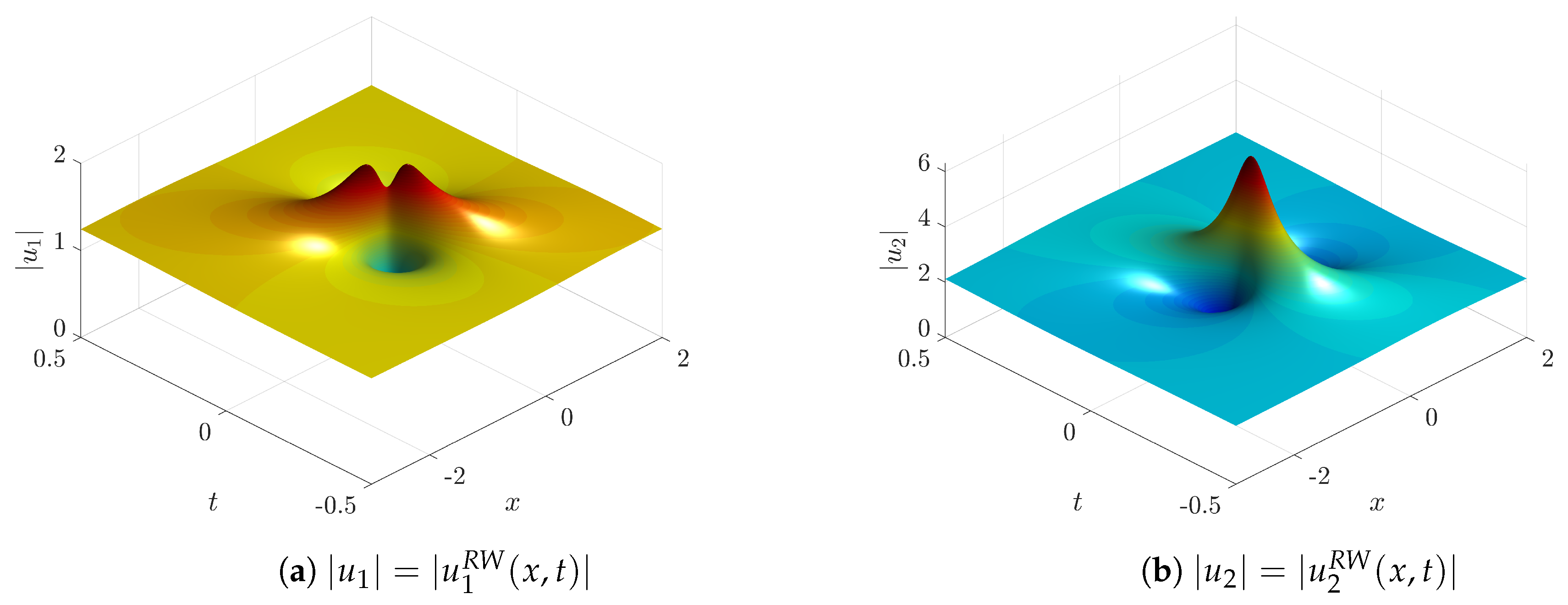
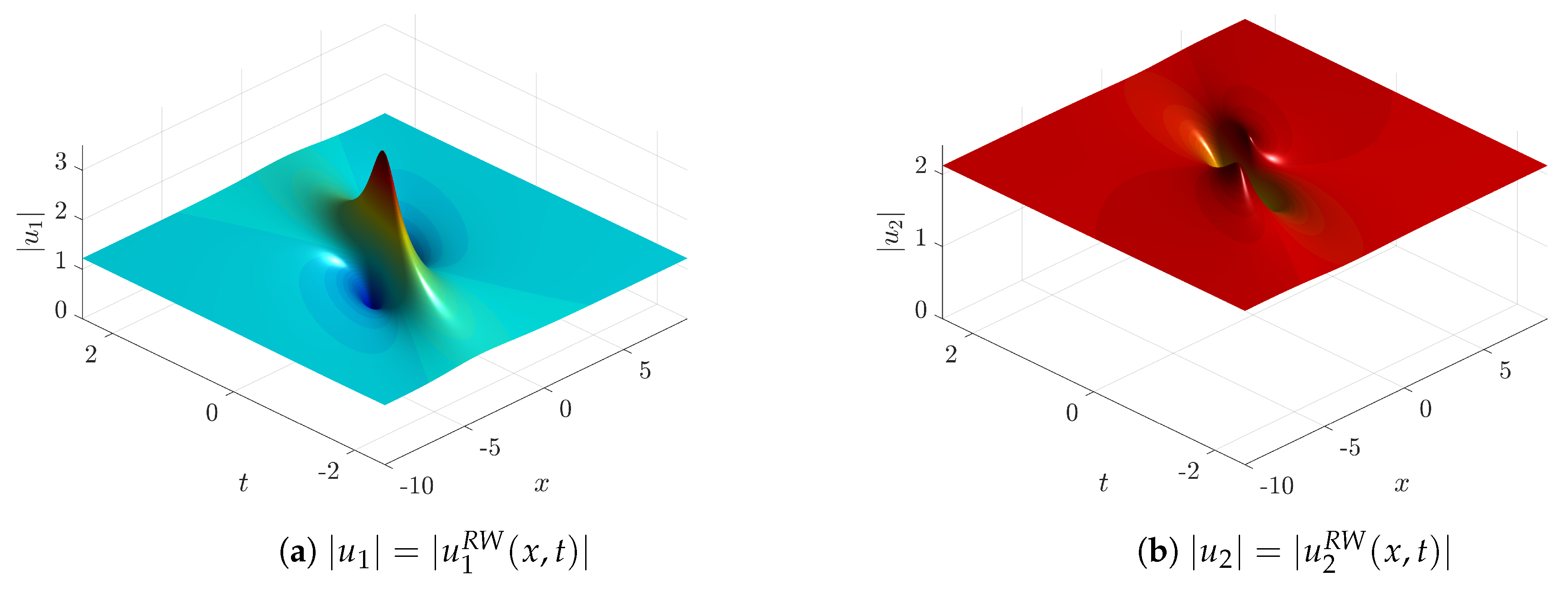
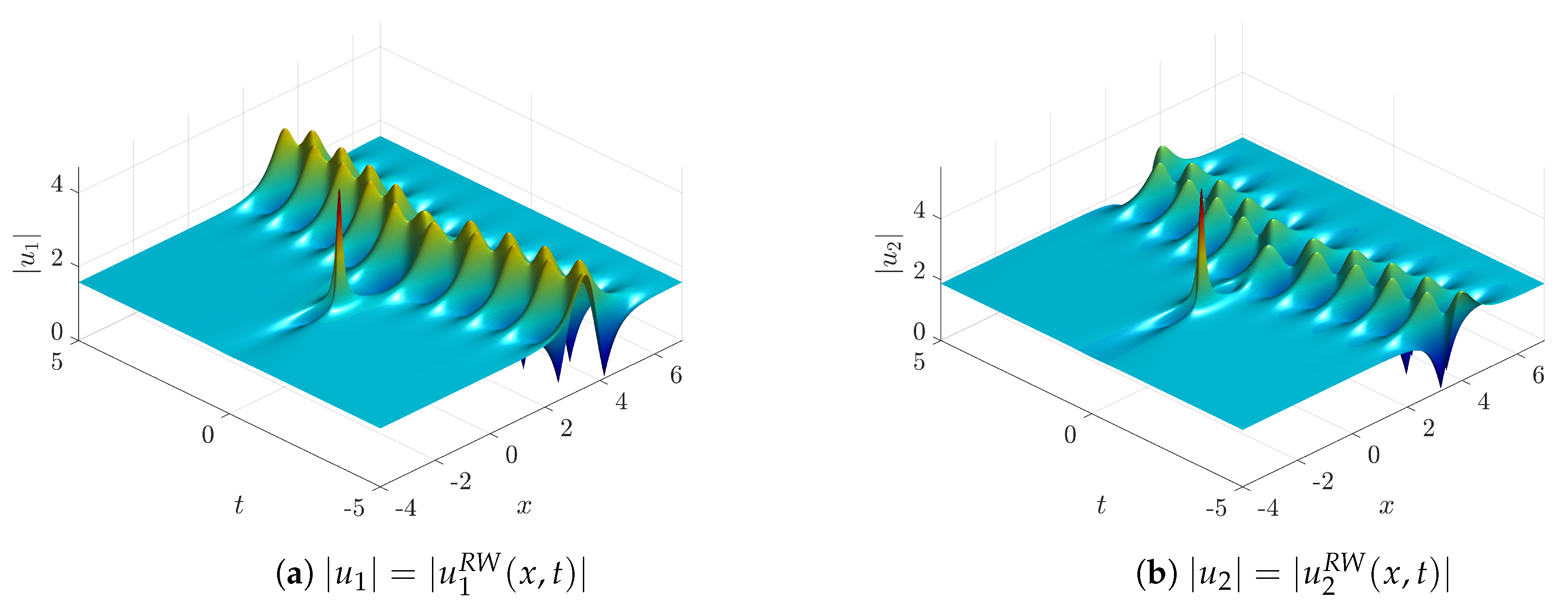
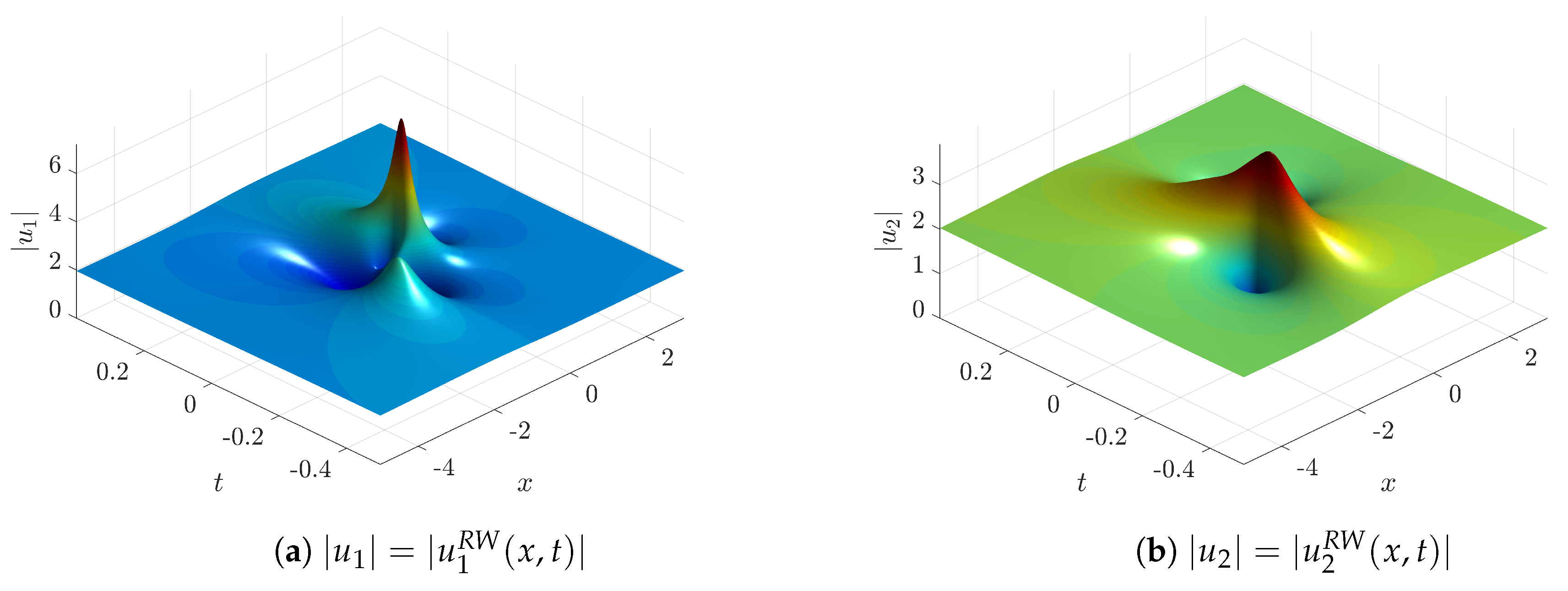
Once all free parameters have been fixed and a critical value of the spectral variable has been computed, Equation (26), obtained from the Darboux (or Darboux–Dressing) method, is the basic tool to plot rogue wave profiles and to explore their properties. Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show examples of RW solutions that are generic and each one attached to one of the four different types of spectra (see captions). It is worth pointing out that solutions are purely rational for the choice $c=c_2=0$ and $c_1=1$; and are generally rational-exponential otherwise. We also note that in each of these figures we choose to fix the numerical values of the parameters r and p and to consequently obtain the values of the wave amplitudes $a_1$ and $a_2$ through the definitions in Equations (20) and (12); this is why the values of the amplitudes may look rather odd. For each solution, one could ask for which choice of the arbitrary constants c, $c_1$ and $c_2$ one would obtain maximal amplitudes. This question can be answered using a Nelder–Mead Simplex Method [59], as implemented in the fminsearch MATLAB_R2018a routine, and an example is given in Figure 11. The corresponding purely rational solution for the same choice of r, p and ${\lambda }_c$ as in Figure 11 is shown in Figure 10.

For the last case, namely $0G2B0L$, we consider two RW solutions, corresponding to the two branches (see Figure 12 and Figure 13); numerical evidence suggests that the RW corresponding to the brach associated to ${\lambda }_c$ with the larger imaginary part has a larger amplitude, as one would expect by inspecting the gain function.

As for non-generic choices of the parameters $r,p$ and q such as $r=0$ or $q=0$, we briefly mention below RW solutions that enjoy an explicit analytical expression together with new physical features, such as amplitude bumps (depressions), which are higher (lower) than that of the Peregrine soliton.

The first example of non-generic solutions is that of RWs over two co-propagating coupled background waves, e.g., the plane–wave solution of Equation (11) with $q=0$ (see Figure 14). The following solution is the analogue of the Peregrine rogue wave in the present case of two coupled NLS equations [38,60]. Indeed, as for the NLS equation, the parameters for this solution are $q=0$ and, as for the focusing interaction, $s_1=s_2=-1$. Thus, p has to be strictly non-vanishing and negative $p=-a_1^2-a_2^2$. The critical value is imaginary, ${\lambda }_c=i\sqrt{-p}$, and $w_1=w_2=0,w_3=-{\lambda }_c$, $z_1=z_2=-p$, $z_3=0$. The parameter m is set to be $m=-ip$ and g is found to be $g=2p$. The expression of this (vector Peregrine) RW, with no loss of generality because of translation symmetry, finally reads

$$u_1=e^{-2ipt}\left(a_1\frac{L}{B}+a_2\frac{M}{B}\right),u_2=e^{-2ipt}\left(a_2\frac{L}{B}-a_1\frac{M}{B}\right)$$

(32)

where

$$\begin{array}{cc}\hfill L& =\frac{3}{2}-8p^2{t}^2+2p{x}^2-8ipt+{|f|}^2{e}^{2x\sqrt{-p}},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill M& =4f(x\sqrt{-p}+2ipt-\frac{1}{2})e^{(x\sqrt{-p}-ipt)},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill B& =\frac{1}{2}+8p^2{t}^2-2p{x}^2+{|f|}^2{e}^{2x\sqrt{-p}}.\hfill \end{array}$$

(35)

The effect of coupling here is in the presence of an exponential term, which shows itself in Figure 14 in the generation of a dark component in addition to the expected bright peak. Obviously, if $f=a_2=0$, Equation (32) reduces to the known Peregrine soliton.

Our second example of RW solution (see Figure 15) is more than non-generic as it is just unique. It corresponds to the only case of a triple eigenvalue of the matrix $W(\lambda )$ in Equation (14) $w_1=w_2=w_3=-1/3{\lambda }_c$ where the critical value is ${\lambda }_c=i3\sqrt{3}/2q$. Because of scale invariance, the mismatch wave number $q\ne 0$ is arbitrary but strictly non-zero. Since the amplitudes are equal $a_1=a_2=2q$ and in the focusing region $s_1=s_2=-1$, the parameters $(r,p)=(0,-8q^2)$ belong to the border of the spectral region $0G2B0L$ (see Figure 1). The RW solution in this case takes the following expression

$$\begin{array}{ccc}{u}_1\hfill & =\hfill & 2q{e}^{i(qx-15q^{2}t)}\left(1+\frac{3\sqrt{3}{\theta }^{*}{A}^{*}{A}_1}{{|A|}^2+|A_1{|}^2+{|A_2|}^2}\right)\hfill \\ u_2\hfill & =\hfill & 2q{e}^{-i(qx+15q^{2}t)}\left(1+\frac{3\sqrt{3}\theta A^{*}{A}_2}{{|A|}^2+|A_1{|}^2+{|A_2|}^2}\right),\theta =\frac{1}{2}(-\sqrt{3}+i),\hfill \end{array}$$

(36)

which is fully algebraic as specified by the following expressions

$$\begin{array}{cc}\hfill A& =c+c_1{\xi }_1+c_2({\xi }_2-i{\theta }^{*}),\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill A_1& =c+c_1({\xi }_1+{\theta }^{*})+c_2({\xi }_2+{\theta }^{*}{\xi }_1+i\sqrt{3}),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill A_2& =c+c_1({\xi }_1+\theta )+c_2({\xi }_2+\theta {\xi }_1),\hfill \end{array}$$

(39)

with ${\xi }_1=-2qx-4i\sqrt{3}{q}^{2}t$ and ${\xi }_2=(1/2){\zeta }_1^2-4i{q}^{2}t$.

4. Conclusions

The common assumption that a surface wave in deep water with small steepness and weak nonlinearity is sufficiently well modelled by the cubic nonlinear Schrödinger equation has been supported by open sea observations and tank experiments. This satisfactory situation seems to also cover rogue wave formation due to instability of long wave trains. In this respect, one learns from the NLS equation that instability is present only in the focusing regime, and that the tallest amplitude is that of the one soliton (Peregrine) solution whose discrete eigenvalue coincides with the extreme of the spectrum branch in the complex plane of the spectral variable of the NLS equation. One also understands that the instability band is finite and of base-band type as it involves only very long wave lengths. The extension of these results to a background state of two such regular, and weakly resonant, wave trains has been the main motivation of the present work. As a result, the coupling of two NLS equations leads to a far richer dynamics.

Few novel and peculiar features of the coupled wave system are known, such as the occurrence of a novel instability with defocusing self- and cross-interactions ($s_1=s_2=1$). The present work is a further contribution to our understanding of the effects of coupling. A crucial effective parameter, with no analogue in the scalar NLS case, is the difference $2q$ of the wave numbers of the two background plane waves. Only if this parameter vanishes, e.g., the two wave trains co-propagate, the stability spectrum looks the same as the one we find from the NLS equation. In the opposite case, i.e., if these wave numbers differ from each other, the spectrum itself looks more complicated with gaps, branches and, especially, loops, which mark a peculiar difference with respect to the NLS dynamics. Indeed, it has been found that, in addition to the baseband instability, as for the Benjamin–Feir instability, a loop of the spectrum causes the instability band to be of passband type. Computing the spectrum leads to relevant information on the stability of small perturbations of the periodic background. Thus, in Figure 1, one can read that, if, for instance, the spectrum is of 2G 0B 1L type in the defocussing region for $0<r<4q^2$, one should expect only one instability passband with a finite range of wave lengths. A predictive power comes also from our plots of the gain function. These make evident the difference between the contribution to the exponential growth due to a branch, and that due to a loop.

Again, and regarding rogue waves, only if $q=0$, a rogue wave solution that is the vector analogue of the Peregrine solution exists. In the opposite case, i.e., if $q\ne 0$, several rogue waves with novel features are possible. Since their corresponding discrete eigenvalues do still lie, as for the NLS, at the extremes of branches of the stability spectrum, these solutions have been fully classified in the entire parameter space. Some of them have been numerically computed and plotted by giving in addition (see captions) their relative maximum amplitude, $max|u_1^{(RW)}|/a_1$ and $max|u_2^{(RW)}|/a_2$, by varying x and t. The outcome of these calculations is that rogue waves exist with relative maximum amplitude larger than 3. This aspect of our work is clearly worthy of further work. Contacts of these results with observations are still to come as only in few rather special states, such as crossing sea, two integrable coupled NLS envelope equations may be derived from Euler equations. However, appropriate experimental settings in flume are likely to be more feasible.