Equations for Deep Water Counter Streaming Waves and New Integrals of Motion

Abstract

The waves on a free surface of 2D deep water can be split into two groups: the waves moving to the right, and the waves moving to the left. A specific feature of the four-wave interactions of water waves allows to describe the evolution of the two groups as a system of two equations. The fundamental consequence of this decomposition is the conservation of the “number of waves” in each particular group. The envelope approximation for the waves in each group of counter streaming waves is obtained.

1. Introduction

A potential flow of an ideal incompressible 2D fluid with a free surface is described by the following classical system of equations:

$$\begin{array}{cccc}\hfill {\varphi }_{xx}+{\varphi }_{zz}& =& 0\hfill & ({\varphi }_z\to 0,z\to -\infty ),\\ \hfill {\eta }_t+{\eta }_x{\varphi }_x& =& {\varphi }_z{|}_{z=\eta }\hfill & \\ \hfill {\varphi }_t+\frac{1}{2}({\varphi }_x^2+{\varphi }_z^2)+\eta & =& 0{|}_{z=\eta },\hfill & \end{array}$$

where $\eta (x,t)$ is the profile of the surface, $\varphi (x,z,t)$ is the velocity potential. This system is hamiltonian (see [1]), and the Hamiltonian variables are $\eta (x,t)$, and $\psi (x,t)=\varphi (x,\eta (x,t),t)$—the potential at the surface. The equations of motions are given by the following equations:

$$\frac{\partial \psi }{\partial t}=-\frac{\delta H}{\delta \eta }\frac{\partial \eta }{\partial t}=\frac{\delta H}{\delta \psi },$$

(1)

and the Hamiltonian truncated (to fourth order) is given by:

$$\begin{array}{ccc}\hfill H& =& \frac{1}{2}\int {\eta }^2+\psi \widehat{k}\psi dx-\frac{1}{2}\int \{{(\widehat{k}\psi )}^2-{({\psi }_x)}^2\}\eta dx+\frac{1}{2}\int \{{\psi }_{xx}{\eta }^2\widehat{k}\psi +\psi \widehat{k}(\eta \widehat{k}(\eta \widehat{k}\psi ))\}dx,\hfill \end{array}$$

(2)

where the linear operator $\widehat{k}$ acts in Fourier–space as a multiplication by the modulus of wavenumber k:

$$\widehat{k}f(x)\Rightarrow \left|k\right|f_k.$$

This Hamiltonian is the starting point to derive the so-called Zakharov equation in 1968. The evolution of the envelope, $\mathsf{\Psi }(x,t)$, of a modulated planar wave with a wavenumber $k_0$, and a frequency ${\omega }_0$ given by the formula:

$$\eta (x,t)=\frac{1}{2}exp(i{k}_{0}x-i{\omega }_{0}t)\mathsf{\Psi }(x,t)+c.c.$$

is described by the well known Nonlinear Schrödiger (NLS) equation:

$$i(\dot{\mathsf{\Psi }}+v_g{\mathsf{\Psi }}_x)=\frac{{\omega }_0}{8k_0^2}{\mathsf{\Psi }}_{xx}+\frac{{\omega }_0{k}_0^2}{2}{\left|\mathsf{\Psi }\right|}^2\mathsf{\Psi },(\mathrm{where}{v}_g\mathrm{is\; the\; group\; velocity},v_g=\frac{{\omega }_0}{2k_0}).$$

In 1994 a remarkable property of the interaction of water waves was discovered, namely, the coefficient of the four-waves interaction in the Hamiltonian vanishes on the resonance manifold, see [2]. This discovery allowed to greatly simplify the Zakharov equation, and the so-called “compact equation” for unidirectional water waves was derived, see [3,4].

Recently, in the work [5], it has been discovered that the four–waves interaction coefficient vanishes for more than just the wavenumbers on the resonance manifold, and this allowed to formulate the water wave equations in a canonical way that is also referred to as the “super compact” way. Moreover, we would like to emphasize that the NLS, the compact, and the super compact equations are all valid for the unidirectional waves. In what follows we will present a new system of two equations that describe the evolution of two almost planar counter streaming waves.

2. The Counter Streaming Waves

The Zakharov equation for water waves can be derived in two steps:

• Firstly, the normal canonical variables, $a_k$ are introduced as follows:

  $$\begin{array}{cc}\hfill & {\eta }_k=\sqrt{\frac{{\omega }_k}{2g}}(a_k+a_{-k}^{*}),{\psi }_k=-i\sqrt{\frac{}{2{\omega }_k}}(a_k-a_{-k}^{*}),\hfill \end{array}$$

  where ${\omega }_k=\sqrt{k}$, and ${\eta }_k$ and ${\psi }_k$ denote the Fourier transform that is defined as follows:

  $$f_k=\frac{1}{\sqrt{2\pi }}\int f(x)e^{-ikx}dx,f(x)=\frac{1}{\sqrt{2\pi }}\int f_k{e}^{ikx}dk.$$
• Secondly, the canonical transformation from $a_k$ to $b_k$ is chosen to cancel all non resonant terms in the Hamiltonian, both cubic and forth order. The details of this transformation can be found in the reference [6].

As a result the Hamiltonian (2) acquires the form:

$$\begin{array}{cc}\hfill H=& \int {\omega }_k{b}_k{b}_k^{*}dk+\frac{1}{2}\int T_{k{k}_1}^{k_2{k}_3}{b}_k^{*}{b}_{k_1}^{*}{b}_{k_2}{b}_{k_3}{\delta }_{k+k_1-k_2-k_3}dkd{k}_{1}d{k}_{2}d{k}_3\hfill \end{array}$$

where $b_k$ is a normal canonical complex variable, and the matrix element, $T_{k{k}_1}^{k_2{k}_3}$, satisfies the symmetry conditions

$$T_{k{k}_1}^{k_2{k}_3}=T_{k_2{k}_3}^{k_{1}k}=T_{k{k}_1}^{k_2{k}_3}=T_{k{k}_1}^{k_3{k}_2}.$$

(3)

The explicit (yet cumbersome) expression for $T_{k{k}_1}^{k_2{k}_3}$ can be found in the reference [1,2], however we will need the diagonal entries of $T_{k{k}_1}^{k_2{k}_3}$ that are given by:

$$T_{k{k}_1}^{k{k}_1}=\frac{k{k}_1}{2\pi }\min (|k|,|k_1|).$$

(4)

The equation of motion is given by the following relation:

$$\frac{\partial b_k}{\partial t}+i\frac{\delta H}{\delta b_k^{*}}=0,$$

(5)

and after the calculation of the variational derivative, we may write:

$$\begin{array}{c}\hfill i{\dot{b}}_k={\omega }_k{b}_k+\int T_{k{k}_1}^{k_2{k}_3}{b}_{k_1}^{*}{b}_{k_2}{b}_{k_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3.\end{array}$$

(6)

This equation takes into account the main nonlinear process, the four-waves interaction, and neglects higher order wave interactions. Besides energy and momentum, this equation admits a specific integral of motion, the “number of waves”, that can be introduced as follows::

$$N={\int }_{-\infty }^{\infty }{\left|b_k\right|}^{2}dk.$$

(7)

For one-dimensional waves $T_{k{k}_1}^{k_2{k}_3}$ has a very important property (see [5]):

$$T_{k{k}_1}^{k_2{k}_3}\equiv 0\mathrm{if}k{k}_1{k}_2{k}_3<0,$$

(8)

that allows to simplify the equation of motion, and provides new integrals of motion. It is convenient to write the function $b(x,t)$ as a sum of two analytic functions in the complex pane $z=x+iy$:

$$\begin{array}{c}\hfill b(x,t)=b^{+}(x,t)+b^{-}(x,t)\mathrm{or}{b}_k=b_k^{+}+b_k^{-}\end{array}$$

(9)

$$\begin{array}{c}{b}^{+}(x,t)\mathrm{is\; analytic\; in\; upper\; half-plane}\\ b^{-}(x,t)\mathrm{is\; analytic\; in\; lower\; half-plane}.\end{array}$$

$b^{+}(x,t)$ has only the positive Fourier modes $b_k^{+}$, while $b^{-}(x,t)$ has only the negative ones that are denoted by $b_k^{-}$. Such a splitting is introduced for the first time, and it leads to an elegant system of two equations. By plugging Equation (9) into the equation of motion (6) one finds that

$$\begin{array}{c}i{\dot{b}}_k^{+}+i{\dot{b}}_k^{-}={\omega }_k{b}_k^{+}+{\omega }_k{b}_k^{-}+\hfill \\ +\int \left[b_{k_1}^{{+}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{+}+2b_{k_1}^{{-}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{-}+b_{k_1}^{{-}^{*}}{b}_{k_2}^{-}{b}_{k_3}^{-}+2b_{k_1}^{{+}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{-}\right]T_{k{k}_1}^{k_2{k}_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3+\hfill \\ \bcancel{\cancel{+\int \left[b_{k_1}^{{-}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{+}+b_{k_1}^{{+}^{*}}{b}_{k_2}^{-}{b}_{k_3}^{-}\right]T_{k{k}_1}^{k_2{k}_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3,}}\hfill \end{array}$$

(10)

and last term in Equation (10) vanishes. Indeed, let us consider the first crossed out term:

$$\begin{array}{c}\hfill k_1<0,k_2>0,k_3>0\end{array}$$

$$\begin{array}{c}\hfill k=-k_1+k_2+k_3>0\end{array}$$

$$\begin{array}{c}\hfill k{k}_1{k}_2{k}_3<0\Rightarrow T_{k{k}_1}^{k_2{k}_3}\equiv 0.\end{array}$$

In a similar manner, one may show that the second crossed out term vanishes too.

Each remaining term in the Equation (10) consists of either the positive, or the negative Fourier modes. This is another consequence of the property Equation (8), and hence this equation can be splitted into two: one for the positive k, and the other for the negative k:

$$\begin{array}{c}i{\dot{b}}_k^{+}={\omega }_k{b}_k^{+}+\int \left[b_{k_1}^{{+}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{+}+2b_{k_1}^{{-}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{-}\right]T_{k{k}_1}^{k_2{k}_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3\hfill \\ i{\dot{b}}_k^{-}={\omega }_k{b}_k^{-}+\int \left[b_{k_1}^{{-}^{*}}{b}_{k_2}^{-}{b}_{k_3}^{-}+2b_{k_1}^{{+}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{-}\right]T_{k{k}_1}^{k_2{k}_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3\hfill \end{array}$$

(11)

This system of two equations describes interaction of two groups of waves propagating in opposite direction, and include the standing waves. The Hamiltonian for this system may be written as follows:

$$\begin{array}{c}H=\int {\omega }_k\left[\right|b_k^{+}{|}^2+|b_k^{-}{|}^2]dk+\hfill \\ +\frac{1}{2}\int \left[b_k^{{+}^{*}}{b}_{k_1}^{{+}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{+}+b_k^{{-}^{*}}{b}_{k_1}^{{-}^{*}}{b}_{k_2}^{-}{b}_{k_3}^{-}\right]T_{k{k}_1}^{k_2{k}_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3+\hfill \\ +2\int b_k^{{+}^{*}}{b}_{k_1}^{{-}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{-}{T}_{k{k}_1}^{k_2{k}_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3,\hfill \end{array}$$

(12)

and the two equations of motion are given by:

$$\frac{\partial b_k^{+}}{\partial t}+i\frac{\delta H}{\delta b_k^{{+}^{*}}}=0,\frac{\partial b_k^{-}}{\partial t}+i\frac{\delta H}{\delta b_k^{{-}^{*}}}=0.$$

(13)

This system has two new integrals of motion, “number of waves” traveling to the right, and “number of waves” traveling to the left, and each of them is conserved individually. Indeed, consider the time derivative of the “number of waves” traveling to the right:

$$\begin{array}{c}\frac{\partial }{\partial t}\int {\left|b^{+}\right|}^{2}dk=i\int \left[b_k^{{+}^{*}}{\omega }_k{b}_k^{+}-b_k^{+}{\omega }_k{b}_k^{{+}^{*}}\right]dk+\hfill \\ +i\int \left[b_k^{{+}^{*}}{b}_{k_1}^{{+}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{+}-b_k^{+}{b}_{k_1}^{+}{b}_{k_2}^{{+}^{*}}{b}_{k_3}^{{+}^{*}}\right]T_{k{k}_1}^{k_2{k}_3}{\delta }_{k+k_1-k_2-k_3}dkd{k}_{1}d{k}_{2}d{k}_3+\hfill \\ +2i\int \left[b_k^{{+}^{*}}{b}_{k_1}^{{-}^{*}}{b}_{k_2}^{+}{b}_{k_3}^{-}-b_k^{+}{b}_{k_1}^{-}{b}_{k_2}^{{+}^{*}}{b}_{k_3}^{{-}^{*}}\right]T_{k{k}_1}^{k_2{k}_3}{\delta }_{k+k_1-k_2-k_3}dkd{k}_{1}d{k}_{2}d{k}_3\equiv 0\hfill \end{array}$$

due to symmetry condition Equation (3). Thus, the system of equations for waves on the surface of 2D deep water conserves two additional integrals given by:

$$\begin{array}{c}\hfill N^{+}={\int }_0^{\infty }{\left|b_k^{+}\right|}^{2}dk\\ \hfill N^{-}={\int }_{-\infty }^0{\left|b_k^{-}\right|}^{2}dk.\end{array}$$

(14)

A trivial calculation shows that the total momentum

$$M={\int }_{-\infty }^{\infty }k\left[|b_k^{+}{|}^2-{\left|b_k^{-}\right|}^2\right]]dk$$

is also conserved.

It should be emphasized that the equations, and the existence of new integrals holds only if four wave interactions are taken into account, and the higher order interactions are negligible. It is known that the five wave interactions do not vanish, see [7]. In this case the “number of waves” is not conserved. For example, in [8] a numerical simulation of waves dynamics was studied in the framework of fully nonlinear equations and, of course, number of waves was not conserved.

It should mentioned that the system Equation (11) can be drastically simplified by applying a canonical transformation similar to that in [3,4,5], and allows one to write this system in x-space, in a super compact way. The set of super compact equations was first reported in [9] and will be the subject of a separate article. In what follows, we consider the case of two almost monochromatic, counter-streaming waves, and do a narrow band approximation.

3. Narrow Bands Approximation

System of Equation (11) has simple solution—two counter-streaming monochromatic waves:

$$\begin{array}{ccc}\hfill b^{+}(x,t)& =& B^{+}{e}^{i(k^{+}x-{\omega }^{+}t)}\hfill \\ \hfill b^{-}(x,t)& =& B^{-}{e}^{i(k^{-}x-{\omega }^{-}t)}.\hfill \end{array}$$

(15)

Here

$$\begin{array}{cc}\hfill & k^{+}>0,k^{-}<0,{\omega }^{+}>0,{\omega }^{-}>0\hfill \end{array}$$

and $B^{+}$ and $B^{-}$ are arbitrary complex constants. For ${\omega }^{+}$ and ${\omega }^{-}$ the following relation are valid:

$$\begin{array}{c}{\omega }^{+}={\omega }_{k^{+}}+T_{k^{+}{k}^{+}}^{k^{+}{k}^{+}}|B^{+}{|}^2+2T_{k^{+}{k}^{-}}^{k^{+}{k}^{-}}{\left|B^{-}\right|}^2\\ {\omega }^{-}={\omega }_{k^{-}}+T_{k^{-}{k}^{-}}^{k^{-}{k}^{-}}|B^{-}{|}^2+2T_{k^{+}{k}^{-}}^{k^{+}{k}^{-}}{\left|B^{+}\right|}^2.\end{array}$$

(16)

From system of Equations (11) one can easily derive equations for two envelopes of two modulated counter-streaming waves trains. $B^{+}$ and $B^{-}$ are now slowly modulated functions of x so, that

$$\begin{array}{ccc}\hfill b^{+}(x,t)& =& B^{+}(x,t)e^{i(k^{+}x-{\omega }_{k^{+}}t)}\hfill \\ \hfill b^{-}(x,t)& =& B^{-}(x,t)e^{i(k^{-}x-{\omega }_{k^{-}}t)},\hfill \end{array}$$

or

$$\begin{array}{ccc}\hfill b_k^{+}& =& B^{+}(k-k^{+})e^{i(k^{+}x-{\omega }_{k^{+}}t)},|k-k^{+}|<<|k^{+}|\hfill \\ \hfill b_k^{-}& =& B^{-}(k-k^{-})e^{i(k^{-}x-{\omega }_{k^{-}}t)}.|k-k^{-}|<<|k^{-}|.\hfill \end{array}$$

(17)

These spectra are schematically shown in the Figure 1. One of them is located in the vicinity of some positive wave number and the other—in the vicinity of negative one.

Under the assumption Equation (17), one may treat the coefficients $T_{k{k}_1}^{k_2{k}_3}$ as constants in the vicinity of $k^{+}$ and $k^{-}$, and the following equations can be derived:

$$\begin{array}{c}i{\dot{B}}_k^{+}=\left[k\frac{\partial {\omega }_k}{\partial k}{|}_{k=k^{+}}+\frac{k^2}{2}\frac{{\partial }^2{\omega }_k}{\partial k^2}{|}_{k=k^{+}}\right]B_k^{+}+\hfill \\ \int \left[T_{k^{+}{k}^{+}}^{k^{+}{k}^{+}}{B}_{k_1}^{{+}^{*}}{B}_{k_2}^{+}{B}_{k_3}^{+}+2T_{k^{+}{k}^{-}}^{k^{+}{k}^{-}}{B}_{k_1}^{{-}^{*}}{B}_{k_2}^{+}{B}_{k_3}^{-}\right]{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3\hfill \\ i{\dot{B}}_k^{-}=\left[k\frac{\partial {\omega }_k}{\partial k}{|}_{k=k^{-}}+\frac{k^2}{2}\frac{{\partial }^2{\omega }_k}{\partial k^2}{|}_{k=k^{-}}\right]B_k^{-}+\hfill \\ \int \left[T_{k^{-}{k}^{-}}^{k^{-}{k}^{-}}{B}_{k_1}^{{-}^{*}}{B}_{k_2}^{-}{B}_{k_3}^{-}+2T_{k^{+}{k}^{-}}^{k^{+}{k}^{-}}{B}_{k_1}^{{+}^{*}}{B}_{k_2}^{+}{B}_{k_3}^{-}\right]{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3.\hfill \end{array}$$

(18)

It x-space the two equations can be written as follows:

$$\begin{array}{c}i({\dot{B}}^{+}+v_g^{+}{B^{+}}^{\prime })=\frac{{\omega }_k{}^{+}}{8{k^{+}}^2}{B^{+}}^{\prime \prime }+\left[T_{k^{+}{k}^{+}}^{k^{+}{k}^{+}}|B^{+}{|}^2+2T_{k^{+}{k}^{-}}^{k^{+}{k}^{-}}{\left|B^{-}\right|}^2\right]B^{+}\\ i({\dot{B}}^{-}+v_g^{-}{B^{-}}^{\prime })=\frac{{\omega }_k{}^{-}}{8{k^{-}}^2}{B^{-}}^{\prime \prime }+\left[T_{k^{-}{k}^{-}}^{k^{-}{k}^{-}}|B^{-}{|}^2+2T_{k^{+}{k}^{-}}^{k^{+}{k}^{-}}{\left|B^{+}\right|}^2\right]B^{-},\end{array}$$

(19)

where

$$v_g^{+}=\frac{1}{2}\sqrt{\frac{g}{k^{+}}},v_g^{-}=-\frac{1}{2}\sqrt{\frac{g}{|k^{-}|}}.$$

It should be noted that a similar system of equations was derived in [10] for polarized light propagation.

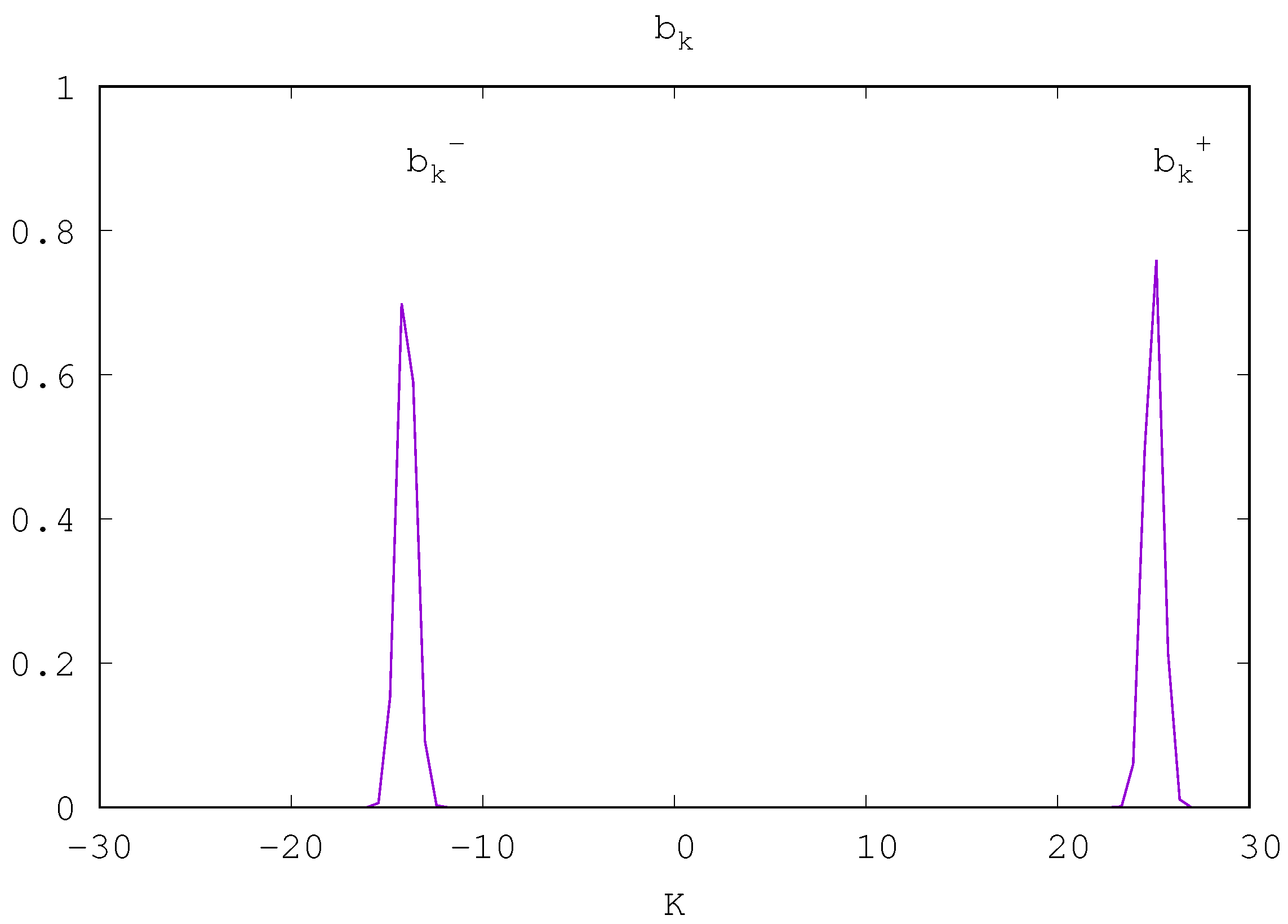
4. The Nonlinear Standing Wave

The Equation (19) have a solution in the form of a standing wave. Given the following substitution

$$B^{+}(x,t)=B(x)e^{i\mathsf{\Omega }t},B^{-}(x,t)=B^{*}(x)e^{i\mathsf{\Omega }t},k_{-}=-k_{+}=k$$

the two Equation (19) reduce to a single one:

$$i\mathsf{\Omega }B+v_g{B}_x+i\frac{{\omega }_k}{8k^2}{B}_{xx}-i{k}^2{\left|B\right|}^{2}B=0.$$

One can look for the solution in the form

$$B=R{e}^{i\varphi }.$$

Then the following equations for R and $\varphi$ hold:

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial x}\left[R^2-\frac{1}{2k}{R}^2{\varphi }_x\right]=0\Rightarrow {\varphi }_x& =& 2k(1-\frac{r_0^2}{R^2})\hfill \\ \hfill \frac{v_g}{4k}{R}_{xx}+\left[\mathsf{\Omega }+v_{g}k\right]R-v_{g}k\frac{r_0^4}{R^3}-k^2{R}^3& =& 0\hfill \end{array}$$

and the solution can be found in terms of the elliptic functions. In particular, a solitary solution given by the formula:

$$R^2=r_0^2-\frac{a^2}{{\cosh }^2(\lambda x)}.$$

exists. This solution depends on four independent constants: $\mathsf{\Omega }$, $r_0$, a and $\lambda$.

5. Conclusions

• A simple system of two Equations (11) was derived for waves on the surface of 2D deep water.
• The special structure of the coefficient of four wave interaction Equation (8) allows to divide waves into two groups: the one traveling to the left and the other traveling to the right. Each group is described by the analytic function: one is analytic in the lower half-plane and the other is analytic in the upper half-plane.
• Due to the property of Equation (8), the system that describes water waves has two additional constants of motion, the numbers of waves that travel in opposite directions.
• An exact analytic solution for a nonlinear standing wave in the narrow-band approximation limit has been derived.