Abstract
In this work, a systematic investigation of the migration of sedimenting particles in a viscoelastic Couette flow is presented, using finite element 3D simulations. To this end, a novel computational approach is presented, which allows us to simulate a periodic configuration of rigid spherical particles accurately and efficiently. To study the different contributions to the particle migration, we first investigate the migration of particles sedimenting near the inner wall, without an externally-imposed Couette flow, followed by the migration of non-sedimenting particles in an externally-imposed Couette flow. Then, both flows are combined, i.e., sedimenting particles with an externally-imposed Couette flow, which was found to increase the migration velocity significantly, yielding migration velocities that are higher than the sum of the combined flows. It was also found that the trace of the conformation tensor becomes asymmetric with respect to the particle center when the particle is initially placed close to the inner cylinder. We conclude by investigating the sedimentation velocity with an imposed orthogonal shear flow. It is found that the sedimentation velocity can be both higher or lower then the Newtonian case, depending on the rheology of the suspending fluid. Specifically, a shear-thinning viscosity is shown to play an important role, which is in-line with previously-published results.
1. Introduction
Suspensions of particles in viscoelastic fluids are encountered in many natural, biological, and industrial processes. Examples of these suspensions are blood, paint, and pharmaceuticals. Therefore, the behavior of particles suspended in a single viscoelastic fluid is of great interest. Many practical applications also show the occurrence of cross-streamline migration of particles. Examples are separation of particles with different sizes, suspensions in microfluidic devices where migration can lead to non-homogenous particle distributions, cells in blood causing clots, which are obstructing the flow, and other biosensing applications [1]. Furthermore, Couette flow devices are often used as a rheometer, to measure the rheology of suspensions. Therefore, the migration behavior of the particles is of great interest, since migration of particles will change the rheology of the fluid.
Understanding the sedimentation behavior of particles in a viscoelastic shear flow can for example be used to optimize the hydraulic fracturing process for obtaining natural gas. In this process, solid particles in polymeric solutions are pumped into hydraulically-induced fractures under high pressure. The particles must keep the fractures open in order to increase the rate of gas recovery. In vertically-oriented fractures, sedimentation causes the particle to settle. Therefore, sedimentation should be limited in order to limit settling and place the particles far into the fracture to increase gas recovery [2].
Migration of a sedimenting particle in a channel near a vertical wall was investigated by Singh and Joseph [3]. They found that a falling particle initially placed close enough to the wall will migrate towards the wall. However, in a Newtonian liquid, the sphere moves away from the vertical wall and attains a steady position between the channel center and the wall.
When the particle was placed in a shear flow, D’Avino et al. [4] found that three different regimes can be recognized in the migration of the particle, depending on the distance of the particle from the wall, where the migration velocity is initially linear with the particle position, but increases when the particle approaches the wall and decreases again when the particle is in very close proximity to the wall.
Migration of a particle in a viscoelastic fluid in a Couette flow was numerically and experimentally investigated by D’Avino et al. [5]. It was found that elasticity promotes migration of the particle towards the outer cylinder for almost every initial position. Only if the particle was initially placed very close to the inner cylinder, it would move towards it. Furthermore, a maximum in the migration velocity was found when the particle moves closer to the outer cylinder. High Newtonian solvent viscosity and shear thinning reduce the migration rate.
The sedimentation of particles in a flow without shear has been studied extensively. A dimensionless number called the sedimentation Weissenberg number relates the polymer relaxation time scale to the flow time scale. It has been shown that at high values for , the deformation of the polymer is dominated by the flow due to the movement of the particle. This can cause significant extension of the polymer around the particle, causing pronounced elastic effects in the wake of the sphere that decrease the particle mobility [6,7,8].
Many research works have also been devoted to the sedimentation of a particle in a shear flow [9]. Van den Brule et al. [10] performed experiments to gain more insight into the effects of fluid elasticity on the settling velocity of spherical particles suspended in viscoelastic fluids. Here, the settling velocity of a spherical particle was measured in three different fluids: a Newtonian fluid, a Boger fluid and a shear-thinning fluid. From this study, it could be concluded that fluid elasticity plays a significant role in reducing the settling velocity of a spherical particle in a viscoelastic fluid. Shear-thinning, however, increased the settling velocity of the particles, since now the viscosity decreases with increasing shear rate. This was also found in another study [11]. Padhy et al. [12] numerically investigated the effect of viscoelasticity on the settling velocity of a particle in a cross-shear flow. Padhy et al. [12] calculated the drag on a particle in their simulations and found that the drag in viscoelastic fluids is increased indirectly through the increase of viscous stresses. The dominant contribution to the viscous stresses becomes asymmetric when sedimentation and shear flow are combined, leading to a decrease in settling velocity. The coupling between the two flows needs to be non-linear for the increase in drag to be substantial. This non-linear coupling is only present in viscoelastic fluids.
Murch et al. [13] recently numerically investigated the growth of viscoelastic wings and how this reduces the particle mobility in a viscoelastic shear flow. They found that for high shear Weissenberg numbers and sedimentation Weissenberg numbers of , the particle mobility is decreased due to the growth of viscoelastic wings around the particle.
Migration is often a problem in flows that are more complex than simple shear, or pure sedimentation. In the current paper, a first step up in complexity is offered, by combining two flows that yield migration. The finite element method is used to investigate numerically the influence of both the sedimentation and shear Weissenberg number on the migration and sedimentation of a particle in a viscoelastic fluid under orthogonal shear in a Couette flow device. The mass of the particle is varied via the downward force on the particle to create different local shear rates around the falling particle, leading to different sedimentation Weissenberg numbers. Furthermore, the orthogonal shear rate is varied to create different shear Weissenberg numbers. The influence of both Weissenberg numbers on the sedimentation and migration of the particle is investigated, using a Giesekus model. Migration of the particle close to the inner cylinder of the Couette is studied systematically to see how the different flow types influence the migration of the particle and what happens if the two are combined.
2. Problem Statement
The shear flow is created in a Couette flow device, by rotating the outer cylinder with a velocity , while keeping the inner cylinder stationary. When studying sedimentation, a force is applied to the particle in the z-direction. To minimize the computational costs, only a part of the Couette flow device is modeled, as is shown in Figure 1. Periodicity is assumed on surfaces and . The top and bottom of the domain are assumed to be far enough away from the particle, to not feel the presence of the particle. The angle , together with the inner radius , the outer radius , and the height H define the size and shape of the domain. The spherical particle has radius a, and its boundary is denoted by . A cylindrical coordinate system will be used throughout this paper, with components, using the convention . The computational domain of the Couette is denoted by . Note that the positive z-direction is directed in the gravitation direction.
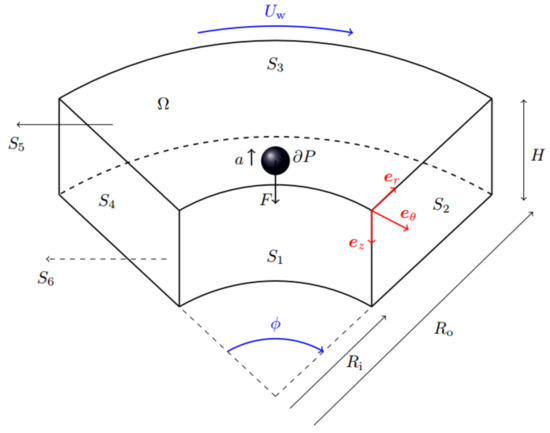
Figure 1.
Problem description of a rigid, spherical particle suspended in a viscoelastic Couette flow. The Couette flow is set up by moving the outer cylinder in the tangential direction, with velocity , while the inner cylinder remains stationary. Simultaneously, a force acts on the particle in the z-direction, causing it to sediment. The inner cylinder boundary is denoted by , the outer cylinder boundary is denoted by . The top and bottom of the Couette are denoted by and , respectively. The periodic side boundaries are denoted by and , where is rotated over an angle with respect to surface .
2.1. Governing Equations
2.1.1. Balance Equations
It is assumed that the fluid is incompressible, that inertia can be neglected, and that there are no external body forces acting on the fluid. This leaves the following equations for the balance of momentum and balance of mass:
where is the fluid velocity and is the Cauchy stress tensor, which consists of three contributions:
where p is the pressure, the unit tensor, and the solvent or Newtonian viscosity. Furthermore, is the rate of deformation tensor, and represents the viscoelastic stress tensor, given by:
where is the conformation tensor and G the polymer modulus, which equals . Here, is the polymer viscosity and the polymer relaxation time. The evolution of the conformation tensor can be described by the following equation using the Giesekus model [14]:
where is the mobility parameter and denotes the upper-convected derivative, which is defined as:
where is the material derivative denoted by .
2.1.2. Particle Motion
It is assumed that the inertia of the particle can be neglected and that a force is applied to the particle. The balance of forces and the balance of torques that act on the particle can be expressed as follows:
where is the outwardly-directed unit normal vector on the boundary of the particle , is the position of the center point of the particle, and is evaluated on the fluid side of the particle boundary . The translational velocity of the particle is denoted by , which is an unknown in the problem, but will be such that Equation (7) is satisfied. The relation between the particle position and velocity is obtained by the following kinematic equation:
2.2. Boundary Conditions
On the particle boundary and rigid walls and , a no-slip condition is imposed. On , the velocity is set to zero, whereas on , the velocity is tangential to the curved surface. Periodicity of the surfaces and is assumed. Surfaces and are assumed to be far enough from the particle to not feel the presence of the particle. Symmetry is prescribed in surfaces and , i.e., the velocities in the r- and -direction are left free, while the velocity in the z-direction is prescribed to be zero. The velocities on the side curves of surfaces and are periodic in the - and r-direction. This yields the following boundary conditions:
where is the particle angular velocity and the subscripts containing a number denoting the velocities on the surfaces up to , respectively. Equation (16) imposes a periodic boundary condition for the velocities on surfaces and . The traction vector on the surface with outwardly-directed normal is denoted by . The rotation of the velocities and tractions from surfaces to is performed by the rotation tensor . More details on the rotation tensor can be found in Appendix A and Appendix B. On surface , the solution of the conformation of of the problem without a particle is prescribed since this surface is an inflow surface due to the rigid body movement of the whole mesh with the particle, as will be explained in Section 3.3. This conformation is obtained by solving a separate 1D problem of a Couette flow without the particle and using the steady state value of . This means that for the conformation tensor, the following boundary condition is applied:
Furthermore, a periodic boundary condition is also applied for the conformation tensor on surfaces and . This periodic boundary condition is imposed by the following equation in the same way as is done for the velocities, but now for a tensor instead of a vector:
An initial condition is needed for the conformation tensor . In order to reduce the computation time, the steady-state solution for the problem without a particle is prescribed as the initial condition for the conformation:
2.3. Arbitrary Lagrange–Euler Formulation
The domain is described with a boundary-fitted mesh that is moved in time in such a way that the mesh moves with the particle, but not necessarily with the fluid. Therefore, the governing equations have to be rewritten in the Arbitrary Lagrange–Euler (ALE) formulation [15]. The movement of the grid has to be compensated. This only applies to the evolution equation of the conformation tensor, since this is the only equation that contains a convective term. The material derivative in Equation (6) is now written as:
where denotes the time derivative in a fixed grid point and is the mesh velocity. Details about the mesh velocity will be explained in Section 3.3.
3. Numerical Method
The finite element method is used to solve the problem. For the velocity and the pressure, isoparametric, tetrahedral (Taylor–Hood) elements are used, whereas for the conformation, tetrahedral elements are used. In order to solve the constitutive equation, the log-conformation representation [16] and DEVSS-G are used for stability [17].
3.1. Weak Formulation
In this section, the weak formulation of the balance equations is presented. The motion of the particle is enforced as a constraint, using the combined equation of motion approach [18]. The periodic boundary condition for the velocity is also enforced as a constraint, using Lagrange multipliers. The weak form of this problem can now be formulated as follows: find , p, , , and such that:
for all admissible test functions . Furthermore, , and denotes an inner product on domain , whereas is an inner product on ; and are parameters for SUPG and DEVSS-G stabilization, respectively, and . More information on log-conformation stabilization and the function can be found in [16], whereas more information on the DEVSS-G method and the projected velocity gradient can be found in [17]. A finite element method on moving meshes aligned with the particle boundary is used to solve the equations. Since the elements are aligned with the particle boundary, the inner product on can be calculated in the nodes. This is done using a collocation method [18]:
where is the number of collocation points, which corresponds to the nodes on the particle boundary. Furthermore, and are the Lagrange multiplier and coordinate of the kth collocation point, respectively. The same approach can be used for the weak formulation of the periodic boundary condition on the velocity. Note that the periodic surfaces have to be meshed such that the meshes are also periodic.
3.2. Implementation Periodic Boundary Conditions
In order to impose periodic boundary conditions for the velocity, the velocity has to be prescribed such that the , and components on and are equal. This means that is equal to , but rotated. The actual implementation is done in Cartesian coordinates. The same approach is used for the periodic boundary condition for the conformation tensor, only now, a tensor rotation is used instead of a vector rotation. More details on the implementation can be found in Appendix A and Appendix B.
3.3. Mesh Movement
Since the mesh will move in time, it is necessary to move the mesh to track the particle boundary. This is done using the ALE method. The starting mesh in the ALE method is used until it becomes too distorted. When this happens, a new mesh, covering the same domain as the old one, is generated using Gmsh [19], and the solution on the old mesh is projected onto the new one. The projection problem is solved to obtain the solution variables on the new mesh. This remeshing and solving the projection problem is done in the same way as was done by Jaensson et al. [20]. However, the projection leads to inaccuracies, and the remeshing procedure is very time consuming. Therefore, the number of remeshing steps should be reduced as much as possible during the simulations.
The mesh velocity can be set to an arbitrary value, and this can be exploited to reduce the remeshing steps, or even avoid remeshing [15]. Therefore, the whole mesh moves as a rigid body with the particle in the - and z-direction, while the mesh still deforms in the r-direction due to the movement of the particle. The mesh displacement in the r-direction due to the migration of the particle can be obtained by solving a Laplace equation, in order to guarantee a smooth mesh motion [15].
3.3.1. Prescribing the Conformation Tensor
Since the conformation tensor obeys a hyperbolic partial differential transport equation, the conformation has to be prescribed at inflow boundaries [21,22]. The bottom surface of the domain can be seen as an inflow surface, since the whole mesh is moved as a rigid body with the particle in the z-direction. Therefore, a solution of the conformation tensor from the same problem without a particle is prescribed at surface .
3.4. Time Integration
The time stepping approach now contains the following steps:
Step 1: Compute the particle position at the beginning of every time step. The new particle position can be found using an explicit Euler scheme for Equation (9):
For subsequent time steps, however, a second-order Adams–Bashforth scheme is used:
Step 2: Update the mesh, using the new particle position as explained in Section 3.3.
Step 3: The mesh velocities can now be obtained by numerically differentiating the mesh coordinates. For the first time step, the mesh velocity is obtained in each node using a backward differencing scheme:
where are the nodal coordinates of the mesh. For subsequent time steps, a second-order backward differencing scheme is used:
The z- and -component of the mesh velocity are set equal to the particle velocity in the z- and -direction. In this way, the whole mesh moves with the particle.
Step 4: Compute and . The method of D’Avino and Hulsen [23] for decoupling the momentum balance from the constitutive equation is applied, using DEVSS-G for stability [17].
Step 5: After solving for the new velocities and pressures, the actual conformation tensor is found using a second-order, semi-implicit Gear scheme with conformation prediction for Equation (5) using SUPG and the log-conformation representation for stability. The conformation tensor is solved component wise, meaning that not all conformation tensor components are known at the same time. Because of this, it is not possible to enforce periodicity of on surfaces and via a constraint. Therefore, an iteration is performed until the periodic solution for is found. During this iteration, the conformation tensor has to be described on the inflow-nodes of surfaces and . See Section 3.3.1. Therefore, it is first computed which of the nodes on surface are inflow nodes by computing whether is positive. Here, is the normal vector of surface . Due to periodicity, outflow nodes on have to be inflow nodes on .
4. Results
In this section, the convergence of the migration problem will be investigated. After that, the results of the migration of a sedimenting particle without Couette flow, migration of a particle in a Couette flow without sedimentation, and migration of a particle with the two flows combined will be discussed. Finally, the results of the sedimentation of a particle in a Couette flow for two different sets of fluid parameters will be discussed. In order to increase the sedimentation Weissenberg number, the applied downward force on the particle is increased. Since a force is applied on the particle, the sedimentation velocity of the particle is not known a priori. Therefore, the sedimentation Weissenberg number is defined as follows:
where is the Stokes velocity defined as . The shear Weissenberg number is defined as:
The ratio between the solvent viscosity and the total viscosity can be expressed as the ratio between the solvent viscosity and the polymer viscosity and can be described as . The viscosity ratio is chosen to be 0.35, together with a non-linear parameter of 0.2. The particle is positioned initially at a distance from the inner cylinder of the Couette.
The outer radius of the outer cylinder has a value of 90-times the particle radius, while the radius of the inner cylinder has a value of 50-times the particle radius, yielding a gap size of 40-times the particle radius. The height of the Couette flow device is 80-times the particle radius. To save computational costs, only a part of the Couette flow device is modeled, where surface is rotated over an angle of = 45° with respect to surface . By using = 45°, we actually model a Couette flow with eight particles in it, because of the periodic boundary conditions. For this angle, the distance between the particles is larger than 40-times the particle radius, which is large enough to exclude the effect of particle–particle interactions [12].
4.1. Convergence
In this section, the convergence of the migration problem will be investigated. Convergence was the hardest to obtain for a high shear Weissenberg number combined with a high sedimentation Weissenberg number. Therefore, a convergence study was performed for a shear Weissenberg number of and a sedimentation Weissenberg number of . In order to choose a mesh with elements small enough that convergence is reached, the migration velocity of a particle, made dimensionless by dividing by , was plotted for different element sizes around the particle. For these simulations, meshes were constructed with six elements across the gap of the Couette flow device and , , and elements on the equator of the particle. This element size was extended over a distance a from the particle and then slowly increased to the element size of the surrounding mesh over a distance . The mesh was refined near the inner radius of the Couette, where 15 elements were placed along the inner radius. The mesh for is shown in Figure 2. The results for mesh convergence are shown in Figure 3a. Time convergence was studied by plotting again the dimensionless migration velocity of the particle, for a mesh with , but now with different time step sizes . The result is shown in Figure 3b. Note that we use quadratic elements for the velocity, meaning that means 61 nodes on the equator of the particle, and six elements across the gap means 13 nodes across the gap.
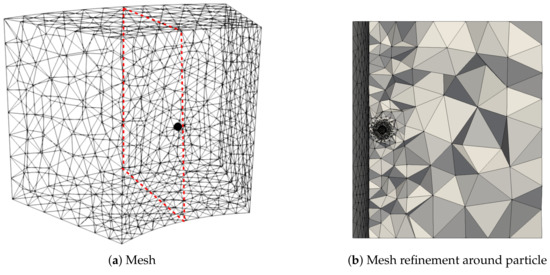
Figure 2.
Mesh that is refined around the particle boundary and at the inner cylinder for . Red dotted lines in (a) indicate the cross-section shown in (b).
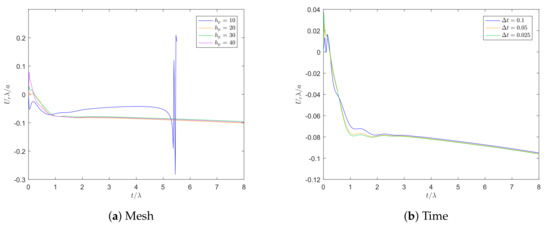
Figure 3.
Migration velocity of a particle placed at a distance from the inner cylinder of a Couette for different element sizes around the particle and different time step sizes .
These figures show that for small enough element sizes and time step sizes, the lines superimpose. The convergence is studied here for the most complicated scenario of high Weissenberg numbers and the particle placed originally close to the inner cylinder. Since Figure 3 shows relatively good convergence, we expected that convergence would be better for the less difficult scenarios. In order to have a good balance between accuracy and computational costs, a element size of and a time step size of were chosen for the simulations.
4.2. Migration
In this section, it is investigated how the two complex flows (shear and sedimentation) influence the migration of a particle placed close to the inner cylinder of a Couette flow device. In order to do this, first the effect of the two separate complex flows is investigated. This is done for different initial particle positions in the Couette flow device, close to the inner cylinder. The dimensionless particle radial position is defined as:
where is the radial position of the center of the particle at time and a is the particle radius. Therefore, indicates how many times the particle radius is away from the inner cylinder. The migration velocity at time is used in the figures in this Results Section. For a time that is ten-times the relaxation time of the fluid, it was assumed that the viscoelastic stresses were fully developed, and therefore, all transient effects were due to the migration of the particle. For the representation of the results, the cross-section indicated in red in Figure 2 was used. From here on, this cross-section is referred to as .
4.2.1. Migration for a Falling Particle without Shear in Couette Flow
The migration of a falling particle close to the inner cylinder of the Couette was first investigated without applying a shear flow. This means that the velocity of the outer cylinder . The result is shown in Figure 4. Here, the migration velocity of the particle is made dimensionless with .
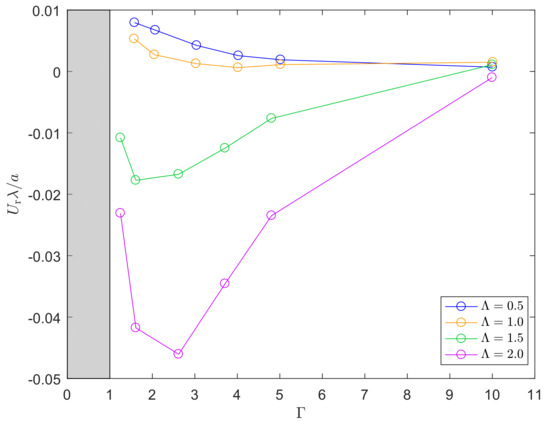
Figure 4.
Migration velocity of the particle at different positions from the inner cylinder without shear and varying sedimentation Weissenberg number at time . The shaded area indicates the inaccessible region.
This figure shows that the movement of the particle towards the inner cylinder slows down significantly when the particle approaches the inner cylinder. For small values of , it even seems to become positive, i.e., the particle is migrating away from the inner cylinder. This effect of the wall is much more severe for the case of a migrating particle in a Couette flow without sedimentation than for a migrating particle without shear, but with sedimentation, as we will see in Section 4.2.2. The figure also shows that the migration velocity goes to zero when the particle position is further away from the inner cylinder. The movement of the particle towards the inner cylinder speeds up for increasing (i.e., higher negative ). The trace of the conformation tensor around the particle for initial particle positions and and without shear is shown using in Figure 5 at time . This figure shows that the trace of the conformation tensor around the particle becomes slightly asymmetric and larger at the side of the particle close to the cylinder, when the particle is positioned close to the inner cylinder.
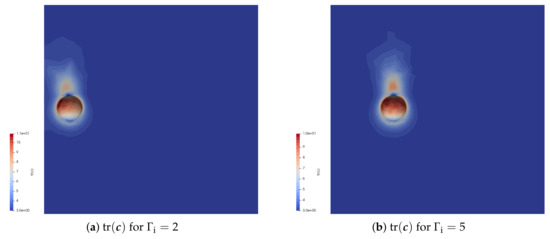
Figure 5.
The trace of the conformation tensor around the particle for different initial positions from the inner cylinder at time for and using .
4.2.2. Migration of a Particle in Couette Flow without Sedimentation
The migration of the particle is now investigated for the case where there is no sedimentation, but the shear rate is varied. This means that the downward force on the particle is set to zero and the velocity of the outer cylinder is varied. The result is shown in Figure 6.
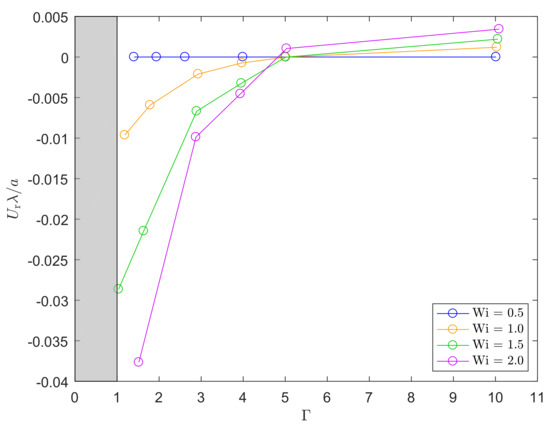
Figure 6.
Migration velocity of the particle at different positions from the inner cylinder without sedimentation and varying shear Weissenberg number at time . The shaded area indicates the inaccessible region.
This figure shows that the movement of the particle towards the inner cylinder speeds up with increasing shear Weissenberg number. For low values of Wi, the migration velocity is nearly zero, independent of the position of the particle. For particles close to the inner cylinder, the migration velocity is negative, indicating that the particle migrates towards the inner cylinder. For larger distances from the inner cylinder, the migration velocity is positive for high values of Wi, i.e., the particle seems to migrate away from the inner cylinder. Figure 7 shows the trace of the conformation tensor around the migrating particle with and no sedimentation, for an initial position and at time using . This figure shows that the presence of the inner cylinder causes the trace of the conformation to by asymmetric around the particle when the particle is placed close to it. The conformation is higher at the side of the particle close to the inner cylinder, indicating that the polymers are more stretched in the small gap between the particle and the inner cylinder.
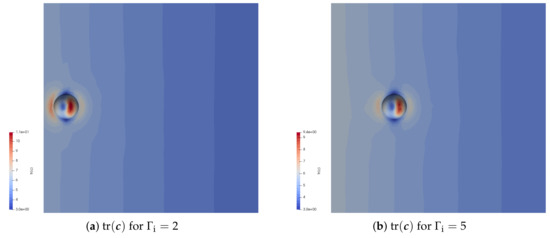
Figure 7.
The trace of the conformation tensor around the particle for different initial positions from the inner cylinder at time for and , using .
4.2.3. Migration of a Falling Particle in a Shear Flow
Now, the two complex flows are combined by first fixing the shear Weissenberg number () and varying the sedimentation Weissenberg number and vice versa. The results are shown in Figure 8.
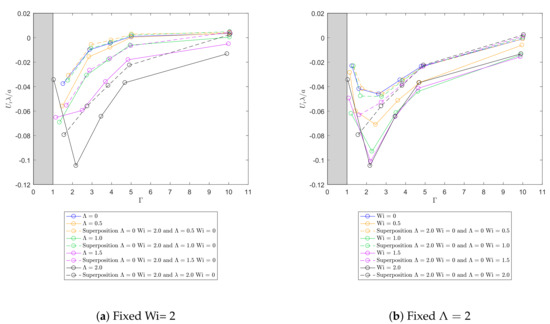
Figure 8.
Migration velocity of a particle placed at different initial positions from the inner cylinder with combined complex flows (solid lines) and the superposition of the two separate flows (dashed lines) at time . The shaded area indicates the inaccessible region.
Both figures show that when the particle approaches the inner cylinder , this slows down the movement of the particle towards it for high shear and sedimentation Weissenberg numbers. Here, the particle nearly touches the inner cylinder at , drastically reducing the mobility of the particle in the r-direction. Furthermore, it can be observed that combining the two complex flows (solid lines) leads to significantly larger migration velocities than the superposition of the migration velocities of the two separate flows (dashed lines). This effect was more pronounced for large values of both Weissenberg numbers, indicating that for large values of and high Wi, the coupling of the flows becomes non-linear, and therefore, the migration velocity for the combination of the two flows will no longer be a simple superposition of the migration velocities of the two separate flows.
Figure 9 shows the trace of the conformation tensor at time for initial particle positions and for and , using . This figure again shows that the trace of the conformation tensor is larger at the side of the particle close to the cylinder, when the particle approaches it. For the trace of the conformation tensor is symmetric and high at both sides of the particle due to the shear flow.
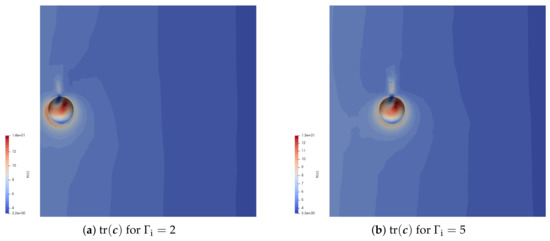
Figure 9.
The trace of the conformation tensor around the particle for different initial positions from the inner cylinder at time for and , using .
Contour plots of the migration velocities for the two flows combined are shown in Figure 10 for .
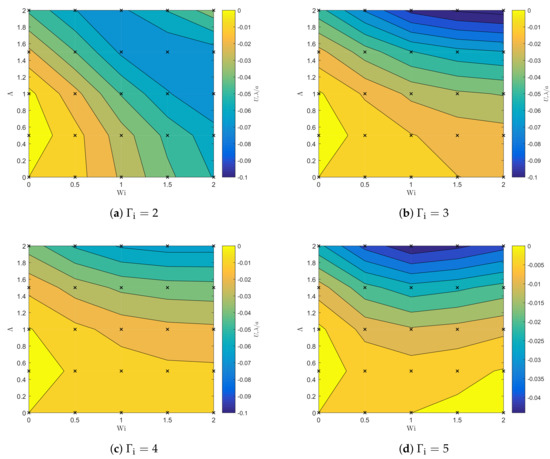
Figure 10.
Contour plots of the migration velocities for combined shear and sedimentation flows. Markers x indicate the data points; between these points, the data are interpolated using the MATLAB® function contourf.
These contour plots show, that it is possible to influence the migration velocity of a particle by combining shear and sedimentation flows and changing the shear and sedimentation Weissenberg numbers. Figure 10b for example shows that the migration velocity can be accelerated, when both Weissenberg numbers are high. The migration can be slowed down by lowering one, or both of these Weissenberg numbers.
4.3. Sedimentation
To investigate the influence of shear and sedimentation Weissenberg number on the sedimentation of a particle, the two complex flows are combined. The particle is now placed initially in the middle of the Couette flow device. Simulations are performed for two different sets of material parameters shown in Table 1. Here, Fluid 1 is used to mimic a Boger fluid with a large value for and small value for [24], so the effect of shear thinning can be excluded from the results. Fluid 2 has a much higher value for , meaning that the fluid is more shear thinning, and a slightly lower value for . These parameters are the same as for the migration simulations. The zero-shear viscosity is the same for both fluids.

Table 1.
Material parameters.
The sedimentation velocity for both fluids, scaled with the sedimentation velocity in a Newtonian fluid with viscosity , is plotted as a function of the shear Weissenberg number for different sedimentation Weissenberg numbers in Figure 11.
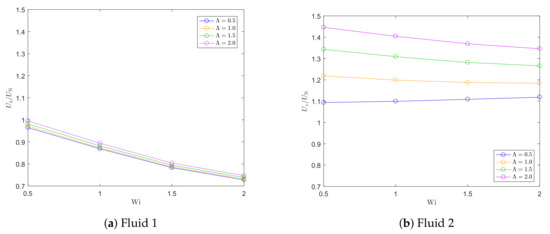
Figure 11.
Sedimentation velocity as a function of Wi for increasing for Fluid 1 and Fluid 2.
This figure shows that the sedimentation velocity is indeed decreasing with increasing shear Weissenberg number. This effect is much more pronounced in Fluid 1 than in Fluid 2. Furthermore, the sedimentation velocity is higher in Fluid 2 than in Fluid 1, and for small Wi, the sedimentation velocity is almost equal to the sedimentation velocity of a particle in a Newtonian fluid in Fluid 1, whereas it is higher than the Newtonian velocity in Fluid 2. This confirms that shear thinning is increasing the sedimentation velocity of a falling particle, also decreasing the effect of elasticity that causes the sedimentation velocity to decrease for higher Wi, as was also found in the literature [10,11]. The contour plots of the sedimentation velocity for both fluids are shown in Figure 12.
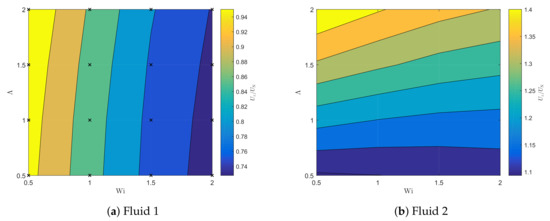
Figure 12.
Contour plots of the sedimentation velocity of Fluid 1 and Fluid 2. Markers x indicate the data points; between these points, the data are interpolated using the MATLAB® function contourf.
The contour plots also clearly show different behavior for the two fluids. For Fluid 1, the sedimentation velocity clearly decreases with increasing Wi, while for Fluid 2, the sedimentation velocity seems almost independent of Wi for small , whereas the effect of decreasing velocity for increasing Wi for higher is much less pronounced as for Fluid 1. For Fluid 2, the effect of increasing is also bigger than for Fluid 1.
5. Conclusions
A numerical model was developed in order to investigate numerically the influence of shear and sedimentation Weissenberg number on the migration and sedimentation of a particle in a Couette flow device. DEVSS-G and the log-conformation representation are used for numerical stability. To reduce computational costs, only a part of the Couette flow device is modeled. Periodic boundary conditions are applied at the symmetry planes, using vector and tensor rotations. We believe that this domain excludes the effect of particle–particle interactions. In order to reduce the amount of remeshing steps, the mesh moves as a rigid body with the particle in the - and z-direction, while it still deforms due to the movement of the particle in the r-direction. This is done using the ALE method.
The particle was initially placed at different positions close to the inner cylinder of the device. First, the influence of the two separate complex flows was investigated by either applying no velocity on the outer cylinder, and therefore , or applying no downward force on the particle, and therefore . The suspending fluid is a Giesekus fluid.
First, the migration velocity of a falling particle without applying a shear flow was studied. It was found that the migration velocity was almost zero when the particle was far away from the inner cylinder. When the particle approached the inner cylinder, the particle migrated towards it, and this migration velocity was increased by increasing . At a certain position, the particle got so close to the inner cylinder that the mobility of the particle in the r-direction was drastically decreased, decreasing the migration velocity. Secondly, the migration of a particle in a Couette flow, without sedimentation, was studied. Here, it was found that for small values of Wi, there was no migration. When Wi was increased, the particle started to migrate towards the inner cylinder when it was initially placed close to it. When the particle was initially positioned further away from the cylinder, the particle migrated away from it. When the two flows were combined, it was found that combining the two complex flows leads to a higher migration velocity than the sum of the migration velocities of the two separate flows. This effect was more pronounced for higher Weissenberg numbers, indicating that for high values of and Wi, the coupling of the two flows becomes non-linear. The trace of the conformation tensor was found to be asymmetric around the particle when the particle was in close proximity of the inner cylinder. The trace of the conformation is higher at the side of the particle close to the inner cylinder, indicating that the polymers are more stretched here.
To study the influence of shear and sedimentation Weissenberg number on the sedimentation of a particle, two different sets of material parameters were used, where Fluid 2 is much more shear thinning than Fluid 1 and fluid 1 has a large , mimicking a Boger fluid. It was confirmed that shear thinning increases the sedimentation velocity of the particle. Furthermore, it was found that the sedimentation velocity indeed decreases for increasing Wi in Fluid 1, whereas this effect was less pronounced for Fluid 2. For small values of , this effect was not seen at all for Fluid 2, indicating that shear thinning opposes the effect of elasticity.
Author Contributions
This study was a part of the graduation project of M.M.A.S. She was responsible for developing the computational model and for performing the simulations and data analysis. She was supervised by N.O.J., who also contributed to the interpretation of the results. N.O.J., M.A.H. and P.D.A. contributed to the critical revision of the article.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Periodic Boundary Condition Velocity
A schematic overview of the domain in 2D is shown in Figure A1. The domain is shown in 2D for clarity, because the velocity in the z-direction does not undergo a rotation. The z-component is now the vector pointing into the paper.
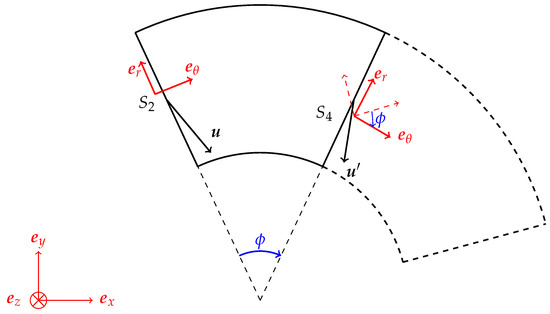
Figure A1.
Schematic overview of a 2D curve with periodic boundary conditions.
To obtain the velocity components on surface equal to the velocity components on , has to be rotated over a counterclockwise angle , since surface is rotated over an angle with respect to surface . The rotation of a vector can be performed by taking the dot product with a tensor , which rotates the vector in a constant coordinate system. After applying the rotation, the velocity on surface equals the velocity on . In a Cartesian coordinate system (, , ), the rotation is expressed as follows:
The same approach can be used to calculate the traction components on surfaces and , in order to obey the periodic boundary conditions.
Appendix B. Periodic Boundary Condition Conformation Tensor
Appendix B.1. Tensor Rotation
Periodic boundary conditions for the conformation tensor are needed on surfaces and , since only a part of the Couette flow device is modeled. This is done following the same principle as for the periodic boundary conditions for the velocity, only now a tensor rotation has to be performed instead of a vector rotation. The formula to rotate a tensor can be derived as follows:
The rotation of an arbitrary vector can be performed by taking the product of a tensor that performs a rotation with this vector. Now, the rotated vector of is obtained:
where is a tensor that performs a rotation in a constant coordinate system. Furthermore, the inner product of a rotated tensor with a rotated vector gives a rotated vector , and the same thing holds for the unrotated tensor and vectors:
If these equations are combined with Equation (A5), the following can be obtained:
Equation (A8) can be multiplied with , (), to obtain:
Appendix B.2. Conformation Tensor
Periodic boundary conditions for the conformation tensor are applied to surfaces and . This means that the components , , , , , , , , and on the inflow nodes of surfaces and have to be equal to the components , , , , , , , , and on the outflow nodes of surfaces and , but rotated. Since the surface is rotated over an angle compared to surface , the components of on the inflow nodes have to be rotated over the same angle . Using the result of Equation (A10), this gives the following equation for rotating the conformation tensor :
Since, , , and , it can be concluded that the conformation tensor is symmetric.
References
- Kim, Y.; Yoo, J. Three-dimensional focusing of red blood cells in microchannel flows for bio-sensing applications. Biosens. Bioelectron. 2009, 24, 3677–3682. [Google Scholar] [CrossRef] [PubMed]
- Economides, M.; Nolte, K. Reservoir Stimulation; Prentice Hall: Hoboken, NJ, USA, 1989. [Google Scholar]
- Singh, P.; Joseph, D. Sedimentation of a sphere near a vertical wall in an Oldroyd-B fluid. J. Non-Newton. Fluid Mech. 2000, 94, 179–203. [Google Scholar] [CrossRef]
- D’Avino, G.; Tuccillo, T.; Maffettone, P.; Greco, F.; Hulsen, M. Numerical simulations of particle migration in a viscoelastic fluid subjected to shear flow. Comput. Fluids 2010, 39, 709–721. [Google Scholar] [CrossRef]
- D’Avino, G.; Snijkers, F.; Pasquino, R.; Hulsen, M.; Greco, F.; Maffettone, P.; Vermant, J. Migration of a sphere suspended in viscoelastic liquids in Couette flow: Experiments and simulations. Rheol. Acta 2012, 51, 215–234. [Google Scholar] [CrossRef]
- Chilcott, M.; Rallison, J. Creeping flow of dilute polymer solutions past cylinders and spheres. J. Non-Newton. Fluid Mech. 1988, 29, 381–432. [Google Scholar] [CrossRef]
- Harlen, O.; Rallison, J.; Chilcott, M. High-Deborah-number flows of dilute polymer solutions. J. Non-Newton. Fluid Mech. 1990, 34, 319–349. [Google Scholar] [CrossRef]
- Arigo, M.; Rajagopalan, D.; Shapley, N.; McKinley, G. The sedimentation of a sphere through an elastic fluid. Part 1. Steady motion. J. Non-Newton. Fluid Mech. 1995, 60, 225–27. [Google Scholar] [CrossRef]
- D’Avino, G.; Maffettone, P. Particle dynamics in viscoelastic liquids. J. Non-Newton. Fluid Mech. 2015, 215, 80–104. [Google Scholar] [CrossRef]
- Van den Brule, B.; Gheissary, G. Effects of fluid elasticity on the static and dynamic settling of a spherical particle. J. Non-Newton. Fluid Mech. 1993, 49, 123–132. [Google Scholar] [CrossRef]
- Padhy, S.; Rodriguez, M.; Shaqfeh, E.; Iaccarino, G.; Morris, J.; Tonmakayakul, N. The effect of shear thinning and walls on the sedimentation of a sphere in an elastic fluid under orthogonal shear. J. Non-Newton. Fluid Mech. 2013, 201, 120–129. [Google Scholar] [CrossRef]
- Padhy, S.; Shaqfeh, E.; Iaccarino, G.; Morris, J.; Tonmakayakul, N. Simulations of a sphere sedimenting in a viscoelastic fluid with cross shear flow. J. Non-Newton. Fluid Mech. 2013, 197, 48–60. [Google Scholar] [CrossRef]
- Murch, W.; Krishnan, S.; Shaqfeh, E.; Iaccarino, G. Growth of viscoelastic wings and the reduction of particle mobility in a viscoelastic shear flow. Phys. Rev. Fluids 2017, 2, 103302. [Google Scholar] [CrossRef]
- Giesekus, H. A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J. Non-Newton. Fluid Mech. 1982, 11, 69–109. [Google Scholar] [CrossRef]
- Hu, H.; Patankar, N.; Zhu, M. Direct numerical simulations of fluid-solid systems using the arbitrary Lagrangian-Eulerian technique. J. Comput. Phys. 2001, 169, 427–462. [Google Scholar] [CrossRef]
- Hulsen, M.; Fattal, R.; Kupferman, R. Flow of viscoelastic fluids past a cylinder at high Weissenberg number: Stabilized simulations using matrix logarithms. J. Non-Newton. Fluid Mech. 2005, 127, 27–39. [Google Scholar] [CrossRef]
- Bogaerds, A.; Grillet, A.; Peters, G.; Baaijens, F. Stability analysis of polymer shear flows using the extended pom-pom constitutive equations. J. Non-Newton. Fluid Mech. 2002, 108, 187–208. [Google Scholar] [CrossRef]
- Glowinski, R.; Pan, T.; Hesla, T.; Joseph, D. A distributed Lagrange multiplier/fictitious domain method for particulate flows. Int. J. Multiph. Flow 1999, 25, 755–794. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J. Gmsh: A 3D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1–24. [Google Scholar] [CrossRef]
- Jaensson, N.; Hulsen, M.; Anderson, P. Stokes-Cahn-Hilliard formulations and simulations of two-phase flows with suspended rigid particles. Comput. Fluids 2015, 111, 1–17. [Google Scholar] [CrossRef]
- Van der Zanden, J.; Hulsen, M. Mathematical and physical requirements for successful computations with viscoelastic fluid models. J. Non-Newton. Fluid Mech. 1988, 29, 93–117. [Google Scholar] [CrossRef]
- Renardy, M. Inflow boundary conditions for steady flows of viscoelastic fluids with differential constitutive laws. J. Non-Newton. Fluid Mech. 1988, 18, 445–454. [Google Scholar]
- D’Avino, G.; Hulsen, M. Decoupled second-order transient schemes for the flow of viscoelastic fluids without a viscous solvent contribution. J. Non-Newton. Fluid Mech. 2010, 165, 1602–1612. [Google Scholar] [CrossRef]
- Snijkers, F.; D’Avino, G.; Maffettone, P.; Greco, F.; Hulsen, M.; Vermant, J. Effect of viscoelasticity on the rotation of a sphere in shear flow. J. Non-Newton. Fluid Mech. 2011, 166, 363–372. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).