DEM/CFD Simulations of a Pseudo-2D Fluidized Bed: Comparison with Experiments
Abstract
:1. Introduction
2. Modeling Strategy
2.1. Gas Phase Modeling
2.2. Discrete Particle Modeling
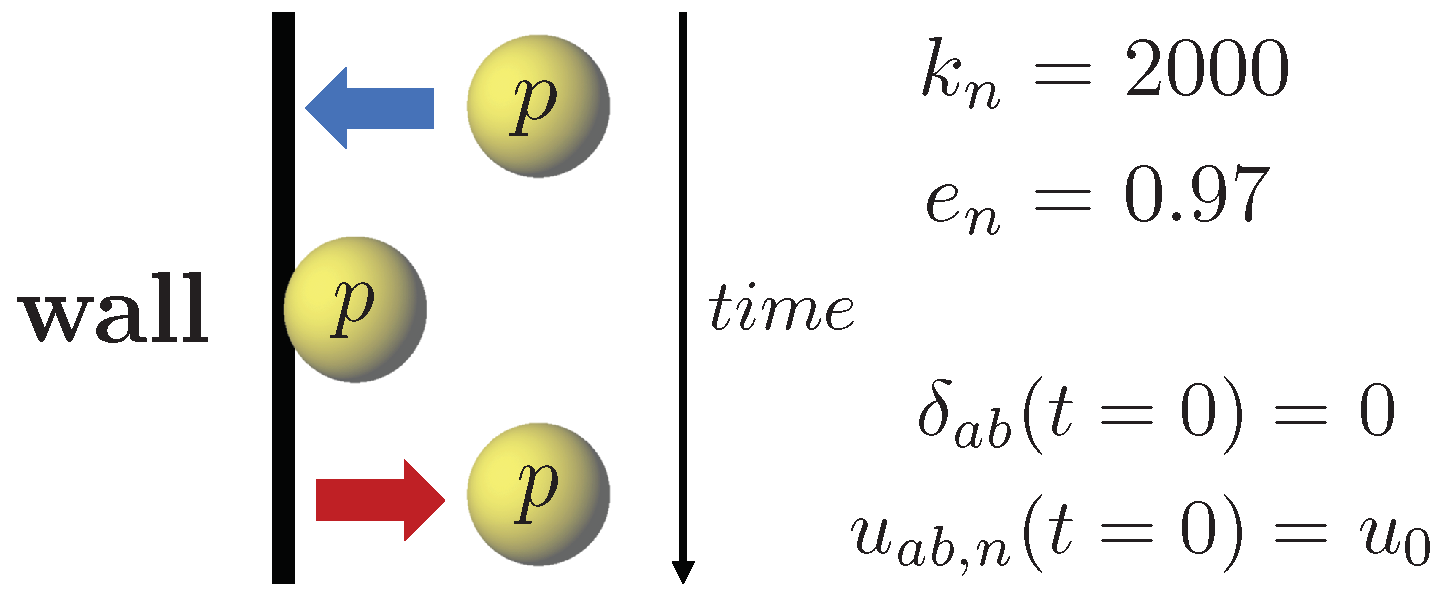
2.2.1. Modeling of Collisions
2.2.2. Closure for Drag
2.2.3. Other Forces
2.3. Phase Coupling
2.4. Numerical Schemes
2.4.1. Fluid Advancement Procedure
- Lagrangian phase advancementFirst, the particles are advanced. The full description of this step is available in Section 2.4.2. After being relocated on the grid, can be computed using Equation (30).
- Density prediction for scalar advancementThe density predictor is then determined by the mean of the mass conservation equation (Equation (3)):
- Velocity predictionOnce is known, the velocity can be predicted reusing the dynamic pressure gradient of the previous time step:
- Velocity correctionVelocity correction is performed by updating the pressure gradient:The Poisson equation aiming at calculating is obtained by taking the divergence of Equation (37) and inserting the condition imposed by the following equation of mass conservation written for :The Poisson equation finally reads:This linear system requires an efficient and accurate iterative solver. For all our simulations, a Deflated Preconditioned Conjugate Gradient (DPCG) algorithm [23] is used.
2.4.2. Particle Advancement Procedure
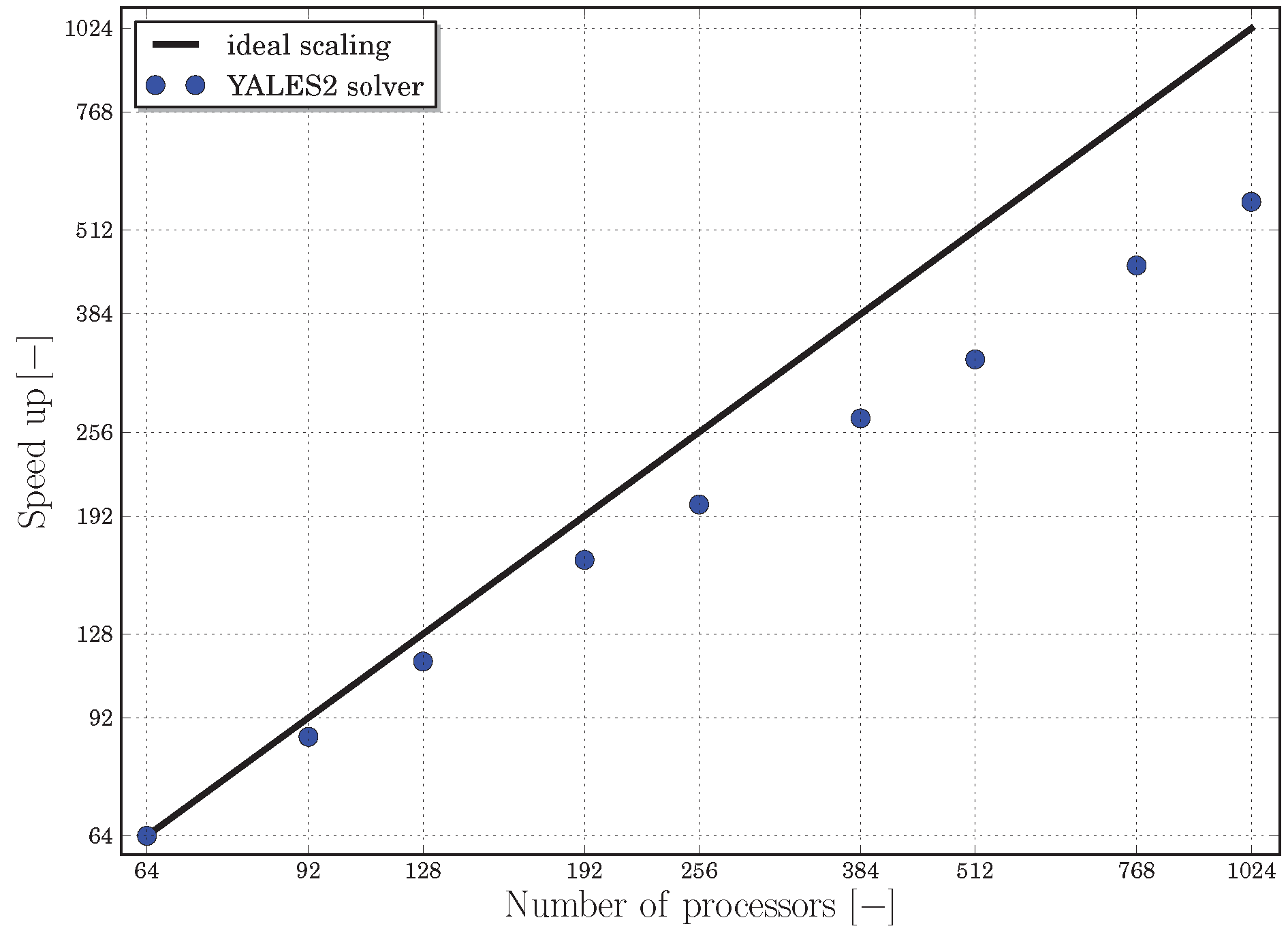
2.5. Performances and Parallelism
2.6. Assessment of the Solver Performances
3. Simulation Cases
3.1. Configuration and Meshes
3.2. Description of the Simulation Cases
4. Results
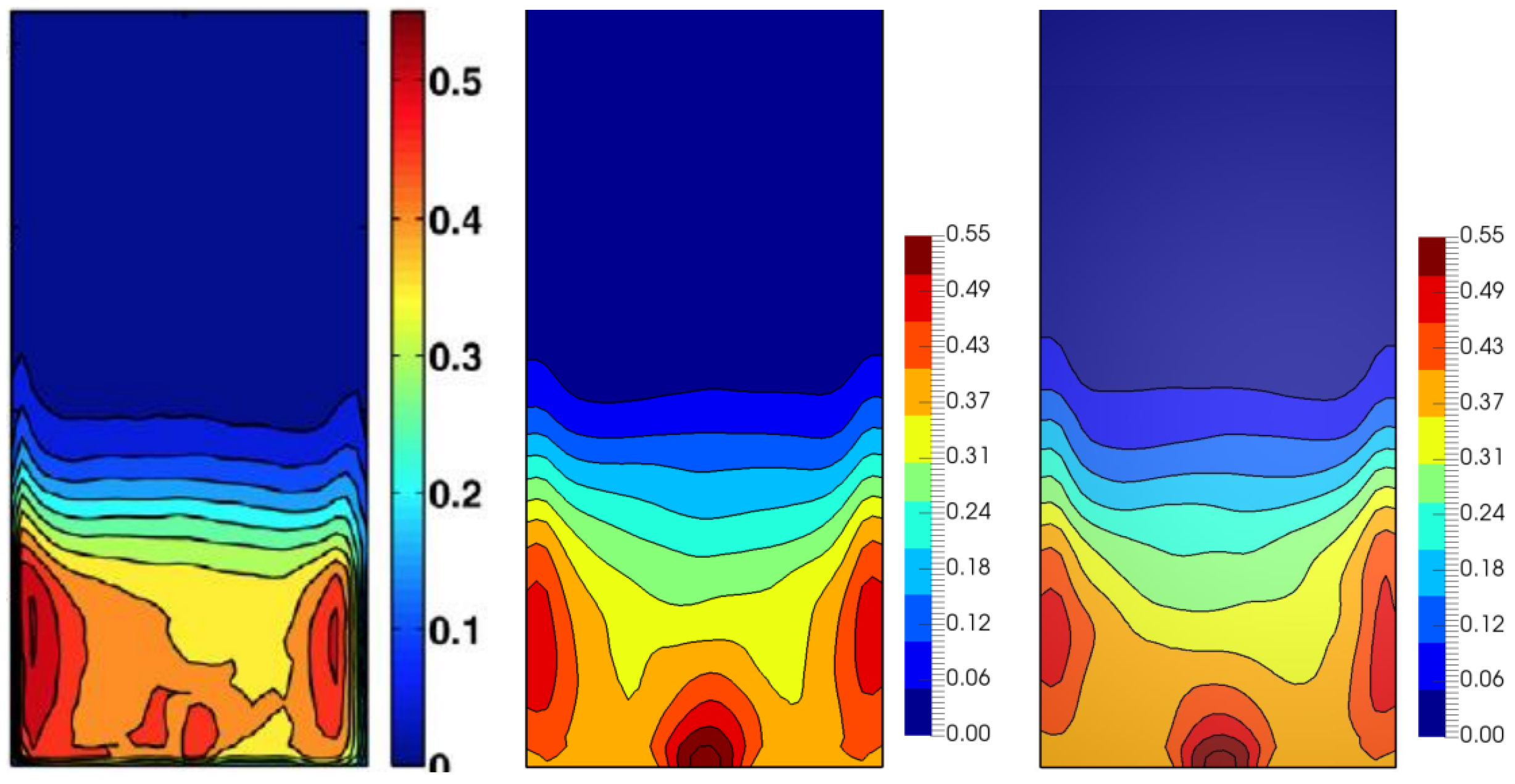
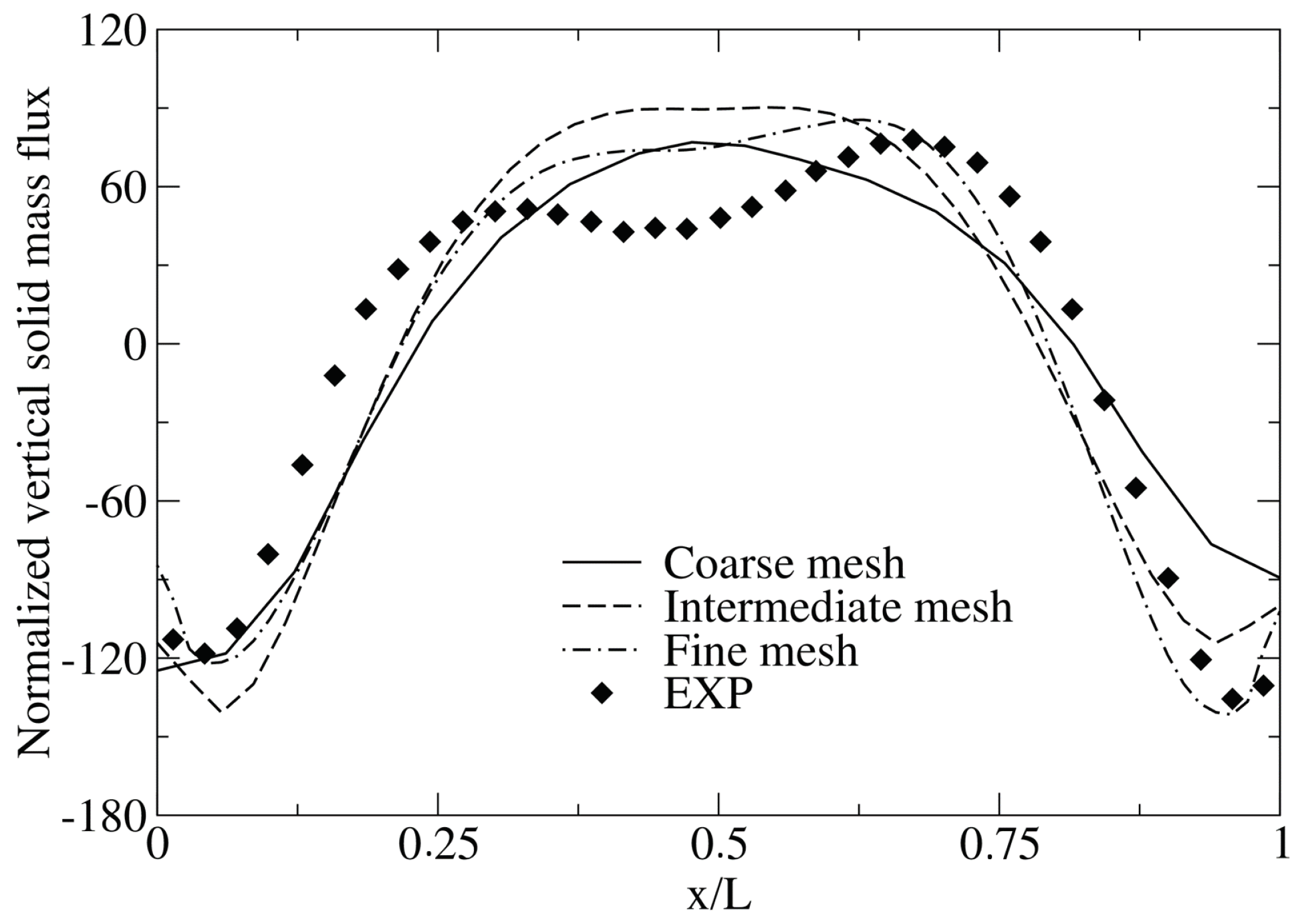
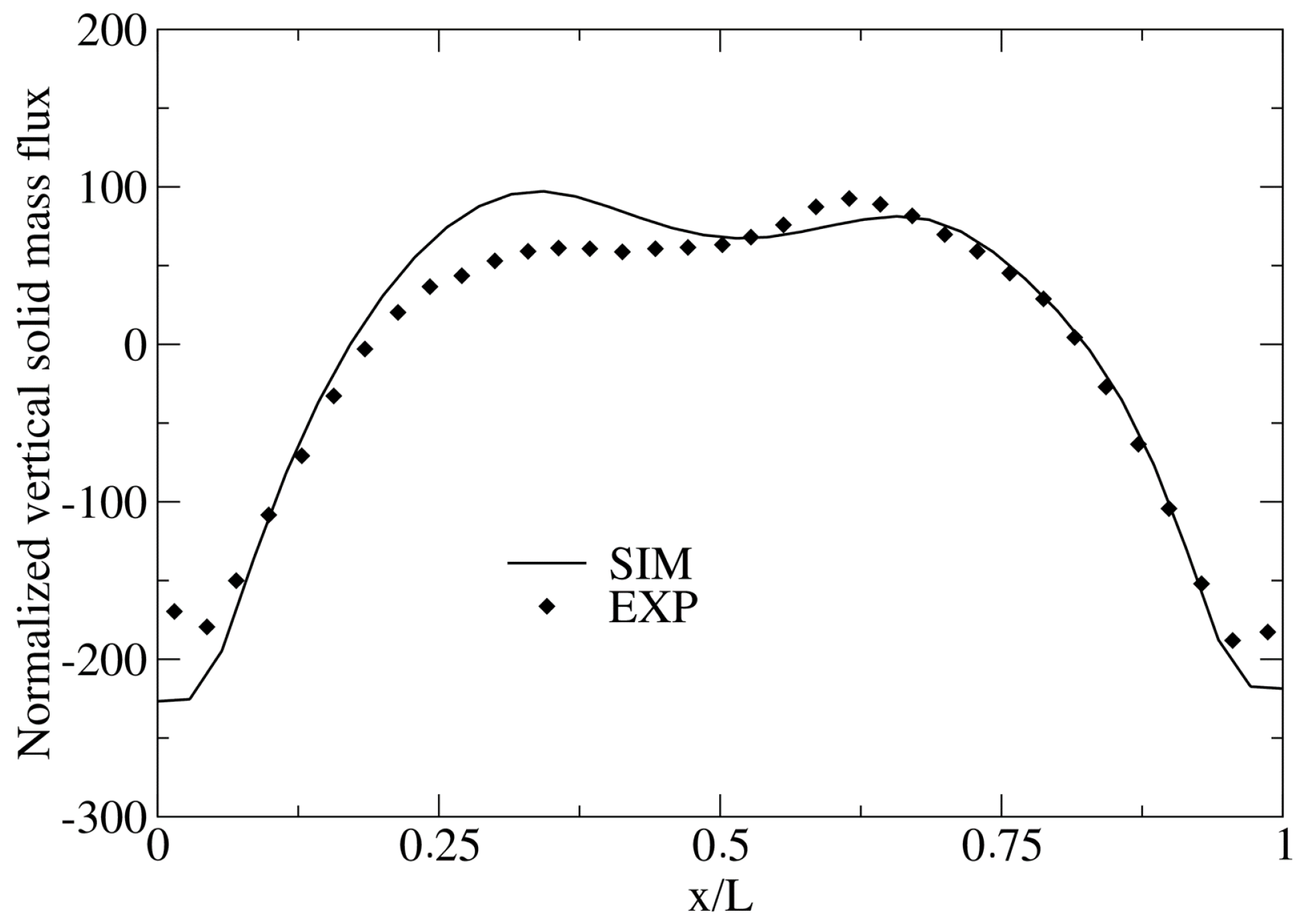
4.1. Effect of the Grid Refinement
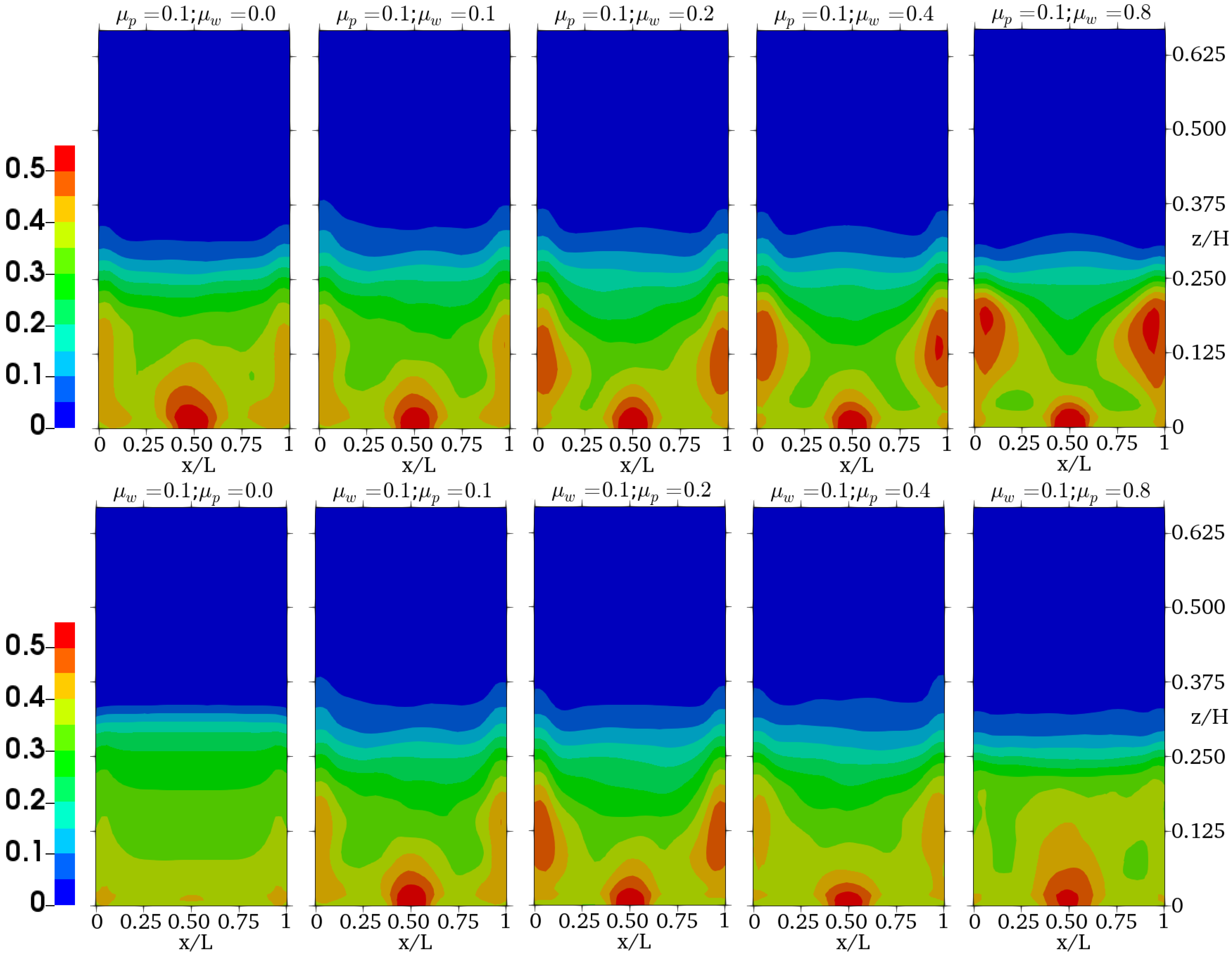
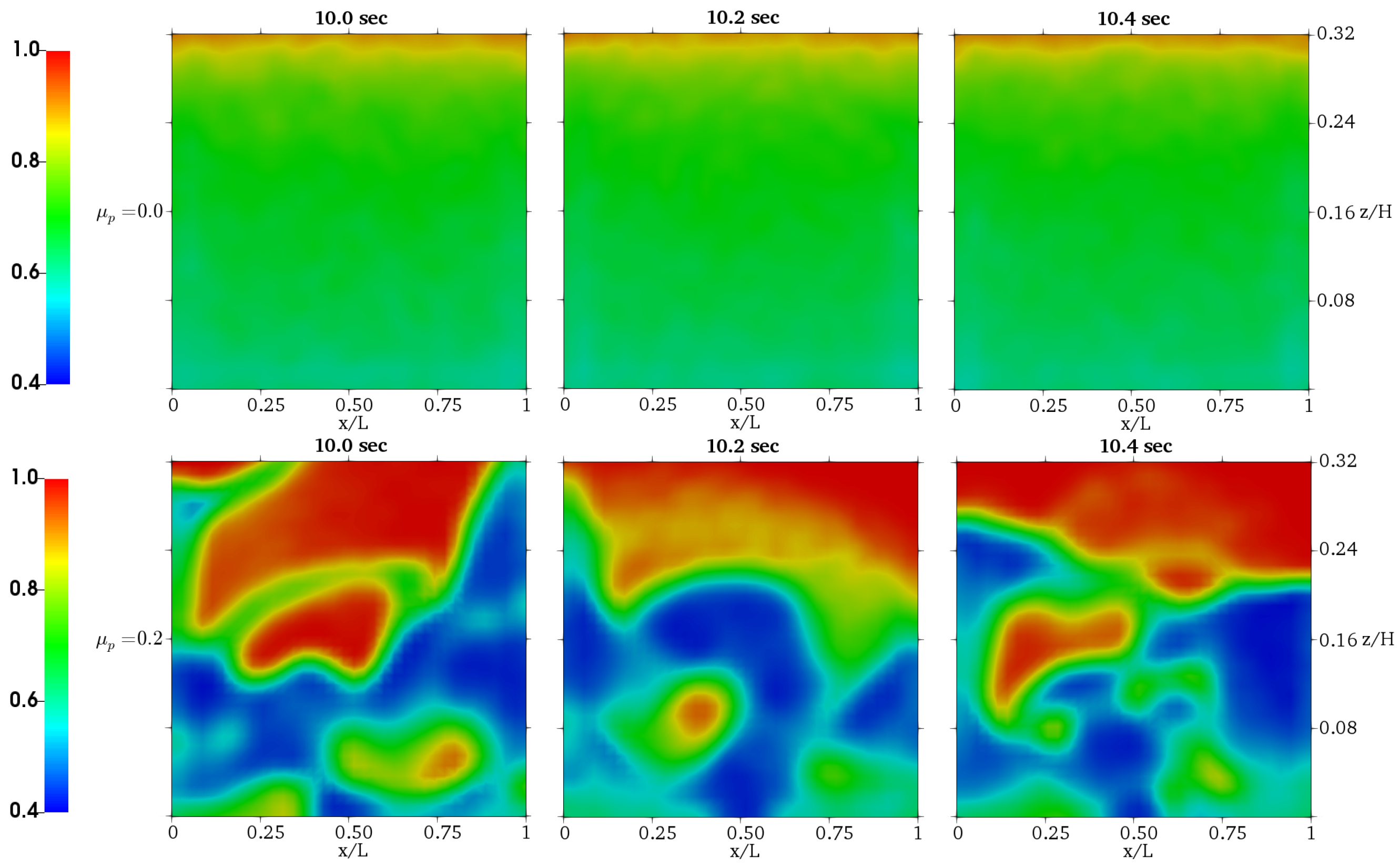
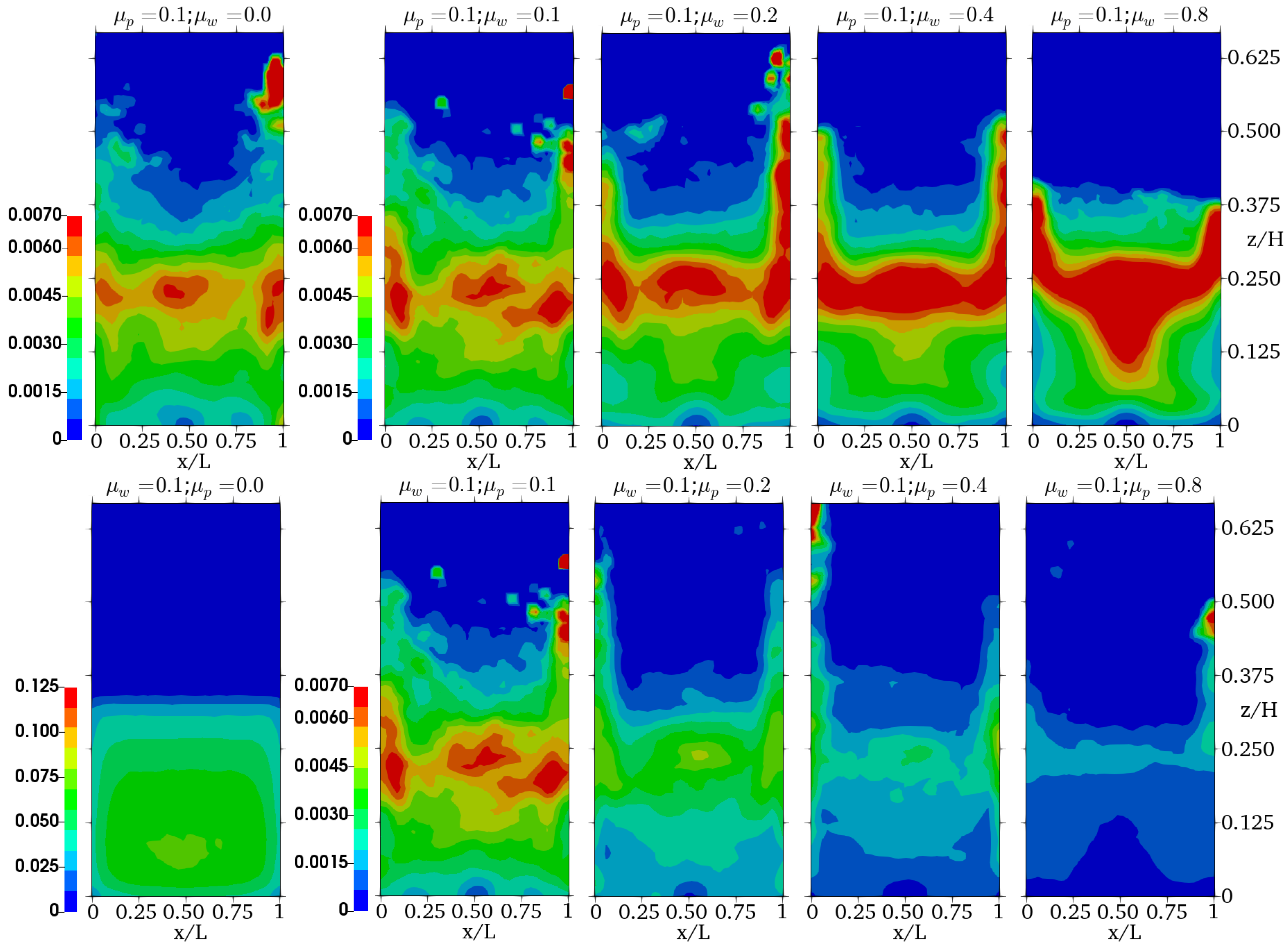
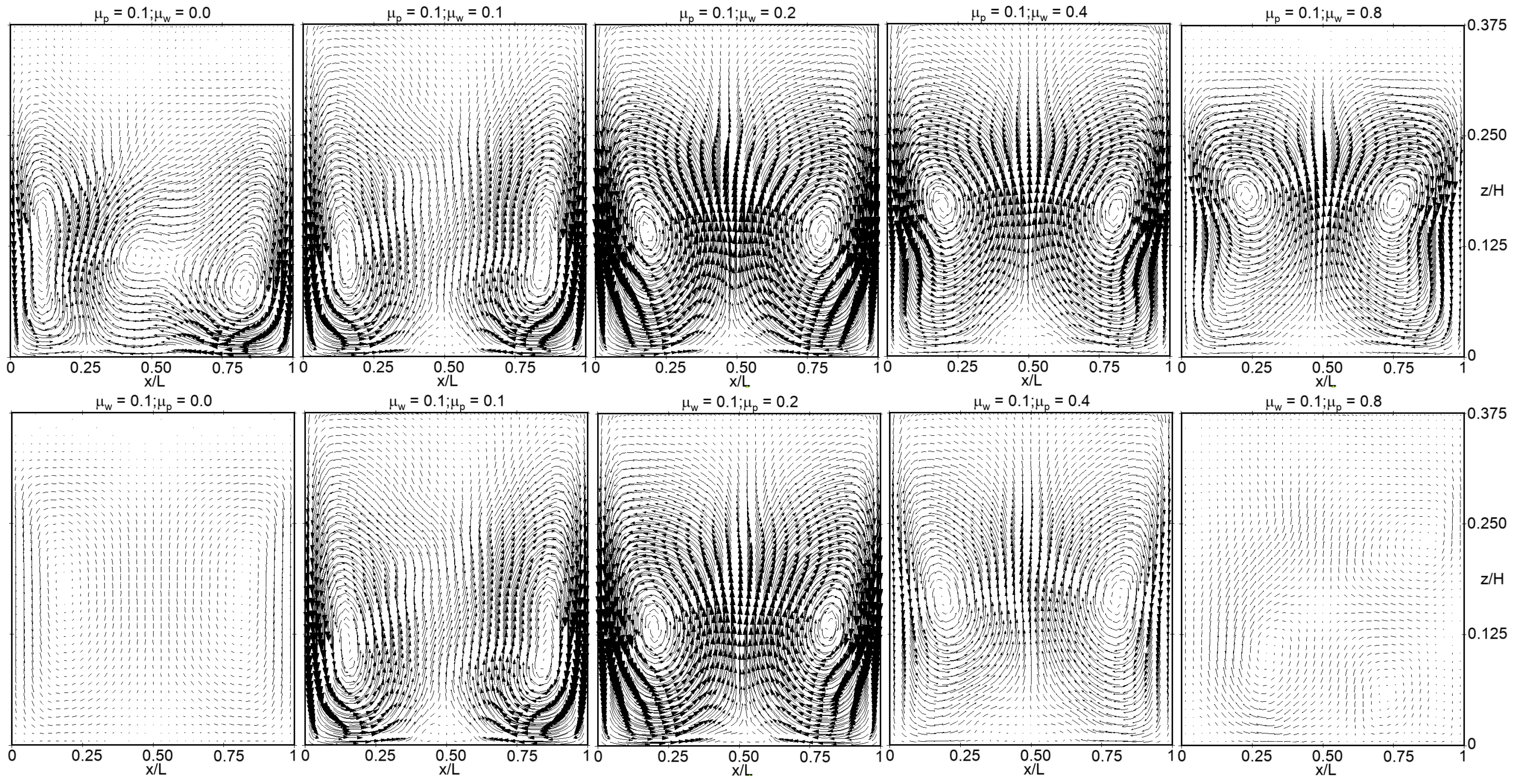
4.2. Investigation of the Frictional Effects
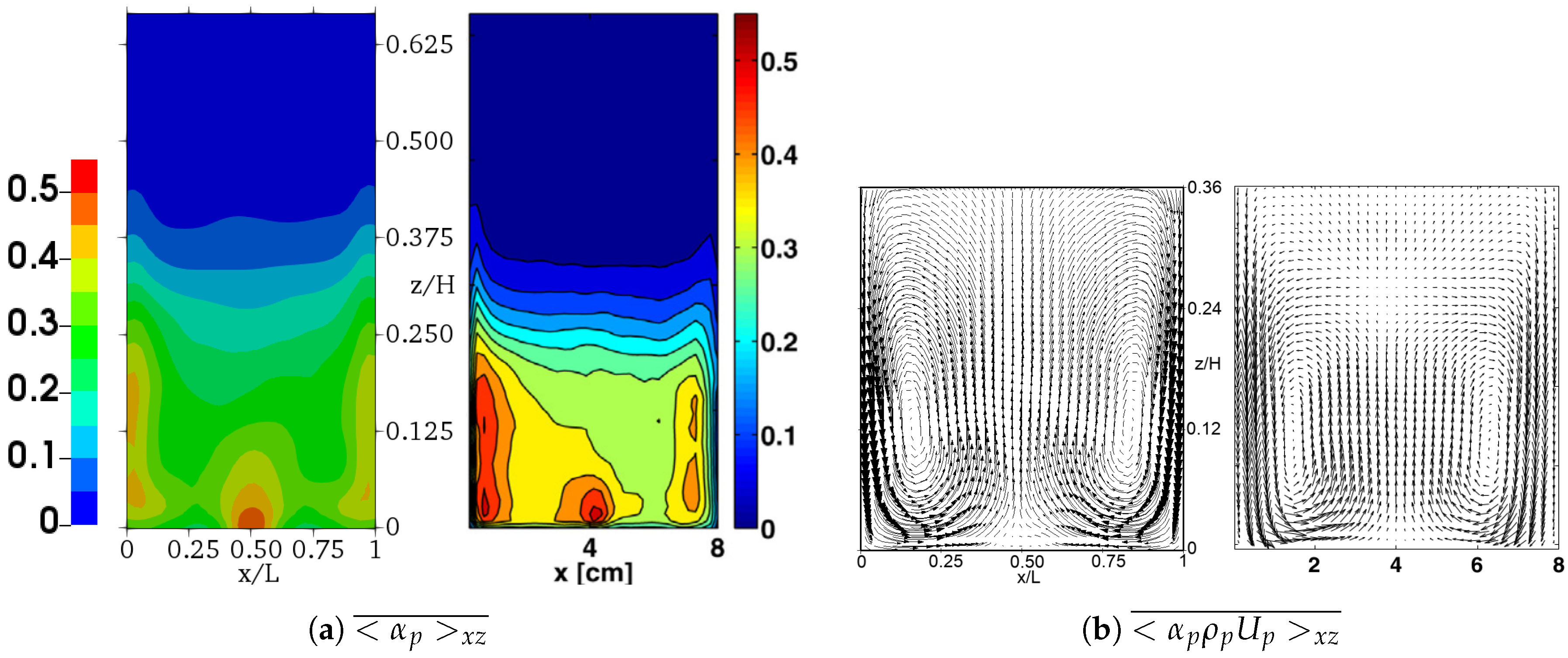
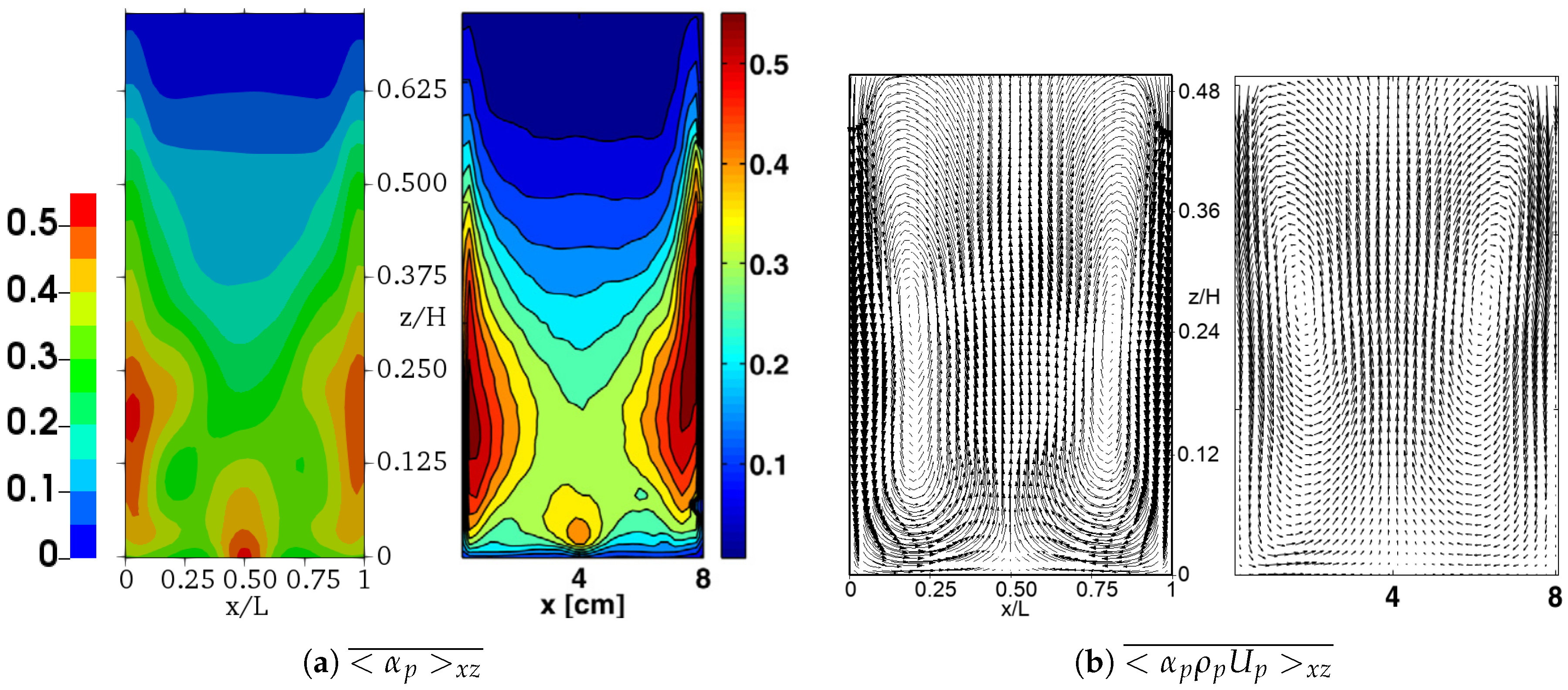
4.3. Application of the Results to Other Physical Configurations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFL | Courant-Friedrichs-Lewy |
| DEM | Discrete Element Method |
| DPCG | Deflated Preconditioned Conjugate Gradient |
| DPM | Discrete Particle Model |
| DNS | Direct Numerical Simulation |
| LES | Large-Eddy Simulation |
| MPI | Message Passing Interface |
| PCM | Particle Centroid Method |
| RK | Runge–Kutta |
| SC | Surrounding Cell |
| TFM | Two Fluid Model |
| BN | Blue Nodes |
| GN | Green Nodes |
| RN | Red Nodes |
Appendix A. Influence of LES Model on the Numerical Results
References
- Tenneti, S.; Subramaniam, S. Particle-resolved direct numerical simulation for gas-solid flow model development. Annu. Rev. Fluid Mech. 2014, 46, 199–230. [Google Scholar] [CrossRef]
- Pepiot, P.; Desjardins, O. Numerical analysis of the dynamics of two-and three-dimensional fluidized bed reactors using an Euler–Lagrange approach. Powder Technol. 2012, 220, 104–121. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Cleary, P.W. Industrial particle flow modelling using discrete element method. Eng. Comput. 2009, 26, 698–743. [Google Scholar] [CrossRef]
- Deen, N.G.; Annaland, M.V.S.; Van der Hoef, M.A.; Kuipers, J.A.M. Review of discrete particle modeling of fluidized beds. Chem. Eng. Sci. 2007, 62, 28–44. [Google Scholar] [CrossRef]
- Sundaresan, S. Reflections on mathematical models and simulation of gas-particle flows. In Proceedings of the 10th International Conference on Circulating Fluidized Beds and Fluidization Technology; Knowlton, T., PSRI, Eds.; ECI Symposium Series; Princeton University: Princeton, NJ, USA, 2011. [Google Scholar]
- Jackson, R. The Dynamics of Fluidized Particles; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Capecelatro, J.; Desjardins, O. An Euler–Lagrange strategy for simulating particle-laden flows. J. Comput. Phys. 2013, 238, 1–31. [Google Scholar] [CrossRef]
- Moureau, V.; Domingo, P.; Vervisch, L. Design of a massively parallel CFD code for complex geometries. C. R. Mécanique 2011, 339, 141–148. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Pierce, C.D.; Moin, P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 2004, 504, 73–97. [Google Scholar] [CrossRef]
- Moureau, V.; Domingo, P.; Vervisch, L. From large-eddy simulation to direct numerical simulation of a lean premixed swirl flame: Filtered laminar flame-pdf modeling. Combust. Flame 2011, 158, 1340–1357. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Columns. J. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Wen, C.Y.; Yu, Y.H. A generalized method for predicting the minimum fluidization velocity. AlChE J. 1966, 12, 610–612. [Google Scholar] [CrossRef]
- Huilin, L.; Gidaspow, D. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures. Chem. Eng. Sci. 2003, 58, 3777–3792. [Google Scholar] [CrossRef]
- Sun, R.; Xiao, H. Diffusion-based coarse graining in hybrid continuum–discrete solvers: Applications in CFD-DEM. Int. J. Multiph. Flow 2015, 72, 233–247. [Google Scholar] [CrossRef]
- Mendez, S.; Gibaud, E.; Nicoud, F. An unstructured solver for simulations of deformable particles in flows at arbitrary Reynolds numbers. J. Comput. Phys. 2014, 256, 465–483. [Google Scholar] [CrossRef]
- Kraushaar, M. Application of the Compressible and Low-Mach Number Approaches to Large-Eddy Simulation of Turbulent Flows in Aero-Engines. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulouse, France, 2011. [Google Scholar]
- Van der Vorst, H.A. Parallel iterative solution methods for linear systems arising from discretized pde’s. In Special Course on Parallel Computing in CFD; France Workshop Lecture Notes; 1995; Available online: https://www.semanticscholar.org/paper/Parallel-Iterative-Solution-Methods-for-Linear-from-Vorst/907dfb316057751b85e8620cf02d4fecb9ed731d (accessed on 12 February 2019).
- Van der Hoef, M.A.; Ye, M.; van Sint Annaland, M.; Andrews, A.T.; Sundaresan, S.; Kuipers, J.A.M. Multiscale modeling of gas-fluidized beds. Adv. Chem. Eng. 2006, 31, 65–149. [Google Scholar]
- Lubachevsky, B.D. How to simulate billiards and similar systems. J. Comput. Phys. 1991, 94, 255–283. [Google Scholar] [CrossRef]
- Fede, P.; Moula, G.; Ingram, A.; Dumas, T.; Simonin, O. 3D Numerical simulation and PEPT experimental investigation of pressurized gas-solid fluidized bed hydrodynamic. Presented at the ASME 2009 Fluids Engineering Division Summer Meeting, Vail, CO, USA, 2–6 August 2009. [Google Scholar]
- Patil, A.V.; Peters, E.A.J.F.; Kuipers, J.A.M. Comparison of CFD-DEM heat transfer simulations with infrared/visual measurements. Chem. Eng. J. 2015, 277, 388–401. [Google Scholar] [CrossRef]
- Lorenz, A.; Tuozzolo, C.; Louge, M.Y. Measurements of impact properties of small, nearly spherical particles. Exp. Mech. 1997, 37, 292–298. [Google Scholar] [CrossRef]
- Goldschmidt, M.J.V.; Beetstra, R.; Kuipers, J.A.M. Hydrodynamic modelling of dense gas-fluidised beds: Comparison and validation of 3D discrete particle and continuum models. Powder Technol. 2004, 142, 23–47. [Google Scholar] [CrossRef]
- Gorham, D.A.; Kharaz, A.H. Results of particle impact tests. In Impact Research Group Report IRG 13; The Open University: Milton Keynes, UK, 1999. [Google Scholar]
- Yang, L.; Padding, J.J.; Kuipers, J.H. Investigation of collisional parameters for rough spheres in fluidized beds. Powder Technol. 2017, 316, 256–264. [Google Scholar] [CrossRef]
- Hoomans, B.P.B.; Kuipers, J.A.M.; Briels, W.J.; van Swaaij, W.P.M. Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidised bed: A hard-sphere approach. Chem. Eng. Sci. 1996, 51, 99–118. [Google Scholar] [CrossRef]
- Li, T.; Gopalakrishnan, P.; Garg, R.; Shahnam, M. CFD–DEM study of effect of bed thickness for bubbling fluidized beds. Particuology 2012, 10, 532–541. [Google Scholar] [CrossRef]
- Ishibashi, I.; Perry, C., III; Agarwal, T.K. Experimental determination of contact friction for spherical glass particles. Soils Found. 1994, 34, 79–84. [Google Scholar] [CrossRef]
- Sandeep, C.S.; Senetakis, K. Effect of Young’s modulus and surface roughness on the inter-particle friction of granular materials. Materials 2018, 11, 217. [Google Scholar] [CrossRef]
 ) moving towards a neighboring cell (
) moving towards a neighboring cell (  ).
).  : mesh nodes.
: mesh nodes.  : contour of node 3 control volume. : interpolation weight of particle p on node i.
: contour of node 3 control volume. : interpolation weight of particle p on node i.
 ) moving towards a neighboring cell (
) moving towards a neighboring cell (  ).
).  : mesh nodes.
: mesh nodes.  : contour of node 3 control volume. : interpolation weight of particle p on node i.
: contour of node 3 control volume. : interpolation weight of particle p on node i.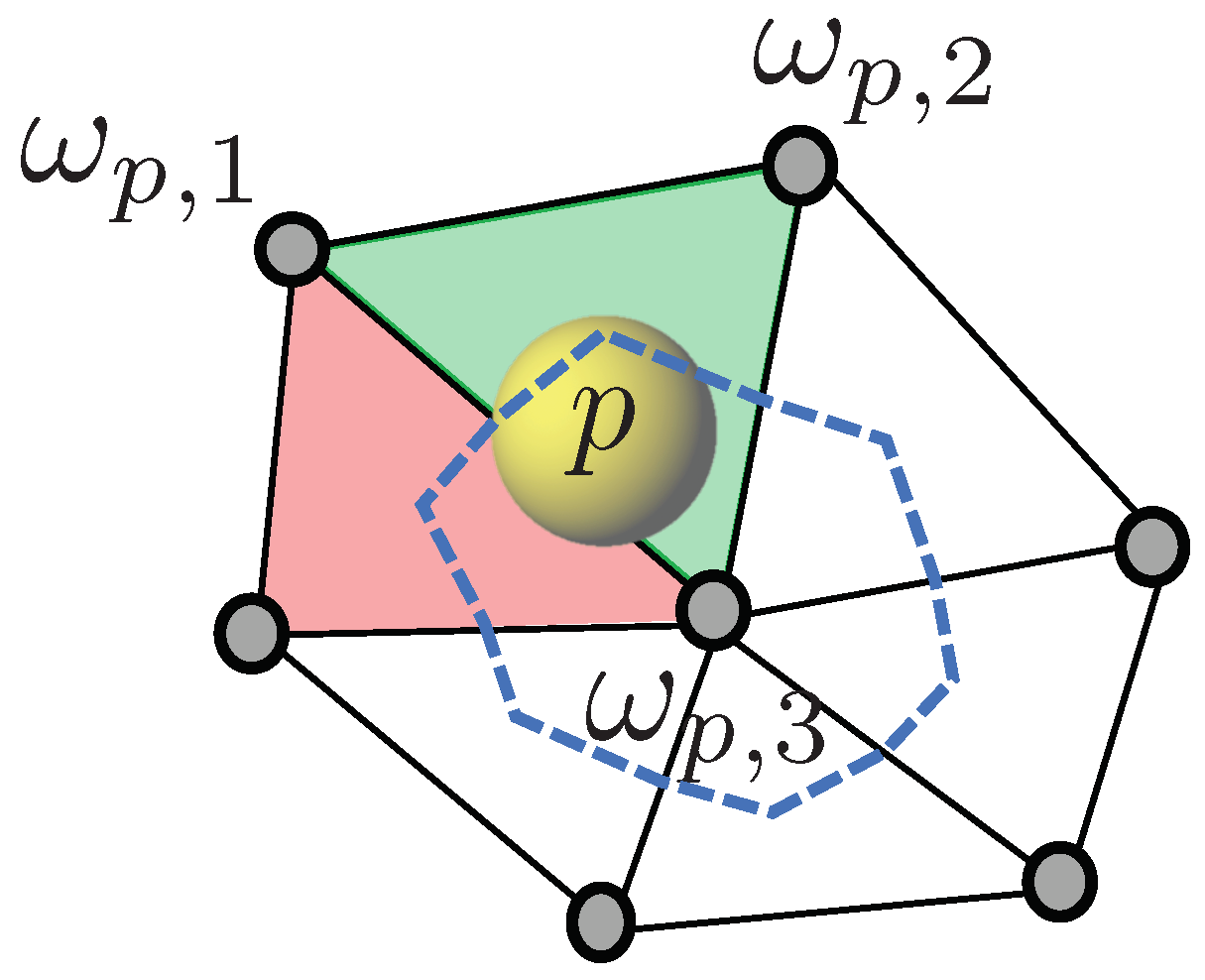
 : mesh nodes. The control volumes of nodes (
: mesh nodes. The control volumes of nodes (  ), (
), (  ), (
), (  ), (
), (  ), (
), (  ), (
), (  ), (
), (  ) are shown. The control volume of node is composed of surfaces , , , , and . On the right: 3D representation of a regular Cartesian mesh part.
) are shown. The control volume of node is composed of surfaces , , , , and . On the right: 3D representation of a regular Cartesian mesh part.  : node .
: node .  : nodes at faces’ center.
: nodes at faces’ center.  : nodes at edges’ center.
: nodes at edges’ center.  : nodes at corners.
: nodes at corners.
 : mesh nodes. The control volumes of nodes (
: mesh nodes. The control volumes of nodes (  ), (
), (  ), (
), (  ), (
), (  ), (
), (  ), (
), (  ), (
), (  ) are shown. The control volume of node is composed of surfaces , , , , and . On the right: 3D representation of a regular Cartesian mesh part.
) are shown. The control volume of node is composed of surfaces , , , , and . On the right: 3D representation of a regular Cartesian mesh part.  : node .
: node .  : nodes at faces’ center.
: nodes at faces’ center.  : nodes at edges’ center.
: nodes at edges’ center.  : nodes at corners.
: nodes at corners.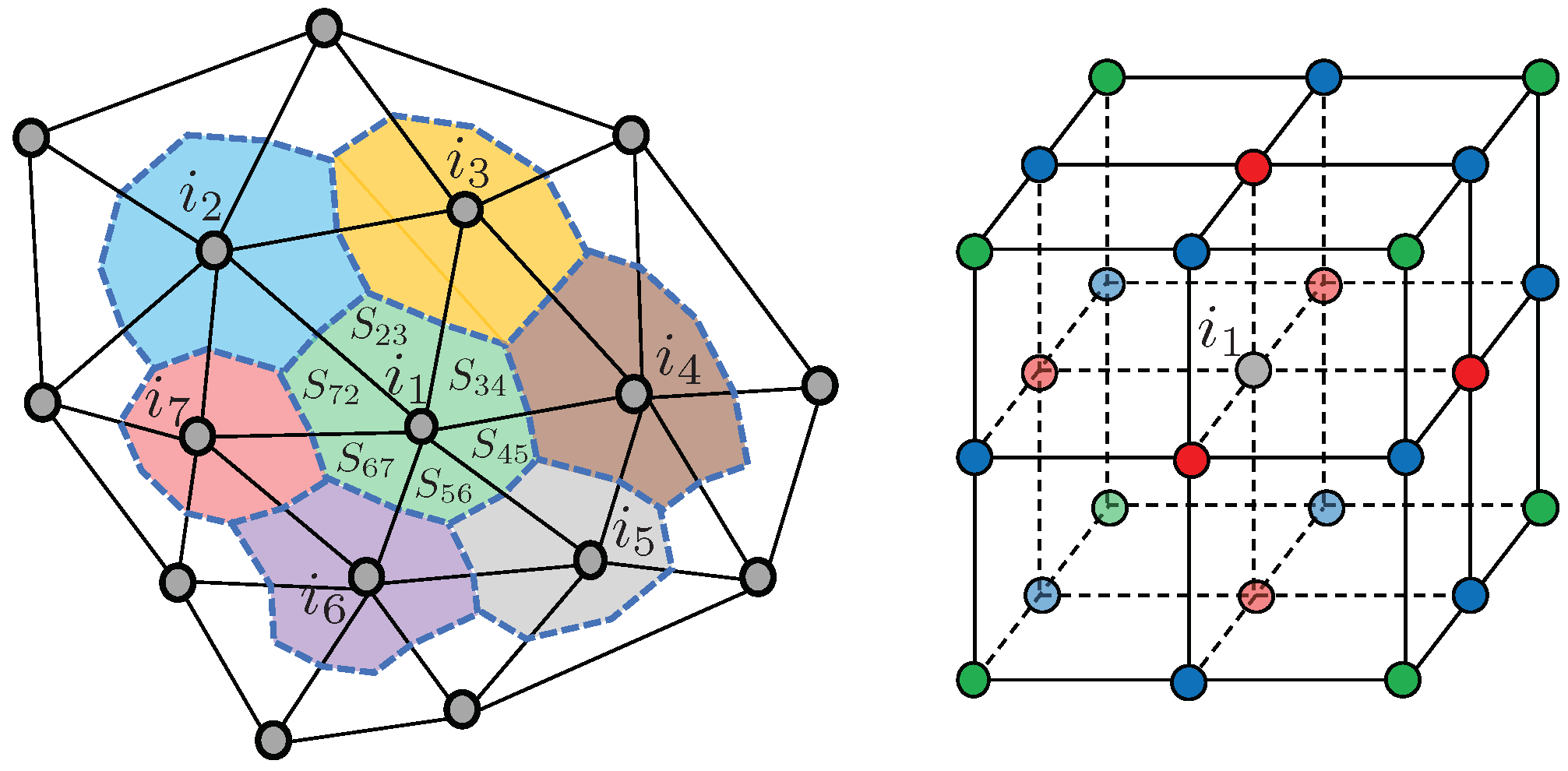
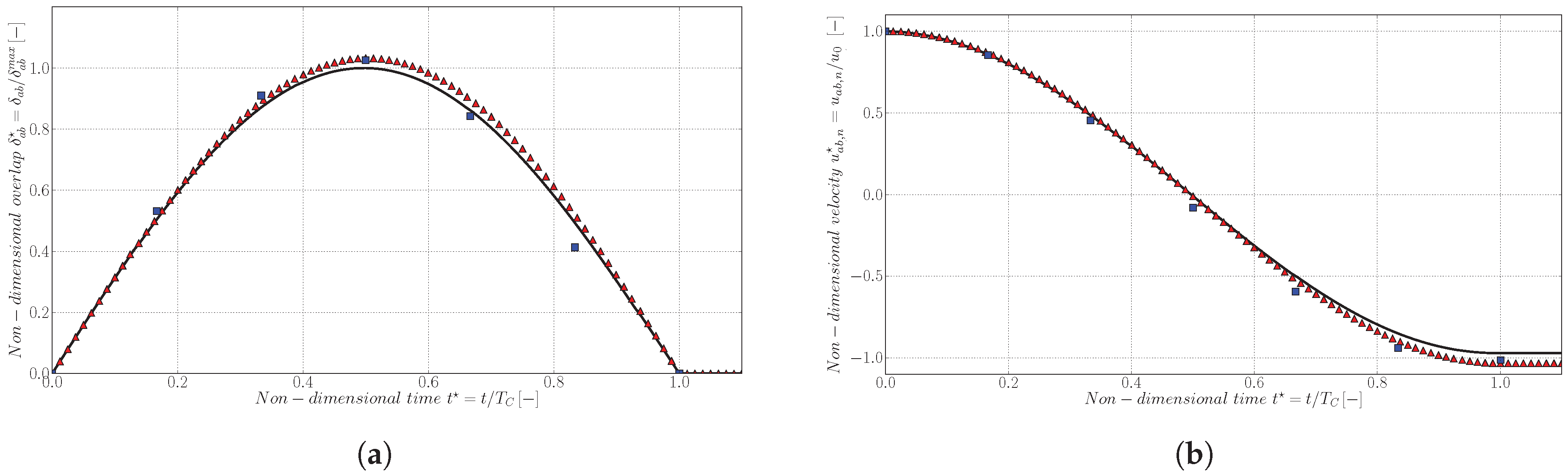
 ), Euler method with (
), Euler method with (  ) and RK2 method with (
) and RK2 method with (  ).
).
 ), Euler method with (
), Euler method with (  ) and RK2 method with (
) and RK2 method with (  ).
).
 : mesh nodes.
: mesh nodes.  : superimposed Cartesian grid. The particle of interest is noted p in the central cell (
: superimposed Cartesian grid. The particle of interest is noted p in the central cell (  ). The particles of which center belongs to this cell or one of the surrounding ones (
). The particles of which center belongs to this cell or one of the surrounding ones (  ) are stored as potential collision partners of particle p.
) are stored as potential collision partners of particle p.
 : mesh nodes.
: mesh nodes.  : superimposed Cartesian grid. The particle of interest is noted p in the central cell (
: superimposed Cartesian grid. The particle of interest is noted p in the central cell (  ). The particles of which center belongs to this cell or one of the surrounding ones (
). The particles of which center belongs to this cell or one of the surrounding ones (  ) are stored as potential collision partners of particle p.
) are stored as potential collision partners of particle p.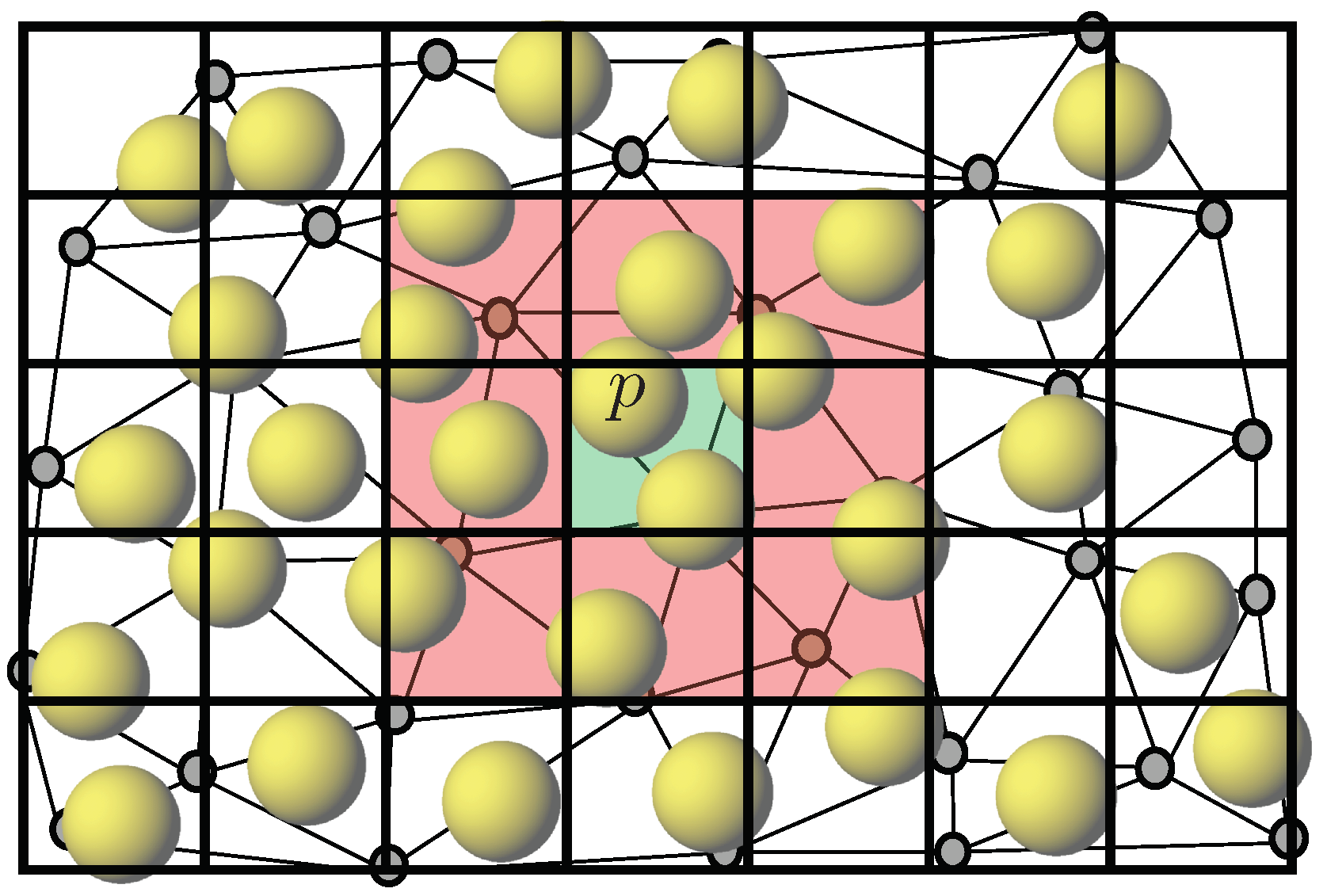
 ) and its closest neighbors are ranked , , , and . A particle entering the white cell halo around will be sent to as a ghost particle by the processor it belongs to.
) and its closest neighbors are ranked , , , and . A particle entering the white cell halo around will be sent to as a ghost particle by the processor it belongs to.
 ) and its closest neighbors are ranked , , , and . A particle entering the white cell halo around will be sent to as a ghost particle by the processor it belongs to.
) and its closest neighbors are ranked , , , and . A particle entering the white cell halo around will be sent to as a ghost particle by the processor it belongs to.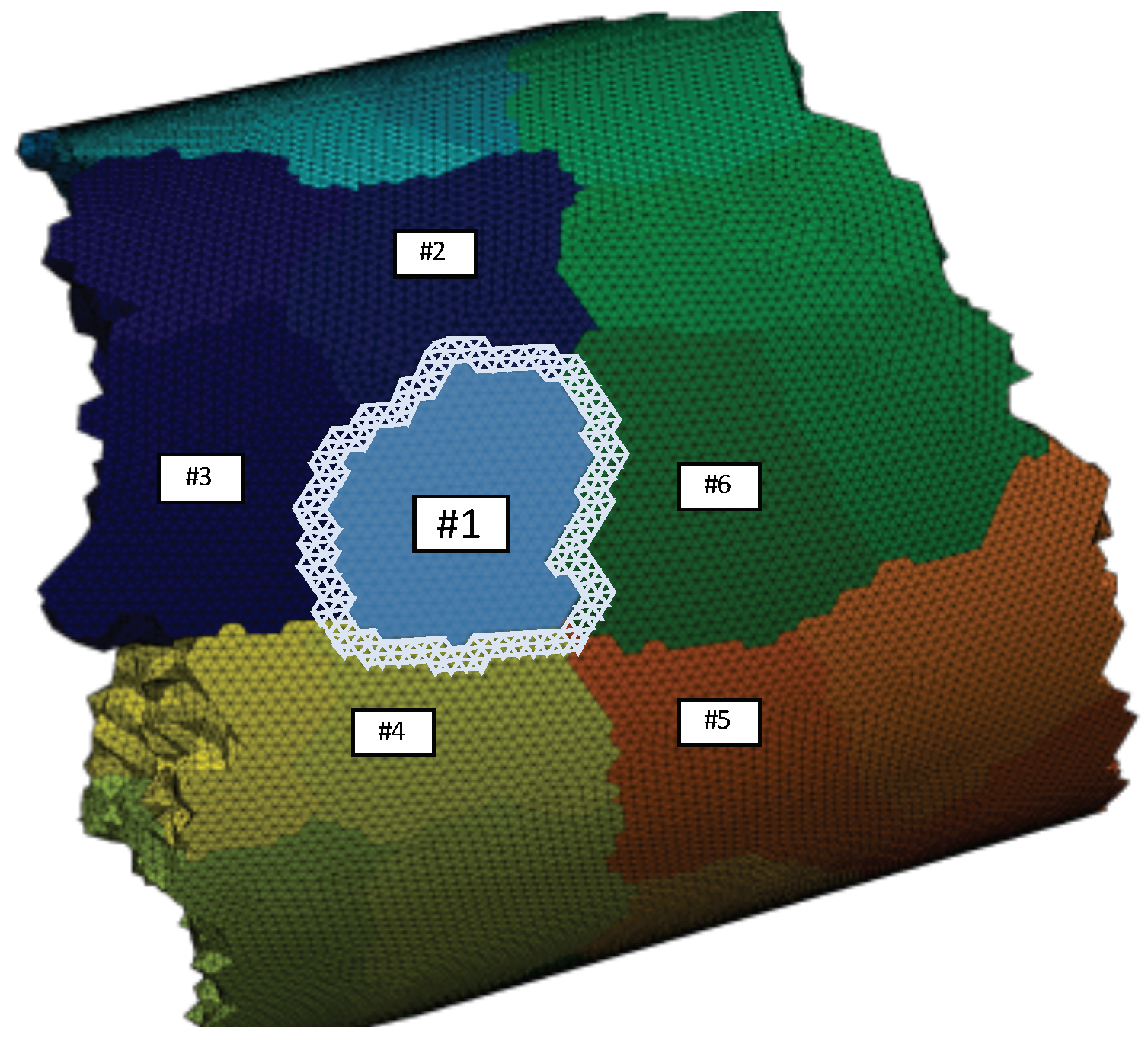

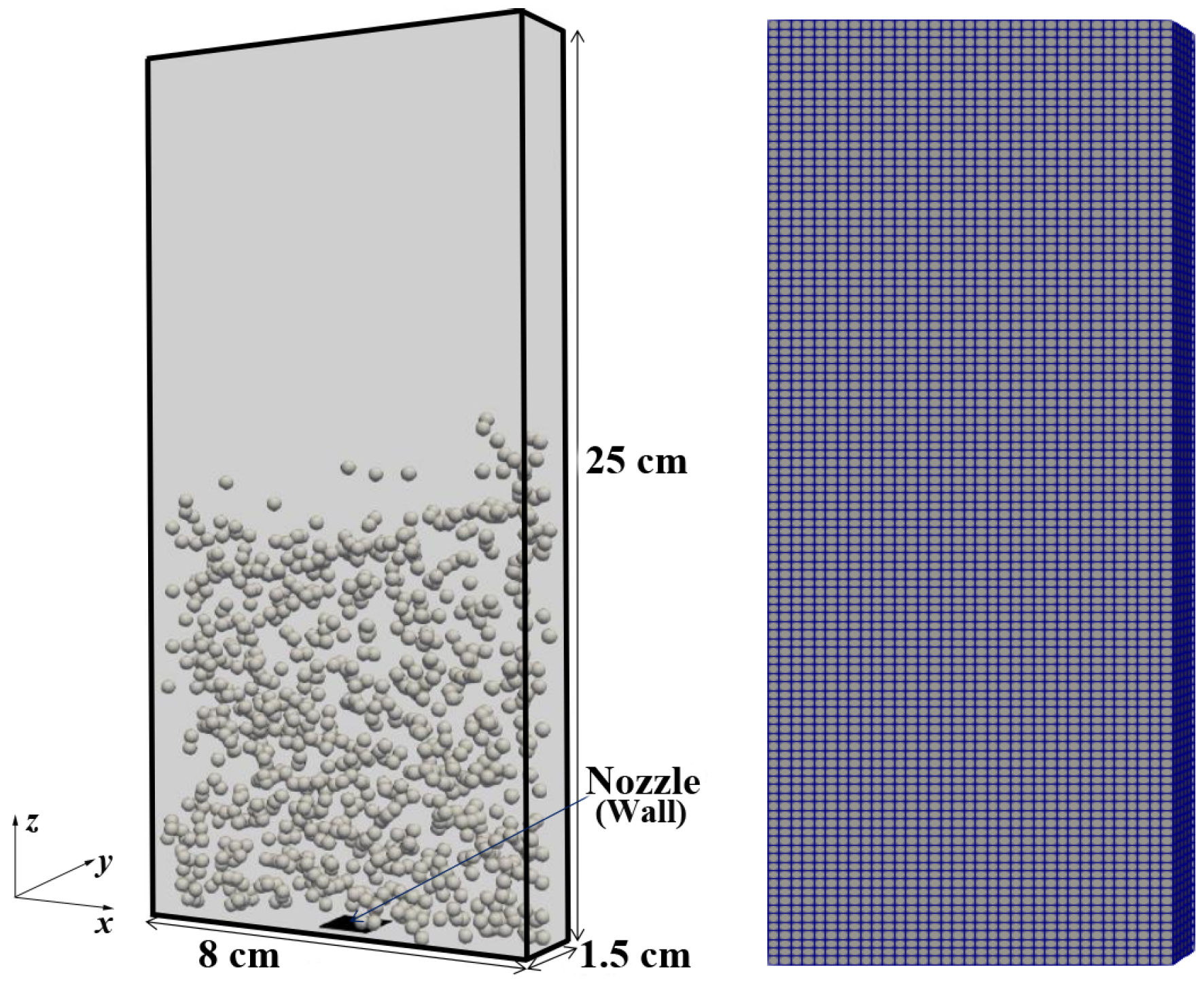
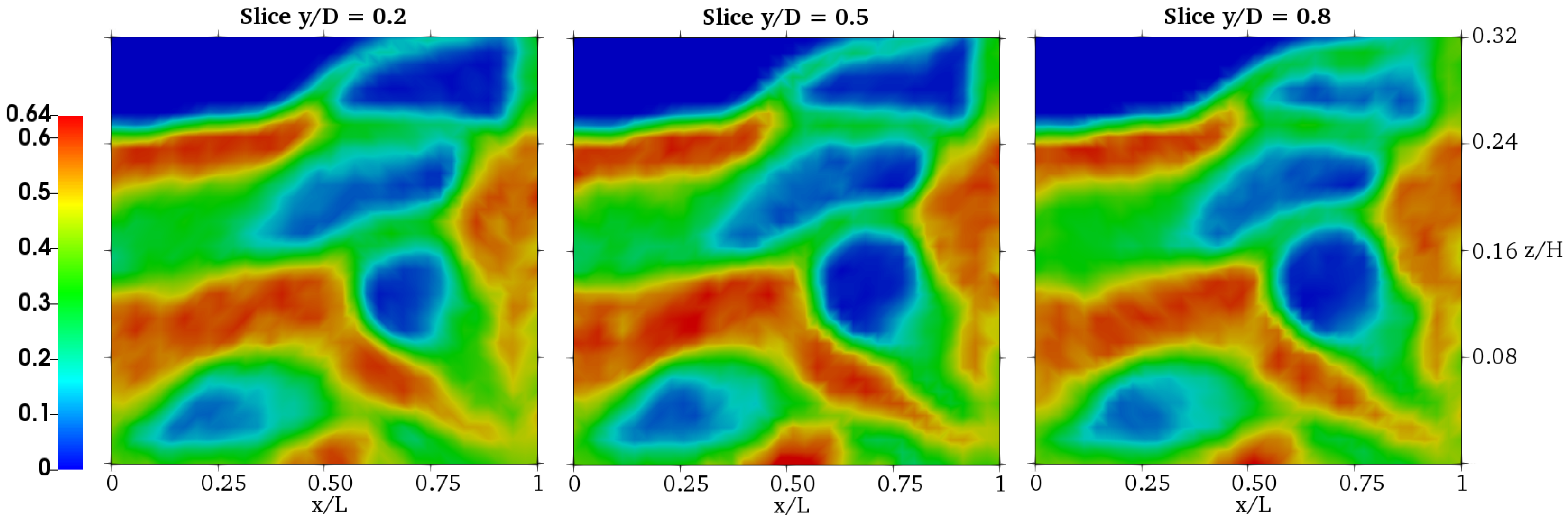
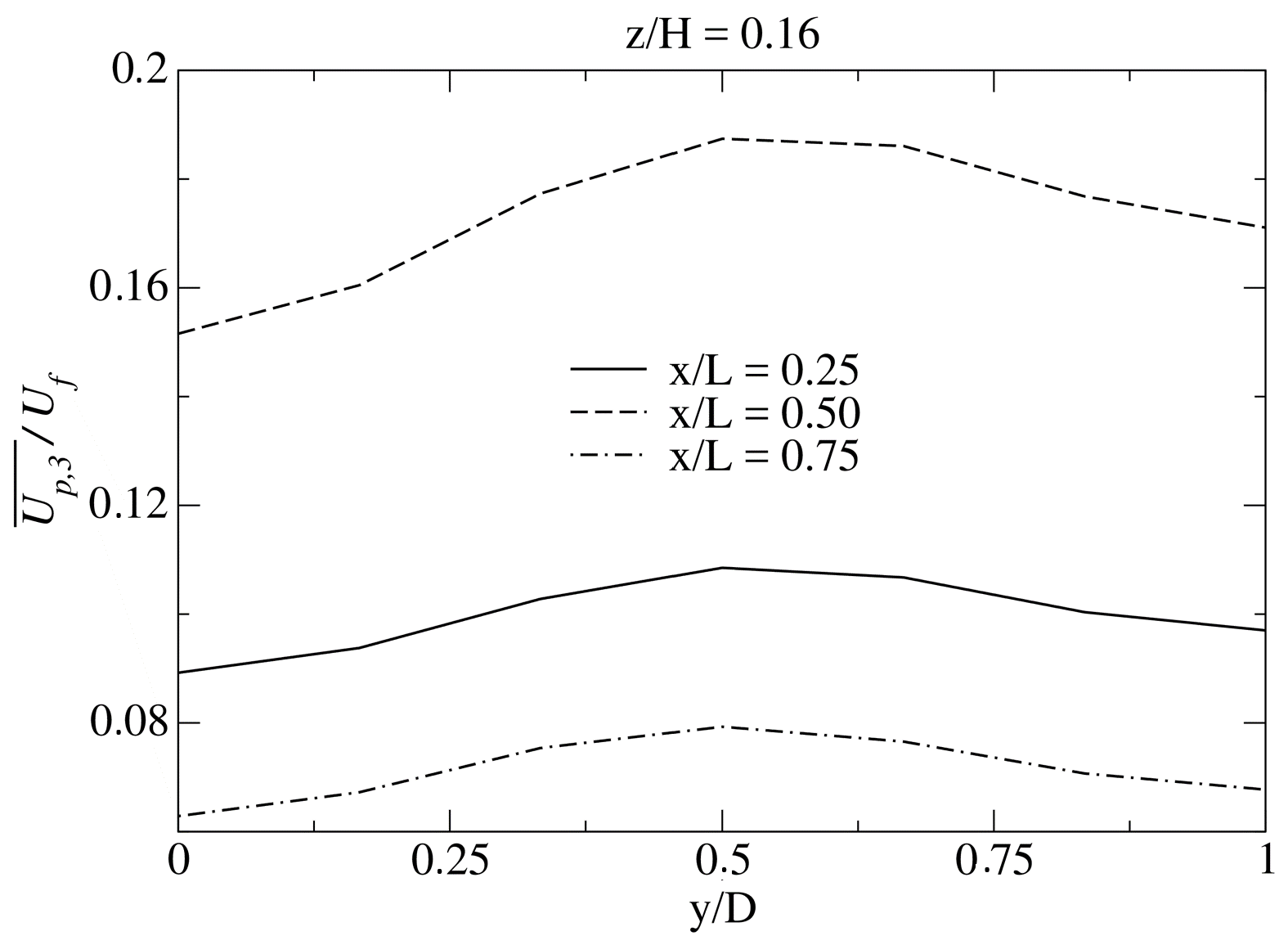
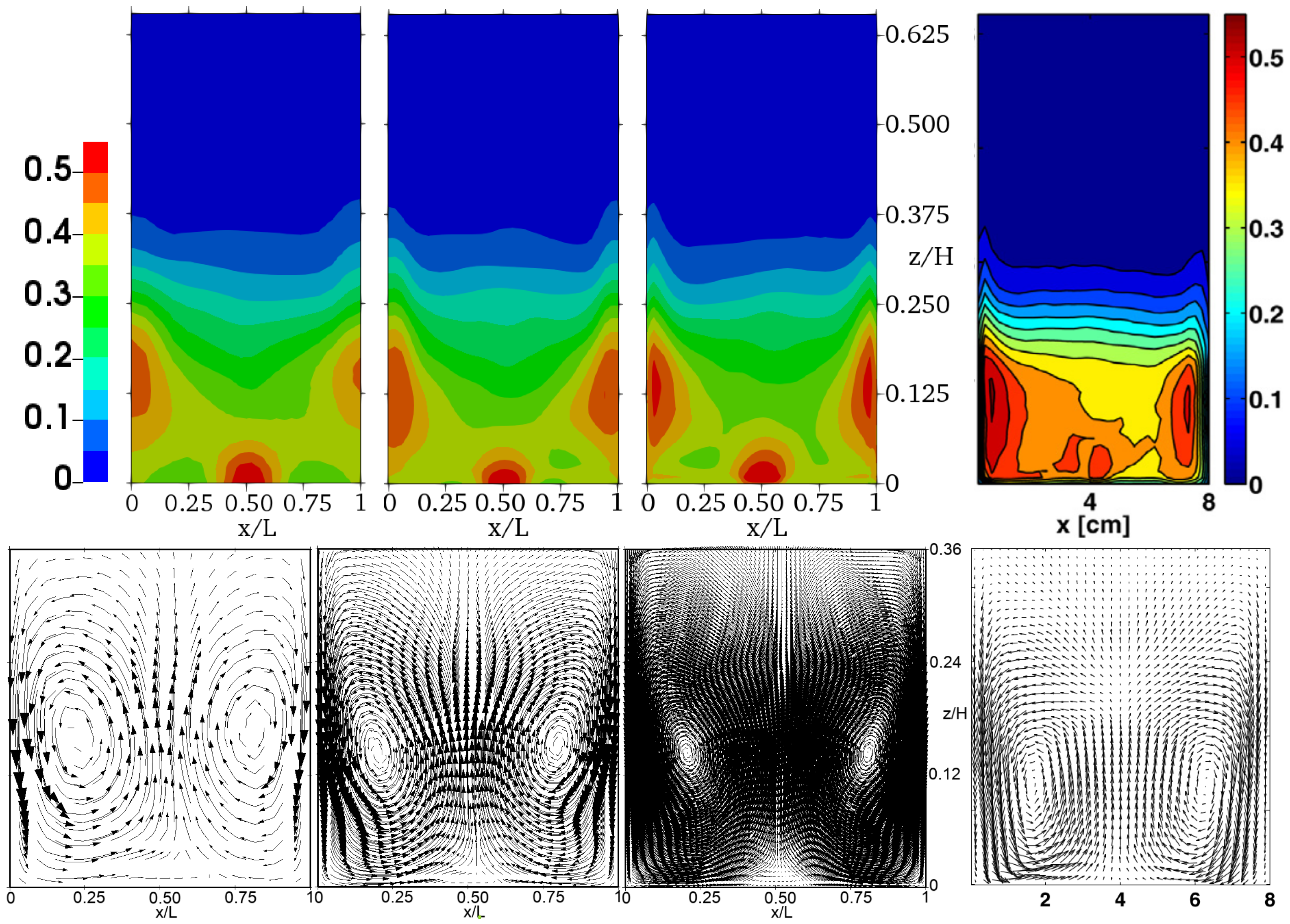

| Gas Properties (at C) | |
| Density, | kg/m |
| Viscosity, | Pa·s |
| Particle Properties | |
| Mean diameter, | 1 mm |
| Density, | 2500 kg/m |
| Norm. coef. of rest., | |
| Solid/gas density ratio, | 2146 |
| Mesh | Number of Cells | Bottom Wall | Mesh Size/Particle Diameter Ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | |||||||||
| Coarse | 17 | 3 | 55 | 2805 | 3 | 3 | 4.706 | 5.000 | 4.545 |
| Intermediate | 35 | 6 | 110 | 23,100 | 5 | 4 | 2.286 | 2.500 | 2.273 |
| Fine | 70 | 12 | 220 | 184,800 | 10 | 8 | 1.143 | 1.250 | 1.136 |
| Simulation | Bed | (m/s) | Friction Coefficients | Mesh | |||
|---|---|---|---|---|---|---|---|
| Cases | Mass (g) | at 20 C | |||||
| C1 | 75 | 70 | ∼4 | Coarse | |||
| C2 | Intermediate | ||||||
| C3 | Fine | ||||||
| C4 | 75 | 70 | ∼4 | Intermediate | |||
| C5 | 75 | 70 | ∼4 | Intermediate | |||
| C6 | 75 | 100 | ∼5.5 | Intermediate | |||
| C7 | 125 | 90 | ∼ 5 | Intermediate | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamidouche, Z.; Dufresne, Y.; Pierson, J.-L.; Brahem, R.; Lartigue, G.; Moureau, V. DEM/CFD Simulations of a Pseudo-2D Fluidized Bed: Comparison with Experiments. Fluids 2019, 4, 51. https://doi.org/10.3390/fluids4010051
Hamidouche Z, Dufresne Y, Pierson J-L, Brahem R, Lartigue G, Moureau V. DEM/CFD Simulations of a Pseudo-2D Fluidized Bed: Comparison with Experiments. Fluids. 2019; 4(1):51. https://doi.org/10.3390/fluids4010051
Chicago/Turabian StyleHamidouche, Ziad, Yann Dufresne, Jean-Lou Pierson, Rim Brahem, Ghislain Lartigue, and Vincent Moureau. 2019. "DEM/CFD Simulations of a Pseudo-2D Fluidized Bed: Comparison with Experiments" Fluids 4, no. 1: 51. https://doi.org/10.3390/fluids4010051
APA StyleHamidouche, Z., Dufresne, Y., Pierson, J.-L., Brahem, R., Lartigue, G., & Moureau, V. (2019). DEM/CFD Simulations of a Pseudo-2D Fluidized Bed: Comparison with Experiments. Fluids, 4(1), 51. https://doi.org/10.3390/fluids4010051





