Use of Computational Fluid Dynamics to Analyze Blood Flow, Hemolysis and Sublethal Damage to Red Blood Cells in a Bileaflet Artificial Heart Valve
Abstract
1. Introduction
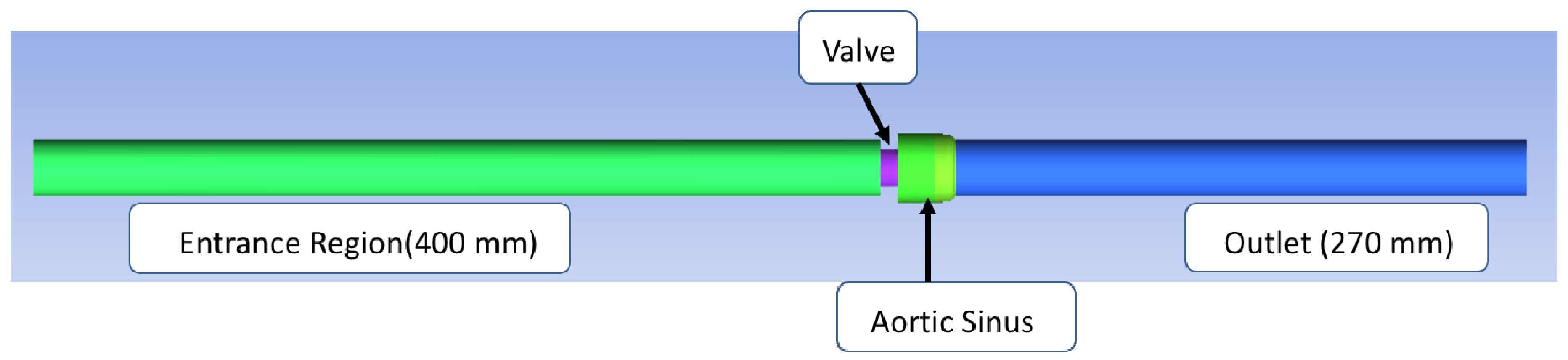
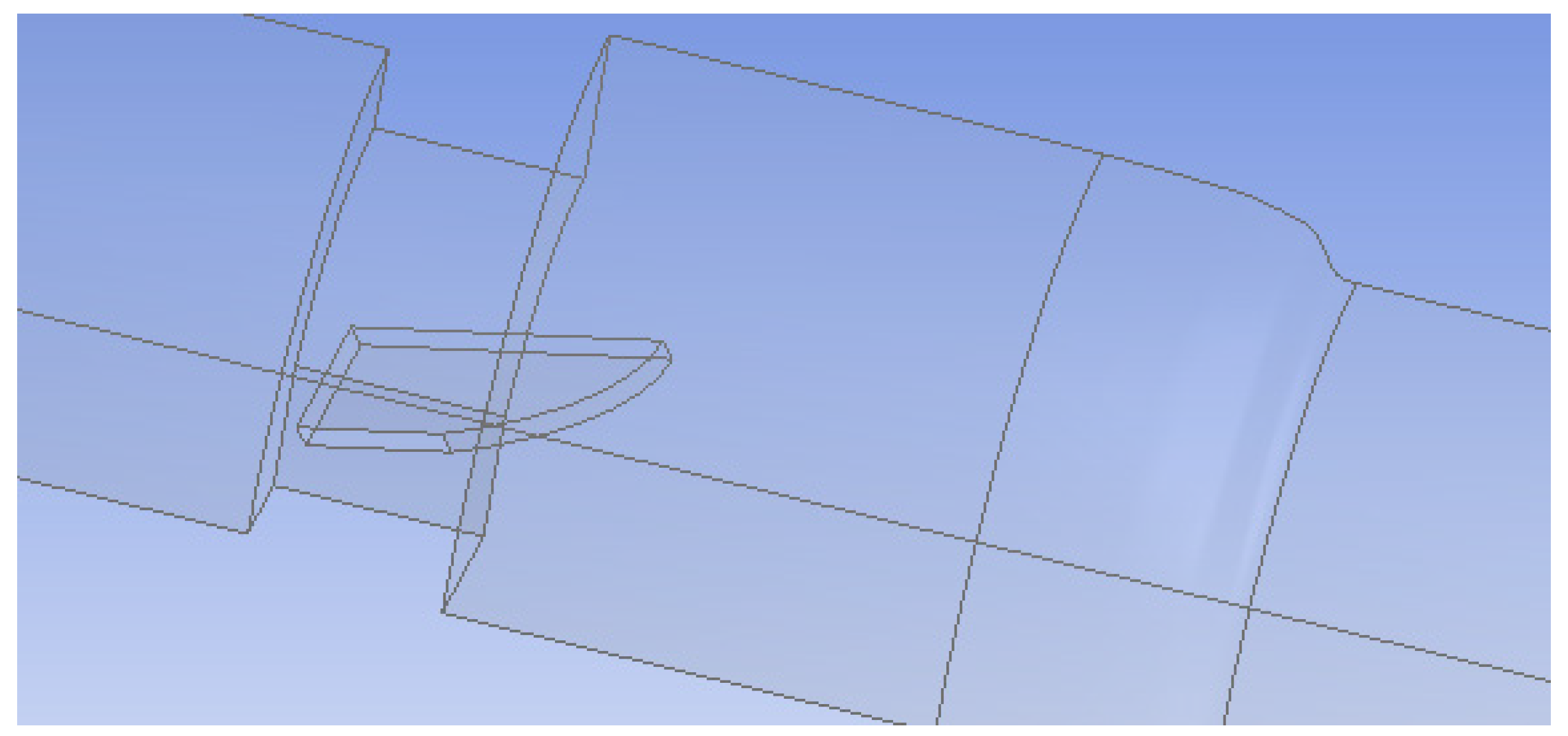
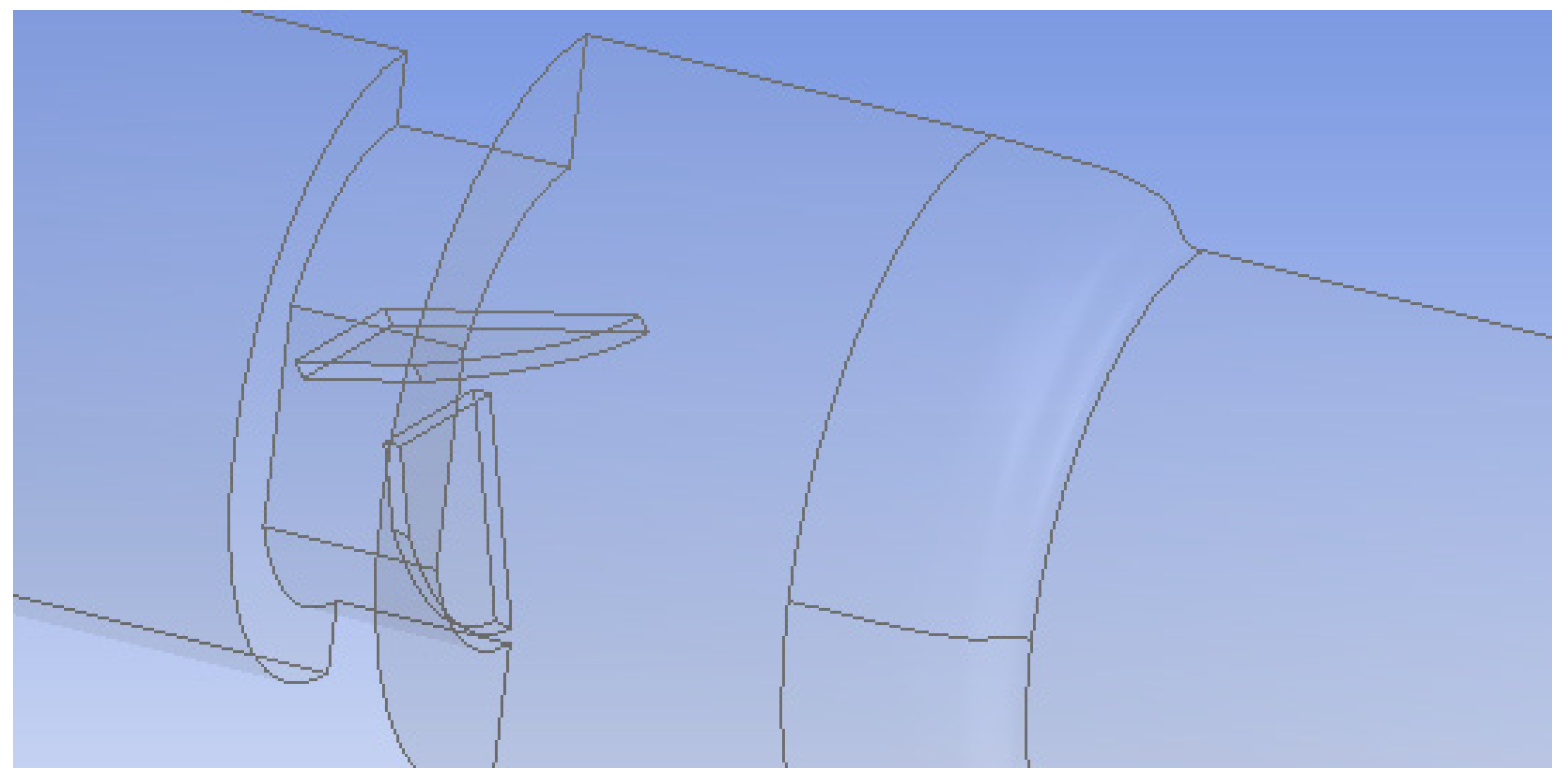
2. Methods
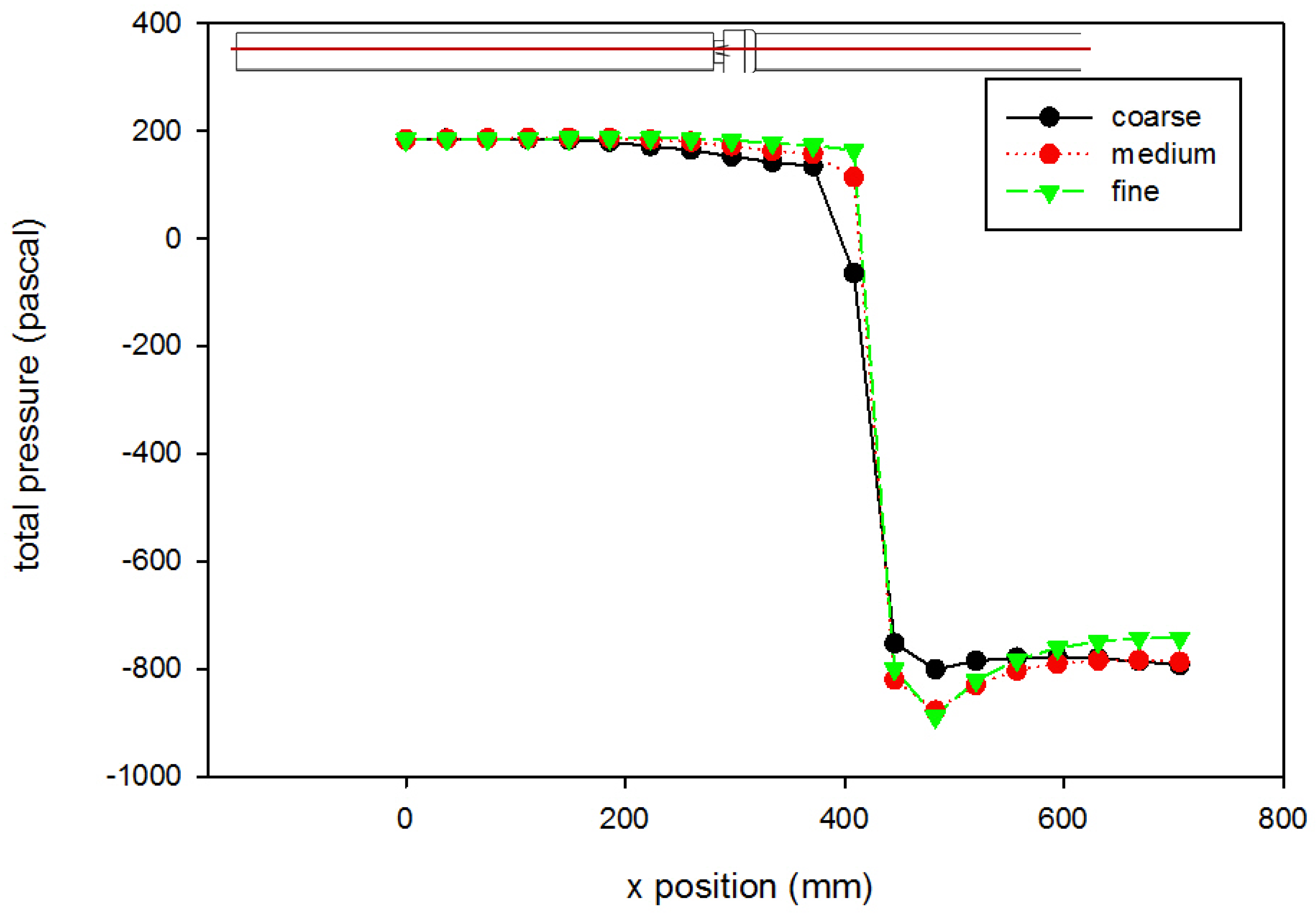
Flow Simulation
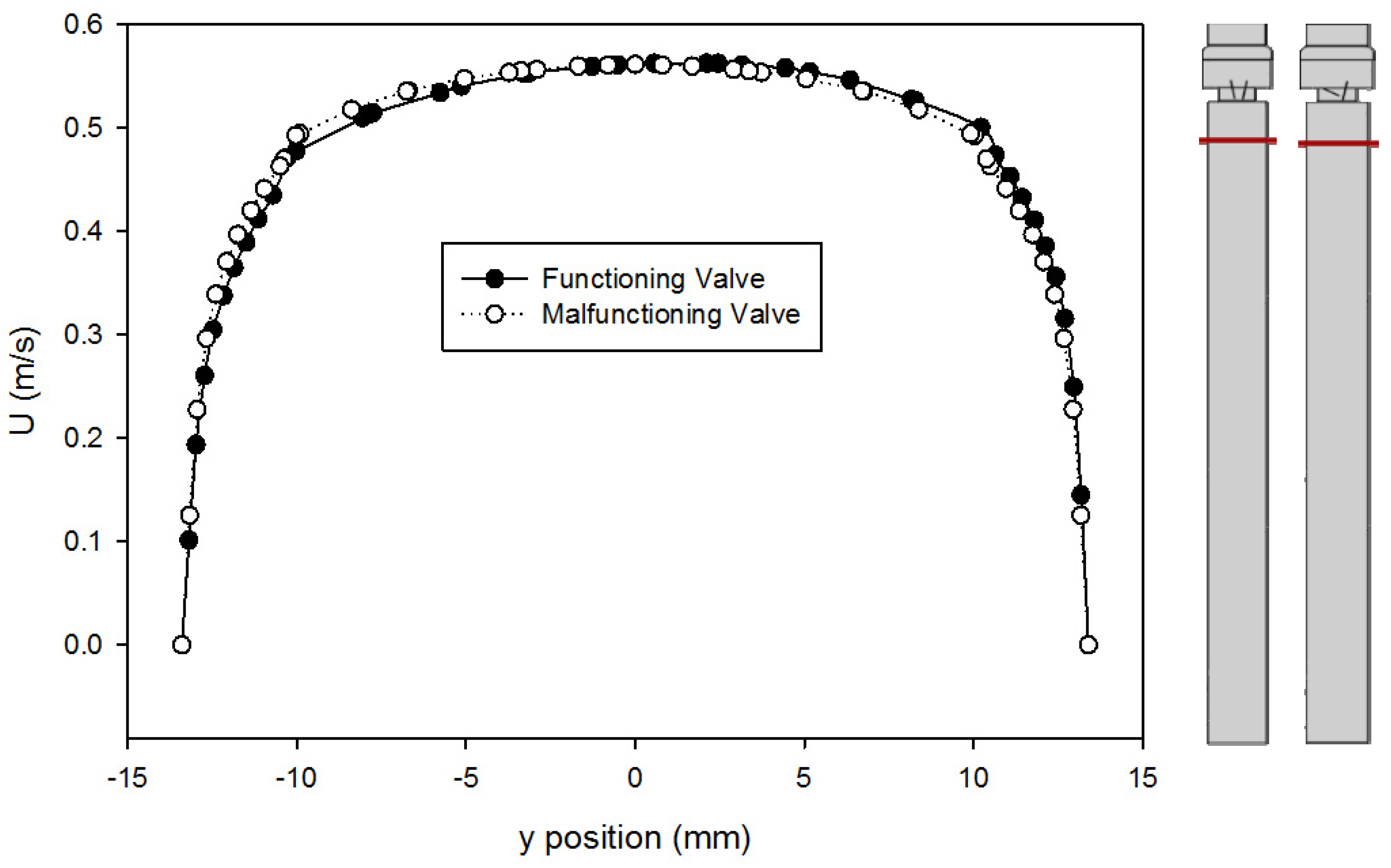
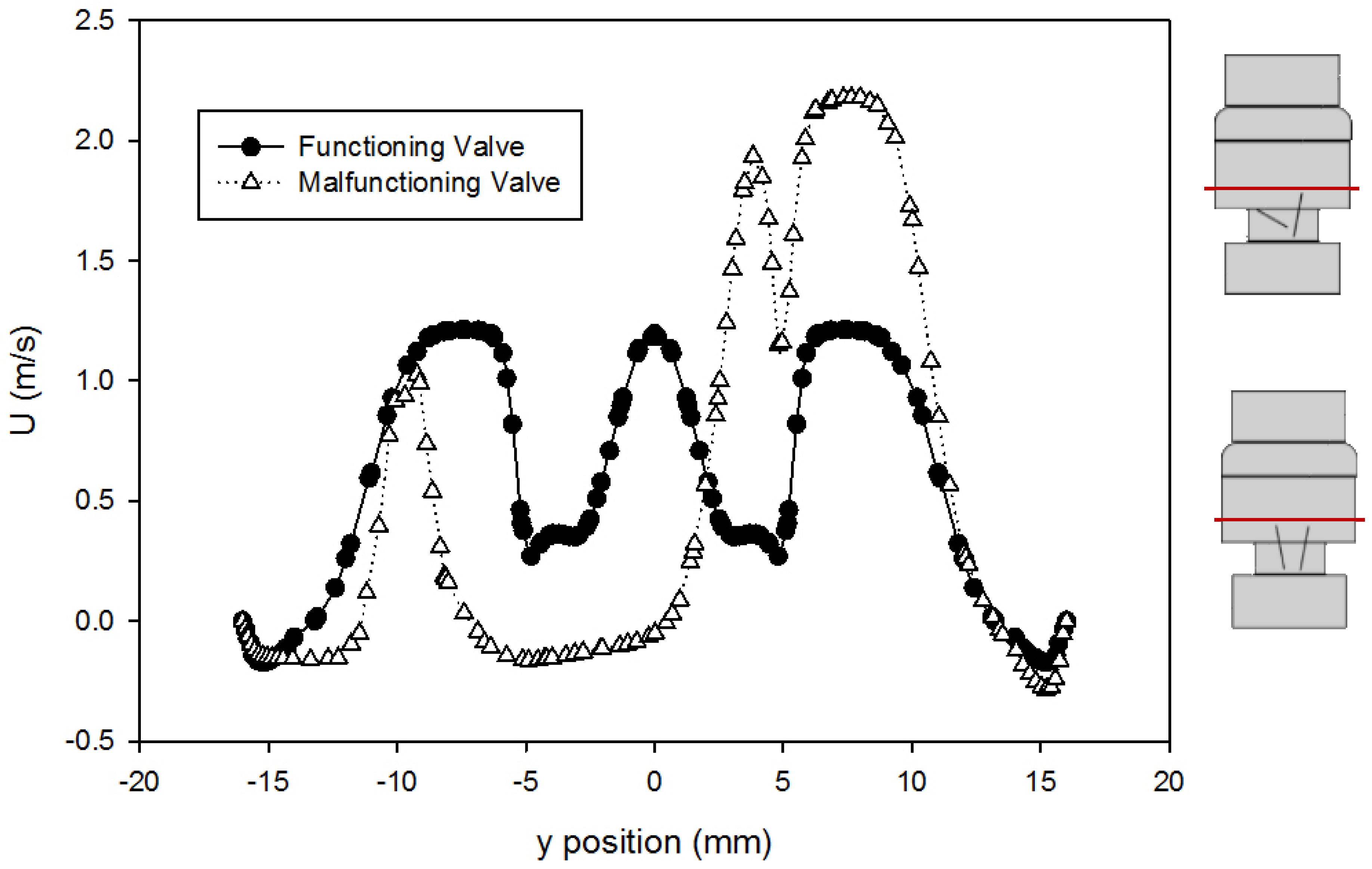
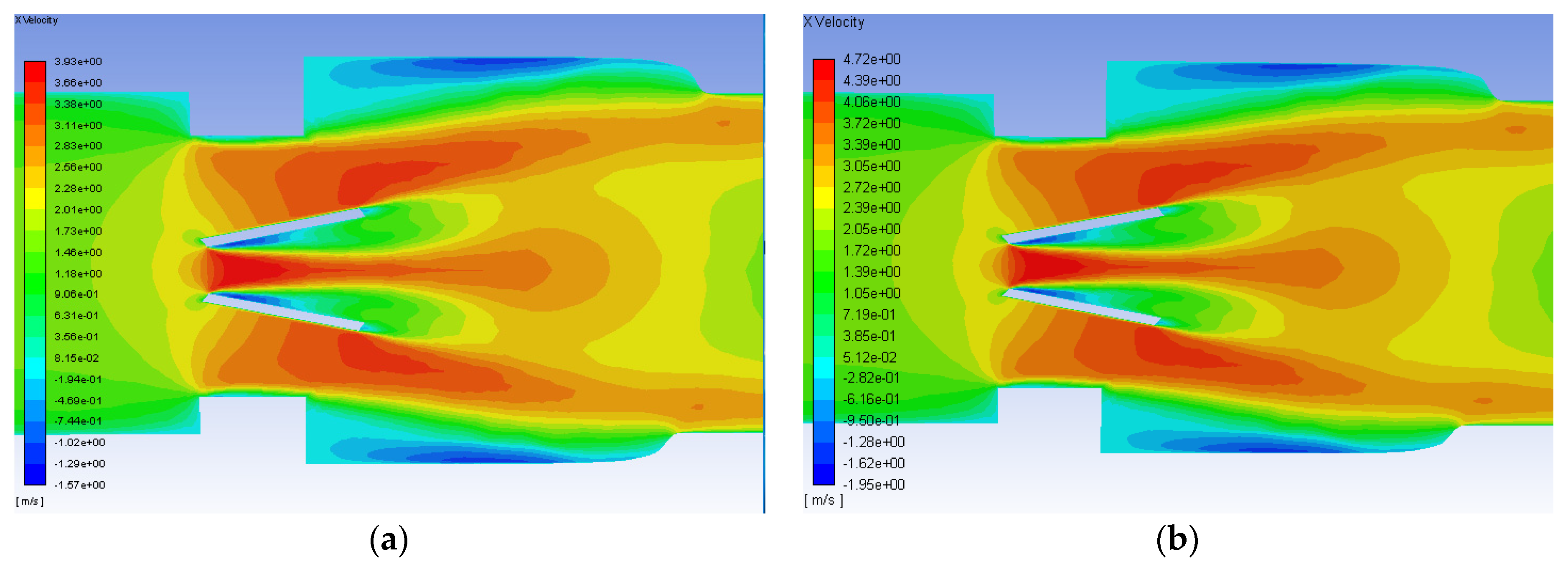
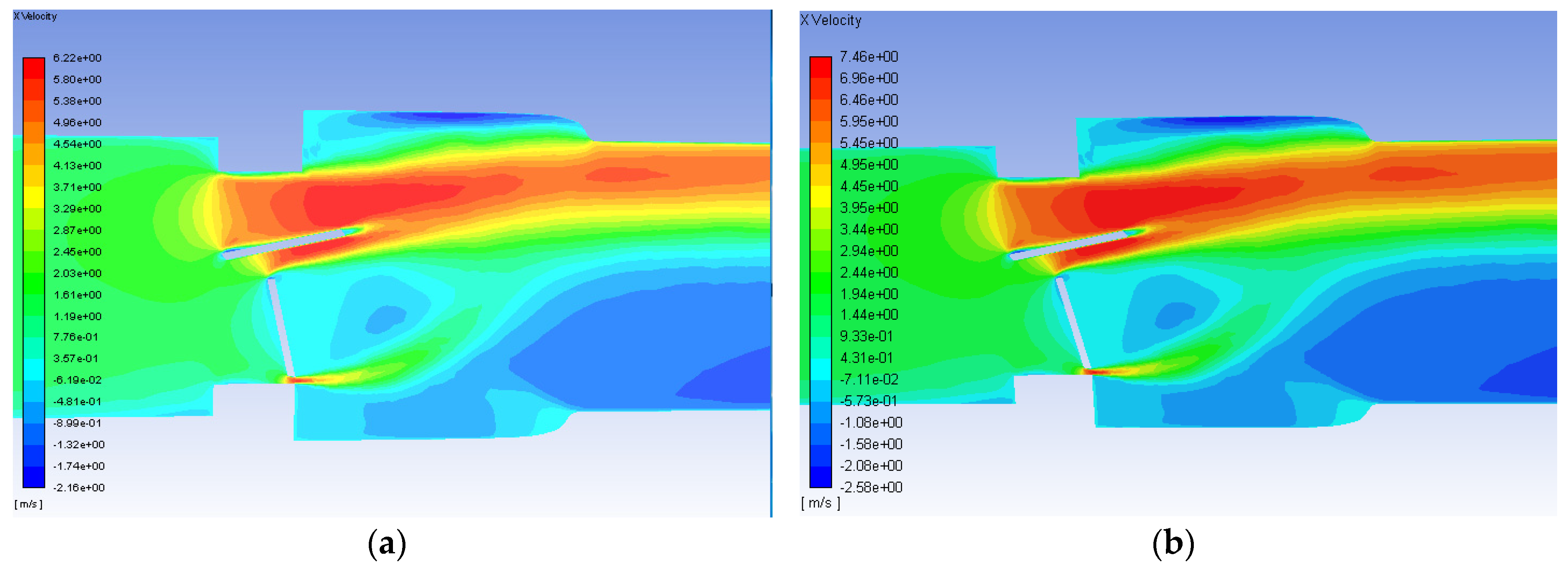
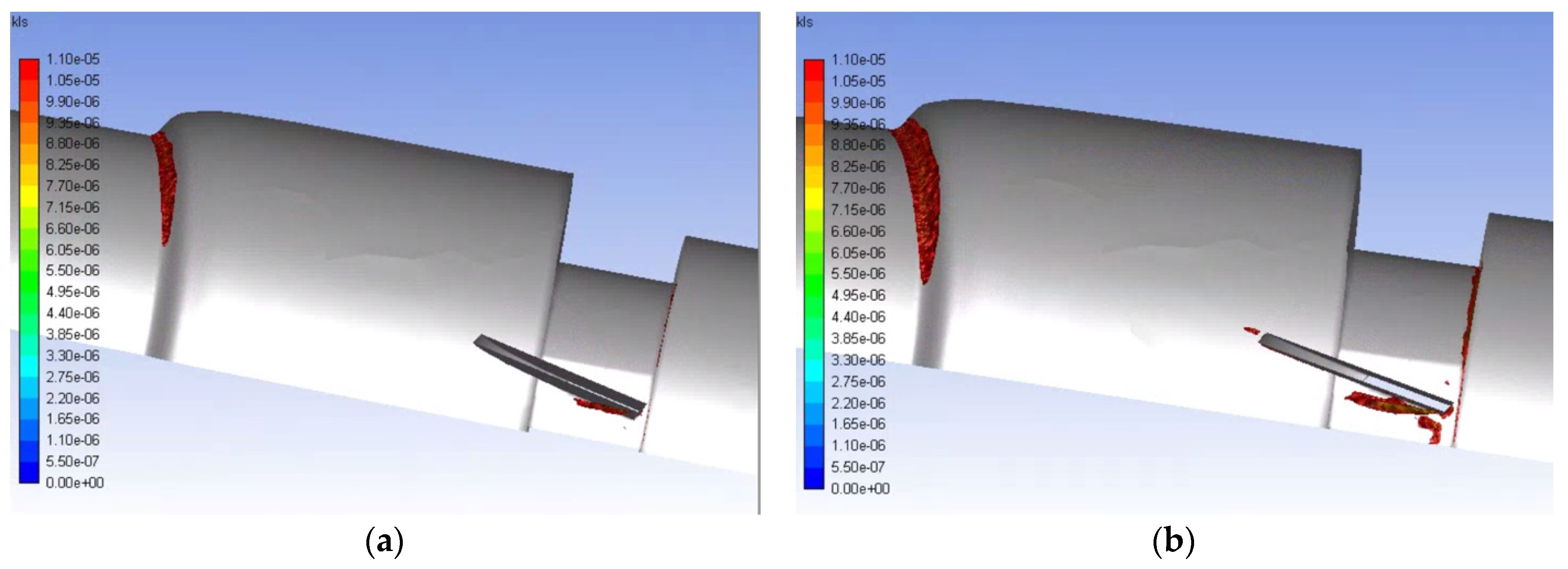
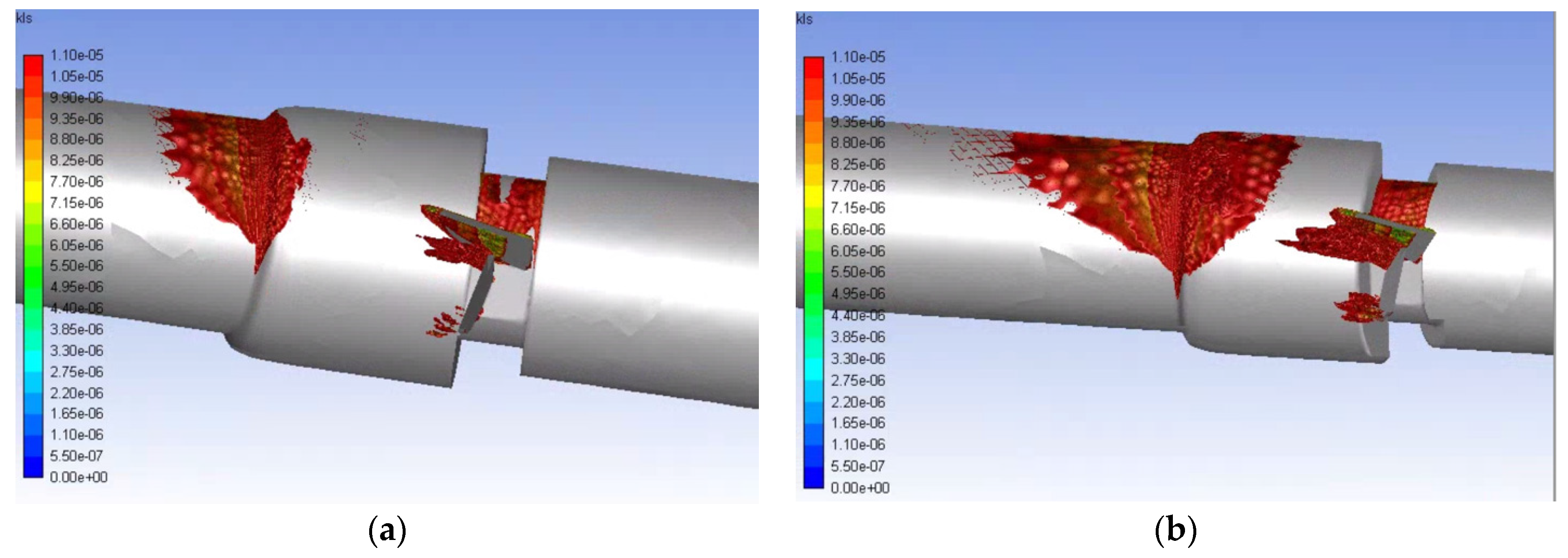
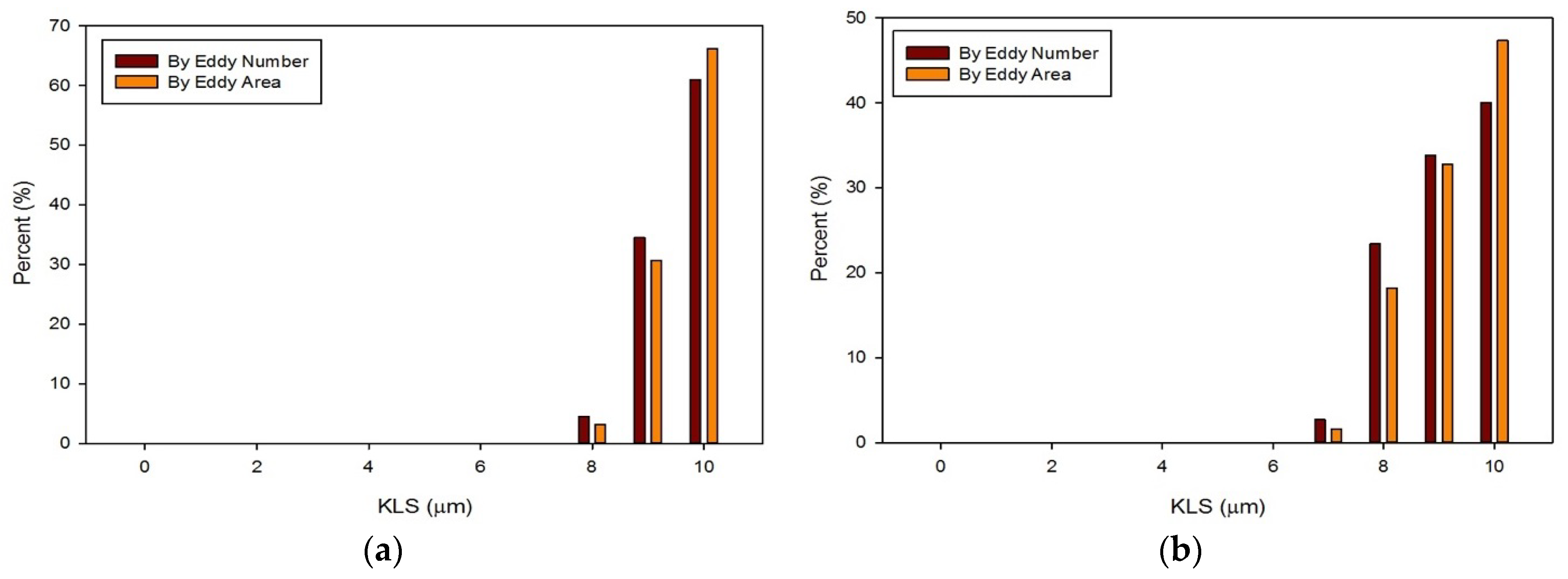
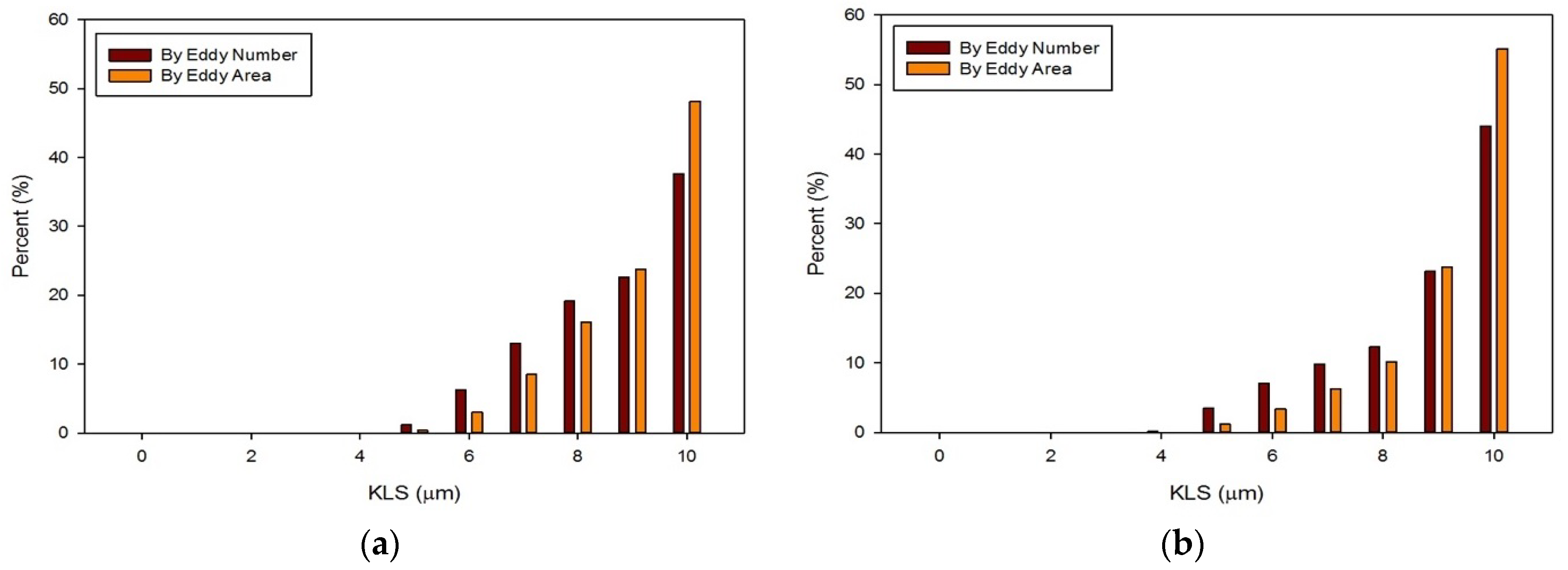
3. Results and Discussion
4. Summary and Conclusions
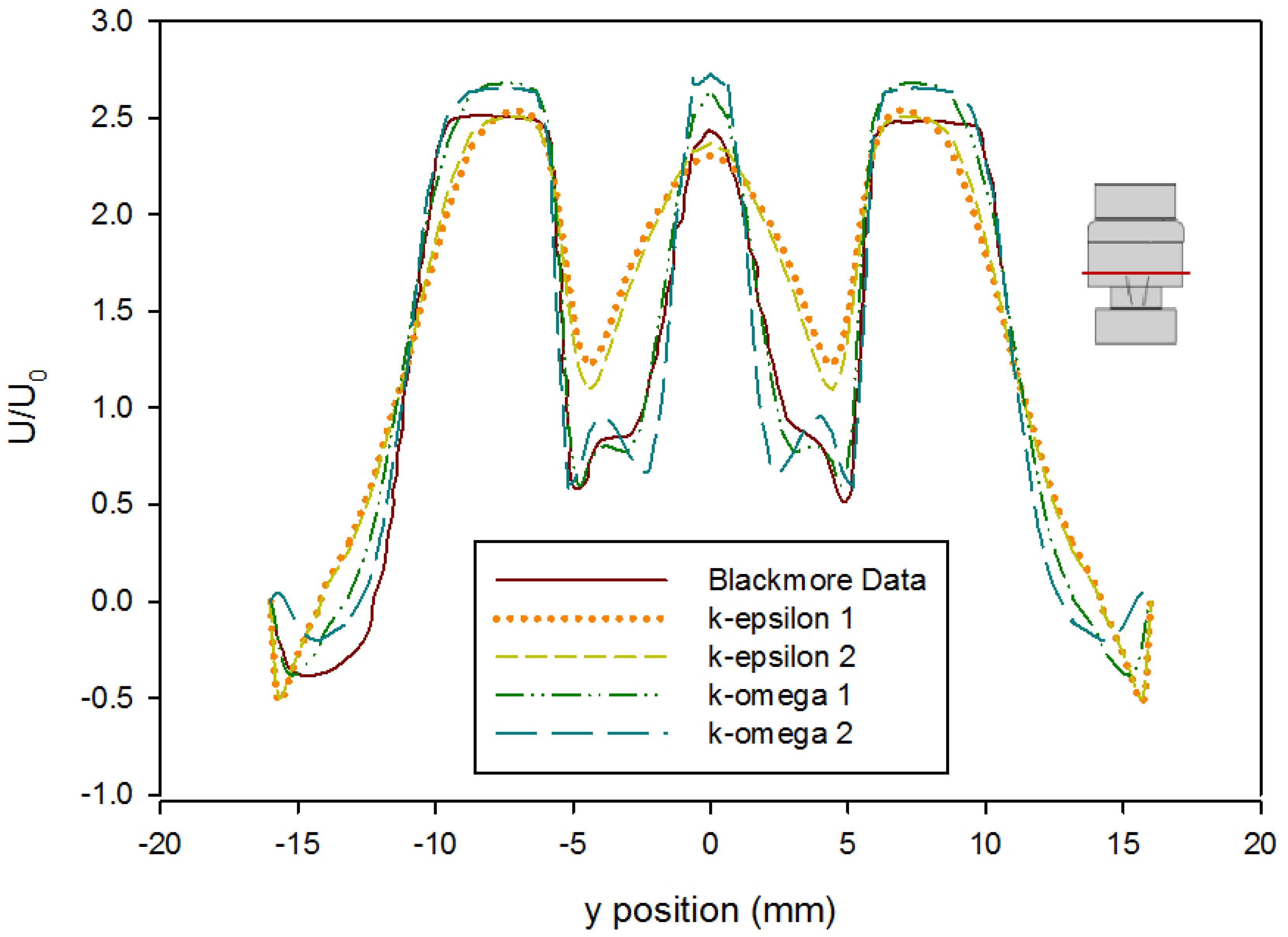
- The CFD model of the functioning valve gave good agreement with velocity data from literature using a medium mesh density and first order k-ω SST turbulence model with curvature and low-Re corrections. This validates the results of the heart valve simulations and gives confidence to other results obtained.
- Simulations within the malfunctioning valve indicated a larger number of small eddies formed on the side of the valve and sinus near the fully open, functioning leaflet, when compared to the nearly closed, malfunctioning leaflet. Again, this is due to a larger amount of fluid flow in this region, creating more areas of turbulence and higher turbulent dissipation rates.
- Results showed that an increased flowrate corresponds with an increase in eddy intensity because of the increase in the number and areas of eddies of smaller sizes. It was also found that at the same flowrate, when compared to the functioning valve, the malfunctioning valve showed increased eddy intensity and eddies farther down the flow field. This means that an increase in flowrate or a malfunction in the valve can increase both eddy intensity and distribution, resulting in greater hemolysis.
- The hemolysis predictions were lower than others in the literature [26,27] and support the view that current artificial heart valves do not cause a significant amount of hemolysis when functioning properly. Adapting the method to subhemolytic injury to cells could provide further improvement in the design of valve prostheses.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blackwell, D.; Villarroel, M.A. Tables of Summary Health Statistics for U.S. Adults: 2015 National Health Interview Survey. National Center for Health Statistics. Available online: http://www.cdc.gov/nchs/nhis/SHS/tables.htm (accessed on 28 January 2019).
- Murphy, S.L.; Xu, J.; Kochanek, K.D.; Curtin, S.C.; Arias, E. Deaths: Final Data for 2015. Natl. Vital Stat. Rep. 2017, 66, 1–75. [Google Scholar]
- Dasi, L.P.; Simon, H.A.; Sucosky, P.; Yoganathan, A.P. Fluid Mechanics of Artificial Heart Valves. Clin. Exp. Pharmacol. Physiol. 2009, 36, 225–237. [Google Scholar] [CrossRef] [PubMed]
- Hund, S.J.; Antaki, J.F.; Massoudi, M. On the representation of turbulent stresses for computing blood damage. Int. J. Eng. Sci. 2010, 48, 1325–1331. [Google Scholar] [CrossRef] [PubMed]
- Antiga, L.; Steinman, D.A. Rethinking turbulence in blood. Biorheology 2009, 46, 77–81. [Google Scholar] [PubMed]
- Casa, L.D.; Deaton, D.H.; Ku, D.N. Role of high shear rate in thrombosis. J. Vasc. Surg. 2015, 61, 1068–1080. [Google Scholar] [CrossRef]
- Slepian, M.J.; Sheriff, J.; Hutchinson, M.; Tran, P.; Bajaj, N.; Garcia, J.G.N.; Scott Saavedra, S.; Bluestein, D. Shear-mediated platelet activation in the free flow: Perspectives on the emerging spectrum of cell mechanobiological mechanisms mediating cardiovascular implant thrombosis. J. Biomech. 2017, 50, 20–25. [Google Scholar] [CrossRef] [PubMed]
- Bluestein, D.; Chandran, K.B.; Manning, K.B. Towards non-thrombogenic performance of blood recirculating devices. Ann. Biomed. Eng. 2010, 38, 1236–1256. [Google Scholar] [CrossRef]
- Simak, J.; Gelderman, M.P. Cell membrane microparticles in blood and blood products: Potentially pathogenic agents and diagnostic markers. Transfus. Med. Rev. 2006, 20, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Marom, G. Numerical Methods for Fluid-Structure Interaction Models of Aortic Valves. Arch. Comput. Method Eng. 2015, 22, 595–620. [Google Scholar] [CrossRef]
- Zhou, F.; Cui, Y.Y.; Wu, L.L.; Yang, J.; Liu, L.; Maitz, M.F.; Brown, I.G.; Huang, N. Analysis of Flow Field in Mechanical Aortic Bileaflet Heart Valves Using Finite Volume Method. J. Med. Biol. Eng. 2016, 36, 110–120. [Google Scholar] [CrossRef]
- Khalili, F.; Gamage, P.P.T.; Sandler, R.H.; Mansy, H.A. Adverse Hemodynamic Conditions Associated with Mechanical Heart Valve Leaflet Immobility. Bioengineering (Basel) 2018, 5, 74. [Google Scholar] [CrossRef] [PubMed]
- Shahriari, S.; Maleki, H.; Hassan, I.; Kadem, L. Evaluation of shear stress accumulation on blood components in normal and dysfunctional bileaflet mechanical heart valves using smoothed particle hydrodynamics. J. Biomech. 2012, 45, 2637–2644. [Google Scholar] [CrossRef] [PubMed]
- Shapira, Y.; Vaturi, M.; Sagie, A. Hemolysis Associated with Prosthetic Heart Valves A Review. Cardiol. Rev. 2009, 17, 121–124. [Google Scholar] [CrossRef] [PubMed]
- Taimeh, Z.; Koene, R.J.; Furne, J.; Singal, A.; Eckman, P.M.; Levitt, M.D.; Pritzker, M.R. Erythrocyte aging as a mechanism of anemia and a biomarker of device thrombosis in continuous-flow left ventricular assist devices. J. Heart Lung Transplant. 2017, 36, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Yacoub, M.H.; Keeling, D.H. Chronic haemolysis following insertion of ball valve prostheses. Br. Heart J. 1968, 30, 676–678. [Google Scholar] [CrossRef] [PubMed]
- Kloster, F.E. Diagnosis and management of complications of prosthetic heart valves. Am. J. Cardiol. 1975, 35, 872–885. [Google Scholar] [CrossRef]
- Maraj, R.; Jacobs, L.E.; Ioli, A.; Kotler, M.N. Evaluation of hemolysis in patients with prosthetic heart valves. Clin. Cardiol. 1998, 21, 387–392. [Google Scholar] [CrossRef]
- Amidon, T.M.; Chou, T.M.; Rankin, J.S.; Ports, T.A. Mitral and Aortic Paravalvular Leaks with Hemolytic-Anemia. Am. Heart J. 1993, 125, 266–268. [Google Scholar] [CrossRef]
- Tanis, W.H.; van den Brink, R.; Symersky, P.; Budde, R.; Chamuleau, S. Differentiation of thrombus from pannus as the cause of acquired mechanical prosthetic heart valve obstruction by non-invasive imaging: A review of the literature. Eur. Heart J. Cardiovasc. Imaging 2014, 15, 119–129. [Google Scholar] [CrossRef]
- Sucha, D.; Symersky, P.; van den Brink, R.B.A.; Tanis, W.; Laufer, E.M.; Meijs, M.F.L.; Habets, J.; de Mol, B.A.; Mali, W.P.; Chamuleau, S.A.; et al. Diagnostic evaluation and treatment strategy in patients with suspected prosthetic heart valve dysfunction: The incremental value of MDCT. J. Cardiovasc. Comput. 2016, 10, 398–406. [Google Scholar] [CrossRef]
- Madukauwa-David, I.D.; Pierce, E.L.; Sulejmani, F.; Pataky, J.; Sun, W.; Yoganathan, A.P. Suture dehiscence and collagen content in the human mitral and tricuspid annuli. Biomech. Model. Mechanobiol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Mecozzi, G.; Milano, A.D.; De Carlo, M.; Sorrentino, F.; Pratali, S.; Nardi, C.; Bortolotti, U. Intravascular hemolysis in patients with new-generation prosthetic heart valves: A prospective study. J. Thorac. Cardiovasc. Surg. 2002, 123, 550–556. [Google Scholar] [CrossRef]
- Shivakumaraswamy, T.M.P.; Radhakrishnan, B.; Khandekar, J.; Agrawal, N.; Patwardhan, A.; Khandeparkar, J. Intravascular hemolysis in patients with normally functioning mechanical heart valves in mitral position. Indian J. Thoracis Cardiovasc. Surg. 2006, 22, 215–218. [Google Scholar] [CrossRef]
- Sabzi, F.; Khosravi, D. Hemolytic Anemia after Aortic Valve Replacement: A Case Report. Acta Medica Iranica 2015, 53, 585–589. [Google Scholar] [PubMed]
- Susin, F.M.; Espa, S.; Toninato, R.; Fortini, S.; Querzoli, G. Integrated strategy for in vitro characterization of a bileaflet mechanical aortic valve. Biomed. Eng. Online 2017, 16, 29. [Google Scholar] [CrossRef] [PubMed]
- de Tullio, M.D.; Nam, J.; Pascazio, G.; Balaras, E.; Verzicco, R. Computational prediction of mechanical hemolysis in aortic valved prostheses. Eur. J. Mech. B-Fluid 2012, 35, 47–53. [Google Scholar] [CrossRef]
- Toninato, R.; Fadda, G.; Susin, F.M. A Red Blood Cell Model to Estimate the Hemolysis Fingerprint of Cardiovascular Devices. Artif. Organs 2018, 42, 58–67. [Google Scholar] [CrossRef]
- Yin, W.; Ngwe, E.C.; Rubenstein, D.A. A Biocompatible Flow Chamber to Study the Hemodynamic Performance of Prosthetic Heart Valves. Asaio J. 2012, 58, 470–480. [Google Scholar] [CrossRef]
- Giersiepen, M.; Wurzinger, L.J.; Opitz, R.; Reul, H. Estimation of Shear Stress-Related Blood Damage in Heart-Valve Prostheses—Invitro Comparison of 25 Aortic Valves. Int. J. Artif. Organs 1990, 13, 300–306. [Google Scholar] [CrossRef]
- Blackshear, P.L.; Dorman, F.D.; Steinbach, J.H. Some Mechanical Effects That Influence Hemolysis. Trans. Am. Soc. Artif. Int. Organs 1965, 11, 112. [Google Scholar] [CrossRef]
- Heuser, G.; Opitz, R. A Couette Viscometer for Short-Time Shearing of Blood. Biorheology 1980, 17, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Fraser, K.H.; Zhang, T.; Taskin, M.E.; Griffith, B.P.; Wu, Z.J. A Quantitative Comparison of Mechanical Blood Damage Parameters in Rotary Ventricular Assist Devices: Shear Stress, Exposure Time and Hemolysis Index. J. Biomech. Eng. 2012, 134, 081002. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Taskin, M.E.; Fang, H.B.; Pampori, A.; Jarvik, R.; Griffith, B.P.; Wu, Z.J. Study of Flow-Induced Hemolysis Using Novel Couette-Type Blood-Shearing Devices. Artif. Organs 2011, 35, 1180–1185. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Niu, S.Q.; Chen, Z.S.; Zhang, T.; Griffith, B.P.; Wu, Z.J. Shear-Induced Hemolysis: Species Differences. Artif. Organs 2015, 39, 795–802. [Google Scholar] [CrossRef] [PubMed]
- Leverett, L.B.; Lynch, E.C.; Alfrey, C.P.; Hellums, J.D. Red Blood-Cell Damage by Shear-Stress. Biophys. J. 1972, 12, 257. [Google Scholar] [CrossRef]
- Arvand, A.; Hormes, M.; Reul, H. A validated computational fluid dynamics model to estimate hemolysis in a rotary blood pump. Artif. Organs 2005, 29, 531–540. [Google Scholar] [CrossRef]
- Chan, W.K.; Wong, Y.W.; Ding, Y.; Chua, L.P.; Yu, S.C.M. Numerical Investigation of the Effect of Blade Geometry on Blood Trauma in a Centrifugal Blood Pump. Artif. Organs 2002, 26, 785–793. [Google Scholar] [CrossRef]
- Song, X.W.; Throckmorton, A.L.; Wood, H.G.; Antaki, J.F.; Olsen, D.B. Computational fluid dynamics prediction of blood damage in a centrifugal pump. Artif. Organs 2003, 27, 938–941. [Google Scholar] [CrossRef]
- Arora, D.; Behr, M.; Pasquali, M. A tensor-based measure for estimating blood damage. Artif. Organs 2004, 28, 1002–1015. [Google Scholar] [CrossRef]
- Vitale, F.; Nam, J.; Turchetti, L.; Behr, M.; Raphael, R.; Annesini, M.C.; Pasquali, M. A multiscale, biophysical model of flow-induced red blood cell damage. Aiche J. 2014, 60, 1509–1516. [Google Scholar] [CrossRef]
- Taskin, M.E.; Fraser, K.H.; Zhang, T.; Wu, C.F.; Griffith, B.P.; Wu, Z.J.J. Evaluation of Eulerian and Lagrangian Models for Hemolysis Estimation. Asaio J. 2012, 58, 363–372. [Google Scholar] [CrossRef] [PubMed]
- Stein, P.D.; Sabbah, H.N. Turbulent Blood-Flow in Ascending Aorta of Humans with Normal and Diseased Aortic Valves. Circ. Res. 1976, 39, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Sabbah, H.N.; Stein, P.D. Turbulent Blood-Flow in Humans—Primary Role in Production of Ejection Murmurs. Circ. Res. 1976, 38, 513–525. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.A. A Relationship between Reynolds Stresses and Viscous Dissipation—Implications to Red-Cell Damage. Ann. Biomed. Eng. 1995, 23, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Yen, J.H.; Chen, S.F.; Chern, M.K.; Lu, P.C. The effect of turbulent viscous shear stress on red blood cell hemolysis. J. Artif. Organs 2014, 17, 178–185. [Google Scholar] [CrossRef]
- Lee, H.; Tatsumi, E.; Taenaka, Y. Experimental Study on the Reynolds and Viscous Shear Stress of Bileaflet Mechanical Heart Valves in a Pneumatic Ventricular Assist Device. Asaio J. 2009, 55, 348–354. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, N.J.; Dooley, P.N. Models of flow-induced loading on blood cells in laminar and turbulent flow, with application to cardiovascular device flow. Ann. Biomed. Eng. 2007, 35, 1347–1356. [Google Scholar] [CrossRef]
- Aziz, A.; Werner, B.C.; Epting, K.L.; Agosti, C.D.; Curtis, W.R. The cumulative and sublethal effects of turbulence on erythrocytes in a stirred-tank model. Ann. Biomed. Eng. 2007, 35, 2108–2120. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.S.; Lu, P.C.; Chu, S.H. Turbulence characteristics downstream of bileaflet aortic valve prostheses. J. Biomech. Eng. 2000, 122, 118–124. [Google Scholar] [CrossRef]
- Dooley, P.N.; Quinlan, N.J. Effect of Eddy Length Scale on Mechanical Loading of Blood Cells in Turbulent Flow. Ann. Biomed. Eng. 2009, 37, 2449–2458. [Google Scholar] [CrossRef]
- Ozturk, M.; O’Rear, E.A.; Papavassiliou, D.V. Hemolysis Related to Turbulent Eddy Size Distributions Using Comparisons of Experiments to Computations. Artif. Organs 2015, 39, E227–E239. [Google Scholar] [CrossRef] [PubMed]
- Ozturk, M.; Papavassiliou, D.V.; O’Rear, E.A. An approach for assessing turbulent flow damage to blood in medical devices. Journal of biomechanical engineering. J. Biomech. Eng. 2017, 139, 011008. [Google Scholar] [CrossRef] [PubMed]
- Sutera, S.P.; Mehrjardi, M.H. Deformation and Fragmentation of Human Red Blood-Cells in Turbulent Shear-Flow. Biophys. J. 1975, 15, 1–10. [Google Scholar] [CrossRef]
- Kameneva, M.V.; Burgreen, G.W.; Kono, K.; Repko, B.; Antaki, J.F.; Umezu, M. Effects of turbulent stresses upon mechanical hemolysis: Experimental and computational analysis. Asaio J. 2004, 50, 418–423. [Google Scholar] [CrossRef] [PubMed]
- Forstrom, R.J. A New Measure of Erythrocyte Membrane Strength-The Jet Fragility Test. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1969. [Google Scholar]
- Hutchinson, C. Stereoscopic PIV in steady Flow Through a Bileaflet Mechanical Heart Valve. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2009. [Google Scholar]
- Raghav, V.S.S.; Saikrishnan, N. Experimental Assessment of Flow Fields Associated with Heart Valve Prostheses Using Particle Image Velocimetry (PIV): Recommendations for Best Practices. Cardiovasc. Eng. Technol. 2018, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Blackmore, A.S.P. Large Eddy simulations and Particle Image velocimetry Experiments within a BIMHV Flow Near Peak Systole. In Proceedings of the International Symposium on Turbulence and Shear Flow Phenomena (PTFP-8), Poitiers, France, 23–30 August 2013; TSFP DIGITAL LIBRARY ONLINE. Begell House Inc.: Danbury, CT, USA, 2013. [Google Scholar]
- Hutchison, C.; Sullivan, P.; Ethier, C.R. Measurements of steady flow through a bileaflet mechanical heart valve using stereoscopic PIV. Med. Biol. Eng. Comput. 2011, 49, 325–335. [Google Scholar] [CrossRef] [PubMed]
- Hwang, H.Y.; Choi, J.-W.; Kim, H.-K.; Kim, K.-H.; Kim, K.-B.; Ahn, H. Paravalvular Leak After Mitral Valve Replacement: 20-Year Follow-Up. Ann. Thoracic Surg. 2015, 100, 1347–1352. [Google Scholar] [CrossRef] [PubMed]
- Smadi, O.; Hassan, I.; Pibarot, P.; Kadem, L. Numerical and experimental investigations of pulsatile blood flow pattern through a dysfunctional mechanical heart valve. J. Biomech. 2010, 43, 1565–1572. [Google Scholar] [CrossRef] [PubMed]
- Jahandardoost, M.; Fradet, G.; Mohammadi, H. Effect of heart rate on the hemodynamics of bileaflet mechanical heart valves’ prostheses (St. Jude Medical) in the aortic position and in the opening phase: A computational study. Proc. Inst. Mech. Eng. H 2016, 230, 175–190. [Google Scholar] [CrossRef]
- Khalili, F.G.P.; Mansy, H.A. Hemodynamics of a Bileaflet Mechanical Heart Valve with Different Levels of Dysfunction. J. Appl. Biotechnol. Bioeng. 2017, 2. [Google Scholar] [CrossRef]
- Ko, T.Y.; Lin, M.S.; Lin, L.C.; Liu, Y.J.; Yeh, C.F.; Huang, C.C.; Chen, Y.H.; Chen, Y.S.; Kao, H.L. Frequency and Significance of Intravascular Hemolysis Before and After Transcatheter Aortic Valve Implantation in Patients with Severe Aortic Stenosis. Am. J. Cardiol. 2018, 121, 69–72. [Google Scholar] [CrossRef] [PubMed]
- Cho, I.J.; Moon, J.; Shim, C.Y.; Jang, Y.; Chung, N.; Chang, B.C.; Ha, J.W. Different Clinical Outcome of Paravalvular Leakage After Aortic or Mitral Valve Replacement. Am. J. Cardiol. 2011, 107, 280–284. [Google Scholar] [CrossRef] [PubMed]

| Model Version | a | b | c | d | e |
|---|---|---|---|---|---|
| Equation (3) | - | 5.57 × 10−4 | 2.45 × 10−5 | 2.67 × 10−6 | 1.14 × 10−6 |
| Equation (4) | 1.62 × 10−7 | 1.82 × 10−7 | 3.08 × 10−5 | 3.42 × 10−6 | 1.72 × 10−6 |
| Mesh | Cells | Faces | Nodes |
|---|---|---|---|
| Coarse | 117,950 | 263,649 | 37,829 |
| Medium | 943,600 | 2,080,556 | 284,342 |
| Fine | 7,548,800 | 16,529,904 | 2,204,660 |
| Error Type | k-epsilon 1 | k-epsilon 2 | k-omega 1 | k-omega 2 |
|---|---|---|---|---|
| Mean Absolute Error | 0.187 | 0.165 | 0.072 | 0.104 |
| Root Mean Square Error | 0.109 | 0.086 | 0.016 | 0.028 |
| Fluid | Density (kg/m3) | Kinematic Viscosity (m2/s) | Dynamic Viscosity (Pa·s) |
|---|---|---|---|
| Test Fluid | 1796 | 1.57 × 10−6 | - |
| Blood | 1050 | - | 0.002 |
| Model Version | Functioning Valve | Malfunctioning Valve | ||
|---|---|---|---|---|
| 1.25 m/s | 1.5 m/s | 1.25 m/s | 1.5 m/s | |
| Equation (3) | 0.675% | 0.716% | 0.833% | 0.818% |
| Equation (4) | 1.097% | 1.135% | 1.273% | 1.314% |
| Model Version | Functioning Valve | Malfunctioning Valve | ||
|---|---|---|---|---|
| 1.25 m/s | 1.5 m/s | 1.25 m/s | 1.5 m/s | |
| Equation (3) | 8.806 × 10−9% | 2.402 × 10−8% | 1.995 × 10−7% | 6.615 × 10−7% |
| Equation (4) | 4.496 × 10−9% | 1.867 × 10−8% | 1.405 × 10−7% | 4.264 × 10−7% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
James, M.E.; Papavassiliou, D.V.; O’Rear, E.A. Use of Computational Fluid Dynamics to Analyze Blood Flow, Hemolysis and Sublethal Damage to Red Blood Cells in a Bileaflet Artificial Heart Valve. Fluids 2019, 4, 19. https://doi.org/10.3390/fluids4010019
James ME, Papavassiliou DV, O’Rear EA. Use of Computational Fluid Dynamics to Analyze Blood Flow, Hemolysis and Sublethal Damage to Red Blood Cells in a Bileaflet Artificial Heart Valve. Fluids. 2019; 4(1):19. https://doi.org/10.3390/fluids4010019
Chicago/Turabian StyleJames, Madison E., Dimitrios V. Papavassiliou, and Edgar A. O’Rear. 2019. "Use of Computational Fluid Dynamics to Analyze Blood Flow, Hemolysis and Sublethal Damage to Red Blood Cells in a Bileaflet Artificial Heart Valve" Fluids 4, no. 1: 19. https://doi.org/10.3390/fluids4010019
APA StyleJames, M. E., Papavassiliou, D. V., & O’Rear, E. A. (2019). Use of Computational Fluid Dynamics to Analyze Blood Flow, Hemolysis and Sublethal Damage to Red Blood Cells in a Bileaflet Artificial Heart Valve. Fluids, 4(1), 19. https://doi.org/10.3390/fluids4010019







