The Use of Semigeostrophic Theory to Diagnose the Behaviour of an Atmospheric GCM
Abstract
1. Introduction
2. Materials and Methods
2.1. The SG Approximation to the UM Equations
2.2. The Diagnostic Equations
2.3. Application
2.4. Computational Aspects
3. Results
3.1. Experimental Setup
3.2. Comparison of Diagnostic and Model-Derived Ageotriptic Winds
3.3. Use of a Modified Static Stability to Represent Latent Heat Release
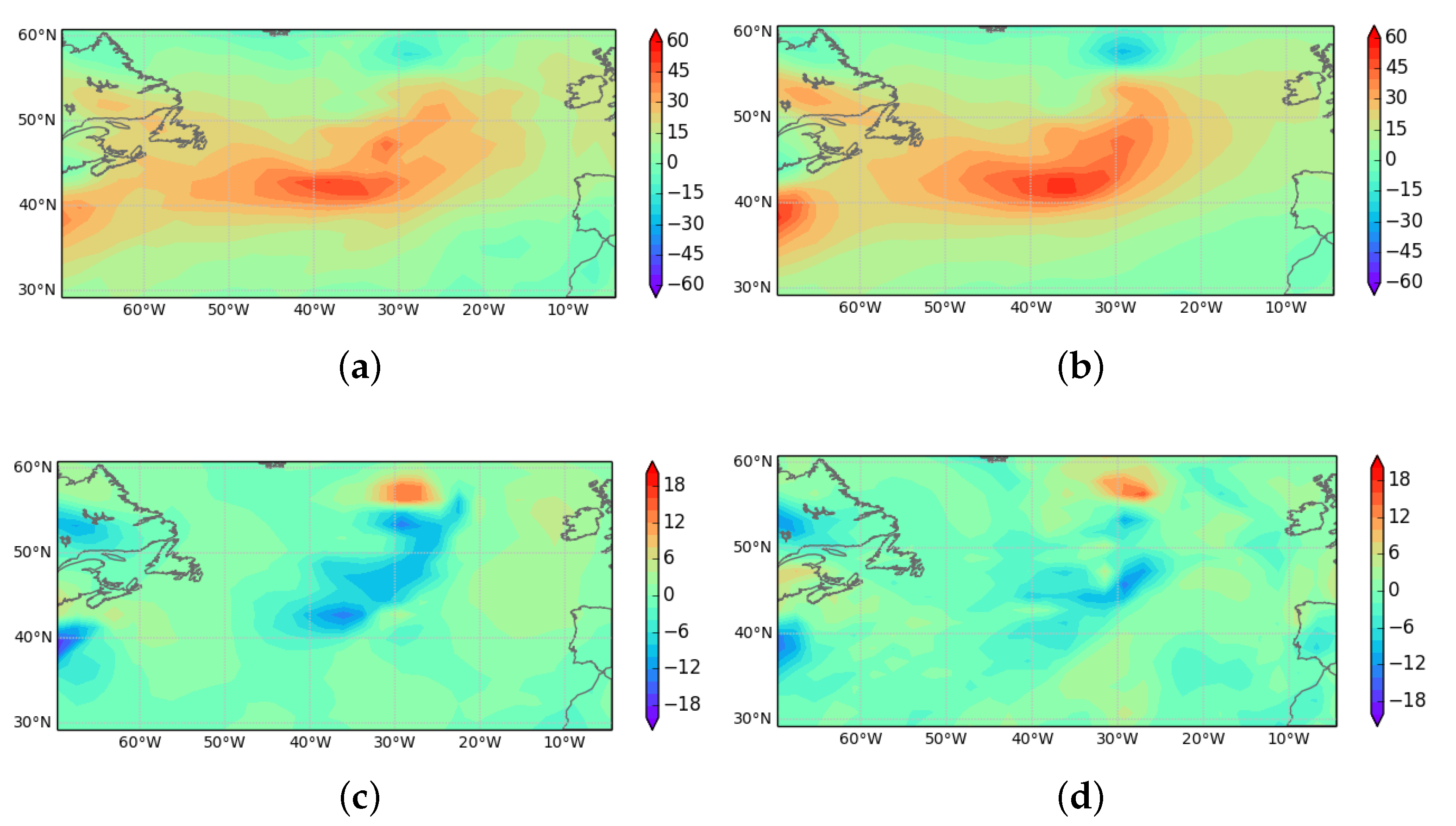
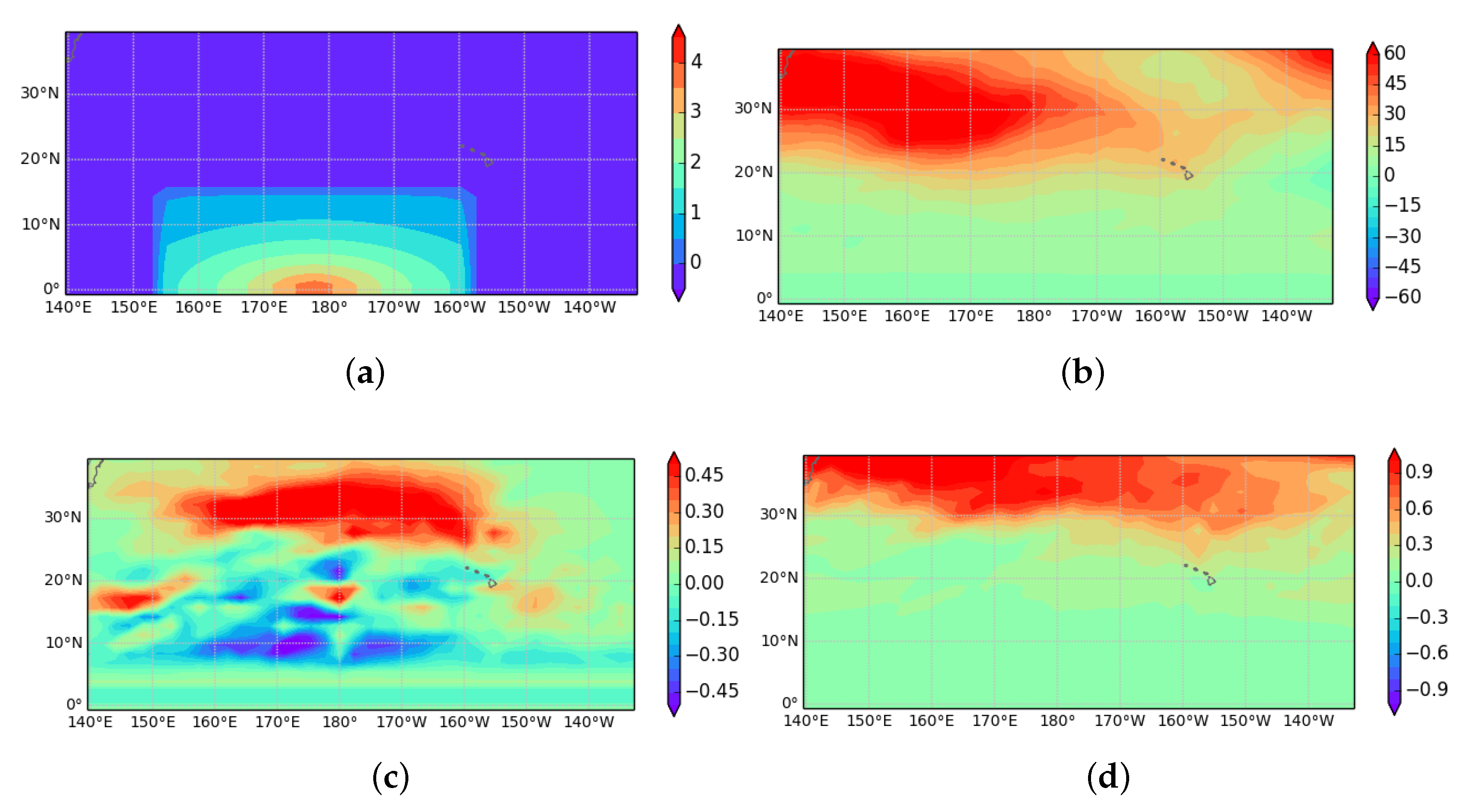
3.4. Effect of Tropical Heating on the Subtropical Jet
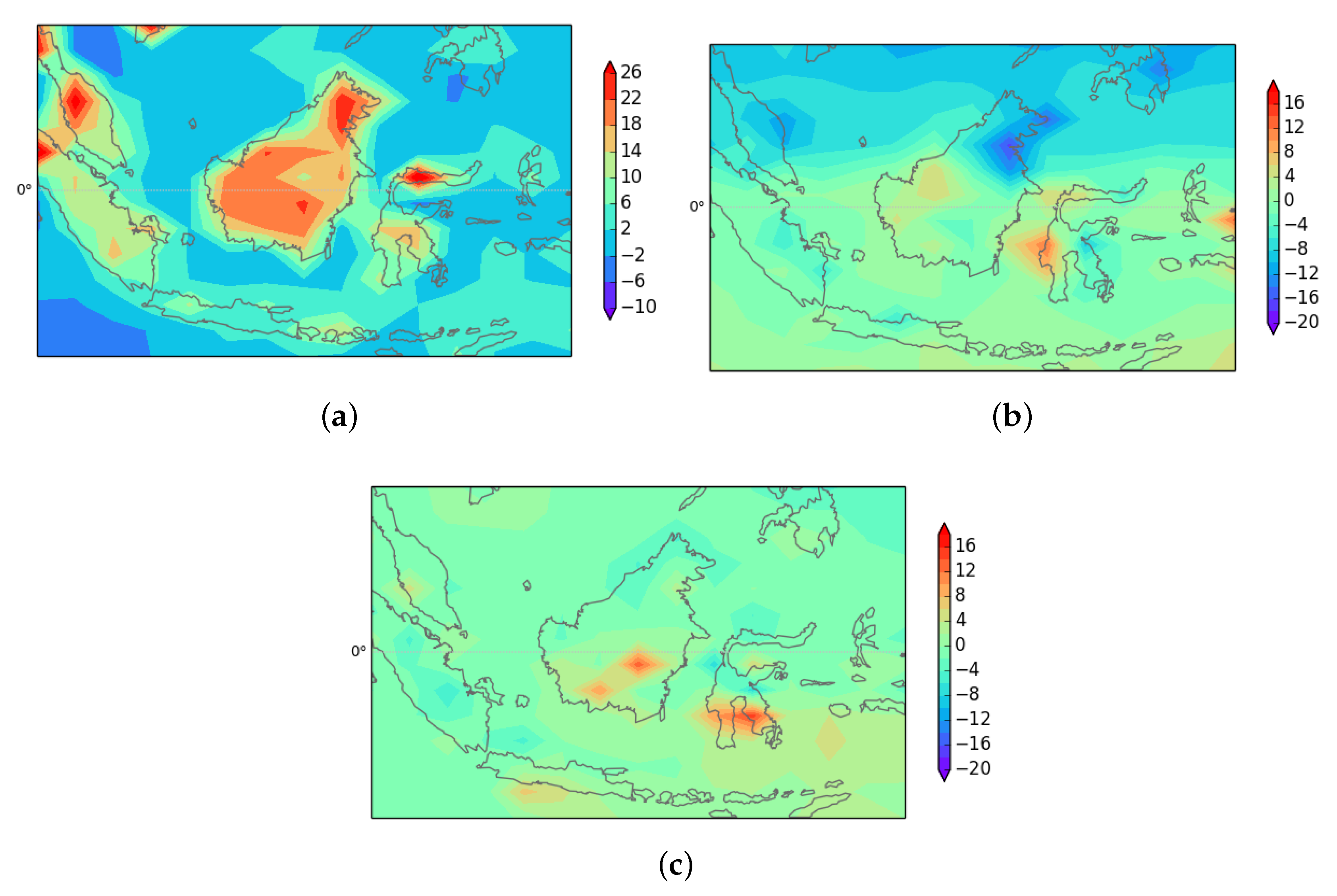
3.5. Effect of Boundary Layer Heating
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GCM | General Circulation Model |
| SEE | Sawyer–Eliassen equation |
| SG | semi-geostrophic |
| SGT | semi-geotriptic |
| UM | Unified Model |
| WTG | Weak Temperature Gradient |
References
- Brown, A.; Milton, S.; Cullen, M.; Golding, B.; Mitchell, J.; Shelly, A. Unified modeling and prediction of weather and climate: A 25-year journey. Bull. Am. Meteorol. Soc. 2012, 93, 1865–1877. [Google Scholar] [CrossRef]
- Martin, G.M.; Milton, S.F.; Senior, C.A.; Brooks, M.E.; Ineson, S.; Reichler, T.; Kim, J. Analysis and reduction of systematic errors through a seamless approach to modeling weather and climate. J. Clim. 2010, 23, 5933–5957. [Google Scholar] [CrossRef]
- Sobel, A.H.; Nilsson, J.; Polvani, L.M. The weak temperature gradient approximation and balanced tropical moisture waves. J. Atmos. Sci. 2001, 58, 3650–3665. [Google Scholar] [CrossRef]
- Beare, R.J.; Cullen, M.J.P. Diagnosis of boundary-layer circulations. Philos. Trans. R. Soc. A 2013, 371, 20110474. [Google Scholar] [CrossRef] [PubMed]
- Cullen, M.J.P. A Mathematical Theory of Large-Scale Atmospheric Flow; Imperial College Press: London, UK, 2006; 259p, ISBN 1-86094-518-X. [Google Scholar]
- Malardel, S.; Thorpe, A.J.; Joly, A. Consequences of the geostrophic momentum approximation on barotropic instability. J. Atmos. Sci. 1997, 54, 103–112. [Google Scholar] [CrossRef]
- Cullen, M.J.P.; Mawson, M.H. An idealised simulation of the Indian monsoon using primitive-equation and quasi-equilibrium models. Quart. J. R. Meteorol. Soc. 1992, 118, 153–164. [Google Scholar]
- Eliassen, A. The quasi-static equations of motion with pressure as independent variable. Geofys. Publ. 1950, 17, 3–43. [Google Scholar]
- Charney, J.G. On the scale of atmospheric motions. Geofys. Publ. 1948, 17, 4–17. [Google Scholar]
- Phillips, N.A. Geostrophic motion. Rev. Geophys. 1963, 1, 123–176. [Google Scholar] [CrossRef]
- Eliassen, A. Geostrophy. Quart. J. R. Meteorol. Soc. 1984, 110, 1–12. [Google Scholar] [CrossRef]
- Hoskins, B.J. The mathematical theory of frontogenesis. Ann. Rev. Fluid Mech. 1982, 14, 131–151. [Google Scholar] [CrossRef]
- Cullen, M.J.P.; Douglas, R.J.; Roulstone, I.; Sewell, M.J. Generalised semi-geostrophic theory on a sphere. J. Fluid Mech. 2005, 531, 123–157. [Google Scholar] [CrossRef]
- Cullen, M.J.P. Analysis of the semi-geostrophic shallow water equations. Phys. D 2008, 237, 1461–1465. [Google Scholar] [CrossRef]
- Cheng, J.; Cullen, M.J.P.; Feldman, M. Semi-geostrophic system with variable Coriolis parameter. Arch. Ration. Mech. Anal. 2016, 1–58. [Google Scholar] [CrossRef]
- Schubert, W.H. Semi-geostrophic theory. J. Atmos. Sci. 1985, 42, 1770–1772. [Google Scholar] [CrossRef]
- Xu, Q. Extended Sawyer-Eliassen Equation for Frontal Circulations in the Presence of small Viscous Moist Symmetric Stability. J. Atmos. Sci. 1989, 46, 2671–2683. [Google Scholar] [CrossRef]
- Cullen, M.J.P. Semigeostrophic solutions for flow over a ridge. Quart. J. R. Meteorol. Soc. 2007, 133, 491–501. [Google Scholar] [CrossRef]
- Thorpe, A.J.; Pedder, M.A. The semi-geostrophic diagnosis of vertical motion. II: Results for an idealized baroclinic wave life cycle. Quart. J. R. Meteorol. Soc. 1999, 125, 1257–1276. [Google Scholar]
- Wernli, H.; Fehlmann, R.; Luthi, D. The Effect of Barotropic Shear on Upper-Level Induced Cyclogenesis: Semigeostrophic and Primitive Equation Numerical Simulations. J. Atmos. Sci. 1998, 55, 2080–2094. [Google Scholar] [CrossRef]
- Ragone, F.; Badin, G. A study of surface semi-geostrophic turbulence: Freely decaying dynamics. J. Fluid Mech. 2016, 792, 740–774. [Google Scholar] [CrossRef]
- Jin, F.; Hoskins, B.J. The direct response to tropical heating in a baroclinic atmosphere. J. Atmos. Sci. 1995, 52, 307–319. [Google Scholar] [CrossRef]
- Schubert, W.H.; Ciesieleski, P.E.; Stevens, D.E.; Kuo, H.-C. Potential vorticity modelling of the ITCZ and the Hadley circulation. J. Atmos. Sci. 1991, 48, 1493–1509. [Google Scholar] [CrossRef]
- Wood, N.; Staniforth, A.; White, A.; Allen, T.; Diamantakis, M.; Gross, M.; Melvin, T.; Smith, C.; Vosper, S.; Zerroukat, M.; et al. An inherently mass-conserving semi-implicit semi-Lagrangian discretization of the deep-atmosphere global nonhydrostatic equations. Quart. J. R. Meteorol. Soc. 2014, 140, 1505–1520. [Google Scholar] [CrossRef]
- White, A.A.; Hoskins, B.J.; Roulstone, I.; Staniforth, A. Consistent approximate models of the global atmosphere: Shallow, deep, hydrostatic, quasi-hydrostatic and non-hydrostatic. Quart. J. R. Meteorol. Soc. 2005, 131, 2081–2108. [Google Scholar] [CrossRef]
- Beare, R.J.; Cullen, M.J.P. Validating weather and climate models at small Rossby numbers: Including a boundary layer. Quart. J. R. Meteorol. Soc. 2016, 142, 2636–2645. [Google Scholar] [CrossRef]
- Holton, J.R.; Hakim, G.J. An Introduction to Dynamic Meteorology, 5th ed.; Academic Press: Cambridge, MA, USA, 2013; ISBN 978-0-12-384866-6. [Google Scholar]
- Booth, J.F.; Polvani, L.; O’Gorman, P.A.; Wang, S. Effective stability in a moist baroclinic wave. Atmos. Sci. Lett. 2015, 16, 56–62. [Google Scholar] [CrossRef]
- Hinch, E.J. Perturbation Methods; Cambridge University Press: Cambridge, UK, 1991; ISBN 0-521-37310-7. [Google Scholar]
- Matthews, A.J.; Hoskins, B.J.; Masutani, M. The global response to tropical heating in the Madden-Julian oscillation during the northern winter. Quart. J. R. Meteorol. Soc. 2004, 130, 1991–2011. [Google Scholar] [CrossRef]
- Smith, R.K.; Spengler, T. The dynamics of heat lows over elevated terrain. Quart. J. R. Meteorol. Soc. 2011, 137, 250–263. [Google Scholar] [CrossRef]

© 2018 Crown Copyright, Met Office. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cullen, M. The Use of Semigeostrophic Theory to Diagnose the Behaviour of an Atmospheric GCM. Fluids 2018, 3, 72. https://doi.org/10.3390/fluids3040072
Cullen M. The Use of Semigeostrophic Theory to Diagnose the Behaviour of an Atmospheric GCM. Fluids. 2018; 3(4):72. https://doi.org/10.3390/fluids3040072
Chicago/Turabian StyleCullen, Mike. 2018. "The Use of Semigeostrophic Theory to Diagnose the Behaviour of an Atmospheric GCM" Fluids 3, no. 4: 72. https://doi.org/10.3390/fluids3040072
APA StyleCullen, M. (2018). The Use of Semigeostrophic Theory to Diagnose the Behaviour of an Atmospheric GCM. Fluids, 3(4), 72. https://doi.org/10.3390/fluids3040072