Comparison of Blade Element Method and CFD Simulations of a 10 MW Wind Turbine
Abstract
1. Motivation and State of the Art
2. Simulation Approaches
2.1. Blade Element and Momentum
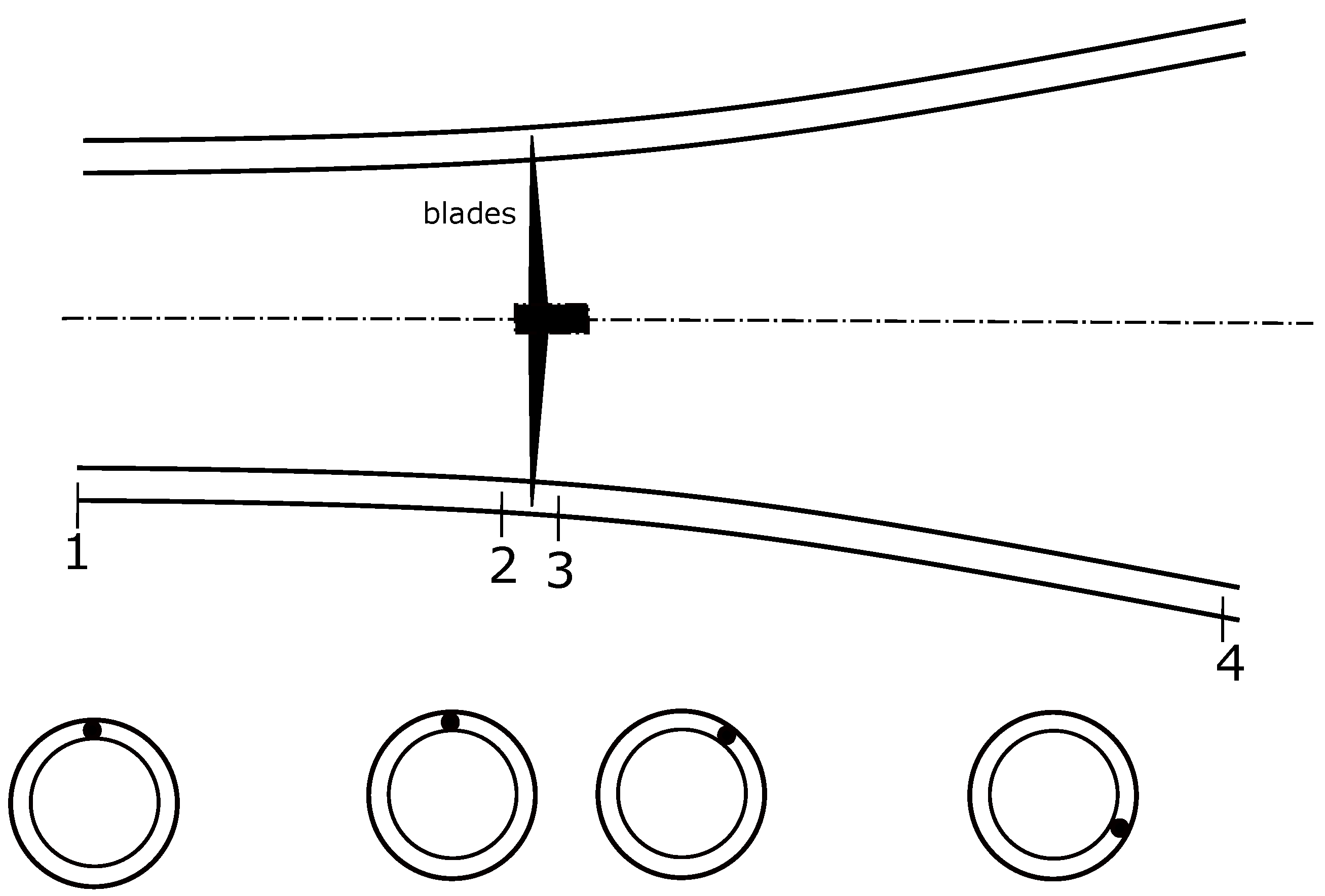
2.1.1. One Dimensional Momentum Theory and the Momentum Transfer
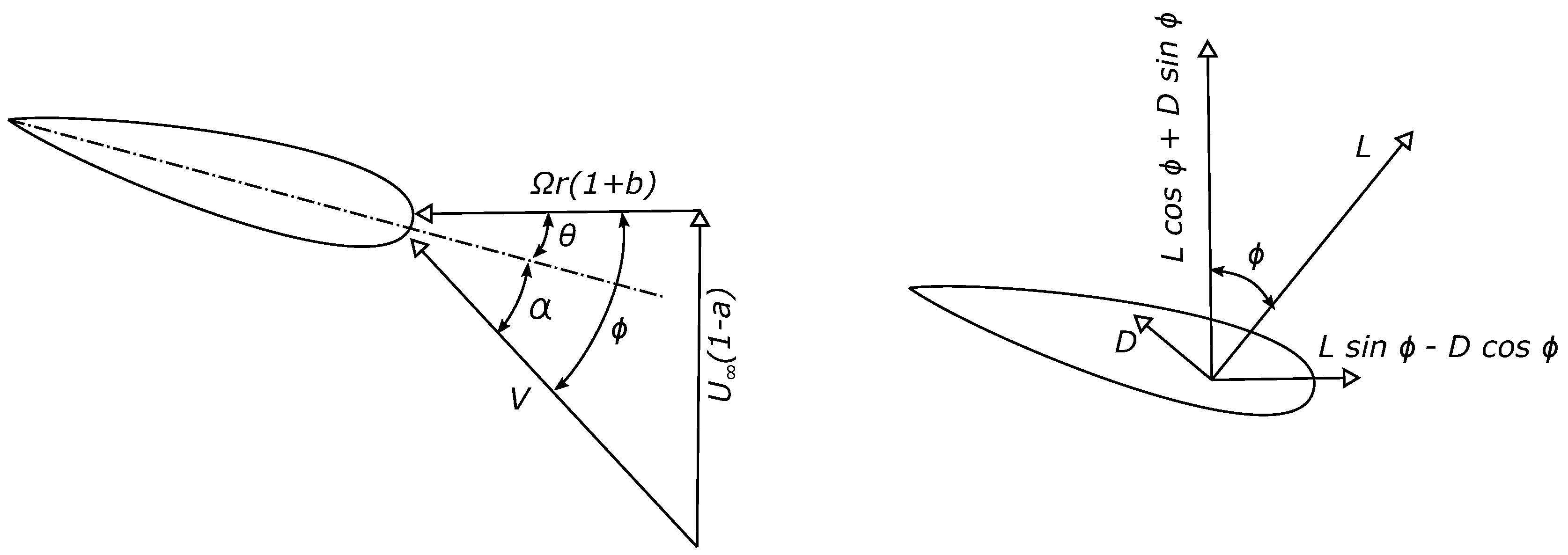
2.1.2. Blade Element Theory
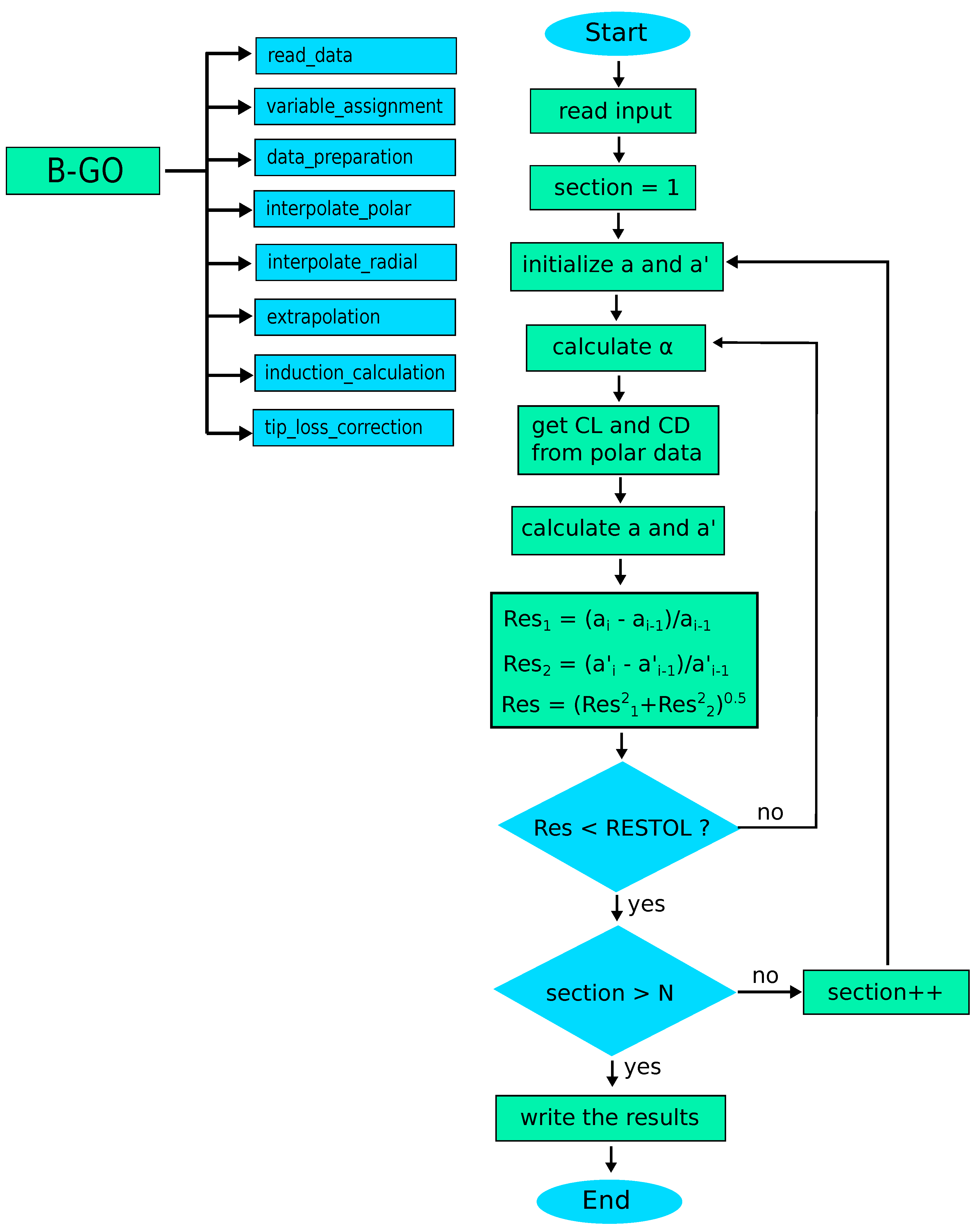
2.1.3. B-GO Code Description
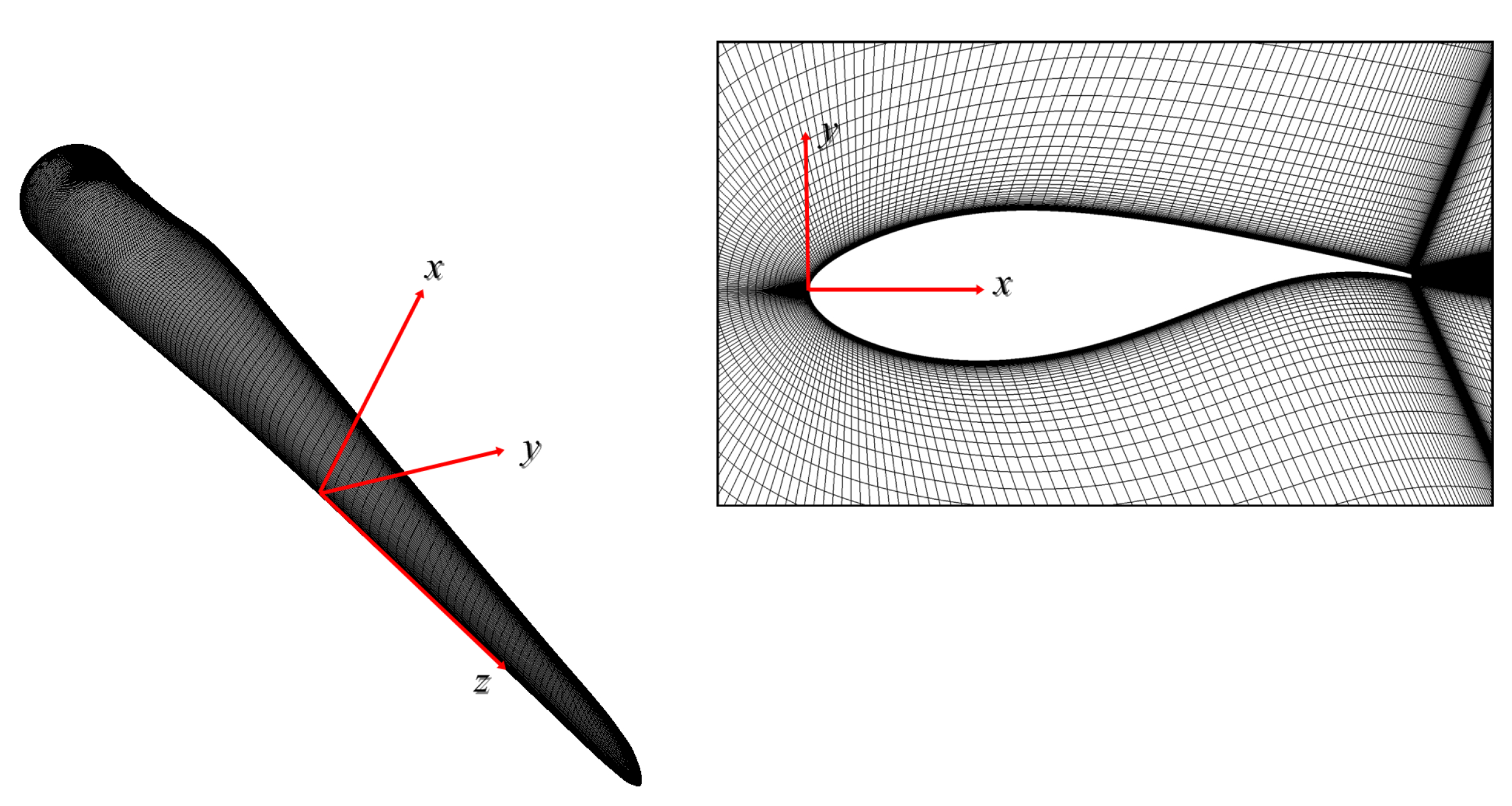
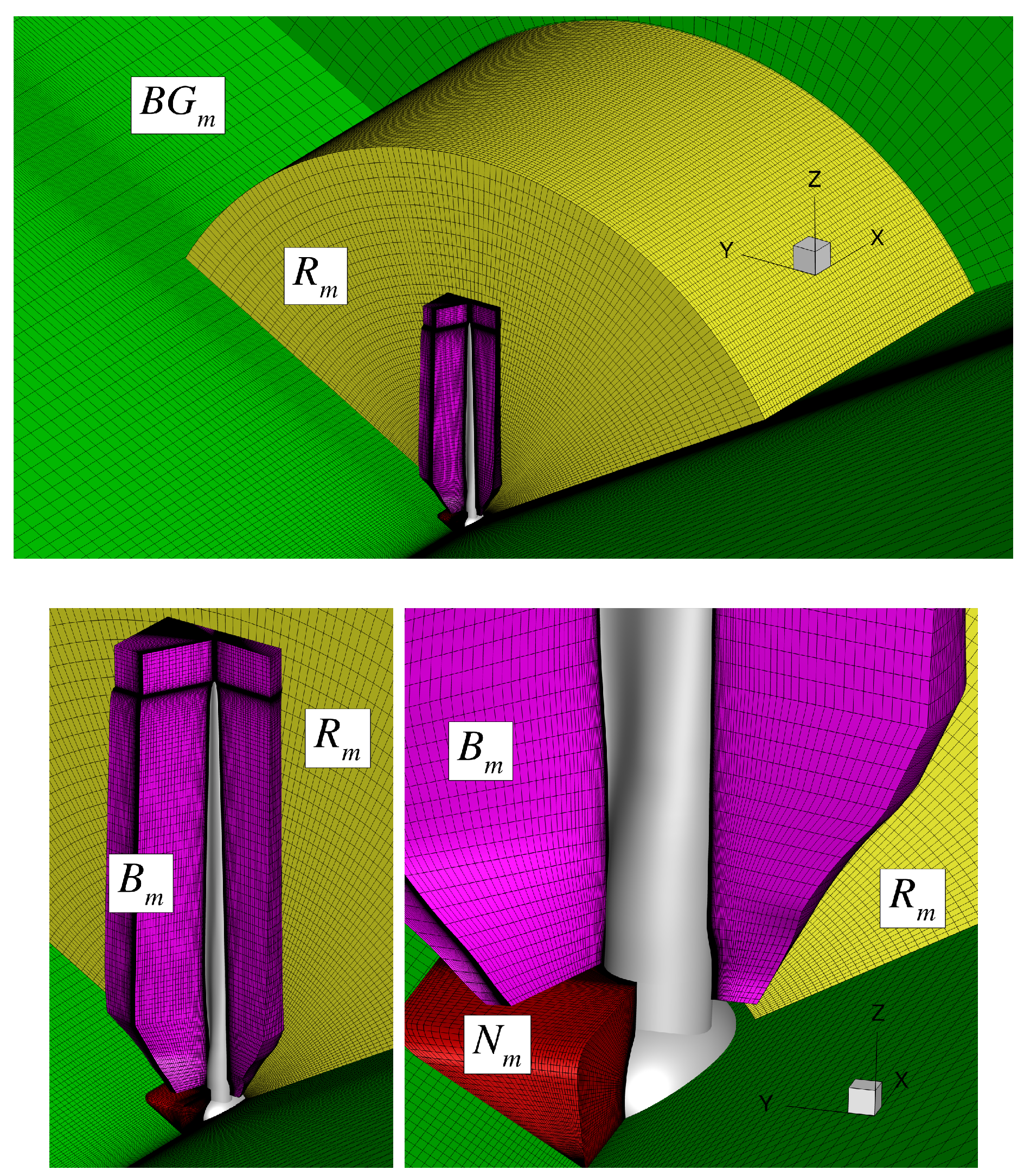
2.2. Computational Fluid Dynamics
3. Results and Discussion
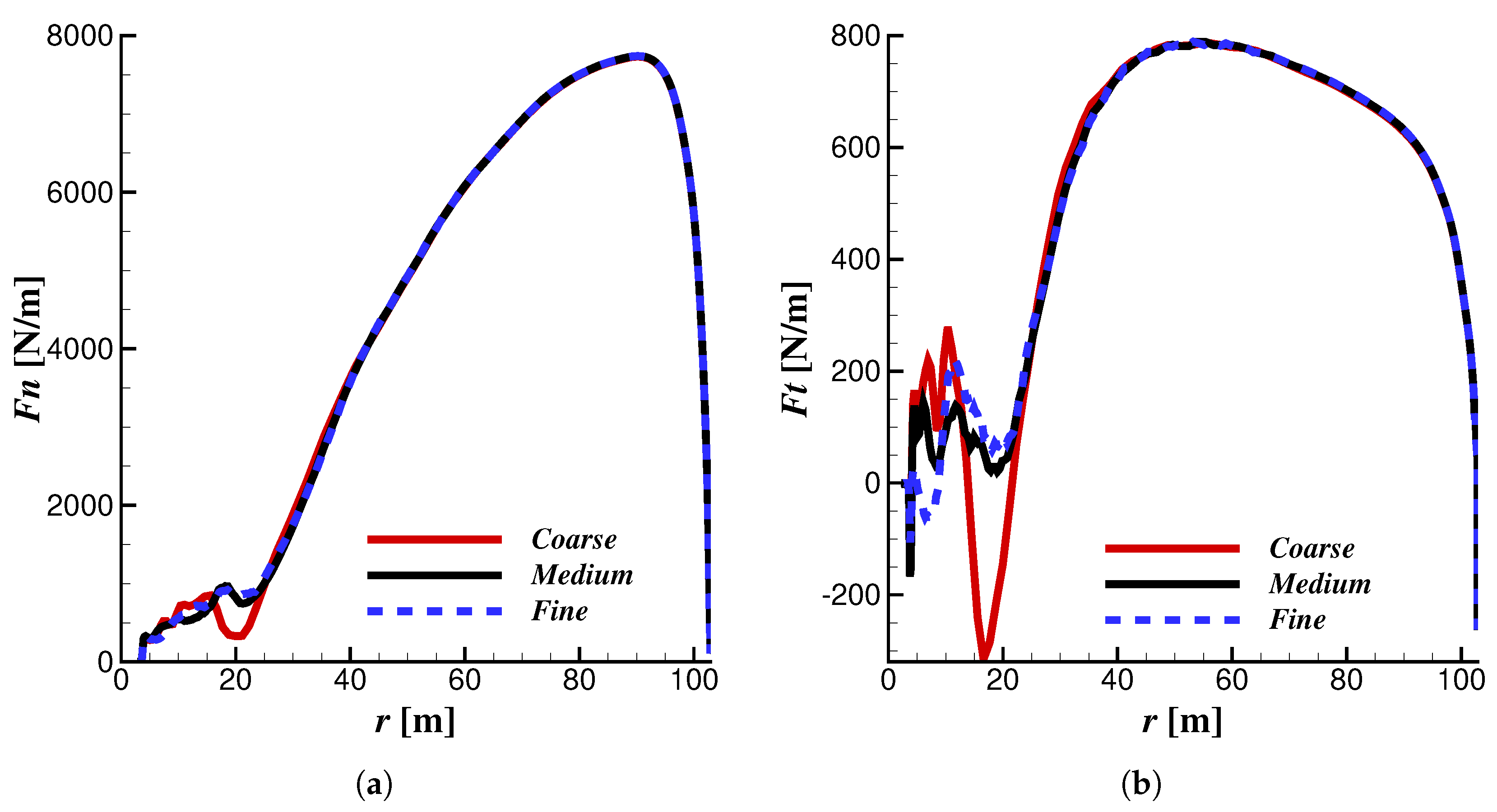
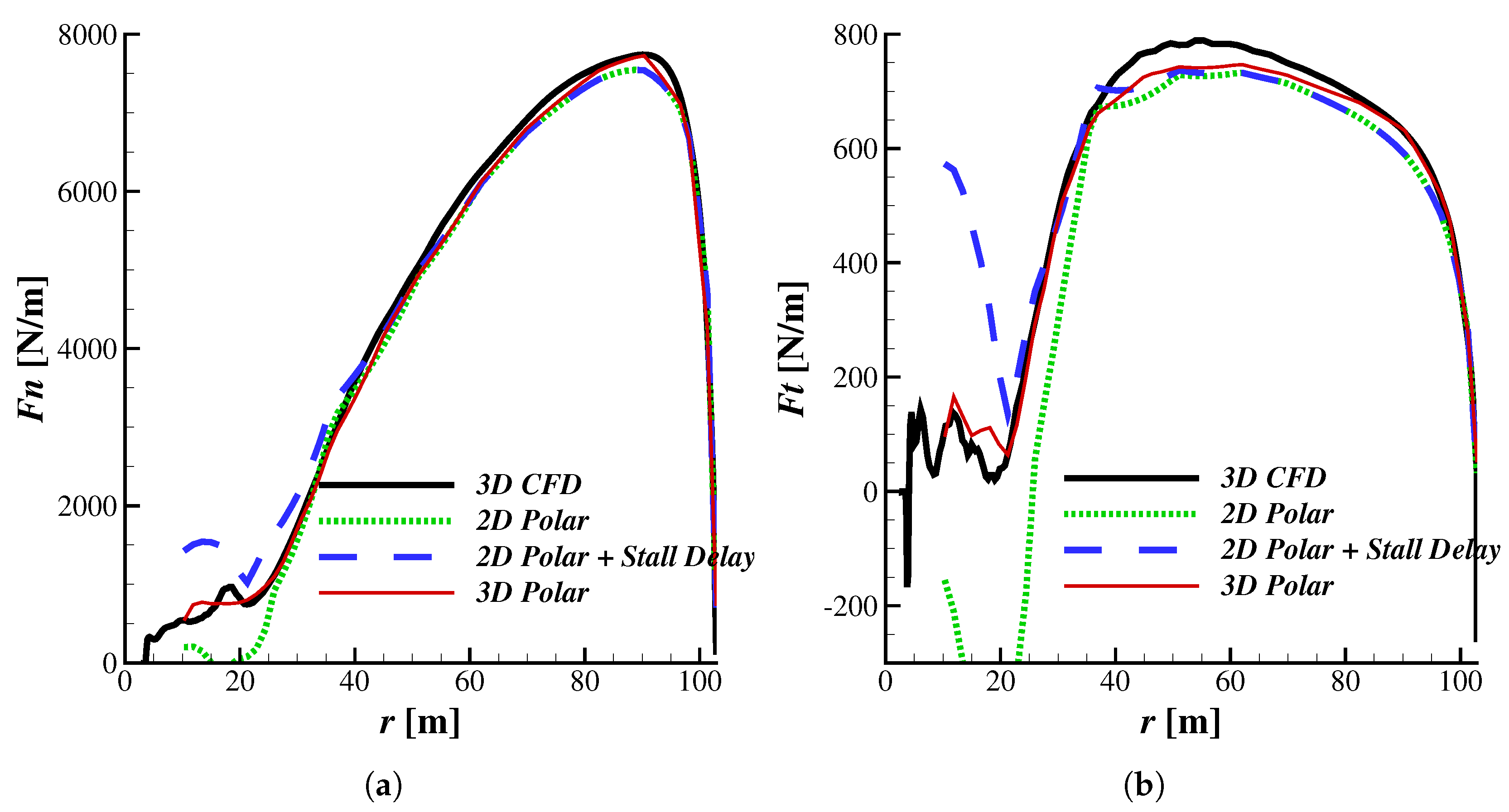
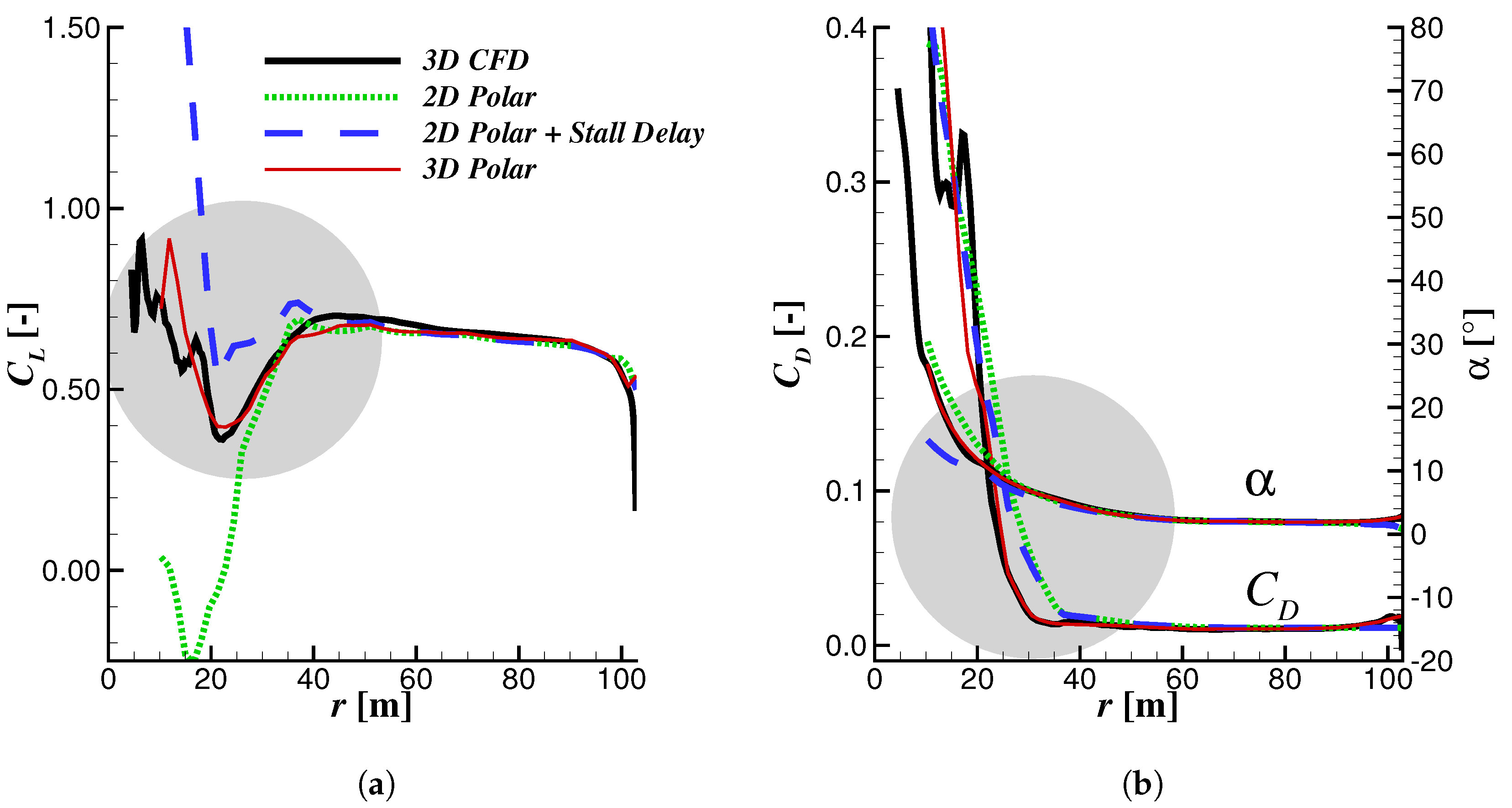
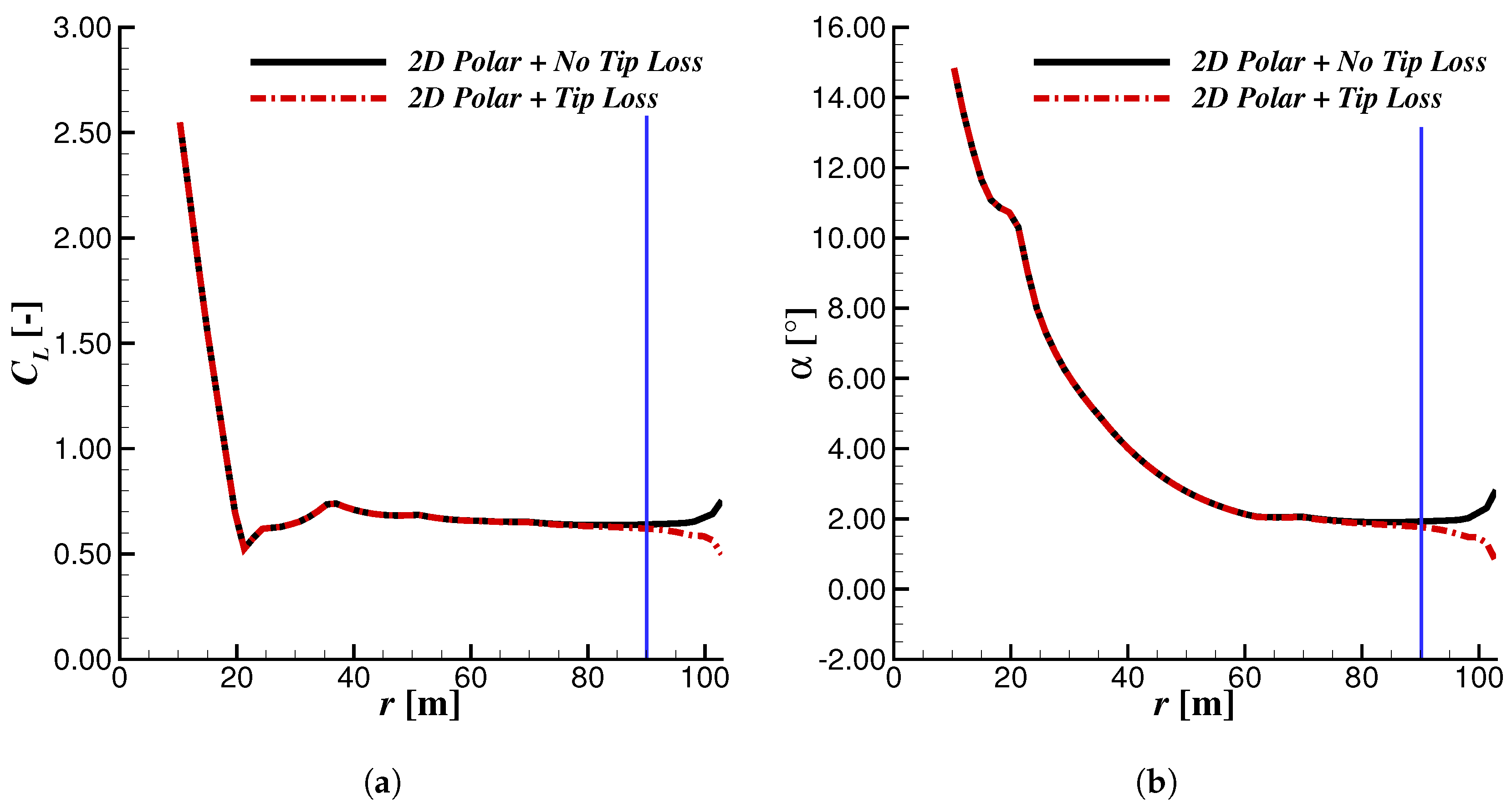
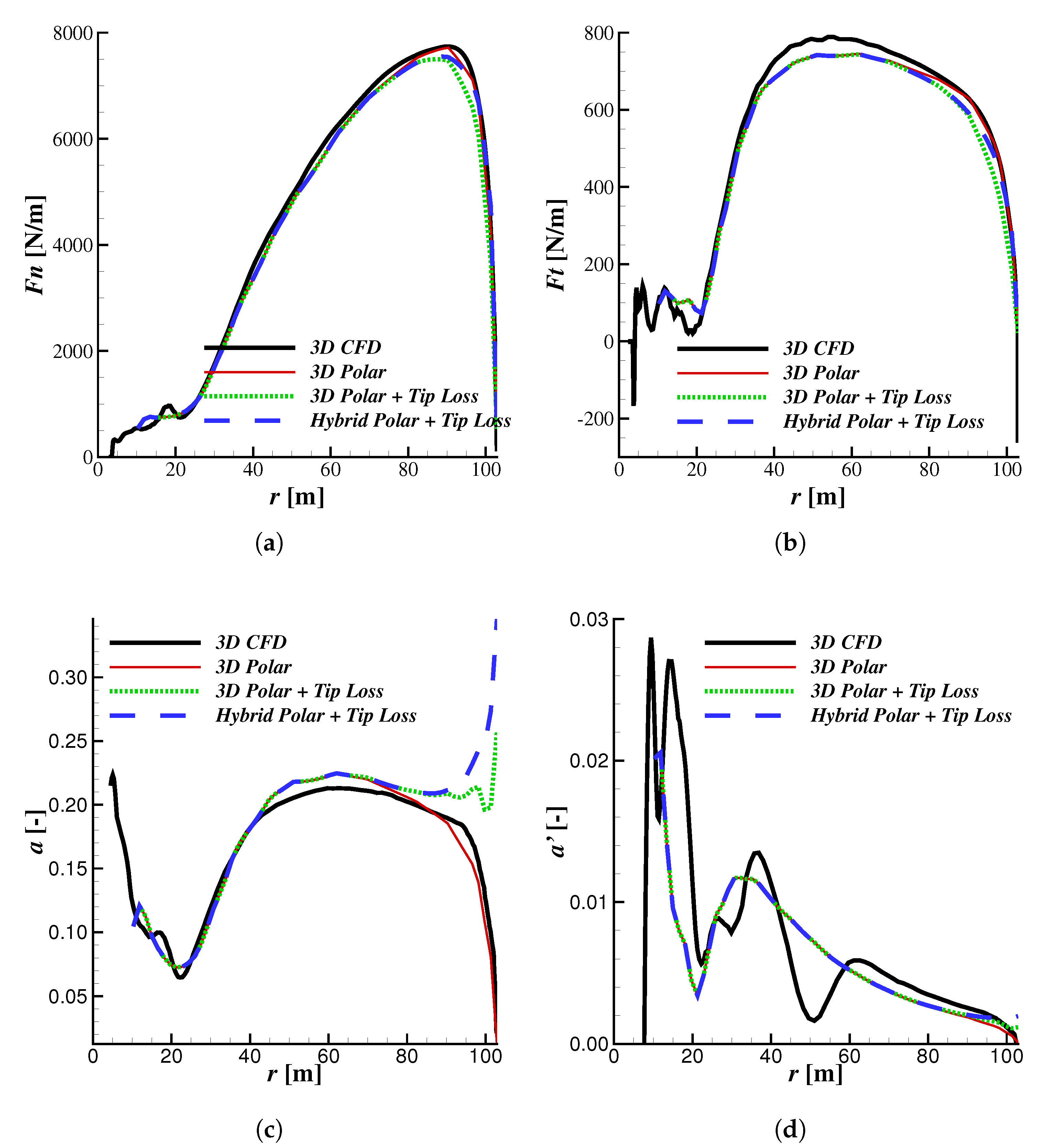
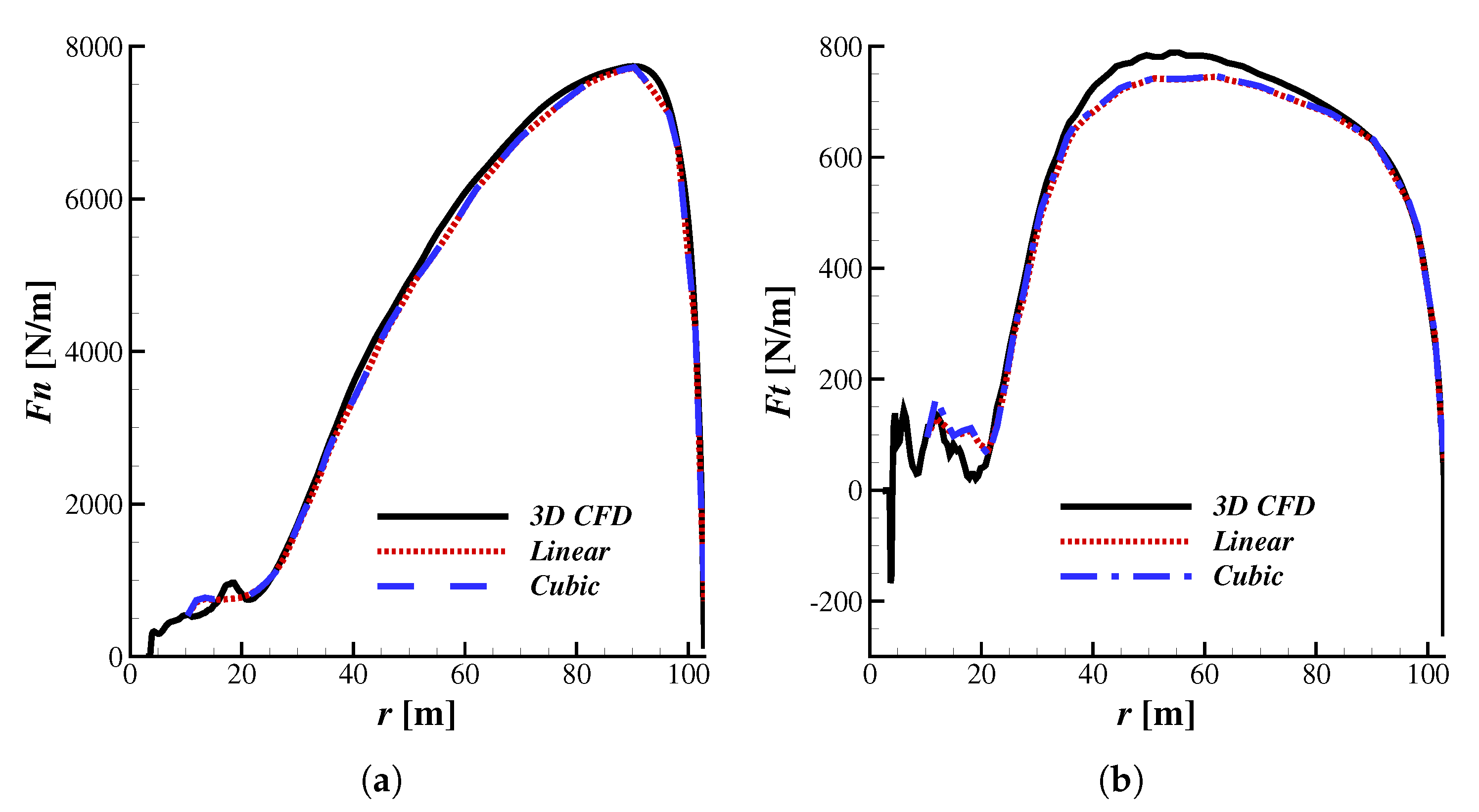
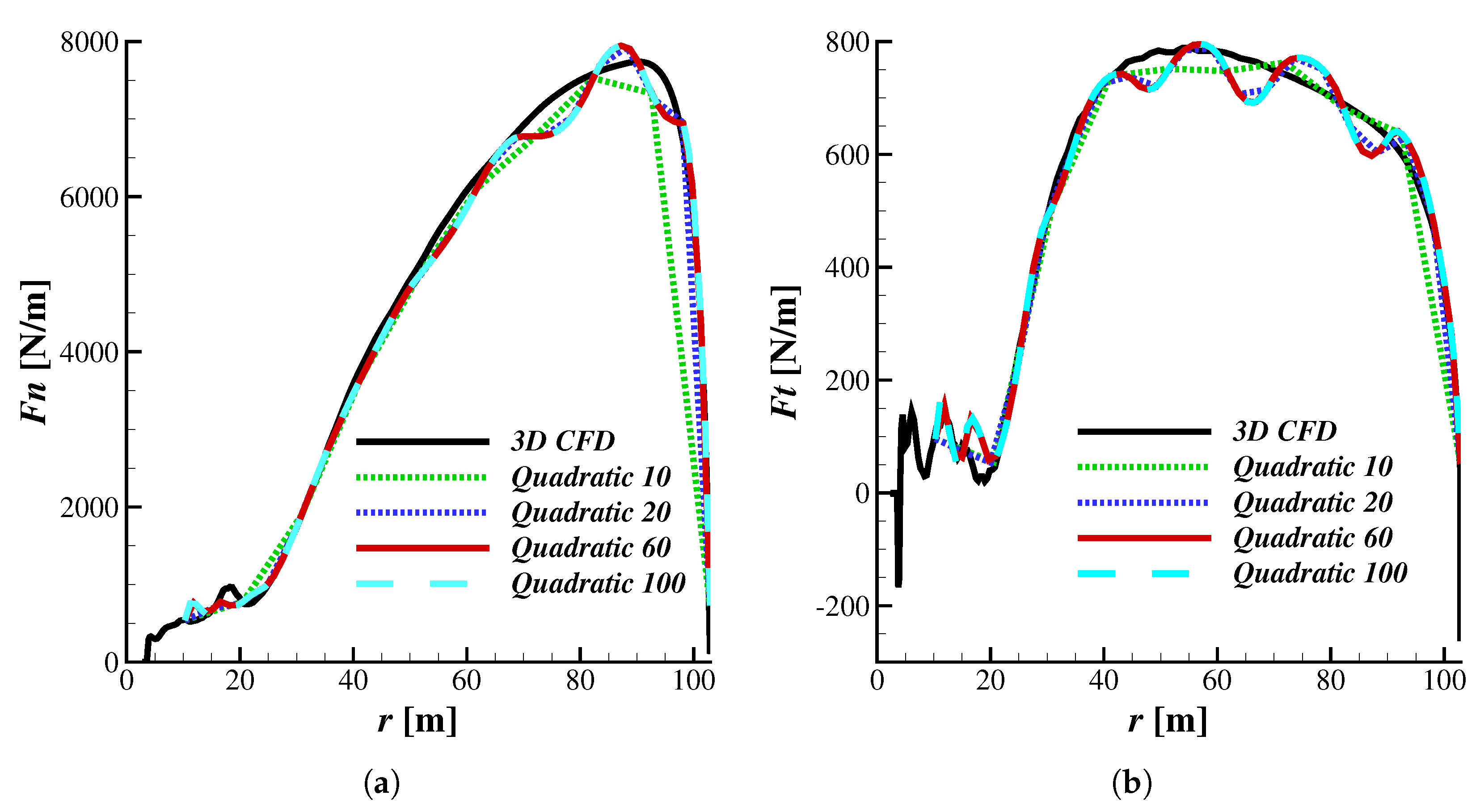
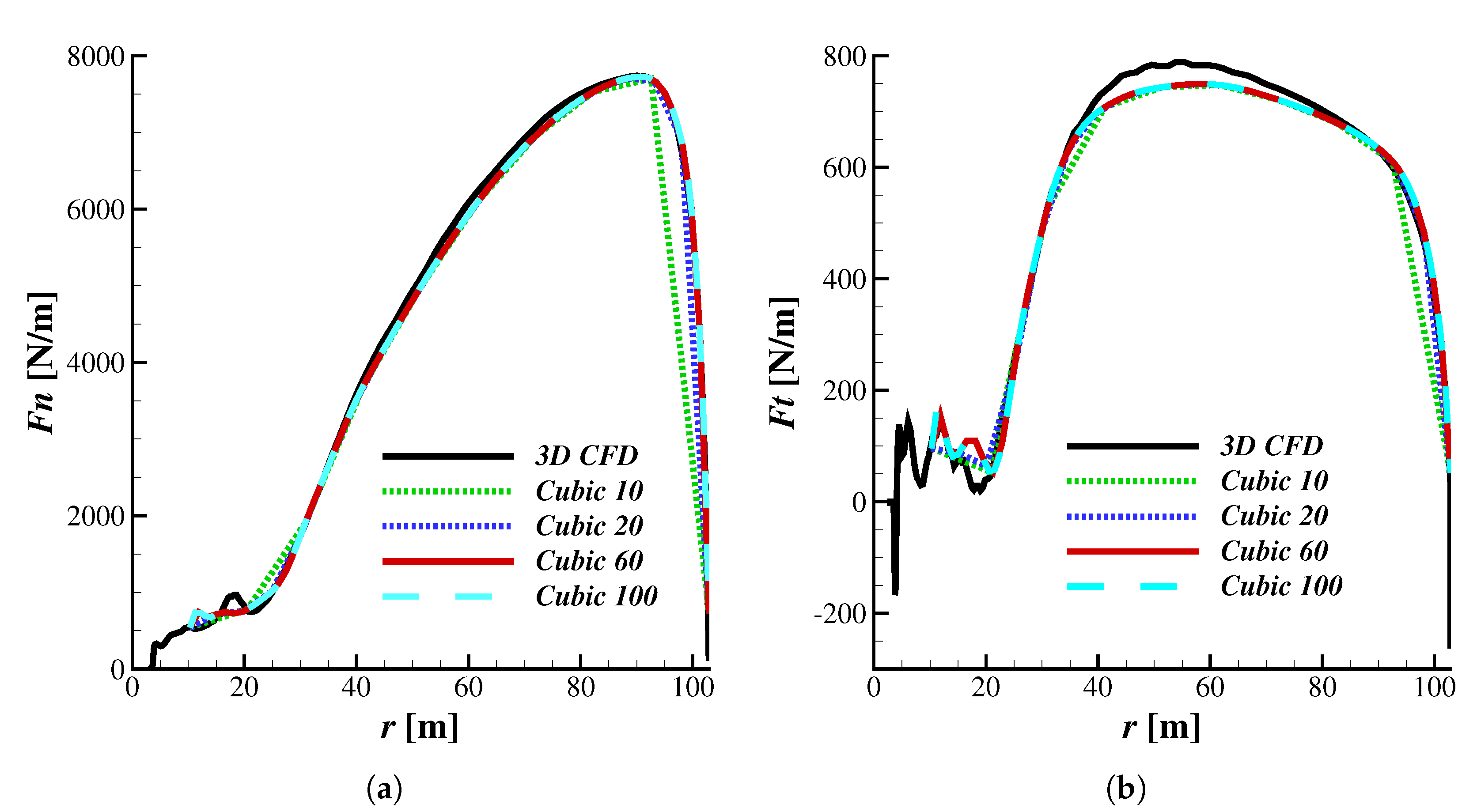
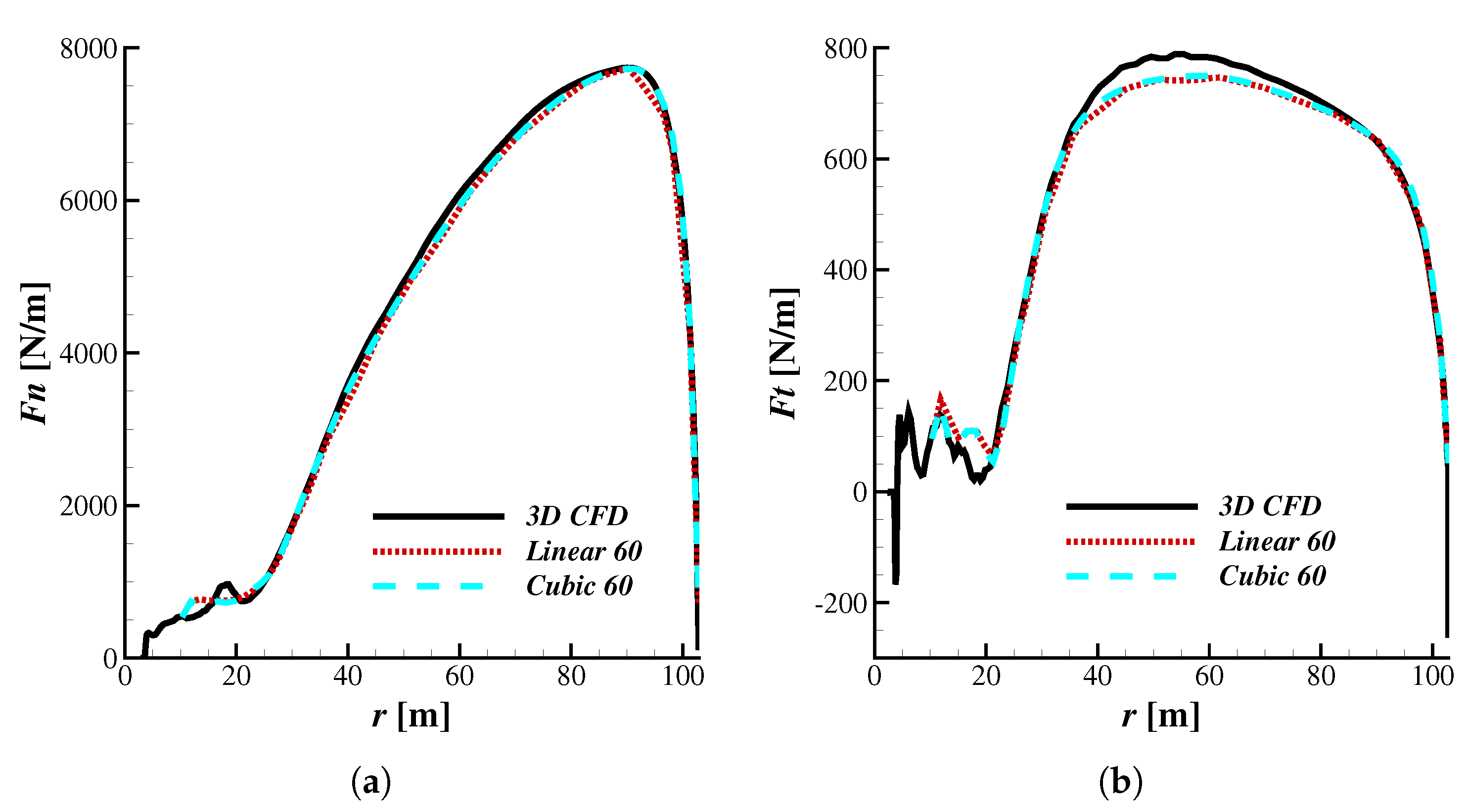
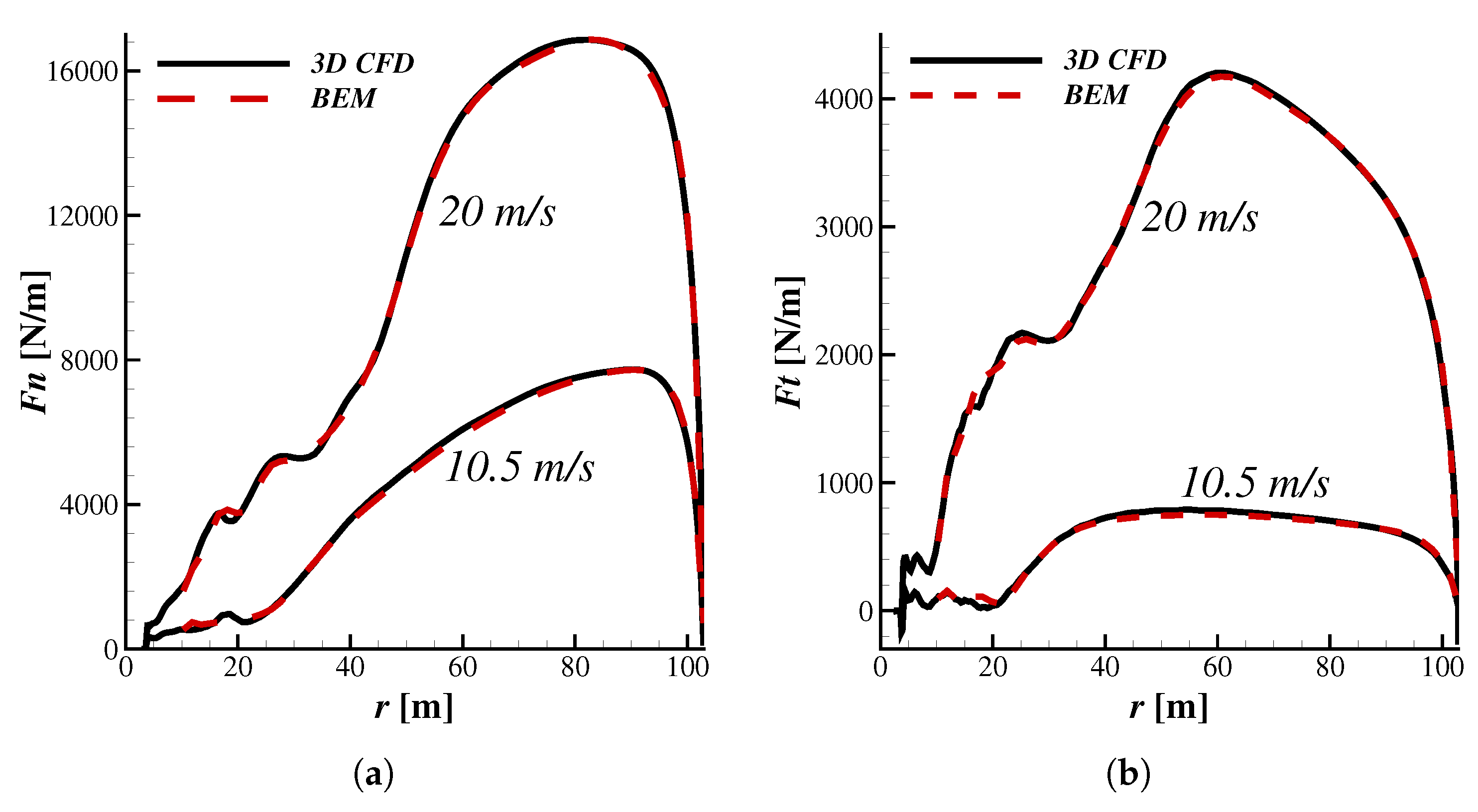
3.1. 3D CFD and BEM Comparison
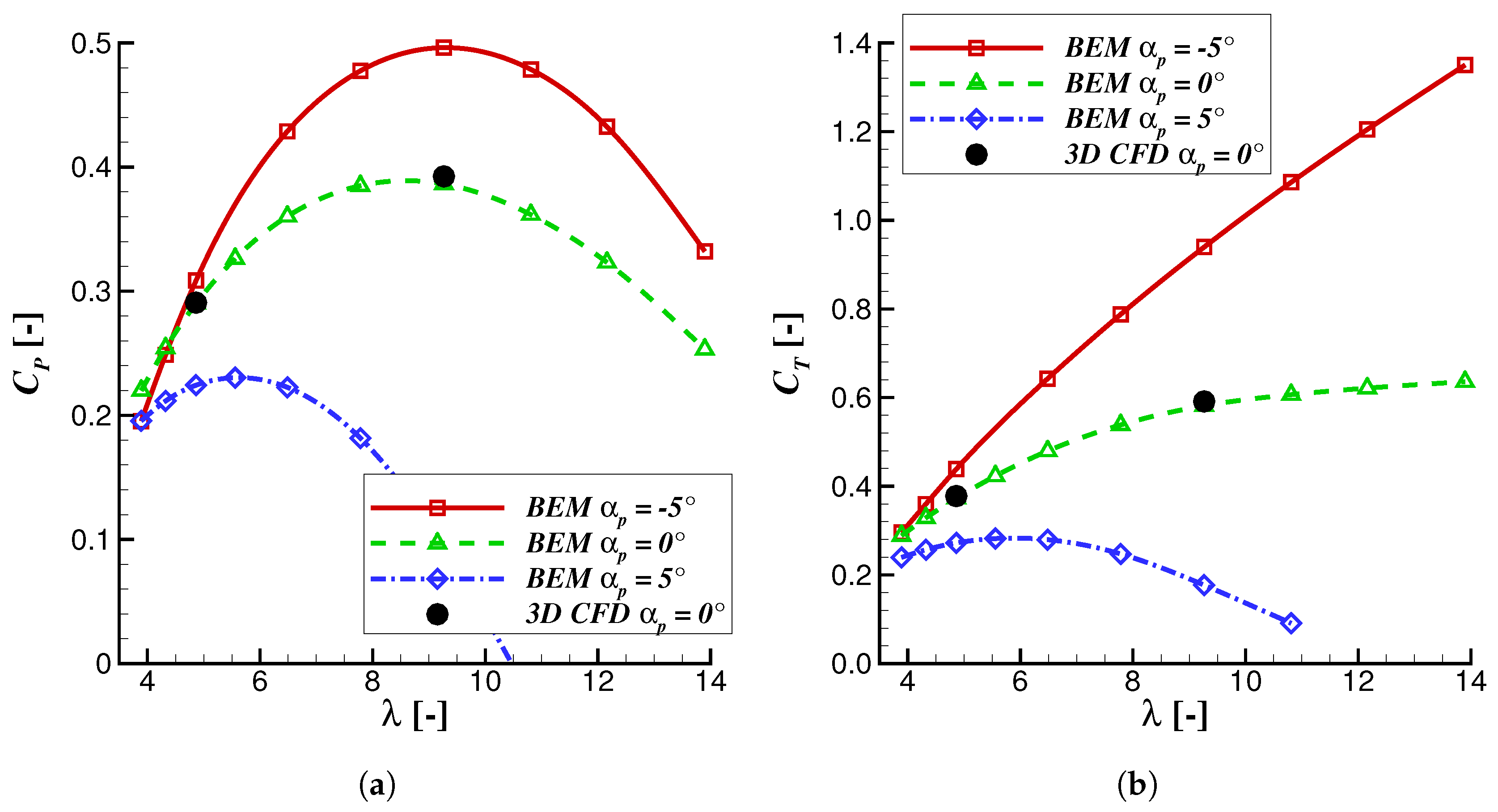
3.2. Simulations at Various Operating Conditions
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Bangga, G.; Hutomo, G.; Syawitri, T.; Kusumadewi, T.; Oktavia, W.; Sabila, A.; Setiadi, H.; Faisal, M.; Hendranata, Y.; Lastomo, D.; et al. Enhancing BEM simulations of a stalled wind turbine using a 3D correction model. J. Phys. Conf. Ser. 2018, 974, 012020. [Google Scholar] [CrossRef]
- Hutomo, G.; Bangga, G.; Sasongko, H. CFD studies of the dynamic stall characteristics on a rotating airfoil. Appl. Mech. Mater. 2016, 836, 109–114. [Google Scholar] [CrossRef]
- Bangga, G.; Lutz, T.; Dessoky, A.; Krämer, E. Unsteady Navier-Stokes studies on loads, wake, and dynamic stall characteristics of a two-bladed vertical axis wind turbine. J. Renew. Sustain. Energy 2017, 9, 053303. [Google Scholar] [CrossRef]
- Betz, A. Das Maximum der theoretisch möglichen Ausnutzung des Windes durch Windmotoren. Zeitschrift Gesamte Turbinenwesten 1920, 20, 307–309. [Google Scholar]
- Gasch, R.; Twele, J. Wind Power Plants: Fundamentals, Design, Construction and Operation; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Glauert, H. The Elements of Aerofoil and Airscrew Theory; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Ingram, G. Wind Turbine Blade Analysis Using the Blade Element Momentum Method Version 1.0; School of Engineering, Durham University: Durham, UK, 2005. [Google Scholar]
- Prandtl, L.; Betz, A. Vier Abhandlungen zur Hydrodynamik und Aerodynamik; Universitätsverlag Göttingen: Göttingen, Germany, 2010; Volume 3. [Google Scholar]
- Himmelskamp, H. Profile Investigations on a Rotating Airscrew; MAP: Göttingen, Germany, 1947. [Google Scholar]
- Sørensen, J.N. Three-Level, Viscous-Inviscid Interaction Technique for the Prediction of Separated Flow Past Rotating Wing. Ph.D. Thesis, Technical University of Denmark (DTU), Lyngby, Denmark, 1986. [Google Scholar]
- Snel, H.; Houwink, R.; Bosschers, J.; Piers, W.; Van Bussel, G.; Bruining, A. Sectional prediction of 3D effects for stalled flow on rotating blades and comparison with measurements. In Proceedings of the European Community Wind Energy Conference, HS Stevens and Associates, LÃ1, Travemuende, Germany, 8–12 March 1993; Volume 4. [Google Scholar]
- Du, Z.; Selig, M. The effect of rotation on the boundary layer of a wind turbine blade. Renew. Energy 2000, 20, 167–181. [Google Scholar] [CrossRef]
- Bangga, G. Three-Dimensional Flow in the Root Region of Wind Turbine Rotors; Kassel University Press GmbH: Kassel, Germany, 2018. [Google Scholar]
- Bangga, G.; Kim, Y.; Lutz, T.; Weihing, P.; Krämer, E. Investigations of the inflow turbulence effect on rotational augmentation by means of CFD. J. Phys. Conf. Ser. 2016, 753, 022026. [Google Scholar] [CrossRef]
- Bangga, G.; Lutz, T.; Jost, E.; Krämer, E. CFD studies on rotational augmentation at the inboard sections of a 10 MW wind turbine rotor. J. Renew. Sustain. Energy 2017, 9, 023304. [Google Scholar] [CrossRef]
- Bangga, G.; Lutz, T.; Krämer, E. Root flow characteristics and 3D effects of an isolated wind turbine rotor. J. Mech. Sci. Technol. 2017, 31, 3839–3844. [Google Scholar] [CrossRef]
- Wood, D. A three-dimensional analysis of stall-delay on a horizontal-axis wind turbine. J. Wind Eng. Ind. Aerodyn. 1991, 37, 1–14. [Google Scholar] [CrossRef]
- Duque, E.P.; Burklund, M.D.; Johnson, W. Navier-Stokes and comprehensive analysis performance predictions of the NREL phase VI experiment. In Proceedings of the Wind Energy Symposium, Reno, NV, USA, 6–9 January 2003; pp. 43–61. [Google Scholar]
- Pape, A.L.; Lecanu, J. 3D Navier–Stokes computations of a stall-regulated wind turbine. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2004, 7, 309–324. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Cañada Flintridge, CA, USA, 1998; Volume 2. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Bangga, G.; Weihing, P.; Lutz, T.; Krämer, E. Effect of computational grid on accurate prediction of a wind turbine rotor using delayed detached-eddy simulations. J. Mech. Sci. Technol. 2017, 31, 2359–2364. [Google Scholar] [CrossRef]
- Boorsma, K.; Schepers, J. New MEXICO experiment. Preliminary Overview with Initial Validation Technical Report ECN-E–14-048 ECN. 2014. Available online: https://www.ecn.nl/docs/library/report/2014/e14048.pdf (accessed on 16 October 2018).
- Sørensen, N.; Hansen, N.; Garcia, N.; Florentie, L.; Boorsma, K.; Gomez-Iradi, S.; Prospathopoulus, J.; Barakos, G.; Wang, Y.; Jost, E.; et al. AVATAR D2. 3–Power Curve Predictions. AVATAR Proj. 2015. Available online: http://www.eera-avatar.eu/fileadmin/mexnext/user/report-d2p3.pdf (accessed on 16 October 2018).
- Schneider, M.S.; Nitzsche, J.; Hennings, H. Accurate load prediction by BEM with airfoil data from 3D RANS simulations. J. Phys. Conf. Ser. 2016, 753, 082016. [Google Scholar] [CrossRef]
- Guma, G.; Bangga, G.; Jost, E.; Lutz, T.; Krämer, E. Consistent 3D CFD and BEM simulations of a research turbine considering rotational augmentation. J. Phys. Conf. Ser. 2018, 1037, 022024. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’S Guide; Technical Report No. NREL/EL-500-38230; National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Marten, D.; Wendler, J.; Pechlivanoglou, G.; Nayeri, C.; Paschereit, C. QBLADE: An open source tool for design and simulation of horizontal and vertical axis wind turbines. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 264–269. [Google Scholar]
- Heramarwan, H. Sensitivity of Wind Turbine Loads to Variation of Aerodynamic Polars Predicted by BEM and Free Vortex Approaches. Bachelor’s Thesis, University of Stuttgart, Stuttgart, Germany, 2018. [Google Scholar]
- Marten, D.; Pechlivanoglou, G.; Nayeri, C.; Paschereit, C. Integration of a WT Blade Design tool in XFOIL/XFLR5. In Proceedings of the 10th German Wind Energy Conference (DEWEK 2010), Bremen, Germany, 17–18 November 2010; pp. 17–18. [Google Scholar]
- McCrink, M.; Gregory, J.W. Blade element momentum modeling of low-Re small UAS electric propulsion systems. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015; p. 3296. [Google Scholar]
- Li, L. MATLAB User Manual; The MathWorks, Inc.: Natick, MA, USA, 2001. [Google Scholar]
- Masters, I.; Chapman, J.; Willis, M.; Orme, J. A robust blade element momentum theory model for tidal stream turbines including tip and hub loss corrections. J. Mar. Eng. Technol. 2011, 10, 25–35. [Google Scholar] [CrossRef]
- Moriarty, P.J.; Hansen, A.C. AeroDyn Theory Manual; National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Sørensen, J.N. General Momentum Theory for Horizontal Axis Wind Turbines; Springer: Berlin, Germany, 2016; Volume 4. [Google Scholar]
- Spera, D.A. Wind Turbine Technology; The American Society of Mechanical Engineers: New York, NY, USA, 1994. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics—Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Jameson, A. Multigrid algorithms for compressible flow calculations. In Lecture Notes in Mathematics; Springer: Berlin, Germany, 1986; Volume 1228, pp. 166–201. [Google Scholar]
- Favre, A. Equations des gaz turbulents compressibles, part 1 et 2. J. Mech. 1965, 4, 391. [Google Scholar]
- Hinze, J. Turbulence; McGraw-Hill: New York, NY, USA, 1975; Volume 218. [Google Scholar]
- Lekou, D.; Chortis, D.; Chaviaropoulos, P.; Munduate, X.; Irisarri, A.; Madsen, H.; Yde, K.; Thomsen, K.; Stettner, M.; Reijerkerk, M. Avatar Deliverable d1.2 Reference Blade Design. Technical Report, ECN Wind Energy. 2015. Available online: http://www.eera-avatar.eu/publications-results-and-links/ (accessed on 16 October 2018).
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.; Andersen, P.; Natarajan, A.; Hansen, M. Design and Performance of a 10 MW Turbine; Technical Report; Technical University of Denmark: Lyngby, UK, 2013. [Google Scholar]
- Pointwise Inc. Gridgen Version 15 User Manual; Pointwise Inc.: Fort Worth, TX, USA, 2012. [Google Scholar]
- Kroll, N.; Rossow, C.C.; Becker, K.; Thiele, F. The MEGAFLOW project. Aerosp. Sci. Technol. 2000, 4, 223–237. [Google Scholar] [CrossRef]
- Aumann, P.; Bartelheimer, W.; Bleecke, H.; Kuntz, M.; Lieser, J.; Monsen, E.; Eisfeld, B.; Fassbender, J.; Heinrich, R.; et al. FLOWer Installation and User Manual; Deutsches Zentrum fur Luft- und Raumfahrt: Cologne, Germany, 2008. [Google Scholar]
- Bangga, G.; Weihing, P.; Lutz, T.; Krämer, E. Hybrid RANS/LES simulations of the three-dimensional flow at root region of a 10 MW wind turbine rotor. In New Results in Numerical and Experimental Fluid Mechanics XI; Springer: Berlin, Germany, 2018; pp. 707–716. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130. [Google Scholar] [CrossRef]
- Chaviaropoulos, P.; Hansen, M.O. Investigating three-dimensional and rotational effects on wind turbine blades by means of a quasi-3D Navier-Stokes solver. J. Fluids Eng. 2000, 122, 330–336. [Google Scholar] [CrossRef]
- Bangga, G.; Guma, G.; Lutz, T.; Krämer, E. Numerical simulations of a large offshore wind turbine exposed to turbulent inflow conditions. Wind Eng. 2018, 42, 88–96. [Google Scholar] [CrossRef]
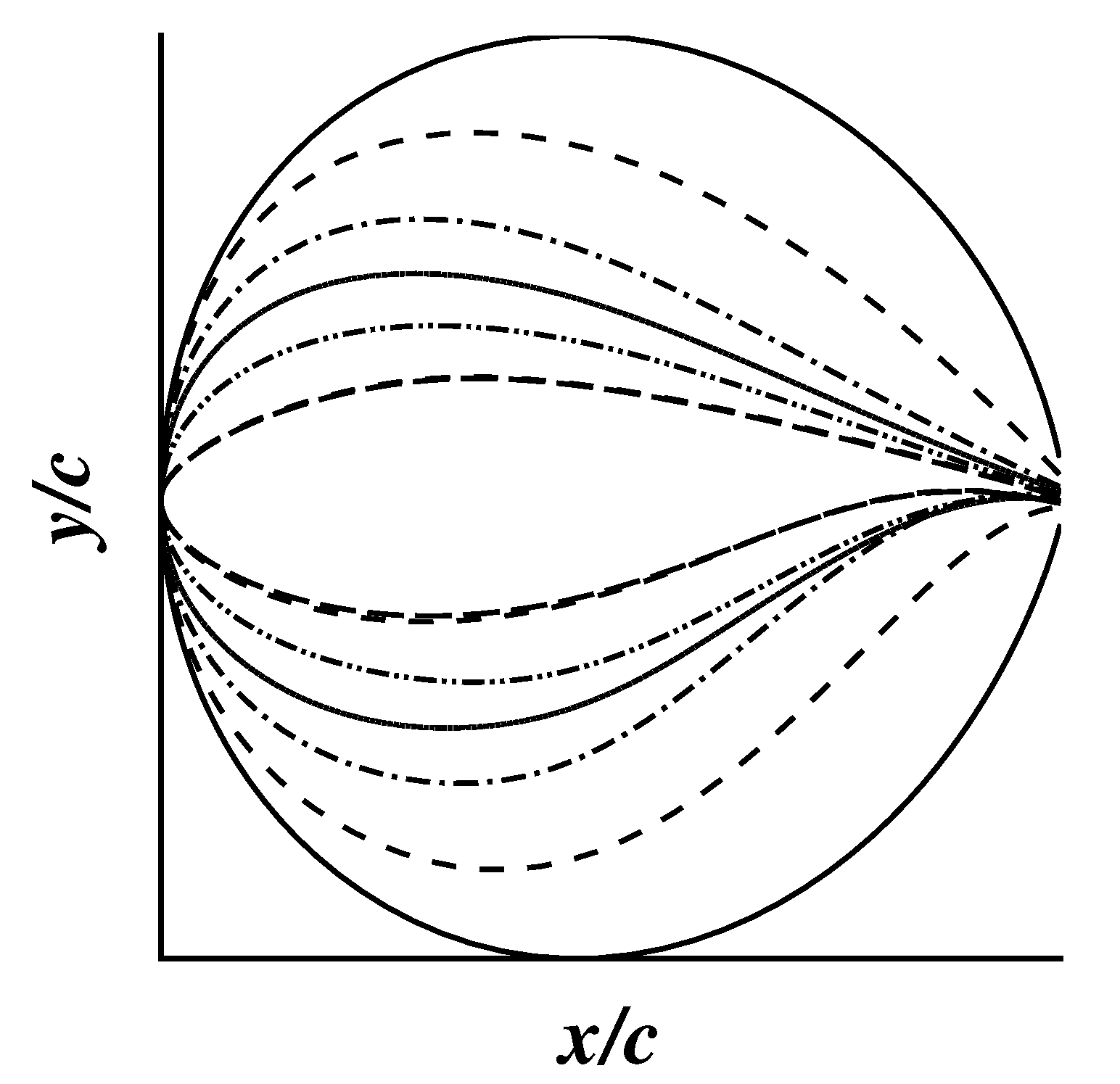

| Airfoil Thickness [] | Airfoil Type |
|---|---|
| 60.0% | Artificial, based on thickest available DU |
| 40.1% | DU 00-W2-401 |
| 35.0% | DU 00-W2-350 |
| 30.0% | DU 97-W300 |
| 24.0% | DU 91-W2-250 (modified for 24%) |
| 21.0% | Based on DU 00-W212, added trailing edge thickness |
| Parameter | Power | Thrust |
|---|---|---|
| Value fine | 9.28 × 10 W | 1.330 × 10 N |
| Value medium | 9.26 × 10 W | 1.328 × 10 N |
| Value coarse | 9.20 × 10 W | 1.326 × 10 N |
| Extrapolated rel. error | ||
| -fine | 0.12% | 0.27% |
| -medium | 0.36% | 0.47% |
| -coarse | 1.02% | 0.58% |
| Grid convercence index | 0.15% | 0.34% |
| [%] | [%] | |||||
|---|---|---|---|---|---|---|
| r = 15 m | r = 60 m | r = 90 m | r = 15 m | r = 60 m | r = 90 m | |
| 2D Polar | 99.01 | 3.45 | 2.56 | 598.24 | 6.67 | 6.06 |
| 2D Polar + Stall Delay | 127.80 | 3.19 | 2.56 | 468.88 | 6.48 | 6.06 |
| 3D Polar | 11.84 | 3.08 | 0.24 | 19.58 | 4.81 | 0.33 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bangga, G. Comparison of Blade Element Method and CFD Simulations of a 10 MW Wind Turbine. Fluids 2018, 3, 73. https://doi.org/10.3390/fluids3040073
Bangga G. Comparison of Blade Element Method and CFD Simulations of a 10 MW Wind Turbine. Fluids. 2018; 3(4):73. https://doi.org/10.3390/fluids3040073
Chicago/Turabian StyleBangga, Galih. 2018. "Comparison of Blade Element Method and CFD Simulations of a 10 MW Wind Turbine" Fluids 3, no. 4: 73. https://doi.org/10.3390/fluids3040073
APA StyleBangga, G. (2018). Comparison of Blade Element Method and CFD Simulations of a 10 MW Wind Turbine. Fluids, 3(4), 73. https://doi.org/10.3390/fluids3040073






