One Dimensional Model for Droplet Ejection Process in Inkjet Devices
Abstract
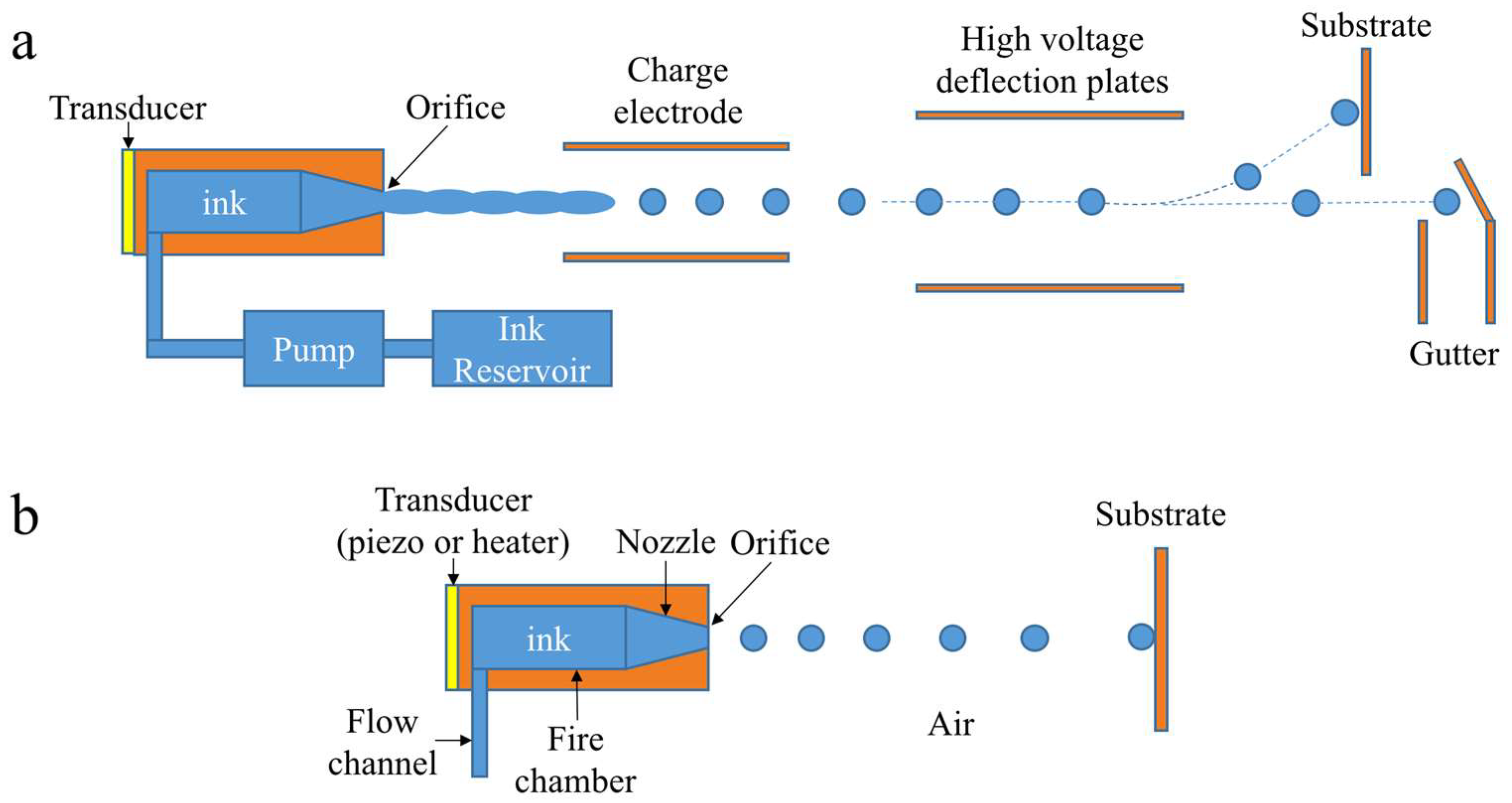
:1. Introduction
2. Mathematical Model
2.1. Droplet Formation Model
2.2. Nozzle Dynamics Model
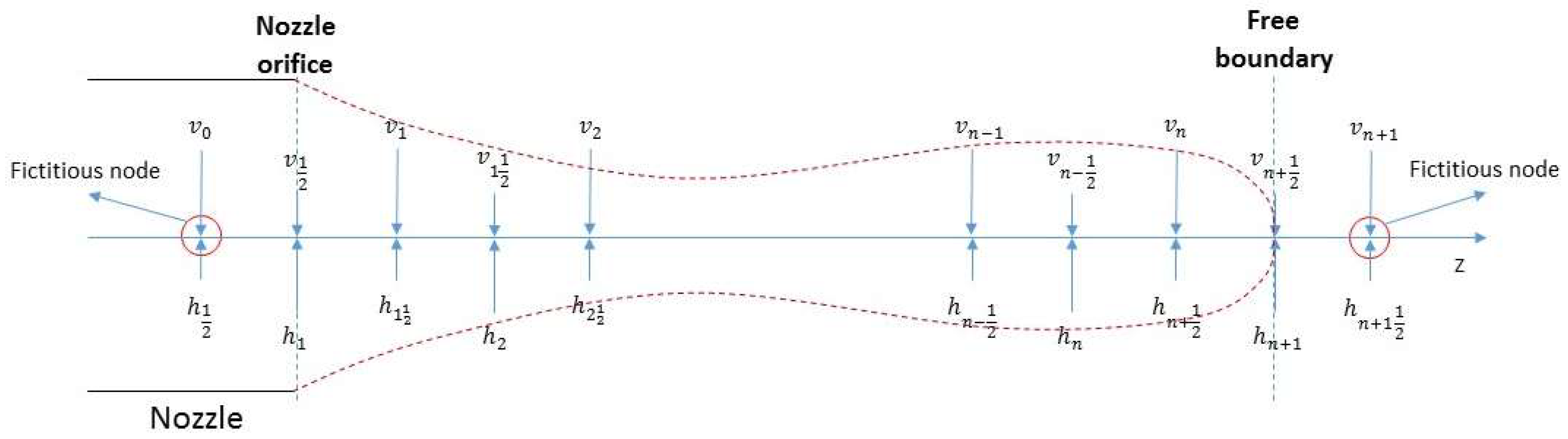
3. Numerical Method
3.1. Solution Method for Droplet Formation
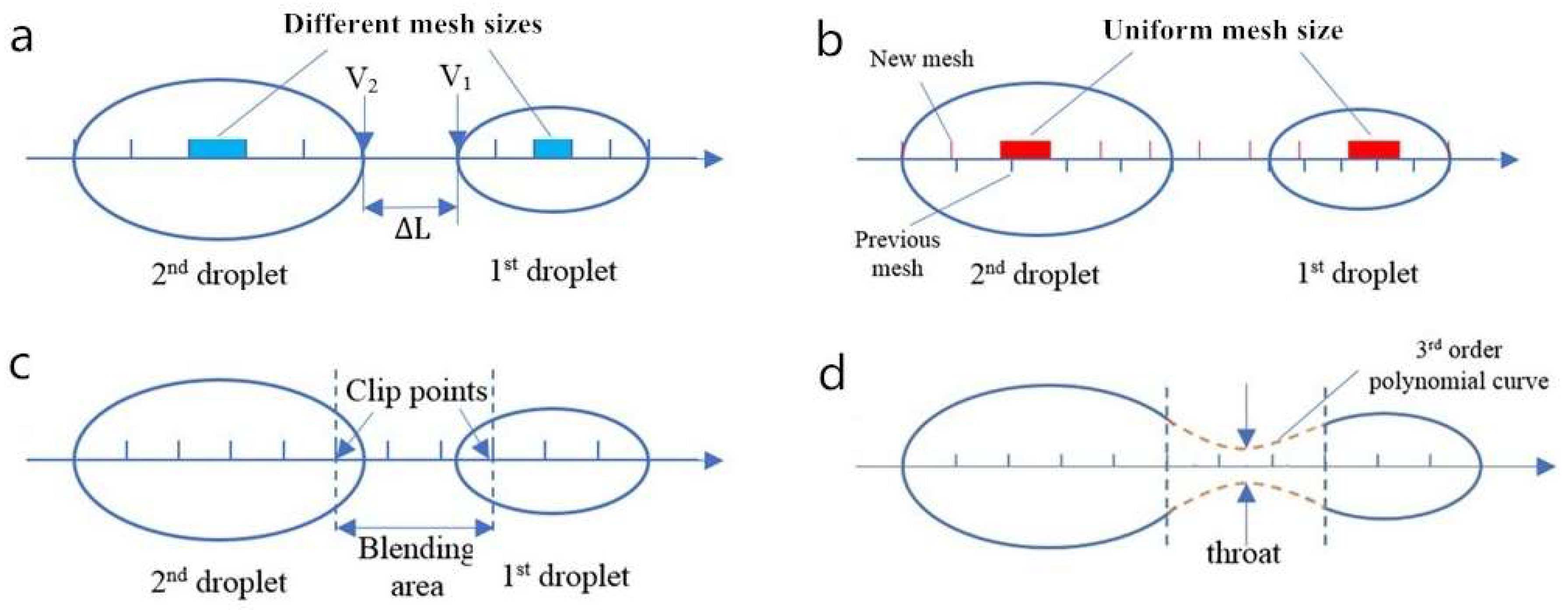
3.2. Treatment of Droplet Ends and Droplet Breakup
3.3. Treatment of Droplet Coalescence
3.4. Coupling of Nozzle Dynamics and Droplet Formation
4. Numerical Tests
4.1. Infinite Microthread
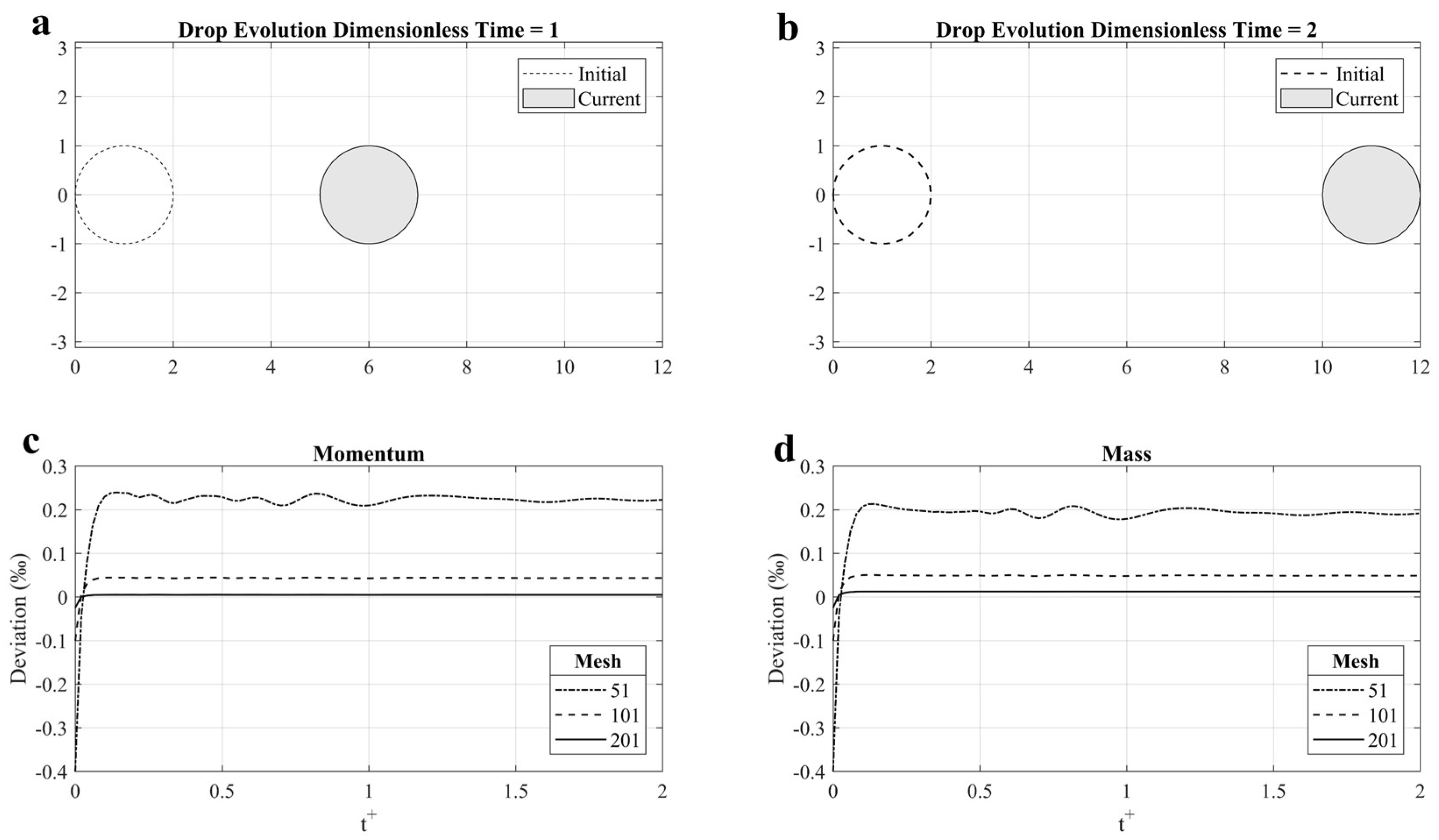
4.2. Free Flying Droplet
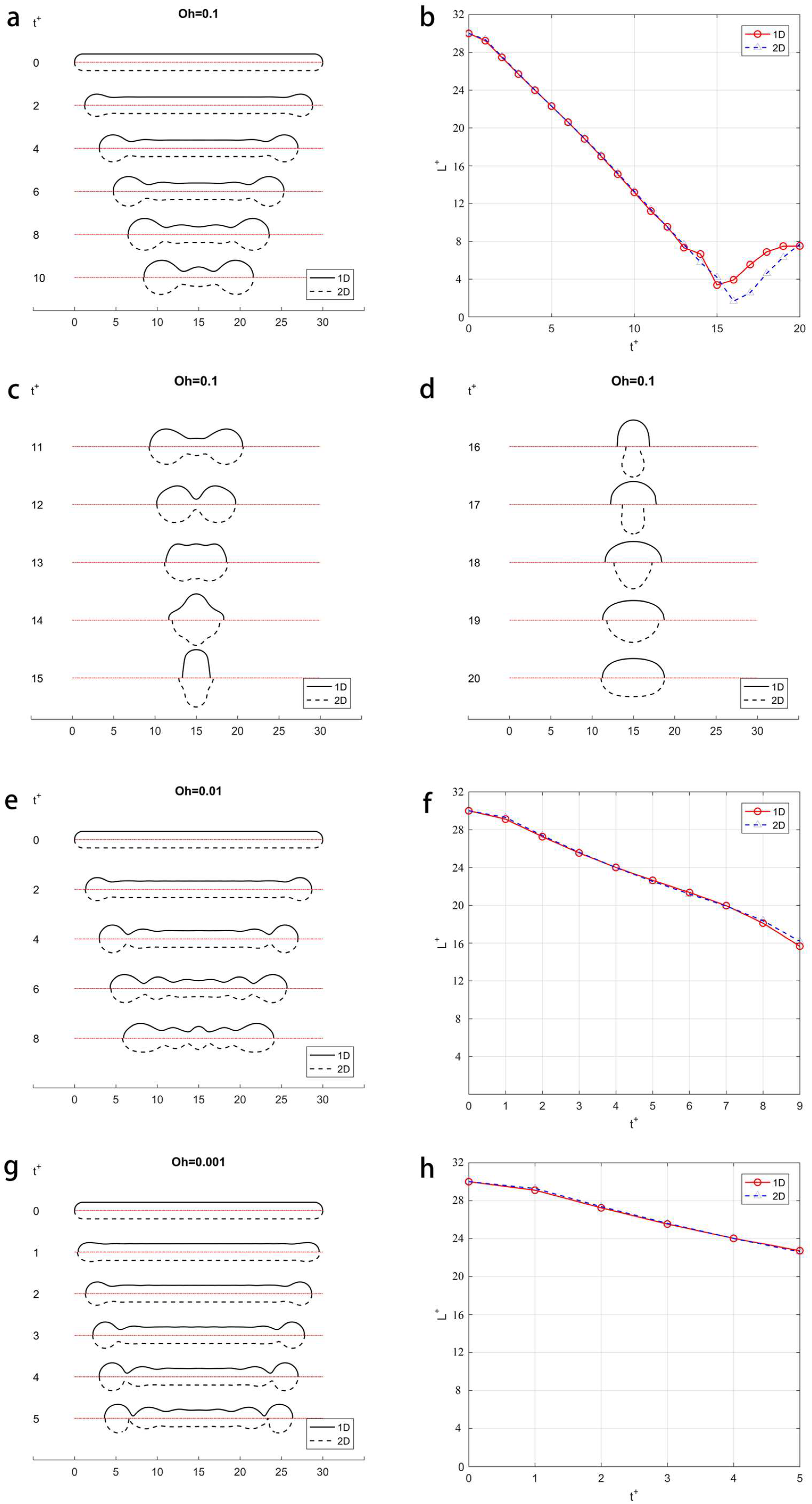
4.3. Liquid Filament Contraction
4.4. Step Driving Pressure
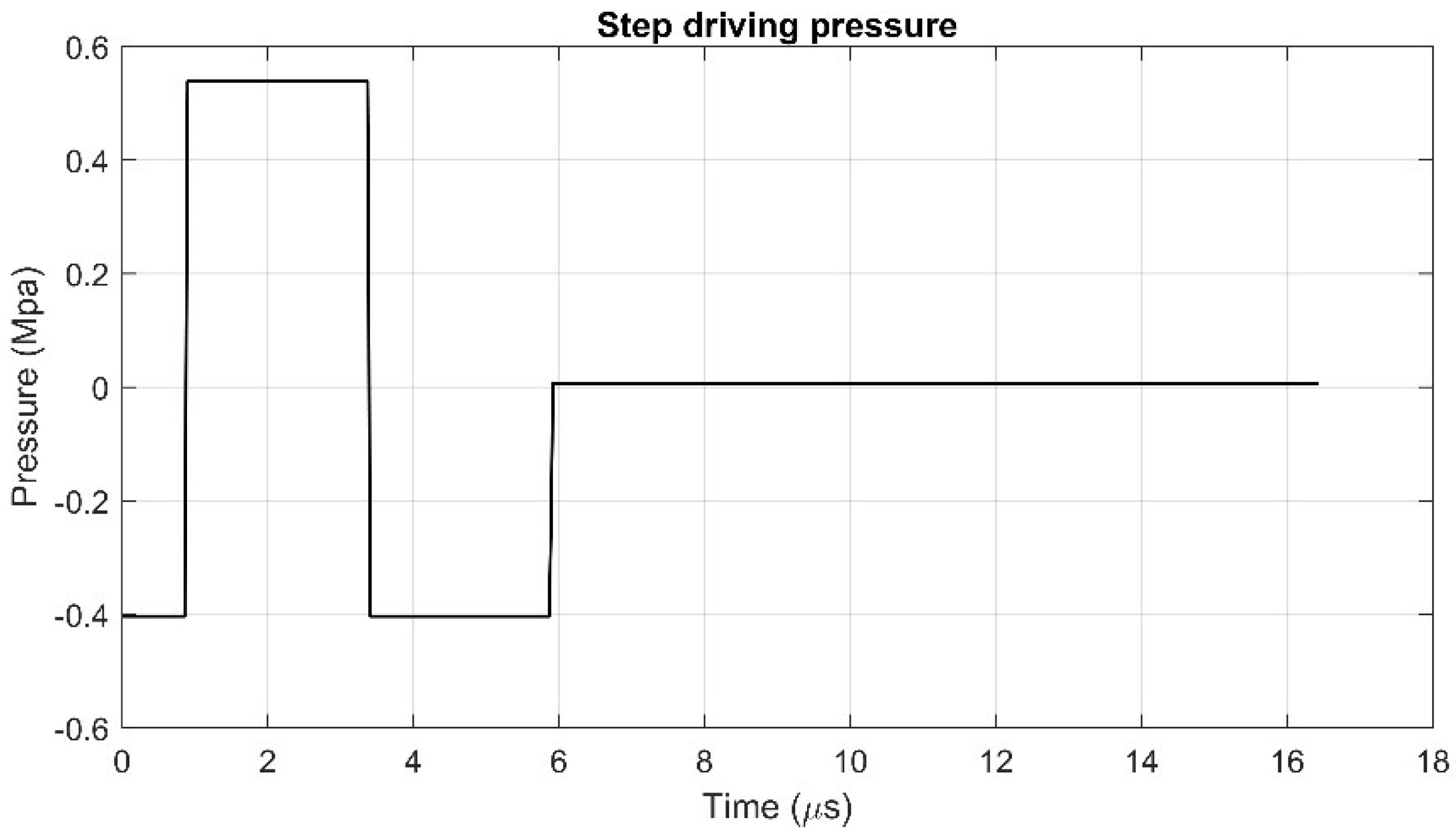
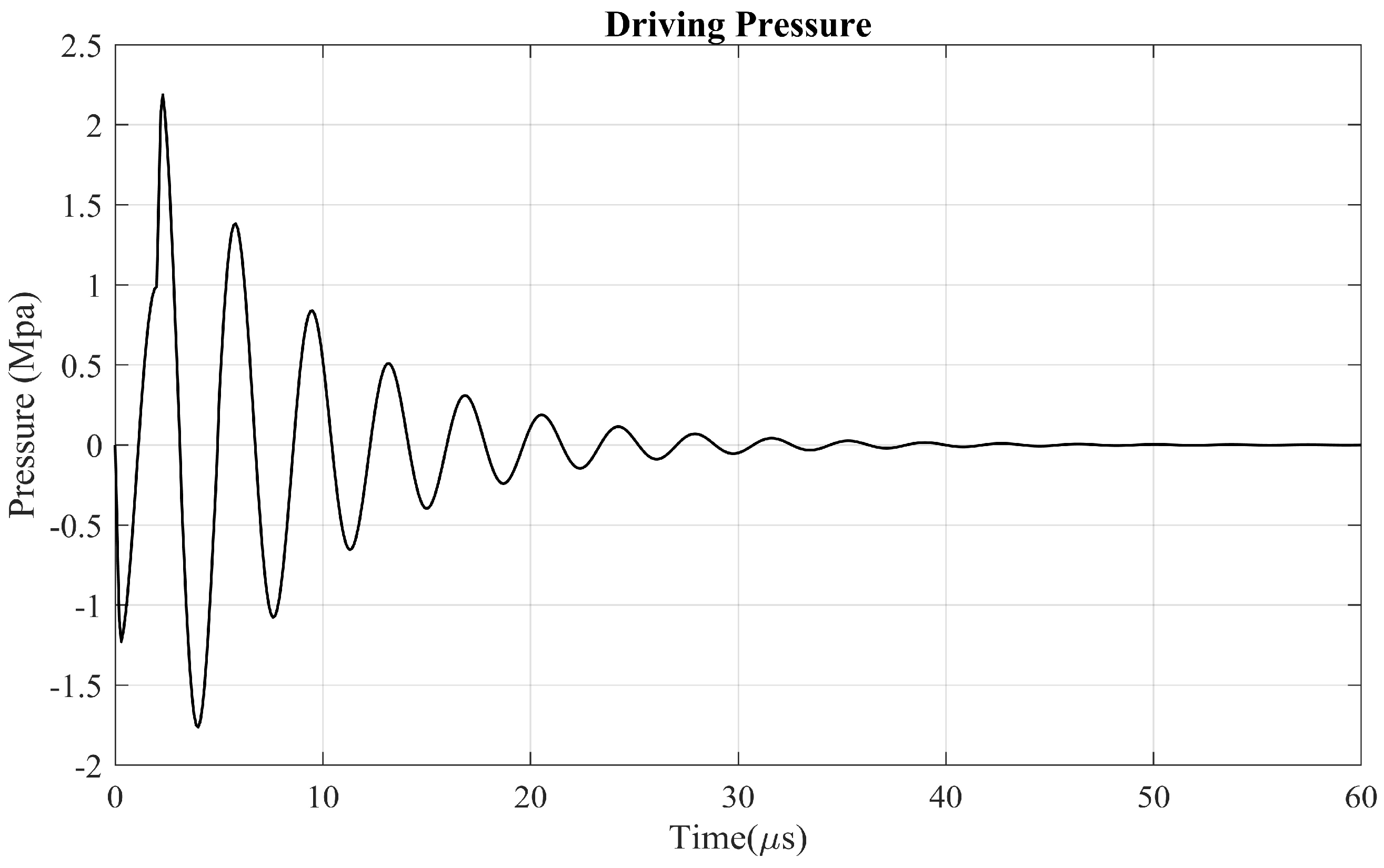
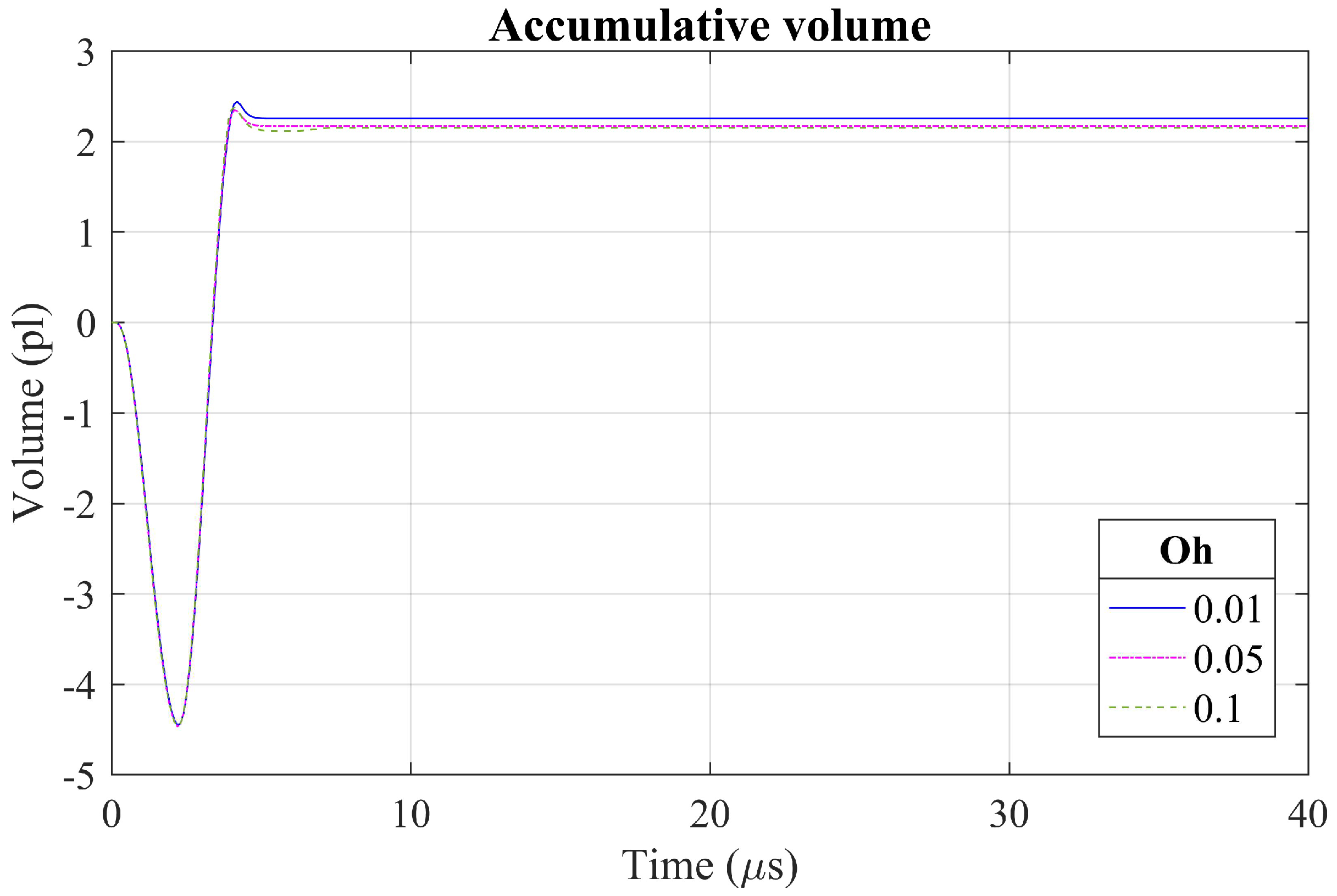
5. Example of Droplet Ejection Simulation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Calvert, P. Inkjet Printing for Materials and Devices. Chem. Mater. 2001, 13, 3299–3305. [Google Scholar] [CrossRef]
- Thomas, H.R.; Hopkinson, N.; Erasenthiran, P. High speed sintering—continuing research into a new rapid manufacturing process. In Proceedings of the 17th SFF Symposium, Austin TX, USA, 14–16 August 2006; pp. 682–691. [Google Scholar]
- Yoshihiro, K.; Hodges, S.; Cook, B.S.; Zhang, C.; Abowd, G.D. Instant inkjet circuits: Lab-based Inkjet Printing to Support Rapid Prototyping of UbiComp Devices. In Proceedings of the 2013 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Zurich, Switzerland, 08–12 September 2013; pp. 363–372. [Google Scholar] [CrossRef]
- Daly, R.; Harrington, T.S.; Martin, G.D.; Hutchings, I.M. Inkjet printing for pharmaceutics—A review of research and manufacturing. Int. J. Pharm. 2015, 494, 554–567. [Google Scholar] [CrossRef] [PubMed]
- Derby, B. Printing and prototyping of tissues and scaffolds. Science 2012, 338, 921–926. [Google Scholar] [CrossRef] [PubMed]
- Bash, C.E.; Patel, C.D.; Sharma, R.K. Inkjet assisted spray cooling of electronic. In Proceedings of the ASME 2003 International Electronic Packaging Technical Conference and Exhibition, Maui, Hawaii, USA, 6–11 July 2003; Volume 2, pp. 119–127. [Google Scholar]
- Hoath, S.D. Fundamentals of Inkjet Printing: The Science of Inkjet and Droplets; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Dong, H.; Carr, W.W.; Morris, J.F. Visualization of drop-on-demand inkjet: Drop formation and deposition. Rev. Sci. Instrum. 2006, 77, 085101. [Google Scholar] [CrossRef]
- Hutchings, I.M.; Martin, G.D.; Hoath, S.D. High speed imaging and analysis of jet and drop formation. J. Imaging Sci. Technol. 2007, 51, 438–444. [Google Scholar] [CrossRef]
- Van der Bos, A.; van der Meulen, M.J.; Driessen, T.; van den Berg, M.; Reinten, H.; Wijshoff, H.; Versluis, M.; Lohse, D. Velocity profile inside piezoacoustic inkjet droplets in flight: Comparison between experiment and numerical simulation. Phys. Rev. Appl. 2014, 1, 014004. [Google Scholar] [CrossRef]
- Staat, H.J.J.; van der Bos, A.; van den Berg, M.; Reinten, H.; Wijshoff, H.; Versluis, M.; Lohse, D. Ultrafast imaging method to measure surface tension and viscosity of inkjet-printed droplets in flight. Exp. Fluids 2017, 58. [Google Scholar] [CrossRef]
- Fromm, J.E. Numerical Calculation of the Fluid Dynamics of Drop-on-Demand Jets. IBM J. Res. Dev. 1984, 28, 322–333. [Google Scholar] [CrossRef]
- Morrison, N.F.; Harlen, O.G. Viscoelasticity in inkjet printing. Rheol. Acta 2010, 49, 619–632. [Google Scholar] [CrossRef]
- Castrejón-Pita, J.R.; Morrison, N.F.; Harlen, O.G.; Martin, G.D.; Hutchings, I.M. Experiments and Lagrangian simulations on the formation of droplets in drop-on-demand mode. Phys. Rev. E 2011, 83, 036306. [Google Scholar] [CrossRef] [PubMed]
- Castrejon-Pita, J.R.; Morrison, N.F.; Harlen, O.G.; Martin, G.D.; Hutchings, I.M. Experiments and Lagrangian simulations on the formation of droplets in continuous mode. Phys. Rev. E 2011, 83, 16301. [Google Scholar] [CrossRef] [PubMed]
- Morrison, N.F.; Harlen, O.G.; Hoath, S.D. Towards satellite free drop-on-demand printing of complex fluids. In 2014 International Conference on Digital Printing Technologies; Society for Imaging Science and Technology: Springfield, VA, USA, 2014; pp. 162–165. [Google Scholar]
- Knight, B. Computer modeling of a thermal inkjet device. In IS&T Seventh International Congress on Advances in Non-Impact Printing Technologies; Society for Imaging Science: Springfield, VA, USA, 1991. [Google Scholar]
- Asai, A. Three-Dimensional Calculation of Bubble Growth and Drop Ejection in a Bubble Jet Printer. J. Fluids Eng. 1992, 114, 638. [Google Scholar] [CrossRef]
- Liou, T.M.; Shih, K.C.; Chau, S.W.; Chen, S.C. Three-dimensional simulations of the droplet formation during the inkjet printing process. Int. Commun. Heat Mass Transf. 2002, 29, 1109–1118. [Google Scholar] [CrossRef]
- Wu, H.-C.; Hwang, W.-S.; Lin, H.-J. Development of a three-dimensional simulation system for micro-inkjet and its experimental verification. Mater. Sci. Eng. A 2004, 373, 268–278. [Google Scholar] [CrossRef]
- Wu, H.-C.; Lin, H.-J.; Kuo, Y.-C.; Hwang, W.-S. Simulation of Droplet Ejection for a Piezoelectric Inkjet Printing Device. Mater. Trans. 2004, 45, 893–899. [Google Scholar] [CrossRef]
- Tan, H.; Torniainen, E.; Markel, D.P.; Browning, R.N.K. Numerical simulation of droplet ejection of thermal inkjet printheads. Int. J. Numer. Methods Fluids 2015, 77, 544–570. [Google Scholar] [CrossRef]
- Yu, J.-D.; Sakai, S.; Sethian, J. A coupled level set projection method applied to ink jet simulation. Interfaces Free Bound. 2003, 5, 459–482. [Google Scholar] [CrossRef]
- Der Yu, J.; Sakai, S.; Sethian, J. A coupled quadrilateral grid level set projection method applied to ink jet simulation. J. Comput. Phys. 2005, 206, 227–251. [Google Scholar] [CrossRef]
- Suh, Y.; Son, G. A Level-Set Method for Simulation of a Thermal Inkjet Process. Numer. Heat Transf. Part B Fundam. 2008, 54, 138–156. [Google Scholar] [CrossRef]
- Harlen, O.G.; Morrison, N.F. Simulations of drop formation in complex rheological fluids-can rheology improve jetting performance? In NIP & Digital Fabrication Conference; Society for Imaging Science and Technology: Springfield, VA, USA, 2016; pp. 378–381. [Google Scholar]
- Tan, H. An adaptive mesh refinement based flow simulation for free-surfaces in thermal inkjet technology. Int. J. Multiph. Flow 2016, 82, 1–16. [Google Scholar] [CrossRef]
- Feng, J. A general fluid dynamic analysis of drop ejection in drop-on-demand ink jet devices. J. Imaging Sci. Technol. 2002, 46, 398–408. [Google Scholar]
- Sen, A.K.; Darabi, J. Droplet ejection performance of a monolithic thermal inkjet print head. J. Micromech. Microeng. 2007, 17, 1420–1427. [Google Scholar] [CrossRef]
- Lindemann, T.; Sassano, D.; Bellone, A.; Zengerle, R.; Koltay, P. Three-Dimensional CFD-Simulation of a Thermal Bubble Jet Printhead. In Proceedings of the NSTI Nanotechnology Conference and Trade Show, Boston, MA, USA, 7–11 March 2004; Volume 2, pp. 227–230. [Google Scholar]
- Zhou, H.; Gué, A.M. Simulation model and droplet ejection performance of a thermal-bubble microejector. Sens. Actuators B Chem. 2010, 145, 311–319. [Google Scholar] [CrossRef]
- Adams, R.L.; Roy, J. A One-Dimensional Numerical Model of a Drop-On-Demand Ink Jet. J. Appl. Mech. 1986, 53, 193. [Google Scholar] [CrossRef]
- Lee, H.C. Drop Formation in a Liquid Jet. IBM J. Res. Dev. 1974, 18, 364–369. [Google Scholar] [CrossRef]
- Fromm, J. A numerical study of drop-on-demand ink jets. In Proceedings of the 2nd International Colloquium on Drops and Bubbles, San Jose, CA, USA, 1 March 1982. [Google Scholar]
- Shield, T.W.; Bogy, D.B.; Talke, F.E. A numerical comparison of one-dimensional fluid jet models applied to drop-on-demand printing. J. Comput. Phys. 1986, 67, 327–347. [Google Scholar] [CrossRef]
- Green, A.E. On the non-linear behaviour of fluid jets. Int. J. Eng. Sci. 1976, 14, 49–63. [Google Scholar] [CrossRef]
- Wallace, D. A Method of Characteristics Model of a Drop-on-Demand Ink-Jet Device Using an Integral Method Drop Formation Model; ASME Publication: New York, NY, USA, 1989. [Google Scholar]
- Eggers, J.; Dupont, D.F. Drop formation in a one-dimensional approximation of the Navier-Stokes equation. J. Fluid Mech. 1994, 262, 205–221. [Google Scholar] [CrossRef]
- Ambravaneswaran, B.; Wilkes, E.D.; Basaran, O.A. Drop formation from a capillary tube: Comparison of one-dimensional and two-dimensional analyses and occurrence of satellite drops. Phys. Fluids 2002, 14, 2606–2621. [Google Scholar] [CrossRef]
- Yildirim, O.E.; Xu, Q.; Basaran, O.A. Analysis of the drop weight method. Phys. Fluids 2005, 17, 1–13. [Google Scholar] [CrossRef]
- Hanchak, M. One Dimensional Model of Thermo-Capillary Driven Liquid Jet Break-up with Drop Merging; University of Dayton: Dayton, OH, USA, 2009. [Google Scholar]
- Furlani, E.P.; Hanchak, M.S. Nonlinear analysis of the deformation and breakup of viscous microjets using the method of lines. Int. J. Numer. Methods Fluids 2011, 65, 563–577. [Google Scholar] [CrossRef]
- Van Hoeve, W.; Gekle, S.; Snoeijer, J.H.; Versluis, M.; Brenner, M.P.; Lohse, D. Breakup of diminutive Rayleigh jets. Phys. Fluids 2010, 22, 122003. [Google Scholar] [CrossRef]
- Notz, P.K.; Basaran, O.A. Dynamics and breakup of a contracting liquid filament. J. Fluid Mech. 2004, 512, 223–256. [Google Scholar] [CrossRef]
- Driessen, T.; Jeurissen, R.; Wijshoff, H.; Toschi, F.; Lohse, D. Stability of viscous long liquid filaments. Phys. Fluids 2013, 25, 062109. [Google Scholar] [CrossRef]
- Shin, D.Y.; Grassia, P.; Derby, B. Numerical and experimental comparisons of mass transport rate in a piezoelectric drop-on-demand inkjet print head. Int. J. Mech. Sci. 2004, 46, 181–199. [Google Scholar] [CrossRef]
- Lee, Y. Analytical solutions of channel and duct flows due to general pressure gradients. Appl. Math. Model. 2017, 43, 279–286. [Google Scholar] [CrossRef]
- Jiang, H.; Tan, H. One Dimensional Simulation of Droplet Ejection of Drop-on-Demand Inkjet; IMECE, ASME: Tampa, FL, USA, 2017. [Google Scholar]
- Schiesser, W. The Numerical Method of Lines: Integration of Partial Differential Equations; Elsevier: New York, NY, USA, 2012. [Google Scholar]
- Tan, H. Numerical study on splashing of high-speed microdroplet impact on dry microstructured surfaces. Comput. Fluids 2017, 154, 142–166. [Google Scholar] [CrossRef]
- Tan, H. Absorption of picoliter droplets by thin porous substrates. AIChE J. 2017, 63, 1690–1703. [Google Scholar] [CrossRef]
- Kong, X.; Xi, Y.; LeDuff, P.; Li, E.; Liu, Y.; Cheng, L.-J.; Rorrer, G.L.; Tan, H.; Wang, A.X. Optofluidic sensing from inkjet-printed droplets: The enormous enhancement by evaporation-induced spontaneous flow on photonic crystal biosilica. Nanoscale 2016, 8, 17285–17294. [Google Scholar] [CrossRef] [PubMed]
- Tan, H. Three-dimensional simulation of micrometer-sized droplet impact and penetration into the powder bed. Chem. Eng. Sci. 2016, 153, 93–107. [Google Scholar] [CrossRef]
- Rayleigh, L. On the instability of jets. Proc. Lond. Math. Soc. 1878, s1-10, 4–13. [Google Scholar] [CrossRef]
- Ashgriz, N.; Mashayek, F. Temporal analysis of capillary jet breakup. J. Fluid Mech. 1995, 291, 163–190. [Google Scholar] [CrossRef]
- Strutt, J.W. The Theory of Sound; Cambridge University Press: London, UK, 2011; Volume 2. [Google Scholar] [CrossRef]
- Schulkes, R.M.S.M. The contraction of liquid filaments. J. Fluid Mech. 1996, 309, 277. [Google Scholar] [CrossRef]
- Hoepffner, J.; Paré, G. Recoil of a liquid filament: Escape from pinch-off through creation of a vortex ring. J. Fluid Mech. 2013, 734, 183–197. [Google Scholar] [CrossRef]
- Castrejón-Pita, A.A.; Castrejón-Pita, J.R.; Hutchings, I.M. Breakup of Liquid Filaments. Phys. Rev. Lett. 2012, 108, 74506. [Google Scholar] [CrossRef] [PubMed]
- Hoath, S.D.; Jung, S.; Hutchings, I.M. A simple criterion for filament break-up in drop-on-demand inkjet printing. Phys. Fluids 2013, 25, 021701. [Google Scholar] [CrossRef]
- Wijshoff, H. The dynamics of the piezo inkjet printhead operation. Phys. Rep. 2010, 491, 77–177. [Google Scholar] [CrossRef]
- Dong, H.; Carr, W.W.; Morris, J.F. An experimental study of drop-on-demand drop formation. Phys. Fluids 2006, 18, 072102. [Google Scholar] [CrossRef]








| ε = 0.05 | ||||
|---|---|---|---|---|
| k+ = 0.2 | k+ = 0.45 | k+ = 0.7 | k+ = 0.9 | |
| Re = 200 | 25.213 | 12.911 | 10.035 | 14.495 |
| 25.0 | 12.6 | 9.7 | 11.0 | |
| 25.036 | 12.722 | 9.767 | 11.098 | |
| Re = 10 | 26.683 | 14.299 | 11.623 | 14.83 |
| 27.9 | 14.3 | 11.4 | 14.4 | |
| 27.005 | 14.306 | 11.480 | 14.523 | |
| Re = 0.1 | 230.6 | 243.2 | 311.9 | 628.2 |
| 227 | 238 | 305 | 634 | |
| 234.025 | 245.748 | 313.740 | 642.686 | |
| 0.00–0.21 | −60 |
| 0.21–0.82 | +80 |
| 0.82–1.43 | +60 |
| 1.43– | +1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Tan, H. One Dimensional Model for Droplet Ejection Process in Inkjet Devices. Fluids 2018, 3, 28. https://doi.org/10.3390/fluids3020028
Jiang H, Tan H. One Dimensional Model for Droplet Ejection Process in Inkjet Devices. Fluids. 2018; 3(2):28. https://doi.org/10.3390/fluids3020028
Chicago/Turabian StyleJiang, Huicong, and Hua Tan. 2018. "One Dimensional Model for Droplet Ejection Process in Inkjet Devices" Fluids 3, no. 2: 28. https://doi.org/10.3390/fluids3020028
APA StyleJiang, H., & Tan, H. (2018). One Dimensional Model for Droplet Ejection Process in Inkjet Devices. Fluids, 3(2), 28. https://doi.org/10.3390/fluids3020028





