1. Introduction
Climate change is gradually coming to affect all living species by giving rise to new sets of meteorological conditions: record breaking high temperatures, melting glaciers, increasing sea water levels, increasing severity of droughts, floods, tornadoes, and hurricanes, to mention just a few. Hydraulic structures have not been the exception; most of these structures were designed was based on rainfall patterns that, in some cases, no longer conform to the realities of today’s weather conditions. Generally speaking, sizing a hydraulic structure for an ungauged watershed starts with a hydrological analysis that includes: (a) a rainfall frequency analysis; (b) the watershed delineation and estimation of its morphometric parameters; and (c) the direct surface runoff (DSR) calculation using a rainfall-runoff model, assuming it has the same return period of the generating rainfall.
Usually, a rainfall frequency analysis for an ungauged watershed consists of trying to find the probability distribution that best represents the behavior of the extreme events (of different durations) being analyzed, in order to subsequently obtain the value of the precipitation event associated with a given return period to be later used for the DSR estimation. The traditional methods for frequency analysis of extreme values for hydraulic structures design (streamflow, rainfall or rainfall intensity) assume that: (a) the values of the variable are random and independent; (b) the probability distribution functions are stationary; and (c) the return period (
Tr) is the inverse of the probability of exceedance (
p). These assumptions imply that the probability of an event producing excessive precipitations does not change over time (the sample is homogeneous). This approach cannot be applied when the variable being analyzed shows noticeable change of pattern (either increase or decline), which may indicate non-stationary conditions [
1,
2,
3,
4]. In these cases, the typical definition of the return period (
Tr = 1/
p) has to be redefined to account for non-stationarity.
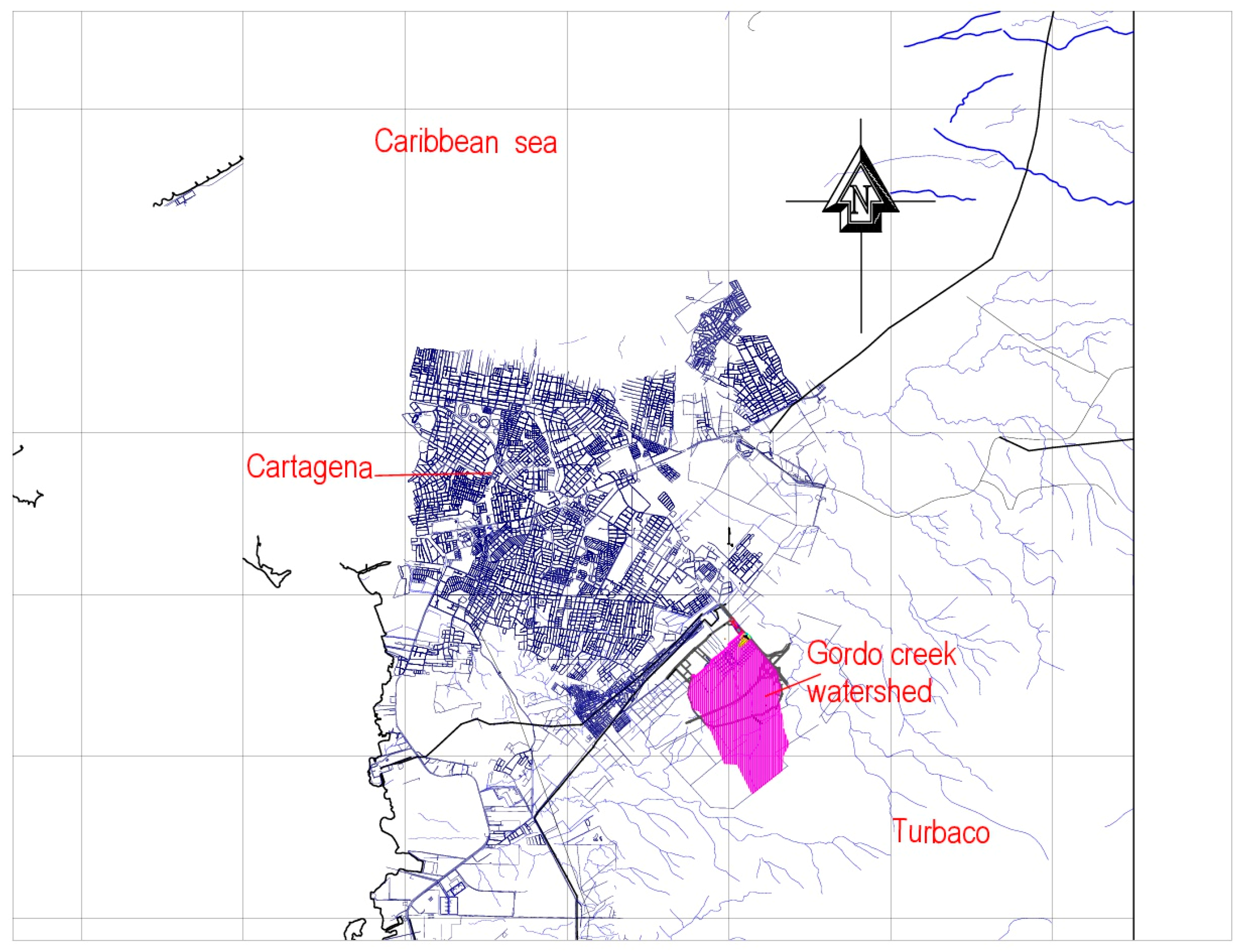
Cartagena de Indias, a city on the Caribbean coast of Colombia, has been lately undergoing recurring floods that can be mainly attributed to different factors that go from uncontrolled development projects—due to the lack of an updated territorial management plan that fits the city’s realities—to poorly designed hydraulic structures for runoff management that do not take future conditions (especially rainfall pattern changes and increase of impervious areas) into account. Most of the runoff of Cartagena de Indias discharges into La Virgen swamp (ciénaga de La Virgen), a waterbody of approximately 502 km2, whose southern shoreline has been populated over the years by illegal low-income settlements that suffer the consequences of both a rising sea level (the swamp is connected to the Caribbean Sea) and an obsolete stromwater system. Furthermore, the cities of Cartagena de Indias (downstream) and Turbaco (upstream) share several watersheds that also drain into the La Virgen swamp. The upstream areas of these watersheds (like the one selected in this study) are mostly rural, which have been gradually converted into impervious areas by local developers that offer more competitive prices than those in Cartagena de Indias. This dynamic will most likely (and rapidly) change the landscape, which brings with it more challenging hydrologic, and hydraulic, conditions.
In this context, Colombian legislation has mandated to analyze the possible effects of climate change on the future rainfall pattern if a stormwater system (channels, pipes, culverts, etc.) is to be designed [
5]. A regional increasing trend of both rainfall and streamflow has been found in some areas of the northern portion of the Colombian Caribbean region [
6,
7]. The studies that carry out assessments for stationary (SC) versus non-stationary (NSC) conditions of streamflow and/or rainfall, typically encompass only performing a statistical analysis (of a trend) without quantifying how the two scenarios may affect real life conditions, both hydrologically and hydraulically speaking. In this study, multiannual 24-h maximum rainfall (P
24h-max) data (from the synoptic weather station located at the Rafael Núñez airport) was used to: (a) assess the trend of the P
24h-max observations over time, specifically for Cartagena de Indias, (b) quantify the rainfall values obtained for several return periods (2, 5, 10, 25, 50, and 100 years) via stationary and non-stationary frequency analyses, (c) carry out a hydrological and hydraulic analysis on the Gordo creek watershed under SC and NSC for different return periods in order to understand the recurring floods reported that affect a commercial and industrial area downstream, and (d) point out the importance of accounting for the effect of climate change in the decision making process in runoff management, especially in flood-prone areas.
4. Results and Discussion
The analysis of the multiannual P
24h-max observations recorded at the Rafael Núñez airport weather station not only evidenced an increasing trend (
Figure 5), but also, in
Table 3, it could be noticed that, before 1985 rainfall events above 148.1 mm (estimated rainfall value for a 10-year return period under stationary conditions in
Table 4) just occurred once (in 1970). After 1985, rainfall events of that magnitude (or higher) have occurred nine times (2011 rainfall was included as it is close enough). Colombian legislation recommends a 50-year return period for the design of open channels for watersheds of an area less than 1000 ha [
5]. In
Table 4 and
Table 5, the rainfall for this return period, even for stationary conditions, was estimated to be nearly 200 mm. However, in
Table 3, a rainfall of 201.8 mm has been already recorded in 1989. From this, it may be inferred that any hydraulic structure to be designed for such return period should be also evaluated for a higher value to test its hydraulic performance.
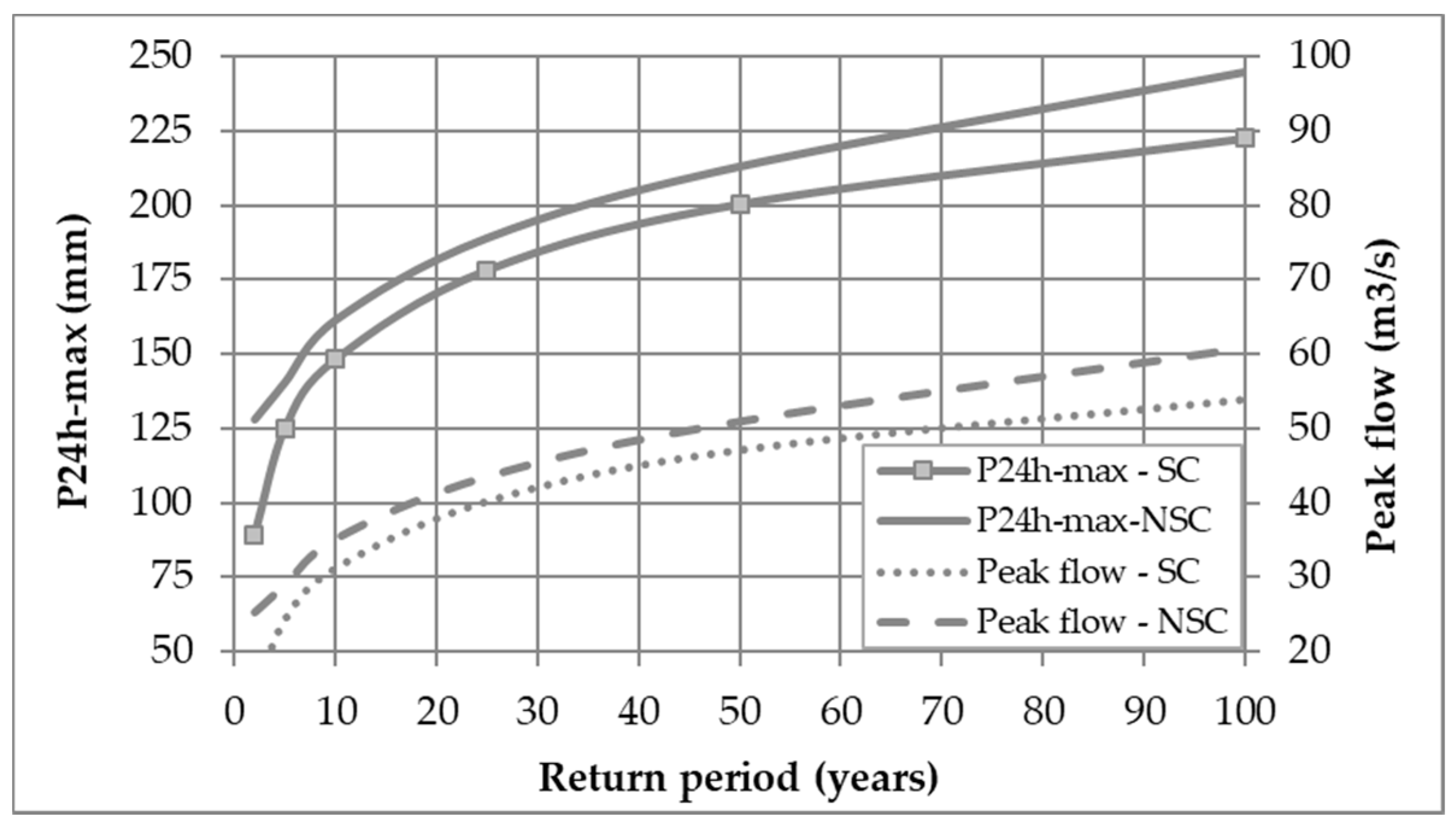
The estimated P
24h-max (
Section 3.1 and
Section 3.2) and the peak flow (
Section 3.5) for several return periods under stationary and non-stationary conditions depicted in
Figure 10 also showed an increase, from 6% to 44% for P
24h-max (
Table 10) and from 8% to 77% for peak flow (
Table 11), depending upon the return period. The increase seen in P
24h-max for return periods of 5 to 100 years are quite similar to each other, with an average value of 1.09. This value is in line with those observed in some areas of the Caribbean region of Colombia [
6,
7]. Despite the fact that a 44% increase in P
24h-max for the 2-year return period looks, at a glance, to be too high when compared to the remaining values, it may be construed as an indication that a more conservative approach might be conducted when designing with this low return period as the probability of exceeding is high.
For the peak flow, the values of the overall increase ratio have the same behavior of that shown by P
24h-max, with the maximum value occurring at a 2-year return period. A 44-percent increase in rainfall (
Table 10) caused a 77-percent peak flow rise (
Table 11). Once again, this indicates the precautions that the designers must take when using this return period. For the other return periods, it may be observed that the increase in P
24h-max resulted in a peak flow increase of a similar range.
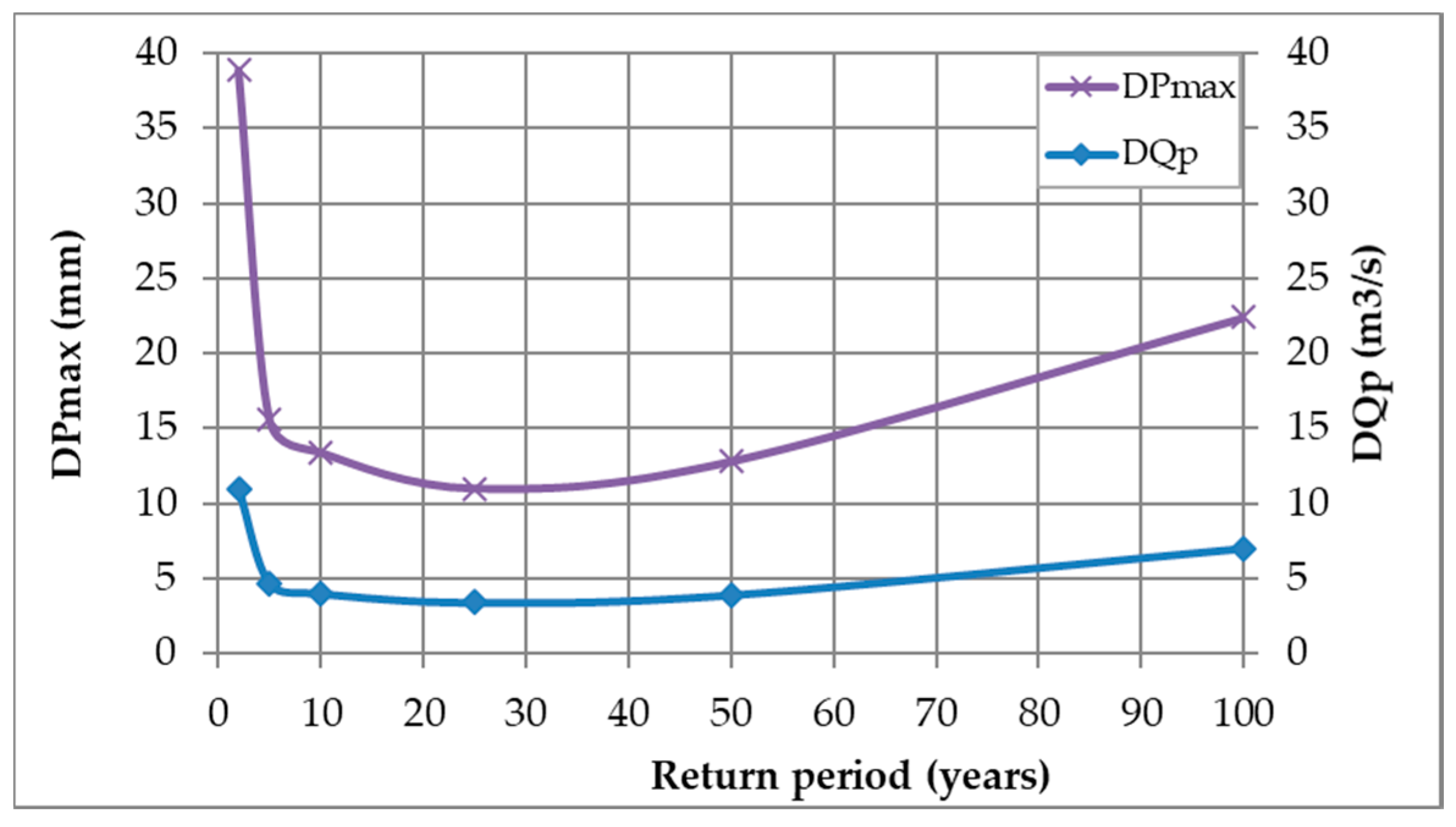
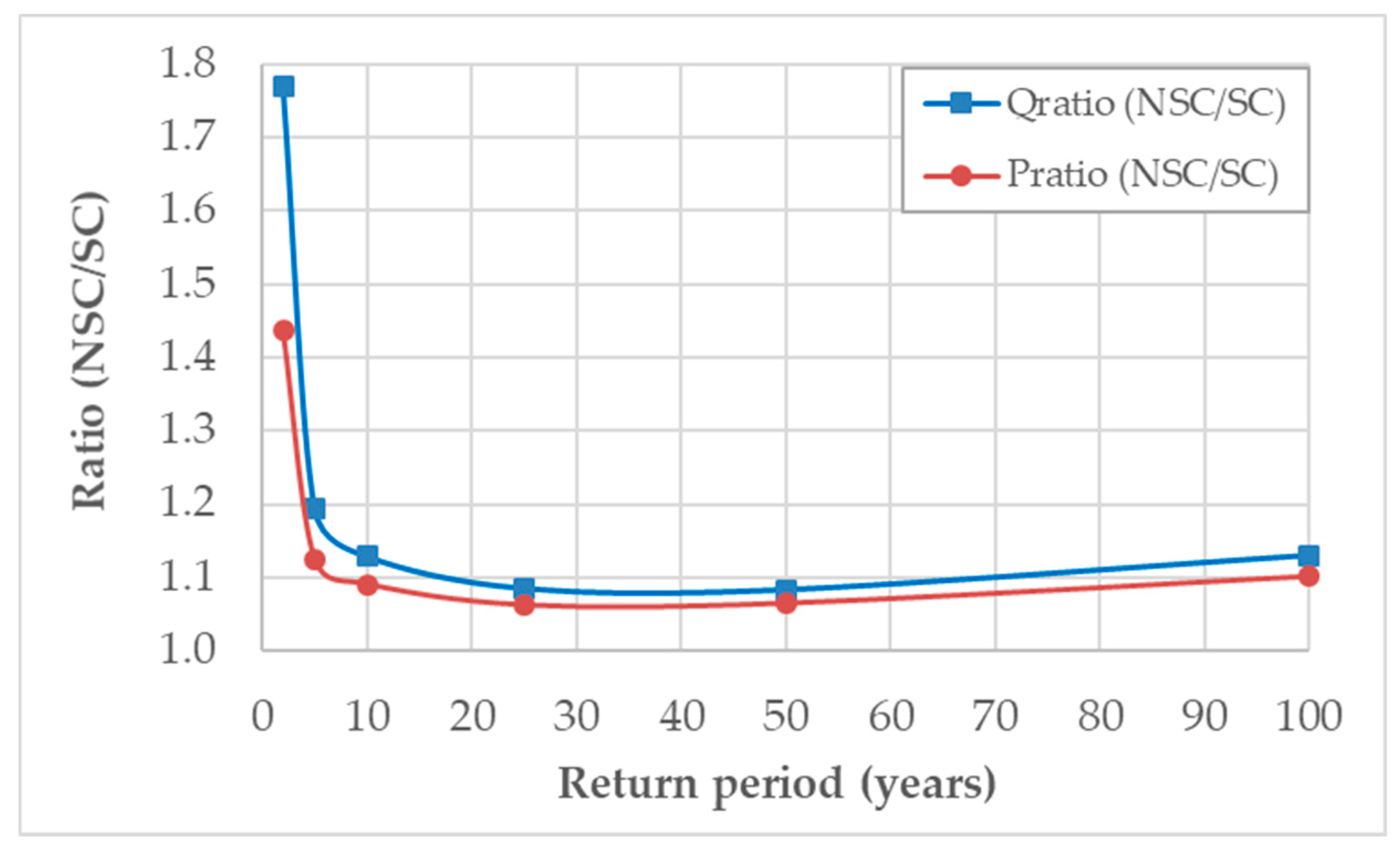
Figure 11 and
Figure 12 show respectively the non-stationary and stationary difference and ratios between P
24h-max and peak flow for different return periods (DPmax, DQp, Pratio and Qratio). As expected, both show how the behavior of P
24h-max, and the watershed’s response to it (the peak flow), have the same trend.
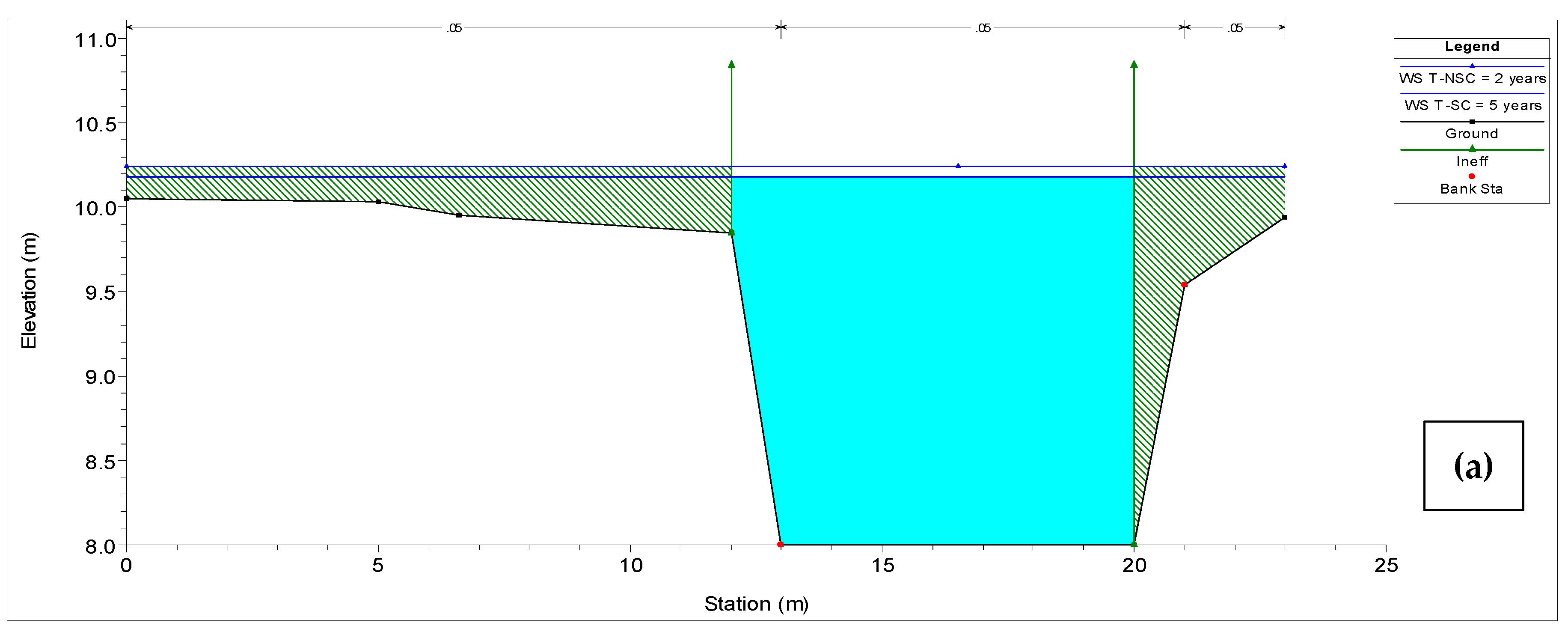
The water level reached after the simulations carried out under stationary and non-stationary conditions indicates that modeling under non-stationary scenario better represents the current hydrological conditions of the Gordo creek watershed, where rainfall events of low magnitude are generating floods every year during the rainy season (during which the soil is saturated most of the time) at the watershed’s outlet, when, in theory, they ought not to. This can be observed, for instance, in the results of the hydraulic simulation at K0+018.5 shown in
Table 12 (P
24h-max, peak flow, and water elevation) and
Figure 13, where the bankfull level (9.94 m) is reached at a lower return period (floods occur more frequently) under non-stationary conditions (
Tr < 2-year). Under stationary conditions, a 2-year return period flow, defined as the mean annual flow (or annual maximum daily flow) [
28,
29], did not result in a bankfull section, which is not what is currently occurring in the study area (floods every year). The change in the rainfall pattern evidenced in previous sections may be the reason for a shift towards more recurrent and higher-than-usual events that cause floods more frequently than in the past. Likewise, statistically speaking, the ACI results obtained in
Section 3.2 (747.5103 for non-stationary and 753.3721 for stationary) demonstrated that the non-stationary condition is more adequate. The AIC test serves to evaluate how good a model is for predicting future values [
30]. The lower the value of the AIC the better the model.
In terms of the flood depth (elevation above bankfull level) at the area of the watershed outlet,
Table 13 and
Figure 14 show the water depth above the bankfull level for different return periods. This sensitivity analysis reveals the necessity for sizing hydraulic structures under non-stationary conditions to avoid more recurring floods. Notwithstanding that the 1-D hydraulic simulation is incapable of delineating the extension of the flooded area beyond the creek’s bank, the difference between NSC and SC elevations in
Table 13 is an indication of what locals and workers of the industrial area have been noticing every year: floods in this area have been gradually worsening in terms of both frequency of occurrence and area covered by water (as well as the water depth marks left at some points that local people use as reference points). Further research is needed, though. Future work in this area must include a more detailed survey (topographic study) covering more area, so as to assess and more accurately quantify (numerically and spatially) the aforementioned anecdotal evidence.
An option for making decisions when designing some hydraulic structures would be to perform a benefit-cost analysis to compare a design under non-stationary conditions versus under stationary condition, taking into account free board heights, allowing handling of the non-stationary peak flow depending on the design return period.
In addition to the already quantified effects of climate change on Cartagena’s P
24h-max pattern and the Gordo creek watershed’s hydrological response, the fact that almost 85% of the watershed is still rural indicates that any increase in the impervious area will both raise the peak flow and reduce the time of concentration. These two variables will worsen the situation at the outlet of Gordo creek watershed unless a series of measures are implemented. For instance, the combination of sustainable urban drainage systems (SUDS) [
31,
32], stormwater storage vaults/tanks (both online and offline), aquifer storage and recovery (ASR) wells, infiltration ponds, among others, have proved to be effective at managing stormwater by: (a) keeping the peak flow at the same magnitude (or lower) when pre-development and post-development scenarios are compared, (b) avoiding the design of larger hydraulic structures, (c) minimizing the risk of floods, and (d) recharging aquifers, as a plus.
5. Conclusions
P24h-max values associated to a given return period are a key variable when estimating design DSR for hydraulic structures for stormwater management, especially in ungauged watersheds. The values obtained in the AIC test carried out in this study, indicated that a frequency analysis under non-stationary conditions represents best the behavior of the rainfall patterns of the P24h-max observations at the Rafael Núñez station. A stationary scenario is, in this case, further from the natural reality, when compared to non-stationary conditions. This was also confirmed by both the increase in the occurrence of P24h-max events greater than or equal to 148.1 mm (value for a 10-year return period under stationary conditions), and the increasing linear trend over time of the overall P24h-max observations. These findings may be an indication that the typical frequency analysis of rainfall under stationary conditions may no longer be applicable when calculating the design rainfall associated with a given return period for sizing hydraulic structures throughout Cartagena de Indias. Furthermore, designing under stationary conditions may have direct implications in the decisions local authorities will be taking in the coming years, given that millions of dollars will be invested in upgrading the city’s stormwater system. The 1-D hydraulic simulation performed herein revealed that the Gordo creek watershed outlet area can be flooded even with an event of 2-year return period (every year)—a situation that had never been observed in the past according to what local people have affirmed. The increase in the P24h-max, though, is not the sole factor to be taken into account when evaluating the reasons behind the more frequent floods reported. Uncontrolled and unplanned urbanization of vegetated areas may and will exacerbate the recurrent floods registered within the study area.
It is noteworthy to mention that sizing larger hydraulic structures for stormwater management as the only solution for the larger rainfall events estimated under non-stationary conditions might be unsuitable and unsustainable in cases where surface area limitations exist (especially in urban areas). Therefore, implementing best management practices for controlling stormwater sources in old and newly constructed areas shall be one of the city’s goals in maintaining the design peak flow values, especially under increasing non-stationary conditions.