Multiscale Stuart-Landau Emulators: Application to Wind-Driven Ocean Gyres
Abstract
1. Introduction
2. Results
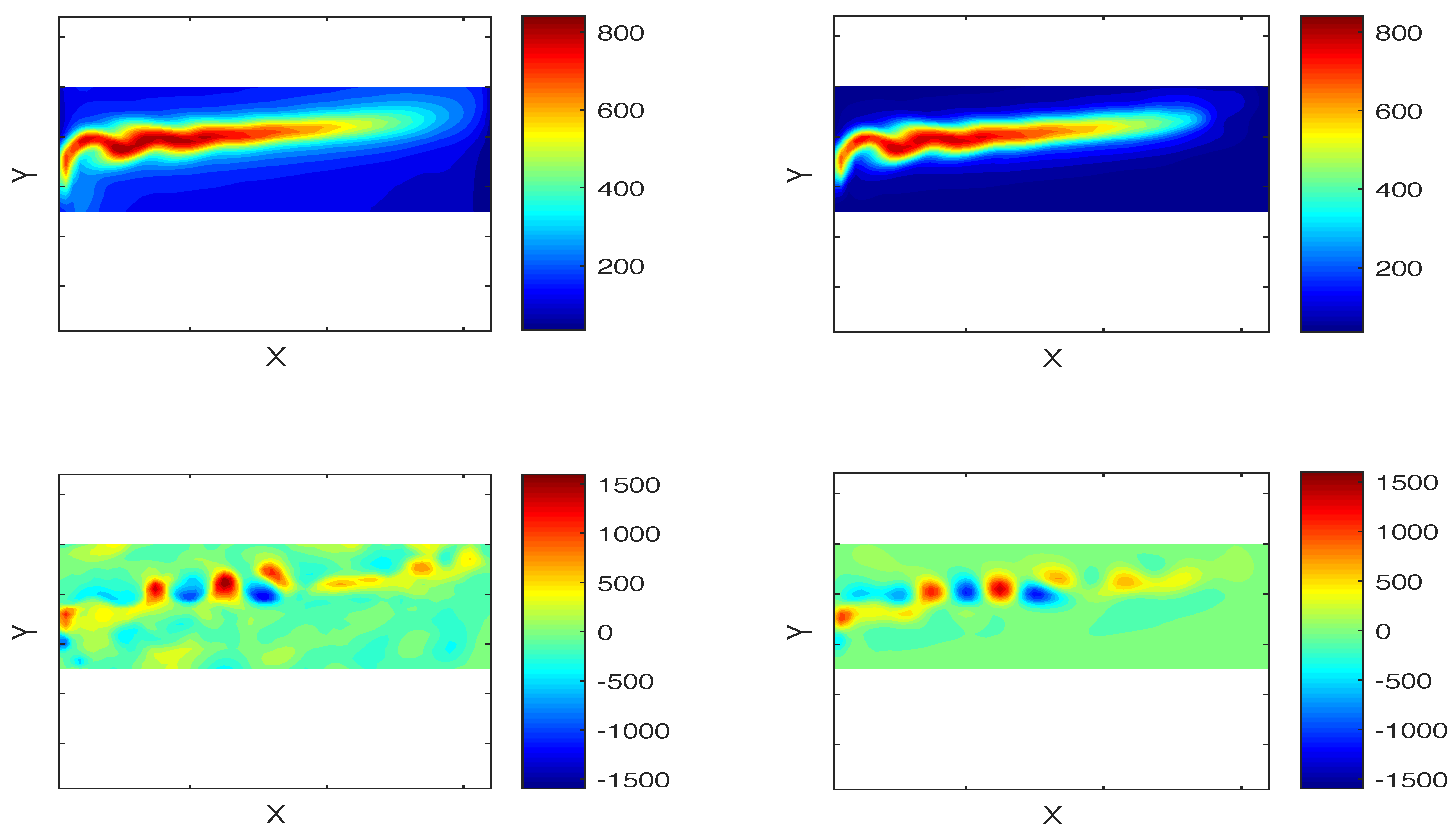
2.1. Oceanic Dataset
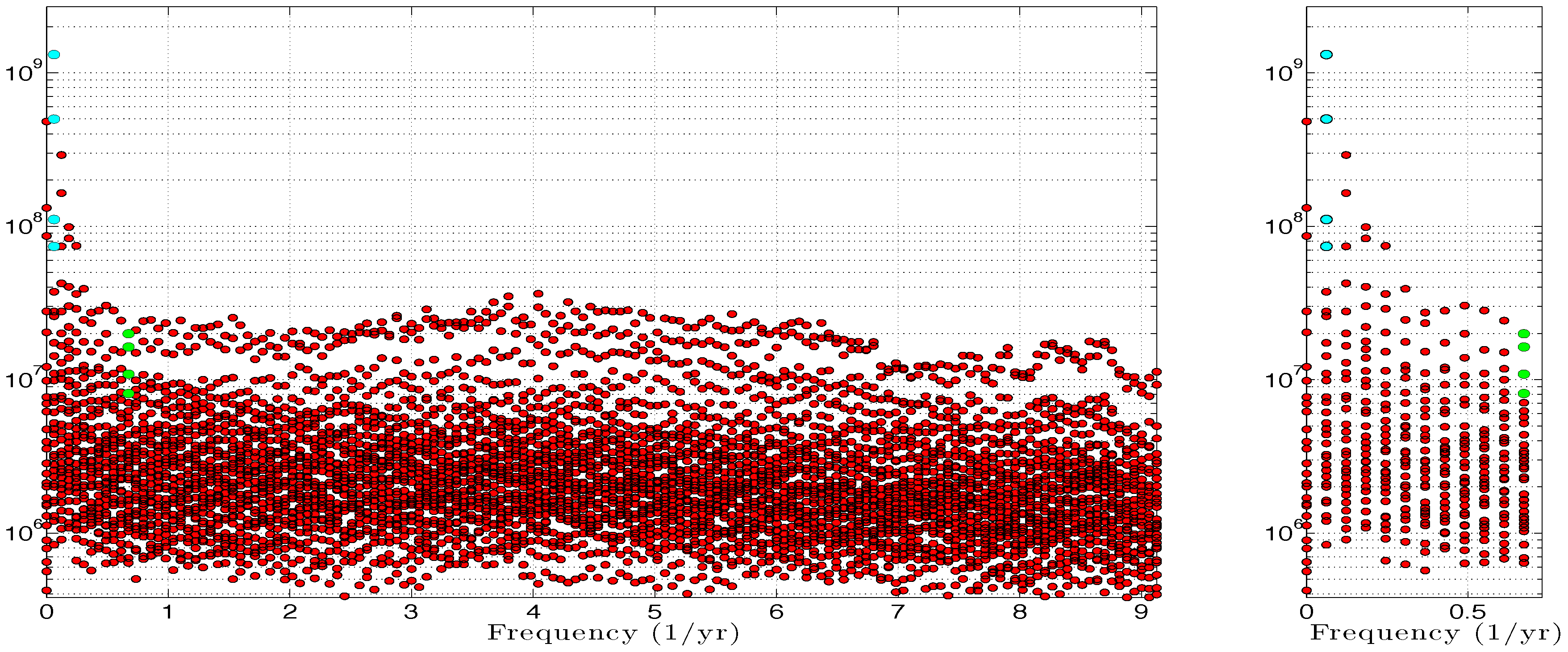
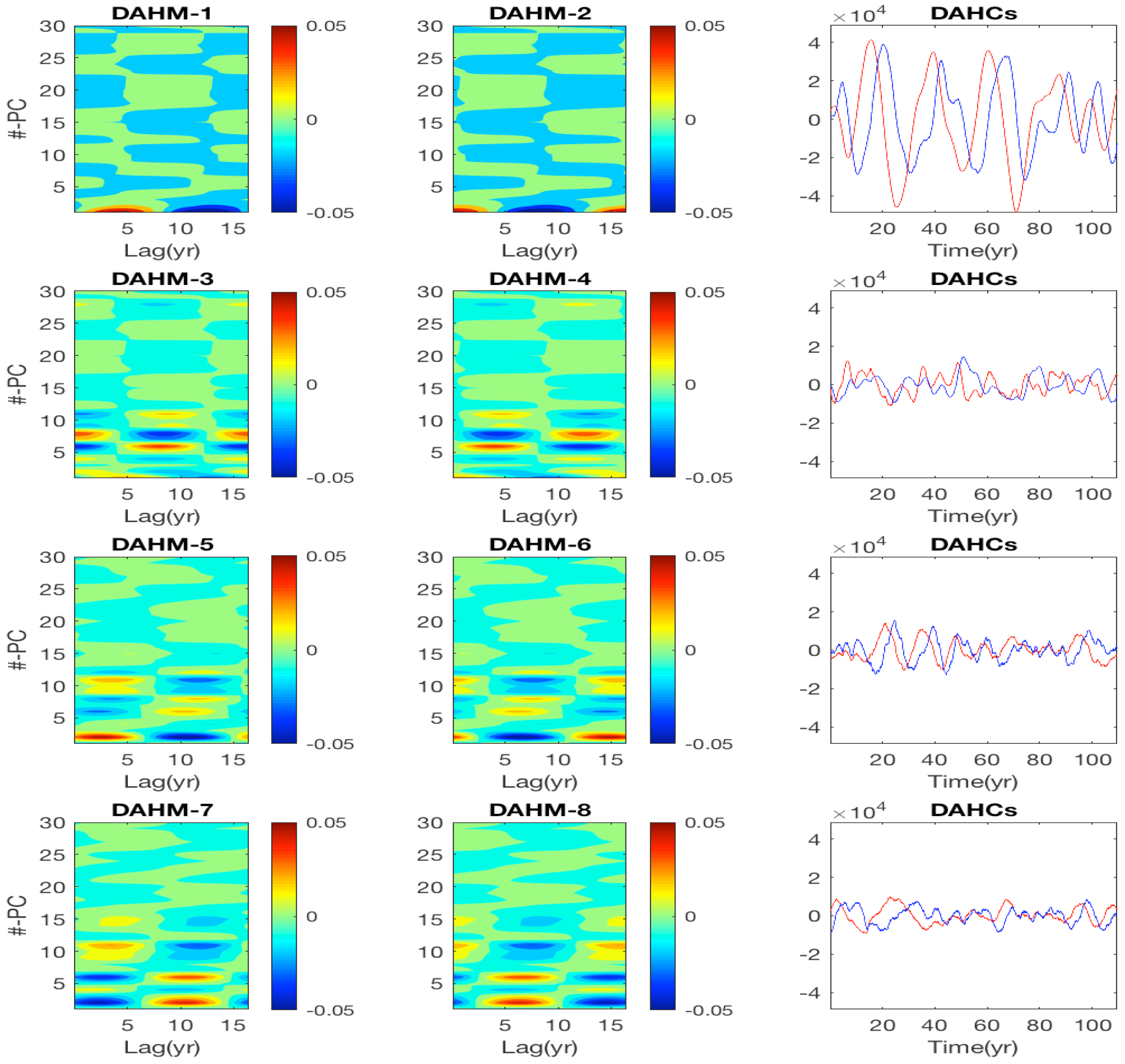
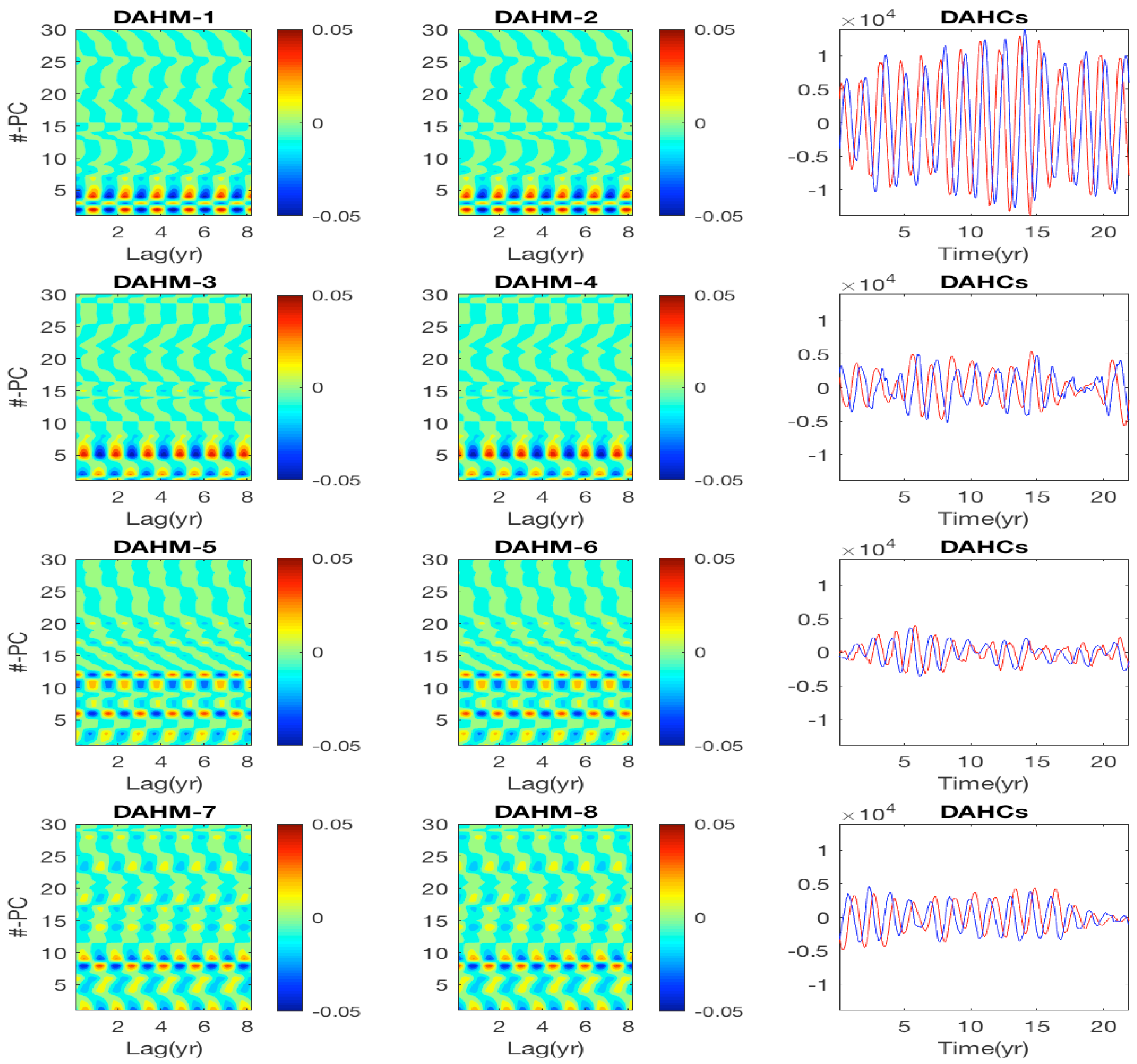
2.2. DAHD, DAH Power Spectrum and DAHMs
2.3. DAH-MSLM Oceanic Emulators
3. Discussion
4. Models and Methods
4.1. Mid-Latitude Ocean Model
4.2. Data-Adaptive Harmonic Decomposition
4.2.1. DAH Eigenelements and Power Spectrum
4.2.2. DAH Coefficients
4.3. Multilayer Stuart–Landau Models
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DAH | Data-adaptive harmonic |
| DAHD | Data-adaptive harmonic decomposition |
| DAHC | Data-adaptive harmonic coefficient |
| DAHM | Data-adaptive harmonic mode |
| EOF | Empirical orthogonal function |
| HRC | Harmonic reconstructed component |
| LFV | Low frequency variability |
| MSLM | Multilayer Stuart–Landau model |
| PCA | Principal component analysis |
| PSD | Power spectral density |
| RC | Reconstructed component |
| RP | Ruelle–Pollicott |
| SDE | Stochastic differential equation |
| SL | Stuart–Landau |
Appendix A. Time Variability of Stochastic Systems and Ruelle–Pollicott Resonances
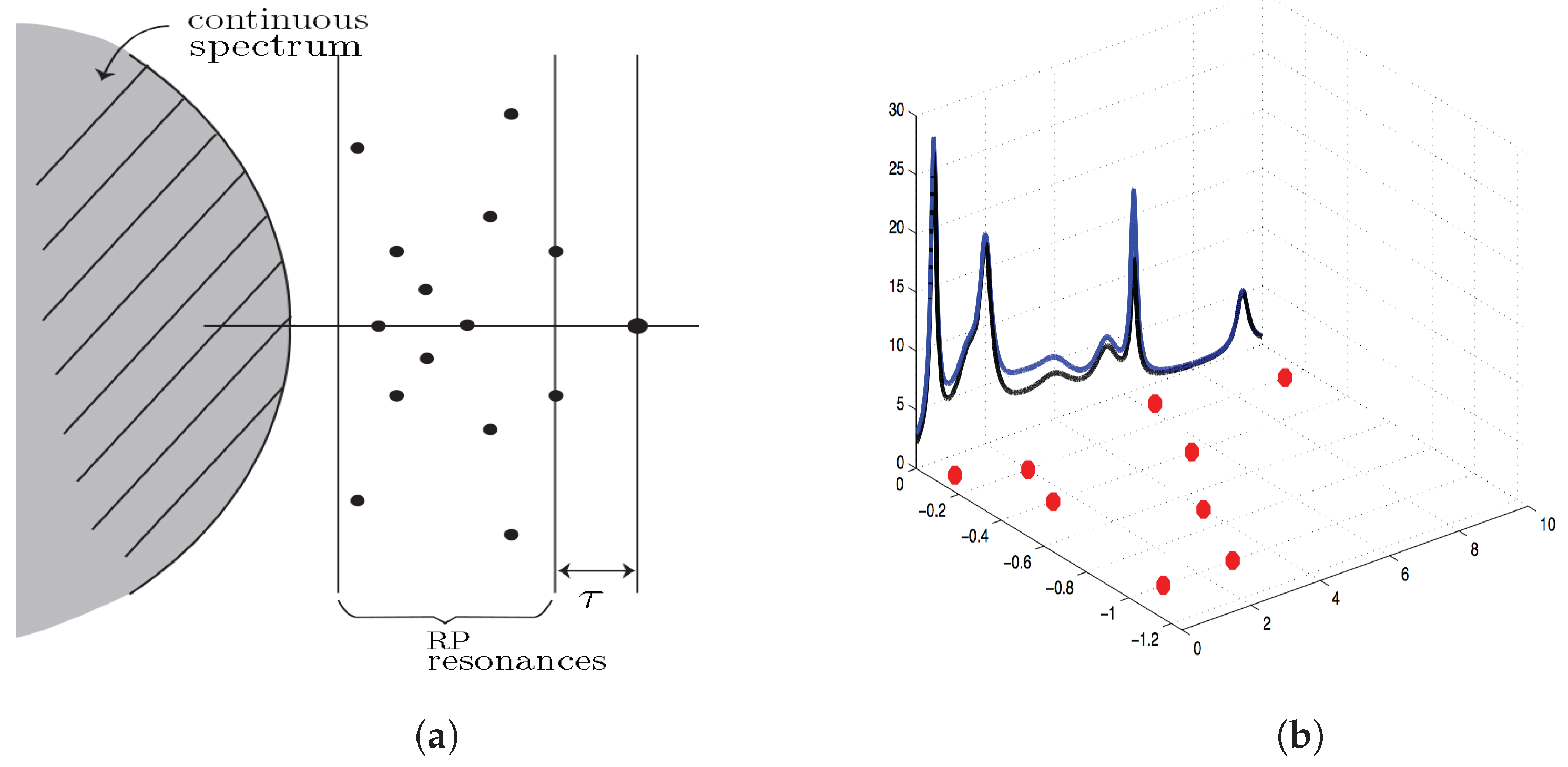
Appendix B. Estimating Resonances from Time Series: The Reduced RP Resonances
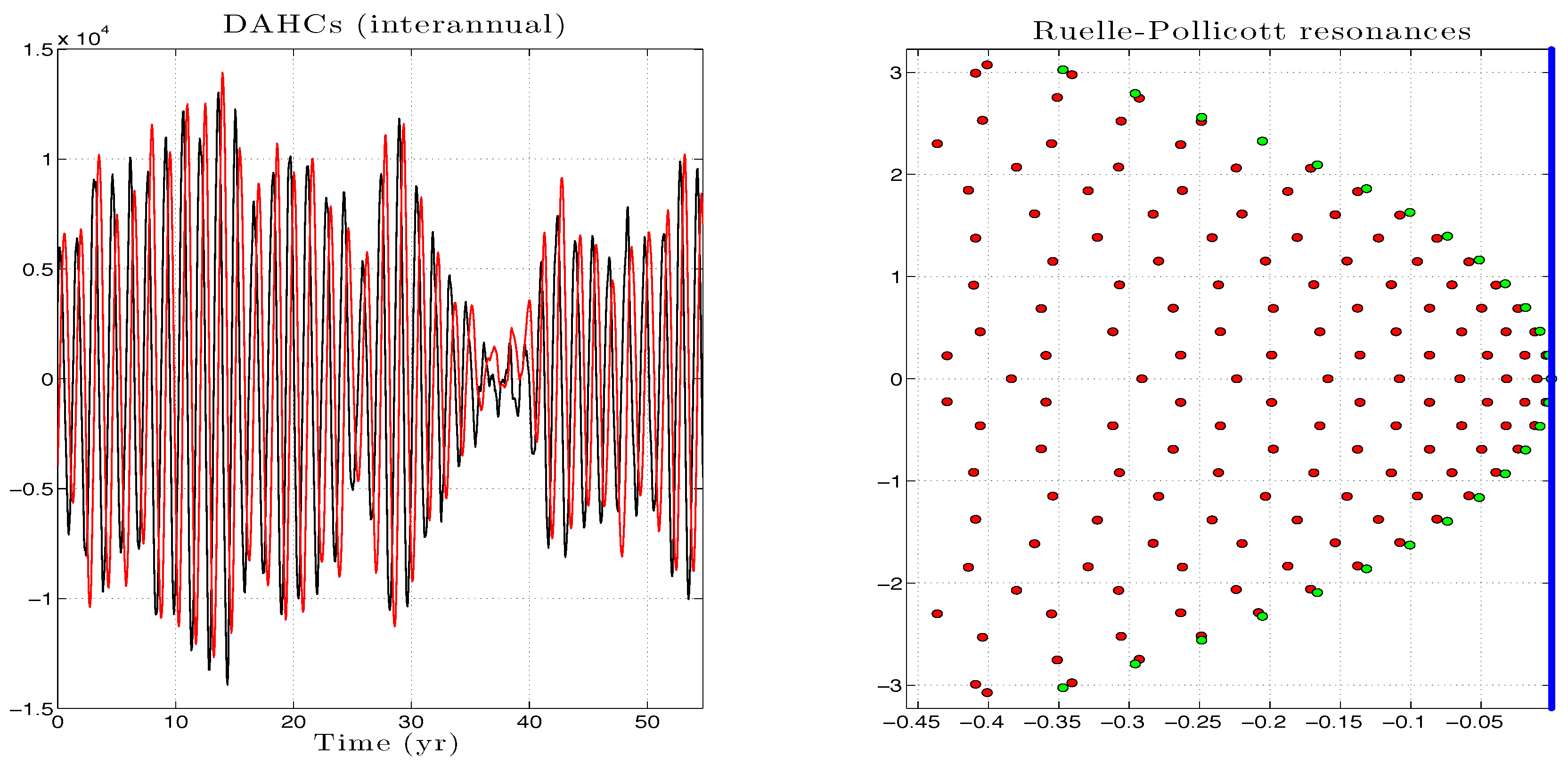
Appendix C. RP Resonances of Stuart–Landau Models: Analytic Approximations
Appendix D. Multilayer Stuart–Landau Modeling of DAHCs
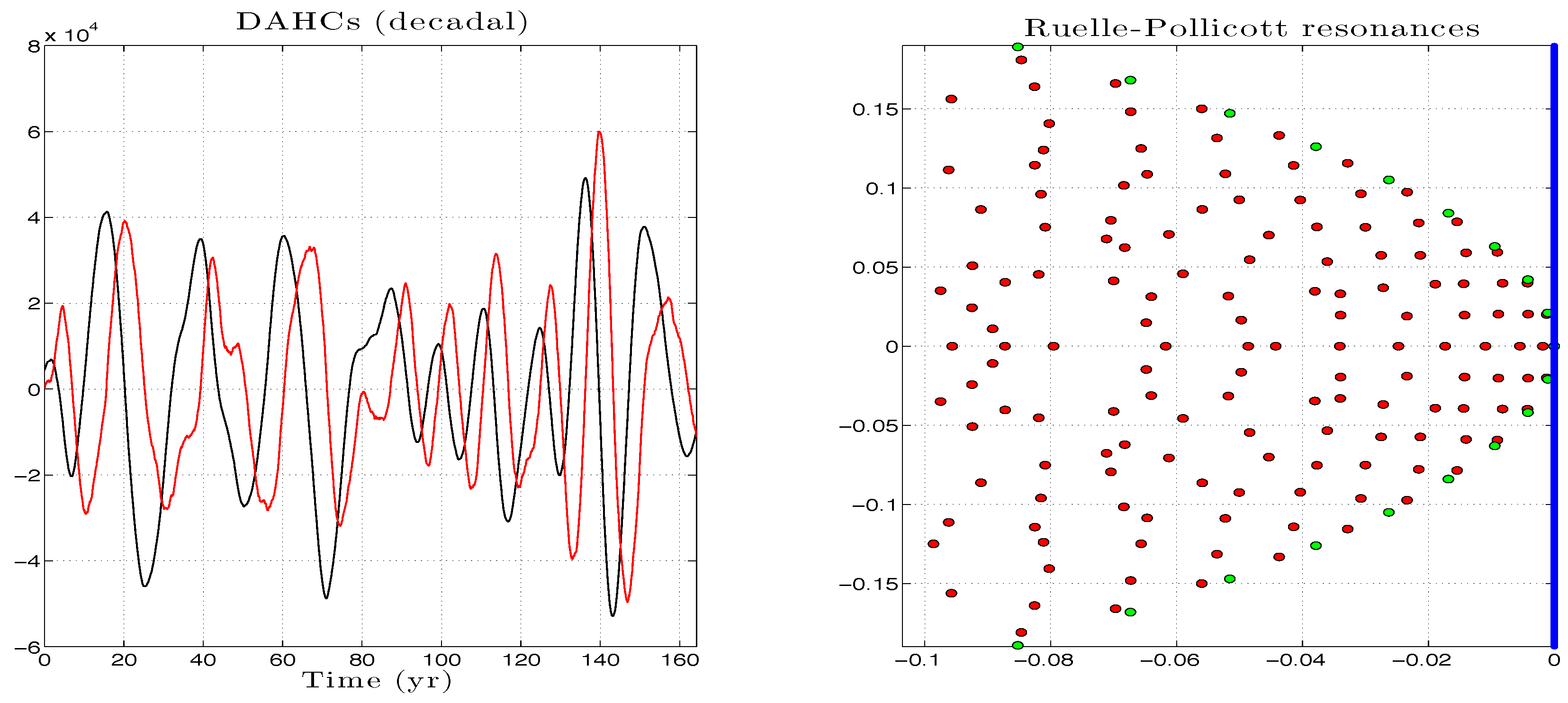
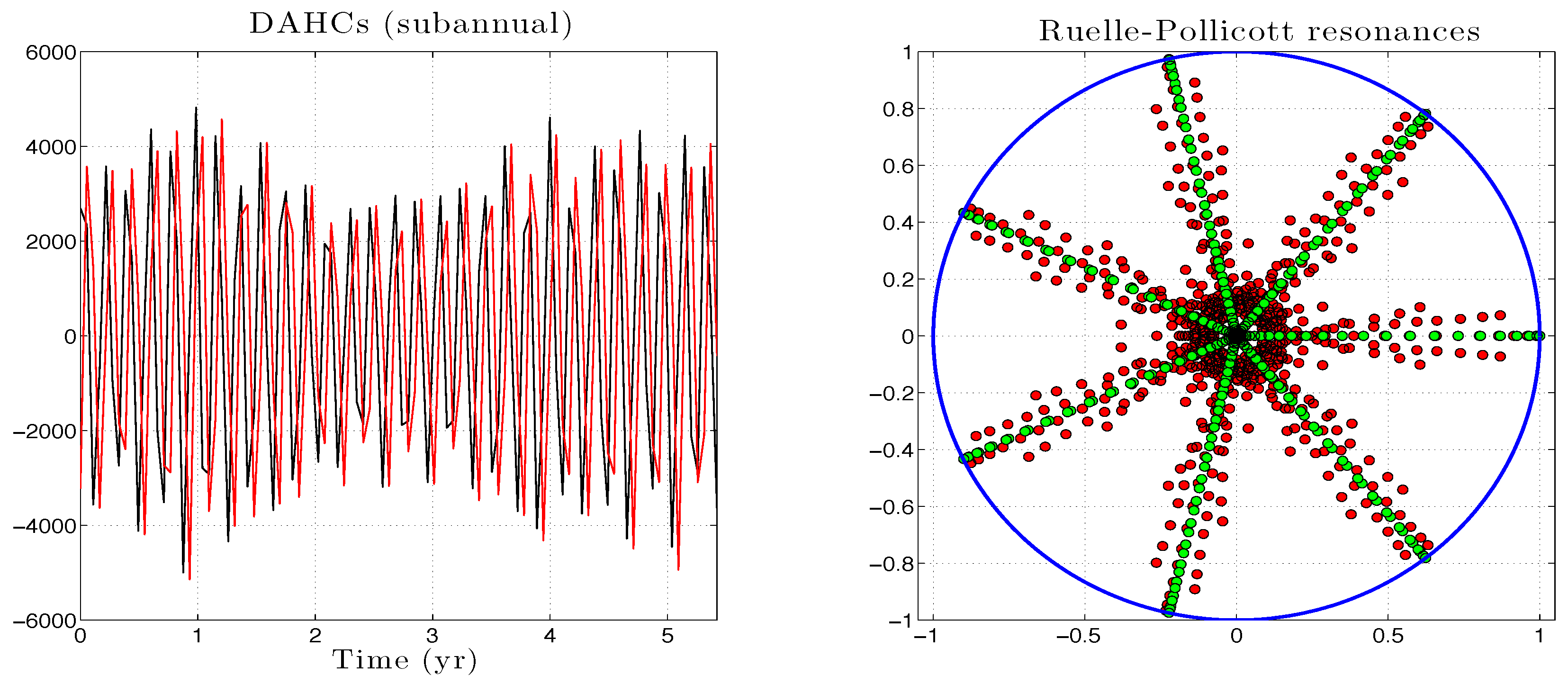
Appendix E. Modeling Skills in the EOF Space
References
- Gent, P.; McWilliams, J. Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 1990, 20, 150–155. [Google Scholar] [CrossRef]
- Eden, C. A closure for meso-scale eddy fluxes based on linear instability theory. Ocean Model. 2011, 39, 362–369. [Google Scholar] [CrossRef]
- Leith, C.E. Stochastic backscatter in a subgrid-scale model: Plane shear mixing layer. Phys. Fluids A Fluid Dyn. 1990, 2, 297–299. [Google Scholar] [CrossRef]
- Berloff, P.S.; McWilliams, J.C. Material transport in oceanic gyres. Part III: Randomized stochastic models. J. Phys. Oceanogr. 2003, 33, 1416–1445. [Google Scholar] [CrossRef]
- Berloff, P.S. Random-forcing model of the mesoscale oceanic eddies. J. Fluid Mech. 2005, 529, 71–95. [Google Scholar] [CrossRef]
- Porta Mana, P.; Zanna, L. Toward a stochastic parameterization of ocean mesoscale eddies. Ocean Model. 2014, 79, 1–20. [Google Scholar] [CrossRef]
- Jansen, M.; Held, I. Parameterizing subgrid-scale eddy effects using energetically consistent backscatter. Ocean Model. 2014, 80, 36–48. [Google Scholar] [CrossRef]
- Berloff, P. Dynamically consistent parameterization of mesoscale eddies. Part I: Simple model. Ocean Model. 2015, 87, 1–19. [Google Scholar] [CrossRef]
- Chorin, A.J.; Hald, O.H.; Kupferman, R. Optimal prediction with memory. Physica D 2002, 166, 239–257. [Google Scholar] [CrossRef]
- Givon, D.; Kupferman, R.; Stuart, A. Extracting macroscopic dynamics: model problems and algorithms. Nonlinearity 2004, 17, R55–R127. [Google Scholar] [CrossRef]
- Chorin, A.J.; Hald, O.H.; Kupferman, R. Prediction from partial data, renormalization, and averaging. J. Sci. Comput. 2006, 28, 245–261. [Google Scholar] [CrossRef]
- Hald, O.H.; Stinis, P. Optimal prediction and the rate of decay for solutions of the Euler equations in two and three dimensions. Proc. Natl. Acad. Sci. USA 2007, 104, 6527–6532. [Google Scholar] [CrossRef] [PubMed]
- Wouters, J.; Lucarini, V. Multi-level dynamical systems: Connecting the Ruelle response theory and the Mori-Zwanzig approach. J. Stat. Phys. 2013, 151, 850–860. [Google Scholar] [CrossRef]
- Temam, R. Infinite-Dimensional Dynamical Systems in Mechanics and Physics, 2nd ed.; Springer: New York, NY, USA, 1997; p. 648. [Google Scholar]
- Ma, T.; Wang, S. Bifurcation Theory and Applications; World Scientific: Singapore, 2005; Volume 53. [Google Scholar]
- Ma, T.; Wang, S. Phase Transition Dynamics; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Chekroun, M.; Liu, H.; McWilliams, J. The emergence of fast oscillations in a reduced primitive equation model and its implications for closure theories. Comput. Fluids 2017, 151, 3–22. [Google Scholar] [CrossRef]
- Chekroun, M.D.; Liu, H.; Wang, S. Approximation of Stochastic Invariant Manifolds: Stochastic Manifolds for Nonlinear SPDEs I; Springer Briefs in Mathematics; Springer: New York, NY, USA, 2015. [Google Scholar]
- Chekroun, M.D.; Liu, H.; Wang, S. Stochastic Parameterizing Manifolds and Non-Markovian Reduced Equations: Stochastic Manifolds for Nonlinear SPDEs II; Springer Briefs in Mathematics; Springer: New York, NY, USA, 2015. [Google Scholar]
- Jolliffe, I. Principal Component Analysis; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Preisendorfer, R.W. Principal Component Analysis in Meteorology and Oceanography; Elsevier: New York, NY, USA, 1988; p. 425. [Google Scholar]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. B 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Mukhin, D.; Gavrilov, A.; Feigin, A.; Loskutov, E.; Kurths, J. Principal nonlinear dynamical modes of climate variability. Sci. Rep. 2015, 5, 15510. [Google Scholar] [CrossRef] [PubMed]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40. [Google Scholar] [CrossRef]
- Coifman, R.R.; Lafon, S. Diffusion maps. Appl. Comput. Harmon. Anal. 2006, 21, 5–30. [Google Scholar] [CrossRef]
- Coifman, R.R.; Kevrekidis, I.G.; Lafon, S.; Maggioni, M.; Nadler, B. Diffusion maps, reduction coordinates, and low dimensional representation of stochastic systems. Multiscale Model. Simul. 2008, 7, 842–864. [Google Scholar] [CrossRef]
- Giannakis, D.; Majda, A.J. Nonlinear Laplacian spectral analysis for time series with intermittency and low-frequency variability. Proc. Natl. Acad. Sci. USA 2012, 109, 2222–2227. [Google Scholar] [CrossRef] [PubMed]
- Froyland, G.; Gottwald, G.A.; Hammerlindl, A. A computational method to extract macroscopic variables and their dynamics in multiscale systems. SIAM J. Appl. Dyn. Syst. 2014, 13, 1816–1846. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Budišić, M.; Mohr, R.; Mezić, I. Applied Koopmanism. Chaos 2012, 22, 047510. [Google Scholar] [CrossRef] [PubMed]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data-driven approximation of the Koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Klus, S.; Koltai, P.; Schütte, C. On the numerical approximation of the Perron-Frobenius and Koopman operator. J. Comput. Dyn. 2016, 3, 51–79. [Google Scholar]
- Klus, S.; Nüske, F.; Koltai, P.; Wu, H.; Kevrekidis, I.; Schütte, C.; Noé, F. Data-driven model reduction and transfer operator approximation. J. Nonlinear Sci. 2017, 1–26. [Google Scholar] [CrossRef]
- Chorin, A.J.; Lu, F. Discrete approach to stochastic parametrization and dimension reduction in nonlinear dynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 9804–9809. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Lin, K.; Chorin, A. Comparison of continuous and discrete-time data-based modeling for hypoelliptic systems. Commun. Appl. Math. Comput. Sci. 2016, 11, 187–216. [Google Scholar] [CrossRef]
- Lu, F.; Lin, K.; Chorin, A. Data-based stochastic model reduction for the Kuramoto–Sivashinsky equation. Phys. D Nonlinear Phenom. 2017, 340, 46–57. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. An artificial neural network (p,d,q)-model for time series forecasting. Expert Syst. Appl. 2010, 37, 479–489. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gupta, H.V.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Mukhin, D.; Kondrashov, D.; Loskutov, E.; Gavrilov, A.; Feigin, A.; Ghil, M. Predicting critical transitions in ENSO models. Part II: Spatially dependent models. J. Clim. 2015, 28, 1962–1976. [Google Scholar] [CrossRef]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 237, 10–26. [Google Scholar] [CrossRef]
- Iliescu, T.; Wang, Z. Variational multiscale proper orthogonal decomposition: Navier-stokes equations. Numer. Methods Partial Differ. Equ. 2014, 30, 641–663. [Google Scholar] [CrossRef]
- Kwasniok, F. Empirical low-order models of barotropic flow. J. Atmos. Sci. 2004, 61, 235–245. [Google Scholar] [CrossRef]
- Sapsis, T.P.; Dijkstra, H.A. Interaction of additive noise and nonlinear dynamics in the double-gyre wind-driven ocean circulation. J. Phys. Oceanogr. 2013, 43, 366–381. [Google Scholar] [CrossRef]
- Penland, C. Random forcing and forecasting using principal oscillation pattern analysis. Month. Wea. Rev. 1989, 117, 2165–2185. [Google Scholar] [CrossRef]
- Penland, C.; Sardeshmukh, P.D. The optimal growth of tropical sea-surface temperature anomalies. J. Clim. 1995, 8, 1999–2024. [Google Scholar] [CrossRef]
- Kravtsov, S.; Kondrashov, D.; Ghil, M. Multilevel regression modeling of nonlinear processes: Derivation and applications to climatic variability. J. Clim. 2005, 18, 4404–4424. [Google Scholar] [CrossRef]
- Kravtsov, S.; Kondrashov, D.; Ghil, M. Empirical model reduction and the modeling hierarchy in climate dynamics. In Stochastic Physics and Climate Modeling; Palmer, T.N., Williams, P., Eds.; Cambridge Univ. Press: Cambridge, UK, 2009; pp. 35–72. [Google Scholar]
- Kondrashov, D.; Kravtsov, S.; Robertson, A.W.; Ghil, M. A hierarchy of data-based ENSO models. J. Clim. 2005, 18, 4425–4444. [Google Scholar] [CrossRef]
- Kondrashov, D.; Chekroun, M.D.; Robertson, A.W.; Ghil, M. Low-order stochastic model and “past-noise forecasting” of the Madden-Julian oscillation. Geophys. Res. Lett. 2013, 40, 5305–5310. [Google Scholar] [CrossRef]
- Majda, A.J.; Harlim, J. Physics constrained nonlinear regression models for time series. Nonlinearity 2012, 26, 201. [Google Scholar] [CrossRef]
- Strounine, K.; Kravtsov, S.; Kondrashov, D.; Ghil, M. Reduced models of atmospheric low-frequency variability: Parameter estimation and comparative performance. Physica D 2010, 239, 145–166. [Google Scholar] [CrossRef]
- Kondrashov, D.; Chekroun, M.D.; Ghil, M. Data-driven non-Markovian closure models. Physica D 2015, 297, 33–55. [Google Scholar] [CrossRef]
- Chekroun, M.D.; Kondrashov, D. Data-adaptive harmonic spectra and multilayer Stuart-Landau models. Chaos 2017, 27. [Google Scholar] [CrossRef] [PubMed]
- Chekroun, M.D.; Neelin, J.D.; Kondrashov, D.; McWilliams, J.C.; Ghil, M. Rough parameter dependence in climate models: The role of Ruelle-Pollicott resonances. Proc. Natl. Acad. Sci USA 2014, 111, 1684–1690. [Google Scholar] [CrossRef] [PubMed]
- Kondrashov, D.; Chekroun, M.D.; Yuan, X.; Ghil, M. Data-adaptive harmonic decomposition and stochastic modeling of Arctic sea ice. In Advances in Nonlinear Geosciences; Tsonis, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Kondrashov, D.; Chekroun, M.D.; Ghil, M. Data-adaptive harmonic decomposition and prediction of Arctic sea ice extent. Dyn. Stat. Clim. Syst. Interdiscip. J. 2018, in press. [Google Scholar]
- Kondrashov, D.; Chekroun, M.D. Data-adaptive harmonic analysis and modeling of solar wind-magnetosphere coupling. J. Atmos. Solar Terr. Phys. 2018, in press. [Google Scholar] [CrossRef]
- Berloff, P.; Hogg, A.M.C.; Dewar, W. The turbulent oscillator: A mechanism of low-frequency variability of the wind-driven ocean gyres. J. Phys. Oceanogr. 2007, 37, 2363–2386. [Google Scholar] [CrossRef]
- Shevchenko, I.V.; Berloff, P.; Guerrero-Lopez, D.; Roman, J.E. On low-frequency variability of the midlatitude ocean gyres. J. Fluid Mech. 2016, 795, 423–442. [Google Scholar] [CrossRef]
- Jiang, S.; Jin, F.F.; Ghil, M. Multiple equilibria, periodic, and aperiodic solutions in a wind-driven, double-gyre, shallow-water model. J. Phys. Oceanogr. 1995, 25, 764–786. [Google Scholar] [CrossRef]
- Nadiga, B.T.; Luce, B.P. Global bifurcation of Shilnikov type in a double-gyre ocean model. J. Phys. Oceanogr. 2001, 31, 2669–2690. [Google Scholar] [CrossRef]
- Simonnet, E.; Dijkstra, H.A. Spontaneous generation of low-frequency modes of variability in the wind-driven ocean circulation. J. Phys. Oceanogr. 2002, 32, 1747–1762. [Google Scholar] [CrossRef]
- Simonnet, E.; Ghil, M.; Ide, K.; Temam, R.; Wang, S. Low-frequency variability in shallow-water models of the wind-driven ocean circulation. Part II: Time-dependent solutions. J. Phys. Oceanogr. 2003, 33, 729–752. [Google Scholar] [CrossRef]
- Dijkstra, H.A.; Ghil, M. Low-frequency variability of the large-scale ocean circulation: A dynamical systems approach. Rev. Geophys. 2005, 43. [Google Scholar] [CrossRef]
- Dijkstra, H. A normal mode perspective of intrinsic ocean-climate variability. Ann. Rev. Fluid Mech. 2016, 48, 341–363. [Google Scholar] [CrossRef]
- Ghil, M. The wind-driven ocean circulation: Applying dynamical systems theory to a climate problem. Discret. Contin. Dyn. Syst. A 2017, 37, 189–228. [Google Scholar] [CrossRef]
- Kondrashov, D.; Berloff, P. Stochastic modeling of decadal variability in ocean gyres. Geophys. Res. Lett. 2015, 42, 1543–1553. [Google Scholar] [CrossRef]
- Gaspard, P. Trace formula for noisy flows. J. Stat. Phys. 2002, 106, 57–96. [Google Scholar] [CrossRef]
- Chekroun, M.; Tantet, A.; Dijkstra, H.; Neelin, J.D. Mixing spectrum in reduced phase spaces of stochastic differential equations. Part I: Theory. arXiv, 2017; arXiv:1705.07573. [Google Scholar]
- Landau, L.D.; Lifshits, E.M. Fluid Mechanics; Pergamon Press: Oxford, UK, 1959. [Google Scholar]
- Ruelle, D.; Takens, F. On the nature of turbulence. Commun. Math. Phys. 1971, 20, 167–192. [Google Scholar] [CrossRef]
- Berloff, P.; Dewar, W.; Kravtsov, S.; McWilliams, J. Ocean eddy dynamics in a coupled ocean–atmosphere model. J. Phys. Oceanogr. 2007, 37, 1103–1121. [Google Scholar] [CrossRef]
- Berloff, P. Dynamically Consistent Parameterization of Mesoscale Eddies. Part II: Eddy Fluxes and and diffusivity from transient impulses. Fluids 2016, 1, 22. [Google Scholar] [CrossRef]
- Engel, K.J.; Nagel, R. A Short Course on Operator Semigroups; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Zakharova, A.; Loos, S.; Siebert, J.; Gjurchinovski, A.; Claussen, J.C.; Schöll, E. Controlling chimera patterns in networks: interplay of structure, noise, and delay in Control of Self-Organizing Nonlinear Systems. In Control of Self-Organizing Nonlinear Systems; Schöll, E., Klapp, S.H.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 35–72. [Google Scholar]
- Selivanov, A.A.; Lehnert, J.; Dahms, T.; Hövel, P.; Fradkov, A.L.; Schöll, E. Adaptive synchronization in delay-coupled networks of Stuart-Landau oscillators. Phys. Rev. E 2012, 85, 016201. [Google Scholar] [CrossRef] [PubMed]
- Cerrai, S. Second-Order PDE’s in Finite and Infinite Dimension: A Probabilistic Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 1762. [Google Scholar]
- Flandoli, F.; Gubinelli, M.; Priola, E. Flow of diffeomorphisms for SDEs with unbounded Holder continuous drift. Bull. Sci. Math. 2010, 134, 405–422. [Google Scholar] [CrossRef]
- Ruelle, D. Locating resonances for Axiom A dynamical systems. J. Stat. Phys. 1986, 44, 281–292. [Google Scholar] [CrossRef]
- Pollicott, M. Meromorphic extensions of generalised zeta functions. Invent. Math. 1986, 85, 147–164. [Google Scholar] [CrossRef]
- Butterley, O.; Liverani, C. Smooth Anosov flows: Correlation spectra and stability. J. Mod. Dyn. 2007, 1, 301–322. [Google Scholar] [CrossRef]
- Dyatlov, S.; Zworski, M. Stochastic stability of Pollicott–Ruelle resonances. Nonlinearity 2015, 28, 3511. [Google Scholar] [CrossRef]
- Froyland, G. Computer-assisted bounds for the rate of decay of correlations. Commun. Math. Phys. 1997, 189, 237–257. [Google Scholar] [CrossRef]
- Crommelin, D.; Vanden-Eijnden, E. Reconstruction of diffusions using spectral data from time series. Commun. Math. Sci. 2006, 4, 651–668. [Google Scholar] [CrossRef]
- Schütte, C.; Fischer, A.; Huisinga, W.; Deuflhard, P. A direct approach to conformational dynamics based on hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. [Google Scholar] [CrossRef]
- Crommelin, D.; Vanden-Eijnden, E. Fitting time series by continuous-time Markov chains: A quadratic programming approach. J. Comput. Phys. 2006, 217, 782–805. [Google Scholar] [CrossRef]
- Tantet, A.; Chekroun, M.; Dijkstra, H.; Neelin, J.D. Mixing Spectrum in Reduced Phase Spaces of Stochastic Differential Equations. Part II: Stochastic Hopf Bifurcation. arXiv, 2017; arXiv:1705.07573. [Google Scholar]
- Chekroun, M.D.; Simonnet, E.; Ghil, M. Stochastic climate dynamics: Random attractors and time-dependent invariant measures. Physica D 2011, 240, 1685–1700. [Google Scholar] [CrossRef]
- Bagheri, S. Effects of weak noise on oscillating flows: Linking quality factor, Floquet modes, and Koopman spectrum. Phys. Fluids 2014, 26, 094104. [Google Scholar] [CrossRef]
- Gaspard, P.; Nicolis, G.; Provata, A.; Tasaki, S. Spectral signature of the pitchfork bifurcation: Liouville equation approach. Phys. Rev. E 1995, 51, 74. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondrashov, D.; Chekroun, M.D.; Berloff, P. Multiscale Stuart-Landau Emulators: Application to Wind-Driven Ocean Gyres. Fluids 2018, 3, 21. https://doi.org/10.3390/fluids3010021
Kondrashov D, Chekroun MD, Berloff P. Multiscale Stuart-Landau Emulators: Application to Wind-Driven Ocean Gyres. Fluids. 2018; 3(1):21. https://doi.org/10.3390/fluids3010021
Chicago/Turabian StyleKondrashov, Dmitri, Mickaël D. Chekroun, and Pavel Berloff. 2018. "Multiscale Stuart-Landau Emulators: Application to Wind-Driven Ocean Gyres" Fluids 3, no. 1: 21. https://doi.org/10.3390/fluids3010021
APA StyleKondrashov, D., Chekroun, M. D., & Berloff, P. (2018). Multiscale Stuart-Landau Emulators: Application to Wind-Driven Ocean Gyres. Fluids, 3(1), 21. https://doi.org/10.3390/fluids3010021





