Kinematics of a Fluid Ellipse in a Linear Flow
Abstract
1. Introduction
2. Definitions and Notation
2.1. A Linear Velocity Field
2.2. A Matrix Basis
2.3. The Kinetic Energy, Stream Function. and Angular Velocity
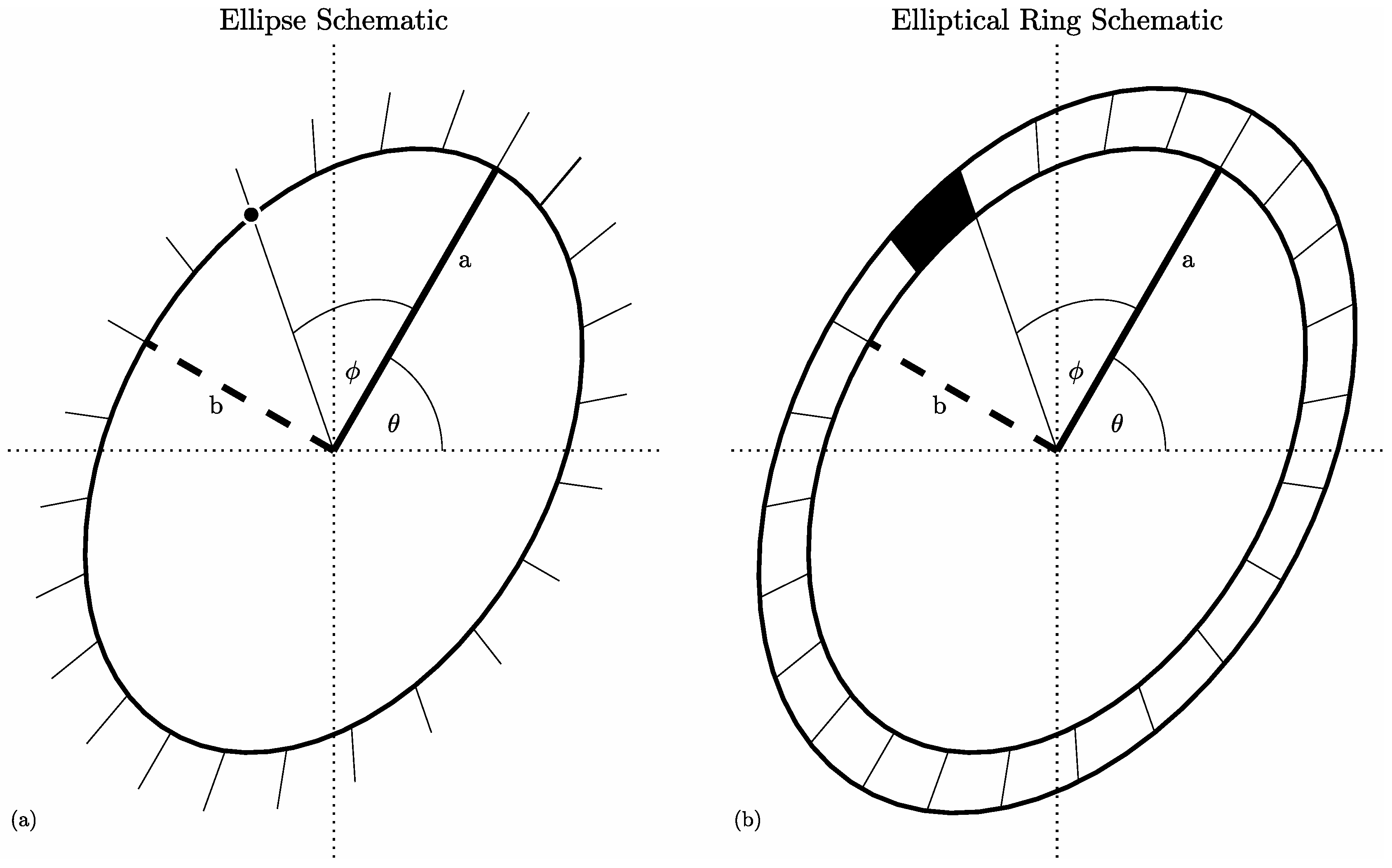
2.4. Measures of Ellipse Size and Shape
2.5. Stream Function and Energy Ellipses
3. Ellipse Kinematics
3.1. A Kinematic Model for Fluid Particles in an Ellipse
3.2. The Ellipse Flow Matrix
3.3. The Ellipse Evolution Equations and Ellipse/Flow Equivalence
3.4. The Kinematic Boundary Condition Approach
4. Integrals of a Fluid Ellipse
4.1. An Elliptical Ring of Fluid
4.2. Moment of Inertia, Angular Momentum, and Circulation
4.3. Physical Properties of an Elliptical Disk of Fluid
4.4. Kinetic Energy
4.5. Computing the Integrals of the Ellipse
4.6. Computing the Kinetic Energy Integral
4.7. A Partitioning of the Ellipse Kinetic Energy
5. The Extended Stokes’ Theorem
5.1. Moment Matrices
5.2. An Extended Stokes’ Theorem
6. Discussion
Acknowledgments
Conflicts of Interest
Appendix A. The Kinematic Boundary Condition
References
- Kida, S. Motion of an elliptic vortex in a uniform shear flow. J. Phys. Soc. Jpn. 1981, 50, 3517–3520. [Google Scholar] [CrossRef]
- Neu, J.C. The dynamics of a columnar vortex in an imposed strain. Phys. Fluids 1984, 27, 2397–2402. [Google Scholar] [CrossRef]
- Ide, K.; Wiggins, S. The dynamics of elliptically shaped regions of uniform vorticity in time-periodic, linear external velocity fields. Fluid Dyn. Res. 1995, 15, 205–235. [Google Scholar] [CrossRef]
- Dritschel, D.G. The stability of elliptical vortices in an external straining flow. J. Fluid Mech. 1990, 210, 223–261. [Google Scholar] [CrossRef]
- Meacham, S.P.; Flierl, G.R. Vortices in shear. Dyn. Atmos. Oceans 1990, 14, 333–386. [Google Scholar] [CrossRef]
- Bayly, B.J.; Holm, D.D.; Lifschitz, A. Three-dimensional stability of elliptical vortex columns in external strain flow. Philos. Trans. R. Soc. A 1996, 354, 895–926. [Google Scholar] [CrossRef]
- Mitchell, T.B.; Rossi, L.F. The evolution of Kirchhoff elliptic vortices. Phys. Fluids 2008, 20, 054103. [Google Scholar] [CrossRef]
- Guha, A.; Rahmani, M.; Lawrence, G.A. Evolution of a barotropic shear layer into elliptical vortices. Phys. Rev. E 2013, 87, 013020. [Google Scholar] [CrossRef] [PubMed]
- Koshel, K.V.; Ryzhov, E.A. Parametric resonance in the dynamics of an elliptic vortex in a periodically strained environment. Nonlinear Process. Geophys. 2017, 24, 1–8. [Google Scholar] [CrossRef]
- Bertozzi, A.L. Heteroclinic orbits and chaotic dynamics in planar fluid flows. SIAM J. Math. Anal. 1988, 19, 1271–1294. [Google Scholar] [CrossRef]
- Polivani, L.M.; Wisdom, J.; DeJong, E.; Ingersoll, A.P. Simple dynamical models of Neptune’s great dark spot. Science 1990, 249, 1393–1398. [Google Scholar] [CrossRef] [PubMed]
- Koshel, K.V.; Ryzhov, E.A.; Zhmur, V.V. Diffusion-affected passive scalar transport in an ellipsoidal vortex in a shear flow. Nonlinear Process. Geophys. 2013, 20, 437–444. [Google Scholar] [CrossRef]
- Ngan, K.; Meacham, S.; Morrison, P.J. Elliptical vortices in shear: Hamiltonian moment formulation and Melnikov analysis. Phys. Fluids 1996, 8, 896–913. [Google Scholar] [CrossRef]
- Vanneste, J.; Young, W.R. On the energy of elliptical vortices. Phys. Fluids 2010, 22, 081701. [Google Scholar] [CrossRef]
- Crosby, A.; Johnson, E.R.; Morrison, P.J. Deformation of vortex patches by boundaries. Phys. Fluids 2013, 25, 023602. [Google Scholar] [CrossRef]
- Melander, M.V.; Zabusky, N.J.; Styczek, A.S. A moment model for vortex interactions of the two-dimensional Euler equations. Part 1. Computational validation of a Hamiltonian elliptical representation. J. Fluid Mech. 1986, 167, 95–115. [Google Scholar] [CrossRef]
- Legras, B.; Dritschel, D. The elliptical model of two-dimensional vortex dynamics. I: The basic state. Phys. Fluids A 1991, 3, 845–854. [Google Scholar] [CrossRef]
- Dritschel, D.; Legras, B. The elliptical model of two-dimensional vortex dynamics. II: Disturbance equations. Phys. Fluids A 1991, 3, 855–869. [Google Scholar] [CrossRef]
- Meacham, S.P.; Morrison, P.J.; Flierl, G.R. Hamiltonian moment reduction for describing vortices in shear. Phys. Fluids 1997, 9, 2310–2328. [Google Scholar] [CrossRef][Green Version]
- Meacham, S.P. Quasigeostrophic, ellipsoidal vortices in a stratified fluid. Dyn. Atmos. Oceans 1992, 16, 189–223. [Google Scholar] [CrossRef]
- McKiver, W.J.; Dritschel, D.G. The motion of a fluid ellipsoid in a general linear background flow. J. Fluid Mech. 2003, 474, 147–173. [Google Scholar] [CrossRef]
- McKiver, W.J.; Dritschel, D.G. The stability of a quasi-geostrophic ellipsoidal vortex in a background shear flow. J. Fluid Mech. 2006, 560, 1–17. [Google Scholar] [CrossRef]
- McKiver, W.J. The ellipsoidal vortex: A novel approach to geophysical turbulence. Adv. Math. Phys. 2015, 2015, 613683. [Google Scholar] [CrossRef]
- Dritschel, D.G. An exact steadily rotating surface quasi-geostrophic elliptical vortex. Geophys. Astrophys. Fluid Dyn. 2011, 105, 368–376. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Heil, W.; Nof, D. Oscillations and rotations of elliptical warm-core rings. J. Geophys. Res. 1985, 20, 11756–11764. [Google Scholar] [CrossRef]
- Young, W.R. Elliptical vortices in shallow water. J. Fluid Mech. 1986, 171, 101–119. [Google Scholar] [CrossRef]
- Cushman-Roisin, B. Exact analytical solutions for elliptical vortices of the shallow-water equations. Tellus 1987, 39, 235–244. [Google Scholar] [CrossRef]
- Kirwan, A.D., Jr.; Liu, J. The shallow-water equations on an F-plane. In Nonlinear Topics in Ocean Physics; Osborne, A.R., Ed.; Italian Physical Society: North-Holland, The Netherlands, 1991; pp. 99–132. [Google Scholar]
- Rogers, C. Elliptic warm-core theory: The pulsrodon. Phys. Lett. A 1989, 138, 267–273. [Google Scholar] [CrossRef]
- Holm, D.D. Elliptical vortices and integrable Hamiltonian dynamics of the rotating shallow-water equations. J. Fluid Mech. 1991, 227, 393–406. [Google Scholar] [CrossRef]
- Ball, F. Some general theorems concerning the finite motion of a shallow rotating liquid lying on a paraboloid. J. Fluid Mech. 1963, 17, 240–256. [Google Scholar] [CrossRef]
- Arai, M.; Yamagata, T. Asymmetric evolution of eddies in rotating shallow water. Chaos 1994, 4, 163–175. [Google Scholar] [CrossRef] [PubMed]
- Stegner, A.; Dritschel, D.G. A numerical investigation of the stability of isolated shallow-water vortices. J. Phys. Oceanogr. 2000, 30, 2562–2573. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Early, J.J.; Samelson, R.M.; Chelton, D.B. The evolution and propagation of quasigeostrophic ocean eddies. J. Phys. Oceanogr. 2011, 41, 1535–1555. [Google Scholar] [CrossRef]
- Lilly, J.M.; Scott, R.K.; Olhede, S.C. Extracting waves and vortices from Lagrangian trajectories. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Waterman, S.; Lilly, J.M. Geometric decomposition of eddy feedbacks in barotropic systems. J. Phys. Oceanogr. 2015, 45, 1009–1024. [Google Scholar] [CrossRef]
- Anstey, J.A.; Zanna, L. A deformation-based parametrization of ocean mesoscale eddy Reynolds stresses. Ocean Model. 2017, 112, 99–111. [Google Scholar] [CrossRef]
- Lilly, J.M.; Olhede, S.C. Bivariate instantaneous frequency and bandwidth. IEEE Trans. Signal Process. 2010, 58, 591–603. [Google Scholar] [CrossRef]
- Lilly, J.M.; Gascard, J.C. Wavelet ridge diagnosis of time-varying elliptical signals with application to an oceanic eddy. Nonlinear Process. Geophys. 2006, 13, 467–483. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Olascoaga, M.J.; Goni, G.J. Oceanic mesoscale eddies as revealed by Lagrangian coherent structures. Geophys. Res. Lett. 2008, 35, L12603. [Google Scholar] [CrossRef]
- Rutherford, B.; Dangelmayr, G.; Montgomery, M.T. Lagrangian coherent structures in tropical cyclone intensification. Atmos. Chem. Phys. 2012, 12, 5483–5507. [Google Scholar] [CrossRef]
- Haller, G.; Beron-Vera, F.J. Geodesic theory of transport barriers in two-dimensional flows. Phys. D 2012, 241, 1680–1702. [Google Scholar] [CrossRef]
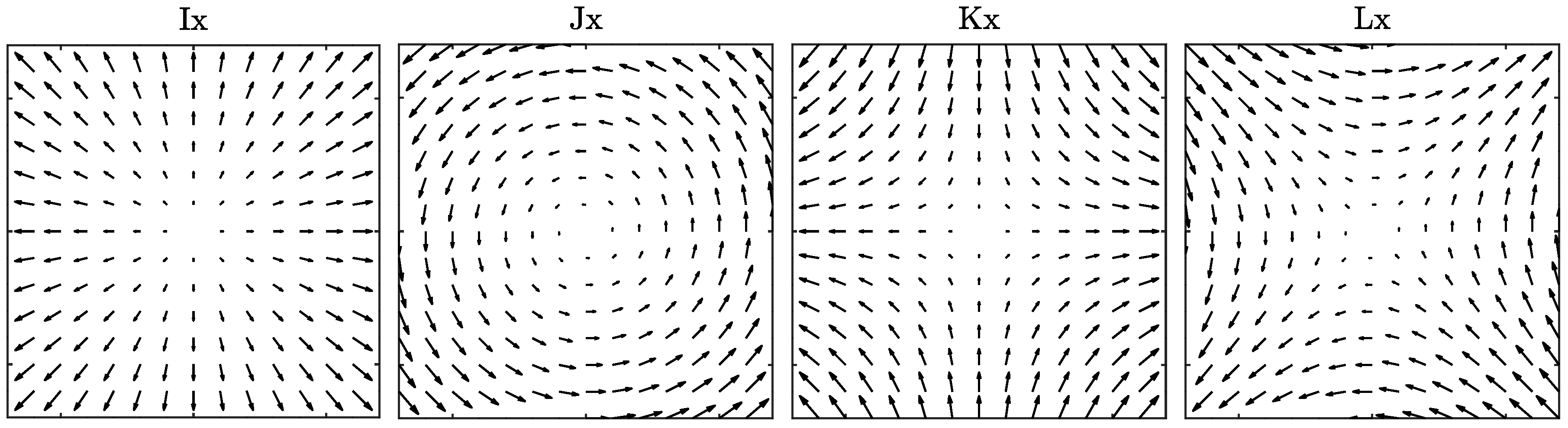
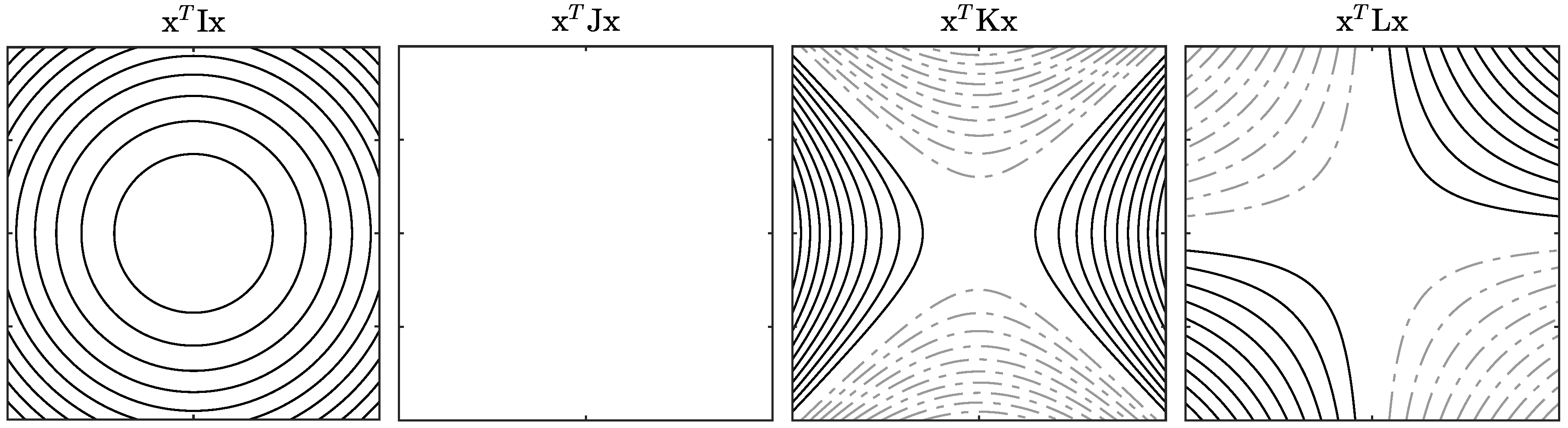
| I | J | K | L | |
|---|---|---|---|---|
| Name | Symbol | Range | ||||
|---|---|---|---|---|---|---|
| Aspect ratio | ||||||
| Linearity | ||||||
| Extension | ||||||
| — |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lilly, J.M. Kinematics of a Fluid Ellipse in a Linear Flow. Fluids 2018, 3, 16. https://doi.org/10.3390/fluids3010016
Lilly JM. Kinematics of a Fluid Ellipse in a Linear Flow. Fluids. 2018; 3(1):16. https://doi.org/10.3390/fluids3010016
Chicago/Turabian StyleLilly, Jonathan M. 2018. "Kinematics of a Fluid Ellipse in a Linear Flow" Fluids 3, no. 1: 16. https://doi.org/10.3390/fluids3010016
APA StyleLilly, J. M. (2018). Kinematics of a Fluid Ellipse in a Linear Flow. Fluids, 3(1), 16. https://doi.org/10.3390/fluids3010016




