Elementary Flow Field Profiles of Micro-Swimmers in Weakly Anisotropic Nematic Fluids: Stokeslet, Stresslet, Rotlet and Source Flows
Abstract
:1. Introduction
2. Results
2.1. Nematic Green Function for the Stokes Equation
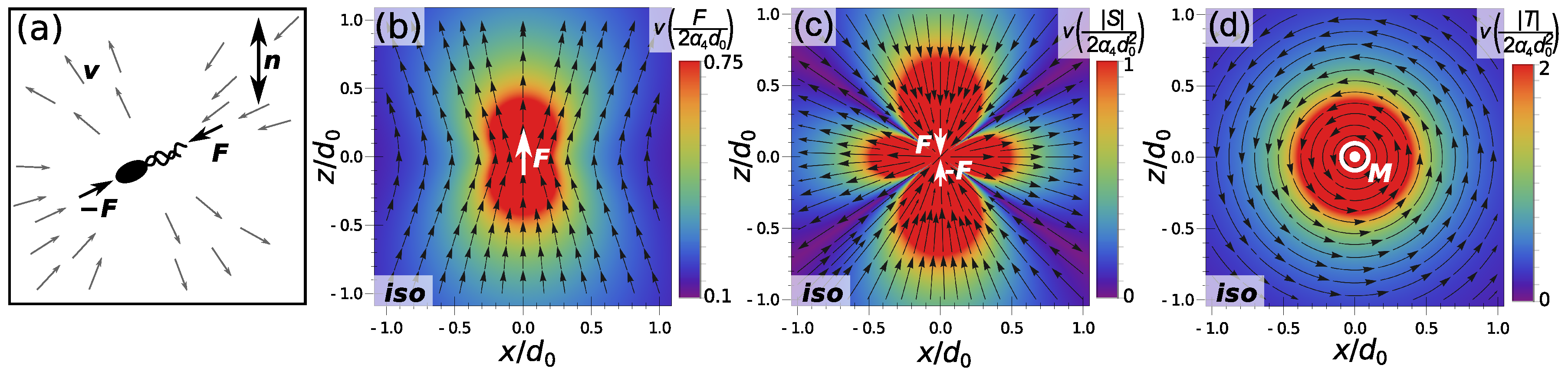
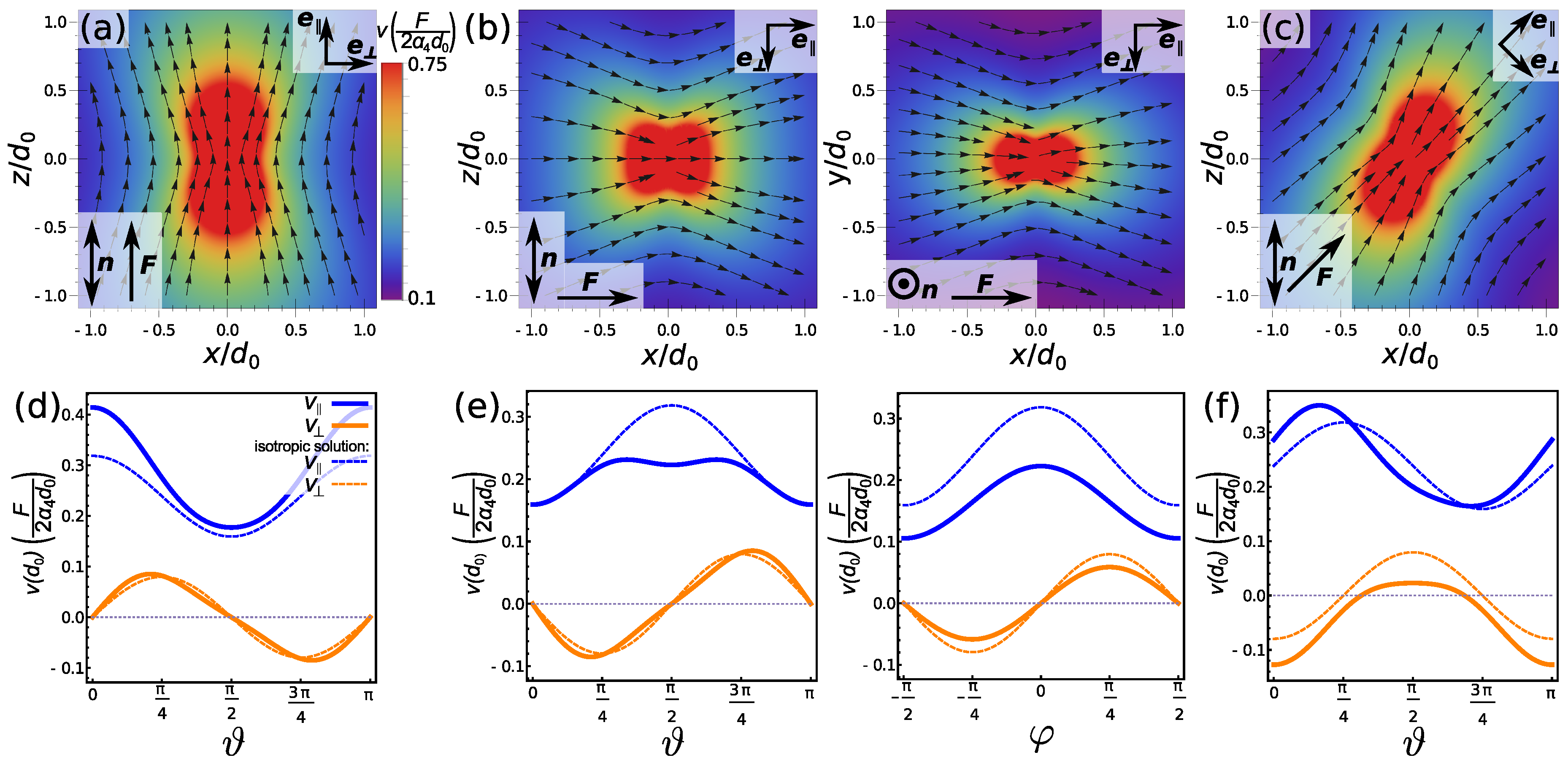
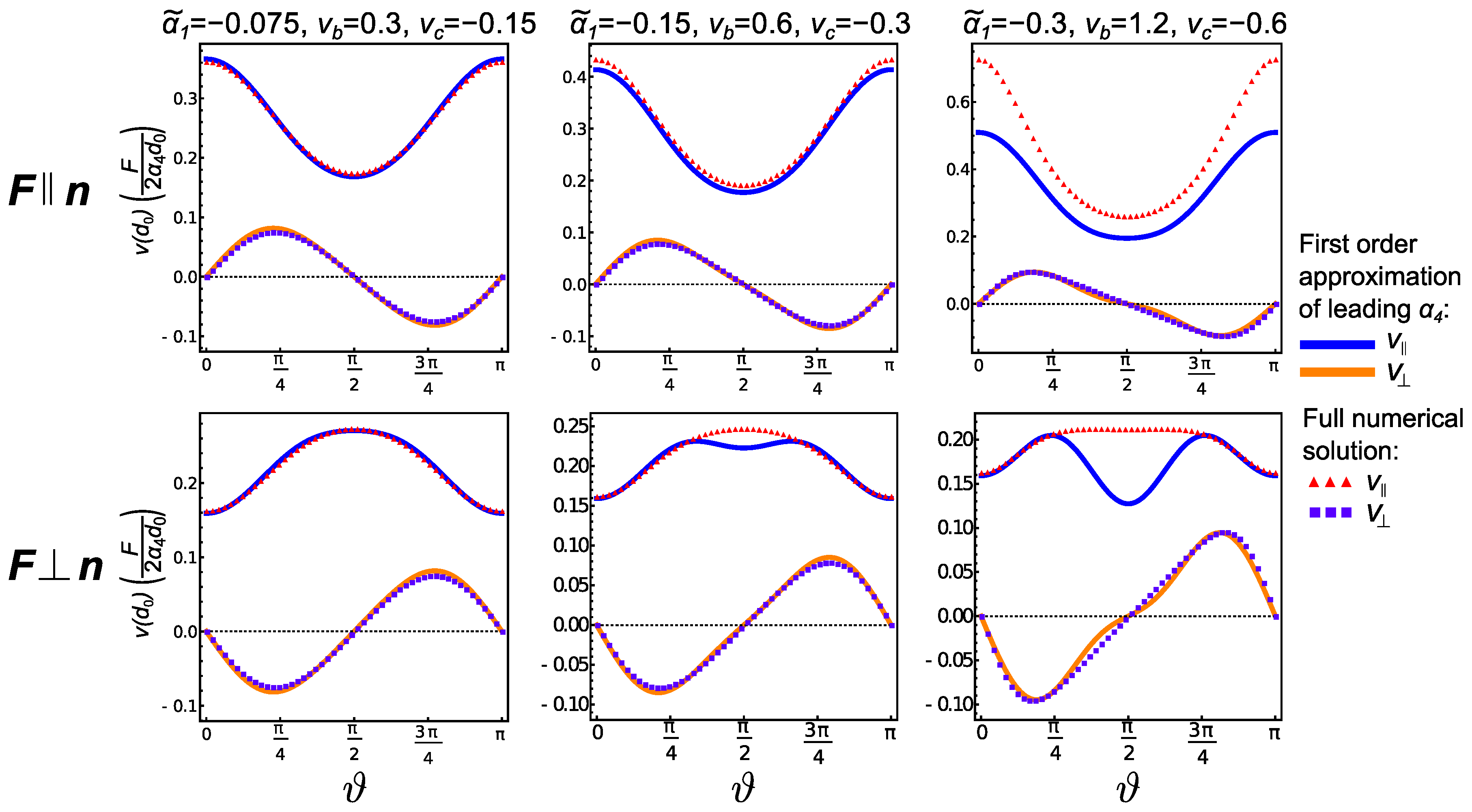
2.2. Flow Fields of Point Force in Nematic Fluid
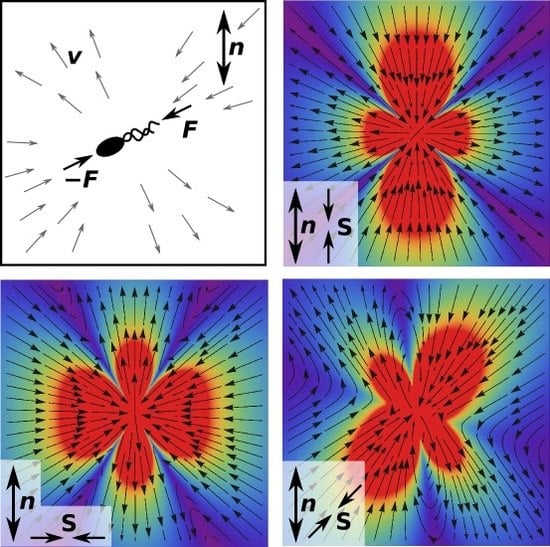
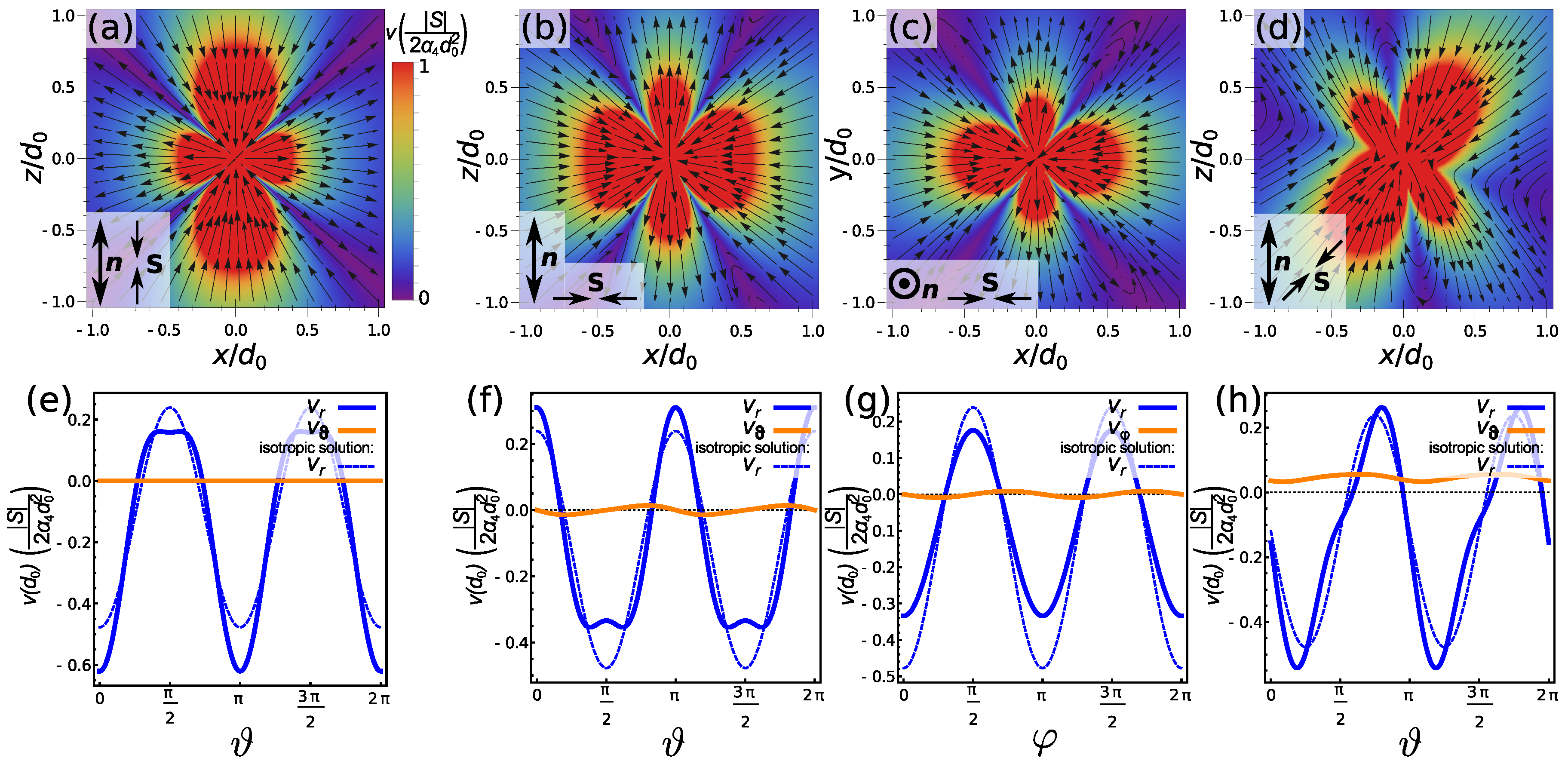
2.3. Flow Field of Force Dipole
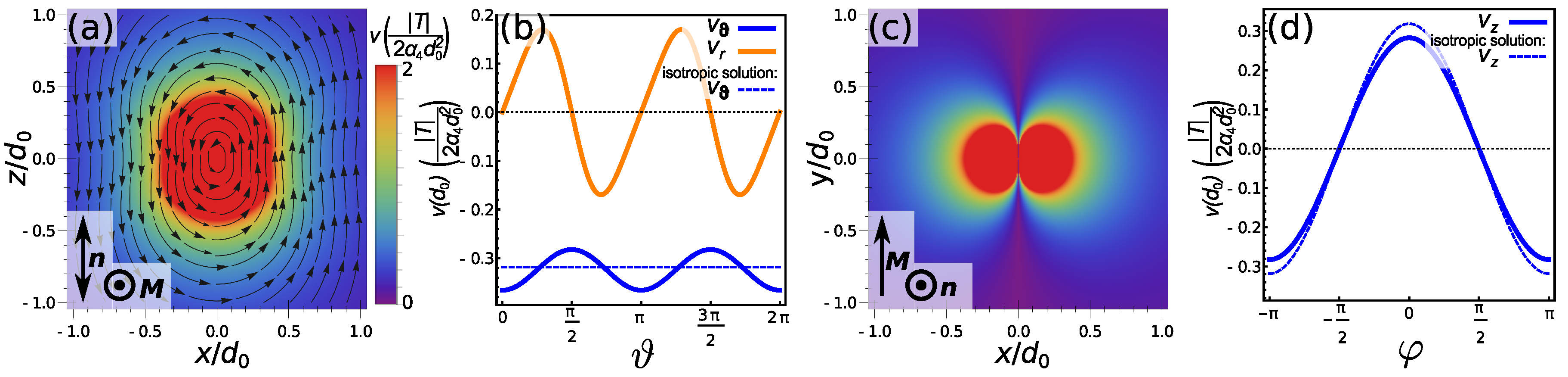
2.3.1. Stresslet Flow Field in Nematics
2.3.2. Rotlet Flow
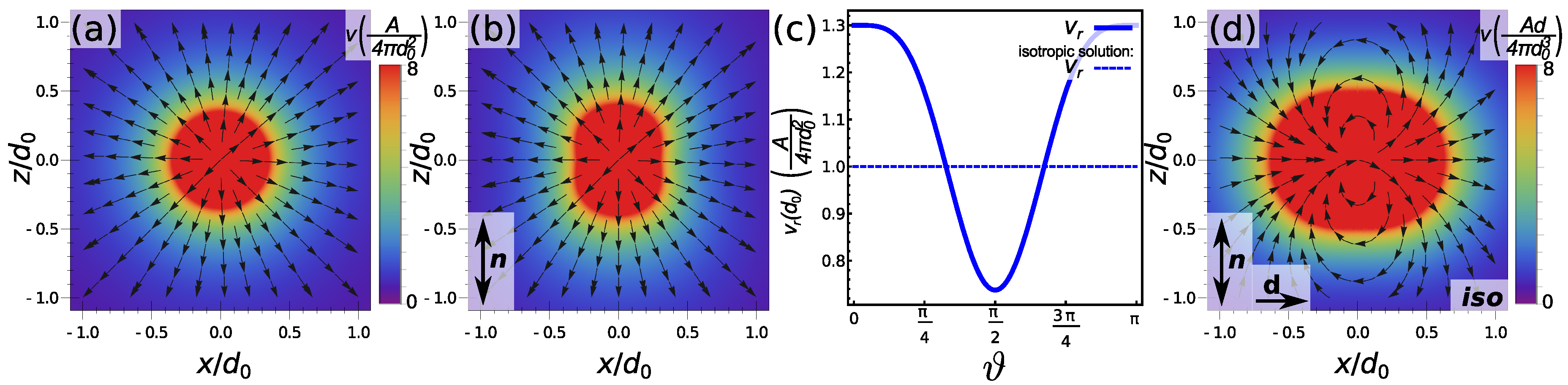
2.4. Flow Fields of Sources and Sinks in Homogeneous Nematics
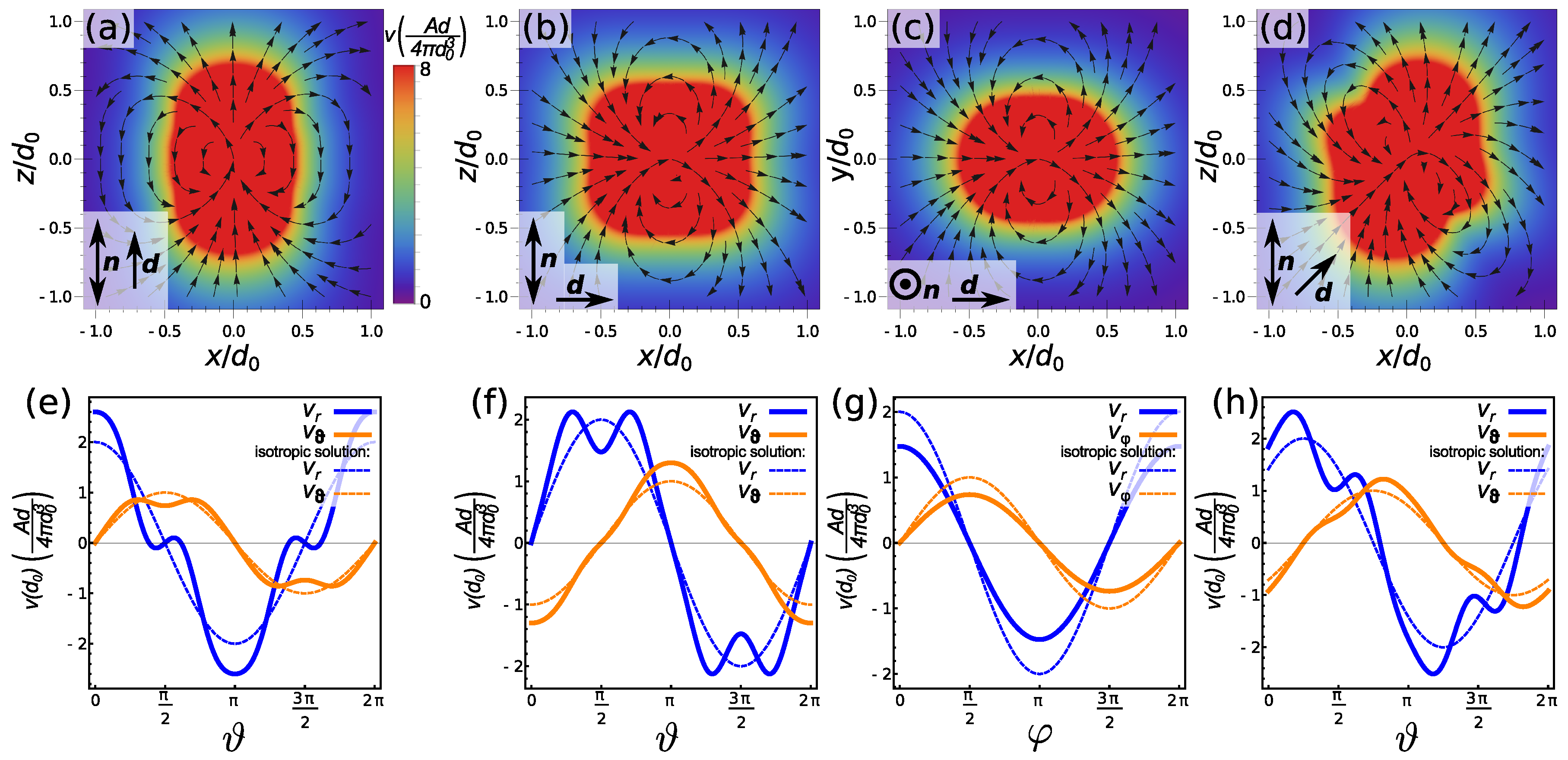
2.5. Source Dipole Flow
3. Discussion
3.1. Assumption of Weakly Anisotropic Nematic Fluid
3.2. Deformations in the Director Profile
3.3. Possible Application to Experiments
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lauga, E.; Powers, T.R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009, 72, 096601. [Google Scholar] [CrossRef]
- Elgeti, J.; Winkler, R.G.; Gompper, G. Physics of microswimmers—Single particle motion and collective behavior: A review. Rep. Prog. Phys. 2015, 78, 056601. [Google Scholar] [CrossRef] [PubMed]
- Bechinger, C.; Leonardo, R.D.; Löwen, H.; Reichhardt, C.; Volpe, G.; Volpe, G. Active particles in complex and crowded environments. Rev. Mod. Phys. 2016, 88, 045006. [Google Scholar] [CrossRef]
- Purcell, E.M. Life at low Reynolds number. Am. J. Phys. 1977, 45, 3–11. [Google Scholar] [CrossRef]
- Zöttl, A.; Stark, H. Emergent behavior in active colloids. J. Phys. Condens. Matter 2016, 28, 253001. [Google Scholar] [CrossRef]
- Sokolov, A.; Apodaca, M.M.; Grzybowski, B.A.; Aranson, I.S. Swimming bacteria power microscopic gears. Proc. Natl. Acad. Sci. USA 2010, 107, 969–974. [Google Scholar] [CrossRef] [PubMed]
- Thampi, S.P.; Doostmohammadi, A.; Shendruk, T.N.; Golestanian, R.; Yeomans, J.M. Active micromachines: Microfluidics powered by mesoscale turbulence. Sci. Adv. 2016, 2, e1501854. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.J.; Breuer, K.S. Enhanced diffusion due to motile bacteria. Phys. Fluids 2004, 16, L78–L81. [Google Scholar] [CrossRef]
- Pushkin, D.O.; Shum, H.; Yeomans, J.M. Fluid transport by individual microswimmers. J. Fluid Mech. 2013, 726, 5–25. [Google Scholar] [CrossRef]
- Hatwalne, Y.; Ramaswamy, S.; Rao, M.; Simha, R. Rheology of active-particle suspensions. Phys. Rev. Lett. 2004, 92, 118101. [Google Scholar] [CrossRef] [PubMed]
- López, H.M.; Gachelin, J.; Douarche, C.; Auradou, H.; Clément, E. Turning bacteria suspensions into superfluids. Phys. Rev. Lett. 2015, 115, 028301. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues; Springer: Heidelberg, Germany, 1981. [Google Scholar]
- Luby-Phelps, K. Cytoarchitecture and physical properties of pytoplasm: volume, viscosity, diffusion, intracellular surface area. Int. Rev. Cytol. 1999, 192, 189–221. [Google Scholar]
- Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402–3429. [Google Scholar] [CrossRef]
- Kumar, A.; Galstian, T.; Pattanayek, S.K.; Rainville, S. The Motility of bacteria in an anisotropic liquid environment. Mol. Cryst. Liq. Cryst. 2013, 574, 33–39. [Google Scholar] [CrossRef]
- Toner, J.; Löwen, H.; Wensink, H.H. Following fluctuating signs: Anomalous active superdiffusion of swimmers in anisotropic media. Phys. Rev. E 2016, 93, 062610. [Google Scholar] [CrossRef] [PubMed]
- Mushenheim, P.C.; Trivedi, R.R.; Roy, S.S.; Arnold, M.S.; Weibel, D.B.; Abbott, N.L. Effects of confinement, surface-induced orientations and strain on dynamical behaviors of bacteria in thin liquid crystalline films. Soft Matter 2015, 11, 6821–6831. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, A.; Zhou, S.; Lavrentovich, O.D.; Aranson, I.S. Individual behavior and pairwise interactions between microswimmers in anisotropic liquid. Phys. Rev. E 2015, 91, 013009. [Google Scholar] [CrossRef] [PubMed]
- Mushenheim, P.C.; Trivedi, R.R.; Tuson, H.H.; Weibel, D.B.; Abbott, N.L. Dynamic self-assembly of motile bacteria in liquid crystals. Soft Matter 2013, 10, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Sokolov, A.; Lavrentovich, O.D.; Aranson, I.S. Living liquid crystals. Proc. Natl. Acad. Sci. USA 2014, 111, 1265–1270. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, R.R.; Maeda, R.; Abbott, N.L.; Spagnolie, S.E.; Weibel, D.B. Bacterial transport of colloids in liquid crystalline environments. Soft Matter 2015, 11, 8404–8408. [Google Scholar] [CrossRef] [PubMed]
- Lavrentovich, O.D. Active colloids in liquid crystals. Curr. Opin. Colloid Interface Sci. 2016, 21, 97–109. [Google Scholar] [CrossRef]
- Krieger, M.S.; Spagnolie, S.E.; Powers, T.R. Locomotion and transport in a hexatic liquid crystal. Phys. Rev. E 2014, 90, 052503. [Google Scholar] [CrossRef] [PubMed]
- Krieger, M.S.; Spagnolie, S.E.; Powers, T. Microscale locomotion in a nematic liquid crystal. Soft Matter 2015, 11, 9115–9125. [Google Scholar] [CrossRef] [PubMed]
- Heuer, H.; Kneppe, H.; Schneider, F. Flow of a nematic liquid crystal around a sphere. Mol. Cryst. Liq. Cryst. 1992, 214, 43–61. [Google Scholar] [CrossRef]
- Kneppe, H.; Schneider, F.; Schwesinger, B. Axisymmetrical flow of a nematic liquid crystal around a sphere. Mol. Cryst. Liq. Cryst. 1991, 205, 9–28. [Google Scholar] [CrossRef]
- Kozachok, M.V.; Lev, B.I. Analytical calculation of the Stokes drag of the spherical particle in a nematic liquid crystal. Condens. Matter Phys. 2014, 17, 79–86. [Google Scholar] [CrossRef]
- Stark, H.; Ventzki, D.; Reichert, M. Recent developments in the field of colloidal dispersions in nematic liquid crystals: the Stokes drag. J. Phys. Condens. Matter 2003, 15, S191. [Google Scholar] [CrossRef]
- Stark, H.; Ventzki, D. Stokes drag of spherical particles in a nematic environment at low Ericksen numbers. Phys. Rev. E 2001, 64, 031711. [Google Scholar] [CrossRef] [PubMed]
- Pokrovskii, V.; Tskhai, A. Slow motion of a particle in a weakly anisotropic viscous fluid. J. Appl. Math. Mech. 1986, 50, 391–394. [Google Scholar] [CrossRef]
- Gómez-González, M.; del Álamo, J.C. Flow of a viscous nematic fluid around a sphere. J. Fluid Mech. 2013, 725, 299–331. [Google Scholar] [CrossRef]
- Drescher, K.; Goldstein, R.E.; Michel, N.; Polin, M.; Tuval, I. Direct measurement of the flow field around swimming microorganisms. Phys. Rev. Lett. 2010, 105, 168101. [Google Scholar] [CrossRef] [PubMed]
- Drescher, K.; Dunkel, J.; Cisneros, L.H.; Ganguly, S.; Goldstein, R.E. Fluid dynamics and noise in bacterial cell-cell and cell-surface scattering. Proc. Natl. Acad. Sci. USA 2011, 108, 10940–10945. [Google Scholar] [CrossRef] [PubMed]
- Pushkin, D.O.; Yeomans, J.M. Fluid mixing by curved trajectories of microswimmers. Phys. Rev. Lett. 2013, 111, 188101. [Google Scholar] [CrossRef] [PubMed]
- Alexander, G.P.; Yeomans, J.M. Dumb-bell swimmers. EPL 2008, 83, 34006. [Google Scholar] [CrossRef]
- Alexander, G.P.; Pooley, C.M.; Yeomans, J.M. Hydrodynamics of linked sphere model swimmers. J. Phys. Condens. Matter 2009, 21, 204108. [Google Scholar] [CrossRef] [PubMed]
- Baskaran, A.; Marchetti, M.C. Statistical mechanics and hydrodynamics of bacterial suspensions. Proc. Natl. Acad. Sci. USA 2009, 106, 15567–15572. [Google Scholar] [CrossRef] [PubMed]
- Saintillan, D.; Shelley, M. Instabilities and pattern formation in active particle suspensions: Kinetic theory and continuum simulations. Phys. Rev. Lett. 2008, 100, 178103. [Google Scholar] [CrossRef] [PubMed]
- Mathijssen, A.J.T.M.; Doostmohammadi, A.; Yeomans, J.M.; Shendruk, T.N. Hydrodynamics of micro-swimmers in films. J. Fluid Mech. 2016, 806, 35–70. [Google Scholar] [CrossRef]
- Reigh, S.Y.; Zhu, L.; Gallaire, F.; Lauga, E. Swimming with a cage: Low-Reynolds-number locomotion inside a droplet. Soft Matter 2017, 13, 3161–3173. [Google Scholar] [CrossRef] [PubMed]
- Marchetti, M.C.; Joanny, J.F.; Ramaswamy, S.; Liverpool, T.B.; Prost, J.; Rao, M.; Simha, R.A. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143–1189. [Google Scholar] [CrossRef]
- Pozrikidis, C. Introduction to Theoretical and Computational Fluid Dynamics, 2nd ed.; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- De Gennes, P.G.; Prost, J. Physics of Liquid Crystals; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Denniston, C.; Orlandini, E.; Yeomans, J. Lattice Boltzmann simulations of liquid crystal hydrodynamics. Phys. Rev. E 2001, 63, 056702. [Google Scholar] [CrossRef] [PubMed]
- Giomi, L.; Kos, Ž.; Ravnik, M.; Sengupta, A. Cross-talk between topological defects in different fields revealed by nematic microfluidics. Proc. Natl. Acad. Sci. USA 2017, 114, E5771–E5777. [Google Scholar] [CrossRef] [PubMed]
- Taratuta, V.G.; Hurd, A.J.; Meyer, R.B. Light-scattering study of a polymer nematic liquid crystal. Phys. Rev. Lett. 1985, 55, 246–249. [Google Scholar] [CrossRef] [PubMed]
- Jamieson, A.M.; Gu, D.; Chen, F.; Smith, S. Viscoelastic behavior of nematic monodomains containing liquid crystal polymers. Prog. Polym. Sci. 1996, 21, 981–1033. [Google Scholar] [CrossRef]
- Kuzuu, N.; Doi, M. Constitutive equation for nematic liquid crystals under weak velocity gradient derived from a molecular kinetic equation. J. Phys. Soc. Jpn. 1983, 52, 3486–3494. [Google Scholar] [CrossRef]
- Herba, H.; Szymański, A.; Drzymala, A. Experimental test of hydrodynamic theories for nematic liquid crystals. Mol. Cryst. Liq. Cryst. 1985, 127, 153–158. [Google Scholar] [CrossRef]
- Cui, M.; Kelly, J.R. Temperature dependence of visco-elastic properties of 5CB. Mol. Cryst. Liq. Cryst. 1999, 331, 49–57. [Google Scholar] [CrossRef]
- Adkins, G. Three-dimensional Fourier transforms, integrals of spherical Bessel functions, and novel delta function identities. arXiv, 2013; arXiv:1302.1830. [Google Scholar]
- Doostmohammadi, A.; Stocker, R.; Ardekani, A.M. Low-Reynolds-number swimming at pycnoclines. Proc. Natl. Acad. Sci. USA 2012, 109, 3856–3861. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Yang, M.; Gompper, G.; Winkler, R.G. Modelling the mechanics and hydrodynamics of swimming E. coli. Soft Matter 2015, 11, 7867–7876. [Google Scholar] [CrossRef] [PubMed]
- Lintuvuori, J.; Würger, A.; Stratford, K. Hydrodynamics defines the stable swimming direction of spherical squirmers in a nematic liquid crystal. Phys. Rev. Lett. 2017, 119, 068001. [Google Scholar] [CrossRef] [PubMed]
- Lubensky, T.C.; Pettey, D.; Currier, N. Topological defects and interactions in nematic emulsions. Phys. Rev. E 1998, 57, 610–625. [Google Scholar] [CrossRef]
- Peng, C.; Turiv, T.; Guo, Y.; Wei, Q.H.; Lavrentovich, O.D. Command of active matter by topological defects and patterns. Science 2016, 354, 882–885. [Google Scholar] [CrossRef] [PubMed]
- Hernàndez-Navarro, S.; Tierno, P.; Farrera, J.A.; Ignés-Mullol, J.; Sagués, F. Reconfigurable swarms of nematic colloids controlled by photoactivated surface patterns. Angew. Chem. Int. Ed. 2014, 53, 10696–10700. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Tovkach, O.; Golovaty, D.; Sokolov, A.; Aranson, I.S.; Lavrentovich, O.D. Dynamic states of swimming bacteria in a nematic liquid crystal cell with homeotropic alignment. New J. Phys. 2017, 19, 055006. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kos, Ž.; Ravnik, M. Elementary Flow Field Profiles of Micro-Swimmers in Weakly Anisotropic Nematic Fluids: Stokeslet, Stresslet, Rotlet and Source Flows. Fluids 2018, 3, 15. https://doi.org/10.3390/fluids3010015
Kos Ž, Ravnik M. Elementary Flow Field Profiles of Micro-Swimmers in Weakly Anisotropic Nematic Fluids: Stokeslet, Stresslet, Rotlet and Source Flows. Fluids. 2018; 3(1):15. https://doi.org/10.3390/fluids3010015
Chicago/Turabian StyleKos, Žiga, and Miha Ravnik. 2018. "Elementary Flow Field Profiles of Micro-Swimmers in Weakly Anisotropic Nematic Fluids: Stokeslet, Stresslet, Rotlet and Source Flows" Fluids 3, no. 1: 15. https://doi.org/10.3390/fluids3010015
APA StyleKos, Ž., & Ravnik, M. (2018). Elementary Flow Field Profiles of Micro-Swimmers in Weakly Anisotropic Nematic Fluids: Stokeslet, Stresslet, Rotlet and Source Flows. Fluids, 3(1), 15. https://doi.org/10.3390/fluids3010015