Abstract
Direct numerical simulations of a turbulent channel flow with a passive scalar at with blowing perturbations is carried out. The blowing is imposed through five spanwise jets located near the upstream end of the channel. Behind the blowing jets (about , where D is the jet diameter), we observe regions of reversed flow responsible for the high temperature region at the wall: hot spots that contribute to further heating of the wall. In between the jets, low pressure regions accelerate the flow, creating long, thin, streaky structures. These structures contribute to the high temperature region near the wall. At the far downstream of the jet (about ), flow instabilities (high shear) created by the blowing generate coherent vortical structures. These structures move hot fluid near the wall to the outer region of the channel; thereby, these are responsible for cooling of the wall. Thus, for engineering applications where cooling of the wall is necessary, it is critical to promote the generation of coherent structures near the wall.
1. Introduction
Jets in cross-flow, which are also known as transverse jets, are common in engineering applications, and the environment. Examples include: gas turbine film-cooling, dilution jets in gas turbine combustors, ash plumes from volcanic eruptions, etc. A comprehensive review of jets in cross-flow can be found in Mahesh [1]. Most of the previous studies focused on the parameters of the jets and cross-flow that affect the flow field. The generation of complex coherent vortical structures was studied in [2,3,4]. However, there is no general consensus about the genesis and evolution of these motions and their effects on passive scalars. The configuration of these vortical motions changes with the characteristic flow parameters like the blowing ratio (the ratio between the mass flow rates/velocities of the cross-flow and the jet) [1].
Blowing and suction have been tested for controlling turbulence, as well. Park and Choi [5] used direct numerical simulations (DNS) on a spatially-developing turbulent boundary layer to study the effect of small blowing and suction perturbations on wall skin friction. They imposed steady blowing and suction through a spanwise slot. Their results show that the skin friction coefficient significantly decreases near downstream and slightly increases far downstream of the slot. The number of coherent vortical structures is also increased downstream. Further, the increase of drag downstream of the slot was attributed to the stretching and tilting of vortices due to blowing. Kim and Sung [6] applied periodic and steady blowing through a spanwise slot to study their effects on the spatially-developing boundary layer. Their results showed that local steady blowing increased the number of vortical structures downstream. Araya et al. [7] studied the effects of steady and unsteady blowing on a turbulent channel flow. They found that forcing frequency, (, where -kinematic viscosity and -friction velocity), is responsible for the local increase in skin friction coefficient. Their findings also include the generation of more vortex structures downstream of blowing. The effects of localized steady blowing on the thermal transport were studied by using DNS in a turbulent channel flow by [8,9]. They imposed the blowing through a spanwise slot. The results of their numerical experiment demonstrate that the critical streamwise length of the blowing slot is 30 wall units. At the critical streamwise length of the slot, they detected a strong enhancement of heat flux. Although the previous studies have found interesting phenomena and mechanisms related to both velocity and thermal fields with blowing perturbations, most studies imposed blowing through spanwise slots. However, the blowing through spanwise slots is rarely encountered in practice. In studies pertaining to gas turbine film-cooling, blowing is imposed through round jets [10]. However, those studies did not focus on local variations of velocity and temperature [11]. Although it is known that jets in cross-flow generate coherent vortical structures and reduce the wall temperature downstream, the influence of vortices on heat fluxes and thereby on wall temperature has not been investigated.
Therefore, we seek to demonstrate the importance of coherent vortical structures in cooling or heating of the wall in a thermal turbulent channel flow. The study uses a turbulent channel flow with small steady blowing perturbations at the bottom wall. Both walls are kept at constant temperatures, and perturbations are set through five holes located at 25% of the channel length from the upstream end of the channel and distributed in the spanwise direction. The results show that the generation of coherent vortical structures increases the wall-normal heat flux compared to the streamwise heat flux. The article is organized as follows. Section 2 describes the numerical procedure. The results are laid out in Section 3, and the conclusions are given in Section 4.
2. Numerical Procedure
In this section, a brief description of the numerical procedure of the current simulations is given. Continuity, momentum and passive scalar transport equations are shown in their non-dimensionalized form by Equations (1)–(3), respectively. The non-dimensional form of the equations was obtained by using velocity scale and length sale h, where is the unitary mean laminar centerline velocity and h is the channel half height. If the dimensional form of the variables is denoted by the superscript , , , , and represent non-dimensional forms of instantaneous velocity, spatial coordinates, instantaneous pressure and the time coordinate. The non-dimensional temperature is given by , where is the constant temperature at the bottom wall and is the temperature at the top wall. Here, , p and represent the density of the fluid, instantaneous velocity components, instantaneous pressure and instantaneous temperature, respectively. In Equation (2), is the instantaneously-changing pressure gradient to maintain a constant flow rate in the channel. The governing equations were discretized in a staggered grid using a second order central differencing scheme. The Reynolds number of the flow is given by , and (=) is the molecular Prandtl number of the fluid, where and stand for the thermal diffusivity and the kinematic viscosity of the fluid. The fractional step method was used in which viscous terms and advective terms are respectively treated implicitly and explicitly. An approximate factorization method was used to invert the large sparse matrix resulting from explicit treatment of viscous terms. Details of the numerical procedure can be found in [12]. The equations are solved for the baseline case (unperturbed) and the perturbed case.
Figure 1 shows the physical domain of the flow, together with the profiles of perturbation velocity. The dimensions of the computational box are: = , = and = . A grid-independence test was performed as detailed in [7]. The number of grid points in the streamwise, spanwise and wall-normal directions is 1153, 193, and 193 respectively. The mesh resolution in the unperturbed case is: , , and . Note that we use the friction velocity of the unperturbed case in the scaling of the velocity field and both thermal and velocity fields were normalized using wall variables. The validation of the first and second order statistics for the unperturbed case is shown in Araya et al. [7] and Dharmarathne et al. [13].
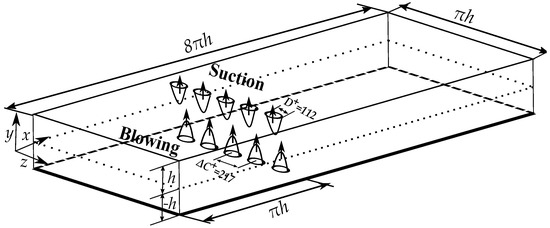
Figure 1.
Schematic of the channel with spanwise local perturbations.
Periodic conditions are prescribed along the streamwise and spanwise directions. The no-slip boundary condition is imposed at both walls, except at locations where the jets are placed. The temperature boundary condition at the bottom wall is 1, and that at the top wall is . The fluid that comes through jets at the bottom wall has a non-dimensional temperature of , and at the top wall, the jet temperature is . The Courant–Friedrichs–Lewy (CFL) parameter remains constant during simulations and the time step – for all cases.
A mean parabolic velocity profile with random fluctuations was used as an initial condition in the entire domain. The molecular Prandtl number, , is , and the friction Reynolds number ( = , where is the friction velocity of the unperturbed channel) is 394. Here, is the shear stress at the wall. The local forcing, , which creates the vertical perturbation, is modeled as follows:
where R is the radius of a blowing/suction jet and is the center of a perturbing jet. Therefore, the range of jets is within , . The circular jets are approximated to the Cartesian grid with a percentage error ≈ . The parameter A represents the ratio of the jet centerline velocity to channel centerline velocity (blowing ratio), and in this study. This value of A complies with the widely-used blowing ratios in gas turbine film cooling [14]. Five equally-spaced jets were imposed at both walls in the spanwise direction; they are located at downstream from as shown in Figure 1. The spanwise separation between the centers of two adjacent jets, , is approximately 217 in wall units, which accommodates the average separation of near-wall streaks in terms of spanwise wavelength, [15], in between two adjacent jets. The diameter of the jets in wall units, , is 112. The value of is approximately equal to the thickness of near-wall high and low speed streaks. In order to ensure the conservation of the mass flow rate inside the computational box, spatially-sinusoidal blowing at the bottom wall was synchronized with sinusoidal suction at the top wall, as shown in Figure 1.
3. Results
First, the effect of blowing on the mean velocity and temperature fields will be demonstrated. The next subsection describes the changes of the velocity and temperature fluctuations due to blowing perturbations. Then, we show the existence of hot and cold spots in the near-wall region by using two-dimensional contours on the plane. We then direct our focus to the heat fluxes, and , in the following section. Subsequently, we show the generation of coherent vortical structures downstream of the jets.
3.1. Mean Velocity and Temperature Field
Figure 2 shows the variation of mean streamwise velocity (Figure 2a) and mean temperature (Figure 2b) along the centerline of the blowing jets (behind the jets, hereafter) at different downstream locations. The mean streamwise velocity at downstream of blowing becomes negative in the near-wall region, as seen in Figure 2a. The negative streamwise mean velocity implies a reversed flow region just behind the blowing jets. The presence of jets obstructs the incoming boundary layer, which in turn creates a reversed flow region behind the jets. This region may significantly change the exchange processes between the wall and the boundary layer. The reversed flow region exists until . The velocity quickly recovers from to . This sudden change of velocity causes steep gradients of velocity. Steep velocity gradients generate more turbulence and increase turbulent momentum and heat transport in that region. The influence of blowing in the near-wall region is considerable even at downstream of the jets. Although the deceleration of the flow in the near-wall region at downstream is not as notable as at downstream, it is noticeable at the outer-layer even at downstream. Interestingly, we can observe a slight flow acceleration in the near-wall region at and downstream. This can be ascribed to the entrainment of accelerated flow in between two jets. The acceleration is a clear manifestation of the three-dimensionality of the perturbations, which may not be seen in slot blowing cases studied previously. The velocity deficit created by the presence of blowing jets gradually moves to the outer-layer of the channel, as suggested by the outward movement of the mean velocity deficit.
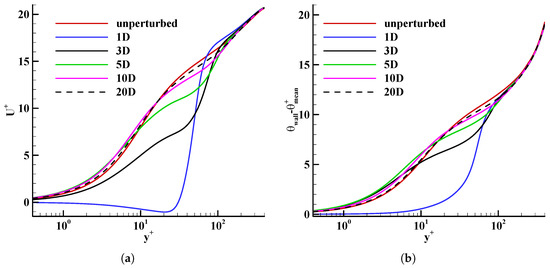
Figure 2.
(a) Mean streamwise velocity variation and (b) mean temperature variation in the wall normal direction behind the jets.
We can observe simultaneous changes of the mean temperature profiles as Figure 2b shows. Due to the reversed flow region in the near-wall region at downstream of blowing, velocity fluctuations might have been reduced. The reduction of velocity fluctuations reduces turbulent heat transport in the near-wall region; therefore, the temperature of the flow close to the wall is nearly similar to that of the wall. At the end of the recirculation region (around ), the mean temperature starts rising rapidly, creating steep temperature gradients. Steep temperature gradients generate temperature fluctuations.
It is peculiar to see that the temperature in the near-wall region at downstream is lower than that of unperturbed flow. Because the mean velocity at downstream is lower than that of the unperturbed flow, one would expect the temperature to be higher than the unperturbed flow. This inconsistency in the near-wall region at downstream becomes more striking since the temperature profile becomes consistent with the velocity profile above the buffer region. Further, the mean temperature profiles at and downstream of the jets are also in compliance with the velocity profiles. The unpredictable behavior of the mean temperature profile (extra cooling effect) at downstream may be attributed to the fluctuations of velocity and temperature fields.
3.2. Fluctuations of Velocity and Temperature
In this section, we discuss the variations of velocity and temperature fluctuations. Figure 3a depicts the root mean square (RMS) value of streamwise velocity fluctuations, , in wall coordinates. At the near-wall region (below ), the profiles of at all downstream locations, except downstream, are not significantly different from the unperturbed flow. At downstream of blowing, streamwise velocity fluctuations are small compared to the unperturbed case. The obstruction of the cross-flow in the presence of blowing jet sets a wake at the immediate downstream of the jets. Since the wake is filled in with slowly-moving fluid, the recirculation region near the downstream of blowing jets attenuates turbulence. Above the reversed flow region (), fluctuations increase rapidly due to the turbulence production caused by steep velocity gradients, and the maximum occurs around . Furthermore, for , and downstream locations, peak values of are in the log-layer. The movement of the peak values of towards the outer-layer could be attributed to the high v fluctuations due to blowing.
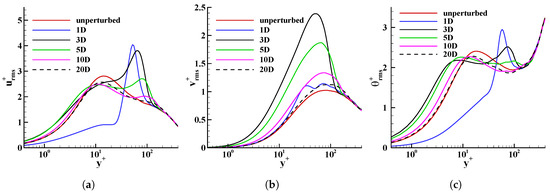
Figure 3.
Variation of (a) streamwise velocity fluctuations; (b) wall normal velocity fluctuations; and (c) temperature fluctuations downstream, behind the jets.
RMS values of wall-normal velocity fluctuations at different downstream locations are shown in Figure 3b. It is interesting to see that at downstream is similar to that of the unperturbed flow particularly in the near-wall region. This indicates that the mechanism that creates wall-normal velocity fluctuations does not change due to the flow reversal just downstream of jets. However, wall-normal velocity fluctuations have considerably increased at downstream. In fact, this location shows the highest increase in from its unperturbed case out of all the observed locations. We speculate that wall-normal velocity fluctuations intensify due to the generation of more coherent vortical structures in the same region. The high fluctuations of wall-normal velocity move warm near-wall fluid upwards. Therefore, the amplification of wall-normal velocity fluctuations at the downstream of blowing may closely correspond to the low wall temperatures observed at downstream. The increase of fluctuations is also significant at and downstream. However, the magnitude of fluctuations gradually reduces as the location moves away from the blowing jet.
Figure 3c depicts the variation of RMS values of temperature fluctuations, . At downstream, temperature fluctuations in the near-wall region are mitigated due to the reversed flow. It seems that temperature fluctuations correspond to streamwise velocity fluctuations at downstream. As the location moves downstream, behaves similar to . Temperature fluctuations in the near-wall region are amplified at the , and downstream locations. The observations of the temperature fluctuations suggest that turbulent mixing is intensified in the near-wall region after downstream. The amplified wall-normal velocity fluctuations and temperature fluctuations relate to the abrupt change in mean temperature at downstream. Moreover, we can predict significant differences between turbulent heat fluxes in the streamwise direction, , and that of the wall-normal direction, .
3.3. Hot Spots Near the Wall
To elucidate the changes of instantaneous and mean temperature in the near-wall region, we observe the temperature field around . Figure 4a illustrates instantaneous high temperature spots (red color) in between jets where the flow is susceptible to acceleration. Right behind the jets where a reverse flow region is observed, high wall temperatures can also be detected. These instantaneous hot spots in between and right behind the jets contribute to the regions of high mean temperature in those regions, as we see in Figure 4b. According to Figure 4a, at behind the jets, the high temperature spots exist. They are also observed on the mean temperature contours. When we move slightly downstream, around , we can see that cold (blue) spots are emerging right behind the jets. These sporadic events are directly coupled with sudden changes of flow phenomena like coherent vortical structure proliferation. The difference of instantaneous temperature between the hot and cold spots around downstream is clearly noticeable. However, the changes that we see in mean temperature contours at the same region is not very distinguishable. Therefore, these instantaneous changes of thermal field are absolutely necessary in the design process. This highlights the importance of understanding the underlying flow physics of the changes in the instantaneous temperature field.
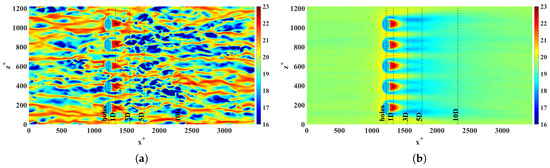
Figure 4.
(a) Instantaneous and (b) mean temperature contours at on the plane. Both instantaneous and mean temperatures are normalized by and , as shown in Section 2.
Comparing the thermal field behind the jets with the unperturbed incoming flow, one can notice a significant reduction of hot spots behind the jets, i.e., –2400. This further confirms the importance of blowing jets in the proliferation of coherent vortical structures, which in turn, promotes the cooling of the wall, particularly beyond . These observations are clearly noticed in both the instantaneous and mean temperature contours, which extend far downstream in the channel, as shown in Figure 4.
3.4. Turbulent Heat Fluxes
This section discusses the changes of turbulent heat fluxes (streamwise heat flux, , and wall-normal heat flux, ) due to blowing. Here, we are particularly interested in heat fluxes in the near-wall region to see which one of and influences temperature more.
In Figure 5, we observe that both and are negligibly small in the near-wall region at downstream. The flow reversal just downstream of blowing jets diminishes the fluctuations of streamwise velocity and temperature. The reduction of fluctuations decreases turbulent transport near the downstream of the blowing jets. This observation complies with the high mean temperature at that location. A clear distinction between and can be seen at the , and downstream locations particularly in the near-wall region. At the , and locations, both and are higher than the respective values of the unperturbed case in the near-wall region until . In between and , one can clearly see that downstream of the perturbations is lower than that of the unperturbed flow.
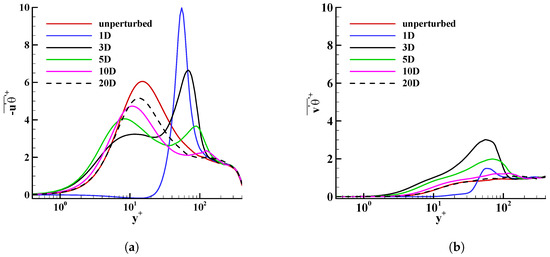
Figure 5.
The variation of turbulent heat fluxes on the plane. (a) along the jets and (b) along the jets.
at downstream locations surpasses unperturbed conditions beyond . On the other hand, is higher than its unperturbed counterpart for most of the boundary layer at all downstream locations, except at downstream. The intensification of at downstream locations suggests a change in the mechanism that generates turbulent heat fluxes. We examine the changes of vortex structures downstream of blowing to see whether the vortex structure generation influences turbulent heat fluxes.
3.5. Generation of Vortex Structures
Figure 6a,b illustrates two-point correlations of streamwise velocity fluctuations, , in the near-wall region at downstream of blowing behind the jets and in between jets, respectively. The streamwise length of demonstrates the flow acceleration in between jets (Figure 6b) in comparison to the deceleration of the flow behind the jets (Figure 6a). It is clear that the streamwise length scale of in between jets is much larger than behind the jets. This suggests that streaks in the near-wall region are stabilized in between jets, while they are destabilized behind the jets. In other words, the flow acceleration in between jets stabilizes low and high speed streaks. The flow acceleration is a result of the favorable pressure gradient that occurs between the jets. Conversely, there exists an adverse pressure gradient behind the jets. This spanwise pressure heterogeneity leads to a difference in coherent vortical structures’ generation in between and behind the jets.
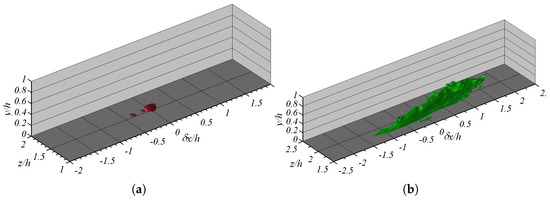
Figure 6.
The two-point correlation of streamwise velocity fluctuations, (a) behind the jets and (b) between the jets.
Figure 7 shows coherent vortical structures identified by [16] iso-contours. The color spectrum of the contours depicts instantaneous temperature on the surfaces of the vortices. The number of coherent vortical structures downstream is higher right behind the blowing jets than that in between blowing jets because of the adverse pressure gradient. The rapid generation of coherent vortical structures has recently also been observed in reverse flow regions, even in high Reynolds number adverse pressure gradient flows, by Vinuesa et al. [17]. In fact, between the jets, the flow is accelerated (this is evident from the streamwise length of shown in Figure 6b), and this shows the evidence of less coherent vortical structures than behind the jets.
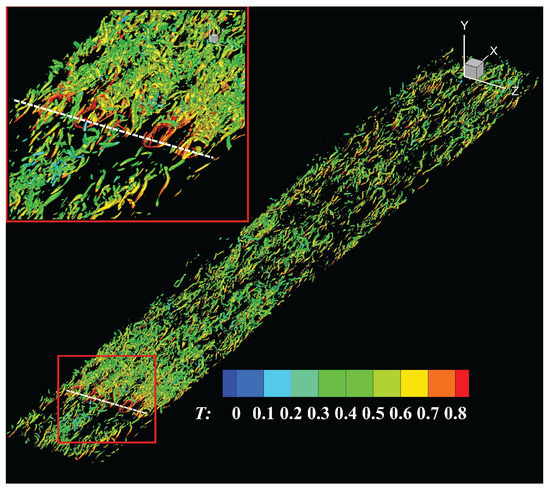
Figure 7.
contours colored with instantaneous temperature. The inset is a zoomed-in view of the flow field near the jets. The dashed white line shows the centerline of the jets. The iso-surfaces are drawn for .
The interaction of the jet and the incoming flow sets Kelvin–Helmholtz instability at the interface of the jet and the cross-flow. The process creates strong spanwise vortices. These spanwise vortices connect with quasi-streamwise vortices that are generated by destabilized low-speed streaks [18] behind the jet due to blowing perturbations. This leads to proliferation of hairpin vortices (as shown in Figure 7) downstream of blowing perturbations. In between jets, flow accelerates due to wall pressure gradient effects induced by blowing perturbations. The accelerated flow stabilizes low-speed streaks and these stabilized streaks are less vulnerable to break up; therefore, suppressing the generation of streamwise vortices downstream. This leads to a significant reduction in the number of vortices between two jets (leading to hot spots). The quasi-heterogeneity of vortex structure generation in the spanwise direction of the flow creates spanwise heterogeneity of turbulent thermal transport, as well. The red color of the temperature contours of Figure 7 directly downstream of blowing jets implies that vortical motions efficiently lift up hot fluid from the near-wall region to the outer region, thus promoting cooling. However, in between jets, heat fluxes are seen to be significantly lower than at from the blowing jets; thus, they do not effectively remove hot fluid from the wall to the outer region. This is contrary to what we observed behind the jets in which high proliferation of coherent vortical structures led to effective cooling of the wall and, thus, generated extensive cold spot regions.
The previous section demonstrated that the wall-normal heat flux is highest around downstream. To see whether this increase of turbulent heat transport has any relation to the generation of coherent vortical structures downstream of blowing, structures are taken on two cross-sectional views at the and downstream locations, as shown in Figure 8a,b, respectively. It can be seen that the number of coherent vortical structures is greater at downstream of blowing jets than at downstream. The generation of more coherent vortical structures amplifies wall-normal velocity fluctuations in the near-wall region.
Figure 8.
Iso-contours of vortices at (a) and (b) downstream of the jets. The iso-contours are drawn for . The instantaneous realization corresponds to .
The wall-normal fluctuations in the near-wall region move low-speed fluid away from the wall. This action increases streamwise velocity fluctuations further from the wall. Figure 9 clearly shows the generation of wall-normal and streamwise velocity fluctuations with respect to the generation of vortex structures downstream of blowing. As the figure depicts, wall-normal velocity fluctuations increase at the near-wall region due to the proliferation of vortices. This is different than what we see in the unperturbed case in general, where wall-normal fluctuations are lower in the near-wall region due to boundary conditions. The increase of in the near-wall region due to the proliferation of vortices moves the peak of away from the wall. The steep mean velocity gradient in the streamwise direction is due to the wake recovery as observed previously in Figure 2a. The velocity gradients in the streamwise direction stretch vortices, and vortex stretching strengthens them. Since vortex stretching and the generation of vortices intensify near downstream, wall-normal turbulent heat fluxes also amplify at the same region. This phenomena transports more heat flux from the wall, which in turn, reduces the temperature at downstream. Importantly, streamwise heat fluxes in the near-wall region do not amplify due to the generation of coherent vortical structures. This is why one could see reduced at , and downstream than that of unperturbed flow (see in Figure 5a), particularly in the near-wall region. However, Figure 5b clearly shows that the generation and stretching of vortices directly affect the wall-normal heat flux throughout the boundary layer.
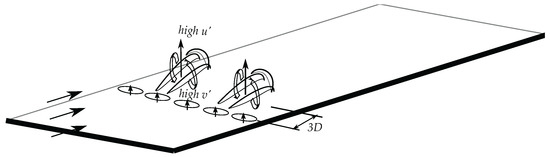
Figure 9.
A schematic of hairpin vortices generated downstream of blowing. Wall-normal and streamwise velocity fluctuations are shown with respect to the vortex structure generation.
4. Conclusions
DNS of turbulent channel flow with small blowing perturbations was performed at a friction Reynolds number () of 394. Due to the obstruction of the flow by the presence of blowing jets, a recirculation region is created downstream of the blowing. The reverse flow region attenuates the intensity of turbulence, which in turn, reduces the turbulent transport of heat fluxes. Thus, it creates a high temperature region at the wall just behind the jets. We observed a peculiar change in mean temperature at downstream at which we noticed low wall temperature even though the mean velocity of the flow is considerably lower than the unperturbed flow. The results show that is lower at downstream than that of the unperturbed flow particularly from to . On the other hand, is higher than that of unperturbed flow throughout the channel. We found that the generation of coherent vortical structures increases near downstream, and they are intensified by vortex stretching due to steep velocity gradients. The results clearly indicate that the proliferation of coherent vortical structures downstream of the jets contributes to the removal of hot fluid from the wall to the outer region. However, in between the jets, the flow is accelerated mainly due to low pressure regions, which prevents the proliferation of coherent vortical structures, leading to high temperature regions.
Acknowledgments
This research was funded by NSF-CBET-ONR:1512393: International Collaboration: The role of initial conditions on LSMs/VLSMsin turbulent boundary layers. We acknowledge Dr. Stefano Leonardi at UT-Dallas for generously allowing us to use channel flow code for this study.
Author Contributions
Suranga Dharmarathne performed the simulations, coded all the post-processing programs and contributed to data analysis and interpretation. Venkatesh Pulletikurthi generated most of the figures, performed the literature review and contributed to data analysis. Luciano Castillo conceptualized the study, performed the data analysis and provided insights and guidance throughout the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mahesh, K. The Interaction of Jets with Crossflow. Annu. Rev. Fluid Mech. 2013, 45, 379–407. [Google Scholar] [CrossRef]
- Keffer, J.; Baines, W. The round turbulent jet in a cross-wind. J. Fluid Mech. 1963, 15, 481–496. [Google Scholar] [CrossRef]
- Kamotani, Y.; Greber, I. Experiments on a turbulent jet in a cross flow. AIAA J. 1972, 10, 1425–1429. [Google Scholar] [CrossRef]
- Yuan, L.L.; Street, R.L.; Ferziger, J.H. Large-eddy simulations of a round jet in cross-flow. J. Fluid Mech. 1999, 379, 71–104. [Google Scholar] [CrossRef]
- Park, J.; Choi, H. Effects of uniform blowing or suction from a spanwise slot on a turbulent boundary layer flow. Phys. Fluids 1999, 11, 3095–3105. [Google Scholar] [CrossRef]
- Kim, K.; Sung, H.J. Effects of unsteady blowing through a spanwise slot on a turbulent boundary layer. J. Fluid Mech. 2006, 557, 423–450. [Google Scholar] [CrossRef]
- Araya, G.; Leonardi, S.; Castillo, L. Numerical assessment of local forcing on the heat transfer in a turbulent channel flow. Phys. Fluids 2008, 20, 085105. [Google Scholar] [CrossRef]
- Tardu, S.; Doche, O. Turbulent passive scalar transport under localized blowing. J. Vis. 2008, 11, 285–298. [Google Scholar] [CrossRef]
- Doche, O.; Tardu, S. Mechanism of wall transfer under steady localized blowing. Int. J. Heat Mass Transf. 2012, 55, 1574–1581. [Google Scholar] [CrossRef]
- Bogard, D.; Thole, K. Gas turbine film cooling. J. Propul. Power 2006, 22, 249–270. [Google Scholar] [CrossRef]
- Coletti, F.; Elkins, C.J.; Eaton, J.K. An inclined jet in cross-flow under the effect of streamwise pressure gradients. Exp. Fluids 2013, 54, 1589. [Google Scholar] [CrossRef]
- Orlandi, P. Fluid Flow Phenomena: A Numerical Toolkit; Fluid Mechanics and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000; Volume 55. [Google Scholar]
- Dharmarathne, S.; Tutkun, M.; Araya, G.; Castillo, L. Structures of scalar transport in a turbulent channel. Eur. J. Mech. B/Fluids 2016, 55 Pt 2, 259–271. [Google Scholar] [CrossRef]
- Bunker, R.S. A review of shaped hole turbine film-cooling technology. J. Heat Transf. 2005, 127, 441–453. [Google Scholar] [CrossRef]
- Moin, P.; Moser, R.D. Characteristic-eddy decomposition of turbulence in a channel. J. Fluid Mech. 1989, 200, 471–509. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Vinuesa, R.; Örlü, R.; Schlatter, P. Characterisation of backflow events over a wing section. J. Turbul. 2017, 18, 170–185. [Google Scholar] [CrossRef]
- Schoppa, W.; Hussain, F. Coherent structure generation in near-wall turbulence. J. Fluid Mech. 2002, 453, 57–108. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).