Abstract
Analysis of a PAT modeling is presented for application in water pipe systems as an interesting and promising energy converter to improve the system energy efficiency. The study is focused on the use of a Computational Fluid Dynamics (CFD) model in conjunction with laboratory data for representing PAT performance. The first stage of the procedure concerns a systematic analysis of the role played by the characteristic PAT parameters in the computational mesh definitions of the CFD model, with the aim of defining the most efficient set of capturing the main features of the PAT behaviour under different operating conditions. In the second stage, comparisons of CFD results and experiments were carried out to examine some system components for better understanding the PAT response. Specifically, the behavior of the pressure distribution along the PAT installation when implemented in a water pipe system are analyzed, and the links between pressure variation and the head drop in different system components responsible for the head losses and net head definition are also examined.
1. Introduction
In water distribution networks pressure reducing valves are generally used to dissipate the excess hydraulic energy and set optimal pressure values to reduce leakage. One of the research lines to improve the management of the pressurized systems is the increase of their energy efficiency. The energy efficiency can be improved through the diminishing of head losses, the reduction of the flow consumption in gravity pipes systems as well as the reduction of the pressure and consequently the leakages in the water distribution systems [1]. Particularly, the last strategy has been a powerful management tool since the 1990s [2,3,4]. Ramos et al. (1999) [5] proposed the use of the pumps working as turbines (PATs) as an alternative solution to reduce the pressure in pipe systems, replacing or in conjunction with the pressure reduction valves. This recovery system has the advantage of possible pressure control regulation and also to be green energy generator. This renewable system, which presents feasibility indexes with payback periods lower than five years, can lead to the improvement of the future water systems sustainability [6].
The knowledge of the operation points of these machines is a difficult task when their rotational speed is variable, because the head and the efficiency values are difficult to predict since the manufacture catalogue does not have these curves available [7]. This lack of knowledge as well as the difficulty to predict the best efficiency point of the pump operating in reverse mode, aims to researchers to propose some empirical methods are proposed in the available literature to identify the best efficiency point (BEP). These methods were summarized by [8] but they cannot accurately cover all machines [7]. This fact joined to the difficulty to predict the efficiency and the recovered head values when the machine operates under variable operation speed (VOS) [9] make necessary the modification of the affinity laws through specific parameters (q, h, p, and n) [10,11]. The modification of these laws is real if the efficiency and head values as a function of the flow are known.
To complement the experimental campaign, the use of a computational fluids dynamic (CFD) model was carried out as long as the model will be previously validated [12]. Hence, the behaviour for different values of head, flow and rotational speed can be estimated in the recovery system [13], increasing the knowledge in terms of pressure variation and head losses as well as their interactions between water system and fluids [14]. Therefore, the use of CFD techniques can make possible the knowledge of the PAT behaviour, reducing economic costs of experimental developments [15,16]. Apart from this, CFD techniques can predict velocities, pressures and turbulence parameters in any node of the represented geometry. In this sense, CFD becomes a virtual laboratory showing researchers accurate information along all the modelled volume.
In this line, different researchers analyzed the variation of the characteristic parameters in hydraulic systems, using CFD techniques [7,17,18]. These analyses showed the suitability to predict the behaviour of the tested recovery machine, but defining the variation trend of specific parameters. A detailed hydraulic loss distribution and a theoretical analysis were performed by Yang et al. (2012) [19]. In this contribution, different machines were simulated by CFD techniques and the results were validated with experimental tests, obtaining the head drop in various machines that had a different specific speed for the nominal speed of each recovery machine.
This research goes deeper in this line and analyses the variations of the head drop for different rotational speeds using a CFD model validated previously. Hence, the objective of this research is to show a PAT behavior under different steady flow conditions obtained by a CFD model. These conditions were compared with the measurements developed in the hydraulic laboratory of Instituto Superior Técnico (Lisbon) in which, the tested PAT operated with variable rotational speeds. Besides, as novelty, the research develops an estimation of the head drop in different connections of the machine (i.e., inlet pipe, volute, impeller, draft tube) for different rotational speeds, showing the significance of a VOS solution in the energy recovery process towards the maximization of the real recovered head for energy production.
2. Numerical and Experimental Procedure
This research presents numerical and experimental developments which were simulated and carried out in the CERIS-Hydraulic Lab of Instituto Superior Técnico at the University of Lisbon. CFD simulations and experimental data collections were developed to analyze the pressure drop behaviour and the influence in the efficiency variation of a PAT energy recovery system.
2.1. PAT Numerical Model
2.1.1. Model Description and Mesh
The setup of the mathematical model was performed using the finite volume method (FVM) with second-order spatial discretization scheme of the convection terms in the governing equations of CFD workbench SolidWorks-FloEFD. The PAT model was built in SolidWorks CAD system as demonstrated in Figure 1. The set of governing equations were discretized and solved using the FVM on a spatially rectangular computational mesh refined locally at the solid/fluid interfaces and in specified fluid regions, where high gradients are expected. A Semi Implicit Method for Pressure-Linked Equations (SIMPLE) algorithm was used to couple the pressure and velocity [20]. A relative error for the convergence criterion was considered to be less than 10−4. The Navier-Stokes equations are supplemented by fluid state equations defining the nature of the fluid, and by empirical dependencies of fluid density and viscosity. FloEFD employs one system of equations to describe both laminar and turbulent flows. The rotating parts were computed in coordinate systems attached to the models rotating parts, i.e., the models’ stationary parts must be axisymmetric with respect to the rotation axis.

Figure 1.
PAT model (a) and mesh (b).
The conservation laws for mass and momentum in the Cartesian coordinate system rotating with angular velocity can be written in the conservation form as follows [20,21]:
where, is the fluid velocity, is the fluid density, is the viscous shear stress tensor. For Newtonian fluids this tensor is defined as [21]:
Following Boussinesq assumption, the Reynolds-stress tensor has the following form [20]:
The Kronecker delta function is equal to unity when i = j, and zero otherwise, is the dynamic viscosity coefficient, is the turbulent eddy viscosity coefficient and is the turbulent kinetic energy. For laminar flows and are zero. In the frame of the k- turbulence model, is defined using two basic turbulence properties, namely, the turbulent kinetic energy k and the turbulent dissipation [21]
where, is a turbulent viscosity factor defined by:
with, , where y is the distance from the wall. This function allows to take into account laminar-turbulent transition.
FloEFD software works with CAD integration, which means that it takes geometrical data from a CAD program directly, suitable for parametric analysis.
Floworks (which is FloEFD as a standalone software) is very professional and accurate. The accuracy depends mainly on the model setup (i.e., meshing, boundary conditions, material properties, rotating and non-rotating zones), being intuitive with calculation stability and friendliness for having the CAD package integration tool. Transfers mechanical assemblies and especially for turbo designs (e.g., mechanical designs) into Floworks models is easy even for very complex geometries. The added value of this commercial software is that in the end the geometry can be already built by a mechanical group, so that the only need is to set up the boundary conditions and perform the mesh. Moreover, if some of the components need to be changed and re-meshed, Floworks in combination with Solidworks does this very fast and trouble free.
Compared to the other tools, FloEFD required less resources and optimally mesh and less calculation time to come up with good overall results, and it shows quite good agreement with experimental measurements too. Although the meshing and solver technology of FloEFD is a non-traditional CFD approach, several authors have proven that FloEFD is as accurate as, or better than, other traditional commercial CFD software in a complex aerodynamic study.
The mesh was determined solely by the computational domain and independent on the solid/fluid interfaces using the following procedure: (1) the computational domain was divided into slices by the basic mesh planes; (2) the mesh cells intersecting with the solid/fluid interface were split uniformly into smaller cells in order to capture the solid/fluid interface with the specified mesh cells; (3) each of the basic mesh cells intersecting with the solid/fluid interface were split uniformly into 8 child cells; (4) each of the child cells intersecting with the interface was in turn split into 8 cells of next level, and so on, until the specified cell size was attained [21]. Then, the rectangular computational domain was automatically constructed, enclosing the solid body with the orthogonal boundary planes to the specified axes of the Cartesian coordinate system [21].
In FloEFD, an optimization process is implemented as part of the global iteration process. Solution Adaptive Refinement (SAR) was used to optimize the mesh distribution in order to minimize the spatial error arising from the discretization of the governing differential equations. For a steady-state calculation, SAR cycles are implemented at a certain iteration frequency. Iterations are chosen on the basis of the estimated residual decrease at current iteration in comparison with residuals calculated after the previous SAR cycle. This approach makes possible to refine the whole solution domain, where potentially any significant disturbances of the flow can appear. The final results are presented in Table 1.

Table 1.
Definition of the mesh and simulations.
Irregular cells computationally represent a hole in the solid domain. If there are numerous irregular cells in a mesh, then a solid wall will no longer provide a physical barrier in the simulation. This can be remedied by increasing the mesh density in the area with the irregular cells. This is accomplished by increasing the global mesh level, shrinking the minimum wall thickness in the mesh settings, or applying a local mesh in the affected zone to impose a higher level of cell refinement. The mesh was refined such that the solution does not depend on the mesh size. To ensure that there was no mesh spacing dependence, a mesh sensitivity study was conduct by activating solution-adaptive meshing. This allowed to increase the number of cells automatically in areas of high flow gradient, and again ensure the flow solution remains unchanged for the purposes of the analysis. Thus, in order to determine the optimum mesh size, mesh sensitivity diagram was plotted to investigate the convergence of results and selection of proper mesh element size (Figure 2).
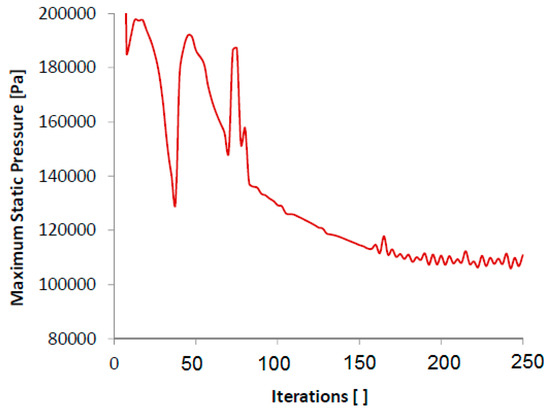
Figure 2.
Convergence of pressure results with different number of iterations.
As a validation of the FVM results, the required outlet pressure can be compared with the experimental work. If the pressure in the simulation meets the experiments at the same section with all similar conditions, the inputs and outputs in the FVM are considered as agreeable values. Moreover, it has been considered a good mesh when the error (in simulated pressure) by comparing simulation results with another mesh is less than 5%.
The used turbulence model is the k-ε model with wall functions. Two additional transport equations were used to describe the turbulent kinetic energy and dissipation [20]:
where, the source terms and were defined as [21]:
The turbulent generation due to buoyancy forces can be written as [20]:
where is the component of gravitational acceleration in direction , the constant and constant is defined as: when , and 0 otherwise;
These constants , , , , were defined empirically. In FloEFD the following typical values were used, , , , and [21].
The default velocity boundary condition at solid walls corresponded to the well-known no-slip condition. The solid walls were also considered to be impermeable. The simulations are carried out using a PC with CPU Intel(R) Core(TM) i7-3517U @ 1.90 GHz, 2.40 GHz and 8.00 GB RAM characteristics. The time taken for each simulation with the finally chosen mesh to the fully convergence starting from previously converged results in coarser mesh is presented in Table 1.
2.1.2. Boundary Conditions
In the CFD simulations, the static pressure (section 2), the volume flow rate (section 1) and the impeller rotational speed (section 3) boundary conditions are assigned to the inflow and outflow boundaries in the geometric model presented in Figure 3. The first initial boundary condition is set upstream of the pipe with inlet volume flow varying from 2.90 L/s to 5.55 L/s. The second initial boundary condition is set at the inside surface for the outlet pipe with a static pressure varying between 112,000 and 113,500 Pa. As for the rotational speed, five rotational speeds of 810, 930, 1050, 1170, 1275 and 1500 rpm are considered.
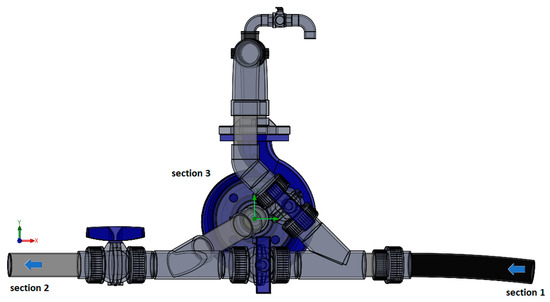
Figure 3.
Boundary sections considered in the CFD model.
Local rotating zones are used for analysis of the fluid flow in the impeller. The rotating solid component is surrounded by an axisymmetric rotating zone, which has its own coordinate system rotating together with the component. The fluid flow equations in the non-rotating zones of the computational domain are solved in the non-rotating Cartesian Global Coordinate System [21]. To connect solutions obtained within the rotating zones and in the non-rotating part of the computational domain, special internal boundary conditions are set automatically at the fluid boundaries of the rotating zones [20]. In addition, the wall surface rotation (without changing the model’s geometry) is specified. All the initial settings and input data remain the same but the volume flow rate and the static pressure is increased according to the experiments.
In the CFD simulations, the pressure opening condition is assigned to the outflow boundary condition, in the geometric model (section 2 in Figure 3). The pressure opening boundary condition, which can be the static pressure, or total pressure, or environment pressure is imposed in the general case when the flow direction and/or magnitude at the model opening are not known a priori, so they are to be calculated as part of the solution. In most cases the static pressure is not known, whereas if the opening connects the computational domain to an external space with known pressure, the total pressure at the opening is known. The local atmospheric pressure condition is used as a total pressure for incoming flows and as a static pressure for outgoing flows. If, during the calculation, a vortex crosses an opening with the environment pressure condition specified at it, this pressure considered as the total pressure at the part of opening through which the flow enters the model and as the static pressure at the part of opening through which the flow leaves the model [14]. For all simulations, a volume flow rate is set at the inlet section represented by section 1 in Figure 3, which is a mean for the model to calculate the flow rate. This allows the verification of the conservation of the mass.
2.2. PAT Experimental Tests
The hydraulic facility that is shown in Figure 4 and Figure 5 is composed by one closed pipe of high density polyethylene. The nominal diameter is 50 mm and its length is 100 m; an air-vessel tank with the volume of 1 m3 is used to stabilize the upstream pressure. This air-vessel allows to regulate the flow and pressure in order to reach the steady flow conditions; a recirculating pump is also necessary since this is a loop pipe system; at downstream of the operating system an open free surface tank with the capacity of 0.5 m3 keeps the recirculating flow constant in the pipe system. The pressure inside of the air-vessel varies between 20 and 35 m w.c.; ball valves located at downstream to induce flow variations are used; an electromagnetic flowmeter is located at upstream; two pressure transducers are used to register the pressure variations in a picoscope acquisition data system to be visualized in the laptop and later processed.
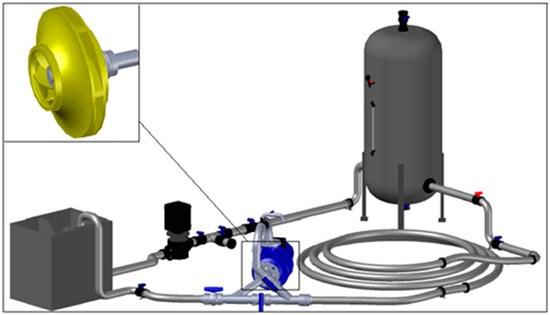
Figure 4.
Scheme of the experimental hydraulic facility at CERIS-IST Lab.

Figure 5.
Components of the experimental facility: (1) HDPE pipe; (2) recirculating pump; (3) air-vessel tank; (4) flowmeter; (5) PAT; (6) picoscope and acquisition data; (7) downstream regulating tank; (8) pressure transducers and (9) general view.
3. Results and Discussion
3.1. PAT Characteristics
The tested and simulated machine is a centrifugal pump working as turbine with a radial impeller (Figure 6). The PAT model is Etarnom 32-125 from KSB. When the machine is operating in the turbine mode, the best efficiency point (BEP) is 3.60 L/s and 4.43 m w.c., reaching an efficiency of 0.62. For these values, the specific speed of the machine is 51 rpm (m, kW) and its nominal rotational speed is 1020 rpm. The characteristics of its impeller are the following: outside diameter with 170 mm; inlet diameter with 90 mm; six blades; the inlet angle of the impeller is 55°; and the outlet angle of the impeller is 45°.
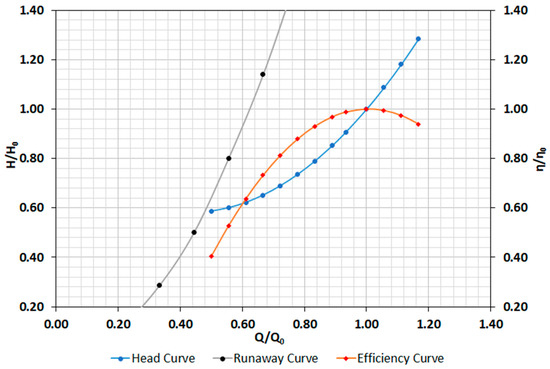
Figure 6.
Characteristic curves of the tested PAT for N = 1020 rpm.
Defined the characteristic parameters of the machine for nominal conditions related with the best efficiency parameters (Q0, H0, and η0), the machine was tested in the hydraulic lab previously described. The experiments were carried out for different rotational speeds and different flows in steady state conditions for different rotational speeds: 810, 930, 1050, 1170, 1275 and 1500 rpm. For each rotational speed, different operation points were recorded with flow values between 2.9 and 5.5 L/s. The below flow limit was established by the runaway curve, where the flow decreases when the speed increases for this type of impeller [22]. In Figure 7, the minimum flows to put the PAT working that was 2.9 L/s for the rotational speed of 810 rpm, while was 4.1 L/s when the machine rotated with 1500 rpm. Figure 7 also shows the increase of the recovered head when the rotational speed grows, keeping the flow constant, a characteristic of radial impellers.
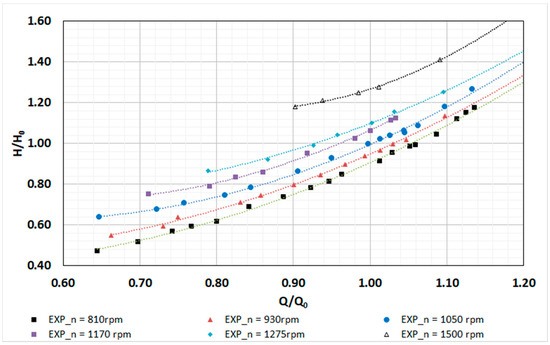
Figure 7.
Experimental results for different rotational speeds.
3.2. CFD and Experiments
The global variables are simulated in the CFD model, namely the head (H) and the hydraulic output torque (T) along with the given variables of discharge (Q) and rotational speed (N) are used to evaluate the overall PAT characteristics. The flow characteristics output of the PAT are displayed using pressure contour plots.
Figure 8 shows the absolute static pressure distribution of the PAT from 810 rpm to 1500 rpm in a cross-section plane of the impeller and along the device for Q = 4.50 L/s. The pressure decreases from upstream to downstream as the fluid flows within the domains and along the impeller, from the inner to the outer region, as energy is transmitted to the shaft.
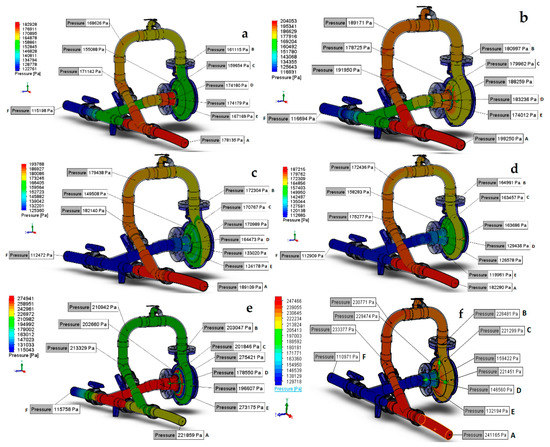
Figure 8.
Absolute static pressure contours for Q = 4.50 L/s: (a) N = 810 rpm; (b) N = 930 rpm; (c) N = 1050 rpm; (d) N = 1170; (e) N = 1275 rpm; (f) N = 1500 rpm.
Comparing the elements of Figure 8, the higher speed corresponds to a lower value of the pressure downstream of the runner. Besides, in the turbulence space between impeller hub and the casing, the reduction of the conversion efficiency results from hydro to mechanical power [16].
Comparing results from N = 810 rpm with N = 1500 rpm, a differential pressure between the upstream and downstream of the runner, at a highest speed corresponds to the increasing net head. In the vortex core, formed downstream of the runner (noticed in Figure 8d–f), lower pressure values were achieved. The vortex formation at the exit of the rotor and extends to downstream thereof related with turbulence and hydrodynamic instability for the not nominal conditions. These effects are associated to the variable pressure fluctuations and efficiency losses.
The validation of the CFD model was done by using the recorded pressure values in the transducers. Figure 9 shows the comparison between experimental and numerical values for different rotational speeds.
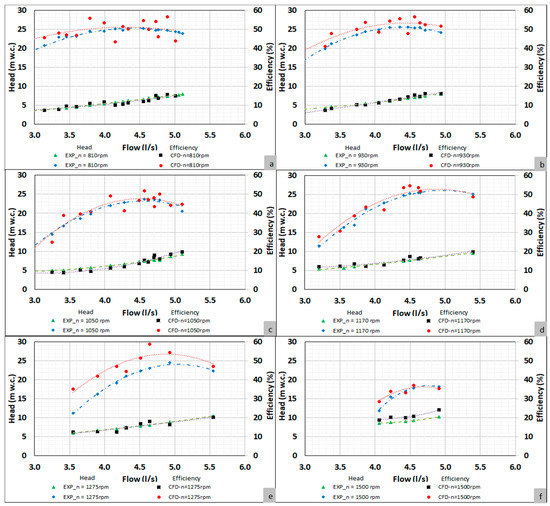
Figure 9.
Experimental and numerical values for different rotational speeds: (a) N = 810 rpm; (b) N = 930 rpm; (c) N = 1050 rpm; (d) N = 1170; (e) N = 1275 rpm; (f) N = 1500 rpm.
Equation (13) defines the mean square error between the experimental data and estimated measurements by the CFD for the same flow value (head or efficiency) according to the number of measured data:
where i is the tested parameter; is the estimated value; is the measured value; and m is the number of measurements.
Table 2 summarizes the mean square errors that were obtained when CFD simulations and experimental results were compared. The error was determined according to developed measures in the control sections A and F (Figure 10). The table shows the error varied between 2 and 9%, reaching lower errors in the head results than in the efficiency values.

Table 2.
Mean square error for each rotational speed.
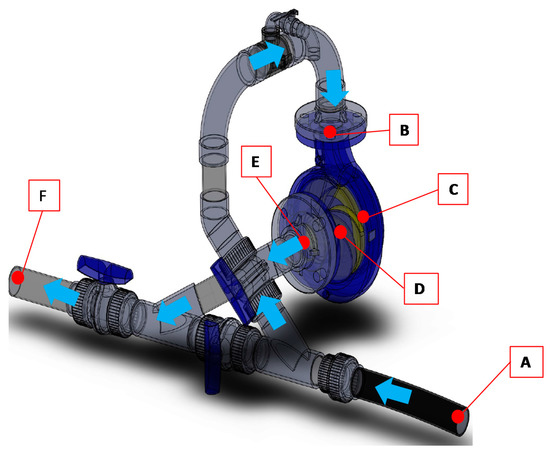
Figure 10.
Definition of referenced sections for pressure drop analyses.
3.3. Head Drop Estimation
Once the mean square error is known, the head drop was analyzed in different sections of the energy converter device. This head estimation was determined through established sections presented in Figure 10.
The difference between points A and F defines the head drops between pressure sensors in the experimental facility. The head losses in the inlet pipe is established by the difference between A and B pressure values. The losses in the volute of the machine can be estimated between B and C values. The impeller head is estimated by the difference between C and D values. The difference between D and F represents the loss in the draft tube that included the losses between impeller outlet and the outlet flange (section E).
Table 3 shows the main results associated to different operating conditions associated for each rotational speed in different cross sections, simulated in the CFD model. Low values of static pressure, in the impeller exit and the draft tube can be identified. The reduction of the pressure, characteristic of the vortex nuclei that occurs downstream of the impellers, can eventually lead to cavitation and rotation in the flow direction. For the operating conditions, the lowest pressure values occurred along the impeller (section D), and near the draft tube (section E).

Table 3.
Simulation pressure results in different cross section (from A to F) in Figure 10 for different rotational speeds.
The analysis of these values obtained using the CFD model and validated with the experiments enabled to estimate the head drop between different cross sections. The estimation of the head drop determined the part of the hydraulic energy that is transmitted by the impeller to the shaft. The head values for each cross section (i.e., inlet pipe, volute, impeller, draft tube) can be observed for different rotational speeds in Figure 11a,c,e,g,i,k. The percentage of the head drop when they are compared to the total head given by the difference of pressure between sections A and F is presented in the right graphs of Figure 11. The mean square error was determined between CFD and experimental for each rotational speed in Table 2. The percentages for each rotational speed can be observed in Figure 11b,d,f,h,j,l.
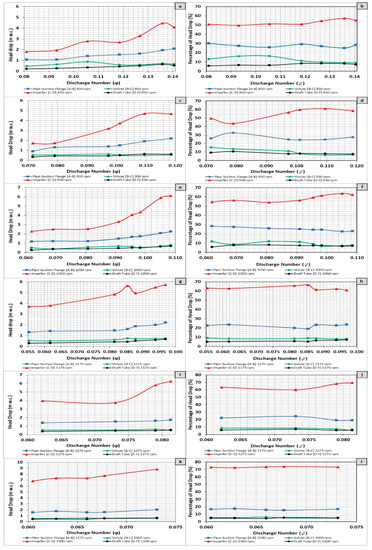
Figure 11.
Head drop variation for different rotational speeds.
Both head drop and its percentage are related in the Figure 11 as function of the discharge number, which is defined by Equation (14):
where Q is the flow in m3/s; N is the rotational speed of the machine in rps; and D is the impeller diameter in m.
All simulations in Figure 11 were developed for flows between 3 and 5 L/s, and showed that the values of the head drop are similar in inlet and outlet pipe (draft tube), varying between 0.8 and 2.2 m w.c. in the inlet pipe and 0.3 and 0.7 m w.c. in the draft tube. The volute losses were around 0.55–0.60 m w.c. and they remained constant for each rotational speed and flow. If the head are analysed in terms of pressure, the volute losses increased slightly with the rotational speed. Finally, for the different simulations, the recovered head by the impeller increased with the rotational speed and flow. For each rotational speed, the average and its standard deviation (-) of the head drop are determined and shown in Figure 12.
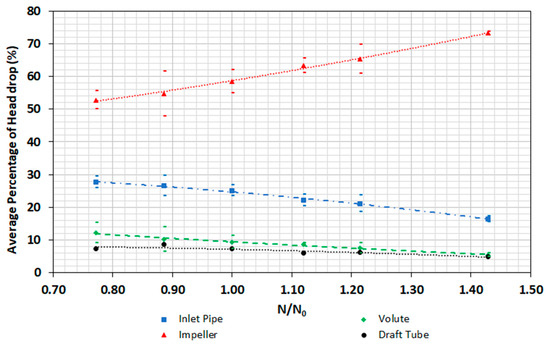
Figure 12.
Discretization of the average percentage of the head drop for different rotational speeds.
If Figure 12 is observed, the percentage of losses of the inlet pipe, volute and draft tube decrease with the rotational speed raising. The draft tube and volute values varied from 10 to 5% approximately when the rotational speed increased from 810 to 1500 rpm. In contrast, if the impeller element is analyzed, the average percentage of head drop increases from 52 to 73% for the same variation of the rotational speed. The standard deviation is also analyzed for all flow range and the values are lower than 5%. The analysis in the discretization of the head drop as well as the rotational speed variation were presented in Figure 6. In this figure, the recovered head increases with the rotational speed indicates the possibility of variable operation speed attaining the maximum value in order to maximize the recovered head using the same energy converter device.
4. Conclusions
The pressure variation analysis by CFD modelling and experimental tests performance of a PAT low-power converter installed in a pipe system with small discharge values constitute an expert answer to improve the system efficiency and the control of the operational pressure management. Related to this, the research proposes sensitivity analyses to several characteristic parameters, identifying the percentage of the head drop in the different parts, for different rotational speeds, in a typical PAT installation and their influence in the real available head.
The influence of the rotational speed variation on the head drop in each system component is an innovative analysis to optimize the hydraulic behaviour in this micro-power system. A significant range of possible applications as pressure reducing system based on the velocity operating strategy of a PAT is discussed for different flow demands. The identification of the pressure drop and the characterization of the equivalent percentage of the total available head between the pipe PAT connection inlet and draft tube connection outlet is of the utmost importance in PAT analyses and implementation in real systems. For this case study, the head drop in the inlet pipe the volute and the draft tube kept constant in absolute terms. Nevertheless, this head drop decreased from 10% to 5% when the percentage related to total head was determined. In contrast, the average percentage of head drop increased from 52 to 73% for the same variation of the rotational speed, particularly from 810 to 1500 rpm.
Therefore, the development of this research, combining experiments and numerical results using CFD model with a mean square error between 2 and 9% gives us a powerful tool for modeling the whole machine performance. The limitation of this study is mainly related to the typology of the machine (i.e., specific speed) that can influence in the percentage of the drop head. Therefore, the development of more studies will be interesting, considering other specific speeds to show the variability of the head drop. Nevertheless, other characteristics, such as the diameter of the pipe in the inlet and outlet of the machine, can present variations in the percentage of head drops, although the trend will be the same of this research for different flow values. This type of analysis improves the knowledge of the behavior of the energy converters. Its development in more case studies will increase the obtained energy efficiency in real applications.
Acknowledgments
This research is supported by the “Program to support the academic career of the faculty of the Universitat Politècnica de València 2016/2017 in the project ‘Maximization of the global efficiency in PATs in laboratory facility`of the first author. The authors wish to thank to the project REDAWN (Reducing Energy Dependency in Atlantic Area Water Networks) EAPA_198/2016 from INTERREG ATLANTIC AREA PROGRAMME 2014–2020 and CERIS (CEHIDRO-IST), the Hydraulic Laboratory, for the support in the conceptual developments and the experiments on PATs.
Author Contributions
The author Helena M. Ramos has contributed with the idea, in the revision of the document, supervising the whole research, and in particular in analyses of the head drop in each system component. Mariana Simao has been involved in the CFD modelling. Modesto Pérez-Sánchez did the experiments in hydraulic lab of IST as well as the analysis of the results between CFD and experiments. P. Amparo López-Jiménez has supervised the whole research and revised the final document.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BEP | Best Efficiency Point |
| CFD | Computational Fluids Dynamics |
| FVM | Finite Volume Methods |
| PATs | Pumps working as Turbines |
| SAR | Solution Adaptive Refinement |
| SIMPLE | Semi Implicit Method for Pressure-Linked Equations |
| VOS | Variable Operation Strategy |
References
- Cabrera, E.; Cobacho, R.; Soriano, J. Towards an energy labelling of pressurized water networks. Procedia Eng. 2014, 70, 209–217. [Google Scholar] [CrossRef]
- Tucciarelli, T.; Criminisi, A.; Termini, D. Leak analysis in pipeline systems by means of optimal valve regulation. J. Hydraul. Eng. 1999, 125, 277–285. [Google Scholar] [CrossRef]
- Lansey, K.E.; Mays, L.W. Optimization model for water distribution system design. J. Hydraul. Eng. 1990, 115, 1401–1418. [Google Scholar] [CrossRef]
- Araujo, L.; Ramos, H.; Coelho, S. Pressure control for leakage minimisation in water distribution systems management. Water Resour. Manag. 2006, 20, 133–149. [Google Scholar] [CrossRef]
- Ramos, H.; Borga, A. Pumps as turbines: An unconventional solution to energy production. Urban. Water. 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.; Ramos, H.; López-Jiménez, P. Energy recovery in existing water networks: Towards greater sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Yang, S.S.; Derakhshan, S.; Kong, F.Y. Theoretical, numerical and experimental prediction of pump as turbine performance. Renew. Energy 2012, 48, 507–513. [Google Scholar] [CrossRef]
- Nautiyal, H.; Varun, K.A. Reverse running pumps analytical, experimental and computational study: A review. Renew. Sustain. Energy Rev. 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. PAT design strategy for energy recovery in water distribution networks by electrical regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Fecarotta, O.; Carravetta, A.; Ramos, H.M.; Martino, R. An improved affinity model to enhance variable operating strategy for pumps used as turbines. J. Hydraul. Res. 2016, 54, 332–341. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M. Methodology for energy efficiency analysis in pressurized irrigation networks. Ph.D. Thesis, Universitat Politècnica Valencia, València, Spain, 2017. [Google Scholar]
- López-Jiménez, P.A.; Escudero-González, J.; Montoya Martínez, T.; Fajardo Montañana, V.; Gualtieri, C. Application of CFD methods to an anaerobic digester: The case of Ontinyent WWTP, Valencia, Spain. J. Water Process. Eng. 2015, 7, 131–140. [Google Scholar] [CrossRef]
- Ramos, H.M.; Simão, M.; Borga, A. Experiments and CFD analyses for a new reaction microhydro propeller with five blades. J. Energy Eng. 2013, 139, 109–117. [Google Scholar] [CrossRef]
- Simao, M.; Mora-Rodriguez, J.; Ramos, H.M. Computational dynamic models and experiments in the fluid-structure interaction of pipe systems. Can. J. Civ. Eng. 2016, 43, 60–72. [Google Scholar] [CrossRef]
- Simão, M.; Ramos, H.M. Hydrodynamic and performance of low power turbines: Conception, modelling and experimental tests. Int. J. Energy Environ. 2010, 1, 431–444. [Google Scholar]
- Nautiyal, H.; Nautiyal, H.; Varun, V.; Kumar, A.; Yadav, S.Y.S. Experimental investigation of centrifugal pump working as turbine for small hydropower systems. Energy Sci. Technol. 2011, 1, 79–86. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Yang, S.S.; Kong, F.Y.; Chen, H.; Su, H.S. Effects of blade wrap angle influencing a pump as turbine. J. Fluids Eng. 2012, 134, 061102. [Google Scholar] [CrossRef]
- Griffini, D.; Insinna, M.; Salvadori, S.; Barucci, A.; Cosi, F.; Pelli, S.; Righini, G.C. On the CFD analysis of a stratified Taylor-Couette system dedicated to the fabrication of nanosensors. Fluids 2017, 2, 8. [Google Scholar] [CrossRef]
- Mentor Graphics Corporation. FloEFD Technical Reference; Mentor Graphics Corporation: Wilsonville, OR, USA, 2011. [Google Scholar]
- Mentor Graphics Corporation. Flow Simulation—Technical Reference; Solid Works 2011; E.U.A., Ed.; Mentor Graphics Corporation: Wilsonville, OR, USA, 2011. [Google Scholar]
- Guidelines for Design of Small Hydropower Plants; Ramos, H. (Ed.) WREAN (Western Regional Energy Agency and Network) and DED (Department of Economic Development—Energy Division): Belfast, Northern Ireland, UK, 2000.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).