A Non-Hydrostatic Depth-Averaged Model for Hydraulically Steep Free-Surface Flows
Abstract
:1. Introduction
2. Governing Equations
3. Numerical Method
4. Model Application and Testing
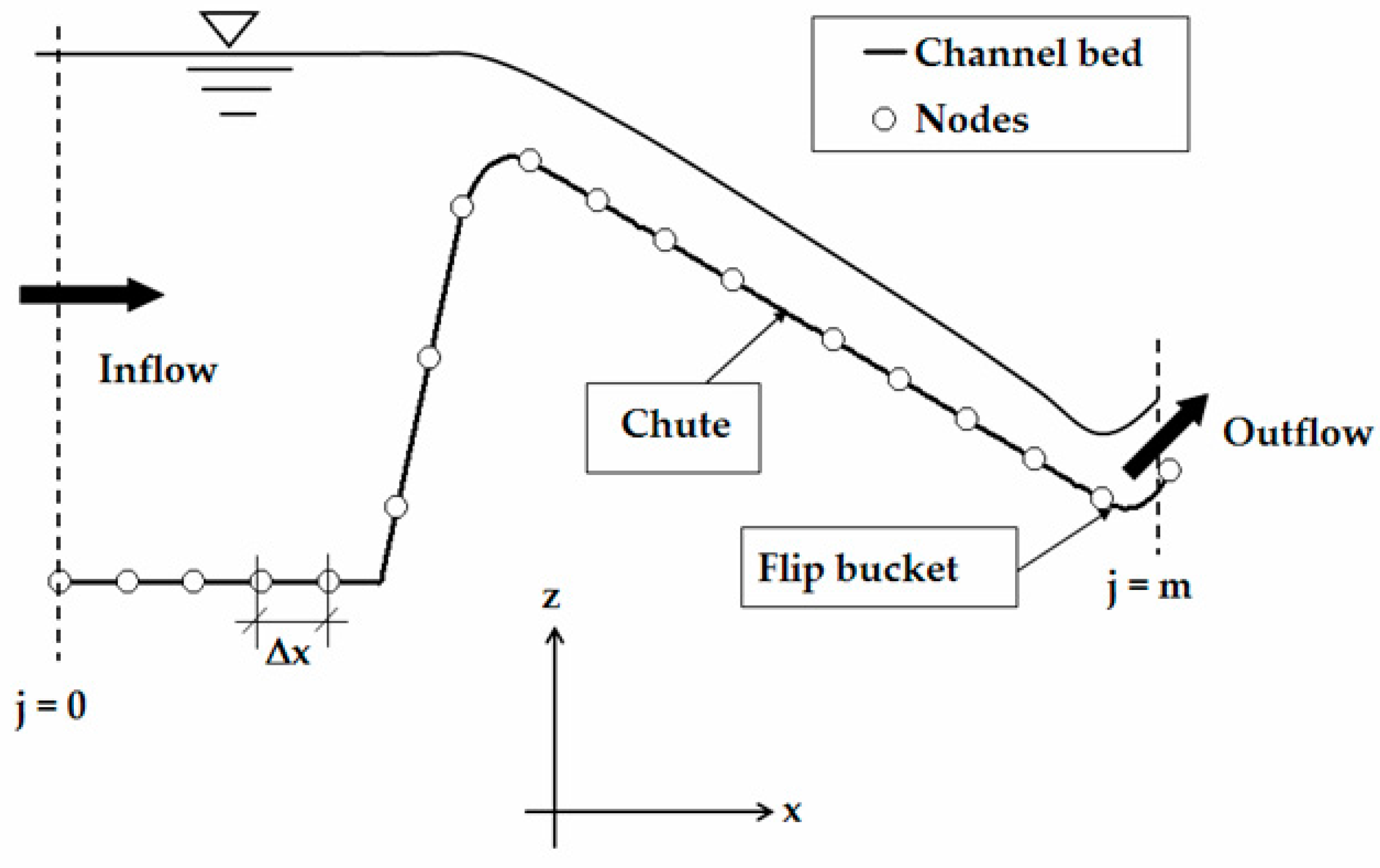
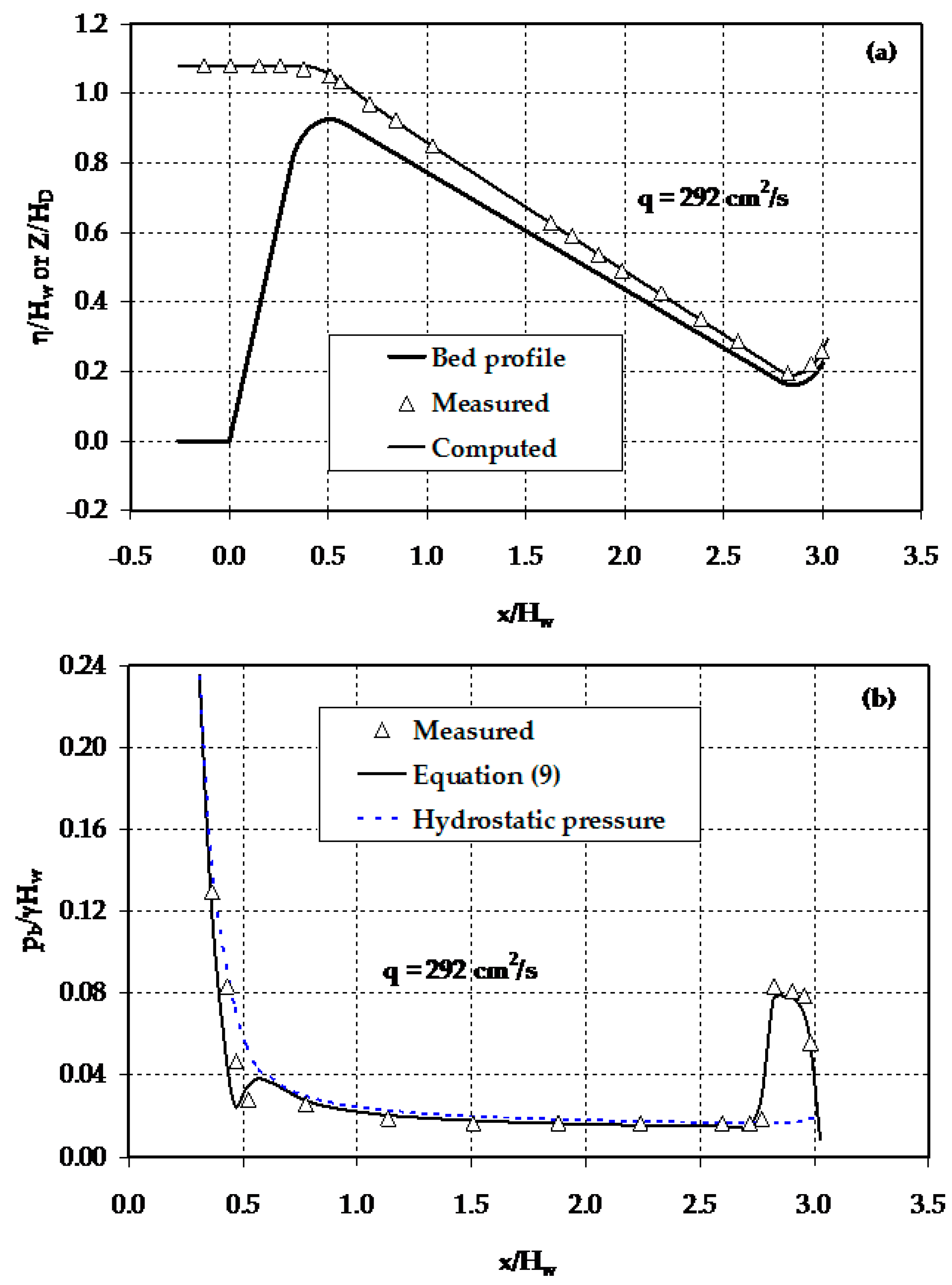
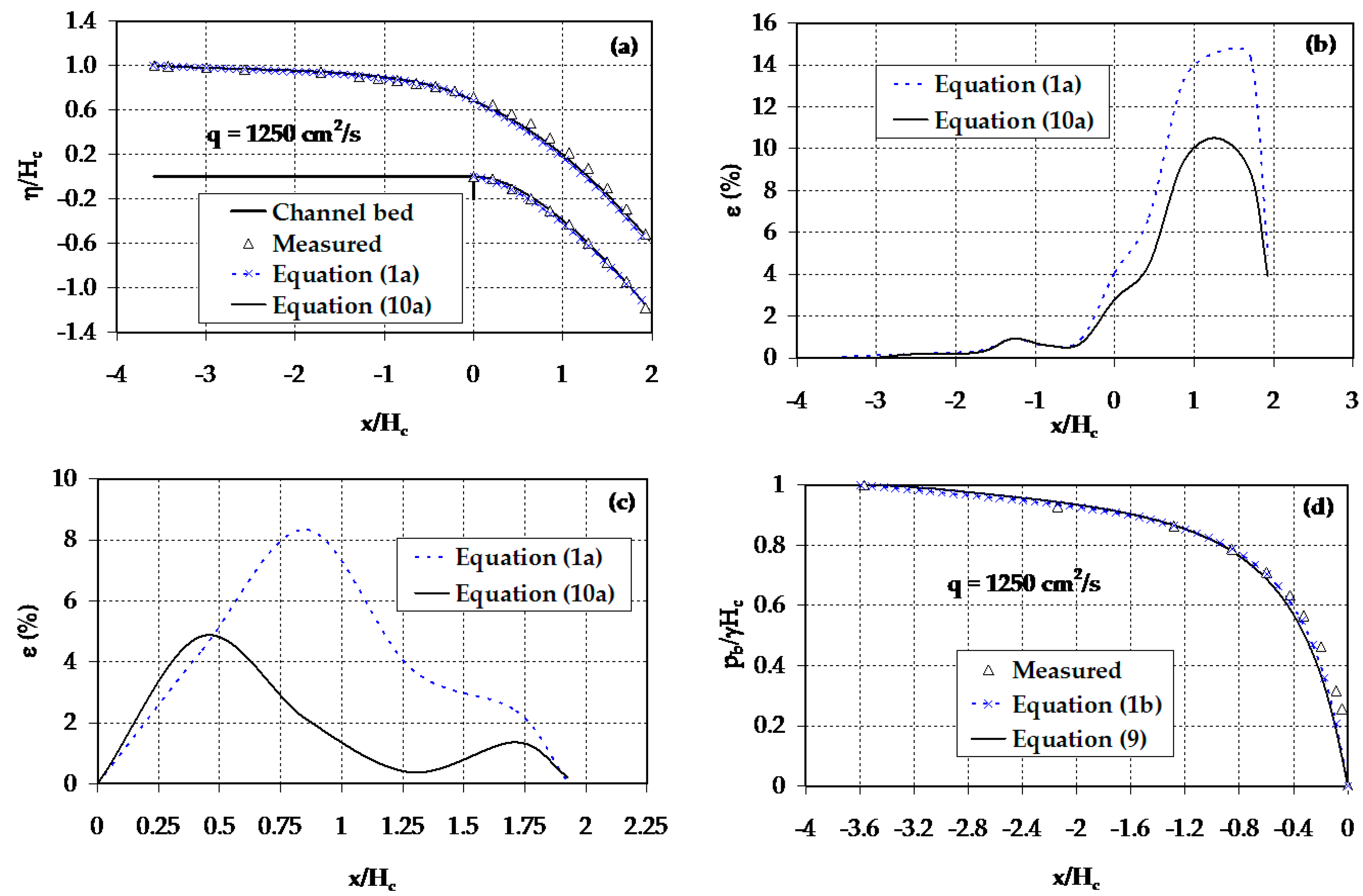
4.1. Non-Hydrostatic Flow over a Spillway
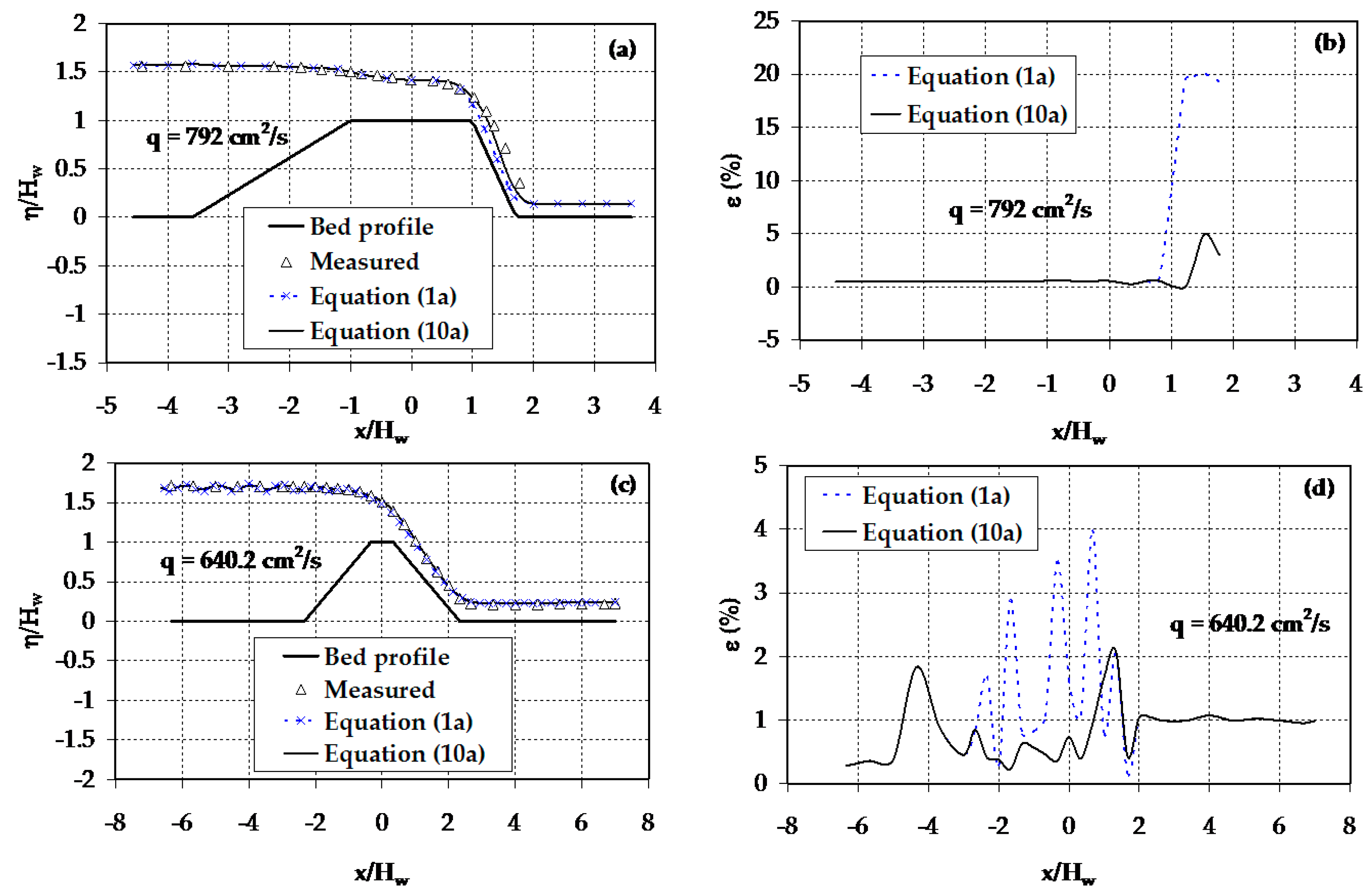
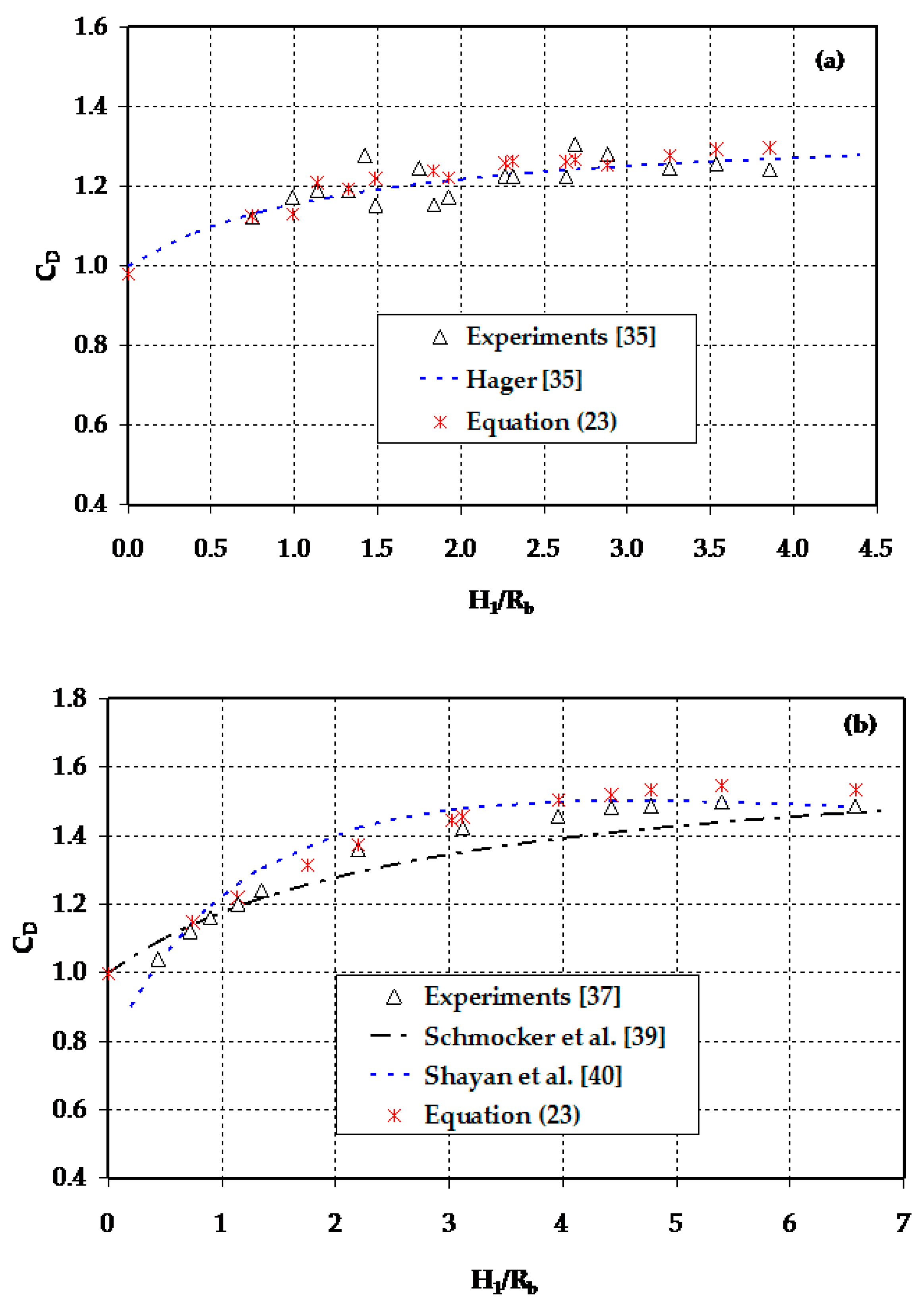
4.2. Flow over Trapezoidal-Shaped Weirs
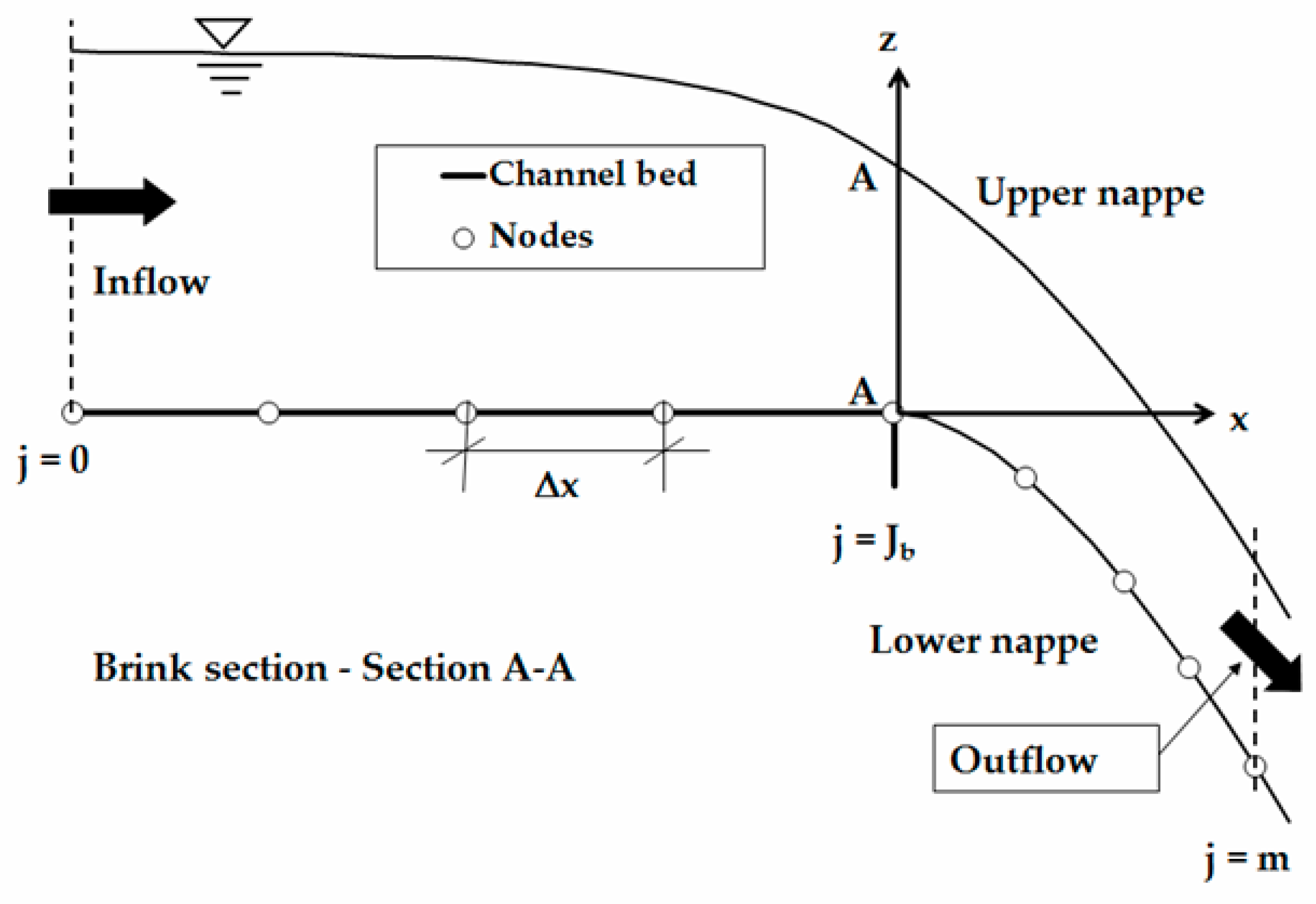
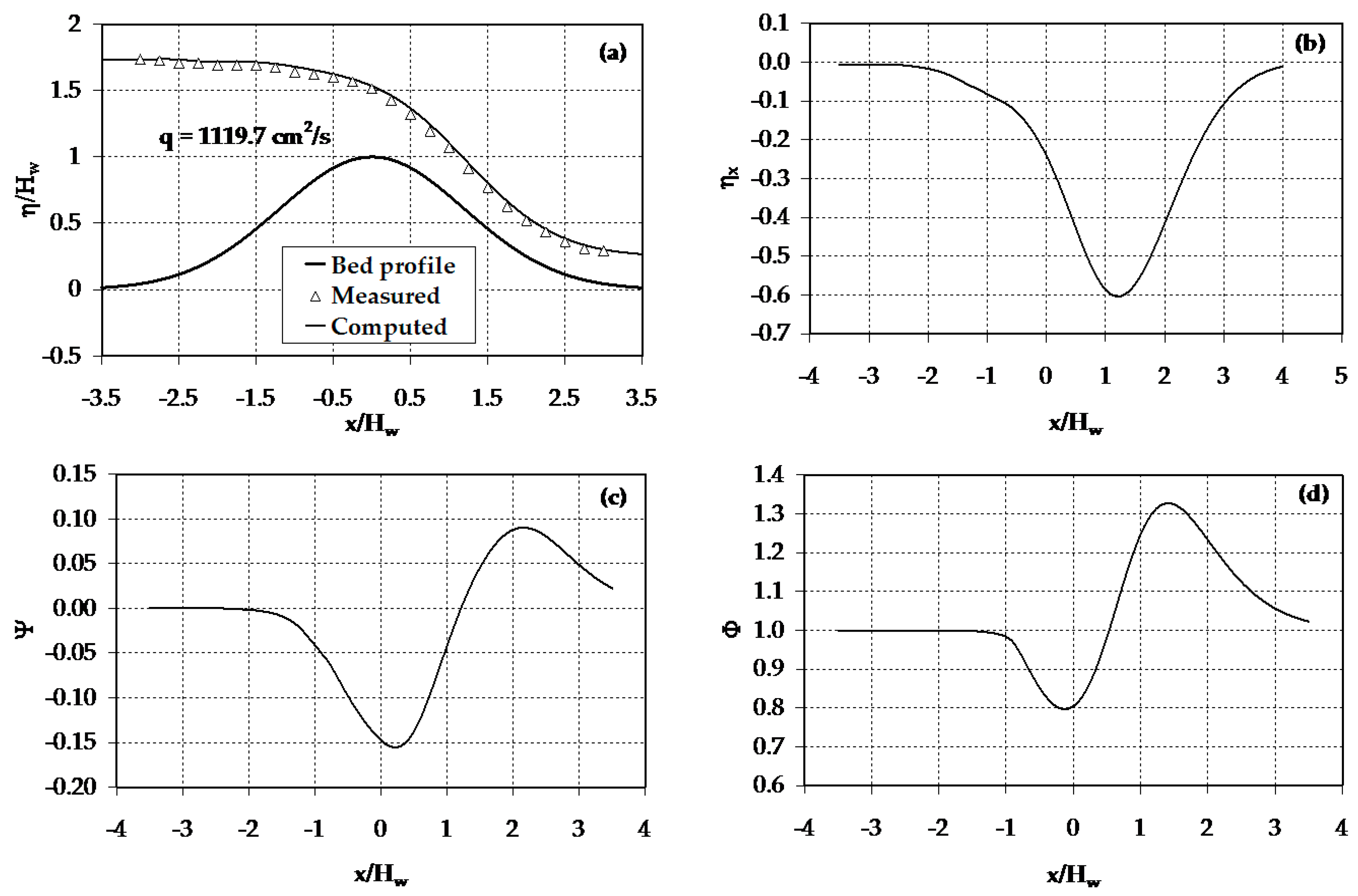
4.3. Curvilinear Overfalls
4.4. Nature of the Higher-Order Curvature Terms
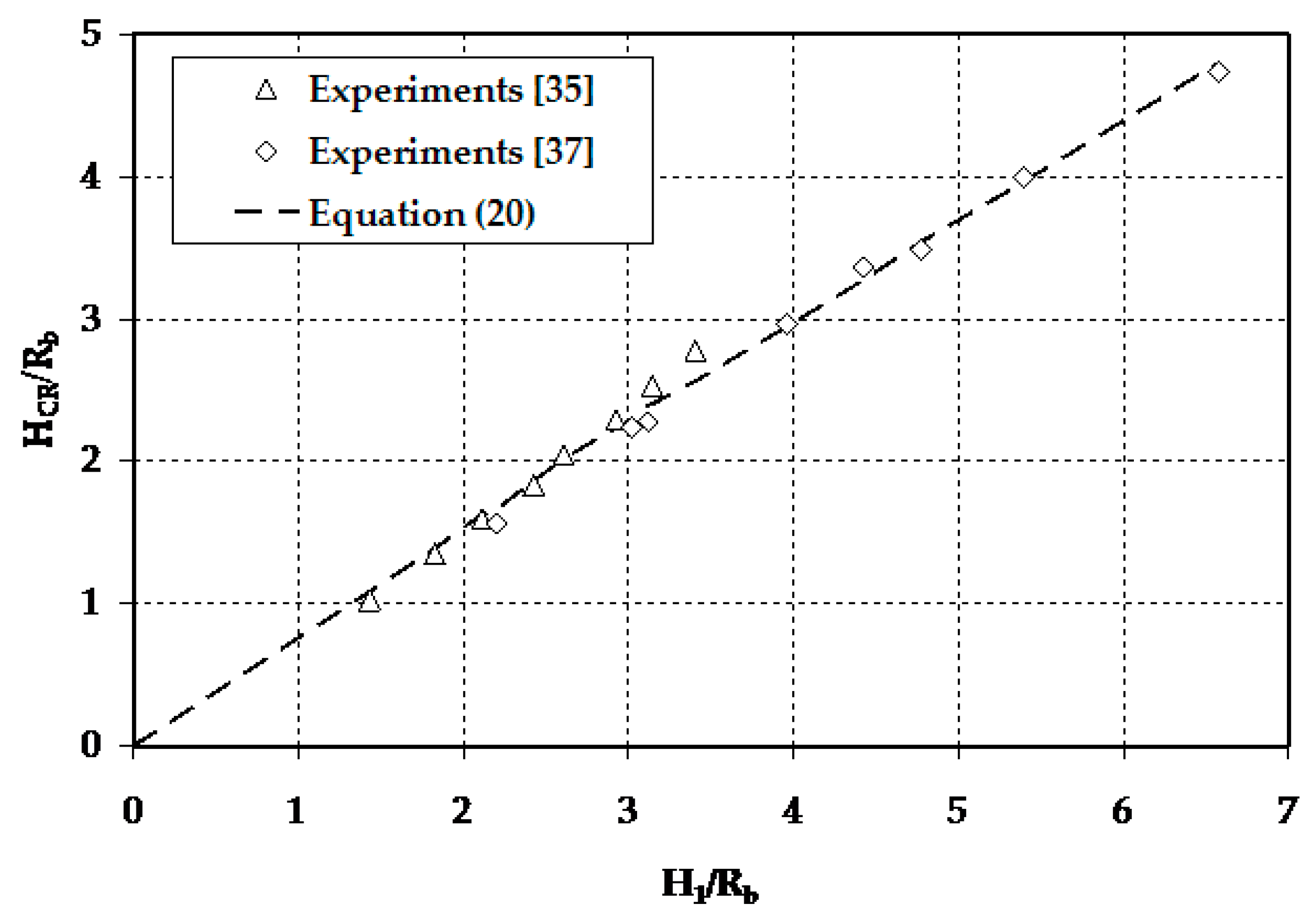
5. Critical Flow Conditions in Curvilinear Free-Surface Flows
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Savage, S.B.; Hutter, K. The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 1989, 199, 177–215. [Google Scholar] [CrossRef]
- Berger, R.C. Free-Surface Flow over Curved Surfaces. Ph.D. Thesis, University of Texas, Austin, TX, USA, 1992. [Google Scholar]
- Berger, R.C.; Carey, G.F. Free-surface flow over curved surfaces-Part I: Perturbation analysis. Int. J. Numer. Method Fluids 1998, 28, 191–200. [Google Scholar] [CrossRef]
- Berger, R.C. Strengths and weaknesses of shallow-water equations in steep open channel flow. In Proceedings of the National Conference on Hydraulic Engineering, ASCE, Buffalo, NY, USA, 1–5 August 1994; Volume 2, pp. 1257–1262. [Google Scholar]
- Keller, J.B. Shallow-water theory for arbitrary slopes of the bottom. J. Fluid Mech. 2003, 489, 345–348. [Google Scholar] [CrossRef]
- Denlinger, R.P.; O’Connell, D.R. Computing non-hydrostatic shallow-water flow over steep terrain. J. Hydraul. Eng. 2008, 134, 1590–1602. [Google Scholar] [CrossRef]
- Fawer, C. Etude de Quelques Écoulements Permanents à Filets Courbes (Study of Some Permanent Flows with Curved Filaments). Docteur ès Sciences Techniques Thèse, Université de Lausanne: Lausanne, Switzerland, 1937. (In French) [Google Scholar] [CrossRef]
- Hager, W.H.; Hutter, K. Approximate treatment of plane channel flow. Acta Mech. 1984, 51, 31–48. [Google Scholar] [CrossRef]
- Hager, W.H. Equations for plane, moderately curved open channel flows. J. Hydraul. Eng. 1985, 111, 541–546. [Google Scholar] [CrossRef]
- Matthew, G.D. Higher-order, one-dimensional equations of potential flow in open channels. Proc. Inst. Civ. Eng. 1991, 91, 187–201. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Hager, W.H. One-dimensional modelling of curvilinear free-surface flow: Generalised Matthew theory. J. Hydraul. Res. 2014, 52, 14–23. [Google Scholar] [CrossRef]
- Zerihun, Y.T. A One-Dimensional Boussinesq-Type Momentum Model for Steady Rapidly-Varied Open Channel Flows. Ph.D. Thesis, Department of Civil and Environmental Engineering, The University of Melbourne, Melbourne, VIC, Australia, 2004. [Google Scholar]
- Benjamin, T.B.; Lighthill, M.J. On cnoidal waves and bores. Proc. R. Soc. A 1954, 224, 448–460. [Google Scholar] [CrossRef]
- Marchi, E. The nappe profile of a free overfall. Rend. Mat. Acc. Lincei. 1992, 3, 131–140. [Google Scholar]
- Marchi, E. On the free overfall. J. Hydraul. Res. 1993, 31, 777–790. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Giráldez, J.V.; Ayuso, J.L. Higher-order critical flow condition in curved-streamline flow. J. Hydraul. Res., 2008, 46, 849–853. [Google Scholar] [CrossRef]
- Dressler, R.F. New nonlinear shallow flow equations with curvature. J. Hydraul. Res. 1978, 16, 205–220. [Google Scholar] [CrossRef]
- Jaeger, C. Engineering Fluid Mechanics; Blackie and Son Limited: London, UK; Glasgow, UK, 1956; pp. 65–135. [Google Scholar]
- Liggett, J.A. Critical depth, velocity profile and averaging. J. Irrig. Drain. Eng. 1993, 119, 416–422. [Google Scholar] [CrossRef]
- Chanson, H. Minimum specific energy and critical flow conditions in open channels. J. Irrig. Drain. Eng. 2006, 132, 498–502. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Chanson, H. Depth-averaged specific energy in open-channel flow and analytical solution for critical irrotational flow over weirs. J. Irrig. Drain. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Rouse, H. Fluid Mechanics for Hydraulic Engineers; McGraw-Hill: New York, NY, USA, 1938; pp. 51–284. [Google Scholar]
- Serre, F. Contribution à l’étude des écoulements permanents et variables dans les canaux (Contribution to the study of permanent and nonpermanent flows in channels). La Houille Blanche 1953, 8, 374–388. (In French) [Google Scholar] [CrossRef]
- Yuan, S.W. Foundations of Fluid Mechanics; Prince Hall International, Inc.: Eaglewood Cliffs, NJ, USA, 1988; p. 149. [Google Scholar]
- White, F.M. Fluid Mechanics, 7th ed.; McGraw-Hill: New York, NY, USA, 2011; p. 280. [Google Scholar]
- Chaudhry, M.H. Open Channel Flow, 2nd ed.; Springer and Media Science LLC: New York, NY, USA, 2008; pp. 18–37. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 10th ed.; Wiley: New York, NY, USA, 1972; p. 877. [Google Scholar]
- Khan, A. Modelling Rapidly-varied Open Channel Flows. Ph.D. Thesis, Department of Civil Engineering, University of Alberta, Edmonton, AB, Canada, 1995. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; pp. 32–33. [Google Scholar]
- Madadi, M.R.; Dalir, A.H.; Farsadizadeh, D. Investigation of flow characteristics above trapezoidal broad-crested weirs. Flow Meas. Instrum. 2014, 38, 139–148. [Google Scholar] [CrossRef]
- Rouse, H. The Distribution of Hydraulic Energy in Weir Flow in Relation to Spillway Design. Master’s Thesis, Massachusetts Institute of Technology, Boston, MA, USA, 1932. [Google Scholar]
- Sivakumaran, N.S. Shallow Flow over Curved Beds. DEng Thesis, Asian Institute of Technology, Bangkok, Thailand, 1981. [Google Scholar]
- Bos, M.G. Discharge Measurement Structures, 3rd ed.; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1989; pp. 40–202. [Google Scholar]
- Ramamurthy, A.S.; Vo, N.D.; Vera, G. Momentum model of flow past a weir. J. Irrig. Drain. Eng. 1992, 118, 988–994. [Google Scholar] [CrossRef]
- Hager, W.H. Critical flow condition in open-channel hydraulics. Acta Mech. 1985, 54, 157–179. [Google Scholar] [CrossRef]
- Ramamurthy, A.S.; Vo, N.D. Application of Dressler theory to weir flow. J. Appl. Mech. 1993, 60, 163–166. [Google Scholar] [CrossRef]
- Vo, N.D. Characteristics of Curvilinear Flow past Circular-Crested Weirs. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 1992. [Google Scholar]
- Chanson, H.; Montes, J.S. Overflow Characteristics of Cylindrical Weirs; Research Report No. CE154; Department of Civil Engineering, University of Queensland: Brisbane, QLD, Australia, 1997. [Google Scholar]
- Schmocker, L.; Halldórsdóttir, B.R.; Hager, W.H. Effect of weir face angles on circular-crested weir flow. J. Hydraul. Eng. 2011, 137, 637–643. [Google Scholar] [CrossRef]
- Shayan, H.K.; Khezerloo, A.B.; Farhoudi, J.; Aminpoor, Y. A discussion to “Discharge coefficient of circular-crested weirs based on a combination of flow around a cylinder and circulation”. J. Irrig. Drain. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Ramamurthy, A.S.; Vo, N.D. Characteristics of circular-crested weir. J. Hydraul. Eng. 1993, 119, 1055–1062. [Google Scholar] [CrossRef]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zerihun, Y.T. A Non-Hydrostatic Depth-Averaged Model for Hydraulically Steep Free-Surface Flows. Fluids 2017, 2, 49. https://doi.org/10.3390/fluids2040049
Zerihun YT. A Non-Hydrostatic Depth-Averaged Model for Hydraulically Steep Free-Surface Flows. Fluids. 2017; 2(4):49. https://doi.org/10.3390/fluids2040049
Chicago/Turabian StyleZerihun, Yebegaeshet T. 2017. "A Non-Hydrostatic Depth-Averaged Model for Hydraulically Steep Free-Surface Flows" Fluids 2, no. 4: 49. https://doi.org/10.3390/fluids2040049
APA StyleZerihun, Y. T. (2017). A Non-Hydrostatic Depth-Averaged Model for Hydraulically Steep Free-Surface Flows. Fluids, 2(4), 49. https://doi.org/10.3390/fluids2040049



