Convective Flow in an Aquifer Layer
Abstract
1. Introduction
2. Governing Systems and Solutions
2.1. Basic State Solutions
2.2. Linear Problem (Order and )
2.2.1. Zeroth Order
2.2.2. Order of
3. Nonlinear Problem
3.1. Order of
3.2. Order of
4. Results
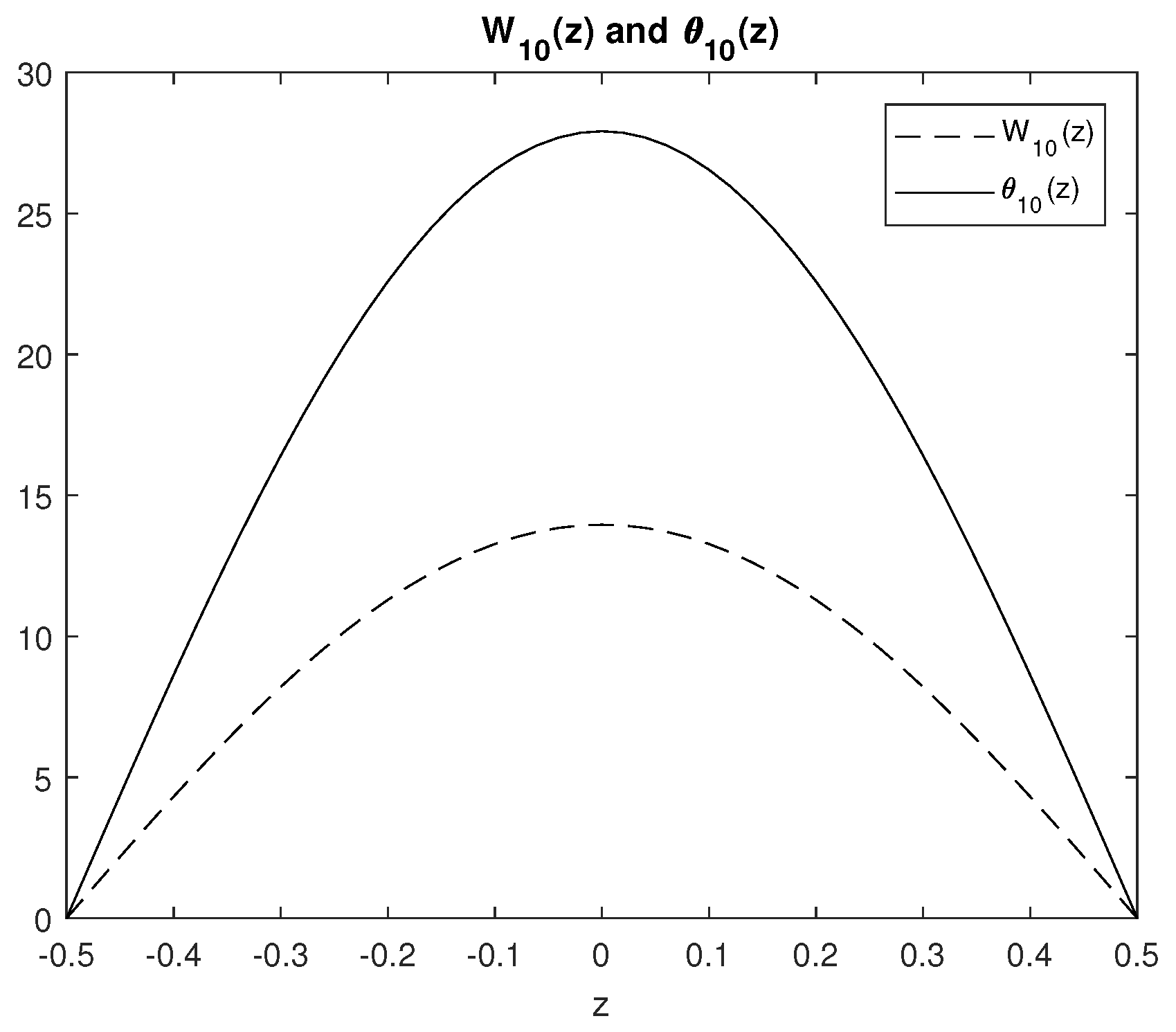
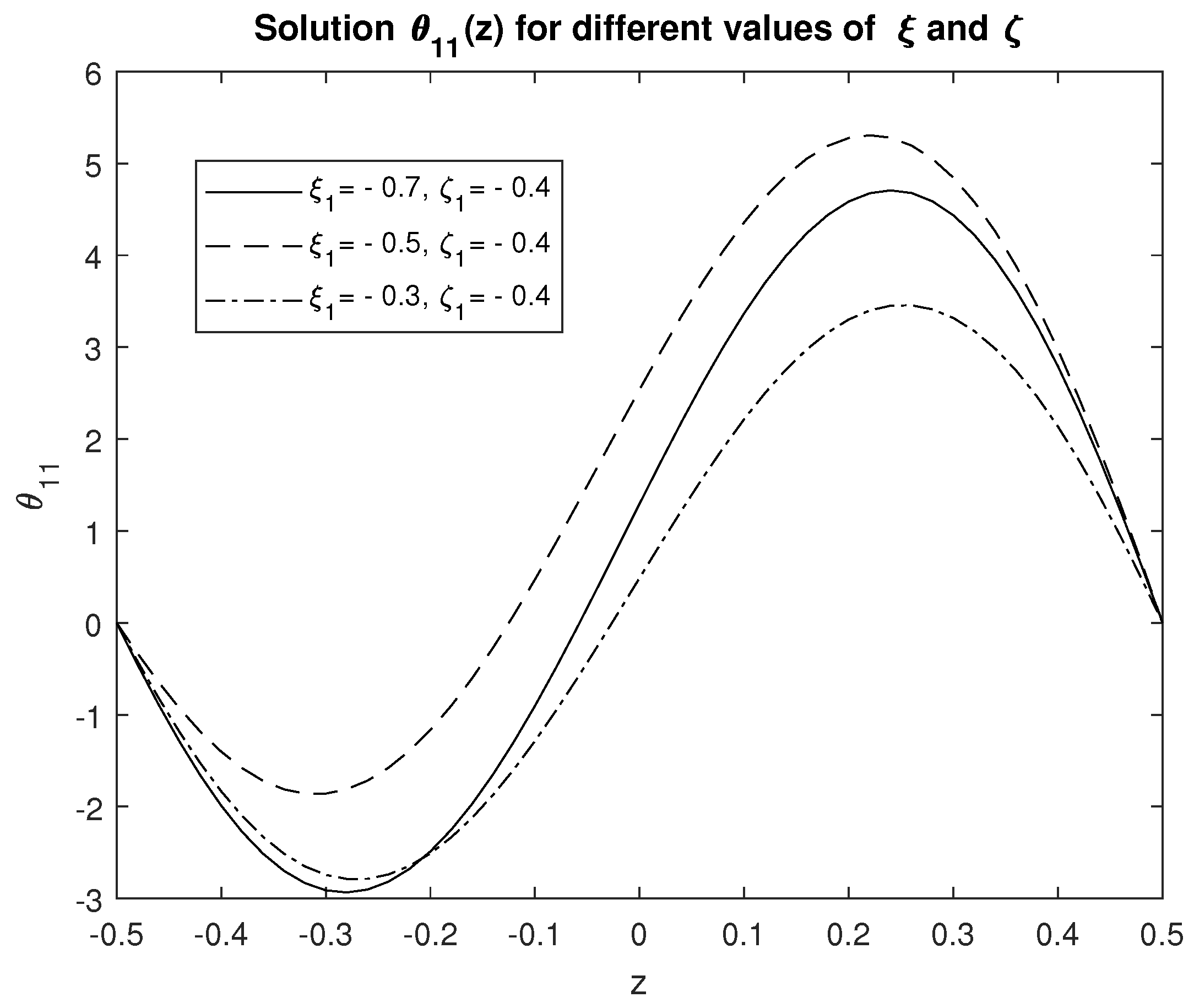
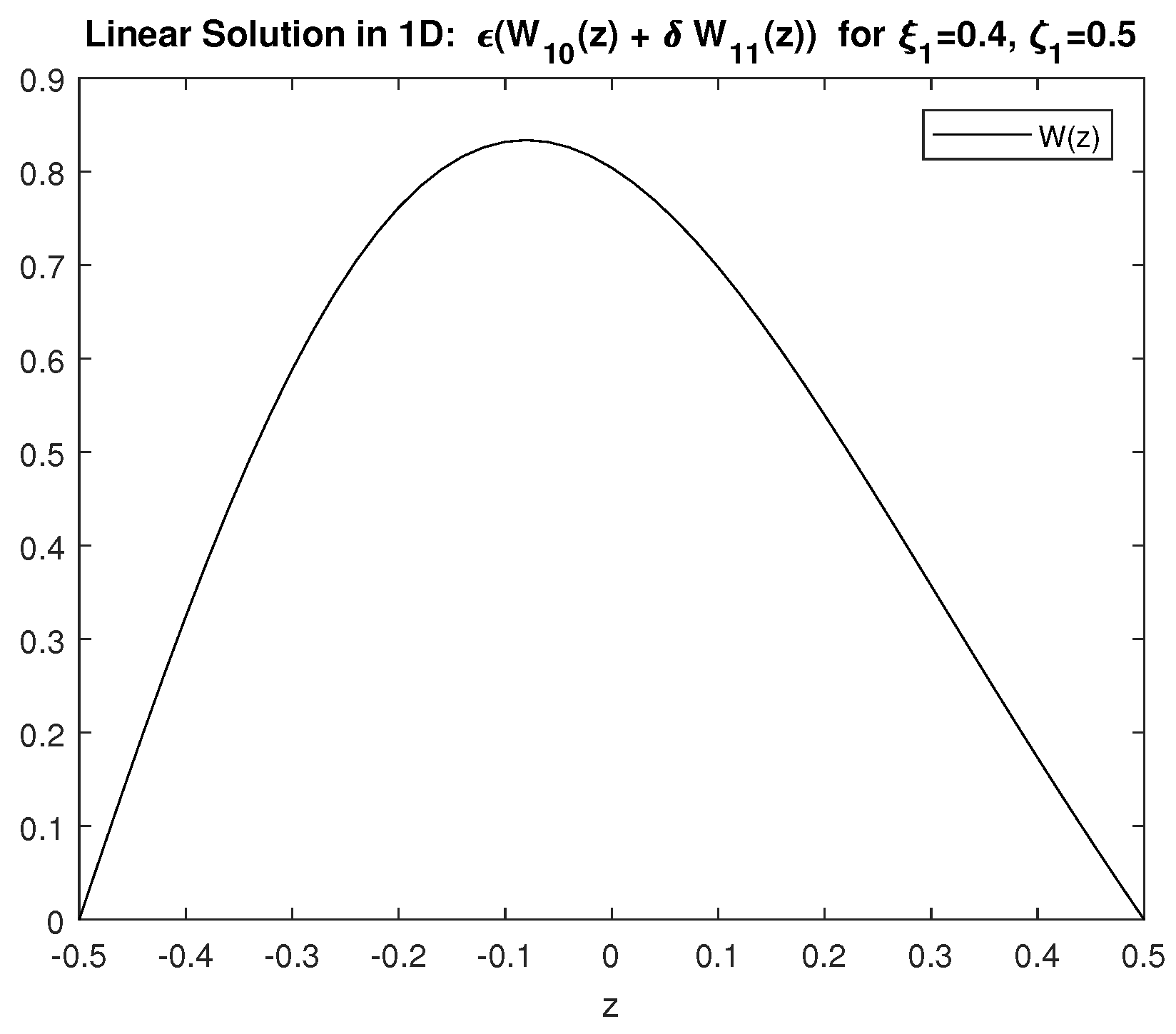
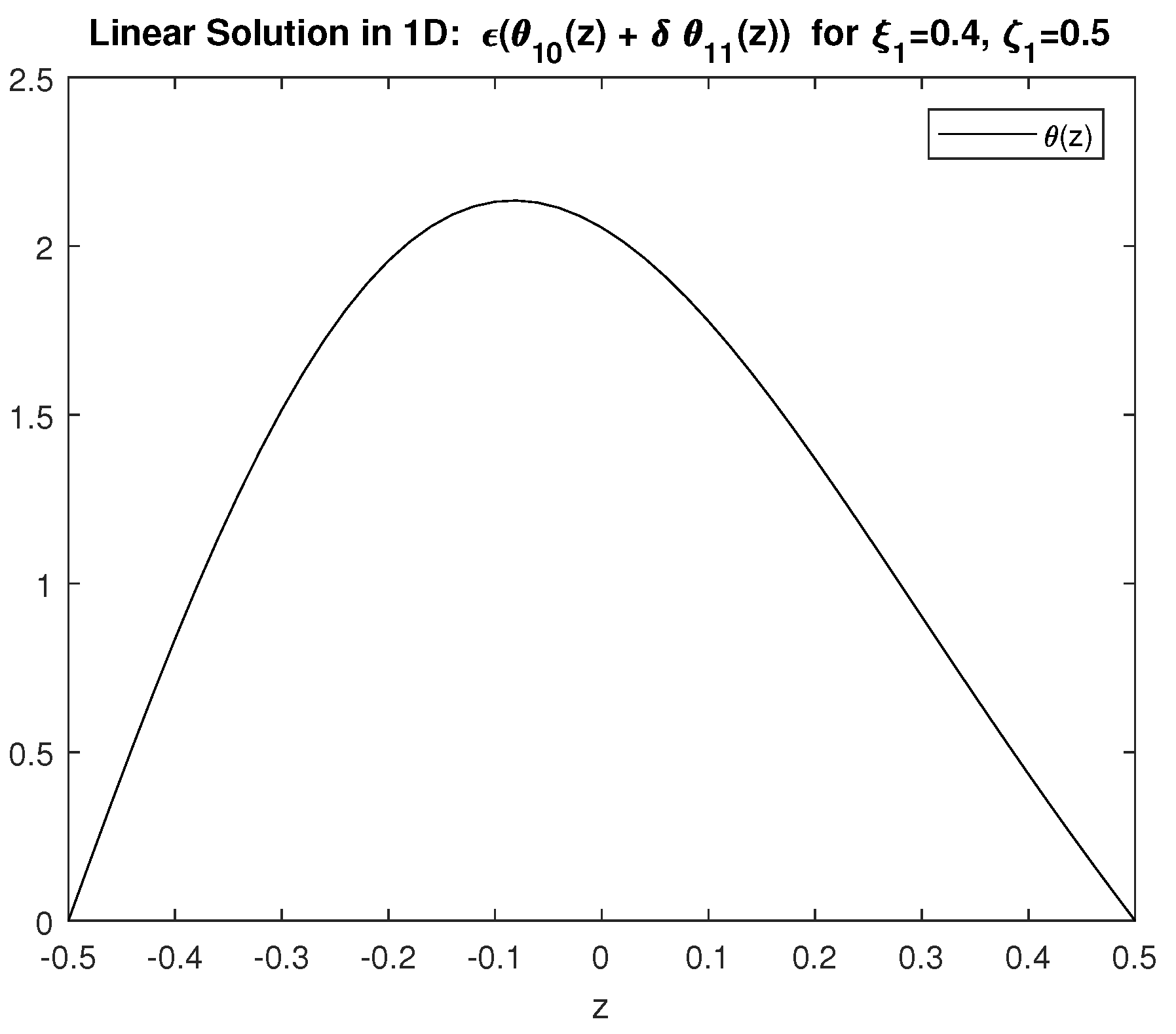
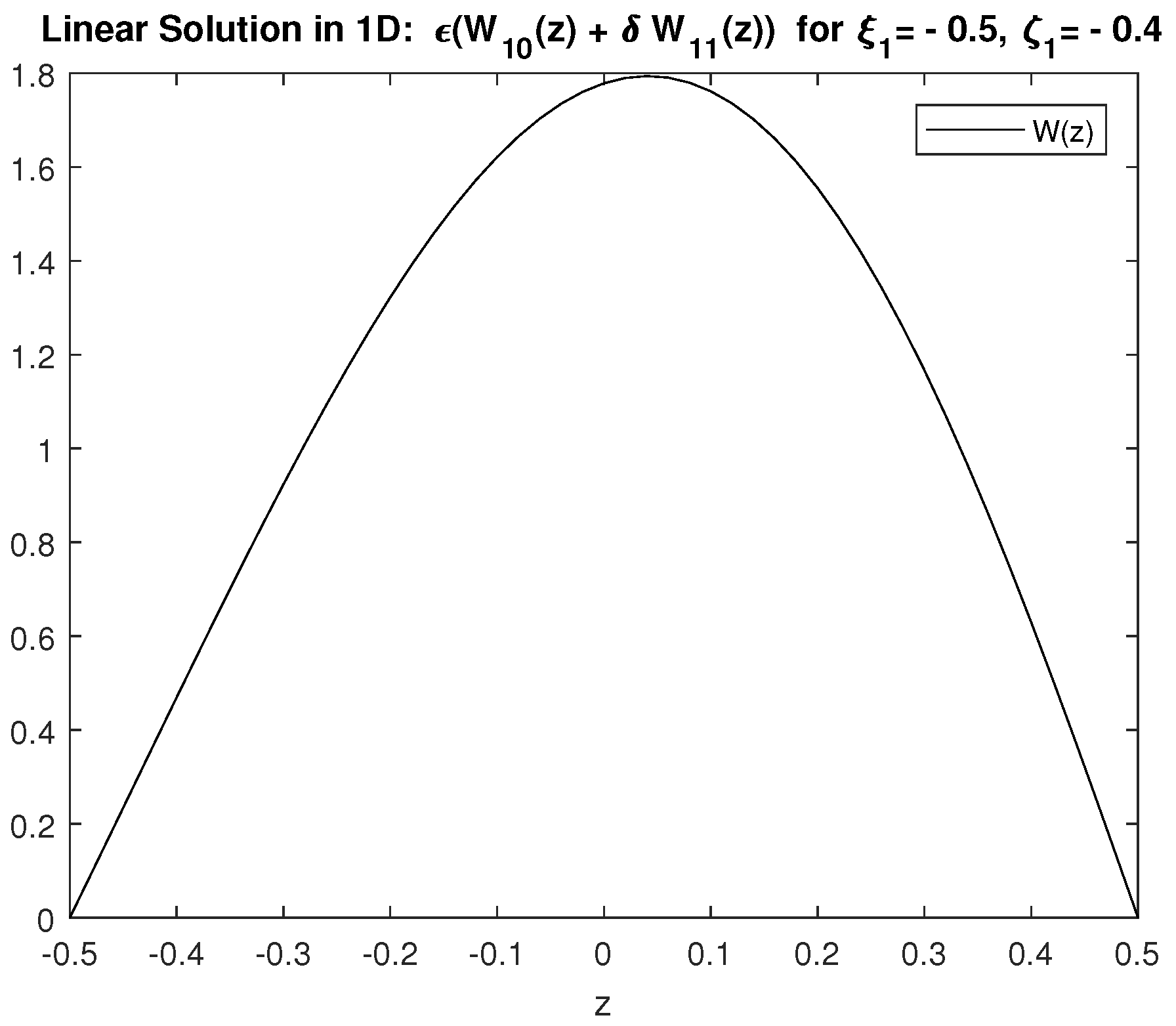
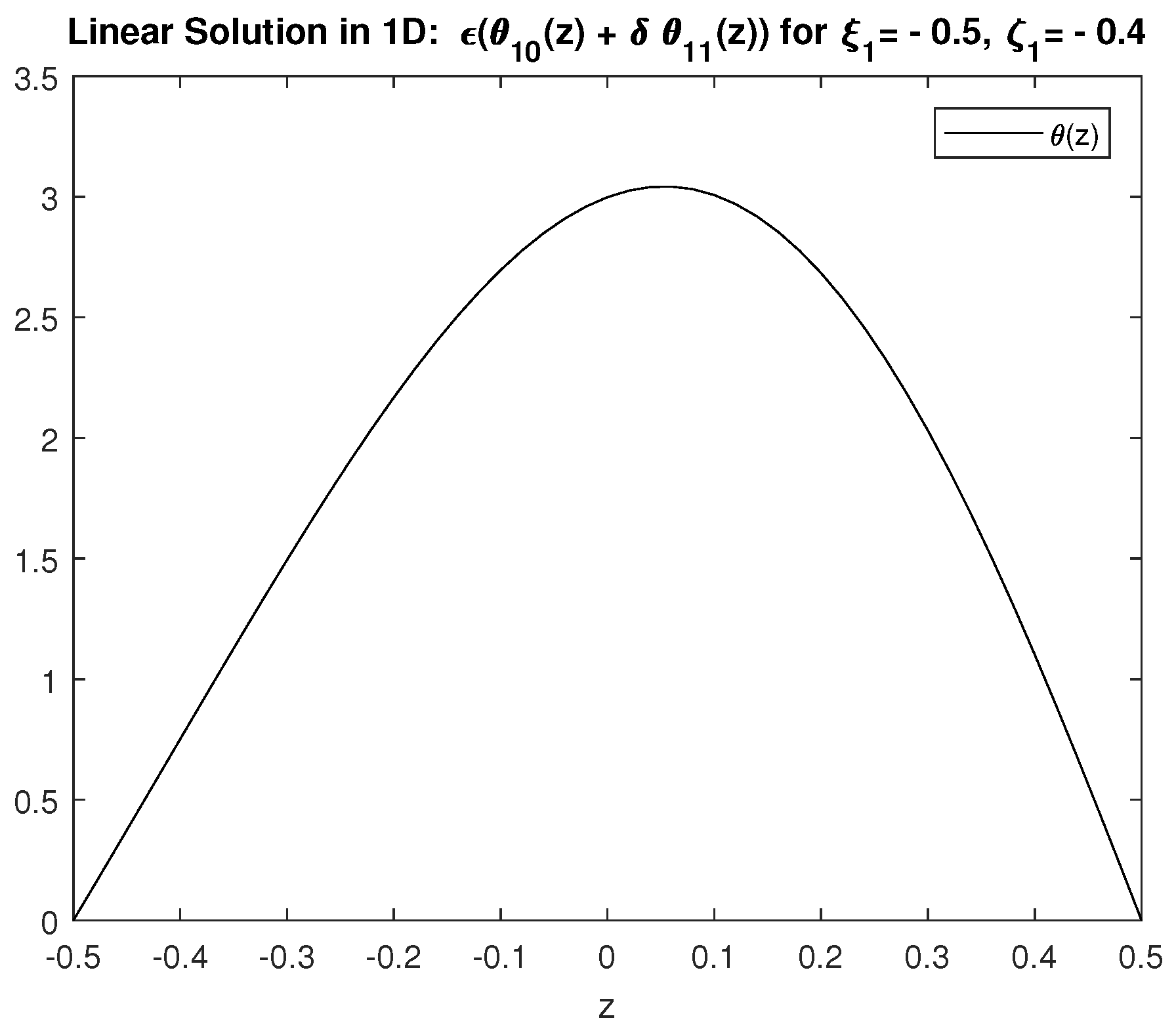
4.1. One-Dimensional Results for the Vertical Dependence of Linear Solutions:
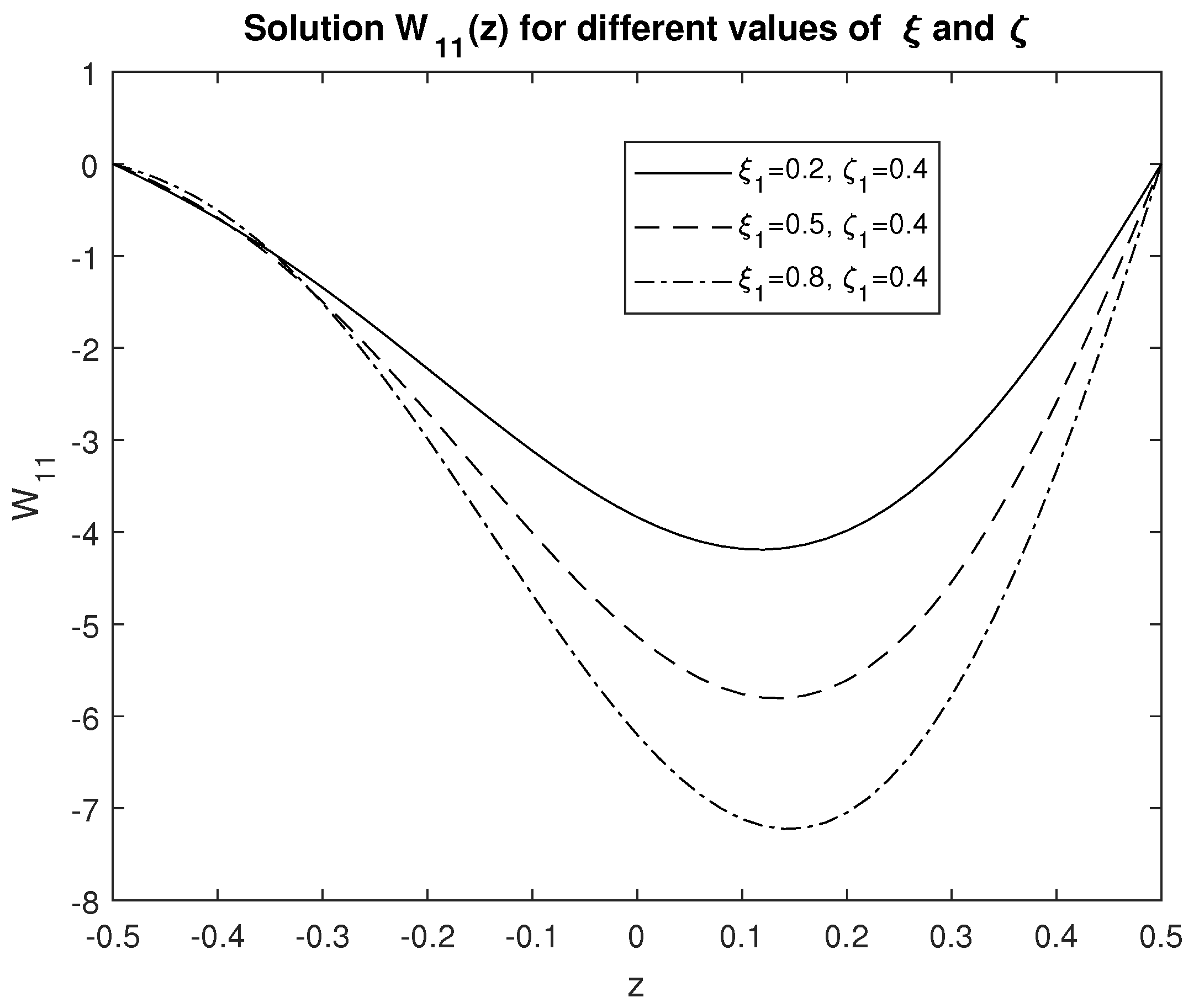
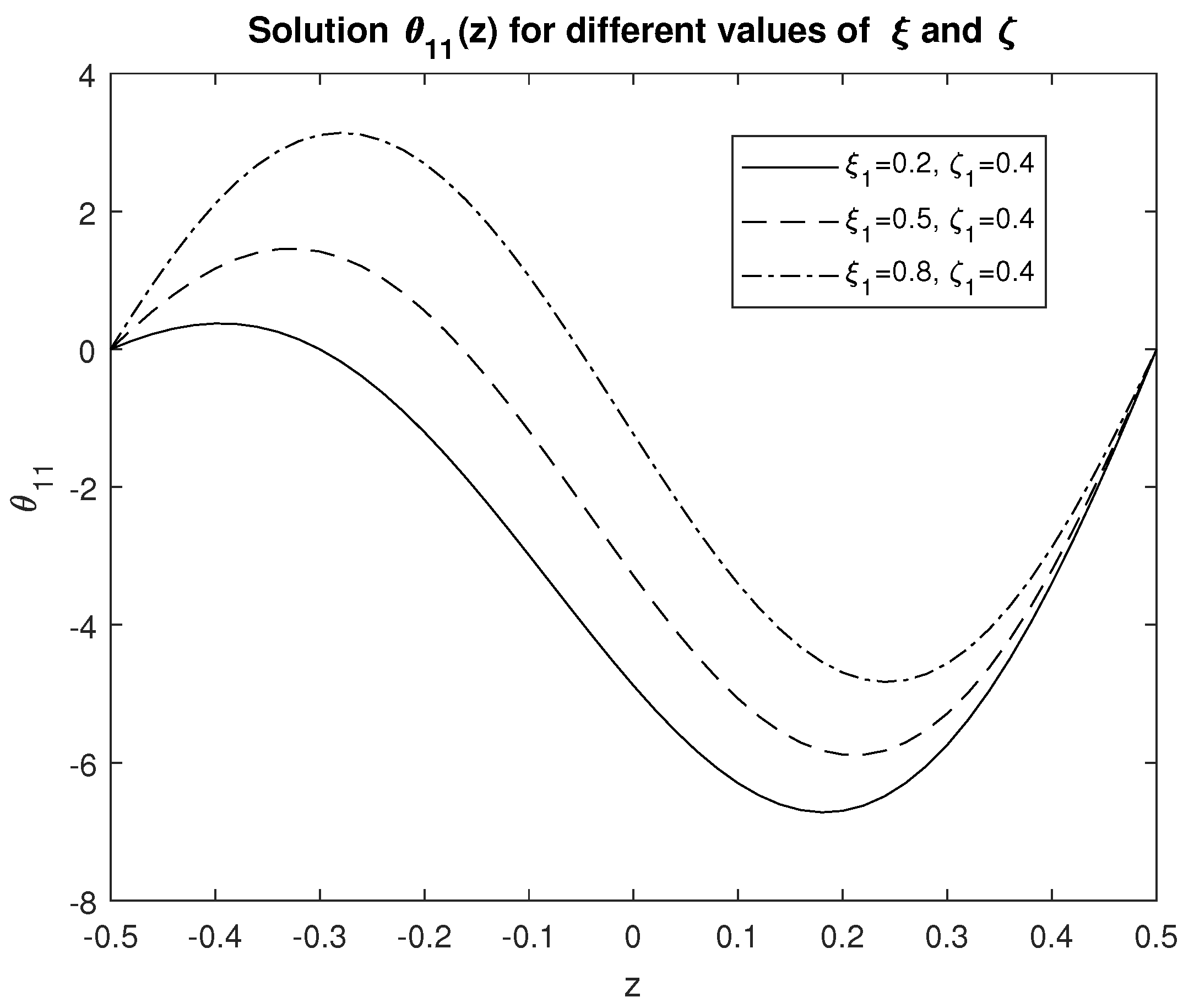
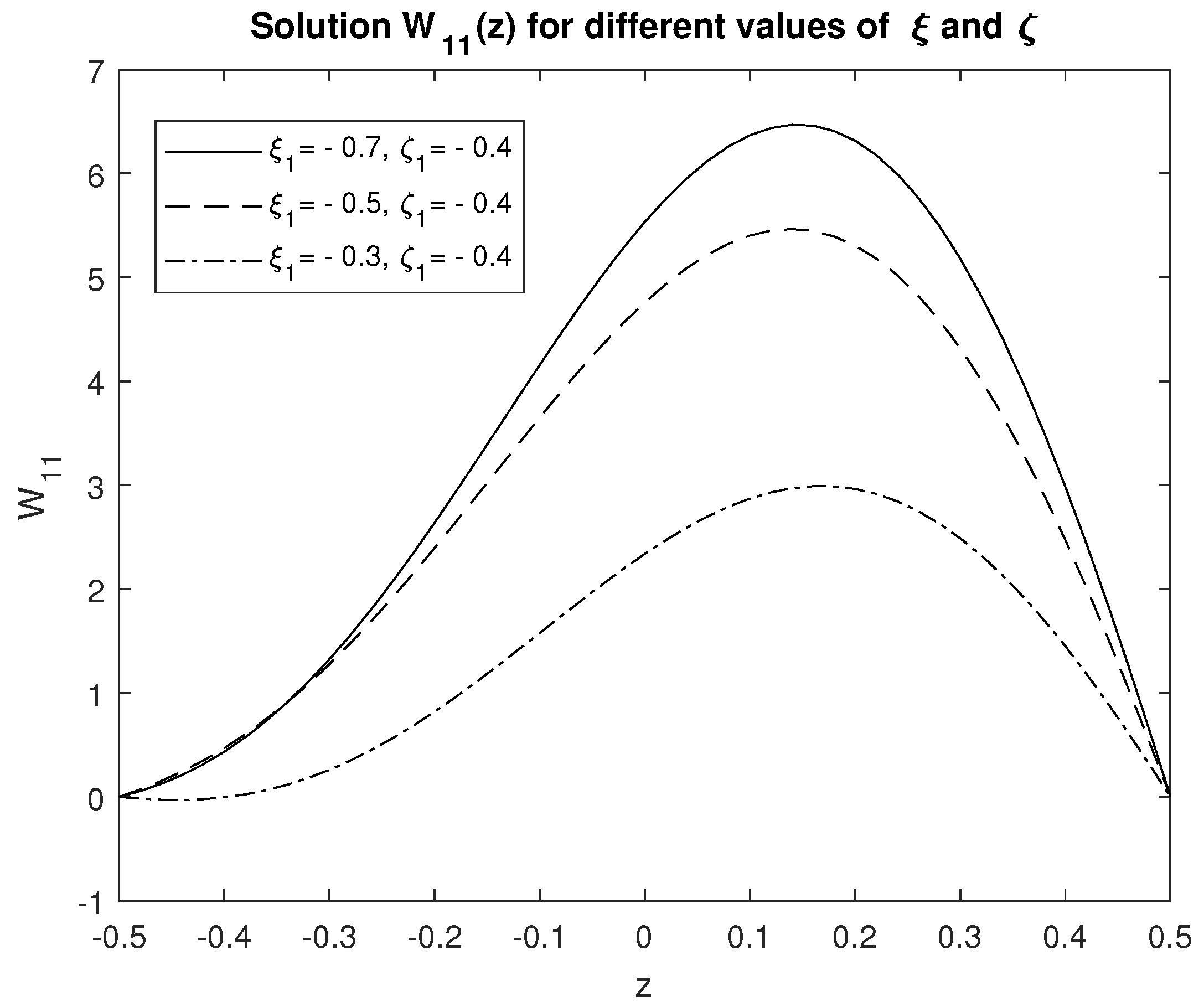
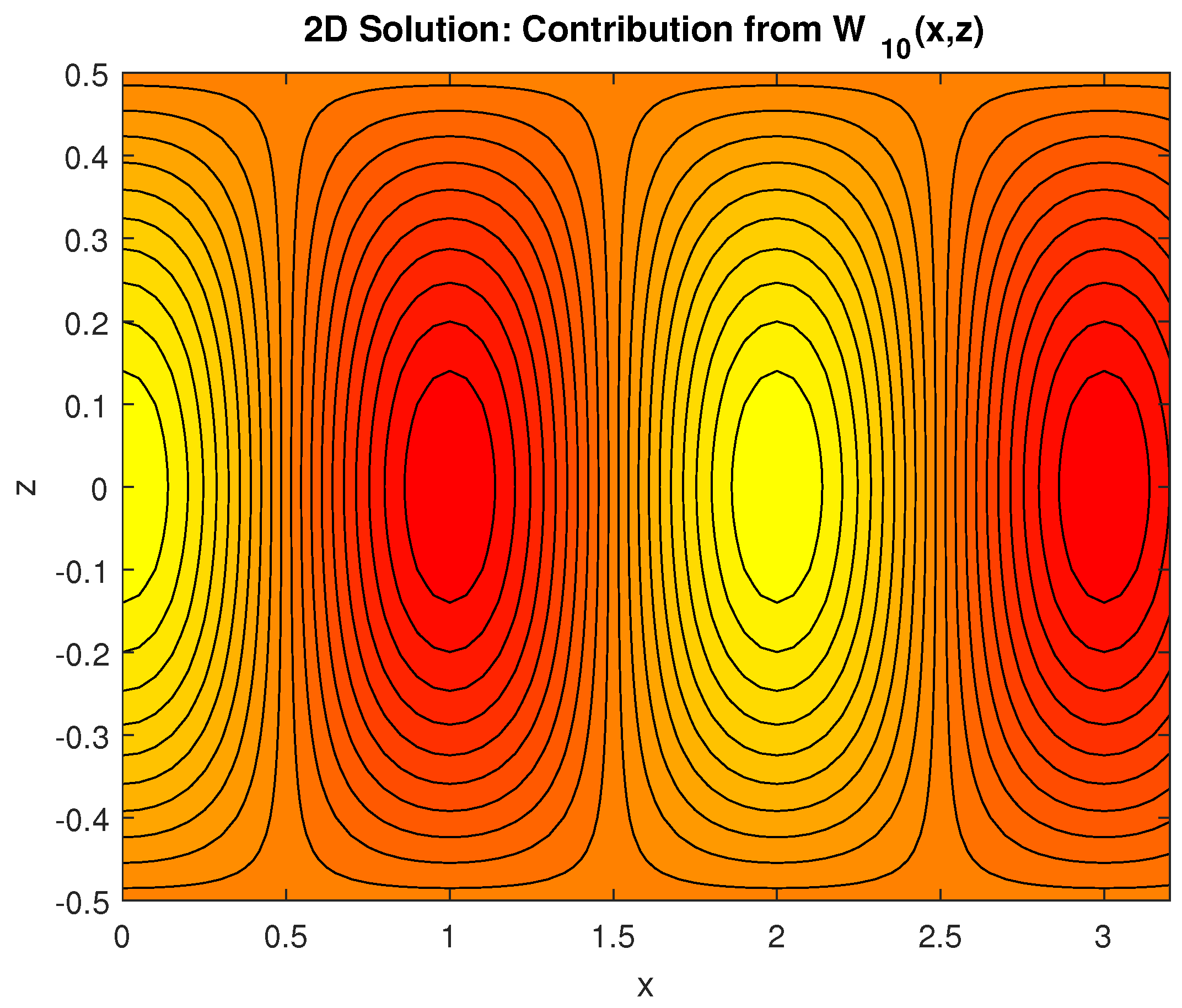
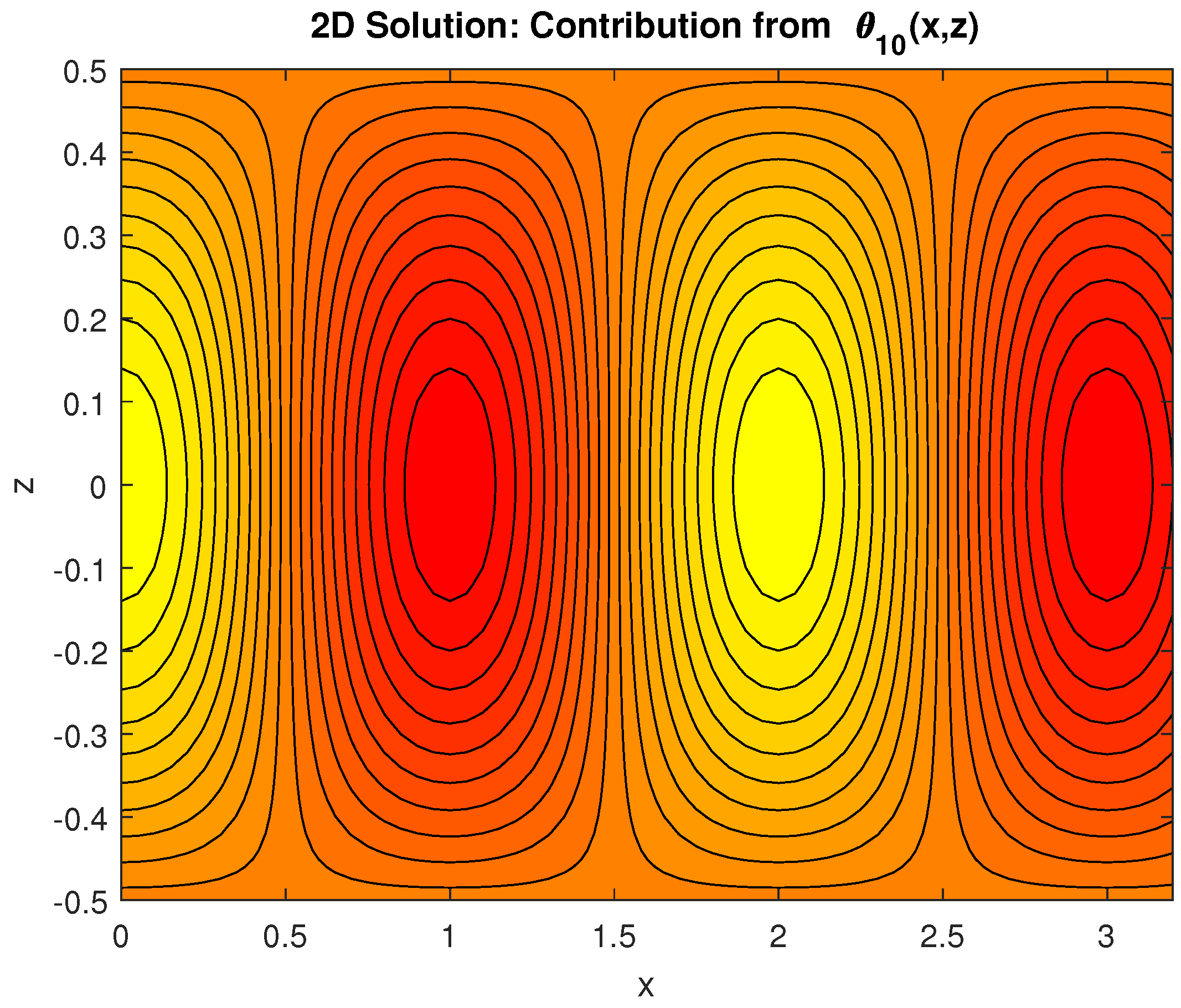
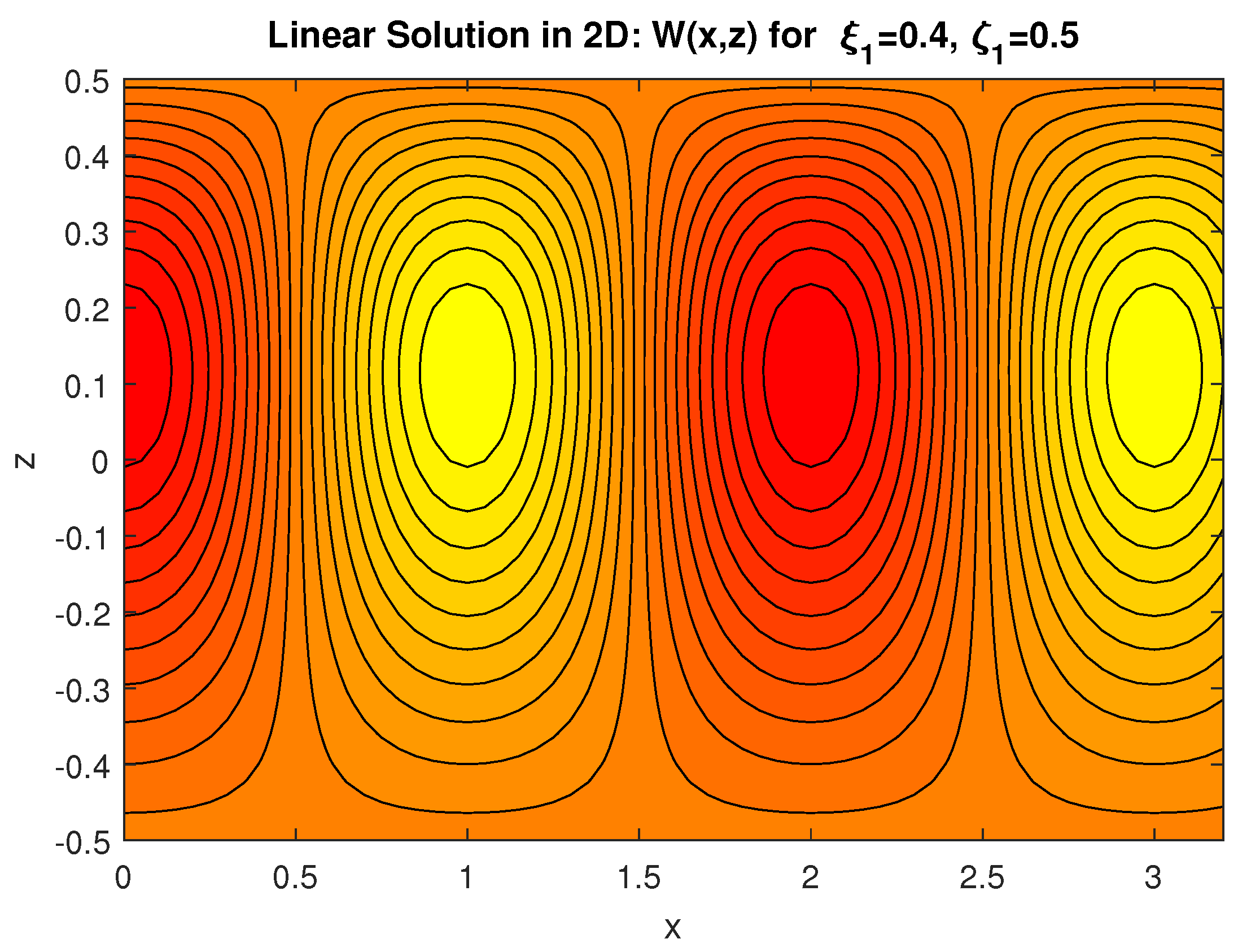
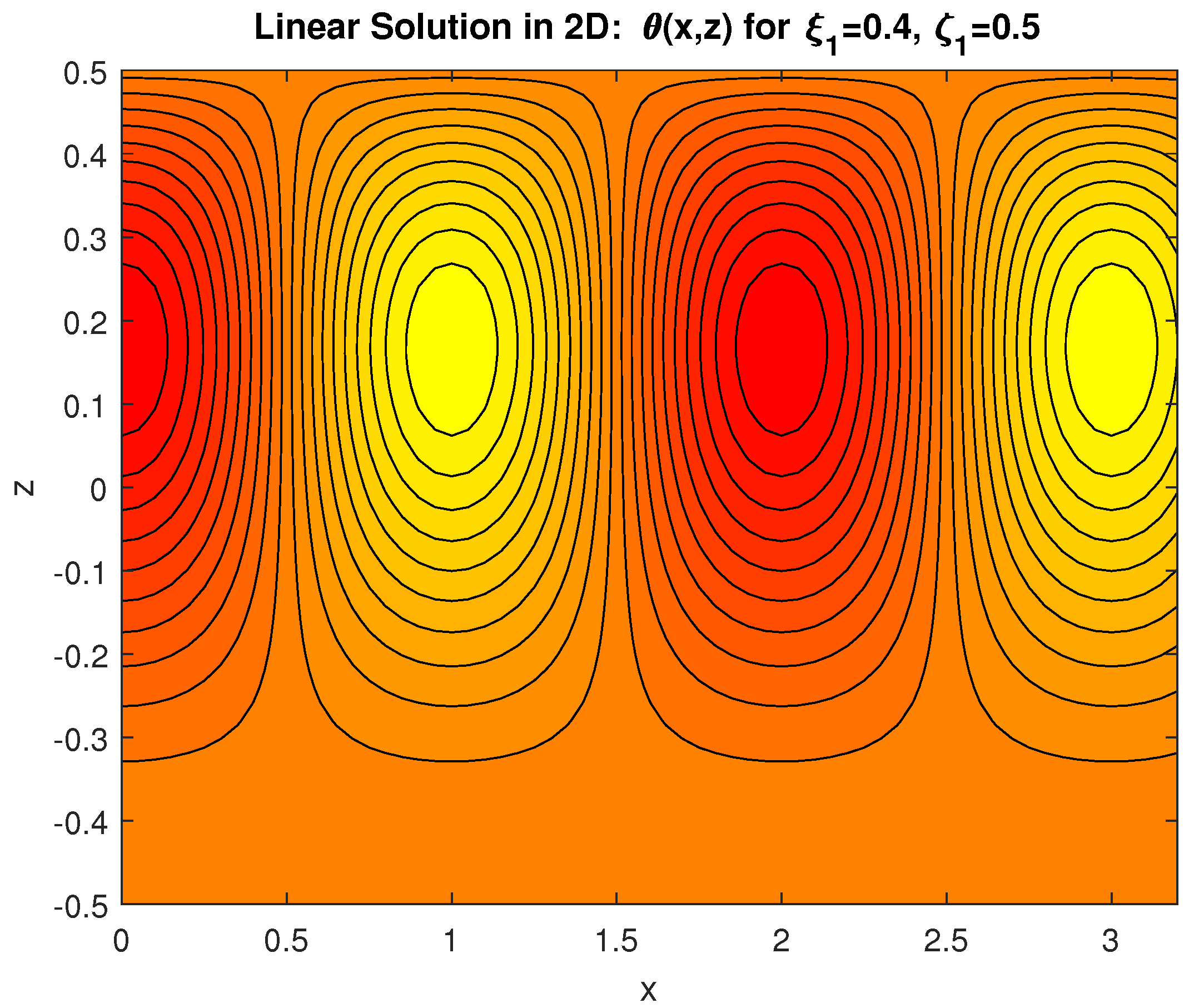
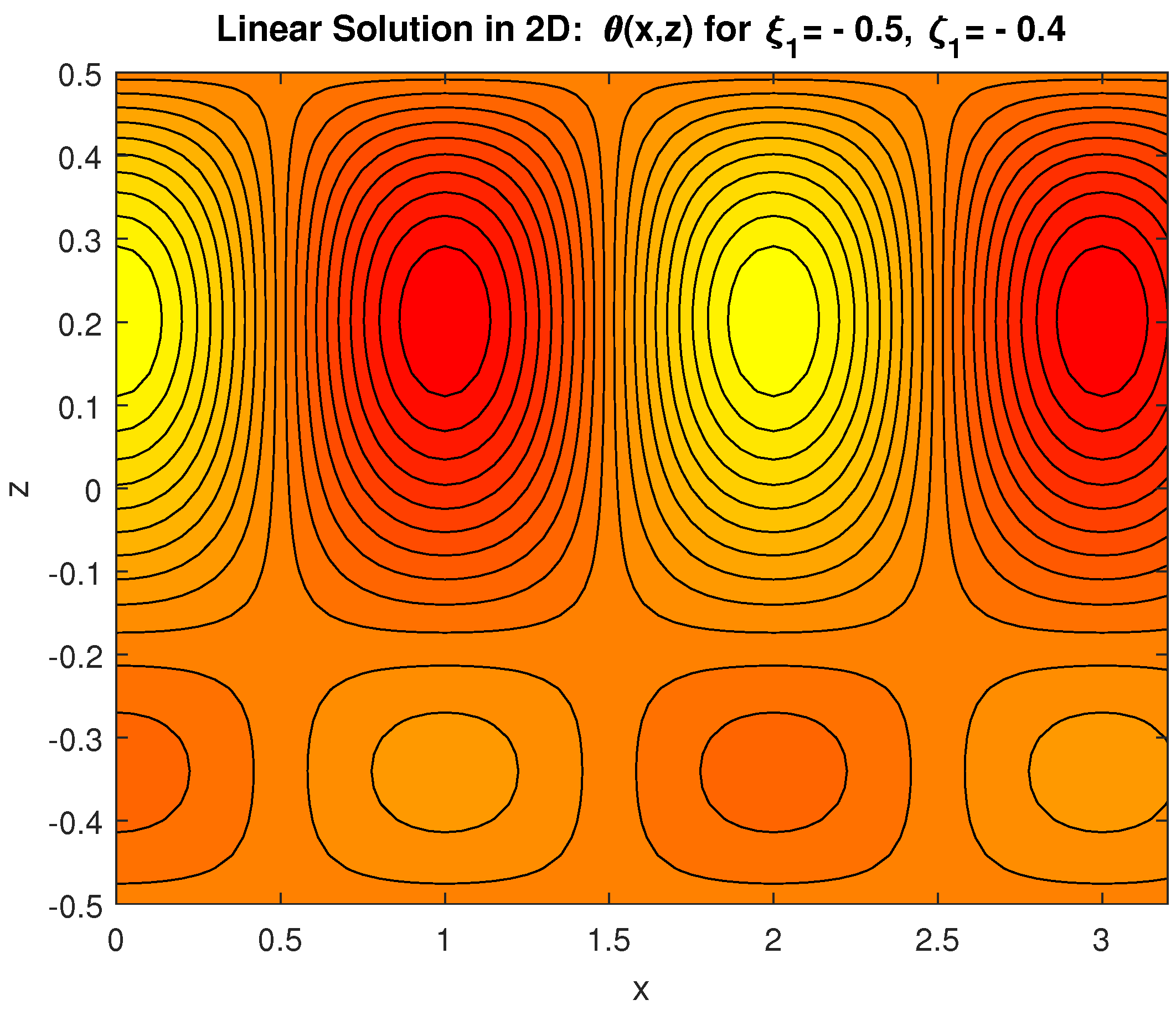
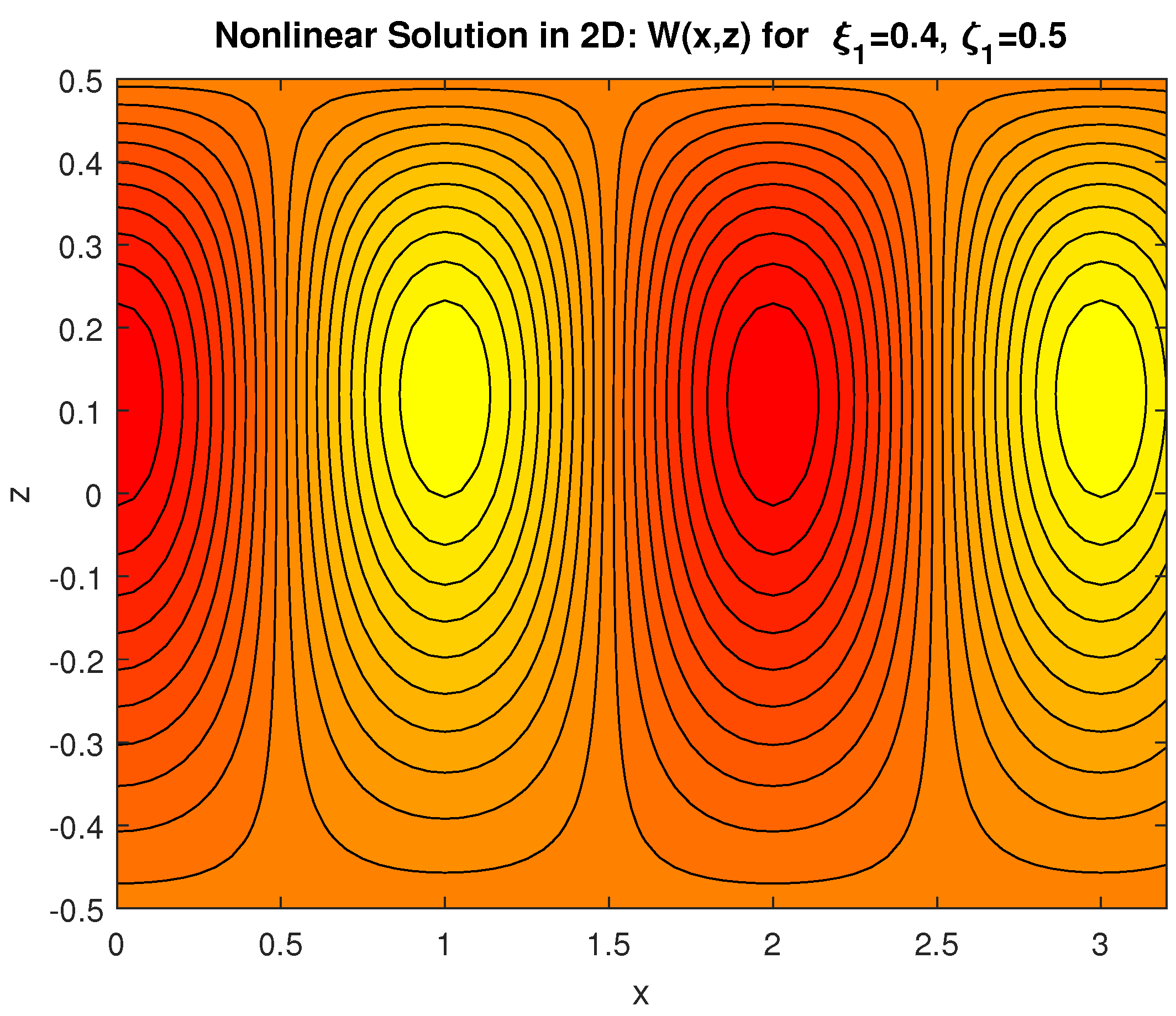
4.2. Two-Dimensional Results for
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rubin, H. A note on the heat dispersion effect on thermal convection in a porous media. J. Hydrol. 1975, 25, 167–168. [Google Scholar] [CrossRef]
- Rubin, H. Seminumerical simulation of singly dispersive convection in ground water. J. Hydrol. 1979, 40, 265–281. [Google Scholar] [CrossRef]
- Rubin, H. Thermal convection in a nonhomogeneous aquifer. J. Hydrol. 1981, 50, 317–331. [Google Scholar] [CrossRef]
- Riahi, D.N. Nonlinear convection in a porous layer with finite conducting boundaries. J. Fluid Mech. 1983, 129, 153–171. [Google Scholar] [CrossRef]
- Vafai, K. Convective flow and heat transfer in variable-porosity media. J. Fluid Mech. 1984, 147, 233–259. [Google Scholar] [CrossRef]
- Riahi, D.N. Preferred pattern of convection in a porous layer with a spatially non-uniform boundary temperature. J. Fluid Mech. 1993, 246, 529–543. [Google Scholar] [CrossRef]
- Riahi, D.N. Modal package convection in a porous layer with boundary imperfections. J. Fluid Mech. 1996, 318, 107–128. [Google Scholar] [CrossRef]
- Fowler, A.C. Mathematical Models in the Applied Sciences; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Bejan, A.; Khair, K.R. Heat and mass transfer by natural convection in a porous medium. Int. J. Heat Mass Transf. 1985, 28, 909–918. [Google Scholar] [CrossRef]
- Bejan, A.; Nield, D.A. Transient forced convection near a suddenly heated plate in a porous medium. Int. Comm. Heat Mass Transf. 1991, 18, 83–91. [Google Scholar] [CrossRef]
- Balasubramanium, R.; Thangaraj, R.P. Thermal convection in fluid layer sandwiched between two porous layers of different permeabilities. Acta Mech. 1998, 130, 81–93. [Google Scholar] [CrossRef]
- Nield, D.A. Convection in a porous medium with inclined temperature gradient. Int. J. Heat Mass Transf. 2000, 34, 87–92. [Google Scholar] [CrossRef]
- Nield, D.A. Some pitfall in the modelling of convective flows in porous media. Transp. Porous Media 2001, 43, 597–601. [Google Scholar] [CrossRef]
- Rees, D.A.S. The onset of Darcy-Brinkman convection in a porous layer : an aysmptotic analysis. Int. J. Heat Mass Transf. 2002, 45, 2213–2220. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in a Porous Media, 4th ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Rees, D.A.S.; Pop, I. Vertical free convection in a porous medium with variable permeability effects. Int. J. Heat Mass Transf. 2000, 43, 2565–2571. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Tyvand, P.A. The Helmholtz equation for convection in two-dimensional porous cavities with conducting boundaries. J. Eng. Math. 2004, 49, 181–193. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Barletta, A. Linear instability of the isoflux Darcy-Benard problem in an inclined porous layer. Transp. Porous Media 2011, 87, 665–678. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Riley, D.S. The three-dimensional stability of finite-amplitude convection in a layered porous medium heated from below. J. Fluid Mech. 1990, 211, 437–461. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Tyvand, P.A. Onset of convection in a porous layer with continuous peridic horizontal stratification. Part I. Two-dimensional convection. Transp. Porous Media 2009, 77, 187–205. [Google Scholar] [CrossRef]
- Bhatta, D.; Muddamallappa, M.S.; Riahi, D.N. On perturbation and marginal stability analysis of magneto-convection in active mushy layer. Transp. Porous Media 2010, 82, 385–399. [Google Scholar] [CrossRef]
- Bhatta, D.; Riahi, D.N.; Muddamallappa, M.S. On nonlinear evolution of convective flow in an active mushy layer. J. Eng. Math. 2012, 82, 385–399. [Google Scholar] [CrossRef]
- Bhatta, D.; Muddamallappa, M.S.; Riahi, D.N. Magnetic and permeability effects on a weakly nonlinear magneto-convective flow in active mushy layer. Int. J. Fluid Mech. Res. 2012, 39, 494–520. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Barletta, A. Onset of convection in a porous layer with continuous peridic horizontal stratification. Part II. Three-dimensional convection. Eur. J. Mech. B Fluids 2014, 47, 57–67. [Google Scholar] [CrossRef]
- Anderson, D.M.; Worster, M.G. Weakly nonlinear analysis of convection in mushy layers during the solidification of binary alloy. J. Fluid Mech. 1995, 302, 307–331. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatta, D.; Riahi, D. Convective Flow in an Aquifer Layer. Fluids 2017, 2, 52. https://doi.org/10.3390/fluids2040052
Bhatta D, Riahi D. Convective Flow in an Aquifer Layer. Fluids. 2017; 2(4):52. https://doi.org/10.3390/fluids2040052
Chicago/Turabian StyleBhatta, Dambaru, and Daniel Riahi. 2017. "Convective Flow in an Aquifer Layer" Fluids 2, no. 4: 52. https://doi.org/10.3390/fluids2040052
APA StyleBhatta, D., & Riahi, D. (2017). Convective Flow in an Aquifer Layer. Fluids, 2(4), 52. https://doi.org/10.3390/fluids2040052



