Anisotropic Wave Turbulence for Reduced Hydrodynamics with Rotationally Constrained Slow Inertial Waves

Abstract

Kinetic equations for rapidly rotating flows are developed in this paper using multiple scales perturbation theory. The governing equations are an asymptotically reduced set of equations that are derived from the incompressible Navier-Stokes equations. These equations are applicable for rapidly rotating flow regimes and are best suited to describe anisotropic dynamics of rotating flows. The independent variables of these equations inherently reside in a helical wave basis that is the most suitable basis for inertial waves. A coupled system of equations for the two global invariants: energy and helicity, is derived by extending a simpler symmetrical system to the more general non-symmetrical helical case. This approach of deriving the kinetic equations for helicity follows naturally by exploiting the symmetries in the system and is different from the derivations presented in an earlier weak wave turbulence approach that uses multiple correlation functions to account for the asymmetry due to helicity. Stationary solutions, including Kolmogorov solutions, for the flow invariants are obtained as a scaling law of the anisotropic wave numbers. The scaling law solutions compare affirmatively with results from recent experimental and simulation data. Thus, anisotropic wave turbulence of the reduced hydrodynamic system is a weak turbulence model for strong anisotropy with a dominant ${\mathbf{k}}_{\perp }$ cascade where the waves aid the turbulent cascade along the perpendicular modes. The waves also enable an appropriate closure of the kinetic equation through averaging of their phases.

1. Introduction

The theory of weak wave dynamics (i.e., the stochastic theory of nonlinear wave interactions) has been extensively studied since the seminal works of Kadomstev [1], Galeev et al. [2], Zakharov and Filonenko [3] and more recently reviewed by Zakharov [4], Balk [5], Choi et al. [6] and Nazarenko [7]. This theory remains one of the few areas where a mathematical framework exists with predictive capabilities for studying the energetics and dynamics associated with fluid turbulence. In this regard, the theory of weak wave turbulence was further explored in recent papers [8,9,10,11] in the context of unstratified rotating turbulent flows. The theory utilizes the incompressible Euler equation for inviscid dynamics in an infinite space, in dimensionless form:

$$({\partial }_t+\mathbf{u}·\nabla )\mathbf{u}+\frac{1}{\mathcal{R}o}\widehat{\mathbf{z}}\times \mathbf{u}=-\frac{1}{\mathcal{R}o}\nabla p,\nabla ·\mathbf{u}=0.$$

(1)

Here $\mathbf{u}=(u,v,w)$ is the three-dimensional velocity field in the Cartesian geometry $\mathbf{x}=(x,y,z)$, p is the pressure field, and $\nabla =({\partial }_x,{\partial }_y,{\partial }_z)$ is the gradient operator. Equation (1) is characterized by system rotation $2\mathsf{\Omega }\widehat{\mathbf{z}}$ along with length, advective velocity, time and pressure scales denoted by $L,U,\frac{L}{U}$ and $2\mathsf{\Omega }LU$, respectively. The Rossby number $\mathcal{R}o=\frac{U}{2\mathsf{\Omega }L}$, describing the relative importance of nonlinear advection to the Coriolis acceleration force, is the sole non-dimensional parameter. Of particular interest is the regime $\mathcal{R}o\ll 1$ for rotationally constrained flows along with the concomitant viewpoint that the dynamics can be partitioned into fast inertial waves evolving on the rotational timescale of $\mathcal{O}({(2\mathsf{\Omega })}^{-1})$, and eddies evolving on the advection timescale of $\mathcal{O}(\frac{L}{U})$. In nondimensional units these timescales are denoted by $\mathcal{O}(\mathcal{R}o)$ and $\mathcal{O}(1)$ respectively. In the Cartesian coordinate system the linear inertial-wave dispersion relation, obtained from Equation (1) for Fourier plane waves with wavevector $\mathbf{k}=(k_x,k_y,k_z)$ and of the form $exp\left\{i(\mathbf{k}·\mathbf{x}-{\omega }_{\mathbf{k}}t)\right\}$, is given by

$${\omega }_{\mathbf{k}}=\pm \frac{1}{\mathcal{R}o}\frac{k_z}{\sqrt{k_x^2+k_y^2+k_z^2}}.$$

(2)

Slow dynamics, to leading order, are geostrophically balanced, i.e.,

$$\widehat{\mathbf{z}}\times \mathbf{u}\approx -\nabla p.$$

(3)

It follows ${\mathbf{u}}_{\perp }\approx {\nabla }^{\perp }p$, with ${\mathbf{u}}_{\perp }=(u,v,0)$ and ${\nabla }^{\perp }=(-{\partial }_y,{\partial }_x,0)$, such that pressure is now identified as the geostrophic streamfunction. On noting ${\nabla }_{\perp }=({\partial }_x,{\partial }_y,0)$ Equation (3) implies that geostrophic motions are horizontally non-divergent with ${\nabla }_{\perp }·{\mathbf{u}}_{\perp }\approx 0$. Moreover, such motions are columnar in nature due to the Taylor-Proudman constraint that enforces axial invariance, i.e., ${\partial }_z(\mathbf{u},p)\approx 0$ [12,13]. Recent work [14,15] has more precisely established this invariance as true provided $k_z\gg \mathcal{O}(\mathcal{R}o)$, thus providing an upper bound to the degree of spatial anisotropy, i.e., ${\partial }_z(\mathbf{u},p)=\mathcal{O}(\mathcal{R}o)$.

Underlying hypotheses for the theory of rotating wave turbulence are: (i) the separation of inertial and advective timescales, i.e., $\mathcal{R}o\ll 1$ and (ii) the non-interaction between geostrophically balanced and inertial waves dynamics [16]. A necessary criterion for this to occur in Equation (1) is $(|\mathbf{u}|,p)=o(\mathcal{R}{o}^{-1})$ which ensures that the nonlinear terms remain small compared to linear terms. It follows from this bound that wave amplitudes can be large outside the slow manifold. Within the $\mathcal{R}o\ll 1$ regime (slow manifold), laboratory experiments [17,18] and sufficiently spatially resolved simulations [11,19,20] have clearly demonstrated the tendency for the inertial wave spectra to evolve anisotropically towards a slow manifold associated with axially invariant geostrophic dynamics ($k_z=0$). Using wave turbulence theory on Equation (1), Galtier [8] predicts an anisotropic energy spectrum $E(k_{\perp },k_z)\sim k_{\perp }^{-5/2}{k}_z^{-1/2}$ and a helicity spectrum $H(k_{\perp },k_z)\sim k_{\perp }^{-3/2}{k}_z^{-1/2}$ contrary to predictions of a $k_{\perp }^{-2}$ solution for $E_{k_{\perp }}$ observed in simulations [21,22]. A critical concern for this discrepancy is that the uniformity of the asymptotic approach of the weak-wave turbulence theory is lost as the slow manifold is approached. Notably, as $k_z\to \mathcal{O}(\mathcal{R}o)$, it is found that inertial waves still exist within the slow manifold and are slow. Such slow waves are not accounted for in weak wave turbulence literature [8,9].

Spectral power laws for anisotropic wave turbulence in the limit of rapid rotation are obtained in this manuscript. Specifically, it is found that $e_{\mathbf{k}}\sim k_{\perp }^{-3}$ (equivalently, $E_{k_{\perp }}\sim k_{\perp }^{-2}$ and $H_{k_{\perp }}\sim k_{\perp }^{-1}$) and are in agreement with power law solutions obtained numerically and experimentally [17,21,22,23] (see Figure 1). These solutions pertain to the slow manifold and hence differ from the power laws for the isotropic flow regime [24] and those obtained by Galtier [8,9] for the flow state outside the slow manifold. A schematic picture of the various regimes of rotating turbulence is also provided in this paper along with the respective power law solutions for each regime. This will serve in broad understanding of rotating turbulent dynamics and specifically, undergird the importance of anisotropy in the slow manifold and its influence on spectral power law solutions. It is also demonstrated that there is, in principle, a simpler approach in obtaining the coupled energy-helicity kinetic equations using the method of Hamiltonian reduction [25] and symmetries than the more algebraically tedious correlation calculations in [8,9]. For clarity and for the sake of averting any confusion, it is important to note that the derivations of the kinetic equations presented here are not the same as the derivations in [8,9]. This point is further elaborated in Section 6.4 and Section 6.5.

2. Reduced-Rotating Hydro-Dynamic Equations, R-RHD

We apply a multi-scale perturbation method directly within the slow manifold to a recently derived set of asymptotically reduced equations for rotationally constrained flows [14,1526,27]. In what follows, we adopt the nomenclature reduced rotating hydrodynamic (R-RHD) for the reduced equations describing an unstratified, non-buoyant rotating fluid. We note that R-RHD capture a slow manifold that is more precisely identified as $k_z\sim \mathcal{O}(\mathcal{R}o)$ and contains not only geostrophic columnar eddies but also anisotropic inertial waves characterized by scales: $k_z/k_{\perp }\ll \mathcal{R}o\ll 1$. The amplitude of these slow waves evolve on slower advective timescale.

At the outset, for convenience to aid our investigation, we centrally locate some notations and definitions involving position vector $\mathbf{x}$ and wavenumber vector $\mathbf{k}$, in Appendix A.1. The detailed derivation of R-RHD is provided in [14,15]. To summarize, the asymptotic framework for Equation (1) is established by assuming the small expansion parameter $\mathcal{R}o$ and a multiple-scale expansion in the axial direction ${\partial }_z={\partial }_{\mathrm{z}}+\mathcal{R}o{\partial }_Z$ with the isotropic scale $\mathrm{z}=z\sim (x,y)$ and the anisotropic columnar length scale $Z=\mathcal{R}oz$. Fluid variables $\mathbf{v}={(\mathbf{u},p)}^T$, where T denotes tranpose, are now written as an asymptotic series in terms of the small parameter, $\mathcal{R}o$:

$$\mathbf{v}={\mathbf{v}}_{\mathbf{0}}+\mathcal{R}o{\mathbf{v}}_{\mathbf{1}}+\mathcal{R}{o}^2{\mathbf{v}}_{\mathbf{2}}+\mathcal{O}(\mathcal{R}{o}^3).$$

(4)

To leading order in Equation (1), we observe a point wise geostrophic balance: $\widehat{\mathbf{z}}\times {\mathbf{u}}_0=-\nabla p_0$. It follows that fluid motions are horizontally non-divergent, i.e., ${\nabla }_{\perp }·{\mathbf{u}}_{0\perp }=0$, with ${\mathbf{u}}_{0\perp }={\nabla }^{\perp }\psi$ where $p_0=\psi$ is the geostrophic stream function as in the classical theory of quasigeostrophy. The Taylor-Proudman constraint [28] associated with the geostrophic balance further requires vertical variations to be negligible on $\mathcal{O}(1)$ vertical scales, i.e., ${\partial }_{\mathrm{z}}{\mathbf{v}}_0\equiv 0$. Importantly, in compliance with the Taylor-Proudman constraint, the multiple scales approach permits variations of $\mathcal{O}(\mathcal{R}{o}^{-1})$ on the Z-scale [14,15]. Hereafter, in the following we set $k_z=\mathcal{R}o{k}_Z$.

At the next order in Equation (1), the requisite solvability conditions, ensuring non-secular behavior of ${\mathbf{v}}_{\mathbf{1}}$, lead to the R-RHD equations describing the evolution of unstratified slow geostrophically balanced motions:

$${\partial }_t\zeta +{\mathbf{u}}_{\perp }·{\nabla }_{\perp }\zeta ={\partial }_{Z}W,$$

(5)

$${\partial }_{t}W+{\mathbf{u}}_{\perp }·{\nabla }_{\perp }W=-{\partial }_Z\psi .$$

(6)

Here ${\mathbf{u}}_{\perp }={\nabla }^{\perp }\psi$, and $\zeta :={\nabla }_{\perp }^2\psi$ and W are the $\widehat{\mathbf{z}}$ components of the vorticity and velocity fields. Akin to classical quasigeostrophic theory, nonlinear vertical advection, $W{\partial }_Z$, is an asymptotically subdominant process and does not appear. However, unlike quasigeostrophic theory the velocity field is isotropic in magnitude with $|{\mathbf{u}}_{\perp }|\sim |W|$, hence the appearance of a prognostic equation for W. Physically, the R-RHD (5) and (6) state that unbalanced vertical pressure gradients drive vertical motions that are materially advected in the horizontal, in turn, vortical stretching due to vertical gradients in W produce vortical motions. The vertical velocity, W, also generates an ageostrophic velocity fleld, ${\mathbf{u}}_{\perp }^{ag}$, such that incompressibility, ${\nabla }_{\perp }·{\mathbf{u}}_{1\perp }^{ag}+{\partial }_{Z}W=0$, holds to $\mathcal{O}(\mathcal{R}o)$. The R-RHD remain valid provided $(|{\mathbf{u}}_{\perp }|,|W|)=o(\mathcal{R}{o}^{-1})$. Consistent with the Euler Equation (1), the R-RHD also conserve, in time, the volume-averaged (over a domain B) kinetic energy ${\mathcal{E}}_V$ and helicity ${\mathcal{H}}_V$:

$${\mathcal{E}}_V\equiv \frac{1}{Vol(B)}\int \mathbf{u}·\mathbf{u}dV=\frac{1}{Vol(B)}\frac{1}{2}\int \left(|{\nabla }_{\perp }{\psi |}^2+W^2\right)dV,$$

(7)

$${\mathcal{H}}_V\equiv \frac{1}{Vol(B)}\int \mathbf{u}·\nabla \times \mathbf{u}dV=2\frac{1}{Vol(B)}\int \left(W\zeta \right)dV.$$

(8)

In what follows, an investigation of wave turbulence will be applied to the R-RHD.

2.1. Geostrophic Inertial Waves and Eddies

We observe that upon linearization, the R-RHD support slow geostrophically balanced inertial waves of the form,

$$\begin{array}{c}\hfill {\widehat{\mathsf{\Psi }}}_{\mathbf{k}}^{s_k}{e}^{i\mathsf{\Phi }(\mathbf{k},s_k{\omega }_{\mathbf{k}})},{\omega }_{\mathbf{k}}=\frac{k_Z}{k_{\perp }}{\omega }_1\end{array}$$

(9)

with planar phase function $\mathsf{\Phi }(\mathbf{k},s_k{\omega }_{\mathbf{k}})=({\mathbf{k}}_{\perp }·{\mathbf{x}}_{\perp }+k_{Z}Z-s_k{\omega }_{\mathbf{k}}t)=({\mathbf{k}}^{\perp }·{\mathbf{x}}^{\perp }+k_{Z}Z-s_k{\omega }_{\mathbf{k}}t)$, ${\omega }_1\sim \mathcal{O}(1)$ with dimension of $\frac{1}{T}$ and can be set to 1 without loss of generality. More explicitly, the phase function can be split into two terms: $e^{i\mathsf{\Phi }(\mathbf{k},s_k{\omega }_{\mathbf{k}})}=e^{-i{s}_k{\omega }_{\mathbf{k}}t}{e}^{i({\mathbf{k}}^{\perp }·{\mathbf{x}}^{\perp }+k_{Z}Z)}$, the temporal phase factor and the spatial Fourier basis. The region of validity of R-RHD is $k_Z\le k_{\perp }$, of special interest is the limit $k_Z\ll k_{\perp }$. When $k_Z=0$ this expression represents vertically invariant modes with ${\omega }_k=0$ (i.e., the 2D modes of turbulent eddies). The circularly polarized wave amplitude vector is

$${\widehat{\mathsf{\Psi }}}_{\mathbf{k}}^{s_k}{e}^{-i{s}_k{\omega }_{\mathbf{k}}t}\equiv \left(\begin{array}{c}{\widehat{\psi }}_{\mathbf{k}}^{s_k}\\ {\widehat{W}}_{\mathbf{k}}^{s_k}\end{array}\right)e^{-i{s}_k{\omega }_{\mathbf{k}}t}=\left(\begin{array}{c}{s}_k/k_{\perp }\\ 1\end{array}\right){\widehat{C}}_{\mathbf{k}}^{s_k},$$

(10)

where $s_k=\pm$ denotes the handedness, ‘+’ for right-handed circularly polarized waves (with positive helicity) and ‘−’ for left-handed circularly polarized waves (with negative helicity). Here, ${\widehat{C}}_{\mathbf{k}}^{s_k}$ is a complex amplitude function ${\widehat{C}}_{\mathbf{k}}^{s_k}={\widehat{c}}_{\mathbf{k}}^{s_k}{e}^{-i{\omega }_{\mathbf{k}}^{s_k}t}$ where ${\omega }_{\mathbf{k}}^{s_k}\equiv s_k{\omega }_{\mathbf{k}}$. The superscript ^{^} represents Fourier coefficients from the Fourier series expansion of a function. In subsequent sections, we invoke the infinite box limit ($L\to \infty$) and switch to Fourier transform variables thusly ${\widehat{c}}_{\mathbf{k}}\to {\left(\frac{L}{2\pi }\right)}^2{\widehat{c}}_{\mathbf{k}}\equiv c_{\mathbf{k}}$ and $\delta (0)={(\frac{L}{2\pi })}^2$ (see ch. 5 and 6 in [7]). The power 2 arises from the fact that the analysis is performed in 2D, i.e., $\mathbf{x}=({\mathbf{x}}_{\perp },\widehat{\mathbf{z}})$, unless otherwise specified.

2.2. Helical Basis for Circularly Polarized Inertial Waves

We note that in wavenumber space the unit vectors $({\widehat{\mathbf{k}}}^{\perp },\widehat{\mathbf{z}},{\widehat{\mathbf{k}}}_{\perp }^{\prime })$, with ${\widehat{\mathbf{k}}}_{\perp }^{\prime }={\mathbf{k}}_{\perp }^{\prime }/k_{\perp }$ and ${\widehat{\mathbf{k}}}^{\perp }={\mathbf{k}}^{\perp }/k_{\perp }$, form a right-handed orthogonal basis. Within the slow manifold, we have ${\widehat{\mathbf{k}}}_{\perp }^{\prime }\leftrightarrow {\widehat{\mathbf{k}}}^{\prime }$ as the direction of wave vector and henceforth we will simply call this vector $\mathbf{k}$ (see Figure 2). The leading order velocity field associated with an inertial wave is given by

$$\begin{array}{ccc}\hfill \mathbf{u}& =& {\mathbf{u}}_{\perp }+W\widehat{\mathbf{z}}\hfill \\ & =& {\nabla }^{\perp }\psi +W\widehat{\mathbf{z}}\hfill \\ & \stackrel{\mathrm{Fourier}\mathrm{modes}}{\to }& \left(i{k}_{\perp }{\widehat{\psi }}_{\mathbf{k}}^{s_k}{\widehat{\mathbf{k}}}^{\perp }+{\widehat{W}}_{\mathbf{k}}^{s_k}\widehat{\mathbf{z}}\right)e^{i\mathsf{\Phi }(\mathbf{k},s_k{\omega }_{\mathbf{k}})}+c.c.\hfill \\ & =& \left({\widehat{U}}_{\mathbf{k}}^{s_k}{\widehat{\mathbf{k}}}^{\perp }+{\widehat{W}}_{\mathbf{k}}^{s_k}\widehat{\mathbf{z}}\right)e^{i\mathsf{\Phi }(\mathbf{k},s_k{\omega }_{\mathbf{k}})}+c.c.\hfill \\ & =& {\widehat{c}}_{\mathbf{k}}^{s_k}{\mathbf{h}}_{\mathbf{k}}^{s_k}{e}^{i\mathsf{\Phi }(\mathbf{k},s_k{\omega }_{\mathbf{k}})}+c.c.\hfill \end{array}$$

(11)

where ${\widehat{U}}_{\mathbf{k}}^{s_k}:=i{k}_{\perp }{\widehat{\psi }}_{\mathbf{k}}^{s_k}$. From (10), ${\widehat{\mathbf{U}}}_{\mathbf{k}}^{s_k}:={({\widehat{U}}_{\mathbf{k}}^{s_k},{\widehat{W}}_{\mathbf{k}}^{s_k})}^T={\widehat{c}}_{\mathbf{k}}^{s_k}{(i{s}_k,1)}^T={\widehat{c}}_{\mathbf{k}}^{s_k}{\mathbf{h}}_{\mathbf{k}}^{s_k}$. Equivalently,

$${\mathbb{U}}_{\mathbf{k}}^{s_k}:={\widehat{\mathbf{U}}}_{\mathbf{k}}^{s_k}{e}^{-i{\omega }_{\mathbf{k}}^{s_k}t}={({\widehat{U}}_{\mathbf{k}}^{s_k},{\widehat{W}}_{\mathbf{k}}^{s_k})}^T{e}^{-i{\omega }_{\mathbf{k}}^{s_k}t}={({\widehat{\mathfrak{U}}}_{\mathbf{k}}^{s_k},{\widehat{\mathfrak{W}}}_{\mathbf{k}}^{s_k})}^T.$$

Here

$${\mathbf{h}}_{\mathbf{k}}^{s_k}:=i{s}_k{\widehat{\mathbf{k}}}^{\perp }+\widehat{\mathbf{z}}$$

(12)

represents the complex helical wave basis (see ref. [29] for details) within the slow manifold incorporating the leading order incompressibility criteria ${\nabla }_{\perp }·\mathbf{u}=0$, i.e., ${\mathbf{k}}_{\perp }·{\mathbf{h}}_{\mathbf{k}}^{s_k}=0$. Notably, as with its counterpart that exists outside the slow manifold (ref. Figure 2), this wave basis exhibits the following property that enables switching across different handedness by a conjugation operation,

$${\mathbf{h}}_{\mathbf{k}}^{-s_k}={\mathbf{h}}_{\mathbf{k}}^{s_k*}.$$

(13)

These findings illustrate that the R-RHD are naturally set up in the helical wave coordinate basis. As stated above in the paragraph following Equation (10), we switch from Fourier series to Fourier transform in the next section, i.e., e.g., ${\widehat{\mathbf{U}}}_{\mathbf{k}}^{s_k}\to {\mathbf{U}}_{\mathbf{k}}^{s_k}$ unless explicitly mentioned. This switch demands a multiplication by a factor ${(\frac{L}{2\pi })}^d,d=2$ which will be explicitly written in the subsequent sections.

3. Dynamical Limits of Turbulence and Multiple Scales Order Parameters

Before we present the derivation of the amplitude and kinetic equations, a note on the time-scales of the different variables is necessary along with their order of magnitude.

3.1. Time Period of Oscillations of Waves and Amplitudes

First we introduce the scalings typically involved in weak wave turbulence [7] as applied to rotating turbulence. In terms of the time periods of oscillations, we have

$$T_f\ll T_{\tau }\ll T_{{\tau }_{NL}},$$

(14)

where $T_f$ is the fast inertial wave time period proportional to $\frac{1}{{\omega }_{f\mathbf{k}}},{\omega }_f={\omega }_{f\mathbf{k}}=\frac{2\mathsf{\Theta }{k}_z}{k}$ as mentioned in [8] (The ${\mathrm{subscript}}_f$ refers to fast waves). $\mathsf{\Theta }$ is the rotation rate of the system. $T_{\tau }$ sets the time scale for weak amplitude oscillations. Typically, $T_f\sim \mathcal{O}(1),T_{\tau }\sim \mathcal{O}(\frac{1}{\mathcal{R}o})$ and $T_{{\tau }_{NL}}\sim \mathcal{O}(\frac{1}{\mathcal{R}{o}^2})$ with $\mathcal{R}o\ll 1$. With these scalings, the wave time period is taken as $T_{\tau }=\frac{1}{\mathcal{R}o}{T}_f$ such that $\frac{\partial }{\partial T_f}\to \frac{\partial }{\partial T_f}+\frac{1}{\mathcal{R}o}\frac{\partial }{\partial T_{\tau }}$. The wave kinetic equations are subsequently derived in an infinite box limit and by taking a large time limit integration as is explained in detail in [7,8,30].

The R-RHD equations introduced in the previous section eliminate the fast inertial waves with frequency ${\omega }_f:=\frac{2\pi }{T_f}$ but retain slow inertial waves with frequency ${\omega }_s:=\frac{2\pi }{T_s}$ which have the dispersion relation ${\omega }_s={\omega }_{s\mathbf{k}}=\frac{k_Z}{k_{\perp }}{\omega }_1$ given in Equation (9) (The ${\mathrm{subscript}}_s$ refers to slow R-RHD waves). This leads to a slight modification of Equation (14) as $T_f\ll T_s\ll T_{\tau }\ll T_{{\tau }_{NL}}$ which we simply write below as,

$$T_f\ll T_s\ll T_{\tau },$$

(15)

where now we may have $T_f\sim \mathcal{O}(\frac{\mathcal{R}o}{ϵ}),T_s\sim \mathcal{O}(\frac{1}{ϵ})$ and $T_{\tau }\sim \mathcal{O}(\frac{1}{{ϵ}^2})$, $ϵ=\frac{k_Z}{k_{\perp }}\ll \mathcal{R}o\ll 1$. We have ${\omega }_s\ll {\omega }_f$ indicating the slowness of the R-RHD waves compared with the fast inertial waves in [8]. However, for the multiple scales analysis carried forth in the subsequent sections, we adopt a new set of slow (or strained) time variables with appropriate order of magnitude as stated below.

3.2. Notations and New Slow Time Variables for the Multiple Scales Derivation Presented in This Paper

For reasons that will soon become clear, we adopt a suitable convention in our multiple scales approach by introducing new strained time variables $\tau ,t_s$ and $t_f$ [31,32,33] (As an analogy, one may think of $t_f$ as the seconds hand on a clock, $t_s$ as the minutes hand on a clock and $\tau$ as the hour hand on a clock. The multiple scales variables $\tau ,t_s$ and $t_f$ must not be conflated with the time period variables $T_{\tau },T_s$ and $T_f$ as they have a distinct interpretation as stated here). The fast wave time scale is $t_f$, the R-RHD slow waves have time scale of $t_s$, while the wave amplitudes introduced in the next section have the slowest time scale denoted by $\tau$. We fix our analysis by setting the most stretched time scale to order one and designate it as the slow time. In other words, we set our frame of reference to this slow time universe. Thus we have the following scale separated temporal variables:

• $\tau \sim \mathcal{O}(1)$: slow time scale of weak amplitudes (slowest time scale),
• $t_s\sim \mathcal{O}(\frac{1}{ϵ})$: slow R-RHD wave time scale, and
• $t_f\sim \mathcal{O}(\frac{1}{ϵ\mathcal{R}o})$: fast inertial wave time scale (filtered out by R-RHD).

Thus with $\tau =ϵt_s$, $ϵ=\frac{k_Z}{k_{\perp }}\ll \mathcal{R}o\ll 1$ defines the magnitude of anisotropy in the flow. The R-RHD wave time derivative is ${\partial }_{t_s}\to {\partial }_{t_s}+ϵ{\partial }_{\tau }$. The interpretation is as provided in [31,32,33] and is articulated as follows. Note that the frame of reference is set to the most slowly elapsing dynamic denoted by $\tau$. As an example, say $ϵ=0.01$. This means for the dynamic in the frame of reference to elapse by unit time ($\tau =1$), the R-RHD waves would have elapsed by 100 units (i.e., $t_s=100$) and the fast inertial waves would have elapsed even more rapidly as seen by an observer in the set frame of reference. We conveniently have the case that within the scope of the amplitude dynamic elapsing at $\tau$, the slow wave dynamic time scale is already infinitely large. However, recall that the R-RHD have filtered out the fast inertial waves by applying a method of multiple scales with $\mathcal{R}o$ as the order parameter as explained in the previous section. This means that from within the frame of reference of the reduced universe of R-RHD, the fast inertial wave is no more accessible and mathematically this means we do not need to track the dynamical universe elapsing at the time scale $t_f$. This means that in our multiple scales analysis we only need to track $\tau$ and $t_s$ (we simply write t for $t_s$ except where we need to distinguish between $t_s$ and $t_f$) with

$$\tau \ll t,\mathrm{or}\mathrm{equivalently},\tau =ϵt,ϵ\ll \mathcal{R}o\ll 1.$$

(16)

Relation (16) is equivalent to $T_{\tau }=\frac{1}{ϵ}{T}_s$ for the same choice of $ϵ$. So in the following we provide order of magnitude estimates for terms involving the slow inertial R-RHD waves ($\omega ,t$) and the non-linear amplitude time scale ($\tau \sim {\tau }_{NL}$) for non-linear advection in the $k_{\perp }$ modes. Consequently, we have $\omega \equiv {\omega }_{\mathbf{k}}=\frac{k_Z}{k_{\perp }}{\omega }_1\sim \mathcal{O}(ϵ)$ representing slow (slow in comparison to the fast inertial waves that are filtered out by the R-RHD) frequency R-RHD waves with ${\omega }_1\sim \mathcal{O}(1)$. This gives us the following limits

$$\omega \tau \sim \mathcal{O}(ϵ)\ll 1,\omega t\sim \mathcal{O}(1).$$

(17)

3.3. Definitions of Turbulence Regimes

In what follows, we will generally abbreviate reference to weak wave turbulence applied to full hydrodynamic equations by Galtier [8] as WT, anisotropic wave turbulence of the reduced hydrodynamic equations developed here, and that developed for reduced magnetohydrodynamics (MHD) [7,34], as AT, and critical balance [27] as CB. Moreover, unless otherwise stated, we will primarily refer to the works by Zakharov et al. [30] and Nazarenko [7] for the section on wave turbulence closure. The terminology anisotropic wave turbulence for reduced hydrodynamic equations is borrowed from the MHD literature [7,34] where the model was developed for reduced MHD equations [7]. This will be explained later in Section 6.2. Based on the order of magnitude scalings prescribed above, we have the following definitions.

WT:

$\begin{array}{|c|}\hline {\omega }_f{T}_{\tau }\gg 1,{\omega }_s{T}_f\ll 1\\ \hline\end{array}$.

AT:

$\begin{array}{|c|}\hline {\omega }_f{T}_{\tau }\gg {\omega }_s{T}_{\tau }\gg 1,{\omega }_s{T}_f\ll 1\\ \hline\end{array}$. In essence, one may envision the AT dynamical regime for hydrodynamics as a zoomed in version of the WT limit in Galtier [8]. In this paper we investigate the subtle variations in the flow dynamic at this magnified scale concealed by the treatment in [8]. Further, in this paper, we perform the multiple scales analysis in the anisotropic regime defined by the order parameter $ϵ=\frac{k_Z}{k_{\perp }}\ll 1$. So the region of validity of AT is also set by the limit where $\frac{k_Z}{k_{\perp }}\ll \mathcal{R}o\ll 1$.

CB:

$\begin{array}{|c|}\hline {\omega }_f{T}_{\tau }\sim 1\\ \hline\end{array}$.

As will be shown subsequently, the dynamic and solutions are distinctly different for WT and AT.

4. Wave Amplitude Equations

In the framework of this paper we consider small amplitude dynamics, where smallness of the amplitude is measured in terms of the extent of anisotropy, i.e., the ratio $\frac{k_Z}{k_{\perp }}\ll 1$. However, rotating fluid motion includes significantly large wave amplitudes of $o(\mathcal{R}{o}^{-1})$ outside the slow manifold. For connectivity and consistency with observed energy spectra as prescribed in this paper, one can therefore envision the scenario whereby the amplitudes of resonantly cascading inertial waves have been sufficiently attenuated once the dominant flow dynamics have reached the slow manifold. We therefore proceed with a multiple scales asymptotic approach in time, where ${\partial }_t\to {\partial }_t+ϵ{\partial }_{\tau }$ and

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}^{ϵ}({\mathbf{x}}_{\perp },Z,t,\tau )& =ϵ{\mathsf{\Psi }}_1({\mathbf{x}}_{\perp },Z,t,\tau )+{ϵ}^2{\mathsf{\Psi }}_2({\mathbf{x}}_{\perp },Z,t,\tau )+\mathcal{O}({ϵ}^3);\hfill \end{array}$$

(18)

where ${\mathsf{\Psi }}_{\mathbf{j}},\forall j=1,2,3...$ is $\mathcal{O}(1)$ to ensure consistency of order in the expansion above.

The order parameter $0<ϵ\ll 1$ is a measure of the wavefield amplitude and $\tau =ϵt$ denotes the slow advective timescale for weak amplitude modulations in comparison to the inertial wave propagation time t. We note that $ϵ{\partial }_{\tau }\sim ϵ{\mathbf{u}}_1·{\nabla }_{\perp }$, indicating that $\tau$ defines the advective timescale. This ensures a necessary separation of temporal scales $\tau$ and t as explained in [16], thereby allowing for a multi-scale treatment of the system with distinct dynamics at every order. The choice of an order parameter, $ϵ$ proportional to $k_Z/k_{\perp }$ has been mentioned by Nazarenko and Scheckochihin [27] and serves as a guiding principle for the theory developed here. This way a systematic multi-scale treatment that captures the anisotropy in the rotating system is developed. A multi-scale approach exploits the presence of scale separation between slow and fast dynamics. This allows the relevance of reduced models for understanding the coupling between slow-fast dynamics. The interested reader is referred to a recent paper by Abramov [35] where a reduced model for multi-scale dynamics is presented that illustrates the power of multiple scales method in a general setting.

At $\mathcal{O}(ϵ)$, the leading order solution can be interpreted as a complex field of waves undergoing resonant interactions on slow inertial timescale. At leading order, $\mathcal{O}(ϵ)$, utilizing Equation (12), we have that planar inertial waves satisfy

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathcal{H}}{\mathbf{U}}_{1\mathbf{k}}^{s_k}=\mathbf{0},{\mathcal{L}}_{\mathcal{H}}\equiv \left[-i{\omega }_{\mathbf{k}}^{s_k}{\mathbf{I}}_2-\frac{k_Z}{k_{\perp }}{\mathbf{J}}_2\right].\end{array}$$

(19)

Here ${\mathbf{J}}_2=\left(\begin{array}{cc}\hfill 0& \hfill 1\\ \hfill -1& \hfill 0\end{array}\right)$ is the Hamiltonian matrix and ${\mathbf{I}}_2$ is the identity matrix. The solution to this system is the helical base vector ${\mathbf{U}}_{1\mathbf{k}}^{s_k}\equiv {\mathbf{h}}_{\mathbf{k}}^{s_k}$. It is important to note that ${\mathcal{L}}_{\mathcal{H}}$ being non-Hermitian, an extended eigen basis, including both the left and right eigenvectors, is required. This extended basis is the complex helical basis $h_{\mathbf{k}}^{s_k}$ introduced earlier in Equation (12). Also of importance to the application of a solvability condition at higher asymptotic orders is the solution ${\mathbf{h}}_{\mathbf{k}}^{-s_k}$ satisfying the adjoint problem ${({\mathcal{L}}_{\mathcal{H}})}^{*T}{\mathbf{h}}_{\mathbf{k}}^{-s_k}\equiv {\mathbf{h}}_{\mathbf{k}}^{-s_{k}T}{\mathcal{L}}_{\mathcal{H}}=\mathbf{0}$ and orthogonality condition $\langle \frac{1}{2}{\mathbf{h}}_{\mathbf{k}}^{-s_k},{\mathbf{h}}_{\mathbf{k}}^{s_k}\rangle =1$. Given system (19), a complex wave field can now be expressed as a superposition of inertial waves and eddies (2D modes) represented in terms of the helical basis:

$${\mathbf{U}}_1=\sum _{s_k}\int \{c_{\mathbf{k}}^{s_k}(\tau ){\mathbf{h}}_{\mathbf{k}}^{s_k}{e}^{i\mathsf{\Phi }(\mathbf{k},s_k{\omega }_{\mathbf{k}})}+c.c.\}d\mathbf{k}.$$

(20)

At $\mathcal{O}({ϵ}^2)$, the next asymptotic order, we have for each helical mode ${\mathbf{h}}_{\mathbf{k}}^{s_k}$,

$$\begin{array}{c}\stackrel{1\mathrm{st}\mathrm{term}}{\overbrace{{\mathcal{L}}_{\mathcal{H}}{\mathbf{U}}_{2\mathbf{k}}^{s_k}}}=-\stackrel{2\mathrm{nd}\mathrm{term}}{\overbrace{{\partial }_{\tau }{c}_{\mathbf{k}}^{s_k}{\mathbf{h}}_{\mathbf{k}}^{s_k}}}-\stackrel{3\mathrm{rd}\mathrm{term}}{\overbrace{\sum _{s_p,s_q}\underset{\mathbf{k}=\mathbf{p}+\mathbf{q}}{\int }\frac{{\mathbf{p}}^{\perp }·{\mathbf{q}}_{\perp }}{p_{\perp }}\left(\begin{array}{c}\hfill \frac{q_{\perp }}{k_{\perp }}{U}_{\mathbf{p}}^{s_p}{U}_{\mathbf{q}}^{s_q}\\ \hfill U_{\mathbf{p}}^{s_p}{W}_{\mathbf{q}}^{s_q}\end{array}\right)e^{i\left((s_p{\omega }_{\mathbf{p}}t)+(s_q{\omega }_{\mathbf{q}}t)-(s_k{\omega }_{\mathbf{k}}t)\right)}d\mathbf{p}d\mathbf{q}}},\hfill \end{array}$$

(21)

where the subscript 1 has been dropped from the right hand side of the above equations. Application of the solvability condition, $\frac{1}{2}({\mathbf{h}}_{\mathbf{k}}^{-s_k}·{\mathcal{L}}_{\mathcal{H}}{\mathbf{U}}_{2\mathbf{k}}^{s_k})=0$, for bounded growth in ${\mathbf{U}}_{2\mathbf{k}}^{s_k}$, gives the wave amplitude equation in terms of the Fourier transform variables over the full $\mathbf{k}$ space as follows:

$$\begin{array}{c}\hfill i{\partial }_{\tau }{c}_{\mathbf{k}}^{s_k}=\frac{1}{2}\sum _{s_p,s_q}\int V_{kpq}^{s_k{s}_p{s}_q}{c}_{\mathbf{p}}^{s_p}{c}_{\mathbf{q}}^{s_q}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}{e}^{i\varphi (\omega )t}d\mathbf{p}d\mathbf{q},\end{array}$$

(22)

where $V_{kpq}^{s_k{s}_p{s}_q}:=\frac{{\mathbf{p}}^{\perp }·{\mathbf{q}}_{\perp }}{p_{\perp }}\left(\frac{q_{\perp }}{k_{\perp }}{s}_k{s}_p{s}_q+s_p\right)$ is the interaction coefficient. Here $\varphi (\omega )=(s_k{\omega }_k-s_p{\omega }_p-s_q{\omega }_q)$. The intermediary steps in the derivation of Equation (22) are given in Appendix A.2.

4.1. Dimensional Consistency of Wave Amplitude Equation (22)

For dimensional analysis, we use $M,L,T$ to represent mass, length and time. Moreover, $[·]$ is used as the dimensional operator, e.g., $\left[W\right]$ denotes the dimension of the variable W. Recall that $c_{\mathbf{k}}\sim L^2{\widehat{c}}_{\mathbf{k}}$ and $[{\widehat{c}}_{\mathbf{k}}]=\left[W\right]=L/T,[V_{kpq}^{s_k{s}_p{s}_q}]=1/L,[{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}]=L^2$, $e^{i\varphi (\omega )t}$ is dimensionless and $\left[d\mathbf{p}d\mathbf{q}\right]=1/L^4$ since we are in 2 dimensions $({\mathbf{x}}_{\perp },\widehat{z})$. Thus, we have $[l.h.s.]=\frac{1}{T}\frac{L^3}{T}=\frac{L^3}{T^2}$ and $[r.h.s.]=\frac{1}{L}\frac{L^3}{T}\frac{L^3}{T}{L}^2\frac{1}{L^2}\frac{1}{L^2}=\frac{L^3}{T^2}$ (Here $l.h.s.$ and $r.h.s.$ mean the left and right hand sides of the concerned equation respectively).

For $s_k=+$, the sum is actually carried over the combinations given by the set $(s_p,s_q)=\{(+,+),(+,-),(-,+)\}$ as the terms with $c_{\mathbf{p}}^{-}{c}_{\mathbf{q}}^{-}$ have null contribution due to the resonance condition. The converse holds for $s_k=-$. Since $\mathsf{\Psi }$ is real valued in the physical space, the corresponding Fourier coefficients satisfy the symmetry condition ${\widehat{c}}_{-\mathbf{k}}^{s_k}={\widehat{c}}_{\mathbf{k}}^{s_k*}$ and the integration over $\mathbf{p},\mathbf{q}$ is performed on the positive spectral space. With this physical information, we re-write Equation (22) in symmetrical form, for $s_k=+$, as follows:

$$\begin{array}{cc}\hfill i{\partial }_{\tau }{c}_{\mathbf{k}}^{+}{e}^{-i{\omega }_{k}t}& =\frac{1}{2}\underset{\mathbf{p},\mathbf{q}>0}{\int }\left[{\tilde{L}}_{kpq}^{+++}{c}_{\mathbf{p}}^{+}{c}_{\mathbf{q}}^{+}{e}^{-i({\omega }_p+{\omega }_q)t}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}+2{\tilde{L}}_{qpk}^{+-+}{c}_{\mathbf{p}}^{-}{c}_{\mathbf{q}}^{+}{e}^{-i({\omega }_q-{\omega }_p)t}{\delta }_{\mathbf{q},\mathbf{p}\mathbf{k}}\right]d\mathbf{p}d\mathbf{q}\hfill \\ & =\underset{\mathbf{p},\mathbf{q}>0}{\int }\left[\frac{1}{2}{\tilde{L}}_{kpq}^{+++}{c}_{\mathbf{p}}^{+}{c}_{\mathbf{q}}^{+}{e}^{-i({\omega }_p+{\omega }_q)t}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}-{\tilde{L}}_{qpk}^{+++}{c}_{\mathbf{p}}^{-}{c}_{\mathbf{q}}^{+}{e}^{-i({\omega }_q-{\omega }_p)t}{\delta }_{\mathbf{q},\mathbf{p}\mathbf{k}}\right]d\mathbf{p}d\mathbf{q},\hfill \end{array}$$

(23)

where the interaction coefficient ${\tilde{L}}_{kpq}^{+++}:=\frac{1}{2}(V_{kpq}^{+++}+V_{kqp}^{+++})=\frac{1}{2}\frac{{\mathbf{p}}^{\perp }·{\mathbf{q}}_{\perp }}{k_{\perp }{p}_{\perp }{q}_{\perp }}(q_{\perp }-p_{\perp })(p_{\perp }+q_{\perp }+k_{\perp })$ is clearly symmetric in the second and third arguments, i.e., ${\tilde{L}}_{kpq}^{+++}={\tilde{L}}_{kqp}^{+++}$ by noting that ${\mathbf{p}}^{\perp }·{\mathbf{q}}_{\perp }=-{\mathbf{q}}^{\perp }·{\mathbf{p}}_{\perp }$. Likewise, ${\tilde{L}}_{qpk}^{+-+}=\frac{1}{2}(V_{qpk}^{+-+}+V_{qpk}^{+-+})=-{\tilde{L}}_{qpk}^{+++}$ by inspection of the definition of $V_{kpq}^{s_k{s}_p{s}_q}$. Hereafter, the integration over $\mathbf{p},\mathbf{q}>0$ is implied. The symmetrization of the nonlinear form is discussed in detail in ch. 6 of the textbook on wave turbulence by Nazarenko [7].

4.2. Spectral Tensor

Having deduced the wave amplitude equation (23), we now proceed with the primary objective of finding the functional forms for stationary energy and helicity spectra, often referred to as Kolmogorov solutions [36]. The relation between energy and helicity in terms of the canonical complex variable, $c_{\mathbf{k}}^{s_k}$ can be understood by carefully analyzing the average spectral tensor for a given spectral mode $\mathbf{k}$.

We review some definitions of terms at the outset. Henceforth, we use the symbol $\mathsf{\Lambda }:=\frac{L}{2\pi }$ to denote the dimensional constant of dimension L. Ensemble average of the squared amplitude function enables us to estimate the energy spectral density. For a given polarity $s_k$, we have

$$\langle C_{\mathbf{k}}^{s_k}{C}_{{\mathbf{k}}^{\prime }}^{s_{k^{\prime }}*}\rangle :=e_{\mathbf{k}}^{s_k}\delta (\mathbf{k}-{\mathbf{k}}^{\prime }).$$

Alternatively, $\langle C_{\mathbf{k}}^{s_k}{C}_{{\mathbf{k}}^{\prime }}^{s_{k^{\prime }}*}\rangle \stackrel{RPA}{=}\langle c_{\mathbf{k}}^{s_k}{c}_{{\mathbf{k}}^{\prime }}^{s_{k^{\prime }}*}\rangle \langle e^{-i({\omega }_{\mathbf{k}}^{s_k}-{\omega }_{{\mathbf{k}}^{\prime }}^{s_{k^{\prime }}})t}\rangle =\langle c_{\mathbf{k}}^{s_k}{c}_{{\mathbf{k}}^{\prime }}^{s_{k^{\prime }}*}\rangle {\delta }_{{\mathbf{k}}^{\prime }}^{\mathbf{k}}=\langle c_{\mathbf{k}}^{s_k}{c}_{\mathbf{k}}^{s_k*}\rangle =e_{\mathbf{k}}^{s_k}\delta (0),$ where the infinite box limit entails $\delta (0)={\mathsf{\Lambda }}^2$ [7]. Here $\delta (\mathbf{k}-{\mathbf{k}}^{\prime })\equiv {\delta }_{\mathbf{k},{\mathbf{k}}^{\prime }}$ is the Dirac delta function and ${\delta }_{{\mathbf{k}}^{\prime }}^{\mathbf{k}}$ is the Kronecker delta function (In this paper, delta function written with arguments both in the superscript and subscript refers to the Kronecker delta whereas the delta function written with arguments either all in the subscript or all within parenthesis refers to the Dirac delta. In other words, ${\delta }_j^i$ is Kronecker delta whereas $\delta (x-y)$ or ${\delta }_{x,y}$ refers to Dirac delta). $RPA$ stands for random phase and amplitude [7]. Thus we have the following relation that is valid when $L\to \infty$,

$$\begin{array}{ccc}\hfill e_{\mathbf{k}}^{s_k}& =\hfill & \hfill {\mathsf{\Lambda }}^2\langle {\widehat{c}}_{\mathbf{k}}^{s_k}{\widehat{c}}_{\mathbf{k}}^{s_k*}\rangle ={\mathsf{\Lambda }}^2{\widehat{e}}_{\mathbf{k}}^{s_k}(\mathrm{r}.\mathrm{h}.\mathrm{s}.\mathrm{in}\mathrm{terms}\mathrm{of}\mathrm{Fourier}\mathrm{coefficients}\mathrm{denoted}\mathrm{by}^),\\ \hfill {\mathsf{\Lambda }}^2{e}_{\mathbf{k}}^{s_k}& =\hfill & \hfill \langle c_{\mathbf{k}}^{s_k}{c}_{\mathbf{k}}^{s_k*}\rangle (\mathrm{r}.\mathrm{h}.\mathrm{s}.\mathrm{in}\mathrm{terms}\mathrm{of}\mathrm{Fourier}\mathrm{transform}\mathrm{variables}).\end{array}$$

(24)

For reference, we list the dimensions of the relevant terms again:

$$\left[{\widehat{c}}_{\mathbf{k}}^{s_k}\right]=\frac{L}{T},\left[c_{\mathbf{k}}^{s_k}\right]=\frac{L^3}{T},\left[{\widehat{e}}_{\mathbf{k}}^{s_k}\right]=\frac{L^2}{T^2},\left[e_{\mathbf{k}}^{s_k}\right]=\frac{L^4}{T^2}\mathrm{and}{\delta }_{{\mathbf{k}}^{\prime }}^{\mathbf{k}}(\mathrm{Kronecker}\mathrm{delta})\mathrm{is}\mathrm{dimensionless}.$$

The average spectral tensor is defined as follows (see p. 179, Section 5.11 in [37]):

$$\begin{array}{c}\frac{1}{2}\langle {\mathcal{U}}_{\mathbf{k}}\rangle :=\frac{1}{2}\langle ({\mathbb{U}}_{\mathbf{k}}\otimes {\mathbb{U}}_{{\mathbf{k}}^{\prime }}^{*})\rangle \hfill \\ =\frac{1}{2}\left(\begin{array}{cc}\langle {\displaystyle \sum _{s_k=\pm }}{c}_{\mathbf{k}}^{s_k}{c}_{{\mathbf{k}}^{\prime }}^{s_k*}\rangle & \langle {\displaystyle \sum _{s_k=\pm }}i{s}_k\frac{k_{\perp }}{k_{\perp }}{c}_{\mathbf{k}}^{s_k}{c}_{{\mathbf{k}}^{\prime }}^{s_k*}\rangle \\ \langle {\displaystyle \sum _{s_k=\pm }}-i{s}_k\frac{k_{\perp }}{k_{\perp }}{c}_{\mathbf{k}}^{s_k}{c}_{{\mathbf{k}}^{\prime }}^{s_k*}\rangle & \langle {\displaystyle \sum _{s_k=\pm }}{c}_{\mathbf{k}}^{s_k}{c}_{{\mathbf{k}}^{\prime }}^{s_k*}\rangle \end{array}\right){\delta }_{{\mathbf{k}}^{\prime }}^{\mathbf{k}}\hfill \\ =\frac{1}{2}\left(\begin{array}{cc}\langle c_{\mathbf{k}}^{+}{c}_{{\mathbf{k}}^{\prime }}^{+*}+c_{\mathbf{k}}^{-}{c}_{{\mathbf{k}}^{\prime }}^{-*}\rangle & \langle \frac{i{k}_{\perp }}{k_{\perp }}(c_{\mathbf{k}}^{+}{c}_{{\mathbf{k}}^{\prime }}^{+*}-c_{\mathbf{k}}^{-}{c}_{{\mathbf{k}}^{\prime }}^{-*})\rangle \\ \langle \frac{-i{k}_{\perp }}{k_{\perp }}(c_{\mathbf{k}}^{+}{c}_{{\mathbf{k}}^{\prime }}^{+*}-c_{\mathbf{k}}^{-}{c}_{{\mathbf{k}}^{\prime }}^{-*})\rangle & \langle c_{\mathbf{k}}^{+}{c}_{{\mathbf{k}}^{\prime }}^{+*}+c_{\mathbf{k}}^{-}{c}_{{\mathbf{k}}^{\prime }}^{-*}\rangle \end{array}\right){\delta }_{{\mathbf{k}}^{\prime }}^{\mathbf{k}}\hfill \\ =\frac{1}{2}\left(\begin{array}{cc}\langle c_{\mathbf{k}}^{+}{c}_{\mathbf{k}}^{+*}+c_{\mathbf{k}}^{-}{c}_{\mathbf{k}}^{-*}\rangle & \langle \frac{i{k}_{\perp }}{k_{\perp }}(c_{\mathbf{k}}^{+}{c}_{\mathbf{k}}^{+*}-c_{\mathbf{k}}^{-}{c}_{\mathbf{k}}^{-*})\rangle \\ \langle \frac{-i{k}_{\perp }}{k_{\perp }}(c_{\mathbf{k}}^{+}{c}_{\mathbf{k}}^{+*}-c_{\mathbf{k}}^{-}{c}_{\mathbf{k}}^{-*})\rangle & \langle c_{\mathbf{k}}^{+}{c}_{\mathbf{k}}^{+*}+c_{\mathbf{k}}^{-}{c}_{\mathbf{k}}^{-*}\rangle \end{array}\right)\hfill \\ =\frac{{\mathsf{\Lambda }}^2}{2}\left(\begin{array}{cc}{e}_{\mathbf{k}}^{+}+e_{\mathbf{k}}^{-}& i\frac{h_{\mathbf{k}}^{+}+h_{\mathbf{k}}^{-}}{k_{\perp }}\\ -i\frac{h_{\mathbf{k}}^{+}+h_{\mathbf{k}}^{-}}{k_{\perp }}& e_{\mathbf{k}}^{+}+e_{\mathbf{k}}^{-}\end{array}\right)=\frac{{\mathsf{\Lambda }}^2}{2}\left(\begin{array}{cc}{e}_{\mathbf{k}}& i\frac{h_{\mathbf{k}}}{k_{\perp }}\\ -i\frac{h_{\mathbf{k}}}{k_{\perp }}& e_{\mathbf{k}}\end{array}\right).\hfill \end{array}$$

(25)

The ensemble averaging of the phase factor results in the appearance of the Kronecker delta function above. The Kronecker and Dirac delta functions may be interpreted as selector functions, i.e., $f(x_i,x_j){\delta }_j^i=f(x_i,x_i)$ and $\int f(x^{\prime })\delta (x^{\prime }-x)d{x}^{\prime }=f(x)$ respectively. The arguments and results that follow in the rest of the paper must be interpreted in the statistical sense whereby the ensemble phase averaging can be regarded as a time averaging operation upon assuming ergodic property of the flow variables. From the relations in (25), it is clear that the following is true,

$$\begin{array}{cc}\hfill e_{\mathbf{k}}^{+}+e_{\mathbf{k}}^{-}& =e_{\mathbf{k}},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill e_{\mathbf{k}}^{+}-e_{\mathbf{k}}^{-}& =\frac{h_{\mathbf{k}}}{k_{\perp }}.\hfill \end{array}$$

(27)

By solving the above equations, we get,

$$\begin{array}{c}\begin{array}{c}\hfill e_{\mathbf{k}}^{+}=\frac{1}{2}\left(e_{\mathbf{k}}+\frac{h_{\mathbf{k}}}{k_{\perp }}\right),\\ \hfill e_{\mathbf{k}}^{-}=\frac{1}{2}\left(e_{\mathbf{k}}-\frac{h_{\mathbf{k}}}{k_{\perp }}\right).\end{array}\end{array}$$

(28)

These expressions are particularly useful in the derivation of the stationary energy and helicity spectra.

5. Zero Helicity Dynamics

In this section, we analyze the special case of a flow with zero helicity, i.e., $h_{\mathbf{k}}\equiv 0$ for all $\mathbf{k}$ such that $e_{\mathbf{k}}^{+}=e_{\mathbf{k}}^{-}=\frac{1}{2}{e}_{\mathbf{k}}$. From (25) this imposes the constraint on the complex amplitude functions $c_{\mathbf{k}}^{-s_k}=c_{\mathbf{k}}^{s_k*}$ where for sake of brevity we will write $c_{\mathbf{k}}^{+*}\equiv c_{\mathbf{k}}^{*}=c_{\mathbf{k}}^{-}$. This entails a reflection symmetry of the wave field and a reduction in the Hamiltonian description of the system [25] because a unique handedness, associated with one of the s variables, now describes the full system as the system described by $s=+$ and $s=-$ are mirror replicas of one another in the statistical sense. This point is explained in more detail in Sen [38]. Newell and Rumpf [39] have exploited this reduction and have studied resonance wave dynamics for the nonlinear Schrödinger’s system.

Now, the inertial waves may be interpreted as occurring in helicity couplets involving ${\mathbf{h}}_{\mathbf{k}}^{+}$ and ${\mathbf{h}}_{\mathbf{k}}^{-}={\mathbf{h}}_{\mathbf{k}}^{+*}$ with wavefield given by

$${\mathbf{U}}_1=\int \{\left(c_{\mathbf{k}}^{+}(\tau ){\mathbf{h}}_{\mathbf{k}}^{+}{e}^{-i{\omega }_{\mathbf{k}}t}\right)e^{i({\mathbf{k}}_{\perp }·{\mathbf{x}}_{\perp }+k_{Z}Z)}+c.c.\}d\mathbf{k}.$$

(29)

5.1. The Hamiltonian

The interaction Hamiltonian for the R-RHD can be expressed as a power series of the complex amplitudes, $C_{\mathbf{k}}:=c_{\mathbf{k}}{e}^{-i{\omega }_{\mathbf{k}}t}$, as follows:

$$H_{int}=H^{(3)}+H^{(4)}+\cdots .$$

(30)

The $H^{(4)}$ component denotes four-wave resonant interactions which are negligibly small and therefore not considered. Resonant self-interactions involving quadratic terms, captured by $H^{(2)}$, evolve on the inertial timescale t and is already accounted for within the operator ${\mathcal{L}}_{\mathcal{H}}$. The full Hamiltonian is $H\approx H^{(2)}+H^{(3)}$ in agreement with the weak wave expansion (18). The wave amplitude Equation (23) is obtained from the well known Hamilton equation

$$i{\partial }_t{C}_{\mathbf{k}}=\frac{\delta H}{\delta C_{\mathbf{k}}^{*}},$$

(31)

where ${\partial }_t{C}_{\mathbf{k}}\to {\partial }_t{C}_{\mathbf{k}}+ϵ{\partial }_{\tau }{C}_{\mathbf{k}}$ and the three wave interaction Hamiltonian $H^{(3)}$ is as follows [7,30]:

$$H^{(3)}=\int \left[{\tilde{L}}_{kpq}^{+++}{C}_{\mathbf{k}}^{*}{C}_{\mathbf{p}}{C}_{\mathbf{q}}+c.c.\right]{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}d\mathbf{k}\mathbf{p}\mathbf{q}.$$

(32)

At the order of the weak nonlinear interactions, Hamilton’s Equation (31) is identical in form to Equation (23) where $\frac{\delta H^{(3)}}{\delta C_{\mathbf{k}}^{*}}$ is the r.h.s. of Equation (23) after invoking the aforementioned Hamiltonian reduction whence $c_{\mathbf{k}}^{-}=c_{\mathbf{k}}^{*}$. Thus the wave amplitude equation of the reduced system ($c_{\mathbf{k}}^{-}=c_{\mathbf{k}}^{*}$) in the ${\mathbf{k}}^{+}$ space is

$$i{\partial }_{\tau }{c}_{\mathbf{k}}=\underset{\mathbf{p},\mathbf{q}>\mathbf{0}}{\int }\left[\frac{1}{2}{\tilde{L}}_{kpq}^{+++}{c}_{\mathbf{p}}{c}_{\mathbf{q}}{e}^{i({\omega }_k-{\omega }_p-{\omega }_q)t}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}-{\tilde{L}}_{qpk}^{+++}{c}_{\mathbf{p}}^{*}{c}_{\mathbf{q}}{e}^{i({\omega }_k+{\omega }_p-{\omega }_q)t}{\delta }_{\mathbf{q},\mathbf{p}\mathbf{k}}\right]d\mathbf{p}d\mathbf{q}.$$

(33)

5.2. Kinetic Equations

By multiplying Equation (33) with $c_{\mathbf{k}}^{*}$ and the complex conjugate of Equation (33) with $c_{\mathbf{k}}$, subsequently subtracting the latter from the former, followed by ensemble averaging and using the results from Section 4.2, we obtain an evolution equation for $e_{\mathbf{k}}\equiv e_{\mathbf{k}}^{+}=e_{\mathbf{k}}^{-}$:

$$\begin{array}{cc}\hfill {\partial }_{\tau }{e}_{\mathbf{k}}& =\Im \left\{{\mathsf{\Lambda }}^{-2}\int {\tilde{L}}_{kpq}^{+++}\langle C_{\mathbf{k}}^{*}{C}_{\mathbf{p}}{C}_{\mathbf{q}}\rangle {\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}-2{\tilde{L}}_{qpk}^{+++}\langle C_{\mathbf{k}}^{*}{C}_{\mathbf{p}}^{*}{C}_{\mathbf{q}}\rangle {\delta }_{\mathbf{q},\mathbf{p}\mathbf{k}}d\mathbf{p}d\mathbf{q}\right\},\hfill \end{array}$$

(34)

where $\mathsf{\Lambda }:=\frac{L}{2\pi }$ and $C_{\mathbf{k}}=c_{\mathbf{k}}{e}^{-i{\omega }_{k}t}$ as stated earlier. Henceforth, we simply write ${\tilde{L}}_{kpq}$ for ${\tilde{L}}_{kpq}^{+++}$. Here, $\Im (···)$ refers to imaginary part of the argument in parenthesis. The triple correlation can be defined as follows:

$$\langle C_{\mathbf{k}}^{*}{C}_{\mathbf{p}}{C}_{\mathbf{q}}\rangle :=J_{kpq}(\tau ){\delta }_{\mathbf{k},\mathbf{pq}}\equiv J_{kpq}^{\mathsf{\Delta }}(\tau ),$$

(35)

where the ${\mathrm{superscript}}^{\mathsf{\Delta }}$ is a convenient way of writing the Dirac delta function ${\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}$. On evaluating the ensemble average and considering the infinite box limit, we have the following reduction:

$$\langle C_{\mathbf{k}}^{*}{C}_{\mathbf{p}}{C}_{\mathbf{q}}\rangle \stackrel{RPA}{=}\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle {\delta }_{\mathbf{p}\mathbf{q}}^{\mathbf{k}}\stackrel{L\to \infty }{=}\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle \frac{{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}}{{\mathsf{\Lambda }}^2}=J_{kpq}(\tau ){\delta }_{\mathbf{k},\mathbf{pq}}\Rightarrow {\mathsf{\Lambda }}^{-2}\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle =J_{kpq}(\tau ).$$

(36)

Here ${\delta }_{\mathbf{p}\mathbf{q}}^{\mathbf{k}}$ is the Kronecker delta function that takes the value 1 when $\mathbf{k}=\mathbf{p}+\mathbf{q}$ and 0 otherwise. The relation (36) implies ${\mathsf{\Lambda }}^{-2}\langle C_{\mathbf{k}}^{*}{C}_{\mathbf{p}}{C}_{\mathbf{q}}\rangle {\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}={\mathsf{\Lambda }}^{-2}\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle {\delta }_{\mathbf{p}\mathbf{q}}^{\mathbf{k}}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}=J_{kpq}{\delta }_{\mathbf{p}\mathbf{q}}^{\mathbf{k}}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}=J_{kpq}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}$. Then Equation (34) can be written as

$${\partial }_{\tau }{e}_{\mathbf{k}}=\Im \left\{\int \left[{\tilde{L}}_{kpq}{J}_{kpq}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}-2{\tilde{L}}_{qpk}{J}_{qpk}{\delta }_{\mathbf{q},\mathbf{p}\mathbf{k}}\right]d\mathbf{p}d\mathbf{q}\right\}=\Im \left\{\int \left[{\tilde{L}}_{kpq}{J}_{kpq}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}-2{\tilde{L}}_{pkq}{J}_{pkq}{\delta }_{\mathbf{p},\mathbf{k}\mathbf{q}}\right]d\mathbf{p}d\mathbf{q}\right\}.$$

(37)

Here we have simply written ${\tilde{L}}_{kpq}\equiv {\tilde{L}}_{kpq}^{+++}$ and hereafter the ${\mathrm{superscript}}^{+++}$ will be implied unless otherwise mentioned. We observe that Equation (37) is not closed in the sense that the left hand side of the equation is a second order correlation function that is expressed in terms of third order correlation functions on the right hand side. For Gaussian distributed fields, odd correlators are null. Hence, we must devise an estimate of $J_{kpq}$ using a property of the fourth order correlator for Gaussian statistics as described in the following section.

5.2.1. Closure

In order to close Equation (37), we need to express the triple correlator in terms of second order correlators. Note that Equation (37) is obtained at $\mathcal{O}({ϵ}^2)$ as explained in Section 4. An estimate of the triple correlator in terms of the second order correlator can be obtained at the previous order of the multiple scales perturbation, i.e., at $\mathcal{O}(ϵ)$, as explained in this section. On applying Wick’s theorem to the Gaussian distributed wave field, quadruple correlation functions are defined as follows [7,30]:

$$\langle C_{\mathbf{k}}^{*}{C}_{\mathbf{p}}^{*}{C}_{\mathbf{q}}{C}_{\mathbf{m}}\rangle :=e_{\mathbf{k}}{e}_{\mathbf{p}}\left[{\delta }_{\mathbf{k},\mathbf{q}}{\delta }_{\mathbf{p},\mathbf{m}}+{\delta }_{\mathbf{k},\mathbf{m}}{\delta }_{\mathbf{p},\mathbf{q}}\right].$$

(38)

The applicability of Wick’s theorem relies on the assumption that the field is Gaussian distributed and this point is further discussed in Section 6.5. Let us first recall some relevant order of magnitude for the terms involved in this section. Since $\varphi (\omega ):=({\omega }_{\mathbf{k}}-{\omega }_{\mathbf{p}}-{\omega }_{\mathbf{q}})\sim \mathcal{O}(ϵ)$, we take $\varphi (\omega )=ϵ{\varphi }_1(\omega )+\mathcal{O}({ϵ}^2)$ where ${\varphi }_1(\omega )\sim \mathcal{O}(1)$ such that ${\varphi }_1(\omega )\tau \sim \mathcal{O}(1)$. Also, $\tau =ϵt$ with $ϵ\ll 1$ implies ${\partial }_t\to {\partial }_t+ϵ{\partial }_{\tau }$ (The total derivative is given by $\frac{d}{dt}=\frac{d}{dt}+\frac{d}{d\tau }\frac{d\tau }{dt}$ and since $\tau =ϵt$, we have $\frac{d\tau }{dt}=ϵ$). We use the definition of $J_{kpq}^{\mathsf{\Delta }}(\tau )$ in (35) and Equation (33) to write a differential equation for $J_{kpq}$. The solution of this differential equation provides us an estimate of $J_{kpq}$ at $\mathcal{O}(ϵ)$ to close the Equation (37) that was derived at $\mathcal{O}({ϵ}^2)$.

$$\begin{array}{ccc}\hfill ({\partial }_t+ϵ{\partial }_{\tau })J_{kpq}(\tau ){\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}& =& ({\partial }_t+ϵ{\partial }_{\tau })\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle \langle e^{i{\varphi }_1(\omega )\tau }\rangle \hfill \\ \hfill \Rightarrow ϵ{\partial }_{\tau }{J}_{kpq}(\tau ){\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}& =& ϵi{\varphi }_1(\omega )\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle \langle e^{i{\varphi }_1(\omega )\tau }\rangle +ϵ\langle e^{i{\varphi }_1(\omega )\tau }\rangle {\partial }_{\tau }\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle \hfill \\ & =& ϵi{\varphi }_1(\omega )J_{kpq}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}+ϵ\langle e^{i{\varphi }_1(\omega )\tau }\rangle {\partial }_{\tau }\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle .\hfill \end{array}$$

The ensemble average of the phase factor can be succinctly captured by the Kronecker delta (This can be readily checked by assuming ergodicity and computing the ensemble average as a large time average), which is equal to $\frac{{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}}{{\mathsf{\Lambda }}^2}$ at the infinite box limit, $\mathsf{\Lambda }:=\frac{L}{2\pi }\to \infty$. Thus at $\mathcal{O}(ϵ)$, for the triadic wave process, we have

$$\begin{array}{cc}(i{\partial }_{\tau }+{\varphi }_1(w))J_{kpq}& =\frac{i}{{\mathsf{\Lambda }}^2}{\partial }_{\tau }\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle \hfill \\ & ={\tilde{L}}_{kpq}(e_{\mathbf{k}}{e}_{\mathbf{p}}+e_{\mathbf{k}}{e}_{\mathbf{q}}-e_{\mathbf{p}}{e}_{\mathbf{q}})(\mathrm{using}\mathrm{Equation}(33)\mathrm{and}\mathrm{def}.(38)\mathrm{as}\mathrm{shown}\mathrm{below})\hfill \\ & =C_{\mathbb{J}}(\mathrm{constant}\mathrm{in}\tau )\hfill \end{array}$$

(39)

The second equality follows from the following calculation. Applying the product rule of differentiation, we have $\frac{i}{{\mathsf{\Lambda }}^2}{\partial }_{\tau }\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}{c}_{\mathbf{q}}\rangle =\frac{1}{{\mathsf{\Lambda }}^2}\langle (i{\partial }_{\tau }{c}_{\mathbf{k}}^{*})c_{\mathbf{p}}{c}_{\mathbf{q}}\rangle +\frac{1}{{\mathsf{\Lambda }}^2}\langle c_{\mathbf{k}}^{*}(i{\partial }_{\tau }{c}_{\mathbf{p}})c_{\mathbf{q}}\rangle +\frac{1}{{\mathsf{\Lambda }}^2}\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}(i{\partial }_{\tau }{c}_{\mathbf{q}})\rangle$. The first term on the r.h.s. is calculated as follows:

(40)

Here, the integral is expressed as a sum to make the calculation explicitly clear for the reader. Note that dimensional consistency demands ${\displaystyle \sum _{\mathbf{m},\mathbf{n}}}\leftrightarrow {\mathsf{\Lambda }}^4\int d\mathbf{mn}$ where ${\mathsf{\Lambda }}^4$ appears here because of the relation ${\delta }_{\mathbf{m},\mathbf{p}}{\delta }_{\mathbf{n},\mathbf{q}}+{\delta }_{\mathbf{m},\mathbf{q}}{\delta }_{\mathbf{n},\mathbf{p}}={\mathsf{\Lambda }}^4\left[{\delta }_{\mathbf{p}}^{\mathbf{m}}{\delta }_{\mathbf{q}}^{\mathbf{n}}+{\delta }_{\mathbf{q}}^{\mathbf{m}}{\delta }_{\mathbf{p}}^{\mathbf{n}}\right]$ in the def. (38). Similarly, $\frac{1}{{\mathsf{\Lambda }}^2}\langle c_{\mathbf{k}}^{*}(i{\partial }_{\tau }{c}_{\mathbf{p}})c_{\mathbf{q}}\rangle ={\tilde{L}}_{kpq}{e}_{\mathbf{k}}{e}_{\mathbf{q}}$ and $\frac{1}{{\mathsf{\Lambda }}^2}\langle c_{\mathbf{k}}^{*}{c}_{\mathbf{p}}(i{\partial }_{\tau }{c}_{\mathbf{q}})\rangle ={\tilde{L}}_{kpq}{e}_{\mathbf{k}}{e}_{\mathbf{p}}$ with $\mathbf{k}=\mathbf{p}+\mathbf{q}$. Thus follows the second equality in Equation (40).

The r.h.s. of Equaiton (40) is independent of time because we are interested in stationary solutions. The solution to the differential Equation (40) is

$$J_{kpq}(\tau )=\kappa e^{i{\varphi }_1(\omega )\tau }+\frac{C_{\mathbb{J}}}{{\varphi }_1(\omega )},\mathrm{where}\kappa \mathrm{is}\mathrm{a}\mathrm{constant}.$$

(41)

By taking the limit $T_{\tau }\to \infty$ for $ϵ\ll 1,{\omega }_s{T}_{\tau }\sim ϵ\frac{1}{{ϵ}^2}\gg 1$, we have the average of the exponential term approach zero because $\frac{1}{2T_{\tau }}{\int }_{-T_{\tau }}^{T_{\tau }}{e}^{i{\varphi }_1(\omega )\tau }d\tau \stackrel{T_{\tau }\to \infty }{\to }0$ when ${\varphi }_1(\omega )\ne 0$. Thus in the long time limit, the estimated average $\overline{J_{kpq}}$ is expressed as follows:

$$J_{kpq}\stackrel{T_{\tau }\to \infty }{\to }\overline{J_{kpq}}:=\frac{C_{\mathbb{J}}}{{\varphi }_1(\omega )}=\frac{{\tilde{L}}_{kpq}}{{\varphi }_1(\omega )}(e_{\mathbf{k}}{e}_{\mathbf{p}}+e_{\mathbf{k}}{e}_{\mathbf{q}}-e_{\mathbf{p}}{e}_{\mathbf{q}})$$

(42)

Thus, we have a reasonable estimate for $J_{kpq}$ in Equation (37) that is obtained as above at $\mathcal{O}(ϵ)$. Recall that the $\mathcal{O}(ϵ)$ solutions described in Section 4 are the slow R-RHD waves that enable this closure procedure. We now plug in this estimate $\overline{J_{kpq}}$ for $J_{kpq}$ in Equation (37) to close the kinetic system. The occurrence of the singularity (${\varphi }_1(\omega )=0$) is averted by circumventing the pole by adding a small term $i\widetilde{ϵ}$ to the denominator. Then we use the identity: $\Im \{\frac{1}{\varphi (\omega )+i\widetilde{ϵ}}\}=-\pi \delta ({\varphi }_1(\omega ))\equiv -\pi \delta (\varphi (\omega ))$ (For a function $f(x)$ that is analytic on the upper half of the complex plane, ${lim}_{\widetilde{ϵ}\to 0^{+}}{\int }_{-\infty }^{\infty }\frac{f(x)}{x-x_0+i\widetilde{ϵ}}dx=P{\int }_{-\infty }^{\infty }\frac{f(x)}{x-x_0}dx-i\pi {\int }_{-\infty }^{\infty }f(x)\delta (x-x_0)dx=P{\int }_{-\infty }^{\infty }\frac{f(x)}{x-x_0}dx-i\pi f(x_0)$, where P refers to the principal value. For the special case when $f(x)=1$, the preceding identity is concisely written as $\frac{1}{x-x_0+i\widetilde{ϵ}}=P\frac{1}{x-x_0}-i\pi \delta (x-x_0)$ where it is generally understood that the integral is taken over the domain with $\widetilde{ϵ}\to 0^{+}$. The imaginary part of the l.h.s., thus, yields the delta function term on the r.h.s. of the identity) and substitute the resulting term for $J_{kpq}$ in Equation (37) to obtain the closed form of the kinetic equation:

$$\begin{array}{cc}\hfill {\partial }_{\tau }{e}_{\mathbf{k}}& =\pi \int [|{\tilde{L}}_{kpq}{|}^2(e_{\mathbf{p}}{e}_{\mathbf{q}}-e_{\mathbf{k}}{e}_{\mathbf{p}}-e_{\mathbf{k}}{e}_{\mathbf{q}}){\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}{\delta }_{{\omega }_k,{\omega }_p{\omega }_q}\hfill \\ & -2|{\tilde{L}}_{pkq}{|}^2(e_{\mathbf{k}}{e}_{\mathbf{q}}-e_{\mathbf{p}}{e}_{\mathbf{k}}-e_{\mathbf{p}}{e}_{\mathbf{q}}){\delta }_{\mathbf{p},\mathbf{k}\mathbf{q}}{\delta }_{{\omega }_p,{\omega }_k{\omega }_q}]d\mathbf{p}d\mathbf{q}.\hfill \end{array}$$

(43)

Recall that $\delta (\varphi (\omega ))\equiv {\delta }_{{\omega }_k,{\omega }_p{\omega }_q}$ because $\varphi (\omega ):={\omega }_{\mathbf{k}}-{\omega }_{\mathbf{p}}-{\omega }_{\mathbf{q}}$. Equation (43), that describes the evolution of the energy spectral density, can be rewritten as a single integral with the interaction operator proportional to the square of ${\tilde{L}}_{kpq}$ by using the Zakharov-Kuznetsov conformal transformation [30,40].

5.2.2. Dimensional Consistency of the kinetic Equation (43)

In Equation (43), $[l.h.s.]=[\frac{e_k}{\tau }]=\frac{L^4}{T^3}$ and $[r.h.s]=[{\tilde{L}}_{kpq}^2][e_{\mathbf{k}}{e}_{\mathbf{q}}][{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}][{\delta }_{{\omega }_{\mathbf{k}},{\omega }_{\mathbf{p}}{\omega }_{\mathbf{q}}}][dpdq]=\frac{1}{L^2}\frac{L^8}{T^4}{L}^{2}T\frac{1}{L^4}=\frac{L^4}{T^3}$. Therefore, the derived kinetic Equation (43) is dimensionally consistent.

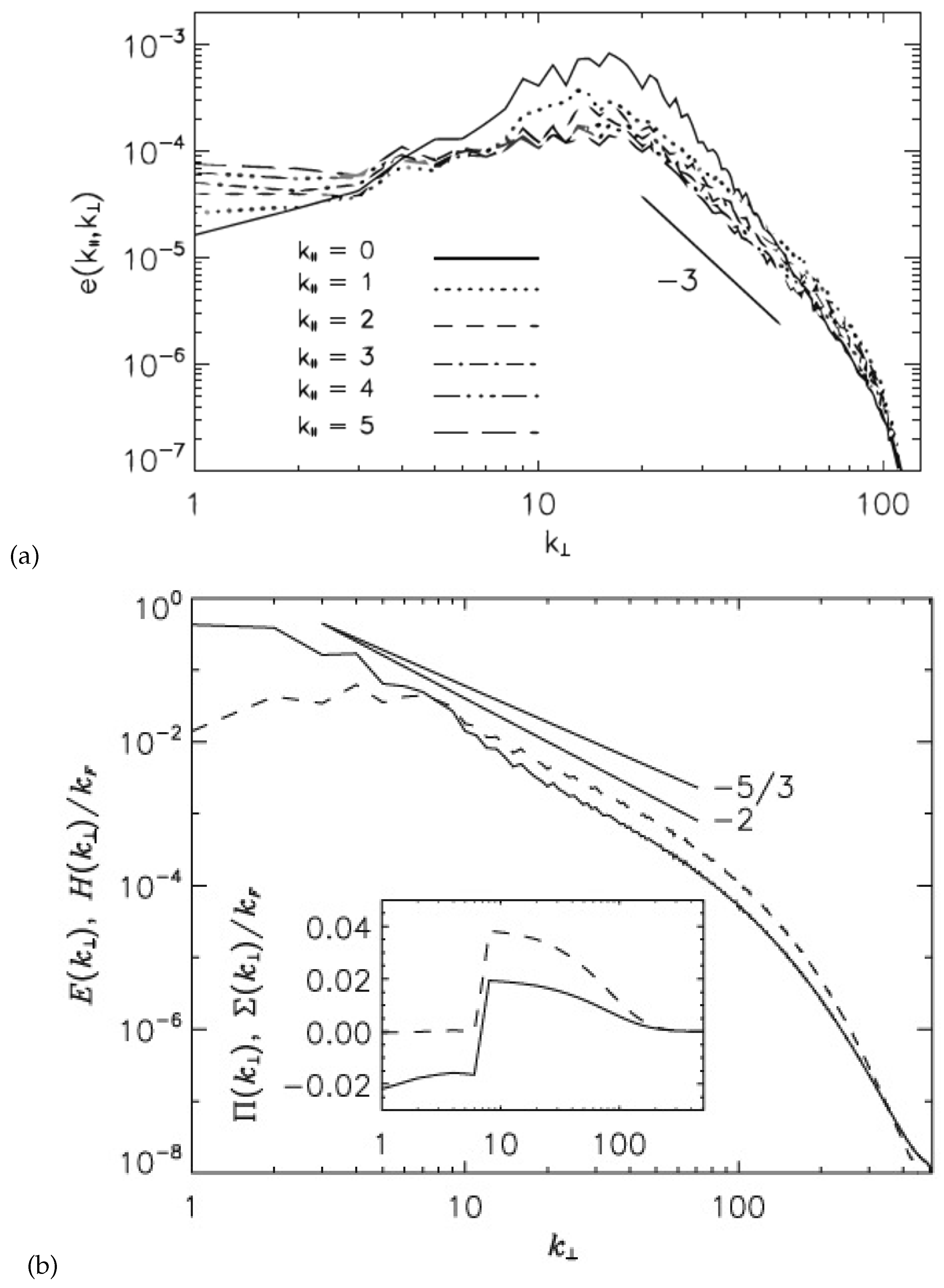
5.2.3. Physical Realizability of Spectrum Prescribed by Equation (43) and Comparison with Quasi-Normal Type Closures

Quasi-Normal family of closures (including modified versions like EDQNM) are well known statistical closures which are widely used in analytical study of turbulence [41,42,43,44]. However, as pointed out by Orszag [42], the original Quasi-Normal closure results in an unphysical negative energy spectrum. This issue was shown to be related to the presence of time-history integrals in the evolution equation of the correlation function. This was corrected in modified versions of the closure, such as Quasi-Normal Markovian and Eddy Damped Quasi-Normal Markovian (EDQNM) closures [37,42,45]. EDQNM is widely used in turbulence predictions and works well in the absence of waves [46]. However, as shown by Bowman et al. [46], Bowman and Krommes [47] and noted in [48,49], in the presence of waves, especially Rossby, inertial and drift waves, EDQNM is unphysical in the sense that the energy spectrum, obtained by performing the closure, becomes negative for dynamically important Fourier modes (see Figure 1 and Figure 2 in [46] and Figure 1 in [47]). This unphysical energy condition, in the presence of waves or mode coupling, is shown to stem from the violation of the realizability criterion $\Re \left\{{\theta }_{\mathbf{kpq}}(t)\right\}\ge 0,\forall t\ge 0$. This is because of the application of the fluctuation-dissipation ansatz that must be invoked in order to capture the two time correlation information within a single parameter, the triad interaction time ${\theta }_{\mathbf{kpq}}$ [50]. Conceptually, this loss of realizability can be checked for a test case by assuming the total damping coefficient to be constant in time but complex valued (e.g., purely imaginary), whence $\Re \left\{{\theta }_{\mathbf{kpq}}\right\}$ can be shown to be oscillatory about zero. In fact, Bowman [50] explicitly shows that the realizability condition is violated for an actual stochastic problem involving three-wave interactions (see ch. III in [50] for details). As a remedy, a realizable Markovian closure was proposed by Bowman et al. [46], Bowman and Krommes [47], Bowman [50].

In contrast, in this paper, a wave turbulence closure [7,30] is used as explained in Section 5.2.1. In this context, it is essential to check the physical realizability of the energy spectrum permitted by the kinetic system derived above. Following the strategy prescribed by Orszag [42] (cf. p. 313, ch. IV), we envision a scenario where, starting with a positive initial condition for the energy spectrum, we assume

$$e_{\mathbf{k}}>0\forall k-\left\{k^{*}\right\}\mathrm{and}\forall \tau \le {\tau }^{*},$$

$$e_{{\mathbf{k}}^{*}}>0\forall \tau <{\tau }^{*},\mathrm{and}{e}_{{\mathbf{k}}^{*}}=0\mathrm{at}\tau ={\tau }^{*}.$$

Here ∀ should be read as for all. The above assumptions mean that physically we have a situation where the energy in a certain mode ${\mathbf{k}}^{*}$ is null at time ${\tau }^{*}$. Specifically, note that $e_{{\mathbf{k}}^{*}}=0$ and $e_{\mathbf{p}},e_{\mathbf{q}}>0$ at $\tau ={\tau }^{*}$. The goal is to investigate if the energy becomes negative for this specific wave mode ${\mathbf{k}}^{*}$ at times $\tau >{\tau }^{*}$. By inspection, it is clear that

$${\partial }_{\tau }{e}_{{\mathbf{k}}^{*}}{|}_{\tau ={\tau }^{*+}}=\pi \int \left[|{\tilde{L}}_{k^{*}pq}{|}^2{\delta }_{{\mathbf{k}}^{*},\mathbf{pq}}{\delta }_{{\omega }_{k^{*}},{\omega }_p{\omega }_q}+2{|{\tilde{L}}_{p{k}^{*}q}|}^2{\delta }_{\mathbf{p},{\mathbf{k}}^{*}\mathbf{q}}{\delta }_{{\omega }_p,{\omega }_{k^{*}}{\omega }_q}\right]e_{\mathbf{p}}{e}_{\mathbf{q}}d\mathbf{p}d\mathbf{q}>0$$

(44)

because $e_{\mathbf{p}},e_{\mathbf{q}}{|}_{\tau ={\tau }^{*}}>0$ and the fact that the terms in the square parentheses are positive. The above inequality is obtained by substituting $e_{{\mathbf{k}}^{*}}=0$ in the r.h.s. of Equation (43) when evaluated at time ${\tau }^{*}$. This means that the mode with null energy receives energy from the interacting modes of the triad and the energy of that mode becomes positive, i.e., the nonlinear transfer to the mode ${\mathbf{k}}^{*}$ is positive and energy is dumped into this mode. The above argument can be extended to any wave mode and for all times $\tau >{\tau }^{*}$ in a straight forward manner. Thus, the spectrum prescribed by Equation (43), and obtained by the wave turbulence closure described in the previous section, is non-negative and physically realizable. This can be attributed to the absence of any time-history integrals in Equation (43). In fact, the separation of time scales, captured by relation (15), enables us to take the long time limit and thereby time dependent oscillatory terms are eliminated as shown in the short paragraph following Equation (41). It is essential to note that the above inequality does not comport with the stationary state of the spectrum for the obvious reason that the derivative is non-zero. So the spectrum eventually adjusts itself to the stationary state permitted by the kinetic system derived earlier and for which the power law solutions are given in a subsequent section.

5.2.4. Invariants of the Closed Kinetic Equations

It can be shown easily that the total interaction energy given by Equation (43) is conserved, i.e., ${\partial }_t\int e_{\mathbf{k}}d\mathbf{k}=0$ using the result of Appendix A.3. The proof in the appendix is essentially a statement of conservation of energy in each wave triad. The form of the interaction coefficient ensures the convergence of the collision integral appearing on the r.h.s. of Equation (43), thereby it meets the first criteria for the realizability of a Kolmogorov spectrum, i.e., stationary energy spectrum solution to (43) [36]. This point is elaborated in Section 5.2.6.

5.2.5. Kolmogorov Solution of the Kinetic Equations

The exact steady state solution of the kinetic Equation (43), as power laws, is obtained by assuming locality of the scale-by-scale energy transfer. This is illustrated in Nazarenko [7], Zakharov et al. [30] and earlier papers referenced therein.

Owing to the constrain imposed by the AT limit $k_Z\ll k_{\perp }$, the turbulence cascade under investigation is in the $k_{\perp }$ direction and $k_Z={\mathbb{B}}_r(k_0)$ (i.e., $k_Z$ is within a relatively small r vicinity of $k_0$) serves as a tracking parameter to ensure that we do not violate the condition: $\frac{k_Z}{k_{\perp }}\ll \mathcal{R}o\ll 1$. The four possible stationary solutions for the anisotropic spectrum, $e_{\mathbf{k}}\sim k_Z^{-x_i}{k}_{\perp }^{-y_i},\forall k_z\ne 0$, are listed as follows [7,30]:

(i)

$x_1=1$ and $y_1=-1$ (Rayleigh-Jeans (RJ) spectrum).

(ii)

$x_2=1$ and $y_2=0$.

(iii)

$x_3=(1+u)$ and $y_3=(2+v)$, where $2u$ and $2v$ are respectively the powers of $k_Z$ and $k_{\perp }$ in $|{\tilde{L}}_{kpq}{|}^2$. Clearly, in our case, $u=0,v=1$. Thus, $x_3=1$ and $y_3=3$.

(iv)

$x_4=1$ and $y_4=7/2$. This solution corresponds to the constant flux in the z-component of the momentum.

Solution (iii), above, corresponds to the only constant energy flux solution, a necessary requirement of Kolmogorov’s theory and of primary concern in this paper. The constancy of energy flux can be easily verified by noting that ${\partial }_t{E}_{\mathbf{k}}:={\partial }_t(2\pi k_{\perp }{e}_{\mathbf{k}})=-{\partial }_{k_{\perp }}\mathsf{\Pi }(k_{\perp },k_Z;t)$; whereby on integrating with respect to $k_{\perp }$ and demanding constant energy flux in the perpendicular direction, we can extract the aforementioned solution. Here, $\mathsf{\Pi }$ denotes the flux of energy. The direction of the flux can be ascertained by comparing the power law solutions of the RJ spectrum with that of the constant energy flux solution, i.e., since $-y_3<-y_1$, the energy cascade is direct and the energy flux is towards smaller scales ( p. 139 in ref. [7]). Thus, the exact solution for the Kolmogorov-Zakharov-Kuznetsov spectra with constant energy flux is as follows:

$$e_{\mathbf{k}}=e(k_{\perp },k_Z)\sim k_{\perp }^{-3}{k}_Z^{-1}.$$

(45)

This result is in agreement with experimental and computational simulations [17,22,23]. Additionally, LaCasce [51] has discussed the observation of a $k^{-3}$ spectrum in the context of barotropic vorticity model using data obtained from several numerical simulations. Moreover, since ${lim}_{k_{\perp }\to \infty }\int e_{\mathbf{k}}d\mathbf{k}$ converges for the spectrum (45), the Kolmogorov spectrum obtained above has finite capacity [7]. The limit $k_{\perp }\to \infty$ is further discussed in the next section.

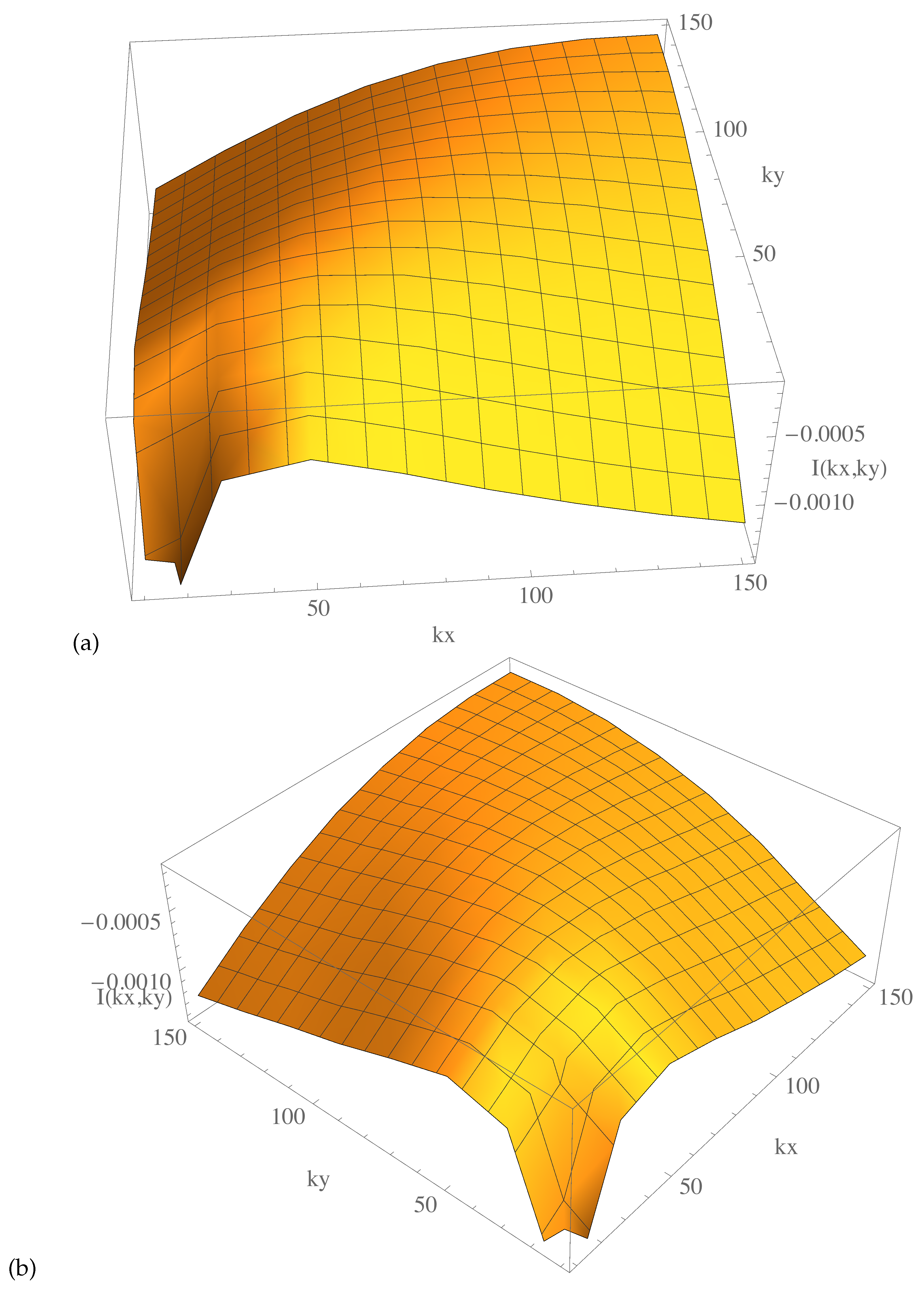
5.2.6. Locality of Interactions and Convergence of Collision Integral

As stated in the previous section, the Kolmogorov solutions obtained above are based on the assumption of locality of interactions. To validate the applicability of the locality assumption, it is sufficient to comment on the convergence of the collision integral on the r.h.s. of Equation (43) for the concerned power law solution [7,30,36]. However, analyzing the convergence of the collision integral is a delicate task [52] and a rigorous commentary is not within the scope of this paper. However, in this section, we will argue on the convergence of the collision integral given by the r.h.s. of Equation (43) based on inspection of the terms in the integrand, the surface over which the integration is performed and numerical integration of the same within the region of validity of the AT limit of R-RHD.

The integral in Equation (43) is in six dimensions, viz., $\int \int \int \int \int \int (···)d{p}_{x}d{p}_{y}d{p}_{Z}d{q}_{x}d{q}_{y}d{q}_Z$ if we further consider the decomposition of the perpendicular modes, ${\mathbf{k}}_{\perp }=(k_x,k_y)$. We have four delta functions, viz., three over the wave numbers and one over the frequency. Integrating over each delta function reduces the dimension of integration by one. So by substituting $\mathbf{q}=\pm (\mathbf{k}-\mathbf{p})$ in the respective integrands, we can completely eliminate integration over the three $\mathbf{q}$ wave numbers. Consequently, re-writing the frequency resonance condition in terms of the substituted expressions for $q_Z$ and ${\mathbf{q}}_{\perp }$, we finally have a surface integral over $p_x$ and $p_y$ dimensions where the surface is defined by $p_Z(p_x,p_y)$. This is illustrated concisely as follows.

$$\begin{array}{cc}\hfill q_i=\pm (k_i-p_i),& i=x,y,Z,\mathrm{where}+\mathrm{is}\mathrm{taken}\mathrm{for}\mathrm{the}\mathrm{first}\mathrm{integrand}\mathrm{and}-\mathrm{for}\mathrm{the}\sec \mathrm{ond}.\hfill \\ \hfill S:& p_Z(p_x,p_y)=\frac{p_{\perp }{k}_Z}{k_{\perp }}\frac{\left(\sqrt{{(k_x-p_x)}^2+{(k_y-p_y)}^2}-\sqrt{k_x^2+k_y^2}\right)}{\left(\sqrt{{(k_x-p_x)}^2+{(k_y-p_y)}^2}-\sqrt{p_x^2+p_y^2}\right)}.\hfill \end{array}$$

(46)

Here $S\equiv p_Z(p_x,p_y)$ defines the surface over which the integration is carried out when the collision integral is projected on the $(p_x,p_y)$ plane. Interestingly, and conveniently, the surface of integration turns out to be identical for both the first and second integrands when projected on the $(p_x,p_y)$ plane. By inspection, the surface S is singular at $k_{\perp }=0$ and $\left(\sqrt{{(k_x-p_x)}^2+{(k_y-p_y)}^2}-\sqrt{p_x^2+p_y^2}\right)=0$. Clearly, $k_{\perp }=0$ is outside the validity of AT because we must have $k_Z\ll k_{\perp },k_Z>0$, so we must not be concerned about the pole at $k_{\perp }=0$. The second condition requires more careful inspection. It defines the equation of a plane in the $(p_x,p_y)$ coordinates because it can be expressed as

$$\alpha p_x+p_y=\frac{{\alpha }^2+1}{2}k,\mathrm{where}{k}_x=\alpha k_y=\alpha k.$$

(47)

Figure 3 illustrates this singular plane on the surface S for two distinct limiting wavenumber configurations: $\alpha =1\Rightarrow p_x+p_y=k$ and $\alpha \ll 1\Rightarrow p_y=k/2$ ($\alpha \gg 1$ is just the opposite case). Equation (47) can also be re-written as follows,

$$\begin{array}{c}(k_x{p}_x+k_y{p}_y)=\frac{1}{2}(k_x^2+k_y^2)\Rightarrow {\mathbf{k}}_{\perp }·{\mathbf{p}}_{\perp }=\frac{1}{2}{k}_{\perp }^2,\mathrm{or}\mathrm{equivalently},{\mathbf{p}}_{\perp }=\frac{1}{2}{\mathbf{k}}_{\perp },\hfill \end{array}$$

(48)

This implies that for the first integral corresponding to the collision integral in Equation (43), we have ${\mathbf{q}}_{\perp }=\frac{1}{2}{\mathbf{k}}_{\perp }$ because of ${\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}$, whence we have ${\mathbf{p}}^{\perp }·{\mathbf{q}}_{\perp }=0$ and thereby ${\tilde{L}}_{kpq}\equiv 0$. Similarly for the second integral we have ${\mathbf{q}}_{\perp }=-\frac{1}{2}{\mathbf{k}}_{\perp }$ because of ${\delta }_{\mathbf{p},\mathbf{k}\mathbf{q}}$ from which we have ${\mathbf{k}}^{\perp }·{\mathbf{q}}_{\perp }=0$ and thereby ${\tilde{L}}_{pkq}\equiv 0$. This means that the integrand is identically zero on the singular plane on S and hence the integration along this singularity may be safely circumvented without blow up. Similarly, averting $p_Z=0$ demands $k_Z\ne 0$ (always true) and ${\mathbf{k}}_{\perp }\ne \frac{1}{2}{\mathbf{p}}_{\perp }$. The latter condition is ensured because ${\tilde{L}}_{kpq},{\tilde{L}}_{pkq}\equiv 0$ when ${\mathbf{k}}_{\perp }=\frac{1}{2}{\mathbf{p}}_{\perp }$ based on very similar arguments as mentioned above.

There are two other regions in Figure 3 that stand out for inspection, viz., $(p_x,p_y)=(0,0)$ and $k_x=p_x,k_y=p_y$ for the value of the integrand is high at these points due to the large values of ${\tilde{L}}_{kpq}$ and ${\tilde{L}}_{pkq}$. These correspond to $p_{\perp }=0$ and $q_{\perp }=0$ respectively and for reasons discussed above are outside the region of validity of AT (R-RHD). Hence these points do not contribute to the integral. In general, the anisotropic limit $\frac{k_Z}{k_{\perp }},\frac{p_Z}{p_{\perp }},\frac{q_Z}{q_{\perp }}\ll 1$ ensures that the region of integration is typically farther away from the singular plane defined by (47) where the value of the integrand is diminishingly small as can be seen from the contour plots in Figure 3. So we know at the very least that we are safe in terms of blow up of the integrand. However, we must still investigate whether or not the accumulation of these small values of the integrand increase in an unbounded fashion over a reasonably large radial wavenumber in the ${\mathbf{k}}_{\perp }$ plane. In order to check this we resort to numerical evaluation of the collision integral (The singular points are carefully excluded for they are found to be inconsequential as discussed above) for a range of perpendicular wave numbers. The general form of the collision integral in the kinetic Equation (43) upon projection on the $(p_x,p_y)$ plane is

$$\begin{array}{cc}\hfill I(k_{\perp },k_Z)& =\underset{S}{\int \int }\left(|{\tilde{L}}_{kp(k-p)}{|}^2(e_{\mathbf{p}}{e}_{\mathbf{k}-\mathbf{p}}-e_{\mathbf{k}}{e}_{\mathbf{p}}-e_{\mathbf{k}}{e}_{\mathbf{k}-\mathbf{p}})-2{|{\tilde{L}}_{pk(p-k)}|}^2(e_{\mathbf{k}}{e}_{\mathbf{p}-\mathbf{k}}-e_{\mathbf{p}}{e}_{\mathbf{k}}-e_{\mathbf{p}}{e}_{\mathbf{p}-\mathbf{k}})\right)dS\hfill \\ & =\underset{p_Z\ne 0,p_{\perp }\gg 0}{\int \int }({|{\tilde{L}}_{kp(k-p)}|}^2(e_{\mathbf{p}}{e}_{\mathbf{k}-\mathbf{p}}-e_{\mathbf{k}}{e}_{\mathbf{p}}-e_{\mathbf{k}}{e}_{\mathbf{k}-\mathbf{p}})\hfill \\ & -2|{\tilde{L}}_{pk(p-k)}{|}^2(e_{\mathbf{k}}{e}_{\mathbf{p}-\mathbf{k}}-e_{\mathbf{p}}{e}_{\mathbf{k}}-e_{\mathbf{p}}{e}_{\mathbf{p}-\mathbf{k}}))\sqrt{{\left(\frac{\partial p_Z}{{\partial }_{p_x}}\right)}^2+{\left(\frac{\partial p_Z}{{\partial }_{p_y}}\right)}^2+1}d{p}_{x}d{p}_y\end{array}$$

(49)

The analytic expression for the Jacobian term $\sqrt{{\left(\frac{\partial p_Z}{{\partial }_{p_x}}\right)}^2+{\left(\frac{\partial p_Z}{{\partial }_{p_y}}\right)}^2+1}$ is too messy to be written explicitly here but can be inspected symbolically using the computer program attached in the Appendix A.5. Most importantly, this term shares the location of the poles with that of the surface $S=p_Z(p_x,p_y)$. Hence no additional caution is required for this term. Since we are interested in analyzing the convergence of this integral, we have ignored the constant multiplier on the r.h.s. of Equation (43). We numerically integrate the function (the integrand in expression (50)) over the surface S defined by Equation (46) by two different methods, viz., adaptive quadrature method and adaptive Monte Carlo method. The numerical integration is performed over S by excluding the singular points described in the previous paragraph as the singularities were either outside the region of validity of AT (R-RHD), i.e., outside the region where $k_Z/k_{\perp }\ll 1$ is true or occurred at points where the integrand is identically zero. The computer program used to generate the plots in this section is given in Appendix A.5. By analyzing Figure 4, it is evident that by staying within the region of validity of AT (R-RHD), as has been elaborated above in this section, the collision integral is convergent. Moreover, it is clear from the results of the numerical integration that the convergence holds for reasonably large values of ${\mathbf{k}}_{\perp }$ thereby permitting an energy cascade to develop. Figure 4 shows that the collision integral on the ${\mathbf{k}}_{\perp }$ plane plateaus away from the boundary of integration (at the boundary, the numerical integration is less accurate) and is very nearly zero as is expected for a stationary solution.

In this section, we have provided direct evidence of the convergence of the collision integral $I(k_{\perp },k_Z)$ by numerical computation to validate the applicability of the locality assumption for seeking the Kolmogorov constant energy flux solution. For a rigorous analysis of convergence of collision integrals in a three wave system, one may refer to the work by Connaughton [52]. Additionally, it is important to note that analysis of stability and evolutionary non-locality of concerned spectra subject to extra perturbative forcing in this anisotropic limit is beyond the scope of the current paper and the interested reader is referred to the work of Balk and Nazarenko [36] and Nazarenko [7] for details.

6. Non-Zero Helicity Dynamics: Interplay of Energy and Helicity

In this section, we deduce a general set of coupled equations for the two invariants of the flow. This is done by formally extending the symmetrical system of the previous section.

6.1. Coupled Equations for Energy and Helicity

Recall that the assumption, $c_{\mathbf{k}}^{-}=c_{\mathbf{k}}^{*}\equiv c_{\mathbf{k}}^{+*}$ implies $h_{\mathbf{k}}=0$, i.e., $\frac{1}{2}{e}_{\mathbf{k}}=e_{\mathbf{k}}^{+}=e_{\mathbf{k}}^{-}$. However, on relaxing such an assumption, a coupled set of equations for energy and helicity may be arrived at by using Equation (28) in Equation (43) (cf. $e_{\mathbf{k}}$ in Equation (43) is actually $e_{\mathbf{k}}^{+}\equiv e_{\mathbf{k}}^{-}$). Thus the closed form coupled energy-helicity equation becomes,

$$\begin{array}{cc}\hfill {\partial }_{\tau }\left(e_{\mathbf{k}}\pm \frac{h_{\mathbf{k}}}{k_{\perp }}\right)& =\frac{\pi }{2}\int \left[{|{\tilde{L}}_{kpq}|}^2\right\{\left(e_{\mathbf{p}}\pm \frac{h_{\mathbf{p}}}{p_{\perp }}\right)\left(e_{\mathbf{q}}\pm \frac{h_{\mathbf{q}}}{q_{\perp }}\right)-\left(e_{\mathbf{k}}\pm \frac{h_{\mathbf{k}}}{k_{\perp }}\right)\left(e_{\mathbf{p}}\pm \frac{h_{\mathbf{p}}}{p_{\perp }}\right)\hfill \\ & -\left(e_{\mathbf{k}}\pm \frac{h_{\mathbf{k}}}{k_{\perp }}\right)\left(e_{\mathbf{q}}\pm \frac{h_{\mathbf{q}}}{q_{\perp }}\right)\}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}{\delta }_{{\omega }_k,{\omega }_p{\omega }_q}-2{|{\tilde{L}}_{pkq}|}^2\{\left(e_{\mathbf{k}}\pm \frac{h_{\mathbf{k}}}{k_{\perp }}\right)\left(e_{\mathbf{q}}\pm \frac{h_{\mathbf{q}}}{q_{\perp }}\right)\hfill \\ & -\left(e_{\mathbf{p}}\pm \frac{h_{\mathbf{p}}}{p_{\perp }}\right)\left(e_{\mathbf{k}}\pm \frac{h_{\mathbf{k}}}{k_{\perp }}\right)-\left(e_{\mathbf{p}}\pm \frac{h_{\mathbf{p}}}{p_{\perp }}\right)\left(e_{\mathbf{q}}\pm \frac{h_{\mathbf{q}}}{q_{\perp }}\right)\left\}{\delta }_{\mathbf{p},\mathbf{k}\mathbf{q}}{\delta }_{{\omega }_p,{\omega }_k{\omega }_q}\right]d\mathbf{p}d\mathbf{q}.\hfill \end{array}$$

(50)

The individual evolution equation for $e_{\mathbf{k}}$ (and $h_{\mathbf{k}}$) follows by adding (and subtracting) the two set of equations expressed concisely by Equation (50) and is given as follows:

$$\begin{array}{c}{\partial }_{\tau }{e}_{\mathbf{k}}\hfill \\ =\frac{\pi }{2}\int [{|{\tilde{L}}_{kpq}|}^2\left\{\left(e_{\mathbf{p}}{e}_{\mathbf{q}}+\frac{h_{\mathbf{p}}{h}_{\mathbf{q}}}{p_{\perp }{q}_{\perp }}\right)-\left(e_{\mathbf{k}}{e}_{\mathbf{p}}+\frac{h_{\mathbf{k}}{h}_{\mathbf{p}}}{k_{\perp }{p}_{\perp }}\right)-\left(e_{\mathbf{k}}{e}_{\mathbf{q}}+\frac{h_{\mathbf{k}}{h}_{\mathbf{q}}}{k_{\perp }{q}_{\perp }}\right)\right\}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}{\delta }_{{\omega }_k,{\omega }_p{\omega }_q}\hfill \\ -2|{\tilde{L}}_{pkq}{|}^2\left\{\left(e_{\mathbf{k}}{e}_{\mathbf{q}}+\frac{h_{\mathbf{k}}{h}_{\mathbf{q}}}{k_{\perp }{q}_{\perp }}\right)-\left(e_{\mathbf{k}}{e}_{\mathbf{p}}+\frac{h_{\mathbf{k}}{h}_{\mathbf{p}}}{k_{\perp }{p}_{\perp }}\right)-\left(e_{\mathbf{p}}{e}_{\mathbf{q}}+\frac{h_{\mathbf{p}}{h}_{\mathbf{q}}}{p_{\perp }{q}_{\perp }}\right)\right\}{\delta }_{\mathbf{p},\mathbf{k}\mathbf{q}}{\delta }_{{\omega }_p,{\omega }_k{\omega }_q}]d\mathbf{p}d\mathbf{q},\hfill \end{array}$$

(51)

and

$$\begin{array}{c}{\partial }_{\tau }{h}_{\mathbf{k}}\hfill \\ =\frac{\pi }{2}\int k_{\perp }[{|{\tilde{L}}_{kpq}|}^2\left\{\left(e_{\mathbf{p}}\frac{h_{\mathbf{q}}}{q_{\perp }}+e_{\mathbf{q}}\frac{h_{\mathbf{q}}}{q_{\perp }}\right)-\left(e_{\mathbf{k}}\frac{h_{\mathbf{p}}}{p_{\perp }}+e_{\mathbf{p}}\frac{h_{\mathbf{k}}}{k_{\perp }}\right)-\left(e_{\mathbf{k}}\frac{h_{\mathbf{q}}}{q_{\perp }}+e_{\mathbf{q}}\frac{h_{\mathbf{k}}}{k_{\perp }}\right)\right\}{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}{\delta }_{{\omega }_k,{\omega }_p{\omega }_q}\hfill \\ -2|{\tilde{L}}_{pkq}{|}^2\left\{\left(e_{\mathbf{k}}\frac{h_{\mathbf{q}}}{q_{\perp }}+e_{\mathbf{q}}\frac{h_{\mathbf{k}}}{k_{\perp }}\right)-\left(e_{\mathbf{k}}\frac{h_{\mathbf{p}}}{p_{\perp }}+e_{\mathbf{p}}\frac{h_{\mathbf{k}}}{k_{\perp }}\right)-\left(e_{\mathbf{p}}\frac{h_{\mathbf{q}}}{q_{\perp }}+e_{\mathbf{q}}\frac{h_{\mathbf{q}}}{q_{\perp }}\right)\right\}{\delta }_{\mathbf{p},\mathbf{k}\mathbf{q}}{\delta }_{{\omega }_p,{\omega }_k{\omega }_q}]d\mathbf{p}d\mathbf{q}.\hfill \end{array}$$

(52)

Equations (51) and (52) clearly reveal the coupled dynamics of energy and helicity in a rapidly rotating fluid flow. The possibility of recovering the total energy and helicity spectrum from the simpler zero helicity case relies on extending the functional on the right hand side of Equation (43) to the non-zero helicity case.

In essence, we have taken a special case of the kinetic equations which has the functional form ${\partial }_t{e}_{\mathbf{k}}=f(\mathbf{k})$ (think of $f(\mathbf{k})$ as the right hand side of Equation (43)) where $h_{\mathbf{k}}=0$, and extended it to the more general case where $h_{\mathbf{k}}\ne 0$. In this general case, the domain of $f(\mathbf{k})$ is still the positive real line because the inequality $|h_{\mathbf{k}}|\le k_{\perp }{e}_{\mathbf{k}}$ implies that $h_{\mathbf{k}}$ and $e_{\mathbf{k}}$ are not independent variables and $e_{\mathbf{k}}\pm \frac{h_{\mathbf{k}}}{k_{\perp }}\ge 0$ is always true. Hence, we have extended the applicability of the kinetic equation from the simpler symmetric case (where $c_{\mathbf{k}}^{*}=c_{\mathbf{k}}^{-}$ because $h_{\mathbf{k}}=0$) to the more general case with non-trivial helicity. This way we have circumvented tedious algebraic computations involving multiple correlation functions (to account for the departure in mirror symmetry in the fully helical case) by first, reducing the Hamiltonian system by invoking reflection symmetry and then formally extending the symmetrical system to the more general helical case. The applicability and implication of this procedure is explained in more details in [38].

6.2. Generalized Solution of Energy and Helicity Spectra

Note that Equation (28) are consistent with the definitions, $e_{\mathbf{k}}=e_{\mathbf{k}}^{+}+e_{\mathbf{k}}^{-}$ and $h_{\mathbf{k}}=k_{\perp }(e_{\mathbf{k}}^{+}-e_{\mathbf{k}}^{-})$. Clearly, the power law solutions do not change for the non-zero helicity case because the homogeneity of the interaction coefficient and the linear dispersion relation remains the same. Thus, $e_{\mathbf{k}}\sim k_{\perp }^{-3}$ for $h_{\mathbf{k}}\ne 0$. Dimensional analysis implies, $h_{\mathbf{k}}\sim k_{\perp }{e}_{\mathbf{k}}\sim k_{\perp }^{-2}$ that is consistent with earlier findings based on numerical simulations [21]. The cylindrically symmetric solutions are:

$$E_{k_{\perp }}=(2\pi k_{\perp }{e}_k)\sim k_{\perp }^{-2},\mathrm{and}{H}_{k_{\perp }}=(2\pi k_{\perp }{h}_k)\sim k_{\perp }^{-1}.$$

(53)

The power law solution obtained here pertains to the perpendicular cascade within the slow manifold, the reader is referred to Bellet et al. [53] for power law solutions of the spectrum in the axial direction. It is important to note that the solutions given by Equation (53) are different from the ones discussed in Pouquet and Mininni [24] as the latter assume isotropy in their arguments to show that the sum of the powers of the wave numbers for $E_{\mathbf{k}}$ and $H_{\mathbf{k}}$ is equal to 4. The solution set of Galtier [8] belongs to the regime where the effect of fast inertial waves is dominant. In the recent work of Galtier [9], it has been shown that within the theory developed in the earlier work of Galtier [8], the power law solutions can be generalized to the empirical form presented in [24]. In contrast, the analysis presented here captures the dynamics in the slow manifold where the flow is highly anisotropic and the effect of the fast inertial waves is sub-dominant, and accounts for a distinct separation of temporal scales, t and $\tau$ as is necessary [16] and explained in the introductory section here. In such a regime in the slow manifold that is devoid of fast inertial wave modulation and where the dynamic is well captured by the R-RHD equations, the stationary power law solutions, that are entirely dependent on the functional form of the interaction term $\tilde{L}$ and the dispersion relation ${\omega }_{\mathbf{k}}$, are given by Equation (53) and is in agreement with results from numerical simulations (e.g., the work of Mininni and Pouquet [21], Teitelbaum and Mininni [22]). It may be interesting to point out here that an identical $k_{\perp }^{-2}$ spectrum for $E_{\perp }^{\pm }$ has been reported in the case of anisotropic MHD turbulence of Alfven waves in the presence of strong external magnetic field (where dominant modes are $k_z\ll k_{\perp }$) [7,34,54]. The analytical results for the anisotropic MHD case were developed based on the reduced MHD model referenced in [7]. Thus it may not be surprising to draw an analogy between the anisotropic MHD wave turbulence and the anisotropic hydrodynamic case discussed in the current paper where the strong magnetic field plays the role of rapid rotation, and the polarized Alfven waves are congruent to the helical inertial waves discussed here (please see the

Table 1. Kinetic wave turbulence: features and parameters.

	Reduced HD	Reduced MHD	Full HD	Critical Balance HD
	(Current Paper)	(Ref. [7,34])	(Ref. [8])	(Ref. [7,27])
name	anisotropic wave	anisotropic wave	weak wave	strong wave
of model	turbulence (AT)	turbulence (AT)	turbulence (WT)	turbulence (CB)
dynamical	strong ${\mathsf{\Theta }}_0$ &	strong $B_0$ &	strong ${\mathsf{\Theta }}_0$	waves balance
features	strong anisotropy	strong anisotropy		nonlinearity
waves	slow inertial	slow Alfven	fast inertial	fast inertial
	waves	waves	waves	waves
anisotropy	very	very	moderate	moderate
(smallness of $\frac{k_Z}{k_{\perp }}$)	strong	strong	to isotropic	to isotropic
governing	kin. eq. deduced	kin. eq. deduced	kin. eq. deduced	unknown
equation	from reduced HD	from reduced MHD	from full HD
			(Navier Stokes)
wave amplitude	weak	weak	weak	large
& nonlinearity
order	$ϵ=\frac{k_Z}{k_{\perp }}\ll 1$	$ϵ=\frac{c_k^{\prime }}{B_0}\ll 1$	$ϵ=\mathcal{R}o\ll 1$	—
parameter	(also, $\frac{k_Z}{k_{\perp }}\ll \mathcal{R}o)$	(also, $\frac{k_Z}{k_{\perp }}\ll 1)$
$E_{k_{\perp }}$	$k_{\perp }^{-2}$	$k_{\perp }^{-2}$	$k_{\perp }^{-5/2}$	$k_{\perp }^{-2}$
spectra

HD = Hydrodynamics; MHD = Magneto-hydrodynamics; CB = critical balance; $\mathcal{R}o=$ Rossby number; ${\mathsf{\Theta }}_0=$ strength of external rotation in reduced HD and full HD; $B_0=$ strength of external magnetic field in reduced MHD; $c_k^{\prime }=$ amplitude fluctuation in reduced MHD; $ϵ=$ order parameter in the perturbative expansion of the amplitudes; kin. eq. = kinetic equation.

in Appendix A.4).

The important point to note here is that rotating turbulence encompasses several different and distinct dynamical regimes, each with distinct set of solutions. Hence, the importance of using reduced equations for distinct asymptotic limits as has been explained by Nazarenko and Scheckochihin [27] (see Appendix A of [27]). Within such a distinct limit of rapid rotation, the R-RHD equations have been derived [14,15,26,27] and a multiple scales perturbation method has been applied in this paper for the asymptotically reduced equations. In the following sections, we attempt to stitch together the important results of weak and strong turbulence of different dynamical regimes in order to clarify the picture of turbulent cascade that has evolved based on recent research literature.

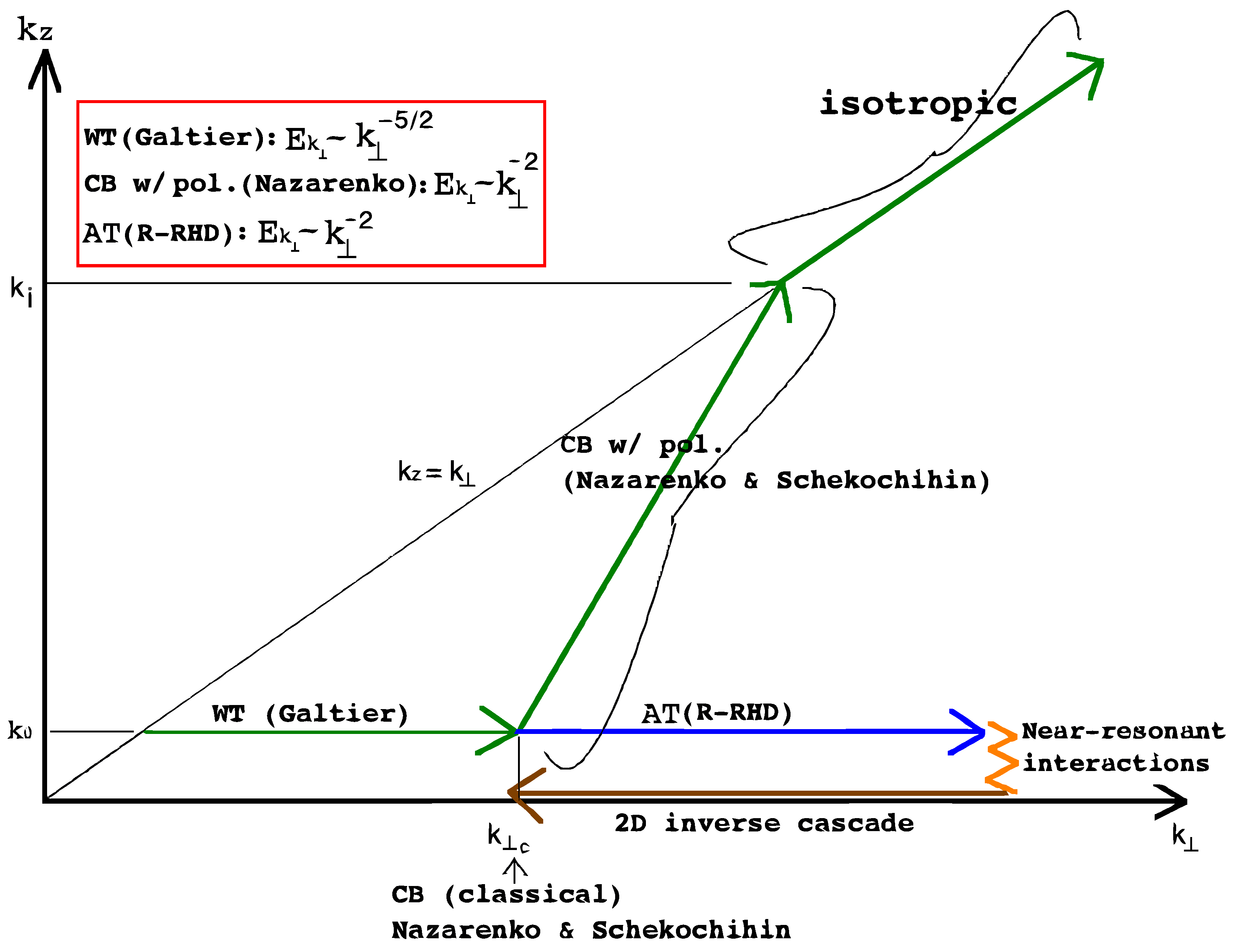
6.3. Hierarchy of Slow Manifolds in Anisotropic Wave Turbulence Diverges from the Critical Balance Route towards Isotropy

The discussion in this section is motivated by the turbulence cascade picture presented by Nazarenko and Scheckochihin [27]. We modify the turbulent cascade schematic based on the results presented here.

The critical balance with polarization alignment argument presented by Nazarenko and Scheckochihin [27] is an attempt to explain the $k_{\perp }^{-2}$ energy spectra observed in several numerical simulations of rotating turbulence [17,21,22,55]. However, as is evident from Figure 5 and the corresponding sketch in [27], the critical balance with polarization alignment leads to a departure from anisotropy and is a path to the recovery of isotropic scales that are prevalent above the Zeeman wavenumber [23]. It must be emphasized that anisotropy is dominant in rotating turbulent flows. It is in this light, we believe that the energy spectra $k_{\perp }^{-2}$ is obtained for anisotropic wave turbulence in the regime of R-RHD defined by AT (${\omega }_f{T}_{\tau }\gg {\omega }_s{T}_{\tau }\gg 1,{\omega }_s{T}_f\ll 1$ and $k_Z\ll k_{\perp }$). In this anisotropic regime, the slow inertial wave frequency is much smaller than the fast inertial wave frequency. This solution prevails as the flow traverses a hierarchy of slow manifold regions with successively decreasing $\frac{k_Z}{k_{\perp }}$ and is the anisotropic wave turbulence solution for the energy spectra within the slow manifold. In summary, there seems to be a bifurcation of the energy spectral solution at the critical balance wavenumber (see Figure 5), two distinct spectra evolve, each with a $k_{\perp }^{-2}$ energy spectra: one leading towards the isotropic scale via critical balance and hence falls within the realm of strong turbulence (Strong wave turbulence is fairly complicated (see secs. 3.2 and 14.6 in [7]) because the wave amplitudes can be $\mathcal{O}(1)$ or higher [56] and the perturbative expansion may not be readily possible. Its description is incomplete as stated by Nazarenko [7]), and the other towards highly anisotropic horizontal scales with $k_Z\ll k_{\perp }$ sustained by small amplitude resonating wave modes.

6.4. Comparison with Weak Turbulence Theory of Galtier

In this section, we contrast the theory presented here with earlier works [8,9]. The main distinctive features are listed below.

• The governing equations on which the wave turbulence theory [8,9] is developed are the Navier-Stokes equations (i.e., Equation (1)). In these equations, the Rossby number $\mathcal{R}o$ appears explicitly and is used as an order parameter in the perturbation analysis and the fast inertial wave dynamic is dominant. In contrast, the governing equations for the analysis presented here are the R-RHD (i.e., Equations (5) and (6)). The asymptotic limit of infinitesimally small $\mathcal{R}o$ is already accounted for in the multiple scales analysis to derive the R-RHD and hence do not explicitly appear in the R-RHD equations. This means that the effect of fast inertial waves is sub-dominant here and the R-RHD equations are hence suitably applicable for the slow manifold dynamics.
• The dynamical regime where the theory [8,9] is valid is ${\omega }_f{T}_{\tau }\gg 1,{\omega }_f{T}_s\gg 1$. This point has been elaborated in great detail in the work of Nazarenko and Scheckochihin [27] (see Section 2 in [27]). The dynamical regime of the R-RHD is ${\omega }_f{T}_{\tau }\gg {\omega }_s{T}_{\tau }\gg 1,{\omega }_s{T}_f\ll 1$ and $k_z\ll k_{\perp }$. It is the limit in which $k_z$ is so small that the turbulent dynamic is populated by slow inertial waves with dispersion relation ${\omega }_k=\frac{k_Z}{k_{\perp }}$ embodying slow oscillations when $\frac{k_Z}{k_{\perp }}\ll 1$ (also see Figure 5 above). In other words, within the slow manifold, $k_z$ is so small that $\frac{k_Z}{k_{\perp }}\ll \mathcal{R}o\ll 1$. The perturbative analysis presented here is applied to the R-RHD where the smallness (weakness) of the wave amplitude is measured by $ϵ\ll 1$ and the slow dispersive three wave system undergoes weak non-linear exchanges at the asymptotic order ${ϵ}^2$ as explained earlier in Section 4 and Section 5.
• In wave turbulence theory of Galtier [8] and Galtier [9], the kinetic equations for energy and helicity are derived by using multiple correlation functions to capture the energetics as well as the absence of symmetry due to helicity. This makes the calculations tediously lengthy. In contrast, the derivation for the helicity kinetic equation is presented here as a natural extension of the symmetrical non-helical system and bypasses the use of calculations using multiple correlation functions. This simpler approach follows a more general philosophy of Hamiltonian reduction exploiting symmetries in the system [25] and their natural extension to understanding asymmetrical phenomena.
• Finally, the spectral power laws obtained for the energy cascade are distinctly different as explained concisely in Figure 5.

Despite the fundamental differences in the region of validity of the two theories, they present a more detailed recipe to better understand turbulent energetics and cascades for rotating flows. A simple schematic towards this goal is presented in Figure 5 above to highlight the key findings in this field.

6.5. Comparison with Weak Turbulence Theory of Newell: Cumulant Hierarchy vs. Wave Amplitude Hierarchy

The fundamental difference between the multiple scales perturbation technique employed in this paper to derive the kinetic equations and the weak wave turbulence theory reviewed by Newell et. al [39] is explained in the following paragraphs.

Weak turbulence calculations, as reviewed by Newell et. al. [39], are computed by taking the closure in the limit $T\to \infty$. The third and higher order cumulants survive at the advective timescale (${\tau }_{NL}$) in the presence of fast inertial waves. This implies prevalence of non-Gaussian statistics. This is the reason for writing a hierarchal system for the cumulants in the perturbation approach, cf. Newell et. al. [39], rather than for the Fourier amplitudes.

The dynamics explained here elapse at the much slower advective time scale (${\tau }_{NL}$) compared to the faster wave timescale $T\to \infty$. At this slower time scale, it is assumed that the third (and higher odd) order cumulants are sub-dominant thereby corroborating the suitability of Gaussian statistics for the wave field. This aspect is detailed by Nazarenko [7] (see p. 64 in Section 5.6). This justifies the applicability of Wick’s theorem in the derivation of the kinetic equations. Consequently, this is also why we employed a hierarchal expansion for the wave amplitude in Equation (18).

7. Coupling between Wave and 2D Modes Through Non-Resonant Interactions

Neither the theory presented in [8] nor the model presented in this manuscript address the issue about the possibility of wave modes pumping the 2D modes. Note that ${\tilde{L}}_{kpq}=0$ when $k_Z=0$ because of the fact that $p_{\perp }=q_{\perp }$. Thus, within the framework of purely resonating wave triads, it is not possible to establish the coupling between wave and purely 2D modes. This should not be surprising because the theory developed is that of dispersive waves that are in resonance. However, a rather phenomenological explanation may be insightful for explaining the coupling between wave and 2D modes, as is presented below.

Suppose that in Equation (22), the triadic resonance condition is modified such that $\varphi (\omega )=s_k{\omega }_k-s_p{\omega }_p-s_q{\omega }_q={\delta }_{\omega }\ll ϵ,{\delta }_{\omega }\ne 0$. This condition represents non-resonant (or near-resonant) interaction of the three wave modes. For small $\frac{{\delta }_{\omega }}{ϵ}\tau$, Taylor expansion implies,

$$e^{i\frac{{\delta }_{\omega }}{ϵ}\tau }\approx 1+i\frac{{\delta }_{\omega }}{ϵ}\tau +...$$

(54)

i.e.,

$$e^{i\frac{{\delta }_{\omega }}{ϵ}\tau }\approx {\left({\delta }_{{\omega }_k^{s_k},{\omega }_p^{s_p}{\omega }_q^{s_q}}\right)}_{{\delta }_{\omega }=0}+i\frac{{\delta }_{\omega }}{ϵ}\tau +....$$

(55)

Thus computing the fast time integral after Taylor-expanding the exponential term reveals that the higher order slow secular terms (cf. presence of $\tau$ in the higher order terms) are inherently embedded in the full system that is not restricted to resonating triadic wave interactions only. These terms account for the coupling with the 2D modes. This is evident by re-writing Equation (22) with the higher order terms as follows,

$$\begin{array}{cc}\hfill i{\partial }_{\tau }{c}_{\mathbf{k}}^{s_k}& =\frac{1}{2}\sum _{s_p,s_q}\int V_{kpq}^{s_k{s}_p{s}_q}{c}_{\mathbf{p}}^{s_p}{c}_{\mathbf{q}}^{s_q}\left[\frac{1}{T}\underset{T}{\int }\underset{\mathrm{res}}{\underbrace{{\left({\delta }_{{\omega }_k^{s_k},{\omega }_p^{s_p}{\omega }_q^{s_q}}\right)}_{{\delta }_{\omega }=0}}}+\underset{\mathrm{non}-\mathrm{res}}{\underbrace{i\frac{{\delta }_{\omega }}{ϵ}\tau +...dt}}\right]{\delta }_{\mathbf{k},\mathbf{p}\mathbf{q}}d\mathbf{p}d\mathbf{q}.\hfill \end{array}$$

(56)

The slow secular behavior of the non-resonant term (after integration) can be efficiently moderated by tuning the damping parameter ${\delta }_{\omega }$. The kinetic equation, that is constructed from the above amplitude equation as explained before, can then be decomposed into two parts with contributions from resonating and non-resonating modes considered separately, as follows:

$${\partial }_{\tau }{e}_{\mathbf{k}}=T_{\mathrm{res}}(\mathbf{k},\tau )+T_{\mathrm{non}-\mathrm{res}}(\mathbf{k},\tau ),$$

(57)

where $T(\mathbf{k},\tau )$ denotes nonlinear transfer of energy to mode $\mathbf{k}$. Thus, retaining only non-resonant interactions, it is possible to establish the aforementioned coupling in the slow manifold, $k_Z=0$. Note that in the case of non-resonant interactions, due to the absence of the frequency delta function, a stationary Kolmogorov (constant flux) solution cannot be obtained. The reader is also referred to the works of Janssen [57] and Annenkov and Shrira [58] for a detailed theory of quasi-resonant interactions in four wave dispersive systems.

8. Conclusions

In conclusion, it is important to emphasize an important point, that of the asymptotic dynamical regime to which the fluid system belongs. In the context of this paper, we have restricted our analysis to the highly anisotropic regime of rapid rotation (i.e., infinitesimally small Rossby number) within the slow manifold where $k_z$ is infinitesimally small. It has been shown that the application of a multiple scales perturbation method within this regime yields a $k_{\perp }^{-3}$ law for the anisotropic energy spectrum, $e_{\mathbf{k}}$ (cf. equivalently a $k_{\perp }^{-2}$ spectrum for the cylindrically symmetric spectrum, $E_{k_{\perp }}$) that is in agreement with results from experimental and numerical simulations [17,21,22,23] as has been stated earlier. An asymptotically reduced system spans a hierarchy of slow manifold regimes and thereby captures the gradual transfer of energy towards the 2D modes. Interestingly, a similar power law solution can also be obtained by applying a critical balance phenomenology (where fast inertial wave time scale balances the nonlinear advection time scale) to the system of rotating turbulence as has been shown in Nazarenko and Scheckochihin [27]. This is the realm of strong turbulence where the nonlinear interactions are strong, meaning ${\omega }_f{T}_{{\tau }_{NL}}\sim \mathcal{O}(1)$. However, the anisotropic limit of rapidly rotating turbulence is farther away from modes where critical balance holds, this has been shown through numerical simulations in Di Leoni et al. [59]. In addition to the discussion in Section 6.3 above, the reader is referred to [27,38] for a detailed discussion on a wave turbulence and critical balance schematic of the energy cascade process. It is important to note that in the analysis presented in this paper, any physical artifact induced by boundary condition is not considered. Interested readers are referred to the work of [60] that describes discrete boundary effects on wave turbulence formalism.

In summary, we have constructed a multiple scales kinetic model for an asymptotically reduced set of equations that is valid in the limit of rapid rotation and in the anisotropic slow manifold regime. Stationary solutions of invariant quantities have been obtained that are consistent with experimental and simulation data reported in recent work. A coupled set of equations has been derived explaining the nature of the inter-dynamics of the two global invariants of the system, viz., energy and helicity. This has been done by extending the symmetrical non-helical system to the more general helical case where the reflection symmetry is broken. This procedure is novel in the sense that it bypasses construction of multiple correlation functions to account for the departure in mirror symmetry in the helical case. This analytical study will serve a useful reference point for theoretical understanding of atmospheric phenomena of planets that require a better knowledge of anisotropic wave dynamics. Moreover, detailed understanding of anisotropic multi-scale wave-eddy interactions, along the lines of the work presented here, will be useful for engineering new parametrization of mesoscale eddy flux in closure schemes for ocean circulation models [61].