Numerical Study of a 3D Eulerian Monolithic Formulation for Incompressible Fluid-Structures Systems

Abstract

An algorithm is derived for a hyperelastic incompressible solid coupled with a Newtonian fluid. It is based on a Eulerian formulation of the full system in which the main variables are the velocities. After a fully implicit discretization in time it is possible to eliminate the displacements and solve a variational equation for the velocities and pressures only. The stability of the method depends heavily on the use of characteristic-Galerkin discretization of the total derivatives. For comparison with previous works, the method is tested on a three-dimensional (3D) clamped beam in a pipe filled with a fluid. Convergence is studied numerically on an axisymmetric case.

1. Introduction

Computer simulation of fluid–structure systems in interaction (FSI) is important for aerospace [1], hemodynamics [2,3], automobile industries [4], etc.

A popular approach to numerically match the velocities and stresses at the fluid–solid interfaces is the arbitrary Lagrangian Eulerian formulation (ALE) whereby at every time step the fluid equations are mapped back into the solid domain [5]. Difficulties with the mesh used in the fluid part arise in the case of large displacements of the solids [6,7].

The immersed boundary method (IBM) proposed by Charles Peskin [2] and analyzed in [8] is efficient for shells in fluid but is more difficult to implement for thick structures [9]. Particles in suspension in a fluid have been simulated by IBM-like methods but mostly for hard particles (see for instance [10,11]).

A third way is the fully Eulerian approach, advocated by Liu et al. [12] and Dunne-Rannacher [13,14] (see also [15,16]). This approach is well suited to problems with large displacements.

In [17,18] a similar monolithic numerical method was proposed for the fluid–structure equations in two dimensions. It was also shown to be energy-stable. For more details on the motivations behind such a radically different approach to FSI, see [18]. The basic idea is to write the equations in terms of velocity, pressure, and displacement, as usual but in an Eulerian frame, and then eliminate the displacement in the time-discretized equations; the result is a monolithic formulation which is well-posed at each time step. Furthermore, to obtain energy stability it was suggested in [18] to update the structure with its own velocity and remesh the fluid domain at every time step.

In this paper we keep the same approach but in 3D. The Cayley–Hamilton theorem was used in 2D and it is different in 3D. Hence, the equations for a structure in Eulerian variables need to be derived again. The analysis is performed for hyper-elastic Mooney–Rivlin incompressible material. The result is not very different except that one coefficient of the constitutive relation is now a nonlinear function of the deformation tensor.

The article has four sections.

• The fully Eulerian formulation is derived in Section 1.
• In Section 2 the equations are discretized implicitly in time as in [18,19]; then the displacements are eliminated and a non-linear system for the velocities and pressures remains. Spatial discretization is obtained by using stable finite element spaces like linear pressures and quadratic velocities on a tetrahedral mesh.
• In Section 3 it is shown that the energy decays at each time step, which is an indication that the method is robust.
• Finally, in Section 4, the method is implemented in 2D for axisymmetric systems and in 3D for general systems. Energy decrease, mass conservation and convergence are analyzed on an axisymmetric case: an elastic torus in a cylindrical canister filled with a fluid at a Reynolds number of a few hundred. Then, the method is carefully evaluated on the test case proposed in [20] and comparisons with previous publications are made.

2. Derivation of the Formulation from the General Laws of Continuum Mechanics

2.1. Notations

The computational domain is denoted ${\Omega }^t$; it is time-dependent and is the union of the fluid part ${\Omega }_f^t$ and solid part ${\Omega }_s^t$. Technically ${\Omega }^t$ must be an open set and so we denote by $\overline{{\Omega }^t}$ its closure. The fluid and solid domains must not overlap: ${\Omega }_f^t\cap {\Omega }_s^t=$ ∅. Initially, ${\Omega }_f^0$ and ${\Omega }_s^0$ are prescribed. Let:

• ${\Sigma }^t={\overline{\Omega }}_f^t\cap {\overline{\Omega }}_s^t$ be the fluid–structure interface, and $\partial {\Omega }^t$ be the boundary of ${\Omega }^t$,
• $\Gamma$ be the part of $\partial {\Omega }^t$ where the structure is clamped or the fluid does not slip. It is assumed to be independent of t.

The following standard notations are used:

• $\mathbf{X}:{\Omega }^0\times \left(0,T\right),\mapsto {\Omega }^t:\mathbf{X}\left(x^0,t\right)$ is the Lagrangian position at t of $x^0$,
• $\mathbf{d}=\mathbf{X}\left(x^0,t\right)-x^0$ is the displacement,
• $\mathbf{u}(X(x^0,t),t)={\partial }_t\mathbf{X}(x^0,t)$ is the Eulerian velocity of the deformation at t and $x=X(x^0,t)$,
• ${\mathbf{F}}_{ji}={\partial }_{x_i^0}{\mathbf{X}}_j$ is the transposed gradient of the deformation,
• $J={\det }_{\mathbf{F}}$ is the Jacobian of the deformation.

Let ${\rho }_f,{\mathbf{\sigma }}_f$ be the density and stress tensor in the fluid, as for the solid with ${\rho }_s,{\mathbf{\sigma }}_s$, respectively. It is convenient to define a unique density and stress tensor by using the set function indicators ${\mathbf{1}}_{{\Omega }_f^t}$ and ${\mathbf{1}}_{{\Omega }_s^t}$:

• $\rho \left(x,t\right)={\mathbf{1}}_{{\Omega }_f^t}(x,t){\rho }_f\left(x,t\right)+{\mathbf{1}}_{{\Omega }_s^t}(x,t){\rho }_s\left(x,t\right)$, the density,
• $\mathbf{\sigma }\left(x,t\right)={\mathbf{1}}_{{\Omega }_f^t}(x,t){\mathbf{\sigma }}_f\left(x,t\right)+{\mathbf{1}}_{{\Omega }_s^t}(x,t){\mathbf{\sigma }}_s\left(x,t\right)$, the stress tensor.

For readability, vectors, tensors and matrices are noted in bold, except x and $x^0$. Unless specified otherwise, all spatial derivatives are with respect to $x\in {\Omega }^t$ and not with respect to $x^0\in {\Omega }^0$. If $\varphi$ is a function of $x=\mathbf{X}\left(x^0,t\right)$,

$${\nabla }_{x^0}\varphi =\left[{\partial }_{x_i^0}\varphi \right]=\left[{\partial }_{x_i^0}{\mathbf{X}}_j{\partial }_{x_j}\varphi \right]={\mathbf{F}}^T\nabla \varphi$$

(1)

When $\mathbf{X}$ is invertible, $\mathbf{d}$ and $\mathbf{F}$ can be seen as functions of $(x,t)$ instead of $(x^0,t)$. They are related by:

$${\mathbf{F}}^T={\nabla }_{x^0}\mathbf{X}={\nabla }_{x^0}\left(\mathbf{d}+x^0\right)={\nabla }_{x^0}\mathbf{d}+\mathbf{I}={\mathbf{F}}^T\nabla \mathbf{d}+\mathbf{I}\Rightarrow \mathbf{F}={\left(\mathbf{I}-\nabla \mathbf{d}\right)}^{-T}$$

(2)

Time derivatives are related by:

$${\mathbb{D}}_t\varphi (x,t):=\frac{d}{dt}\varphi {\left.\left(\mathbf{X}\left(x^0,t\right),t\right)\right|}_{\mathbf{X}\left(x^0,t\right)=x}={\partial }_t\varphi \left(x,t\right)+\mathbf{u}·\nabla \varphi \left(x,t\right)$$

(3)

It is convenient to introduce a notation,

$$\mathbf{Du}=\nabla \mathbf{u}+{\nabla }^{\mathbf{T}}\mathbf{u}.$$

2.2. Conservation Laws

Conservation of momentum and conservation of mass take the same form for the fluid and the solid. With $\mathbf{f}\left(x,t\right)$, the volumic force in the system is:

$$\rho {\mathbb{D}}_t\mathbf{u}=\mathbf{f}+\nabla ·\mathbf{\sigma },\frac{d}{dt}\left(J\rho \right)=0,\mathrm{i}.\mathrm{e}.,J\rho ={\rho }^0$$

with continuity of $\mathbf{u}$ and of $\mathbf{\sigma }·\mathbf{n}$ at the fluid–structure interface ${\mathbf{\sigma }}^t$ in the absence of external surface force, like surface tension. There are also unwritten constraints pertaining to the realizability of the map $\mathbf{X}$. Finally, incompressibility implies $J=1$ and so $\rho ={\rho }^0$ along the Lagrangian trajectories. In particular, if ${\rho }^0$ is piecewise constant and equal to ${\rho }_f$, ${\rho }_s$ in the fluid and the solid, at initial time, then it remains so at later times.

2.3. Constitutive Equations

Three-dimensional hyperelastic incompressible Mooney–Rivilin/neo Hookean materials and Newtonian incompressible fluids are considered.

• For a Newtonian incompressible fluid, ${\mathbf{\sigma }}_f=-p_f\mathbf{I}+\mu \mathbf{Du}$
• For an hyperelastic incompressible material, ${\mathbf{\sigma }}_s=-p_s\mathbf{I}+{\partial }_{\mathbf{F}}\Psi {\mathbf{F}}^T$

where $\Psi$ is an Helmholtz potential, like,

$$\Psi \left(\mathbf{F}\right)=c_1{\mathrm{tr}}_{{\mathbf{F}}^T\mathbf{F}}+c_2\left({\mathrm{tr}}_{{\left({\mathbf{F}}^T\mathbf{F}\right)}^2}-{\mathrm{tr}}_{{\mathbf{F}}^T\mathbf{F}}^2\right).$$

(4)

2.4. The Mooney–Rivlin 3D Stress Tensor

Note that ${\partial }_{\mathbf{F}}{\mathrm{tr}}_{{\mathbf{F}}^T\mathbf{F}}=2\mathbf{F}$ and ${\partial }_{\mathbf{F}}{\mathrm{tr}}_{{\left({\mathbf{F}}^T\mathbf{F}\right)}^2}=4{\mathbf{FF}}^T\mathbf{F}$. Hence,

$${\partial }_{\mathbf{F}}\Psi {\mathbf{F}}^T=\left(2c_1-4c_2{\mathrm{tr}}_{\mathbf{B}}\right)\mathbf{B}+4c_2{\mathbf{B}}^2,\mathrm{where}\mathbf{B}=\mathbf{F}{\mathbf{F}}^T.$$

(5)

In order to compute the tensors at Eulerian points $\left(x,t\right)$ rather than Lagrangian points $\left(x^0,t\right)$, it is necessary to compute $x\to \mathbf{F}\left(x,t\right)$ or $x\to \mathbf{d}\left(x,t\right)$ in terms of $\Psi$. By (2)

$${\mathbf{B}}^{-1}={\mathbf{F}}^{-T}{\mathbf{F}}^{-1}=\left(\mathbf{I}-\nabla \mathbf{d}\right){\left(\mathbf{I}-\nabla \mathbf{d}\right)}^T=\mathbf{I}-\mathbf{D}\mathbf{d}+\nabla \mathbf{d}{\nabla }^T\mathbf{d}.$$

(6)

By Cayley–Hamilton theorem in 3D, for an invertible symmetric matrix,

$${\mathbf{B}}^3-{\mathrm{tr}}_{\mathbf{B}}{\mathbf{B}}^2+\gamma \mathbf{B}-{\det }_{\mathbf{B}}\mathbf{I}=0\mathrm{with}\gamma =\frac{1}{2}({\mathrm{tr}}_{\mathbf{B}}^2-{\mathrm{tr}}_{{\mathbf{B}}^2}),$$

(7)

and by incompressibility ${\det }_{\mathbf{B}}=1$. Multiplying (7) by ${\mathbf{B}}^{-2}$, and the result by ${\mathbf{B}}^{-1}$ leads to polynomial expressions in terms of ${\mathbf{B}}^{-1}$:

$$\begin{array}{ccc}\hfill \mathbf{B}& ={\mathrm{tr}}_{\mathbf{B}}\mathbf{I}-\gamma {\mathbf{B}}^{-1}+{\mathbf{B}}^{-2},{\mathbf{B}}^2\hfill & \hfill =\left({\mathrm{tr}}_{\mathbf{B}}^2-\gamma \right)\mathbf{I}+\left(1-{\mathrm{tr}}_{\mathbf{B}}\gamma \right){\mathbf{B}}^{-1}+{\mathrm{tr}}_{\mathbf{B}}{\mathbf{B}}^{-2}.\end{array}$$

(8)

With the help of (8), (5) becomes:

$$\begin{array}{cc}\hfill {\partial }_{\mathbf{F}}\Psi {\mathbf{F}}^T=& \left(2c_1-4c_2{\mathrm{tr}}_{\mathbf{B}}\right)\mathbf{B}+4c_2{\mathbf{B}}^2=\left(2c_1-4c_2{\mathrm{tr}}_{\mathbf{B}}\right)\left({\mathrm{tr}}_{\mathbf{B}}\mathbf{I}-\gamma {\mathbf{B}}^{-1}+{\det }_{\mathbf{B}}{\mathbf{B}}^{-2}\right)\hfill \\ & +4c_2\left[\left({\mathrm{tr}}_{\mathbf{B}}^2-\gamma \right)\mathbf{I}+\left(1-{\mathrm{tr}}_{\mathbf{B}}\gamma \right){\mathbf{B}}^{-1}+{\mathrm{tr}}_{\mathbf{B}}{\mathbf{B}}^{-2}\right]\hfill \\ \hfill =& 2c_1{\mathbf{B}}^{-2}+\left(4c_2-2c_1\gamma \right){\mathbf{B}}^{-1}+\left(2c_1{\mathrm{tr}}_{\mathbf{B}}-4c_2\gamma \right)\mathbf{I}.\hfill \end{array}$$

Consequently, as a function of $\mathbf{d}$, the 3D Mooney–Rivlin stress tensor is obtained from (6),

$${\partial }_{\mathbf{F}}\Psi {\mathbf{F}}^T=2c_1{\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)}^2+2c_3\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)+\alpha \mathbf{I},$$

(9)

$$c_3:=\frac{c_1}{2}\left({\mathrm{tr}}_{\mathbf{B}}^2-{\mathrm{tr}}_{{\mathbf{B}}^2}-4\right)-4c_2$$

(10)

with a complex expression for $\alpha$ in (10) which is unimportant for the time being because it is absorbed by the pressure.

This is compared with the 2D model of [19] obtained with the same $\Psi$:

$${\partial }_{\mathbf{F}}\Psi {\mathbf{F}}^T=\left\{\begin{array}{cc}2c_1\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)+{\alpha }^{\prime }\mathbf{I},\hfill & 2\mathrm{D}\mathrm{model}.\hfill \\ 2c_1{\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)}^2+2c_3(x,t)\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)+\alpha \mathbf{I},\hfill & 3\mathrm{D}\mathrm{model}.\hfill \end{array}\right.$$

with $c_3$ given by (10).

2.5. From 3D to 2D

In the 3D model, $c_3$ varies with ${\mathrm{tr}}_{\mathbf{B}}$ and ${\mathrm{tr}}_{{\mathbf{B}}^2}$ instead of being constant, like $c_1$ in 2D model. The way to calculate $c_3$ is to compute directly ${\mathrm{tr}}_{\mathbf{B}}$ and ${\mathrm{tr}}_{{\mathbf{B}}^2}$ by (6) which involves a 3 by 3 inverse matrix at each point of the solid domain.

The 3D model degenerates into a 2D system when the geometry and the data are invariant with respect to one coordinate, like a translation invariance with respect to z for instance, in a Cartesian coordinate system, or a rotation invariance in $\theta$, in a cylindrical coordinate system.

Assume invariance with respect to the third coordinate. Then,

$$\mathbf{F}={\left(\begin{array}{cc}\mathbf{I}-{\nabla }_2\mathbf{d}& 0\\ 0& 1\end{array}\right)}^{-T}=\left(\begin{array}{cc}\tilde{\mathbf{F}}& 0\\ \mathbf{0}& 1\end{array}\right)\mathrm{with}\tilde{\mathbf{F}}={(\mathbf{I}-{\nabla }_2\mathbf{d})}^{-T},{\nabla }_2\mathbf{d}=\left(\begin{array}{cc}{\partial }_1{d}_1& {\partial }_1{d}_2\\ {\partial }_2{d}_1& {\partial }_2{d}_2\end{array}\right).$$

Consequently ${\mathrm{tr}}_{{({\mathbf{F}}^T\mathbf{F})}^j}={\mathrm{tr}}_{{({\tilde{\mathbf{F}}}^T\tilde{\mathbf{F}})}^j}+1,j=1,2$, ${({\mathrm{tr}}_{{\mathbf{F}}^T\mathbf{F}})}^2={({\mathrm{tr}}_{{\tilde{\mathbf{F}}}^T\tilde{\mathbf{F}}})}^2+2{\mathrm{tr}}_{{\tilde{\mathbf{F}}}^T\tilde{\mathbf{F}}}+1$,

$$\begin{array}{cc}\hfill \Psi \left(\mathbf{F}\right)& =c_1{\mathrm{tr}}_{{\mathbf{F}}^T\mathbf{F}}+c_2({\mathrm{tr}}_{{\left({\mathbf{F}}^T\mathbf{F}\right)}^2}-{\mathrm{tr}}_{{\mathbf{F}}^T\mathbf{F}}^2)=(c_1-2c_2){\mathrm{tr}}_{{\tilde{\mathbf{F}}}^T\tilde{\mathbf{F}}}+c_2({\mathrm{tr}}_{{\left({\tilde{\mathbf{F}}}^T\tilde{\mathbf{F}}\right)}^2}-{\mathrm{tr}}_{{\tilde{\mathbf{F}}}^T\tilde{\mathbf{F}}}^2)+\mathrm{constant}.\hfill \end{array}$$

(11)

Hence a comparison between the 2D model and the 3D model on a 2D configuration requires replacing the $c_1$ of the 2D Helmholtz potential by $c_1-2c_2$ from the 3D Helmholtz potential.

2.6. Variational Formulation

For simplicity, we shall consider only the case of homogeneous boundary conditions on $\Gamma \subset \partial {\Omega }^t$, i.e., clamped or no-slip, and homogeneous Neumann conditions on $\partial {\Omega }^t\mathsf{\setminus }\Gamma$.

So, given ${\Omega }_f^0$, ${\Omega }_s^0$, $\mathbf{d}$, and $\mathbf{u}$ at $t=0$, we must find $\left(\mathbf{u},p,\mathbf{d},{\Omega }_f^t,{\Omega }_s^t\right)$ with ${\mathbf{u}}_{|\Gamma }=0$ and,

$$\left\{\begin{array}{cc}\hfill {\int }_{{\Omega }^t}& \left(\rho {\mathbb{D}}_t\mathbf{u}·\widehat{\mathbf{u}}-p\nabla ·\widehat{\mathbf{u}}-\widehat{p}\nabla ·\mathbf{u}\right)+{\int }_{{\Omega }_f^t}\frac{\mu }{2}\mathbf{Du}:\mathbf{D}\widehat{\mathbf{u}}\hfill \\ \hfill +{\int }_{{\Omega }_s^t}& \left[c_1{\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)}^2+c_3\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)\right]:\mathbf{D}\widehat{\mathbf{u}}={\int }_{{\Omega }^t}\mathbf{f}·\widehat{\mathbf{u}},\hfill \\ & {\mathbb{D}}_t\mathbf{d}=\mathbf{u},\hfill \end{array}\right.$$

(12)

for all $\left(\widehat{\mathbf{u}},\widehat{p}\right)$ with ${\widehat{\mathbf{u}}}_{|\Gamma }=0$ and where ${\Omega }_s^t$ and ${\Omega }_f^t$ are defined by:

$$\frac{d\chi }{d\tau }=\mathbf{u}\left(\chi \left(\tau \right),\tau \right),\chi \left(t\right)\in {\Omega }_r^t\Rightarrow \chi \left(\tau \right)\in {\Omega }_r^{\tau }\forall \tau \in \left(0,T\right),r=s,f.$$

3. Numerical Schemes

3.1. Characteristic-Galerkin Derivatives

The characteristic–Galerkin method is applied to (12) to discretize the total derivatives.

Let $\mathbf{u}:{\Omega }^t\times (0,T)\mapsto {\mathbb{R}}^3$ be given, Lipschitz in space and continuous in time. Let ${\chi }_{\mathbf{u},x}^t\left(\tau \right)$ be the solution at time $\tau <t$ of:

$$\dot{\chi }\left(\tau \right)=\mathbf{u}\left(\chi \left(\tau \right),\tau \right)\mathrm{with}\chi \left(t\right)=x.$$

So $\chi$ is the particle path in a velocity field $\mathbf{u}$ and ${\chi }_{\mathbf{u},x}^t\left(\tau \right)$ is the position of a particle at time $\tau$ which will be at position x at (future) time t. The method of characteristics relies on the concept of total derivative: for any differentiable function $\mathbf{w}:{\Omega }^t\times (0,T)\mapsto {\mathbb{R}}^m$, $m=1,2,3,\cdots$,

$${\mathbb{D}}_t\mathbf{w}\left(x,t\right):=\frac{d}{d\tau }\mathbf{w}\left(\chi \left(\tau \right),\tau \right){|}_{\tau =t}={\partial }_t\mathbf{w}+\mathbf{u}·\nabla \mathbf{w}.$$

(13)

Given a time step $\delta t$, the position of a particle at time $n\delta t$, which will be at position x at time $(n+1)\delta t$, is approximated by ${\mathbb{Y}}^{n+1}\left(x\right)$:

$${\chi }_{{\mathbf{u}}^{n+1},x}^{\left(n+1\right)\delta t}\left(n\delta t\right)\approx {\mathbb{Y}}^{n+1}\left(x\right):=x-{\mathbf{u}}^{n+1}\left(x\right)\delta t.$$

Then a first-order consistent scheme for the total derivative of $\mathbf{w}$ is:

$${\partial }_t\mathbf{w}+\mathbf{u}·\nabla \mathbf{w}={\mathbb{D}}_t\mathbf{w}\left(x,t\right)\approx \frac{1}{\delta t}\left({\mathbf{w}}^{n+1}\left(x\right)-{\mathbf{w}}^n\left({\mathbb{Y}}^{n+1}\left(x\right)\right)\right).$$

(14)

Combined with a Galerkin approximation in space the scheme has been analyzed in depth in [21] in the variational context of the finite element methods.

3.2. A Monolithic Time–Discrete Variational Formulation

Define ${\displaystyle L_0^2(\Omega )=\{q\in L^2(\Omega ):{\int }_{\Omega }q=0\}}$.

Proposition 1.

The following variational problem is a first order in time-consistent approximation of (12): Find, ${\Omega }^{n+1}$, ${\mathbf{u}}^{n+1}\in {\mathit{H}}_0^1\left({\Omega }^{n+1}\right)$, $p^{n+1}\in L_0^2\left({\Omega }^{n+1}\right)$ such that for all $\widehat{\mathbf{u}}\in {\mathit{H}}_0^1\left({\Omega }^{n+1}\right)$, $\widehat{p}\in L_0^2\left({\Omega }^{n+1}\right)$,

$$\left\{\begin{array}{cc}{\displaystyle {\int }_{{\Omega }^{n+1}}}\hfill & \left({\rho }^{n+1}\frac{{\mathbf{u}}^{n+1}-{\mathbf{u}}^n\circ {\mathbb{Y}}^{n+1}}{\delta t}·\widehat{\mathbf{u}}-p^{n+1}\nabla ·\widehat{\mathbf{u}}-\widehat{p}\nabla ·{\mathbf{u}}^{n+1}\right)+{\int }_{{\Omega }_f^{n+1}}\frac{\mu }{2}\mathbf{D}{\mathbf{u}}^{n+1}:\mathbf{D}\widehat{\mathbf{u}}\hfill \\ & +\delta t{\int }_{{\Omega }_s^{n+1}}\left[2c_1\left(\mathbf{D}{\mathbf{u}}^{n+1}-\nabla {\mathbf{u}}^{n+1}{\nabla }^T{\tilde{\mathbf{d}}}^n-\nabla {\tilde{\mathbf{d}}}^n{\nabla }^T{\mathbf{u}}^{n+1}\right)\left(\mathbf{D}{\tilde{\mathbf{d}}}^n-\nabla {\tilde{\mathbf{d}}}^n{\nabla }^T{\tilde{\mathbf{d}}}^n\right)\right.\hfill \\ & +\left.c_3^n\left(\mathbf{D}{\mathbf{u}}^{n+1}-\nabla {\mathbf{u}}^{n+1}{\nabla }^T{\tilde{\mathbf{d}}}^n-\nabla {\tilde{\mathbf{d}}}^n{\nabla }^T{\mathbf{u}}^{n+1}\right)\right]:\mathbf{D}\widehat{\mathbf{u}}\hfill \\ & +{\int }_{{\Omega }_s^{n+1}}\left[c_1{\left(\mathbf{D}{\tilde{\mathbf{d}}}^n-\nabla {\tilde{\mathbf{d}}}^n{\nabla }^T{\tilde{\mathbf{d}}}^n\right)}^2+c_3^n\left(\mathbf{D}{\tilde{\mathbf{d}}}^n-\nabla {\tilde{\mathbf{d}}}^n{\nabla }^T{\tilde{\mathbf{d}}}^n\right)\right]:\mathbf{D}\widehat{\mathbf{u}}={\int }_{{\Omega }^t}\mathbf{f}·\widehat{\mathbf{u}},\hfill \\ & {\mathbf{d}}^{n+1}={\mathbf{d}}^n\circ {\mathbb{Y}}^{n+1}+\delta t{\mathbf{u}}^{n+1}.\hfill \end{array}\right.$$

(15)

where ${\tilde{\mathbf{d}}}^n$ stands for ${\mathbf{d}}^n\left({\mathbb{Y}}^{n+1}\right)$.

Some comments

• Formula (14) has been used to approximate ${\mathbb{D}}_t\mathbf{u}$ and ${\mathbb{D}}_t\mathbf{d}$ in (12).
• One may wonder why the scheme is applied to $\mathbf{u}$ and not to $\rho \mathbf{u}$. Note that $\rho ={\rho }_f{\mathbf{1}}_{{\Omega }_f^t}+{\rho }_s{\mathbf{1}}_{{\Omega }_s^t}$ is convected by the velocity $\mathbf{u}$. Hence ${\rho }^{n+1}\left(x\right)={\rho }^n\circ {\mathbb{Y}}^{n+1}\left(x\right)$. This shows that discretizing the total derivative of $\mathbf{u}$ or the total derivative of $\rho \mathbf{u}$ gives the same scheme:

  $$\frac{1}{\delta t}\left({\mathbf{w}}^{n+1}\left(x\right)-\mathbf{w}\left({\mathbb{Y}}^{n+1}\left(x\right)\right)\right)=\left({\partial }_t\mathbf{w}+\mathbf{u}·\nabla \mathbf{w}\right){|}_{x,t^{n+1}}+O\left(\delta t\right)\mathrm{with}\mathbf{w}=\mathbf{u}\mathrm{or}\mathbf{w}=\rho \mathbf{u}.$$

  (16)

Proof. 

With the characteristic Galerkin method, a consistent time discretization of (12) would be such that at each time step one must:

Find ${\mathbf{u}}^{n+1}\in {\mathbf{H}}_0^1\left({\Omega }^{n+1}\right)$, $p\in L_0^2\left({\Omega }^{n+1}\right)$, ${\Omega }^{n+1}={\Omega }_f^{n+1}\cup {\Omega }_s^{n+1}$, such that $\forall \widehat{\mathbf{u}}\in {\mathbf{H}}_0^1\left({\Omega }^{n+1}\right)$, $\forall \widehat{p}\in L_0^2\left({\Omega }^{n+1}\right)$; the three relations below hold:

$$\begin{array}{c}{\int }_{{\Omega }^{n+1}}\left({\rho }^{n+1}\frac{{\mathbf{u}}^{n+1}-{\mathbf{u}}^n\circ {\mathbb{Y}}^{n+1}}{\delta t}·\widehat{\mathbf{u}}-p^{n+1}\nabla ·\widehat{\mathbf{u}}-\widehat{p}\nabla ·\mathbf{u}\right)+{\int }_{{\Omega }_f^{n+1}}\frac{\mu }{2}\mathbf{D}{\mathbf{u}}^{n+1}:\mathbf{D}\widehat{\mathbf{u}}\hfill \\ +{\int }_{{\Omega }_s^{n+1}}\left[c_1{\left(\mathbf{D}{\mathbf{d}}^{n+1}-\nabla {\mathbf{d}}^{n+1}{\nabla }^T{\mathbf{d}}^{n+1}\right)}^2+c_3^{n+1}\left(\mathbf{D}{\mathbf{d}}^{n+1}-\nabla {\mathbf{d}}^{n+1}{\nabla }^T{\mathbf{d}}^{n+1}\right)\right]:\mathbf{D}\widehat{\mathbf{u}}={\int }_{{\Omega }^t}\mathbf{f}·\widehat{\mathbf{u}},\hfill \end{array}$$

(17)

$${\mathbf{d}}^{n+1}={\tilde{\mathbf{d}}}^n+\delta t{\mathbf{u}}^{n+1},\mathrm{where}{\tilde{\mathbf{d}}}^n={\mathbf{d}}^n\circ {\mathbb{Y}}^{n+1}$$

(18)

$${\Omega }^{n+1}={\left({\mathbb{Y}}^{n+1}\right)}^{-1}\left({\Omega }^n\right)=\left\{x:{\mathbb{Y}}^{n+1}\left(x\right):=x-\delta t{\mathbf{u}}^{n+1}\left(x\right)\in {\Omega }^n\right\}.$$

(19)

A fully implicit monolithic formulation with variables $\left({\mathbf{u}}^{n+1},p^{n+1}\right)$ can be derived by substituting ${\mathbf{d}}^{n+1}$ in (17) with (18):

$$\begin{array}{cc}{\int }_{{\Omega }^{n+1}}\hfill & \left({\rho }^{n+1}\frac{{\mathbf{u}}^{n+1}-{\mathbf{u}}^n\circ {\mathbb{Y}}^{n+1}}{\delta t}·\widehat{\mathbf{u}}-p^{n+1}\nabla ·\widehat{\mathbf{u}}-\widehat{p}\nabla ·{\mathbf{u}}^{n+1}\right)+{\int }_{{\Omega }_f^{n+1}}\frac{\mu }{2}\mathbf{D}{\mathbf{u}}^{n+1}:\mathbf{D}\widehat{\mathbf{u}}\hfill \\ & +{\int }_{{\Omega }_s^{n+1}}\left[c_1{\left(\mathbf{D}\left({\tilde{\mathbf{d}}}^n+\delta t{\mathbf{u}}^{n+1}\right)-\nabla \left({\tilde{\mathbf{d}}}^n+\delta t{\mathbf{u}}^{n+1}\right){\nabla }^T\left({\tilde{\mathbf{d}}}^n+\delta t{\mathbf{u}}^{n+1}\right)\right)}^2\right.\hfill \\ & \left.+c_3^{n+1}\left(\mathbf{D}\left({\tilde{\mathbf{d}}}^n+\delta t{\mathbf{u}}^{n+1}\right)-\nabla \left({\tilde{\mathbf{d}}}^n+\delta t{\mathbf{u}}^{n+1}\right){\nabla }^T\left({\tilde{\mathbf{d}}}^n+\delta t{\mathbf{u}}^{n+1}\right)\right)\right]:\mathbf{D}\widehat{\mathbf{u}}={\int }_{{\Omega }^t}\mathbf{f}·\widehat{\mathbf{u}}.\hfill \end{array}$$

(20)

System (15) is found by expanding the nonlinear terms in (20), and keeping only the zero order terms and the terms of order one in $\delta t$. ☐

3.3. Spacial Discretization with Finite Elements

Let ${\mathcal{T}}_h^0$ be a triangulation of the initial domain. Spatial discretization can be done with the most popular finite element for fluids: the Lagrangian triangular elements of degree 2 for the space $V_h$ of velocities and displacements and Lagrangian triangular elements of degree 1 for the pressure space $Q_h$, provided that the pressure is different in the structure and the fluid because the pressure is discontinuous at the interface $\mathbf{\sigma }$; therefore $Q_h$ is the space of piecewise linear functions on the triangulations, continuous in ${\Omega }_r^{n+1},r=s,f$. Appropriate couples like $\{V_h,Q_h\}$ are chosen to satisfy the inf-sup condition to avoid checker-board oscillations (see for example [8]). A small penalization with parameter $ϵ$ must be added to impose uniqueness of the pressure when $L_0^2$ is replaced by $Q_h\approx L^2$.

This leads us to find ${\mathbf{u}}_h^{n+1}\in V_{0h}$, $p_h^{n+1}\in Q_h$, ${\Omega }^{n+1}$, such that for all ${\widehat{\mathbf{u}}}_h$, ${\widehat{p}}_h\in V_{0h}\times Q_h$ with,

$${\tilde{\mathbf{d}}}_h^n:={\mathbf{d}}_h^n\circ {\mathbb{Y}}^{n+1},\mathrm{where}{\mathbb{Y}}^{n+1}\left(x\right)=x-{\mathbf{u}}_h^{n+1}\left(x\right)\delta t,$$

the following holds:

$$\left\{\begin{array}{cc}{\int }_{{\Omega }^{n+1}}\hfill & \left({\rho }^{n+1}\frac{{\mathbf{u}}_h^{n+1}-{\mathbf{u}}_h^n\circ {\mathbb{Y}}^{n+1}}{\delta t}·{\widehat{\mathbf{u}}}_h-p_h^{n+1}\nabla ·{\widehat{\mathbf{u}}}_h-{\widehat{p}}_h\nabla ·{\mathbf{u}}_h^{n+1}+ϵ\nabla p_h^{n+1}\nabla {\widehat{p}}_h\right)\hfill \\ & +{\int }_{{\Omega }_f^{n+1}}\frac{\mu }{2}\mathbf{D}{\mathbf{u}}_h^{n+1}:\mathbf{D}{\widehat{\mathbf{u}}}_h\hfill \\ & +\delta t{\int }_{{\Omega }_s^{n+1}}\left[2c_1\left(\mathbf{D}{\mathbf{u}}_h^{n+1}-\nabla {\mathbf{u}}_h^{n+1}{\nabla }^T{\tilde{\mathbf{d}}}_h^n-\nabla {\tilde{\mathbf{d}}}_h^n{\nabla }^T{\mathbf{u}}_h^{n+1}\right)\left(\mathbf{D}{\tilde{\mathbf{d}}}_h^n-\nabla {\tilde{\mathbf{d}}}_h^n{\nabla }^T{\tilde{\mathbf{d}}}_h^n\right)\right.\hfill \\ & +\left.c_3^{n+1}\left(\mathbf{D}{\mathbf{u}}_h^{n+1}-\nabla {\mathbf{u}}_h^{n+1}{\nabla }^T{\tilde{\mathbf{d}}}_h^n-\nabla {\tilde{\mathbf{d}}}_h^n{\nabla }^T{\mathbf{u}}_h^{n+1}\right)\right]:\mathbf{D}{\widehat{\mathbf{u}}}_h\hfill \\ & +{\int }_{{\Omega }_s^{n+1}}\left[c_1{\left(\mathbf{D}{\tilde{\mathbf{d}}}_h^n-\nabla {\tilde{\mathbf{d}}}_h^n{\nabla }^T{\tilde{\mathbf{d}}}_h^n\right)}^2+c_3^{n+1}\left(\mathbf{D}{\tilde{\mathbf{d}}}_h^n-\nabla {\tilde{\mathbf{d}}}_h^n{\nabla }^T{\tilde{\mathbf{d}}}_h^n\right)\right]:\mathbf{D}{\widehat{\mathbf{u}}}_h={\int }_{{\Omega }^{n+1}}\mathbf{f}·{\widehat{\mathbf{u}}}_h\hfill \\ & {\Omega }^{n+1}={\left({\mathbb{Y}}^{n+1}\right)}^{-1}\left({\Omega }^n\right)=\left\{x:{\mathbb{Y}}^{n+1}\left(x\right)\in {\Omega }^n\right\}.\hfill \\ & {\mathbf{d}}_h^{n+1}={\tilde{\mathbf{d}}}_h^n+\delta t{\mathbf{u}}_h^{n+1}.\hfill \end{array}\right.$$

(21)

3.4. Solution Algorithm

Equation (21) must be solved iteratively because ${\Omega }^{n+1}$ is updated by (19). The most natural method is to freeze some coefficients, $c_3$ included, so as to obtain a well-posed linear problem and iterate.

To explain the iteration process let us rename, in (19), ${\rho }^{n+1}$, ${\Omega }^{n+1},{\Omega }_f^{n+1},{\Omega }_s^{n+1}$, ${\mathbb{Y}}^{n+1},c_3^{n+1}$, into $\Omega ,{\Omega }^f,{\Omega }^s$, $\mathbb{Y},c_3$.

• Set $\rho ={\rho }_n$, $c_3=c_3^n$, ${\Omega }^r={\Omega }_r^n,r=f,s$, $\mathbf{u}={\mathbf{u}}_h^n$, $\mathbb{Y}\left(x\right)=x-\mathbf{u}\delta t$,
• Solve system (21). In this study a direct solver is used for the linear system.
• Set $\mathbf{u}={\mathbf{u}}_h^{n+1}$, $\mathbb{Y}\left(x\right)=x-\mathbf{u}\delta t$, ${\Omega }^r={\mathbb{Y}}^{-1}\left({\Omega }_r^n\right),r=s,f$; update $c_3$ and $\rho$.
• If not converged return to step 2.

Remark 1.

${\Omega }_s^{n+1}$ we move the vertices $q^j$ in the solid part by its velocity $\mathbf{u}\left(q^j\right)$. As ${\tilde{\mathbf{d}}}^n$ is moved by $\mathbb{Y}$, it is naturally convected on the new mesh. Similarly, $\rho$ being constant on ${\Omega }^s$, it is well defined on the new mesh. Finally, $c_3$ being defined in terms of $\mathbf{u}$, it is also well defined on the new mesh.

In the fluid region we generate a new mesh with a Delauney–Voronoi automatic mesh generator from the new position of the interface $\mathbf{\sigma }$. There are many other possibilities like solving a Laplace equation in the fluid part with Dirichlet conditions equal to the velocity of the fluid–solid interface. It works equally well but what we advocate is, in our experience, more robust, even if it is at the cost of a possibly greater interpolation error at every step because ${\tilde{\mathbf{u}}}^n$ needs to be projected on the new mesh. A $P^2$ polynomial interpolation is used.

Remark 2.

An earlier study in [17] showed that 2 iterations are necessary but 3 or more make invisible improvements; this result is confirmed in 3D by the numerical tests below.

By inspection of (23) below, notice that this iterative algorithm computes the stationary point of ${\displaystyle \frac{d}{dt}{\int }_{{\Omega }_s^0}\Psi \left(\mathbf{I}+{\nabla }_{x_0}{\mathbf{d}}^T\right)}$. As $\Psi$ is convex, it should be a convergent process, but it requires a more rigorous proof.

4. Stability of the Scheme

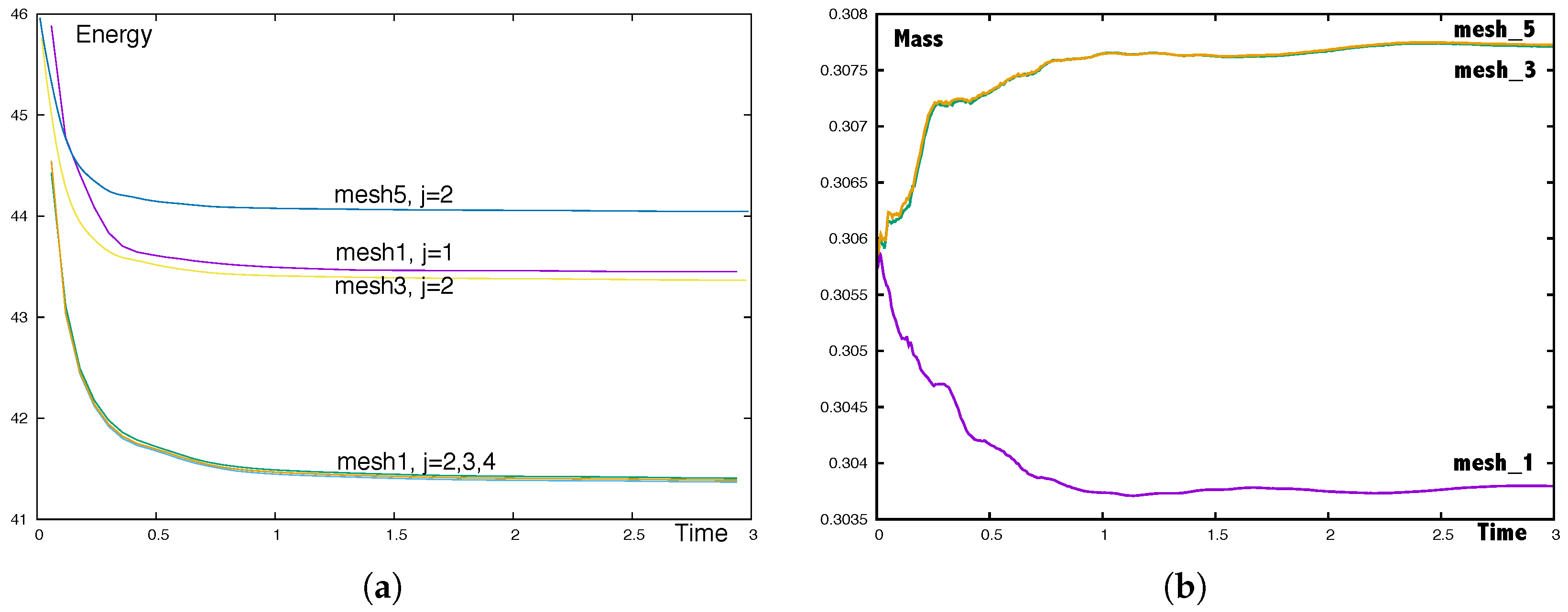
4.1. Conservation of Energy

Proposition 2.

In the continuous case, it holds that:

$$\frac{d}{dt}{\int }_{{\Omega }^t}\frac{\rho }{2}{\left|\mathbf{u}\right|}^2+\frac{{\mu }^f}{2}{\int }_{{\Omega }_f^t}{\left|\mathbf{D}\mathbf{u}\right|}^2+\frac{d}{dt}{\int }_{{\Omega }_s^0}\Psi \left(\mathbf{I}+{\nabla }_{x_0}{\mathbf{d}}^T\right)={\int }_{{\Omega }^t}\mathbf{f}·\mathbf{u}.$$

(22)

Proof. 

Choosing $\widehat{\mathbf{u}}=\mathbf{u}$, $\widehat{p}=-p$ in Equation (12), then one term becomes (9) :

$${\int }_{{\Omega }_s^t}\left[c_1{\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)}^2+c_3\left(\mathbf{D}\mathbf{d}-\nabla \mathbf{d}{\nabla }^T\mathbf{d}\right)\right]:\nabla \mathbf{u}={\int }_{{\Omega }_s^t}\left({\partial }_{\mathbf{F}}\Psi {\mathbf{F}}^T-\alpha \mathbf{I}\right):\nabla \mathbf{u}.$$

(23)

Now, $\frac{d}{dt}\Psi \left(\mathbf{F}\right)={\partial }_{\mathbf{F}}\Psi \left(\mathbf{F}\right):{\partial }_t\mathbf{F}$ and ${\mathbf{F}}^T\nabla \mathbf{u}={\nabla }_{x_0}\mathbf{u}\left(x_0\right)={\partial }_t{\nabla }_{x_0}\mathbf{d}\left(x_0\right)={\partial }_t{\mathbf{F}}^T\left(x_0\right)$, so conservation of the Helmholtz potential $\Psi$ can be derived as follows:

$$\begin{array}{cc}{\int }_{{\Omega }_s^t}\left({\partial }_{\mathbf{F}}\Psi {\mathbf{F}}^T-\alpha \mathbf{I}\right):\nabla \mathbf{u}\hfill & ={\int }_{{\Omega }_s^0}{\partial }_{\mathbf{F}}\Psi :{\nabla }_{x_0}\mathbf{u}={\int }_{{\Omega }_s^0}{\partial }_{\mathbf{F}}\Psi :{\partial }_t{\nabla }_{x_0}\mathbf{d}={\int }_{{\Omega }_s^0}{\partial }_{\mathbf{F}}\Psi :{\partial }_t{\mathbf{F}}^T\hfill \\ & ={\int }_{{\Omega }_s^0}\frac{d}{dt}\Psi \left(\mathbf{F}\right)=\frac{d}{dt}{\int }_{{\Omega }_s^0}\Psi \left(\mathbf{F}\right)=\frac{d}{dt}{\int }_{{\Omega }_s^0}\Psi \left(\mathbf{I}+{\nabla }_{x_0}{\mathbf{d}}^T\right).\hfill \end{array}$$

The other terms in (12) are standard, in particular, with enough regularity on ${\Omega }^t$,

$${\int }_{{\Omega }^t}\left({\partial }_t\mathbf{u}+\mathbf{u}·\nabla \mathbf{u}\right)·\mathbf{u}=\frac{d}{dt}{\int }_{{\Omega }^t}\frac{{\left|\mathbf{u}\right|}^2}{2}.$$

☐

Remark 3.

When $\Psi$ is convex, some regularity can be gained from this energy conservation which can lead to existence of solution up to time T which, loosely speaking, in the most optimistic perspective, is the first time of contact of two boundaries which were not in contact initially (see [22,23,24] etc.).

4.2. Stability of the Scheme Discretized in Time

Lemma 1.

$${\mathbf{F}}^{n+1}={\mathbf{F}}^n+\delta t{\nabla }_{x^0}{\mathbf{u}}^{n+1}.$$

Proof. 

By construction, ${\mathbb{X}}^{n+1}={({\mathbb{Y}}^1\circ {\mathbb{Y}}^2...{\mathbb{Y}}^{n+1})}^{-1}={\left({\mathbb{Y}}^{n+1}\right)}^{-1}\circ {\mathbb{X}}^n$; therefore ${\mathbf{d}}_h^{n+1}={\tilde{\mathbf{d}}}_h^n+\delta t{\mathbf{u}}_h^{n+1}$ implies that:

$${\nabla }_{x^0}{\mathbf{d}}^{n+1}={\nabla }_{x^0}{\mathbf{d}}^n+\delta t{\nabla }_{x^0}{\mathbf{u}}^{n+1}.$$

☐

Theorem 1.

When (17) is used and if $\mathbf{f}=0$ and ${\rho }_r$ is constant in each domain ${\Omega }_r^n,r=s,f$,

$${\int }_{{\Omega }^{n+1}}\frac{{\rho }^{n+1}}{2}{\left|{\mathbf{u}}^{n+1}\right|}^2+\delta t{\int }_{{\Omega }_f^{n+1}}\frac{\mu }{2}{\left|\mathbf{D}{\mathbf{u}}^{n+1}\right|}^2+{\int }_{{\Omega }_s^0}\Psi \left({\mathbf{F}}^{n+1}\right)\le {\int }_{{\Omega }^n}\frac{{\rho }^n}{2}{\left|{\mathbf{u}}^n\right|}^2+{\int }_{{\Omega }_s^0}\Psi \left({\mathbf{F}}^n\right)$$

(24)

Proof. 

The proof is similar to that given in [19] for the 2D case.

With $\widehat{\mathbf{u}}={\mathbf{u}}^{n+1}$, $\widehat{p}=-p^{n+1}$, and $\mathbf{f}=0$, (17) becomes:

$$\begin{array}{c}{\int }_{{\Omega }^{n+1}}\left({\rho }^{n+1}\frac{{\mathbf{u}}^{n+1}-{\mathbf{u}}^n\circ {\mathbb{Y}}^{n+1}}{\delta t}·{\mathbf{u}}^{n+1}\right)+\frac{\mu }{2}{\int }_{{\Omega }_f^{n+1}}{\left|\mathbf{D}{\mathbf{u}}^{n+1}\right|}^2\hfill \\ +{\int }_{{\Omega }_s^{n+1}}\left[c_1{\left(\mathbf{D}{\mathbf{d}}^{n+1}-\nabla {\mathbf{d}}^{n+1}{\nabla }^T{\mathbf{d}}^{n+1}\right)}^2+c_3^{n+1}\left(\mathbf{D}{\mathbf{d}}^{n+1}-\nabla {\mathbf{d}}^{n+1}{\nabla }^T{\mathbf{d}}^{n+1}\right)\right]:\mathbf{D}{\mathbf{u}}^{n+1}=0\hfill \end{array}$$

(25)

We note that ${\rho }_r^n\circ {\mathbb{Y}}^{n+1}\left(x\right)={\rho }_r^{n+1}\left(x\right)$, $x\in {\Omega }_r^{n+1}$; so:

$${\int }_{{\Omega }_r^{n+1}}\left({\rho }_r^n{\mathbf{u}}^n\right)\circ {\mathbb{Y}}^{n+1}·{\mathbf{u}}^{n+1}={\int }_{{\Omega }_r^{n+1}}\left(\sqrt{{\rho }_r^n}{\mathbf{u}}^n\right)\circ {\mathbb{Y}}^{n+1}·\sqrt{{\rho }_r^{n+1}}{\mathbf{u}}^{n+1}$$

Schwartz inequality applied to the right side followed by Young’s inequality leads to:

$$\begin{array}{c}\hfill {\int }_{{\Omega }_r^{n+1}}\left({\rho }_r^n{\mathbf{u}}^n\right)\circ {\mathbb{Y}}^{n+1}·{\mathbf{u}}^{n+1}\le {\left({\int }_{{\Omega }_r^{n+1}}{\left(\sqrt{{\rho }_r^n}{\mathbf{u}}^n\right)}^2\circ {\mathbb{Y}}^{n+1}\right)}^{\frac{1}{2}}{\left({\int }_{{\Omega }_r^{n+1}}{\rho }_r^{n+1}{\left({\mathbf{u}}^{n+1}\right)}^2\right)}^{\frac{1}{2}}\\ \hfill ={\left({\int }_{{\Omega }_r^n}{\left(\sqrt{{\rho }_r^n}{\mathbf{u}}^n\right)}^2\right)}^{\frac{1}{2}}{\left({\int }_{{\Omega }_r^{n+1}}{\rho }_r^{n+1}{\left({\mathbf{u}}^{n+1}\right)}^2\right)}^{\frac{1}{2}}\le \frac{1}{2}{\int }_{{\Omega }_r^{n+1}}{\rho }_r^{n+1}{\left|{\mathbf{u}}^{n+1}\right|}^2+\frac{1}{2}{\int }_{{\Omega }_r^n}{\rho }_r^n{\left|{\mathbf{u}}^n\right|}^2\end{array}$$

Because ${\left({\mathbb{Y}}^{n+1}\right)}^{-1}\left({\Omega }^{n+1}\right)={\Omega }^n$, and ${\det }_{\nabla {\mathbb{Y}}^{n+1}}=1$, for any f,

$${\int }_{{\Omega }^{n+1}}f\left({\mathbb{Y}}^{n+1}\left(x\right)\right)dx={\int }_{{\left({\mathbb{Y}}^{n+1}\right)}^{-1}\left({\Omega }^{n+1}\right)}f\left(y\right){\det }_{{\left(\nabla {\mathbb{Y}}^{n+1}\right)}^{-1}}dy={\int }_{{\Omega }^n}f.$$

(26)

The third integral in (25) can be transformed with Equation (9):

$$\begin{array}{c}\hfill {\int }_{{\Omega }_s^{n+1}}\left[c_1{\left(\mathbf{D}{\mathbf{d}}^{n+1}-\nabla {\mathbf{d}}^{n+1}{\nabla }^T{\mathbf{d}}^{n+1}\right)}^2+c_3^{n+1}\left(\mathbf{D}{\mathbf{d}}^{n+1}-\nabla {\mathbf{d}}^{n+1}{\nabla }^T{\mathbf{d}}^{n+1}\right)\right]:\mathbf{D}{\mathbf{u}}^{n+1}\\ \hfill ={\int }_{{\Omega }_s^{n+1}}{\left.{\partial }_{\mathbf{F}}\Psi {\mathbf{F}}^T\right|}^{n+1}:\nabla {\mathbf{u}}^{n+1}=\frac{1}{\delta t}{\int }_{{\Omega }_s^0}{\partial }_{\mathbf{F}}\Psi \left({\mathbf{F}}^{n+1}\right):\left({\mathbf{F}}^{n+1}-{\mathbf{F}}^n\right)\end{array}$$

(27)

The last equality is due to Lemma 1. Now, by the convexity of $\Psi$:

$${\int }_{{\Omega }_s^0}{\partial }_{\mathbf{F}}\Psi \left({\mathbf{F}}^{n+1}\right):\left({\mathbf{F}}^{n+1}-{\mathbf{F}}^n\right)\ge {\int }_{{\Omega }_s^0}\Psi \left({\mathbf{F}}^{n+1}\right)-{\int }_{{\Omega }_s^0}\Psi \left({\mathbf{F}}^n\right)$$

Finally,

$${\int }_{{\Omega }^{n+1}}\frac{{\rho }^{n+1}}{2}{\left|{\mathbf{u}}^{n+1}\right|}^2+\delta t{\int }_{{\Omega }_f^{n+1}}\frac{\mu }{2}{\left|\mathbf{D}{\mathbf{u}}^{n+1}\right|}^2+{\int }_{{\Omega }_s^0}\Psi \left({\mathbf{F}}^{n+1}\right)\le {\int }_{{\Omega }^n}\frac{{\rho }^n}{2}{\left|{\mathbf{u}}^n\right|}^2+{\int }_{{\Omega }_s^0}\Psi \left({\mathbf{F}}^n\right)$$

(28)

☐

4.3. Energy Inequality for the Fully Discrete Scheme

It was argued in [18] that the same proof holds for scheme discretized with $P^1$ triangular elements for velocity and pressure because then $\mathbb{Y}$ transforms a tetrahedron into a tetrahedron and so (27) holds also in the discrete case. Compatible linear elements are either the $P^1-P^1$ stabilized element or the $P^1$ element for the pressure with $P^1$ also for the velocity but on a mesh where each tetrahedron is divided in sub-tetrahedra from an inner additional vertex. In the first case the above stability analysis needs to be modified to include the stabilization term. Numerical tests in 2D showed that the $P^2-P^1$ element is alright even though energy stability cannot be proved.

5. Numerical Tests

The first set of tests is meant to evaluate the precision of the method. Due to limited computer resources (the program is not parallelized), we chose an axisymmetric example so as to work in 2D with four embedded meshes and study convergence, conservation of mass and energy decay.

The second set concerns a well-documented test case in 3D with experimental comparisons.

Computing time on a Mac-Intel core 2 i7 at 3 GHz ranges from 7sec for ${\mathrm{mesh}}_1$ to 2800sec for ${\mathrm{mesh}}_7$ on the axisymmetric case with two iterations in the solver. For the benchmark 3D case it takes several hours. The computer program is written in the FreeFem++ language [25] (see also www.freefem.org), which is an extension of C++.

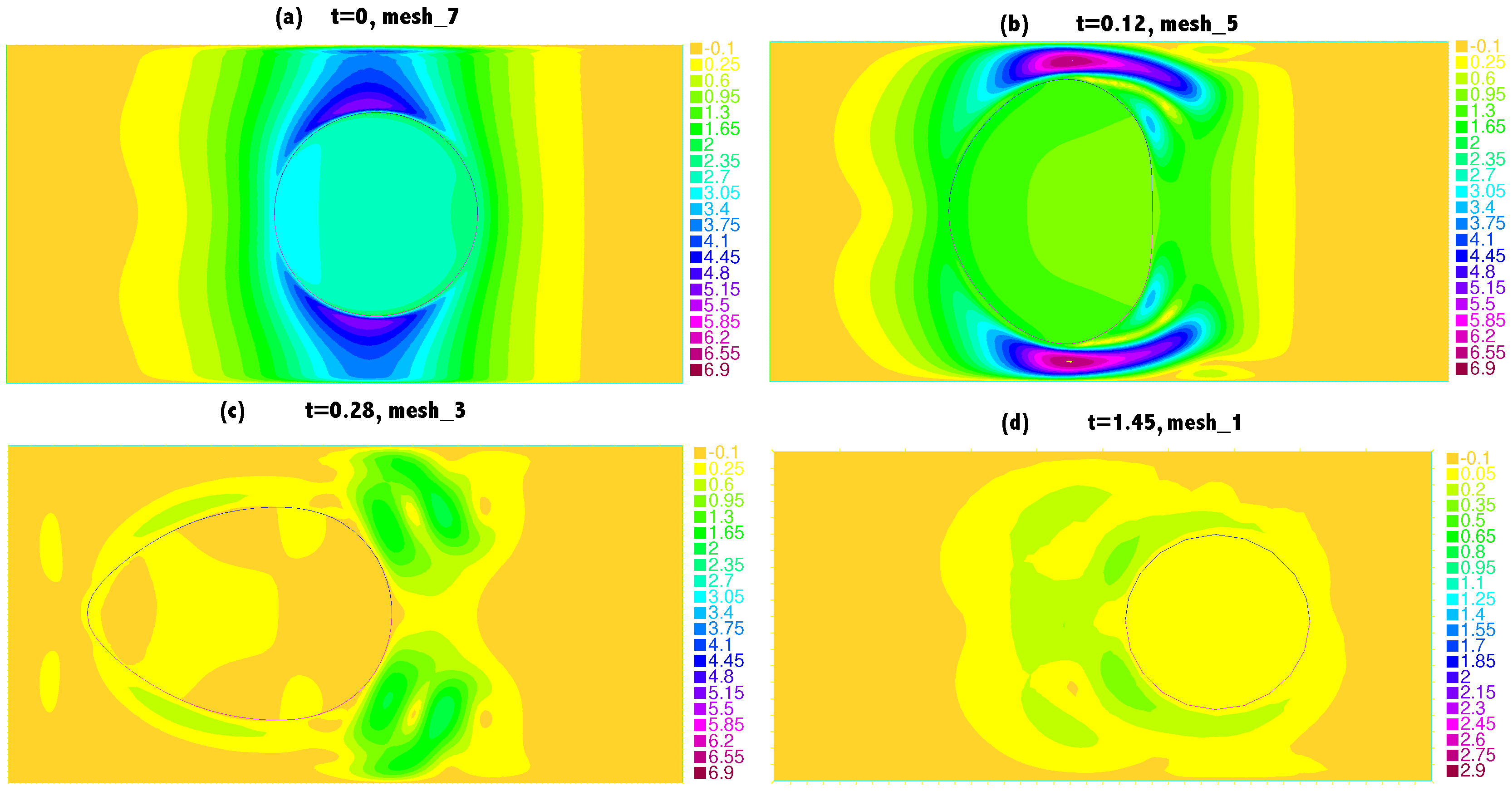
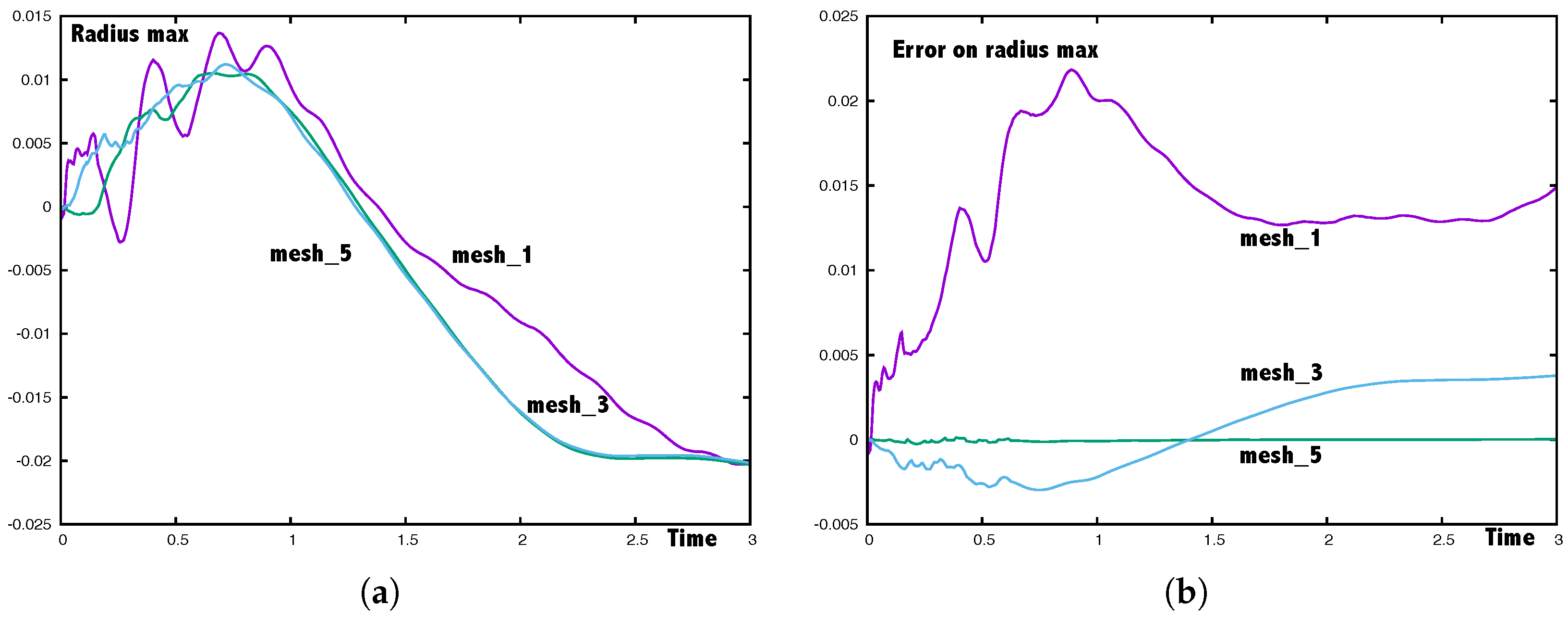
5.1. An Axisymmetric Torus

A torus of rubber-like material is immersed in a fluid filling a cylindrical canister. Assuming axial symmetry, the computational domain is a rectangle $(0,L)\times (0,H)$ with a disk inside of radius R and center $x_c,y_c$.

The disk is the cross-section of the torus which is an incompressible Mooney–Rivlin material characterized by ${\overline{c}}_1=c_1-2c_2$ and ${\rho }_s$, as explained in Section 2.5. The rectangle is filled with a Newtonian fluid characterized by its density ${\rho }_f$ and viscosity ${\mu }_f$.

At time zero a centripetal horizontal uniform velocity $U_0$ is imposed on the torus. Consequently, the torus contracts, and its cross-section, changes to preserve mass, until a position nearest to the axis of symmetry is reached. Then, it bounces away from its axis to a maximal position and repeats these oscillations a few times until fluid viscosity dampens the motion.

The tests are done with $T=3$, corresponding to 2.3 periods; the parameters are:

$$R=0.3,L=2,H=1,,x_c=1.1,y_c=0.5,U_0=-4,{\rho }_s=5,{\rho }_f=1,{\mu }_f=0.01,{\overline{c}}_1=40$$

The problem is solved on four triangulations, called ${\mathrm{mesh}}_i,i=1,3,5,7$; the associated time step size is $\delta t=T/(50\times i)$. The number of triangles in the meshes are 775, 6522, 17,749 and 35,308.

Figure 1 shows the initial state and some snapshots at times of maximum vertical and horizontal elongations, and farthest travel to the right.

Decrease of energy (viscous terms included) and conservation of mass are shown on Figure 2a. Energy is computed using ${\mathrm{mesh}}_1$ and 1, 2, 3 or 4 iterations for the non-linear solver of Section 3.4; the results show that 2 iterations for the nonlinear solver is optimal. Energy is also plotted when ${\mathrm{mesh}}_3$ and ${\mathrm{mesh}}_5$ are used (with 2 iterations). In agreement with the theory, energy decays with time even on a coarse mesh. The decay is due to the numerical dissipation because for the continuous problem it should be constant, and indeed it is less with finer meshes. Note that an impulsive start is not an energy-friendly test case.

Conservation of mass is shown on Figure 2b for ${\mathrm{mesh}}_1$, ${\mathrm{mesh}}_3$ and ${\mathrm{mesh}}_5$. It is within 2%.

To study convergence we take the results obtained with ${\mathrm{mesh}}_7$ as a reference “almost exact” solution. Then, we observe the point on the torus with maximum radius (i.e., farthest to the right). On Figure 3a the maximum radius is shown versus time for the four meshes; on Figure 3b the pointwise error for ${\mathrm{mesh}}_i$, $i=1,3,5$. Convergence is observed; we make no claim on the speed of convergence versus mesh size because ${\mathrm{mesh}}_7$ is probably too coarse to be reliable.

5.2. Clamped Structure in a Fluid

A set of computations of a beam in vacuum or in fluid has been performed at the request of Larma’s PhD advisor, Miguel Fernandez [26]. Experimental measurements are available [20] so it is intended to make them into a well-documented benchmark for the community. The geometry is always a clamped beam in a container; in all but the first case there is a flow in the container but to initialize the computation the position of the beam is computed with a stagnant fluid.

The beam in Hessenthaler’s experiment and Larma’s simulation is not incompressible, as the Poisson ratio is 0.35 instead of 0.5, so we expect discrepencies. The present method can generalized to compressible material and 2D simulations show similar stability properties but the computer program is not yet ready for 3D cases.

5.2.1. Free-Fall of a Clamped Structure in Vacuum

The beam size is $9\times 1\times 1$. The beam is clamped on the right to the $yz$ plane and free to fall under its own weight. The density ${\rho }_s$ is 1, and the gravity is $-0.01$ along y direction. The Mooney–Rivlin coefficients are $c_1=5$ and $c_2=2.5$. Computation stops at $T=100$ after 3200 steps with $\delta t=0.03125$. Results are shown at different times in Figure 4.

At the end of computation, the error of volume is less than $1\%$. A discussion about $c_3$ is found later in Section 5.3.3.

5.2.2. Free-Fall of a Clamped Beam in a Fluid

Second, we consider a flat beam of size $9\times 1\times 4$ with one side attached to a box which is filled with a fluid. The box size is $10\times 7\times 5$. Solid density ${\rho }_s$ is 1. Fluid density ${\rho }_f$ is $0.5$, and viscosity ${\mu }_f$ equals $0.1$. The gravity g is $-0.5$ along the y direction. The Mooney–Rivlin coefficients are $c_1=16.67$ and $c_3=8.33\left({\mathrm{tr}}_{\mathbf{B}}^2-{\mathrm{tr}}_{{\mathbf{B}}^2}-4\right)$. Computation stops at $T=100$ after 200 steps with $\delta t=0.5$.

Computing results are shown in Figure 5; volume error is less than $0.5\%$ at the end.

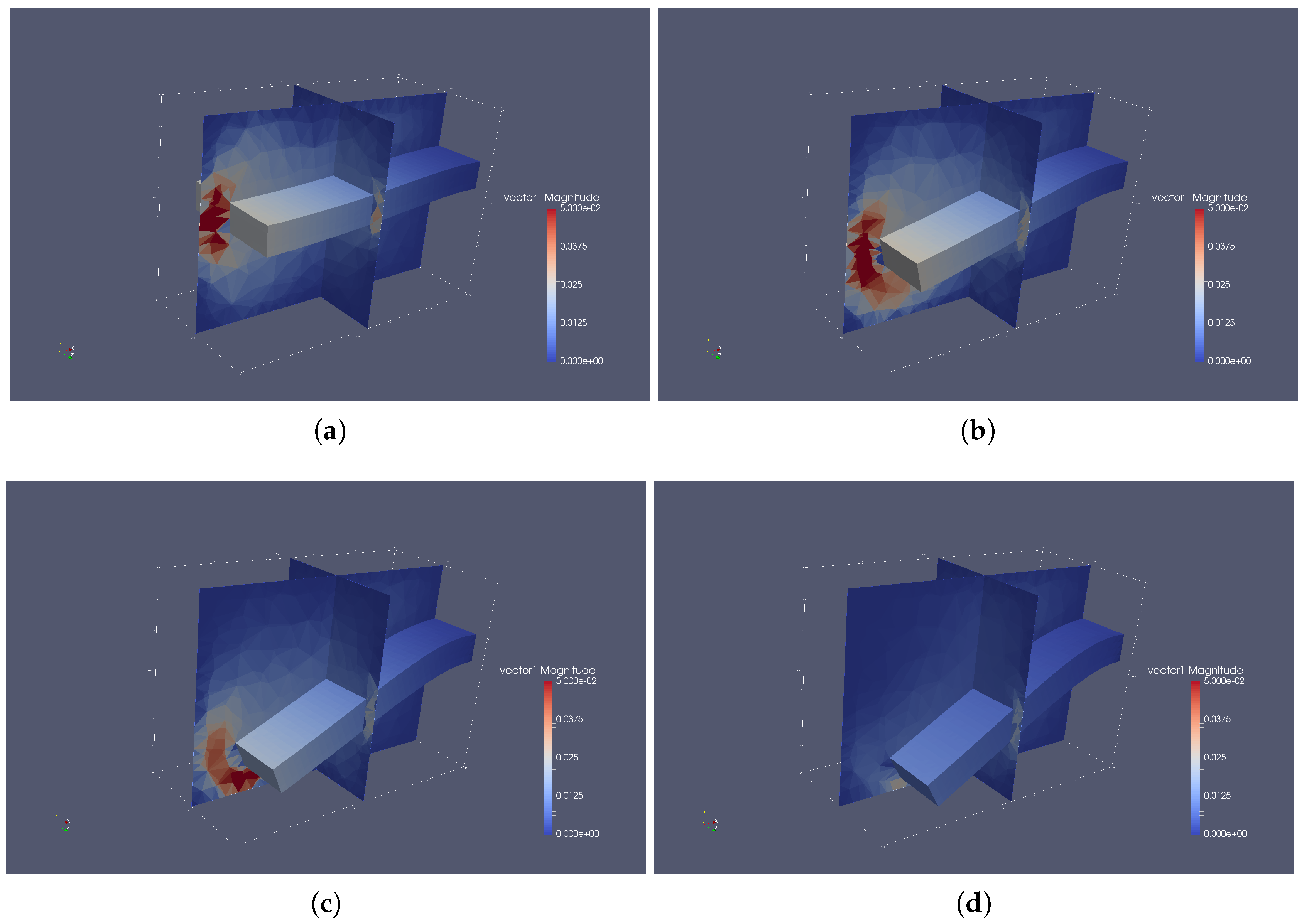
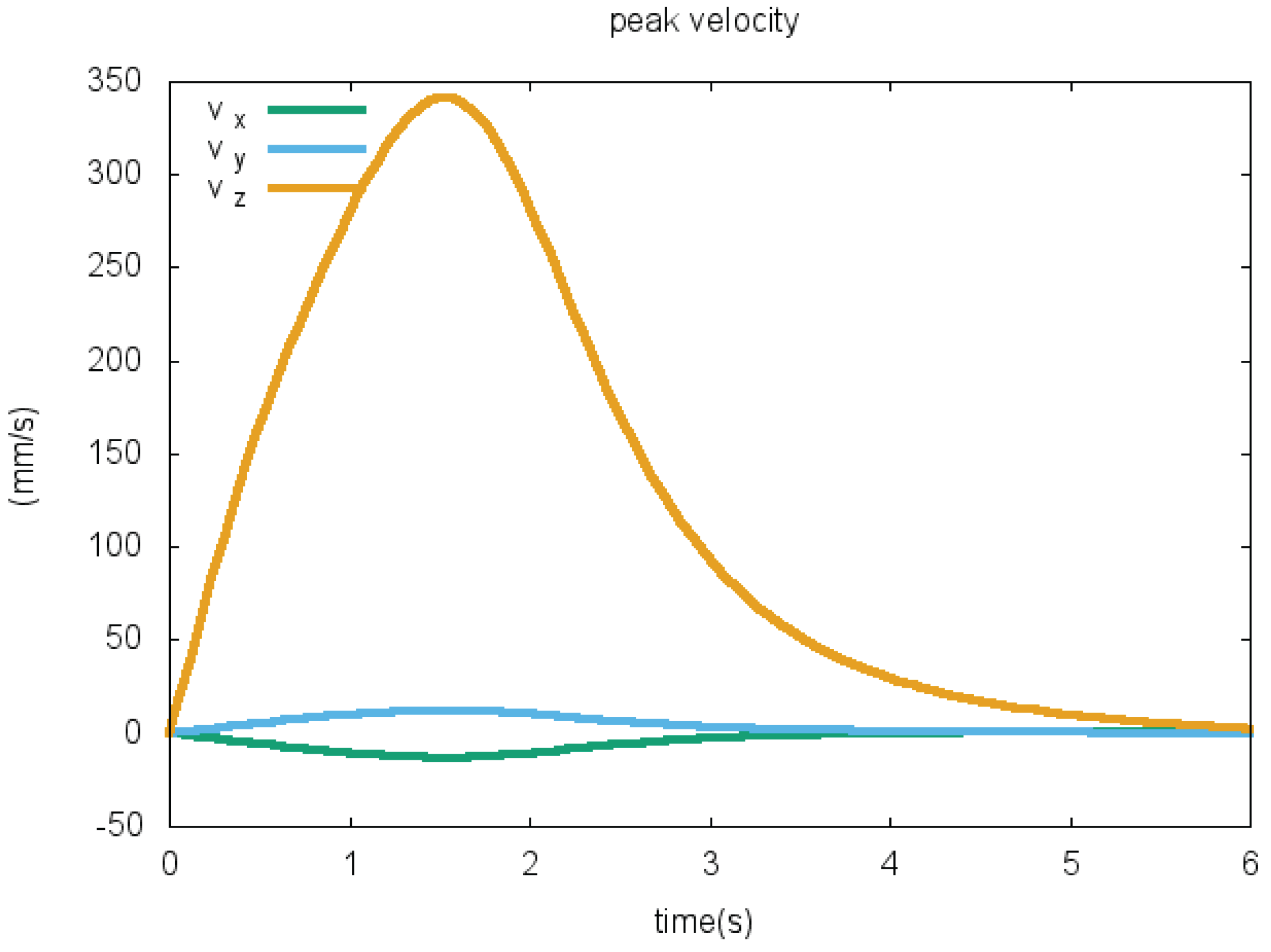
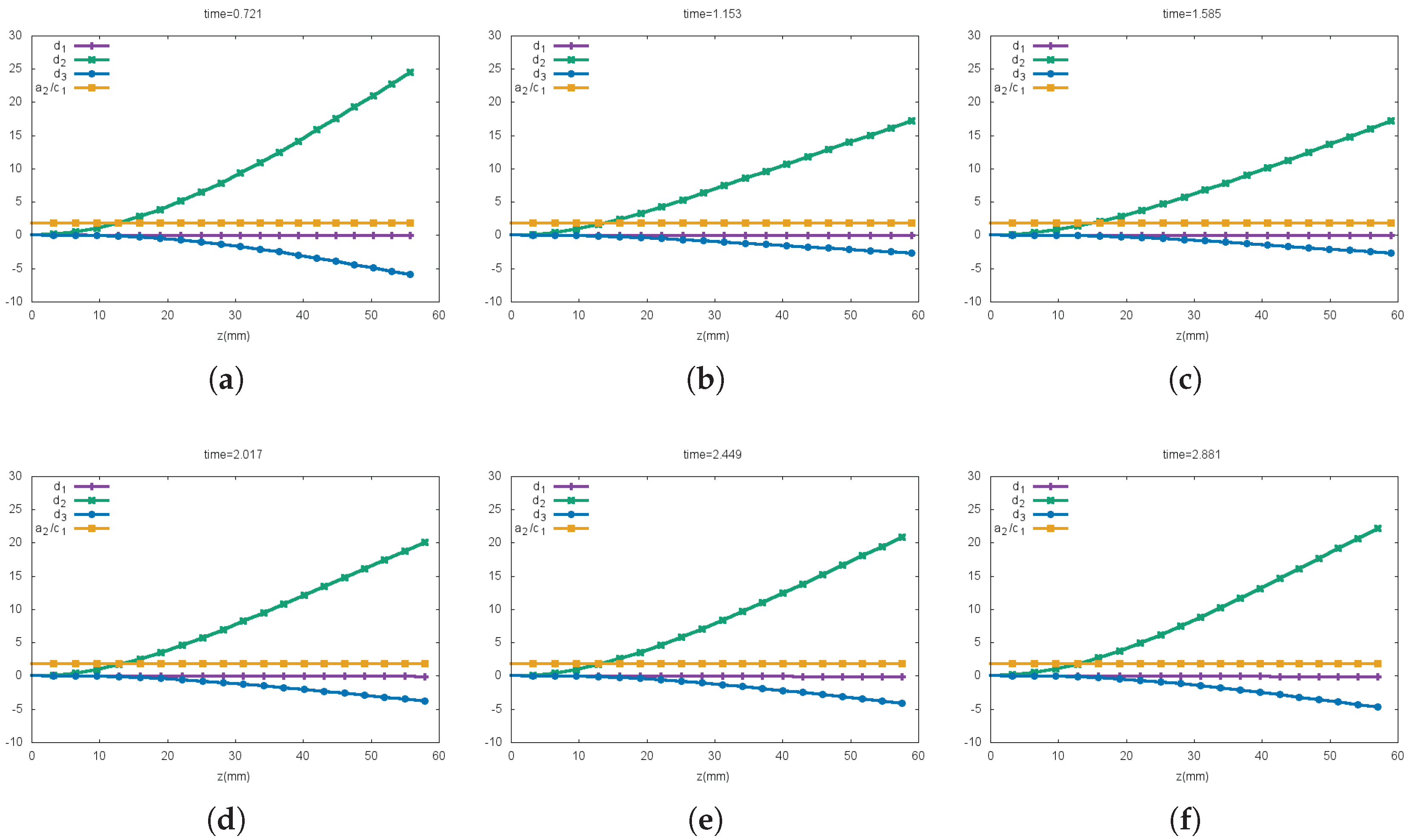
5.3. The Benchmark

An experiment was designed by Hessenthaler et al. [20] to calibrate the computer simulations of Larma [26].

The geometry is a cylindrical chamber with a length of 200 mm, diameter 76.2 mm and axis parallel to $x=y=0$. Two inlet circular wholes are on the left $z=0$ wall, one with center at $\left(0,-27.15,0\right)$, the other at $\left(0,27.15,0\right)$, both of diameter 21.9 mm; the inlet pipes are 20 mm long. A silicon filament clamped on the $z=0$ plane is 2 mm thick, 11 mm wide, and 65 mm long; its center is located at $(0,0,0)$. The computational domain is discretized into ${10}^4$ vertices and adapted to the silicone filament to decrease error during its motion. Geometric schematic is shown in Figure 6.

As in [20], the density of the silicone filament is ${\rho }_s=1.0583\times {10}^{-3}$ g/${\mathrm{mm}}^3$. The incompressible Mooney–Rivlin hyperelastic coefficients are determined by curve-fitting to uni-axial tensile-load displacement test data. In [26] two coefficients are introduced: ${\widehat{c}}_1=103,533.82/2$ Pa and ${\widehat{c}}_2=8891.65/4$ Pa. The Poisson ratio is $\nu =0.315$ in [26] and $c_1=\frac{{\widehat{c}}_1}{2\left(1+\nu \right)}$, $c_2=\frac{{\widehat{c}}_2}{2\left(1+\nu \right)}$. There will be a difference because incompressibility implies $\nu =0.5$. Gravity g is $-9810$ mm/${\mathrm{s}}^2$ along the y-direction. Two numerical tests are made, a steady phase I, and a transient phase $\mathrm{II}$.

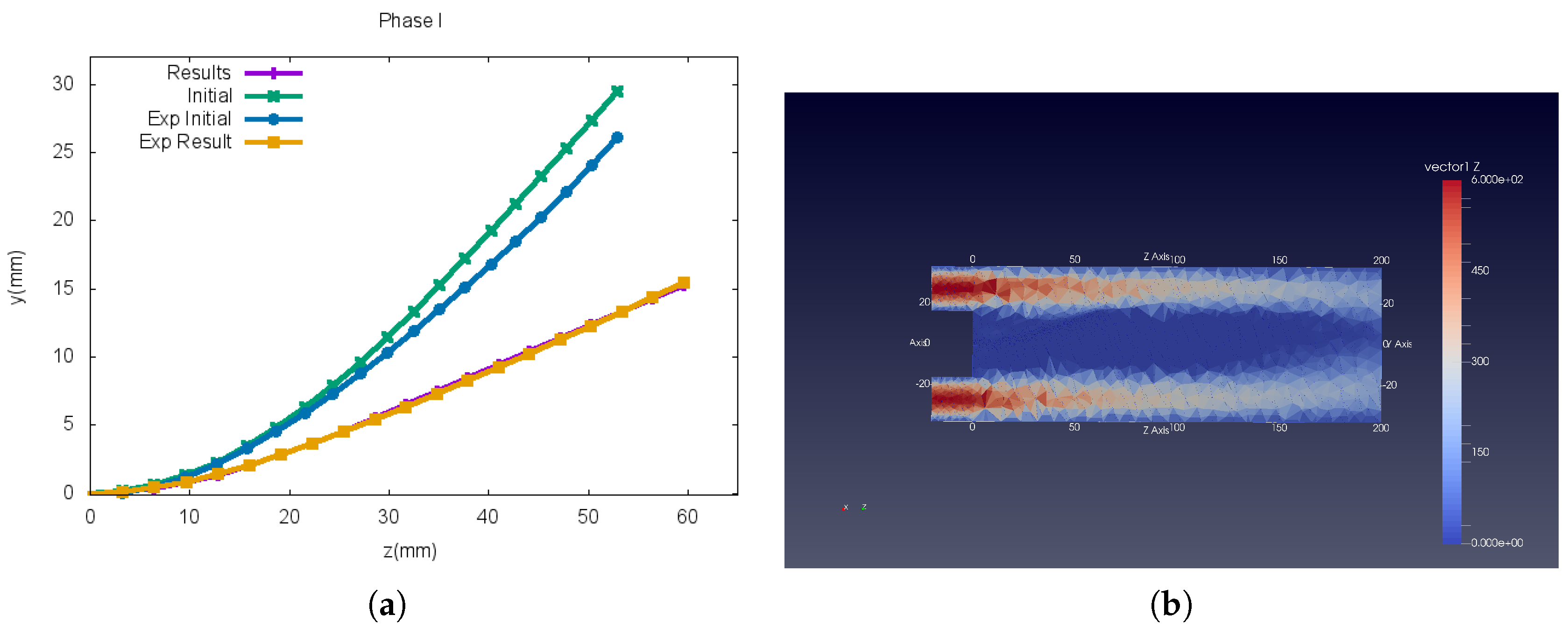
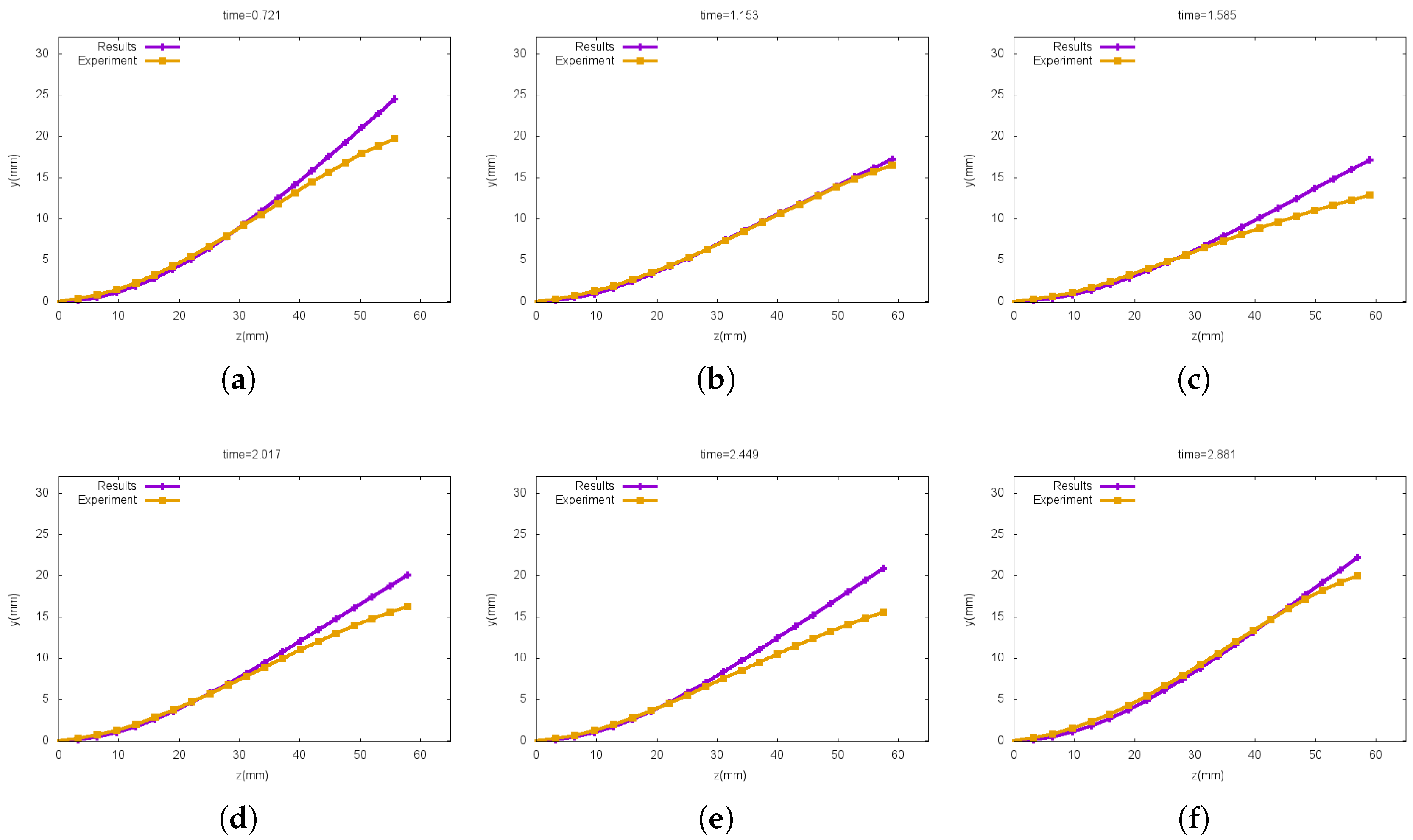
5.3.1. Phase I

In the fluid ${\rho }_f=1.1633\times {10}^{-3}$ g/${\mathrm{mm}}^{-3}$ and ${\mu }_f=1.25\times {10}^{-2}$ Pa·s. A Poiseuille profile flow is applied to the upper and lower pipes with peak velocity of 630 mm/s and 615 mm/s, respectively. The position of center line of the beam along the z direction is recorded as a function of time in Figure 7 and compared with experimental data.

In absence of flow, due to buoyancy forces, the silicone filament reaches an hydrostatic equilibrium with maximum displacement ${\mathbf{d}}_M^0$, at the tip on the right, approximately equal to 29.50 mm in [20] and 31.04 mm in [26]. To compute this displacement we have taken $T=1$ and 1000 steps with $\delta t=0.001$.

Then ${\mathbf{d}}^0$ is taken as initial condition to Phase I as the inflows are turned on; the maximum displacements are now approximately 16.41 mm in [20] and 15.99 mm in [26] . To compute this state we have taken $T=2$, 2000 steps with $\delta t=0.001$. Our results, shown in Figure 7, overlap the experimental data.

5.3.2. Phase II

Finally a transient computation is performed. The fluid properties are ${\rho }_f=1.1640\times {10}^{-3}$ g/${\mathrm{mm}}^{-3}$ and $\mu =1.337\times {10}^{-2}$ Pa·s.

The Poiseuille profile flow applied on the upper pipe has a transient peak velocity ${\widehat{v}}_k\left(t\right)$, $k\in \left[x,y,z\right]$ shown in Figure 8 and corresponds to a smooth interpolation from

Table 1. For phase $\mathrm{II}$, curve–fitting coefficients of inlet peak velocity for ${\widehat{v}}_k\left(t\right)={\mathbf{\sigma }}_{i=1}^3{n}_i{t}^i/{\mathbf{\sigma }}_{j=0}^4{b}_j{t}^j$ with ${\widehat{v}}_k=0$ for $t\in \mathrm{I}\setminus {\mathrm{I}}_k$. Note that the flow in y direction is applied only in the upper inlet.

$\widehat{\mathit{v}}$	${\mathit{n}}_1$	${\mathit{n}}_2$	${\mathit{n}}_3$	${\mathit{d}}_0$	${\mathit{b}}_1$	${\mathit{b}}_2$	${\mathit{b}}_3$	${\mathit{b}}_4$	${\widehat{\mathbf{I}}}_{\mathit{k}}$
${\widehat{v}}_x$	$-11.37$	$-28.99$	7.73	1.38	0.24	3.59	$-3.14$	1	$\left[0,4.07\right]$
${\widehat{v}}_y$	14.95	11.88	$-2.17$	2.06	$-2.0$	4.95	$-3.50$	1	$\left[0,5.51\right]$
${\widehat{v}}_z$	367.10	363.40	$-62.24$	1.21	$-0.38$	3.76	$-3.19$	1	$\left[0,5.27\right]$

. No flow is applied to the lower inflow pipe.

Computation stops at $T=5$ after 1600 steps with $\delta t=0.003125$. The maximum velocity norm of the solid is less than 30 mm/s; the error introduced by the computation is less than 0.1 mm. Deflection of the center line of the silicone filament is recorded versus time and a comparison between numerical results and experimental data is shown in Figure 9 at six different times. These results display a fair—yet not satisfactory—agreement between the simulations and the experimental data. The difference is perhaps due to improper determination of the coefficients of the hyperelastic model, because bending at the end of silicone filament could be observed only when the magnitude of $c_2$ is large enough. Another possible explanation is the wrong Poisson ratio, namely an effect due to incompressibility.

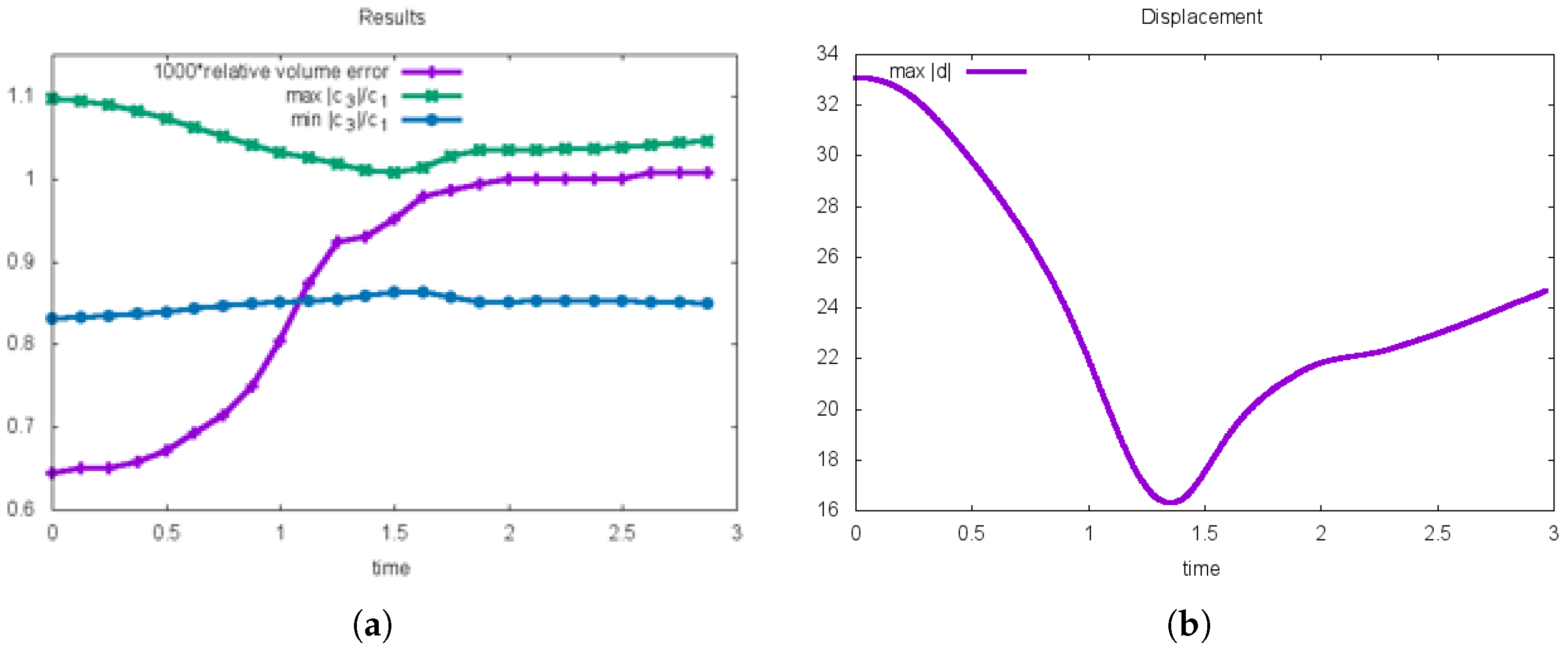
5.3.3. Variation of Coefficient $c_3$

The coefficient $c_3$ in (10) varies with the structural rheology through ${\mathrm{tr}}_{\mathbf{B}}$ and ${\mathrm{tr}}_{{\mathbf{B}}^2}$. We wish to analyze the non-linearity of $c_3=\frac{c_1}{2}\left({\mathrm{tr}}_{\mathbf{B}}^2-{\mathrm{tr}}_{{\mathbf{B}}^2}-4\right)-2c_2$ during the simulation.

Maximum and minimum magnitude of $c_3$ and relative volume error with respect to time are plotted in Figure 10a, and the corresponding maximum magnitude of displacement $\mathbf{d}$ is shown in Figure 10b.

It is interesting to point out that $c_3$ is not very sensitive to the displacement gradients in this simulation as shown in Figure 11: $c_3$ remains fairly constant during the computation, even though $\mathbf{d}$ does not. These results seem reasonable since deflection over the whole silicone filament is fairly uniform. However, we do not rule out that strong deformations could cause a stability problem in the algorithm; this will be investigated in the future.

6. Conclusions

In this study, a fully Eulerian fluid–structure formulation has been presented. An implicit unconditionally stable monolithic finite element scheme based on characteristic–Galerkin discretization has been proposed and studied. At each time step a non-linear system must be solved; however semi-linearization leads to well-posed linear monolithic systems for the velocities and pressures.

What was found in [17,18] for 2D systems could be generalized in 3D with similar stability based on analytical proof that the energy of the discrete system cannot increase.

The numerical method has been implemented with FreeFem++ [25], and validation tests have been presented. For an axisymmetric case, conservation of mass and energy were shown as well as convergence on a sequence of embedded meshes.

The effect of nonlinearity of $c_3$—the major difference with the 2D case—is studied in Section 5.3.3 with validation tests.

In the near future we intend to parallelize the computer program and use it for larger systems, in particular for hemodynamics.