Abstract
Mesoscale filtering and protective layers are replete throughout the natural world. Within the body, arrays of extracellular proteins, microvilli, and cilia can act as both protective layers and mechanosensors. For example, blood flow profiles through the endothelial surface layer determine the amount of shear stress felt by the endothelial cells and may alter the rates at which molecules enter and exit the cells. Characterizing the flow profiles through such layers is therefore critical towards understanding the function of such arrays in cell signaling and molecular filtering. External filtering layers are also important to many animals and plants. Trichomes (the hairs or fine outgrowths on plants) can drastically alter both the average wind speed and profile near the leaf’s surface, affecting the rates of nutrient and heat exchange. In this paper, dynamically scaled physical models are used to study the flow profiles outside of arrays of cylinders that represent such filtering and protective layers. In addition, numerical simulations using the Immersed Boundary Method are used to resolve the three-dimensional flows within the layers. The experimental and computational results are compared to analytical results obtained by modeling the layer as a homogeneous porous medium with free flow above the layer. The experimental results show that the bulk flow is well described by simple analytical models. The numerical results show that the spatially averaged flow within the layer is well described by the Brinkman model. The numerical results also demonstrate, however, that the flow can be highly three-dimensional with fluid moving into and out of the layer. These effects are not described by the Brinkman model and may be significant for biologically relevant volume fractions. The results of this paper can be used to understand how variations in density and height of such structures can alter shear stresses and bulk flows.
1. Introduction
Flows through porous layers are significant to numerous applications in biology, from the microscale problem of blood flow at the endothelial cell membrane to the macroscale problem of water flow through sea grass meadows and kelp forests [1,2]. Flows at the intermediate scales (e.g., the mesoscale) are also significant to many organisms because this is the scale at which many small organisms, such as tiny insects and zooplankton, experience their environment [3,4,5]. This is also the scale at which tiny hairs, or trichomes, may alter the boundary layer at the individual blade level which can, in turn, affect nutrient uptake and exchange [6,7]. Biological flows at the mesoscale, however, have received far less attention than either larger or smaller scale flows, due in part to the fact that the equations of fluid motion cannot be simplified by neglecting either inertia or viscosity.
It is exactly at these intermediate scales where both viscosity and inertia are significant that bristled, hairy and filtering structures help many organisms feed, locomote, smell, signal, exchange nutrients, and perform a variety of sensory and other important and often complex functions. These structures are found in many different types and sizes of organisms, in terrestrial and aquatic environments, and from the cellular level up to the organism level. For example, cilia are hair-like protrusions that can act as antennae on the surface of most eukaryotic cells [8]. Cilia also perform a variety of complex behaviors, including the establishment of left-right symmetry in the vertebrate embryo [9], acoustic streaming in the ear [10], and cell–cell communication in Drosophila [11]. Their presence and function in sponges, one of the earliest developing phyla, suggest that arrays of cilia such as these might represent the beginning of sensory and coordination systems in the animal kingdom [8].
Many examples also exist in the aquatic environment. For example, copepods beat their cephalic appendages to feed or swim, use antennules and swimming legs to escape from predators, or sink in the water column by reducing the use of their appendages [12]. Barnacles use their feeding structures, called cirral fans, to assist in their suspension feeding, sweeping them through the water when flow is slower and holding them out passively when currents are slower [13,14], and the lappets of developing scyphomedusa assist in propulsion as well as feeding [15,16]. On land, bristled, flexible wings help insects feed by lessening the force required to clap their wings together and fling the wings apart [17]. Among mammals, lab rats possess different lengths of whiskers (vibrissae) that are attuned to different resonances, while the whiskers of pinnipeds (seals) allow them to follow prey by tracking hydrodynamic trails in the water [18].
Another way in which small hairs aid organisms by altering the boundary layer over exchange surfaces. For example, trichomes are small hairs or other outgrowths that can be found on the epidermis of a plant during some or all stages of its life. One of the potential functions of the trichomes is to alter the boundary layer to increase the efficiency of gas exchange and transpiration. Turbulent boundary layers experience much higher rates of gas transport than do laminar boundary layers, but unless the windspeed is high, boundary layers can experience laminar flow even if the air around the plant is turbulent [19]. Trichomes have been shown to increase the surface roughness of leaves, producing turbulent boundary layers at lower wind speeds and enhancing gas exchange [20]. Along with increasing the exchange of gases between plants and the atmosphere, trichomes are also important for reducing absorbed solar radiation and leaf temperature, defending against predators, and reducing water film on leaves that could reduce gas exchange [20].
1.1. Relevant Dimensionless Numbers and the Leaky to Solid Transition
An important and complex function of bristles, hairs, and other bioarrays at the mesoscale is that they operate at the transition from leaky to functionally solid layers. When flow is viscous, due to the no-slip condition, a velocity gradient develops between the surface and freestream flow, with smaller or slower objects (lower ) resulting in a thicker (boundary) layer of fluid. The result is that rows of denser (or slower) cylinders operate as solid layers, while cylinders that are faster or farther apart function as leaky sieves.
To accurately describe flow through these filtering, protective, and hairy layers, several dimensionless parameters are needed. The first dimensionless number we will use is the bulk flow Reynolds number, . This Reynolds number describes the relative inertial to viscous forces in the bulk flow and is described by
where is the viscosity of the fluid, is the dynamic viscosity of the fluid, U is a characteristic velocity (here defined as the free stream velocity), and L is a characteristic length scale. For the bulk flow , we use the height of the channel or computational domain as the characteristic length scale. To describe the relative importance of inertial and viscous effects at the level of the cylinders, we use a diameter based Reynolds number, , given by
where D is the diameter of the cylinder. The relevant depends upon the scale being considered. For the bulk average flow within and above the layer, the characteristic length based on the domain height is the more useful . When considering the small scale flow between each individual cylinder, the characteristic length of the diameter and provides the relevant scale. Other important dimensionless numbers include the gap to diameter ratio, . Here, the diameter is set to the diameter of the cylinder, and the gap is set to the distance between the central axes of the nearest cylinders. The height to diameter ration, , is set to the height of the cylinders to the diameter. Dimensionless quantities for several biological systems are given in Table 1.

Table 1.
Measured morphological parameters of various cylinder-like structures in biology. The diameter based Reynolds Number, , was computed using the length scale as the diameter of the cylinders, kinematic viscosity of air or water. The characteristic velocity was chosen as the free stream velocity (approximately 1–2 m/s for trichomes, the wind speed on an average day). Trichome measurements were taken from images using [21,22].
At the organism level, hairy appendages are typically leaky at and higher, while they are paddle-like at and lower [28]. Koehl showed a highly nonlinear transition between leaky- (sieve) and solid- (paddle) like behavior of an array of hairs based on factors such as the hair size, speed, and spacing [28,29,30]. The effective leakiness of these arrays are challenging to describe for biologically relevant problems given the relatively long times it takes the flow to reach steady state and the strong dependence of the effective leakiness upon the spacing and velocity of the array (which may change during their operation). The effective leakiness also depends strongly on the direction of flow and interactions with other boundaries. For example, Loudon and Koehl found a complex relationship between wall nearness and Reynolds number [31], and Jones et al. [5] found that leakiness depends upon the angle of attack of the structure relative to the direction of flow. In addition, while some organisms exist in one regime all of their lives, others may exist in one regime at one life stage and transition to another at a later stage or quickly switch from one to the other as it becomes advantageous [15,32].
It should also be noted that there is an extensive body of work combining experiments, analytical models, and numerical simulations of flow through terrestrial and aquatic canopies [33,34]. These flows are typically very high and are dominated by turbulence, vortex shedding, and rolling eddies. One important dimensionless parameter for these flows is the roughness density , which is defined as the total frontal area of the canopy elements per unit ground area [34]. In this paper, we do not explicitly consider the effect of roughness density on bulk flow through the array, but note that this is an interesting parameter to consider in future work. Since the fluid physics of our parameter space are rather different from the canopy regime, it would be interesting to determine how well and over what parameter space the roughness density describes bulk flow through an array. One potential source of error is that, for flows at , large boundary layers form whose thicknesses change rapidly with . Given that leakiness is not a monotonic or unique function of volume fraction in this regime, it is not clear that the frontal area of the array elements would be an effective metric to describe how the array interacts with the flow. We do, however, note that in general it would be worthwhile to apply the ideas and methods from this body of high work to future studies at the mesoscale.
1.2. Analytical Porous Models
At the microscale () in the field of vascular transport, relatively simple, analytical models have been used to describe the profile of the blood flow above and through the endothelial surface layer (ESL). The endothelial surface layer consists of the glycocalyx and attached plasma proteins and has a significant role in proper cell function since it serves as a vasculoprotective layer, a mechanotransducer, and a molecular filter. Mathematical models of the flow through this layer have been to estimate volumetric flow rates and shear stresses within this layer and at the cell surface. One of the more popular models uses the Brinkman equation where the ESL is treated as a homogenized porous layer [23,35,36,37,38,39,40]. For example, Weinbaum et al. [23] model the glycocalyx as a Brinkman layer and calculate the value of the hydraulic conductivity using estimates of the volume fraction of core proteins and by assuming that the layer has a quasi-periodic structure. To obtain the flow profile for the entire vessel, the flow through this layer is matched to Stokes flow above the layer. They find that the majority of shear stress is imposed on the tip of the core proteins and relatively little is imposed at the membrane. Brinkman models have also been used to describe the flow through layers of microvilli within the kidney that have a mechanosensory role [24].
At the larger scale (), flow through vegetative canopies and beds, including sea grasses, reefs, grass fields, forest canopies, and macrophytes, have been modeled using 1D models with analytical solutions such as Darcy’s law [41], its generalization to the Brinkman law [35], and the Darcy–Forchheimer law [42] describing non-Darcy flow at high velocities. In some applications, modified Brinkman equations have been applied used to model flow through vegetation using a Cantor–Taylor brush configuration [43,44]. In this case, three regions of the flow are considered: (1) a dense layer, (2) a sparse layer, and (3) a layer free of obstructions. The flow fields obtained from these modeling efforts have then been used to understand the flushing of plankton and pollen from sea grass meadows and kelp forests [1,2] and to describe the distributions of zooplankton that use local flow velocity and sheer to initiate reorientation or directed movements [45,46,47]. For a more complete overview of applications, please see the review by Nepf et al. [33].
There are several challenges and limitations when using Brinkman models to describe flow through mesoscale arrays. By design, the Brinkman and similar porous models only describes the average flow through a porous layer and do not reveal smaller scale flow patterns where the fluid bends around obstacles such as various protrusions, transmembrane proteins, bristles, and hairs. Models that describe shear flow or flow within a channel with a porous layer typically assume that there is no flow in the third dimension (e.g., into and out of the layer). For applications where such small scale flow structures are important, it may be necessary to consider more than a model of the averaged flow. Example applications could include anything where a particle is required to diffuse or swim through such a layer. Furthermore, the error introduced by the homogenization of the porous layer will be proportional to the amount of flow in the third dimension. Careful consideration of this amount of flow in the third dimension as a function of obstacle spacing, , and height of the layer has not been carefully described, although studies of specific applications do suggest its importance [5,48,49]. Furthermore, it is not straightforward to analytically determine the value of the effective porosity or leakiness of a particular array. These values are highly nonlinear functions of , volume fraction, geometry, and array height and length. Often, these values must be determined experimentally or numerically for a particular situation.
1.3. Fully Resolved Flow (Not Averaged) Past 3D Structures
Our goal in this paper is to describe the details of flow within idealized biological filtering, protective, and other types of porous layers, and solve an associated fully coupled fluid–structure interaction problem for simplified structures. While numerous studies have considered such flow at small () or large () scales, few studies have focused on the mesoscale (). Some of the challenges of such simulations include different length and time scales and far-from-equilibrium spatially and temporally varying forces [50]. In addition, it is often necessary to solve the full Navier–Stokes equations to resolve the flows within such mesoscale arrays. Given the sensitivity of the flows to any changes in effective viscosity or the thickness of boundaries, these simulations often require highly resolved spatial grids [5], leading to the need for adaptive mesh refinement and parallelized codes.
In this paper, we use several approaches to describe the flow around filtering layers at the mesoscale:
- Flow around physical models of filtering layers is measured using particle image velocimetry.
- A 1D Brinkman model of flow through porous layers is compared to three-dimensional dynamically scaled physical models. The goal is to confirm that the 1D Brinkman model captures bulk flow outside of the porous layers.
- Three-dimensional flow through idealized filtering layers is numerically simulated using the immersed boundary method.
- A 1D Brinkman model of flow within the layer is compared to the numerical simulations. The goal is to confirm that the Brinkman model adequately captures average flow but does not capture movement in the third dimension (which would enhance exchange into and out of the layer).
Note that the models and numerical simulations are also used to examine how changes in volume fraction, height, and arrangement of the filtering layer alters velocity profiles within and around the layer. Two different boundary conditions are considered for experimental and numerical feasibility. In the case of physical models, flow is driven through a channel with a porous layer on both the top and bottom. This is representative of flow through blood vessels and other internal channels. In the numerical simulations, shear flow is considered with a porous layer on the bottom of the domain. This is representative of flow over a leaf or another external surface. It is also a reasonable approximation of flow near the luminal surface of a vessel. Note that the experiments and simulations are being used to illustrate different features of flow through filtering layers. The experiments are used to illustrate whether or not the Brinkman model can describe flow around in finite layers. The simulations are used to determine if the Brinkman model can resolve flows within infinite layers. The experiments and simulations are not constructed for one-to-one comparisons.
2. Methods
2.1. Immersed Boundary Method
To perform the fluid–structure interaction, we implement the immersed boundary method. The immersed boundary method has been successfully applied to numerous different applications from microscale and cellular interactions [40,51,52] to cardiovascular dynamics [53,54], to organismal scale biomechanics, including aquatic locomotion [55,56], insect flight [17,57], muscle–fluid–structure interactions [58,59], and plant biomechanics [60,61], to parachuting [62].
The following outlines the two-dimensional formulation of the immersed boundary method, from which the three dimensional extension is straightforward. For a full review of the method, please see Peskin [63]. Please note that for fluid–structure simulations of rigid bodies, other numerical methods are likely more efficient [64,65]. Our goal is to eventually build up to 3D flexible cylinders in oscillating flows, and Peskin’s immersed boundary method and publicly available codes provides us this flexibility. The governing equations of fluid motion are given by the Navier–Stokes equations:
where is the fluid velocity, is the pressure, is the force per unit area applied to the fluid by the immersed boundary, and are the fluid’s density and dynamic viscosity, respectively. The independent variables are the time t and the position . Note that the variables , and are all written in an Eulerian framework on the fixed Cartesian mesh, .
The interaction equations between the fluid and the boundary are given by:
where is the force per unit length applied by the boundary to the fluid as a function of Lagrangian position, q, and time, is a two-dimensional delta function, gives the Cartesian coordinates at time t of the material point labeled by the Lagrangian parameter, q. Equation (5) applies a singular force from the immersed boundary to the fluid through the external forcing term in Equation (3), and Equation (6) evaluates the local fluid velocity at the boundary. This enforces the no-slip condition and the boundary is then moved at the local fluid velocity. Each interaction equation involves an integral transformation, with a two-dimensional Dirac delta function kernel, , to convert Lagrangian variables to Eulerian variables and vice versa.
The forcing term, , in the integrand of Equation (5) is specific to the application. In a simple case where boundary points are tethered to target points, to hold the boundary nearly fixed, the equation describing the force applied to the fluid by the boundary is
where is a stiffness coefficient and is the prescribed position of the target boundary. Details on other forcing terms can be found in [66,67].
2.2. Description of the Numerical Setup, Example Output, and Validation
We use the immersed boundary method [63] to simulate the fully-coupled fluid–structure interaction (FSI) problem of a single cylinder in a periodic flow. Fluid equations are nondimensionalized and discretized on a Cartesian grid, and boundary equations are discretized on a moving Lagrangian grid. The full Navier–Stokes equations are solved for the fluid domain. We use IBAMR (Boyce Griffith, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA), a software library that provides an adaptive and parallelized framework for the direct numerical simulation of the FSI problem using the immersed boundary method [68].
We use the immersed boundary method [63] to simulate the fully-coupled fluid–structure interaction (FSI) problem of a single cylinder in a periodic flow. Fluid equations are nondimensionalized and discretized on a Cartesian grid, and boundary equations are discretized on a moving Lagrangian grid. The full Navier–Stokes equations are solved for the fluid domain. We use IBAMR (Boyce Griffith, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA), a software library that provides an adaptive and parallelized framework for the direct numerical simulation of the FSI problem using the immersed boundary method [68].
IBAMR is a C++ framework that provides discretization and solver infrastructure for partial differential equations on block-structured locally refined Eulerian grids [69,70] and on Lagrangian meshes. Adaptive mesh refinement (AMR) is capable of higher accuracy between the immersed boundary and the fluid by increasing grid resolution in areas of the domain where vorticity exceeds a certain threshold or that contains an immersed structure. AMR improves computational efficiency by decreasing grid resolution in areas of the domain where low resolution is sufficient.
The Eulerian grid was locally refined near both the immersed boundaries and regions of vorticity where . This Cartesian grid was organized as a hierarchy of four nested grid levels; the finest grid was assigned a resolution of . A 1:4 spatial step size ratio was used between each successive grid level. The Lagrangian spatial step resolution was chosen to be twice the resolution of the finest Eulerian grid, e.g., .
All numerical parameters are provided in Table 2. The height of the domain was set to 1.0, and the lengths in the x- and y-directions were set to , see Figure 1. The domain is periodic in the x- and y directions. The boundary conditions are set in the z-direction to model shear flow. The x-component of the velocity was set to 0.1 m/s at the top of the domain and to 0 at the bottom. The diameter of the cylinder was set to 0.03125 m, and the height was varied from 0.078 m to 0.625 m. Reynolds number () was varied by changing the dynamic viscosity.

Table 2.
Numerical parameters used in the three-dimensional simulations.
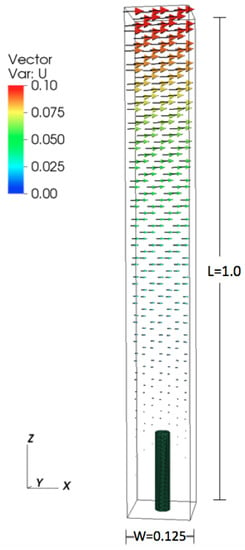
Figure 1.
Numerical set up for the periodic cylinder configuration.
We used several metrics to validate the three-dimensional simulations. Numerical simulations were performed for one cylinder with , = 5, and = 4 with and at the finest level. The average horizontal flow as a function of height agreed to within . The flow between two cylinders over a range of was calculated and compared to analytical results by [71]. Details of this study are reported in [5]. Finally, this implementation of the immersed boundary method has been checked against several standard fluid–structure interaction problems including flow past a sphere as reported in [72,73].
2.3. 1D Analytical Model Using Brinkman Equations
Brinkman’s equation, a generalization of Darcy’s law, states that the force acting on the fluid due to a porous layer is proportional to the local velocity in the layer [35]. Brinkman’s equation is written as
where is is the inverse of the hydraulic permeability.
First, we rewrite the two-dimensional Brinkman equation as
where . We consider a channel consisting of a central main region with unobstructed parallel shear flow (Region I with ) that is bounded on the top and the bottom by identical porous layers (Region II with ). The flow field is assumed to be symmetric about the centerline , and so our analysis will be restricted to the bottom half of the system. The flow is considered to be steady (), fully developed ), and zero in the cross-stream direction ().
Region I:
Using these assumptions, the x-momentum Equation (9) in the free shear flow region (Region I, where ) simplifies to
The y-momentum Equation (10) simplifies to
In other words, the fluid pressure is independent of the y-direction, and only changes in the x-direction.
We are interested in determining a closed-form expression for the velocity of the flow field within this region. To obtain this, Equation (11) is integrated once in y to obtain the velocity gradient
and then integrated once again to arrive at an equation for the streamwise velocity
where the evaluation of constants A and B requires two boundary conditions.
Region II:
To distinguish between the velocity of the flow in Region I, will be used to denote the streamwise x-directional velocity in the porous layer. Starting with the equation set Equations (9) and (10) and using the same assumptions as in Region I with gives
This second order ordinary differential equation can be converted into a set of two first order differential equations by defining a new variable w,
such that Equation (14) can be reduced to
The Equation set (15) and (16) represents a two-dimensional system of non-homogenous, first order differential equations that can be further simplified into a homogenous system by defining a transformation for ,
so that
This system can be written in matrix form as
and solved using conventional linear algebra techniques to give the velocity profile in Region II,
where the constants C and D will be evaluated using the boundary conditions.
At the centerline of the flow domain , velocity is unchanging
Applying this condition to Equation (12), we have
At in Region II, the layer of fluid that is in contact with the channel wall remains at rest (“no slip”). Applying to Equation (12) yields
Between the regions at , matching of the velocities results in
and matching the velocity gradients gives us
Solving Equations (18)–(21), we have the constants
with A given in Equation (18).
Substitution of these constants into Equations (12) and (13) gives us the velocity distributions as
Region I:
Region II:
The average flow velocities can be determined using the integral definitions
Region I
Region II
The viscous fluid flow exerts a tangential shear stress that can be determined as the gradient of the streamwise velocity, given as
Region I
Region II
We also consider the case of simple shear flow where velocity is a positive constant at () and a no-slip condition applies at the bottom (), see Figure 2. In this case, Equation (18) is replaced by
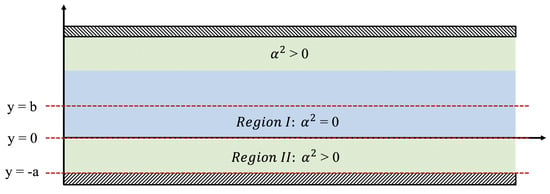
Figure 2.
Depicting the physical setup for the Brinkman equations. There are two regions of interest, namely where and .
Solving Equations (22)–(21) for the constants C and D results in
The other constants can be found in terms of these via Equations (20) and (21) and then applied to Equations (12) and (13) for the solution. In performing these calculations on a computer, it is useful to note that multiplying both the numerator and denominator of D by results in an expression that shares the same denominator as C while also avoiding numerical overflow in domains with large porous regions or values of .
2.4. Physical Models
The dynamically scaled physical models consisting of rigid cylinders are constructed out of pins that are 1 mm in diameter. Figure 3 shows the side and top views of the physical models. The parameters vary for each of the models, and the entire list of design parameters examined herein is presented in Table 3. This setup is inspired by flow through the endothelial surface layer within capillaries. The of the flow in capillaries is (10), using the vessel diameter as the characteristic length and the maximum velocity as the characteristic velocity. The of the flow within the endothelial surface layer is (10), using the core protein diameter as the characteristic length scale and the maximum velocity in a capillary as the characteristic velocity.
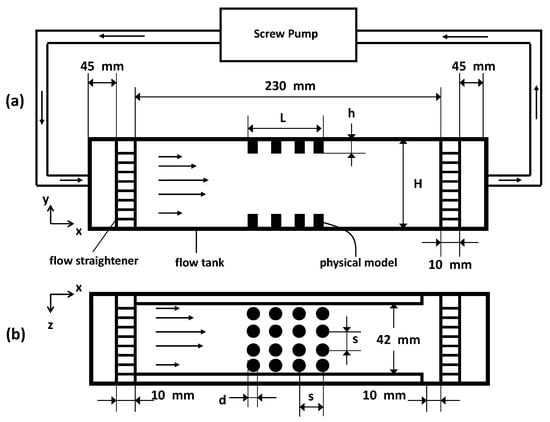
Figure 3.
Schematic of the experimental setup showing the side view (a) and the top view (b) of the flow chamber with the physical model inserted. Flow direction in the tank is from right to left.

Table 3.
Parameters used in the physical model experiments.
To achieve this low value of in these experiments with macroscopically scaled models, both the velocity and the viscosity of the fluid are adjusted. The fluid used is KaroTM brand light corn syrup, with dynamic viscosity () of 1.229 kg·ms, and density () of 1340 kg·m at an ambient room temperature of 20 C.
The models are inserted flush on the top and bottom walls of an optically accessible plexiglass flow tank with dimensions as shown in Figure 3. The fluid is driven by means of a screw pump that is powered by a DC (direct current) motor. To achieve parabolic inflow, the fluid entering and exiting the tank is passed through a set of flow straighteners consisting of a fine mesh. Note that, in the schematic in Figure 3, N is equal to 4 (as seen in the top view). This is merely for the purpose of illustration, as other variations of this parameter are examined as well (see Table 3 for details). The average inflow velocities with which the pump moves the fluid upstream of the models at the entrance is approximately = 0.0002 m/s. Using this value as the velocity scale for the fluid properties mentioned earlier, a value of approximately is achieved in these experiments, using the diameter = 0.001 m of the individual cylinders as the length scale, or using channel height H as the length scale. Since the pins used in the design of the models are opaque, the flow through the layer could not be resolved using particle image velocimetry (PIV) since this method requires optical access to acquire information.
2.5. Experimental Diagnostics
In order to visualize the flow field and quantitatively determine the velocity, two-dimensional particle image velocimetry (PIV) measurements are conducted on the flow over the scale models in the flow tank. Particle image velocimetry is a non-intrusive, two- or three-dimensional technique that can be used to obtain instantaneous information on a flow field by recording and processing the single or multiple exposed images of tracer particles suspended in the fluid. The particle images are then processed using correlation based techniques to construct the velocity vector field of the fluid flow. Detailed reviews of PIV can be found in Adrian [74] and Willert and Gharib [75].
Measurements are made using time-averaged PIV. The laser sheet for the PIV measurements is generated from a 50 mJ double-pulsed Nd:YAG laser manufactured by Continuum Inc. (San Jose, CA, USA), which emits light at a wavelength of 532 nm with a maximum repetition rate of 15 Hz. The laser beam is converted into a planar sheet approximately 3 mm thick using a set of focusing optics. The laser sheet is located in the x–y plane along the center of the flow tank (z = 21 mm in Figure 3). The time interval of separation between two images in an image pair is held constant at 0.1 s throughout all experiments. A 14 bit charge-coupled device (CCD) camera (Imager Intense, LaVision Inc., Ypsilanti, MI, USA) with a 1376×1040 pixel array is used for capturing images. Uniform seeding is accomplished using 10 micron hollow glass spheres that are inserted in the flow tank and mixed to achieve a near homogenous distribution prior to each experiment. For processing the raw images, the software Davis 7.0 provided by LaVision Inc. is used. For each PIV run, 20 images are recorded for processing resulting in a minimum of 10 velocity vector fields from which to generate the mean flow field and statistics.
To check the appropriateness of this Brinkman model to the physical model, a least squares regression is used to find the values of and that best approximate the experimentally determined velocity profile between the two layers as measured by the experiments described in Section 2.4 . The equation describing the flow velocities between the two layers (13) can be restated as follows:
where , b is half of the distance between the layers, and is a constant that depends upon .
3. Results
3.1. Experimental Results
Figure 4 shows some example velocity vector fields obtained from PIV measurements of the flow around the physical models from the side view. For all cases, the diameter and spacing of the pins is kept constant at = 0.001 m and spacing = 0.005 m. For (Figure 4a–c), L = 0.043 m. The length of the layer was decreased in (Figure 4d) to about 0.010 m. The height of the layers was varied from (Figure 4a) 0.008 m, (Figure 4b) 0.022 m, and (Figure 4c,d) 0.028 m. The lengths of the vectors are proportional to the magnitude of the velocity. Flow is from right to left. The backgrounds of the images are snapshots of the fluid and pins. The regions where the model pins are located are enclosed by dashed boxes. In all cases, the flow velocities increase within the space between the layers as seen by the longer vectors present in these regions. In general, the velocity increases as the space between the layers decreases. The flow along the floor moves upwards as it approaches the clump of pins and then downwards as it moves past the pins. The flow between the arrays could not be resolved on account of the opacity of the pins.
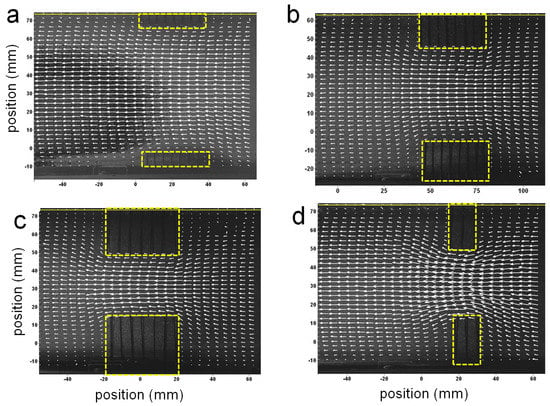
Figure 4.
Some example velocity vector fields obtained from particle image velocimetry (PIV) measurements of the flow around the physical models from the side view. The lengths of the vectors are proportional to the magnitude of the velocity. Flow is from right to left. The background of the images are snapshots of the flow. The regions where the model pins are located are enclosed by yellow boxes. In (a–c) the length of the layer was kept constant, while the height was varied, while in (d) the length was decreased and the height was equal to that of (c).
3.1.1. Comparison of Experimental Results to 1D Theory
Figure 5 shows the experimentally measured velocity profiles between two layers compared to the profiles determined by the Brinkman model. As explained in the methods section above, the values of and are determined using a least squares regression. The top panel shows velocity profiles for layer heights of 8 mm (Figure 5a) and 22 mm (Figure 5b). In both cases, the spacing between the pins is set to 5 mm and the length of the layer is 43 mm. Since the layer density is the same in both cases, one would predict that the value of would remain fairly constant. was determined to be 0.32173 mm for the shorter layer and 0.39993 mm for the taller layer. In the middle panel, the length of the layer is changed from 1 mm (Figure 5c) to 52 mm (Figure 5d), while the spacing and height is held constant (layer height = 28 mm, spacing = 7.5 mm). Although the volume fraction of the layer is unchanged, the value of drops nearly 50% as the layer length is reduced to one row of pins. Since the theoretical model assumes fully developed flow between the layers, it is not surprising the model with held constant would not accurately predict the flow profile. The bottom panel shows the flow profiles for variable layer densities, with layer spacings of mm. As expected, the values of for the models with a higher volume fraction ( mm) is greater than that for the sparser models ( mm).
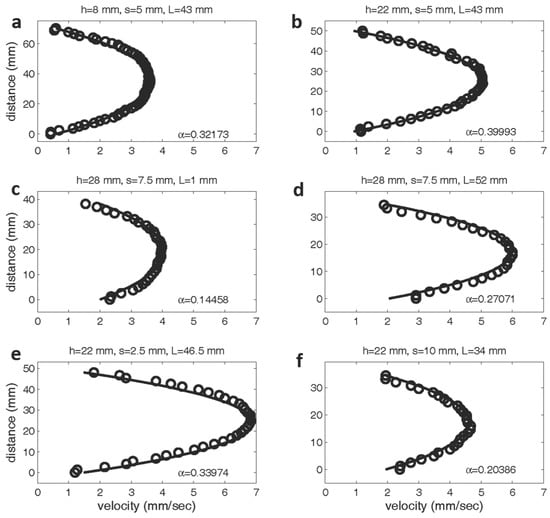
Figure 5.
Experimentally and theoretically determined velocity profiles between two model layers. The experimental data is labeled with open circles, and the theoretical predictions are denoted with a solid line. The values of have units of cm. In the top row, the spacing between pins and layer length is fixed at 5 mm and 43 mm, respectively. The height is varied from 8 mm (a) to 22 mm (b). The middle rows shows the velocity profiles are shown between two layers with a constant height of 28 mm and spacing of 7.5 mm. The length of the layer was varied from 1 mm (c) to 52 mm (d). The bottom row shows profiles for a constant layer height of 22 mm and lengths of 46.5 and 34 mm. The spacing was varied from 2.5 mm (e) to 10 mm (f).
These results show that the flow patterns above the center of the porous layer are well described by the Brinkman equation even when the layer is sparse or made up of clumps of relatively short lengths. Comparison of the experimental flow fields to the results reported by Leiderman et al. [40], where the endothelial surface layer is modeled as a two-dimensional Brinkman ‘clump’ also show good agreement. Since the 1D Brinkman model assumes that there is no flow in the y- and z-directions, this model does not capture the dynamics of the flow turning upward to move over the layer or downward to move past the layer. The 1D model is a good description only at the center of the layer or, at least, not near the ends of sufficiently long layers. Also note that the best fit value of is not constant for a given volume fraction. For example, the shorter the layer, the smaller the effective value of .
To compare the values of hydraulic resistances between the model, experiment, and estimated values for the real world application of flow through capillaries, will be expressed in nondimensional form. Let U, L, and be the characteristic length (height of chamber), velocity (peak velocity), and time scales, respectively. Define , and . Then, x-momentum Equation (9) within the layer becomes:
where is the nondimensional, scaled resistance coefficient. To obtain the nondimensional resistance coefficient in Section 2 of the Results, the channel height (0.0006 cm) is multiplied by the values of in cm. This gives a range of from 1.44 to 562,500. Rapid changes in the flow profile are observed for on the order of 1000. To nondimensionalize the values of that are experimentally derived in Section 3 of the Results, the channel height (8 mm) is multiplied by the values of in mm. This gives a range of from about 130 to 1025. Secomb et al. [76] estimated that the dimensional hydraulic resistivity of rat mesentery was on the order of 10 dynes s/cm. Converting this value to the nondimensional resistance coefficient gives .
3.2. 3D Simulations of Flow through Arrays of Cylinders
3.2.1. Effect of Re
We varied the Reynolds number with . This corresponds to diameter based Reynolds numbers . Over this range, our simulations suggest no significant change in average flow velocity in either direction perpendicular to the cylinder. However, average vertical flow velocity increases with within the cylinder layer. This velocity increase is at its maximum in a plane located at approximately of the cylinder’s height with velocity separation due to disappearing at the base and the top of the cylinder. The difference in average vertical velocity scales linearly with the magnitude of the Reynolds number according to the equation , where is the average magnitude of flow velocity in the z-direction within a plane located at of the cylinder’s height.
Figure 6 shows a sample flow through the cylinders at . The arrows show the direction of flow and the color corresponds to the magnitude. Velocity vectors along planes are taken parallel to the direction of flow and through the center of the cylinder (Figure 6a,c) and between periodic cylinders (Figure 6b,d). Note that the height is set to 0.156 (such that = 5 and = 4). The flow between the cylinders is typically quite small relative to the free stream velocity.
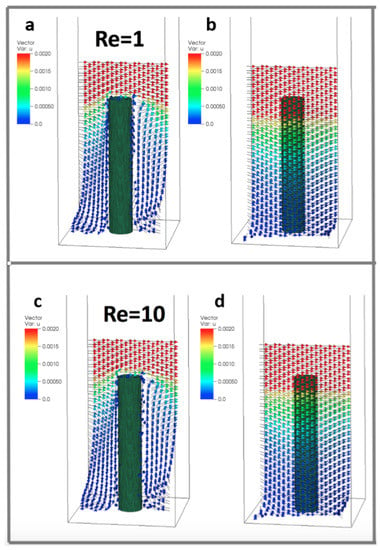
Figure 6.
Velocity vectors along planes taken parallel to the direction of flow and through the center of the cylinder (a,c) and between periodic cylinders (b,d) at (). Reynolds numbers were changed by varying the dynamic viscosity. The height of the cylinder is set to 0.156, such that = 5 and = 4.
3.3. Effect of the Number of Cylinders
To consider the effect of the periodic boundary conditions, we varied the number of cylinders within the periodic domain as 1, 4, and 16 cylinders. The effective spacing between the cylinders was kept constant such that = 4, and the size of the domain was set to 0.125, 0.25, and 0.5. The height of the cylinders was kept fixed such that = 5. The was set to 0.2, 1, and 10 for each number of cylinders (such that ). Across these simulations, the number of cylinders did not appear to have any significant effect on the average flow velocity profile. Some differences were observed in the small scale local velocity fields within the layer. Figure 7 shows velocity vectors within planes taken parallel to the direction of flow at . The planes are taken through the center of the cylinder (Figure 7a), one diameter from the center of a cylinder (Figure 7b), and halfway between rows of cylinders (Figure 7c). Slow moving regions of rotation are observed near the base of the cylinders. If only average flow profiles are desired, periodic boundary conditions with a single cylinder are sufficient to model an array of larger size within the specified parameter space. If details of the flow near the surface are needed, the results suggest that larger periodic domains are required.
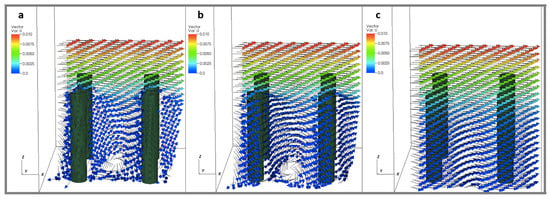
Figure 7.
Velocity vectors taken within planes parallel to the direction of flow at (). The planes are taken through the center of the cylinder (a), one diameter from the center of a cylinder (b), and halfway between rows of cylinders (c). The height of the cylinders were set to 0.156, such that = 5 and = 4.
3.3.1. Effect of Height
To consider the effect of cylinder height, we set the height equal to 0.156, 0.313, 0.469, and 0.625 (corresponding to ). The domain size was fixed at 0.125 and 0.25 with a single cylinder and four cylinders, respectively. The was set to 0.2, 1, and 10. Figure 8 shows the magnitude of the velocity average across the -plane as a function of height within the cylinder layer. The average fluid speed profile appears consistent between all cylinder heights, although for taller cylinders there is less distance between the top of the cylinder and the maximal average flow rates, i.e., there is greater shearing at the top of the taller cylinders. Furthermore, near the bottom of the domain, there is more fluid motion in the y-direction, due to the non-zero and zero shearing in the x-direction at the top and bottom of the domain, respectively. As you measure the flow components moving towards the top of the domain, the fluid begins to move for uniformly in the x-direction, with little motion in the y. However, interestingly, the component ratio of the average flow speeds, shows that as the x-component begins to dominate, it temporarily tapers down to a constant value, ∼0.2, until you measure high enough in the domain, in which case, the x-motion dominates and there appears little or no motion in the y-direction. Moreover, for the ratio of components of the average velocity, a similar trend occurs, where the x-average velocity component dominates. However, rather than the ratio monotonically decrease to zero, as in the case, for each tower height, the ratio hits a relative minimum, shortly increases, and then tapers off to zero as you measure further up the height of the domain. In each case, the relative maximum of the ratio of -average velocities occurs for heights slightly about the height of each cylinder.
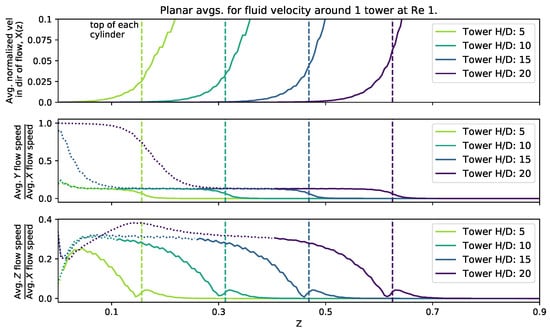
Figure 8.
Magnitude of flow velocity averaged across planes perpendicular to the z-axis for four different cylinder heights. The top of each cylinder is plotted as a vertical dashed line. A dotted line has been used in the y and z plots where the average fluid velocity in the direction of the flow (x) falls below .
3.3.2. Effect of Spacing
To consider the effect of cylinder spacing, we fixed the height at 0.156 and set the domain width to 0.125, 0.25, 0.5, and 1. This provided a range of gap to diameters such that = 4, 8, 16, 32. was kept fixed at 5. The was set to 0.1, 1, and 10 (}).
Figure 9 shows the magnitude of the velocity average across the -plane as a function of effective spacing. It was found that as you measure the average flow speed in the x-direction as a function of z, it increases in almost a linear fashion above the top of the cylinder. Furthermore, high enough above the tower, the ratios of the and components of average velocity taper to zero, while for z-cross-sections below the top of the tower, there are nonlinear relationships between those ratios. Moreover, when the spacing is reduced, there is more average fluid motion in the y- and z-directions within the height of the tower. In the case of the ratio, there exist clear local maximum for spacings of and , one within the height of the cylinder and another slightly above the top of the cylinder. This is in contrary to the case, where the ratio more monotonically tapers towards zero.
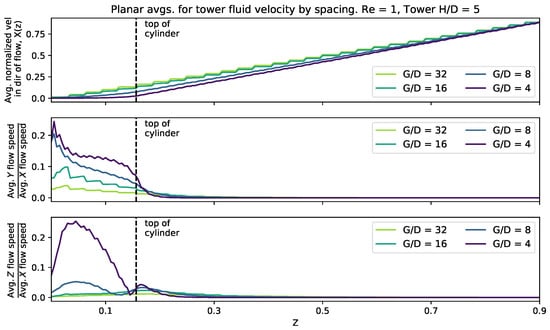
Figure 9.
Magnitude of flow velocity averaged across planes perpendicular to the z-axis for different cylinder spacing. The top of the cylinders is plotted as a vertical dashed line.
3.4. Brinkman vs. Explicit Treatment of Cylinders
We compare the results of the averaged flow as a function of height from the three-dimensional simulations to the 1D analytical model. To begin, we average the flow across the -plane at each height. We then fit the numerical data to the Brinkman model using nonlinear least squares to find the best choice of . Recall that the dimensionless form of is given by , and if L is set to the domain height, then in this case is equal to the dimensionless value . Figure 10 shows a sample of the averaged velocity magnitude from the numerical data vs. height compared to the analytical model. The best fit values of are included. The 3D simulations and analytical results are consistent and give the same flow profiles for the x-component of the average velocity and height, z. Moreover, from finding the best fit porosity coefficient for the analytical model, it appears that, as the height of the tower increases, the porosity coefficient decreases. This is consistent with the results from the experiments, which showed that the best fit value of decreased as the height of the cylinders was increased.
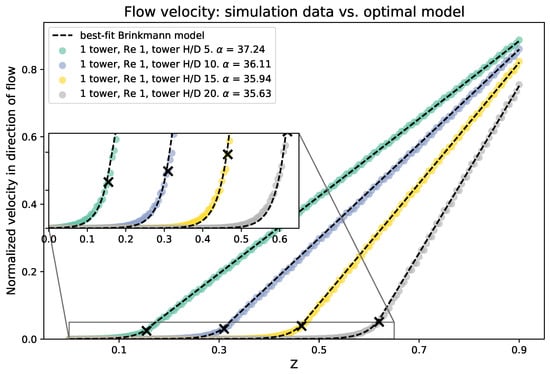
Figure 10.
Average velocity in the direction of the flow for various cylinder heights, compared with the best fitting Brinkman model. The top of each cylinder is marked with a black X. The best choice of porosity is given for each cylinder height in the figure legend.
4. Discussion and Conclusion
The flow through biological filtering layers can be highly three-dimensional. In many porous models, these dynamics are not properly captured. While bulk flow may appear to be in only the x-direction, transient flows in the y- and z-directions are important as they can enhance nutrient and chemical exchange and alter settlement. Our 3D simulation results indicate that the amount of flow through such layers depends nonlinearly on both , layer height, and spacing between successive cylinders. The Brinkman model may only be sufficient for describing flow above the layer and giving bulk flow average estimates flow within the porous layer. To fully resolve the fluid motion in these other directions, fully coupled FSI is necessary, as illustrated by our results.
Moreover, our bulk flow profiles obtained from the physical and numerical models do agree with previous theoretical work. With regard to the endothelial surface layer, the flow rates through the layer are small, and the majority of shear stress is felt on the luminal side [77,78,79]. In regards to trichomes, our results suggest that flow near the leaf surface is slow, and velocities in the vertical direction may be on the order of flow in the tangential direction. Trichomes may also operate near the transition between acting as a leaky and a solid layer. For tiny insects, our results support previous work that the wing’s bristled morphology operates near the leaky-to-solid transition. Finally, the results of this paper show that the Brinkman model is a reasonable approximation of the average flow within and above micro- and mesoscale porous layers even if the volume fraction of obstacles (e.g., core proteins, trichomes, bristles) is relatively low. Assuming that the layer is relatively homogeneous and of reasonable length relative to the height of the layer, the one-dimensional Brinkman model can be used to obtain analytical solutions of the averaged flow profiles and shear stresses.
In this initial study, we have resolved the three-dimensional flows through arrays of rigid, evenly spaced cylinders at . In the biological world, hairs, bristles, and other structures are more complex. Future work should explore the role that flexibility plays on flow. Furthermore, variations in shape, such as those seen in trichomes, may alter the local flow significantly. Accordingly, additional studies are needed to quantify the effect of shape on flow. Finally, we limit our study to , where strong inertial effects such as vortex separation are not observed. Although previous studies have considered flow through obstacles at large scales ( [80,81,82]), additional work is needed to map up transitional flows for .
There are a few ways that the Brinkman model could be extended to describe additional parameter spaces, particularly for high or unsteady flows. At the interface between the porous layer and the open fluid, we have used a normal stress continuity condition, as described by [77] for the low flows characteristic of the endothelial surface layer. An alternative approach would be to use a jump condition in which the jump depends upon the degree of roughness at the porous-free fluid interface [83]. This effect is likely significant at high characteristic of canopy or other macroscopic flows. We note, however, that the normal stress continuity condition does describe average flow well for the range of low considered here. For the case of unsteady flows, a term could be added to the Brinkman equation. A mathematical expression for c can be derived using the Volume-Averaged Navier–Stokes (VANS) approach [84,85].
Acknowledgments
The authors would like to thank the following grant sources: Army Research Office Staff Research Grant to Virginia Pasour; National Science Foundation Division of Mathematical Sciences (NSF DMS) Math Biology and Chemical, Bioengineering, Environmental and Transport Systems Fluid Dynamics (CBET) Fluid Dynamics CAREER Award 1151478, NSF DMS Math Biology and CBET Fluid Dynamics 1022802 to Laura Miller; NSF CBET Fluid Dynamics 1512071 grant to Arvind Santhanakrishnan.
Author Contributions
Laura Miller wrote the simulation code, while Christopher Strickland, Virginia Pasour, and Nicholas A. Battista ran simulations. Christopher Strickland compared 3D simulation data to the analytical models, developed by Arvind Santhanakrishnan. Christina Hamlet, Arvind Santhanakrishnan, and Laura Miller performed the physical modeling experiments. Experimental and numerical ata analysis was performed by Laura Miller, Arvind Santhanakrishnan, Christopher Strickland, and Nicholas A. Battista. Laura Miller, Christopher Strickland, Nicholas A. Battista, and Virginia Pasour wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jackson, G.; Winant, C. Effect of a kelp forest on coastal currents. Cont. Shelf Res. 1983, 2, 75–80. [Google Scholar] [CrossRef]
- Gaylord, B.; Reed, D.; Washburn, L.; Raimondi, P. Physical-biological coupling in spore dispersal of kelp forest macroalgae. J. Mar. Syst. 2004, 49, 19–39. [Google Scholar] [CrossRef]
- Koehl, M.A.R.; Reidenbach, M.A. Swimming by Microscopic Organisms in Ambient Water Flow; Animal Locomotion, Springer: Berlin, Germany, 2010; pp. 117–130. [Google Scholar]
- Sutherland, K.R.; Dabiri, J.O.; Koehl, M.A.R. Simultaneous field measurements of ostracod swimming behavior and background flow. Limnol. Oceanogr. 2011, 1, 135–146. [Google Scholar] [CrossRef]
- Jones, S.K.; Yun, Y.J.J.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Bristles reduce the force required to ‘fling’ wings apart in the smallest insects. J. Exp. Biol. 2016, 219, 3759–3772. [Google Scholar] [CrossRef] [PubMed]
- Koch, E.W. Hydrodynamics, diffusion-boundary layers and photosynthesis of the seagrasses, thalassia testudinum and cymodocea nodosa. Mar. Biol. 1994, 118, 767–776. [Google Scholar] [CrossRef]
- Hurd, C.L. Water motion, marine macroalgal physiology, and production. J. Phycol. 2000, 36, 453–472. [Google Scholar] [CrossRef]
- Ludeman, D.; Farrar, N.; Riesgo, A.; Paps, J.; Leys, S. Evolutionary origins of sensation in metazoans: Functional evidence for a new sensory organ in sponges. BMC Evol. Biol. 2014, 14, 3. [Google Scholar] [CrossRef] [PubMed]
- Babu, D.; Roy, S. Left-right asymmetry: Cilia stir up new surprises in the node. Open Biol. 2013, 3, 130052. [Google Scholar] [CrossRef] [PubMed]
- Lighthill, J. Acoustic streaming in the ear itself. J. Fluid Mech. 1992, 239, 551–606. [Google Scholar] [CrossRef]
- Bornschlogl, T. How filopodia pull: What we know about the mechanics and dynamics of filopodia. Cryoskeleon 2013, 70, 590–603. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Osborn, T. Hydrodynamics of copepods: A review. Surv. Geophys. 2004, 25, 339–370. [Google Scholar] [CrossRef]
- Geierman, C.; Emlet, R. Feeding behavior, cirral fan anatomy, reynolds numbers, and leakiness of balanus glandula, from post-metamophic juvenile to the adult. J. Exp. Mar. Biol. Ecol. 2009, 379, 68–76. [Google Scholar] [CrossRef]
- Alexander, D. The biomechanics of solids and fluids: the physics of life. Eur. J. Phys. 2001, 37, 053001. [Google Scholar] [CrossRef]
- Feitl, K.; Millett, A.; Colin, S.; Dabiri, J.; Costello, J. Functional morphology and fluid interactions during early development of the scyphomedusa aurelia aurita. Biol. Bull. 2009, 217, 283–291. [Google Scholar] [CrossRef] [PubMed]
- Wilson, M.; Peng, J.; Dabiri, J.; Eldredge, J. Lagrangian coherent structures in low reynolds number swimming. J. Phys. Condens. Matter 2009, 21, 204105. [Google Scholar] [CrossRef] [PubMed]
- Miller, L.A.; Peskin, C.S. A computational fluid dynamics of clap and fling in the smallest insects. J. Exp. Biol. 2009, 208, 3076–3090. [Google Scholar] [CrossRef] [PubMed]
- Summarell, C.G.; Ingole, S.; Fish, F.; Marshall, C. Comparative analysis of the flexural stiffness of pinniped vibrissae. PLoS ONE 2015. [Google Scholar] [CrossRef]
- Vogel, S. Life in Moving Fluids: The Physical Biology of Flow, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Schreuder, M.D.J.; Brewer, C.A.; Heine, C. Modelled influences of non-exchanging trichomes on leaf boundary layers and gas exchange. J. Theor. Biol. 2001, 210, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Huwaldt, J.A. Plot Digitizer. Available online: http://plotdigitizer.sourceforge.net/ (accessed on 23 August 2017).
- Hedrick, T.L. Software techniques for two- and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinspir. Biomimetics 2008, 3, 034001. [Google Scholar] [CrossRef] [PubMed]
- Weinbaum, S.; Zhang, X.; Han, Y.; Vink, H.; Cowin, S. Mechanotransduction and flow across the endothelial glycocalyx. Proc. Natl. Acad. Sci. USA 2003, 100, 7988–7995. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Zhang, J. Velocity distributions in laminar and turbulent vegetated flows. J. Hydraul. Res. 2016, 54, 117–130. [Google Scholar] [CrossRef]
- Waldrop, L.D. Ontogenetic scaling of the olfactory antennae and flicking behavior of the shore crab Hemigrapsus oregonensis. Chem. Sens. 2013, 38, 541–550. [Google Scholar] [CrossRef] [PubMed]
- Waldrop, L.D.; Nguyen, Q.; Bantay, R. Scaling of olfactory antennae and kinematics of antennule flicking of the terrestrial hermit crabs coenobita rugosus and coenobita perlatus during ontogeny. PeerJ 2014, 2, e535. [Google Scholar] [CrossRef] [PubMed]
- Szymanski, D.B.; Marks, M.D.; Wicks, S.M. Organzied f-actin is essential for normal tricome morphogenesis in arabidopsis. Plant Cell 1999, 11, 2331–2347. [Google Scholar] [CrossRef] [PubMed]
- Koehl, M. Small-scale fluid dynamics of olfactory antennae. Mar. Freshw. Behav. Physiol. 1996, 27, 127–141. [Google Scholar] [CrossRef]
- Koehl, M. Biomechanics of microscopic appendages: Functional shifts caused by changes in speed. J. Biomech. 2004, 37, 789–795. [Google Scholar] [CrossRef] [PubMed]
- Koehl, M. Transitions in function at low reynolds number: Hair-bearing animal appendages. Math. Methods Appl. Sci. 2001, 24, 1523–1532. [Google Scholar] [CrossRef]
- Loudon, C.; Koehl, M. Sniffing by a silkworm moth: Wing fanning enhances air penetration through and pheromone interception by antennae. J. Exp. Biol. 2000, 203, 2977–2990. [Google Scholar] [PubMed]
- Blough, T.; Colin, S.; Costello, J.; Marques, A. Ontogenetic changes in the bell morphology and kinematics and swimming behavior of rowing medusae: The special case of the limnomedusa liriope tetraphylla. Biol. Bull. 2011, 220, 6–14. [Google Scholar] [CrossRef] [PubMed]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2013, 44, 123–142. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. 1949, 1, 27–34. [Google Scholar] [CrossRef]
- Damiano, E.R.; Long, D.S.; Smith, M.L. Estimation of viscosity profiles using velocimetry data from parallel flows of linearly viscous: Application to microvascular hemodynamics. J. Fluid Mech. 2004, 512, 1–19. [Google Scholar] [CrossRef]
- Smith, M.L.; Long, D.S.; Damiano, E.R.; Ley, K. Near-wall micro-piv reveals a hydrodynamically relevant endothelial surface layer in venules in vivo. Biophys. J. 2003, 85, 637–645. [Google Scholar] [CrossRef]
- Vincent, P.E.; Sherwin, S.J.; Weinberg, P.D. Viscous flow over outflow slits covered by an anisotropic brinkman medium: A model of flow above interendothelial cell clefts. Phys. Fluids 2008, 20, 063106. [Google Scholar] [CrossRef]
- Ferko, M.C.; Bhatnagar, A.; Garcia, M.B.; Butler, P.J. Finite-element stress analysis of a multicomponent model of sheared and focally-adhered endothelial cells. Ann. Biomed. Eng. 2007, 35, 208–223. [Google Scholar] [CrossRef] [PubMed]
- Leiderman, K.M.; Miller, L.A.; Fogelson, A.L. The effects of spatial inhomogeneities on flow through the endothelial surface layer. J. Theor. Biol. 2008, 252, 313–325. [Google Scholar] [CrossRef] [PubMed]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Dalmont: Paris, France, 1856. [Google Scholar]
- Bejan, A. Convection Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Shavit, U.; Bar-Yosef, G.; Rosenzweig, R.; Assouline, S. Modified brinkman equation for a free flow problem at the interface of porous surfaces: The cantor-taylor brush configuration case. Water Resour. J. 2002, 38, 1320–1334. [Google Scholar] [CrossRef]
- Shavit, U.; Rosenzweig, R.; Assouline, S. Free flow at the interface of porous surfaces: Generalization of the taylor brush configuration. Transp. Porous Media 2004, 54, 345–360. [Google Scholar] [CrossRef]
- Grunbaum, D.; Strathmann, R.R. Form, performance and trade-offs in swimming and stability of armed larvae. J. Mar. Res. 2003, 61, 659–691. [Google Scholar] [CrossRef]
- Reidenbach, M.A.; Koseff, J.R.; Koehl, M.A.R. Hydrodynamic forces on larvae affect their settlement on coral reefs in turbulent, wave-driven flow. Limnol. Oceanogr. 2009, 54, 318–330. [Google Scholar] [CrossRef]
- Koehl, M.A.R.; Hadfield, M. Hydrodynamics of larval settlement from a larva’s point of view. Integr. Comp. Biol. 2010, 50, 539–551. [Google Scholar] [CrossRef] [PubMed]
- Cheer, A.; Cheung, S.; Hung, T.; Piedrahita, R.H.; Sanderson, S.L. Computational fluid dynamics of fish gill rakers during crossflow filtration. Bull. Math. Biol. 2012, 74, 981–1000. [Google Scholar] [CrossRef] [PubMed]
- Waldrop, L.D.; Miller, L.A.; Khatri, S. A tale of two antennules: The performance of crab odour-capture organs in air and water. R. Soc. Interface 2016. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R. Low reynolds number hydrodynamics and mesoscale simulations. Eur. Phys. J. Spec. Top. 2016, 225, 2079–2097. [Google Scholar] [CrossRef]
- Atzberger, P.J.; Kramer, P.R.; Peskin, C.S. A stochastic immersed boundary method for fluid–structure dynamics at microscopic length scales. J. Comp. Phys. 2007, 224, 1255–1292. [Google Scholar] [CrossRef]
- Strychalski, W.; Guy, R.D. A computational model of bleb formation. Math. Med. Biol. 2013, 30, 115–130. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C.S.; McQueen, D.M. Fluid Dynamics of the Heart and Its Valves. In Case Studies in Mathematical Modeling: Ecology, Physiology, and Cell Biology; Adler, F.R., Lewis, M.A., Dalton, J.C., Eds.; Prentice-Hall: Upper Saddle River, NJ, USA, 1996; pp. 309–338. [Google Scholar]
- Griffith, B.E. Immersed boundary model of aortic heart valve dynamics with physiological driving and loading conditions. Int. J. Numer. Meth. Biomed. Eng. 2012, 28, 317–345. [Google Scholar] [CrossRef]
- Fauci, L.; Peskin, C. A computational model of aquatic animal locomotion. J. Comput. Phys. 1988, 77, 85–108. [Google Scholar] [CrossRef]
- Hoover, A.P.; Miller, L.A. A numerical study of the benefits of driving jellyfish bells at their natural frequency. J. Theor. Biol. 2015, 374, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.K.; Laurenza, R.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Lift- vs. drag-based for vertical force production in the smallest flying insects. J. Theor. Biol. 2015, 384, 105–120. [Google Scholar] [CrossRef] [PubMed]
- Battista, N.A.; Baird, A.J.; Miller, L.A. A mathematical model and matlab code for muscle-fluid–structure simulations. Integr. Comp. Biol. 2015, 55, 901–911. [Google Scholar] [CrossRef] [PubMed]
- Hamlet, C.; Fauci, L.J.; Tytell, E.D. The effect of intrinsic muscular nonlinearities on the energetics of locomotion in a computational model of an anguilliform swimmer. J. Theor. Biol. 2015, 385, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; He, G.; Wang, S.; Miller, L.A.; Zhang, X.; You, Q.; Fang, S. An immersed boundary method by the lattice boltzmann approach in three dimensions. Comput. Math. Appl. 2011, 61, 3506–3518. [Google Scholar] [CrossRef]
- Miller, L.A.; Santhanakrishnan, A.; Jones, S.K.; Hamlet, C.; Mertens, K.; Zhu, L. Reconfiguration and the reduction of vortex-induced vibrations in broad leaves. J. Exp. Biol. 2012, 215, 2716–2727. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Peskin, C.S. 2d parachute simulation by the immersed boundary method. SIAM J. Sci. Comput. 2006, 28, 2294–2312. [Google Scholar] [CrossRef]
- Peskin, C. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Kempe, T.; Frohlich, J. An improved immersed boundary method with direct forcing for the simulation of particle laden flows. J. Comput. Phys. 2012, 231, 3663. [Google Scholar] [CrossRef]
- Pinelli, A.; Naqavi, I.Z.; Piomelli, U.; Favier, J. Immersed boundary method for generalised finite volume and finite difference navier-stokes solvers. J. Comput. Phys. 2010, 229, 9073–9091. [Google Scholar] [CrossRef]
- Battista, N.A.; Strickland, W.C.; Miller, L.A. Ib2d: A python and matlab implementation of the immersed boundary method. Bioinspir. Biomim. 2017, 12, 036003. [Google Scholar] [CrossRef] [PubMed]
- Battista, N.A.; Strickland, W.C.; Barrett, A.; Miller, L.A. Ib2d reloaded: A more powerful python and matlab implementation of the immersed boundary method. arXiv 2017, arXiv:1707.06928. [Google Scholar]
- Griffith, B.E. An Adaptive and Distributed-Memory Parallel Implementation of the Immersed Boundary (ib) Method. Available online: https://github.com/IBAMR/IBAMR (accessed on 21 October 2014).
- Berger, M.J.; Oliger, J. Adaptive mesh refinement for hyperbolic partial-differential equations. J. Comput. Phys. 1984, 53, 484–512. [Google Scholar] [CrossRef]
- Berger, M.J.; Colella, P. Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 1989, 82, 64–84. [Google Scholar] [CrossRef]
- Cheer, A.Y.L.; Koehl, M.A.R. Paddles and rakes: Fluid flow through bristled appendages of small organisms. J. Theor. Biol. 1987, 129, 17–39. [Google Scholar] [CrossRef]
- Lai, M.-C.; Peskin, C.S. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity. J. Comp. Phys. 2000, 160, 705–719. [Google Scholar] [CrossRef]
- Griffith, B.E.; Luo, X. Hybrid finite differencec/finite element immersed boundary method. Int. J. Numer. Methods Biomed. Eng. 2017. [Google Scholar] [CrossRef]
- Adrian, R.J. Particle–imaging techniques for experimental fluid mechanics. Ann. Rev. Fluid Mech. 1991, 23, 261–304. [Google Scholar] [CrossRef]
- Willert, C.E.; Gharib, M. Digital particle image velocimetry. Exp. Fluids 1991, 10, 181–193. [Google Scholar] [CrossRef]
- Secomb, T.; Hsu, R.; Pries, A. A model for red blood cell motion in glycocalyx-lined capillaries. Am. J. Physiol. Heart Circ. Physiol. 1998, 274, H1016–H1022. [Google Scholar]
- Secomb, T.; Hsu, R.; Pries, A. Effect of the endothelial surface layer on transmission of fluid shear stress to endothelial cells. J. Biorheol. 2001, 38, 143–150. [Google Scholar]
- Damiano, E. The effect of the endothelial-cell glycocalyx on the motion of red blood cells through capillaries. Microvasc. Res. 1998, 55, 77–91. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Weinbaum, S. Lubrication theory in highly compressible porous media: The mechanics of skiing, from red cells to humans. J. Fluid Mech. 2000, 422, 281–317. [Google Scholar] [CrossRef]
- Kim, S.J. 3d Numerical Simulation of Turbulent Open-Channel Flow through Vegetation. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2011. [Google Scholar]
- Bazilevs, Y.; Korobenko, A.; Deng, X.; Yan, J.; Kinzel, M.; Dabiri, J.O. Fsi modeling of vertical-axis wind turbines. J. App. Mech. 2014, 81, 081006. [Google Scholar] [CrossRef]
- Kinzel, M.; Araya, D.B.; Dabiri, J.O. Turbulence in vertical axis wind turbine canopies. Phys. Fluids 2015, 27, 115102. [Google Scholar] [CrossRef]
- Chen, N.; Gunzburger, M.; Wang, X. Asymptotic analysis of the differences between the stokes-darcy system with different interface conditions and the stokes-brinkman system. J. Math. Anal. Appl. 2010, 368, 658–676. [Google Scholar] [CrossRef]
- Whitaker, S. Flow in porous media i: A theoretical derivation of darcy’s law. Transp. Porous Med. 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Whitaker, S. The forchheimer equation: A theoretical development. Transp. Porous Med. 1996, 25, 27–61. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).