A Short Review of Advances in the Modelling of Blood Rheology and Clot Formation
Abstract
:1. Introduction
2. Advances in Modelling
2.1. Constitutive Models for Blood
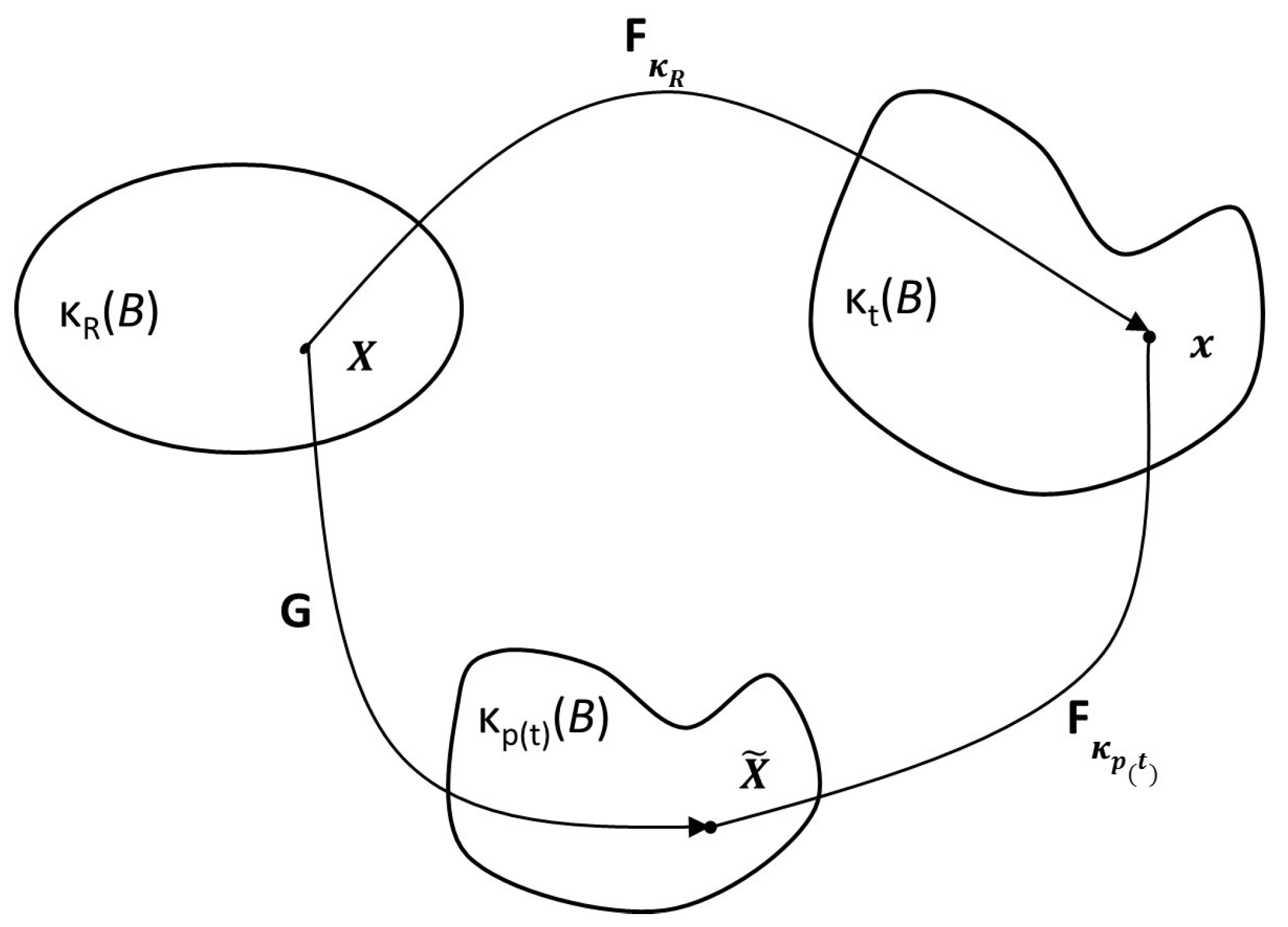
2.1.1. Model of Anand et al. (2013)
2.2. Models for Clot Formation and Lysis
2.2.1. Single-Scale Models
2.2.2. Multi-Scale Models
3. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baillargeon, B.; Rebelo, N.; Fox, D.D.; Taylor, R.L.; Kuhl, E. The Living Heart Project: A robust and integrative simulator for human heart function. Eur. J. Mech. A Solids 2014, 48, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Anand, M.; Rajagopal, K.; Rajagopal, K.R. A model incorporating some of the mechanical and biochemical factors underlying clot formation and dissolution in flowing blood. J. Theor. Med. 2003, 5, 183–218. [Google Scholar] [CrossRef]
- Charm, S.E.; Kurland, G.S. Viscometry of human blood for shear rate of 0–100,000 sec−1. Nature 1965, 206, 617–618. [Google Scholar] [CrossRef] [PubMed]
- Thurston, G.B. Viscoelasticity of human blood. Biophys. J. 1972, 12, 1205–1217. [Google Scholar] [CrossRef]
- Thurston, G.B. Frequency and shear rate dependence of viscoelasticity of blood. Biorheology 1973, 10, 375–381. [Google Scholar] [PubMed]
- Thurston, G.B. Rheological Parameters for the viscosity, viscoelasticity and thixotropy of Blood. Biorheology 1979, 16, 149–162. [Google Scholar] [PubMed]
- McMillan, D.E.; Utterback, N.G.; Nasrinasrabadi, M.; Lee, M.M. An Instrument to evaluate the time dependent flow properties of blood at moderate shear rates. Biorheology 1986, 23, 63–74. [Google Scholar] [PubMed]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef] [PubMed]
- Casson, N. A flow equation for pigment-oil suspensions of the printing ink type. In Rheology of Disperse Systems; Mill, C.C., Ed.; Pergamon Press: Oxford, UK, 1959; pp. 84–104. [Google Scholar]
- Liepsch, D.; Moravec, S. Pulsatile flow of Non-Newtonian fluids in distensible models of human arteries. Biorheology 1984, 21, 571–586. [Google Scholar] [PubMed]
- Cho, Y.I.; Kensey, K.R. Effects of the non-newtonian viscosity of blood on flows in a diseased arterial vessel. Part I: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [PubMed]
- Quemada, D. A non-linear Maxwell model of biofluids: Application to normal blood. Biorheology 1993, 30, 253–265. [Google Scholar] [PubMed]
- Sharp, M.K.; Thurston, G.B.; Moore, J.E. The effect of blood viscoelasticity on pulastile flow in stationary and axially moving tubes. Biorheology 1996, 33, 185–206. [Google Scholar] [CrossRef]
- Phillips, W.M.; Deutsch, S. Toward a constitutive equation for blood. Biorheology 1975, 12, 383–389. [Google Scholar] [PubMed]
- Yeleswarapu, K.K. Evaluation of Continuum Models for Characterizing the Constitutive Behavior of Blood. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 1996. [Google Scholar]
- Sun, N.; De Kee, D. Simple shear, hysteresis and yield stress in biofluids. Can. J. Chem. Eng. 2001, 79, 36–41. [Google Scholar]
- Anand, M.; Rajagopal, K.R. A shear-thinning viscoelastic fluid model for describing the flow of blood. Int. J. Cardiovasc. Med. Sci. 2004, 4, 59–68. [Google Scholar]
- Owens, R.G. A new micro-structure based constitutive model for blood. J. Non-Newton. Fluid Mech. 2006, 40, 57–70. [Google Scholar] [CrossRef]
- Capek, M. A Non-Newtonian Model of Blood Capturing Segregation of Erythrocytes. Unpublished, Necas Center for Mathematical Modeling. 2014. [Google Scholar]
- Massoudi, M.; Phuoc, T.X. Pulsatile flow of blood using a modified second grade fluid model. Comput. Math. Appl. 2008, 56, 199–211. [Google Scholar] [CrossRef]
- Wu, W.T.; Aubry, N.; Massoudi, M.; Antaki, J.F. Transport of platelets induced by red blood cells based on mixture theory. Int. J. Eng. Sci. 2017, 118, 16–27. [Google Scholar] [CrossRef]
- Bodnar, T.; Rajagopal, K.R.; Sequeira, A. Simulation of the three-dimensional flow of blood using a shear-thinning viscoelastic fluid model. Math. Model. Nat. Phenom. 2011, 6, 1–24. [Google Scholar] [CrossRef]
- Anand, M.; Kwack, J.H.; Masud, A. A new generalized Oldroyd-B model for blood flow in complex geometries. Int. J. Eng. Sci. 2013, 72, 78–88. [Google Scholar] [CrossRef]
- Rajagopal, K.R. Multiple Natural Configurations in Continuum Mechanics; Technical Report “Report 6”; Institute of Computational and Applied Mechanics, University of Pittsburgh: Pittsburgh, PA, USA, 1995. [Google Scholar]
- Rajagopal, K.R.; Srinivasa, A.R. A thermodynamic framework for rate-type fluids. J. Non-Newton. Fluid Mech. 2000, 88, 207–227. [Google Scholar] [CrossRef]
- Rajagopal, K.R. On implicit constitutive theories. Appl. Math. 2013, 48, 279–319. [Google Scholar] [CrossRef]
- Mann, K.G. Thrombin formation. Chest 2003, 124, 4S–10S. [Google Scholar] [CrossRef] [PubMed]
- Orfeo, T.; Butenas, S.; Brummel-Ziedins, K.E.; Mann, K.G. The tissue factor requirement in blood coagulation. J. Biol. Chem. 2005, 280, 42887–42896. [Google Scholar] [CrossRef] [PubMed]
- Panteleev, M.A.; Dashkevich, N.M.; Ataullakhanov, F.I. Hemostasis and thrombosis beyond biochemistry: Roles of geometry, flow and diffusion. Thromb. Res. 2015, 136, 699–711. [Google Scholar] [CrossRef] [PubMed]
- Hockin, M.F.; Jones, K.C.; Everse, S.J.; Mann, K.G. A Model for the stoichiometric regulation of blood coagulation. J. Biol. Chem. 2002, 277, 18322–18333. [Google Scholar] [CrossRef] [PubMed]
- Diamond, S.L. Systems biology of coagulation. J. Thromb. Haemost. 2013, 11, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Kuharsky, A.L.; Fogelson, A.L. Surface-mediated control of blood coagulation: The role of binding site densities and platelet deposition. Biophys. J. 1997, 80, 1050–1074. [Google Scholar] [CrossRef]
- Panteleev, M.A.; Ovanesov, M.V.; Kireev, D.A.; Shibeko, A.M.; Sinauridze, E.I.; Ananyeva, N.M.; Butylin, A.A.; Saenko, E.L.; Ataullakhanov, F.I. Spatial propagation and localization of blood coagulation are regulated by intrinsic and protein C Pathways, respectively. Biophys. J. 2006, 90, 1489–1500. [Google Scholar] [CrossRef] [PubMed]
- Anand, M.; Rajagopal, K.; Rajagopal, K.R. A model for the formation, growth, and lysis of clots in quiescent plasma. A comparison between the effects of antithrombin III deficiency and protein C deficiency. J. Theor. Biol. 2008, 253, 725–738. [Google Scholar] [CrossRef] [PubMed]
- Luan, D.; Zai, M.; Varner, J.D. Computationally derived points of fragility of a human cascade are consistent with current therapeutic strategies. PLoS Comput. Biol. 2007, 3, e142. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, M.S.; Denney, W.S.; Jing, H.; Diamond, S.L. Systems biology of coagulation initiation: Kinetics of thrombin generation in resting and activated human blood. PLoS Comput. Biol. 2010, 6, e1000950. [Google Scholar] [CrossRef] [PubMed]
- Susree, M.; Anand, M. A mathematical model for in vitro coagulation of blood: Role of platelet count and inhibition. Sadhana 2017, 42, 291–305. [Google Scholar]
- Shibeko, A.M.; Panteleev, M.A. Untangling the complexity of blood coagulation network: Use of computational modelling in pharmacology and diagnostics. Brief. Bioinform. 2016, 17, 429–439. [Google Scholar] [CrossRef] [PubMed]
- Bodnar, T.; Sequeira, A. Numerical simulation of the coagulation dynamics of blood. Comput. Math. Methods Med. 2008, 9, 83–104. [Google Scholar] [CrossRef]
- Sequeira, A.; Bodnar, T. Blood coagulation simulations using a viscoelastic model. Math. Model. Nat. Phenom. 2014, 9, 34–45. [Google Scholar] [CrossRef]
- Leiderman, K.; Fogelson, A.L. Grow with the flow: A spatial-temporal model of platelet deposition and blood coagulation under flow. Math. Med. Biol. 2011, 28, 47–84. [Google Scholar] [CrossRef] [PubMed]
- Leiderman, K.; Fogelson, A.L. The influence of hindered transport on the development of platelet thrombi under flow. Bull. Math. Biol. 2013, 75, 1255–1283. [Google Scholar] [CrossRef] [PubMed]
- Leiderman, K.; Fogelson, A.L. An overview of mathematical modeling of thrombus formation under flow. Thromb. Res. 2014, 133, S12–S14. [Google Scholar] [CrossRef] [PubMed]
- Fogelson, A.L.; Neeves, K.B. Fluid mechanics of blood clot formation. Annu. Rev. Fluid Mech. 2015, 47, 377–403. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.T.; Jamiolkowski, M.A.; Wagner, W.R.; Aubry, N.; Massoudi, M.; Antaki, J.F. Multi-Constituent Simulation of Thrombus Deposition. Sci. Rep. 2017, 7, 42720. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Chen, N.; Kamocka, M.; Rosen, E.D.; Alber, M.S. A multiscale model of thrombus development. J. R. Soc. Interface 2008, 5, 705–722. [Google Scholar] [CrossRef] [PubMed]
- Jones, K.C.; Mann, K.G. A model for the tissue factor pathway to thrombin. II. A mathematical simulation. J. Biol. Chem. 1994, 269, 23367–23373. [Google Scholar] [PubMed]
- Xu, Z.; Lioi, J.; Mu, J.; Kamocka, M.M.; Liu, X.; Chen, D.Z.; Rosen, E.D.; Alber, M.S. A multiscale model of venous thrombus formation with surface-mediated control of blood coagulation cascade. Biophys. J. 2010, 98, 1723–1732. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Kim, O.; Kamocka, M.M.; Rosen, E.D.; Alber, M.S. Multiscale models of thrombogenesis. Wiley Interdiscip. Rev. Syst. Biol. Med. 2012, 4, 237–246. [Google Scholar] [CrossRef] [PubMed]
- Bessonov, N.; Sequeira, A.; Simakov, S.; Vassilevskii, Y.; Volpert, V. Methods of blood flow modelling. Math. Model. Nat. Phenom. 2016, 11, 1–25. [Google Scholar] [CrossRef]
- Mann, K.G. Is there value in kinetic modeling of thrombin generation? Yes. J. Thromb. Haemost. 2012, 10, 1463–1469. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anand, M.; Rajagopal, K.R. A Short Review of Advances in the Modelling of Blood Rheology and Clot Formation. Fluids 2017, 2, 35. https://doi.org/10.3390/fluids2030035
Anand M, Rajagopal KR. A Short Review of Advances in the Modelling of Blood Rheology and Clot Formation. Fluids. 2017; 2(3):35. https://doi.org/10.3390/fluids2030035
Chicago/Turabian StyleAnand, Mohan, and Kumbakonam Ramamani Rajagopal. 2017. "A Short Review of Advances in the Modelling of Blood Rheology and Clot Formation" Fluids 2, no. 3: 35. https://doi.org/10.3390/fluids2030035
APA StyleAnand, M., & Rajagopal, K. R. (2017). A Short Review of Advances in the Modelling of Blood Rheology and Clot Formation. Fluids, 2(3), 35. https://doi.org/10.3390/fluids2030035




