Aorta Ascending Aneurysm Analysis Using CFD Models towards Possible Anomalies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Patient Data
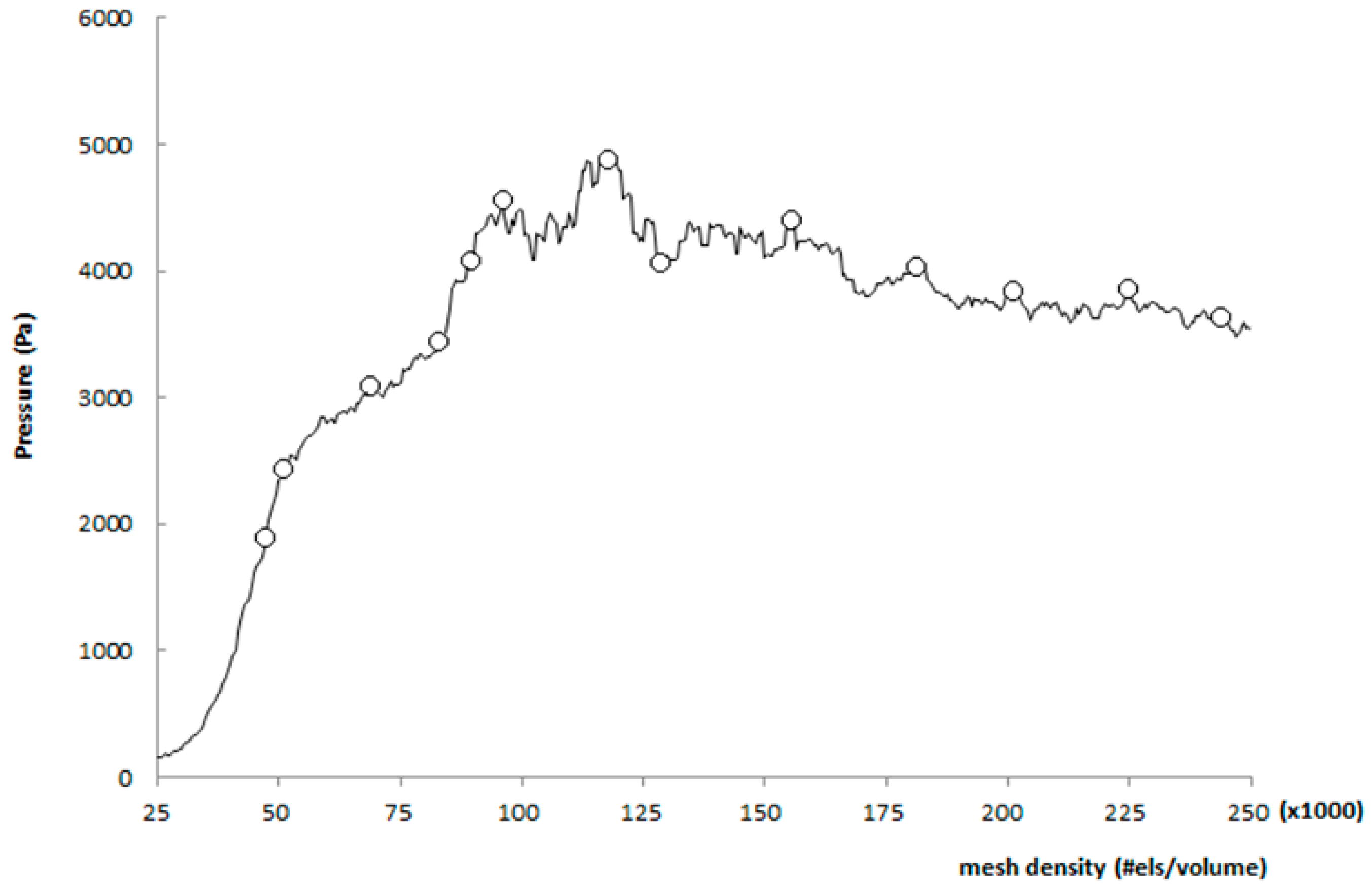
2.2. Model Geometry and Mesh
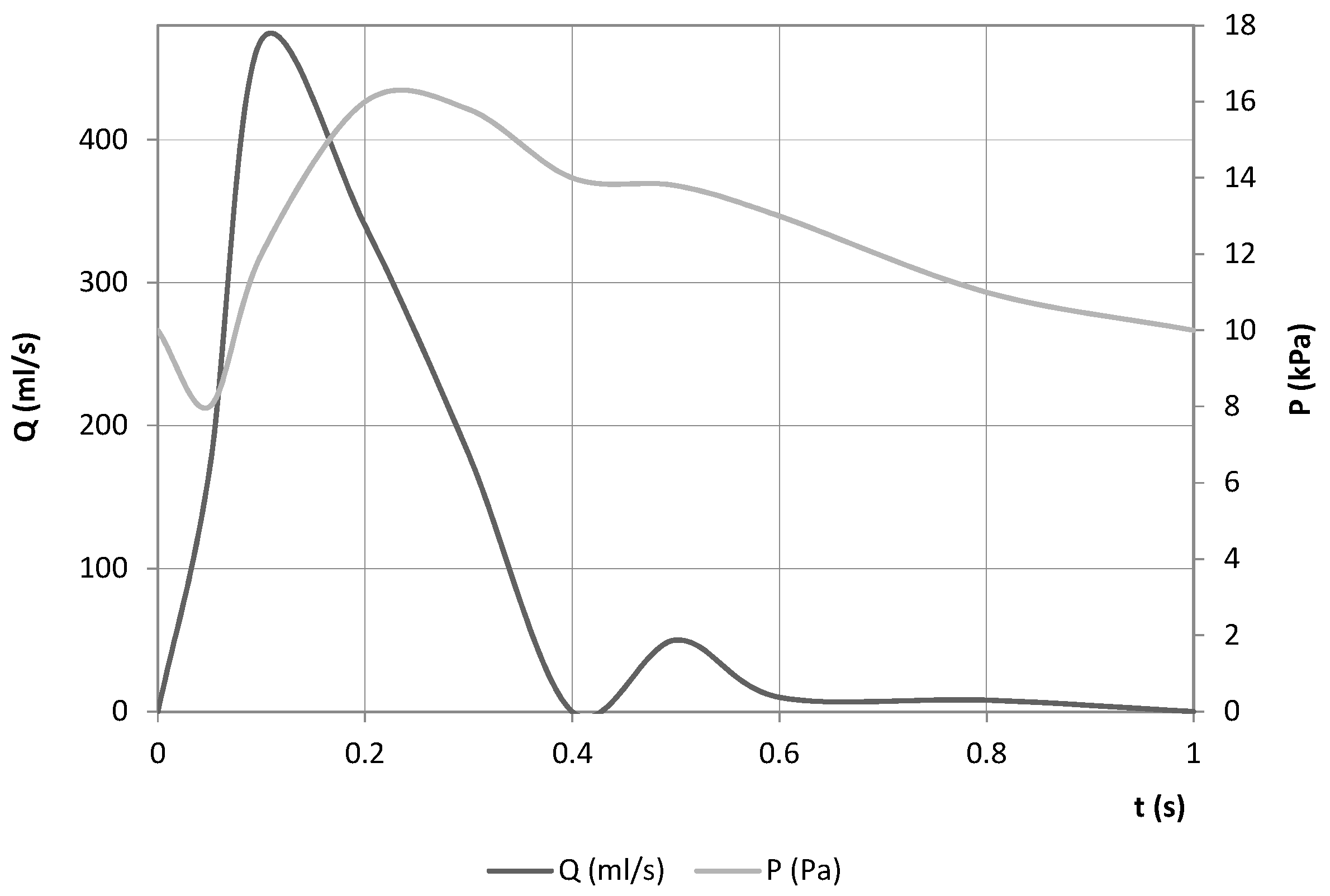
2.3. Boundary Conditions
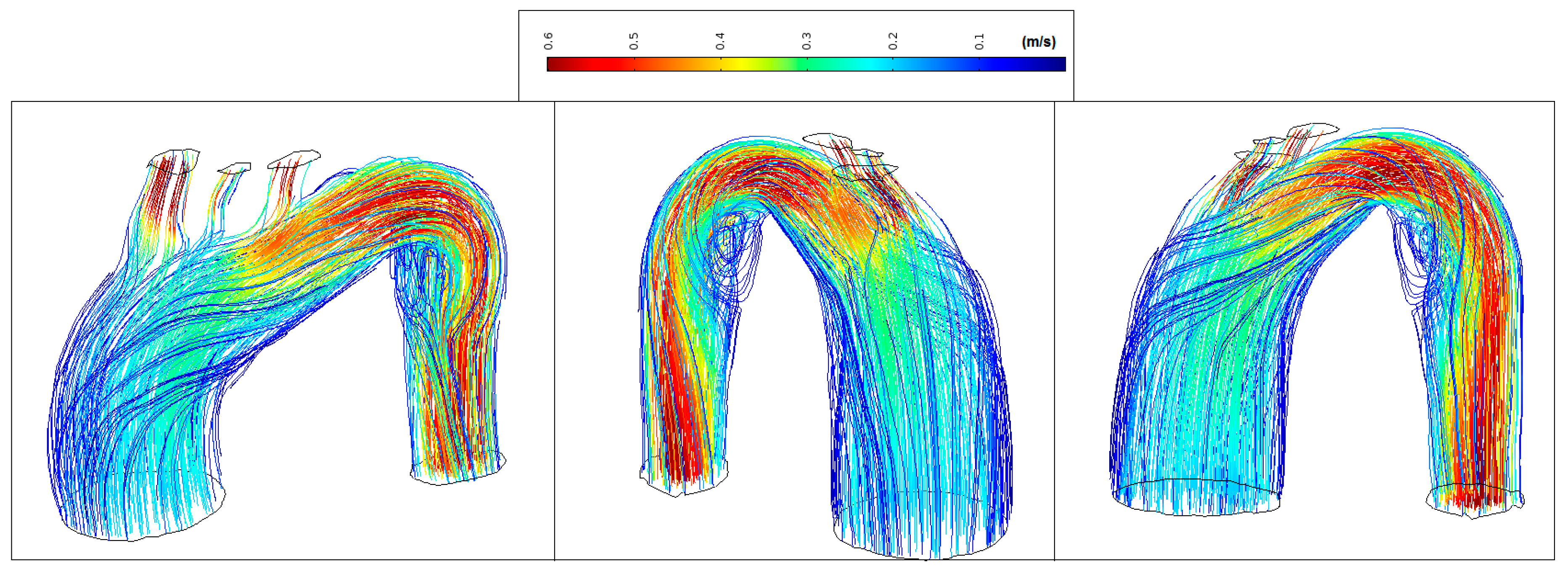
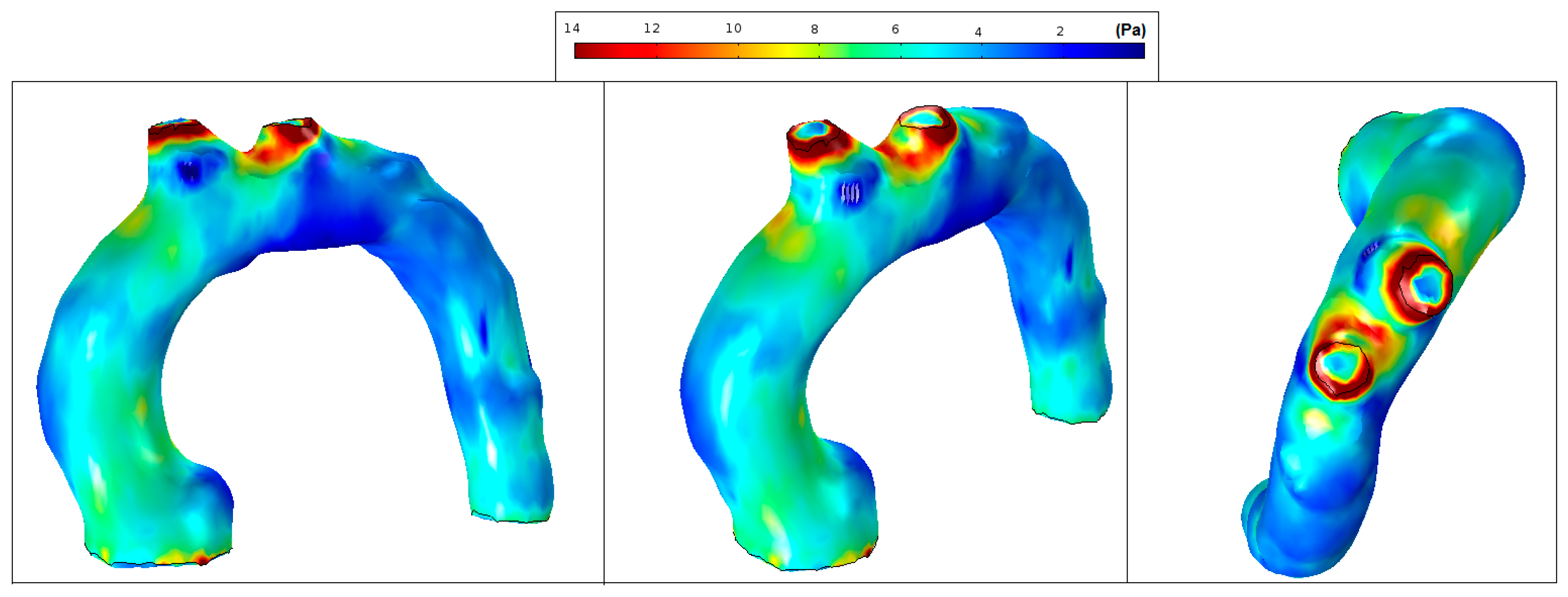
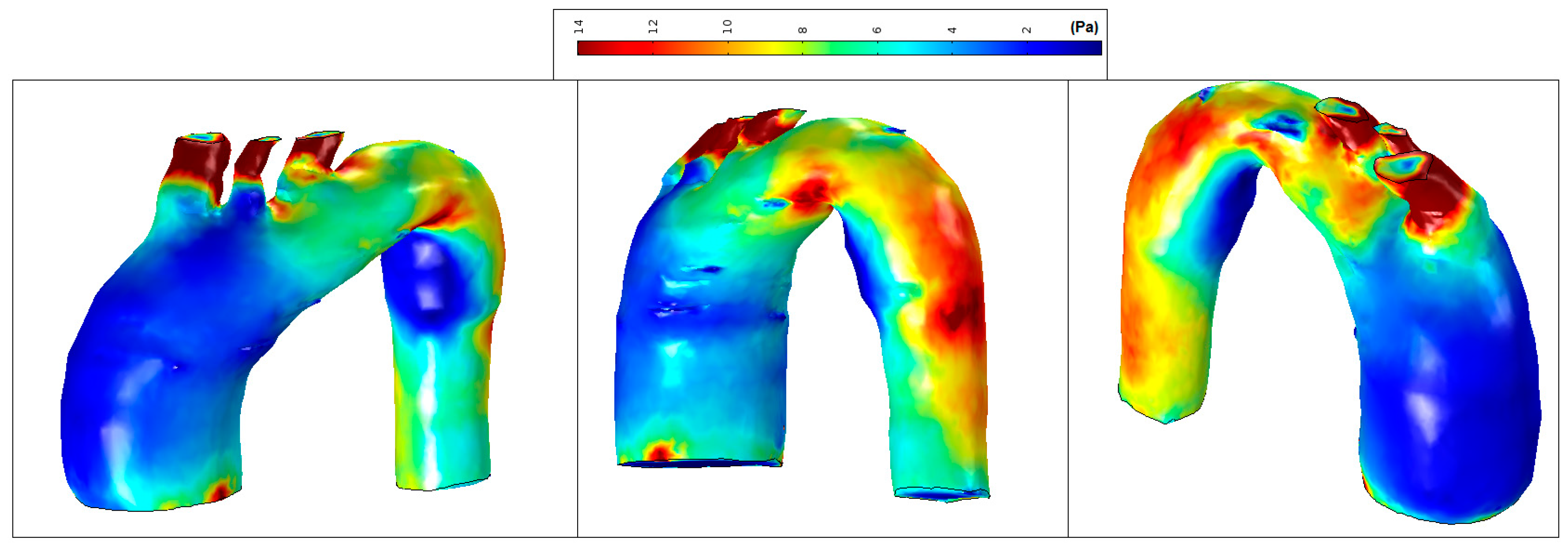
3. Results
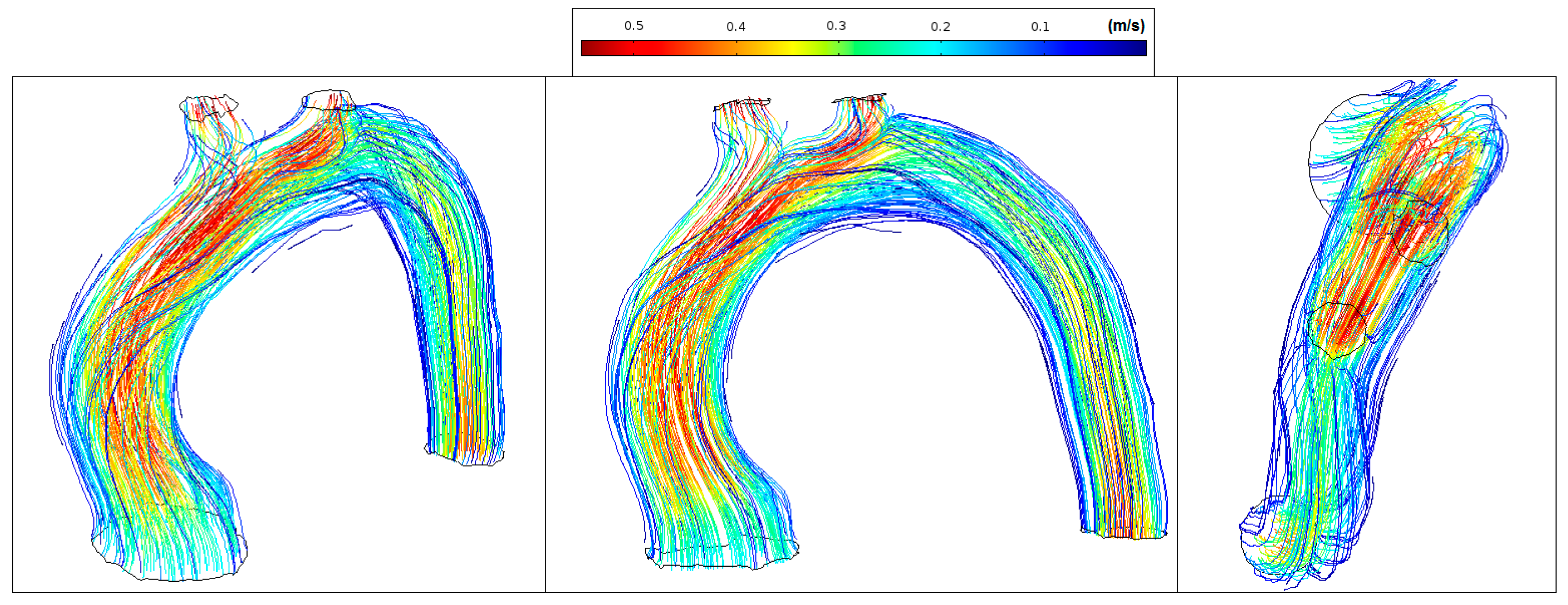
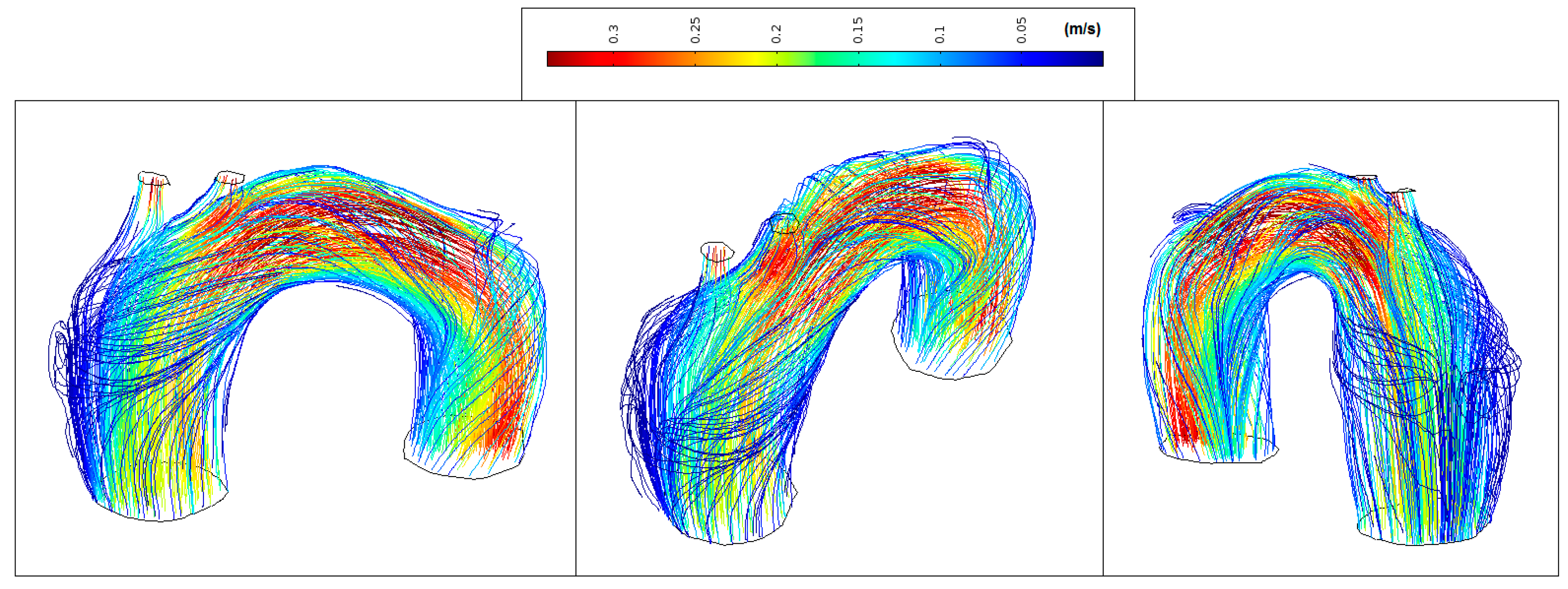
3.1. Blood Velocity
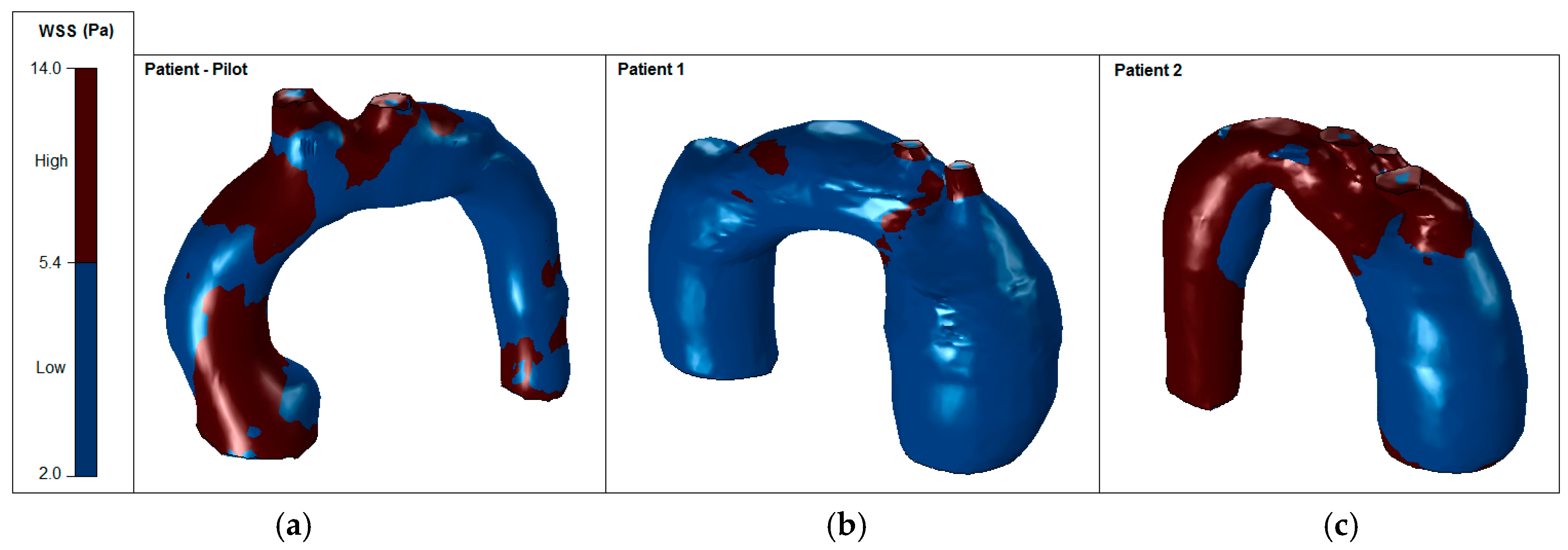
3.2. Wall Shear Stress
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Informed Consent
References
- Biasetti, J.; Hussain, F.; Gasser, T. Blood flow and coherent vortices in the normal and aneurysmatic aortas: A fluid dynamical approach to intra-luminal thrombus formation. J. R. Soc. Interface 2011. [Google Scholar] [CrossRef] [PubMed]
- Soudah, E.; Loong, T.; Bordone, M.; Pua, U.; Narayanan, S. CFD modelling of abdominal aortic aneurysm on hemodynamic loads using a realistic geometry with CT. Comput. Math. Methods Med. 2013. [Google Scholar] [CrossRef] [PubMed]
- Bonow, R.; Mann, D.; Zipes, D.; Libby, P. Braunwald’s Heart Disease. In A Textbook of Cardiovascular Medicine; Elsevier Health Sciences: Amsterdam, The Netherlands, 2011; Volume 2. [Google Scholar]
- Vorp, D. Biomechanics of abdominal aortic aneurysm. J. Biomech. 2007, 40, 1887–1902. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, J. Cardiovascular Solid Mechanics. In Cells, Tissues and Organs; Springer: New York, NY, USA, 2002. [Google Scholar]
- Powell, J.; Brown, L.; Forbes, J. Final 12-year follow-up of surgery versus surveillance in the UK small aneurysm trial. Br. J. Surg. 2007, 94, 702–708. [Google Scholar] [CrossRef] [PubMed]
- Filardi, V. CFD analysis to evaluate hemodynamic parameters in a growing abdominal aortic aneurysm. Vasc. Dis. Manag. 2015, 12, E84–E95. [Google Scholar]
- Biglino, G.; Cosentino, D.; Steeden, J.; De Nova, L.; Castelli, M.; Ntsinjana, H.; Pennati, G.; Taylor, A.; Schievano, S. Using 4D cardiovascular magnetic resonance imaging to validate computational fluid dynamics: A case study. Front. Pediatr. 2015, 3. [Google Scholar] [CrossRef] [PubMed]
- Valverde, I.; Nordmeyer, S.; Uribe, S.; Greil, G.; Berger, F.; Kuehne, T. Systemic-to-pulmonary collateral flow in patients with palliated univentricular heart physiology: Measurement using cardiovascular magnetic resonance 4D velocity acquisition. J. Cardiovasc. Magn. Reson. 2012, 14. [Google Scholar] [CrossRef] [PubMed]
- Francois, C.; Srinivasan, S.; Schiebler, M.; Reeder, S.; Niespodzany, E.; Landgraf, B. 4D cardiovascular magnetic resonance velocity mapping of alterations of right heart flow patterns and main pulmonary artery hemodynamics in tetralogy of Fallot. J. Cardiovasc. Magn. Reson. 2012, 14. [Google Scholar] [CrossRef] [PubMed]
- Geiger, J.; Markl, M.; Jung, B.; Grohmann, J.; Stiller, B.; Langer, M. 4D-MR flow analysis in patients after repair of tetralogy of Fallot. Eur. Radiol. 2011, 21, 1651–1657. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, M.; Toger, J.; Kanski, M.; Bloch, K.; Stahlberg, F.; Heiber, E. Quanification and visualization of cardiovascular 4D velocity mapping accelerated with parallel imaging or k-t BLAST: Head to head comparison and validation at 1.5T and 3T. J. Cardiovasc. Magn. Reson. 2011, 13. [Google Scholar] [CrossRef] [PubMed]
- De Vecchi, A.; Nordsletten, D.; Razavi, R.; Greil, G.; Smith, N. Patient specific fluid/structure ventricular modelling for integrated cardiac care. Med. Biol. Eng. Compt. 2013, 51, 1261–1270. [Google Scholar] [CrossRef] [PubMed]
- COMSOL. Multiphysics User’s Guide; COMSOL Inc.: Burlington, MA, USA, 2012; p. 1372. [Google Scholar]
- De Santis, G.; De Beule, M.; Van Canneyt, K.; Segers, P.; Verdonck, P.; Verhegghe, B. Full-hexahedral structured meshing for image-based computational vascular modeling. Med. Eng. Phys. 2011, 33, 1318–1325. [Google Scholar] [CrossRef] [PubMed]
- Baker, T.; Pebay, P.; Pousin, J. Dynamic meshing for finite element based segmentation of cardiac imagery. In Proceedings of the WCCM V-Fifth World Congress on Computational Mechanics, Vienna, Austria, 2002. [Google Scholar]
- Sochi, T. Non-Newtonian Rheology in Blood Circulation. In Fluid Dynamics; Department of Physics and Astronomy, University College London: London, UK, 2014; Volume 1. [Google Scholar] [CrossRef]
- Herzog, C.; Zwrner, P.; Doll, J.; Nielsen, C.; Nguyen, S.; Savino, G.; Vogl, T.; Costello, P.; Schoepf, U. Significant coronary artery stenosis: comparison on per-patient and per-vessel or per-segment basis at 64-section CT angiography. Radiology 2007, 244, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Bluestein, D.; Dumont, K.; de Beule, M. Intraluminal thrombus and risk of rupture in patient specific abdominal aortic aneurysm—FSI modelling. Comput. Methods Biomechan. Biomed. Eng. 2009, 12, 73–81. [Google Scholar] [CrossRef]
- Vorp, D.; Raghavan, M.; Webster, M. Mechanical wall stress in abdominal aortic aneurysm: Influence of diameter and asymmetry. J. Vasc. Surg. 1998, 27, 632–639. [Google Scholar] [CrossRef]
- Ouriel, K.; Green, R.; Donayre, C.; Shortell, C.; Elliott, J.; DeWeese, J. An evaluation of new methods of expressing aortic aneurysm size: Relationship to rupture. J. Vasc. Surg. 1992, 15, 12–20. [Google Scholar] [CrossRef]
- Shipkowitz, T.; Rodgers, V.G.; Frazin, L.J.; Chandran, K.B. Numerical study on the effect of secondary flow in the human aorta on local shear stresses in abdominal aortic branches. J. Biomech. 2000, 33, 717–728. [Google Scholar] [CrossRef]
- Alastruey, J.; Xiao, N.; Fok, H.; Schaeffter, T.; Figueroa, C. On the impact of modelling assumptions in multi-sacle, subject-specific models of aortic heamodynamics. J. R. Soc. Interface 2016, 13. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.; Choi, J.; Park, C. Asymmetric flows of non-newtonian fluids in a symmetric stenosed artery. Korea-Aust. Rheol. J. 2004, 1, 101–108. [Google Scholar]
- Migliavacca, F.; Petrini, L.; Montanari, V.; Quagliana, I.; Auricchio, F.; Dubini, G. A predictive study of the mechanical behaviour of coronary stents by computer modelling. Med. Eng. Phys. 2005, 27, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Kajzer, W.; Kackmarek, M.; Marciniak, J. Biomechanical analysis of stent-oesophagus system. J. Mater. Process. Technol. 2005, 162–163, 196–202. [Google Scholar] [CrossRef]
- Gundert, T. Improving Cardiovascular Stent Design Using Patient-Specific Models and Shape Optimization. Master’s Thesis, Marquette University, Milwaukee, WI, USA, 2011; p. 104. [Google Scholar]
- Kleinstreuer, C.; Li, Z. Analysis and computer program for rupture-risk prediction of abdominal aortic aneurysms. Biomed. Eng. Online 2006, 5. [Google Scholar] [CrossRef] [PubMed]
- Vorp, D.; Lee, P.; Wang, D. Association of intraluminal thrombus in abdominal aortic aneurysm with local hypoxia and wall weakening. J. Vasc. Surg. 2001, 34, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Nicholls, S.; Gardner, J.; Meissner, M.; Johans, K. Rupture in small abdominal aortic aneurysms. J. Vasc. Surg. 1998, 28, 884–888. [Google Scholar] [CrossRef]
- Bauer, M.; Siniawski, H.; Pasic, M.; Schaumann, B.; Hetzer, R. Different hemodynamic stress of the ascending aorta wall in patients with bicuspid and tricuspid aortic valve. J. Card. Surg. 2006, 21, 21820. [Google Scholar] [CrossRef] [PubMed]
- Morbiducci, U.; Ponzini, R.; Rizzo, G.; Cadioli, M.; Esposito, A.; Montevecchi, F.M.; Redaelli, A. Mechanistic insight into the physiological relevance of helical blood flow in the human aorta an in vivo study. Biomech. Model. Mechanobiol. 2010, 10, 339–355. [Google Scholar] [CrossRef] [PubMed]
- Hsu, M.C.; Kamensky, D.; Bazilevs, Y.; Sacks, M.S.; Hughes, T.J. Fluid-structure interaction analysis of bioprosthetic heart valves: Significance of arterial wall deformation. Comput. Mech. 2014, 54, 10551071. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-H.; Liu, K.S.; Jhong, G.H.; Liu, S.J.; Hsu, M.Y.; Wang, C.J.; Hung, K.C. Finite element analysis of helical flows in human aortic arch: A novel index. Biomicrofluidics 2014, 8, 024111. [Google Scholar]
- Bonomi, D.; Vergara, C.; Faggiano, E.; Stevanella, M.; Conti, C.; Redaelli, A.; Puppini, G.; Faggian, G.; Formaggia, L.; Luciani, G.B. Influence of the aortic valve leaflets on the fluid-dynamics in aorta in presence of a normally functioning bicuspid valve. Biomechan. Model. Mechanobiol. 2015, 14, 1349–1361. [Google Scholar] [CrossRef] [PubMed]
- Morbiducci, U.; Ponzini, R.; Rizzo, G.; Cadioli, M.; Esposito, A.; De Cobelli, F.; Del Maschio, A.; Montevecchi, F.M.; Redaelli, A. In vivo quantification of helical blood flow in human aorta by time-resolved three-dimensional cine phase contrast magnetic resonance imaging. Ann. Biomed. Eng. 2009, 37, 516–531. [Google Scholar] [CrossRef] [PubMed]
- Guzzetti, S.; Passerini, T.; Slawinski, J.; Villa, U.; Veneziani, A.; Sunderam, V. Platform and algorithm effects on computational fluid dynamics applications in life sciences. Future Gener. Comput. Syst. 2017, 67, 382–396. [Google Scholar] [CrossRef]
- Suh, G.Y.; Les, A.S.; Tenforde, A.S.; Shadden, S.C.; Spilker, R.L.; Yeung, J.J.; Cheng, C.P.; Herfkens, R.J.; Dalman, R.L.; Taylor, C.A. Hemodynamic changes quantified in abdominal aortic aneurysms with increasing exercise intensity using MR exercise imaging and image-based computational fluid dynamics. Ann. Biomed. Eng. 2011, 39, 2186–2202. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, Vol 1: Fluid Mechanics, 2nd ed.; Wiley: Hoboken, NJ, USA, 1987; ISBN 978-0-471-80245-7. [Google Scholar]
- Carreau, P.J.; De Kee, D.C.R.; Chhabra, R.P. Rheology of Polymeric Systems, Principles and Applications; Hanser/Gardner Publications: Cincinnati, OH, USA, 1997; p. 520. [Google Scholar]
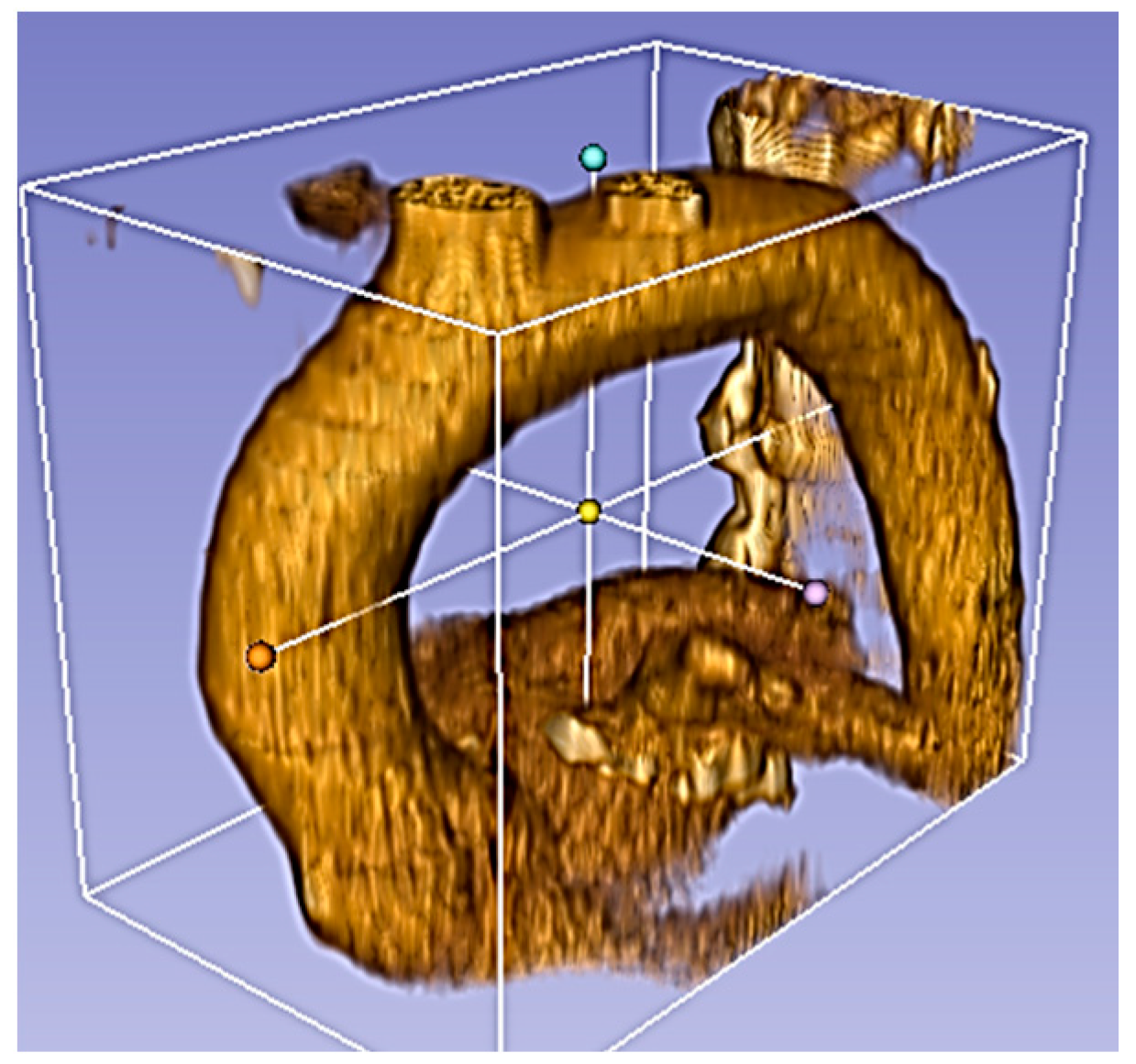
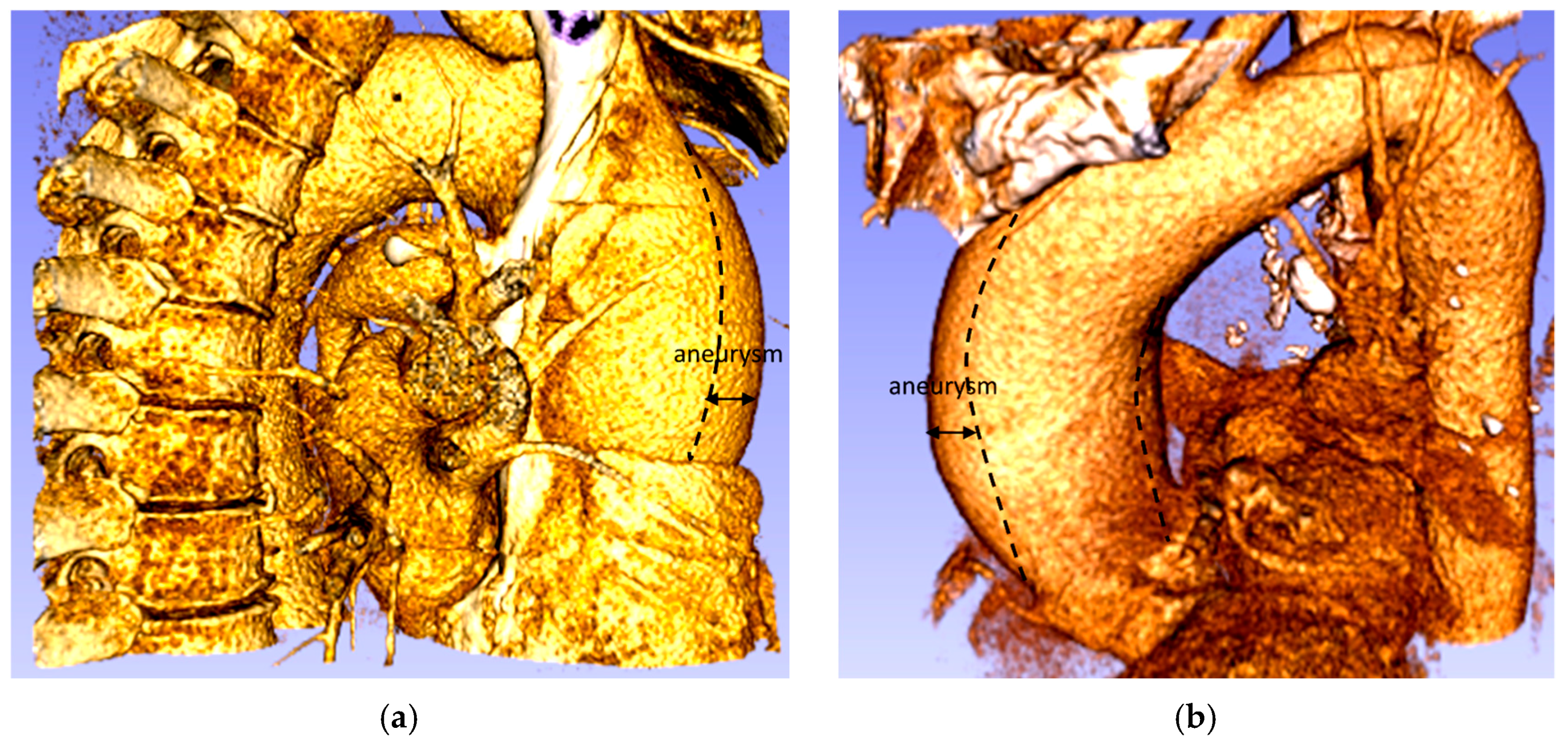
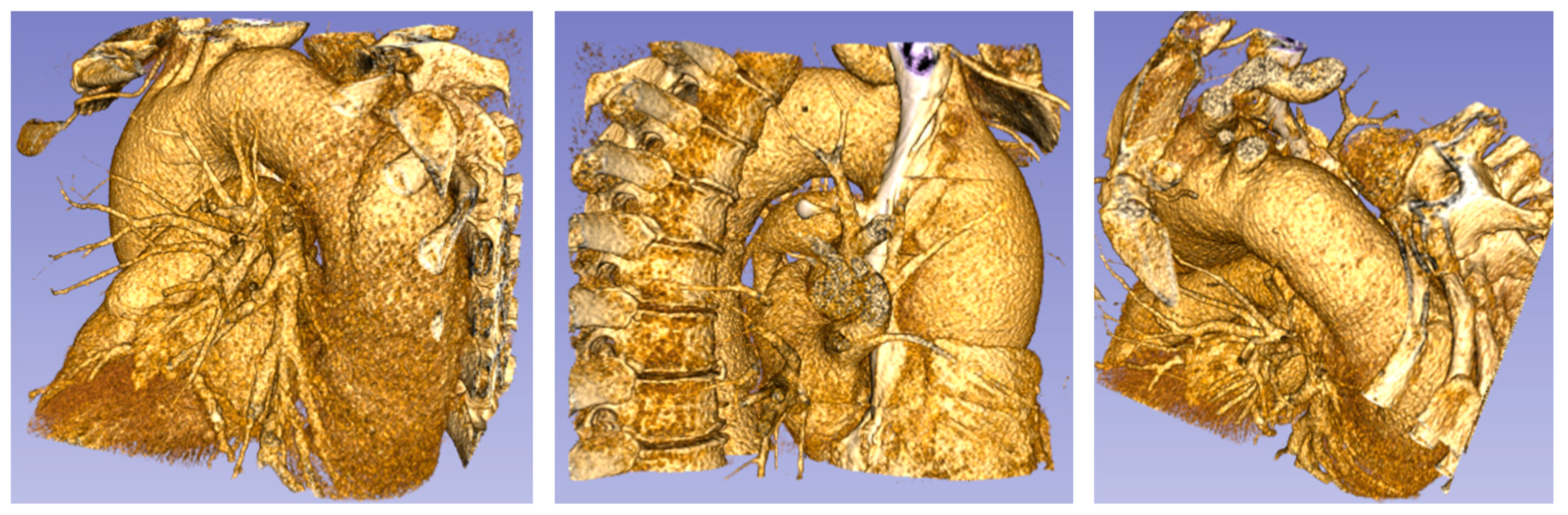
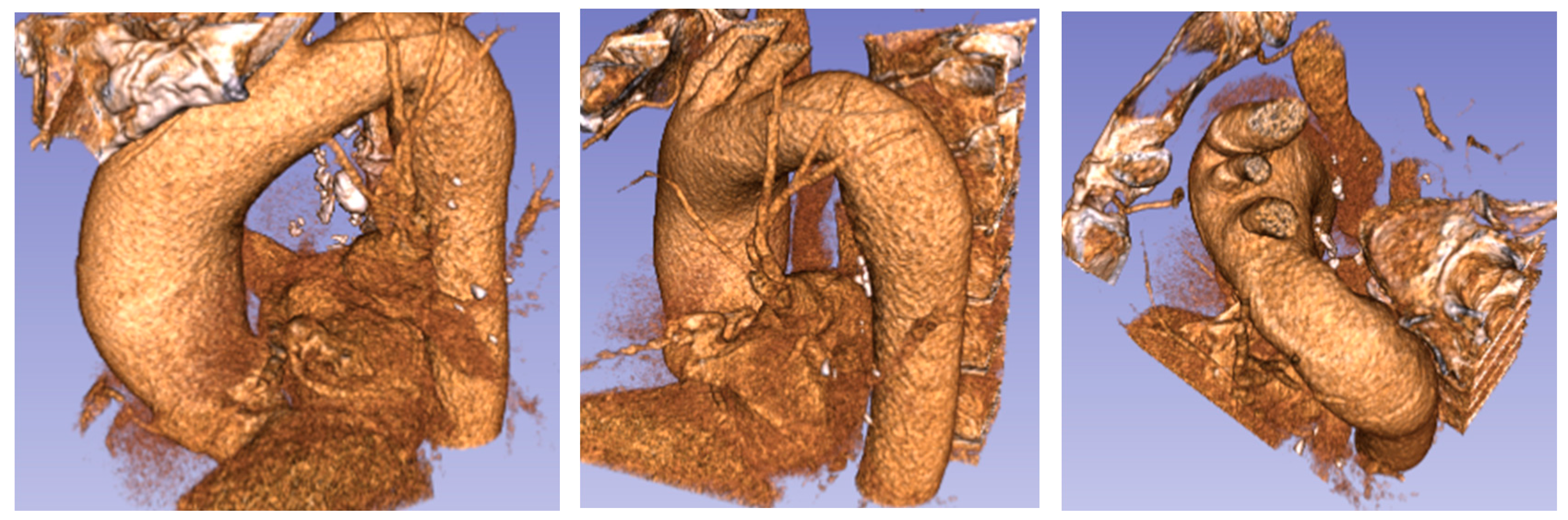
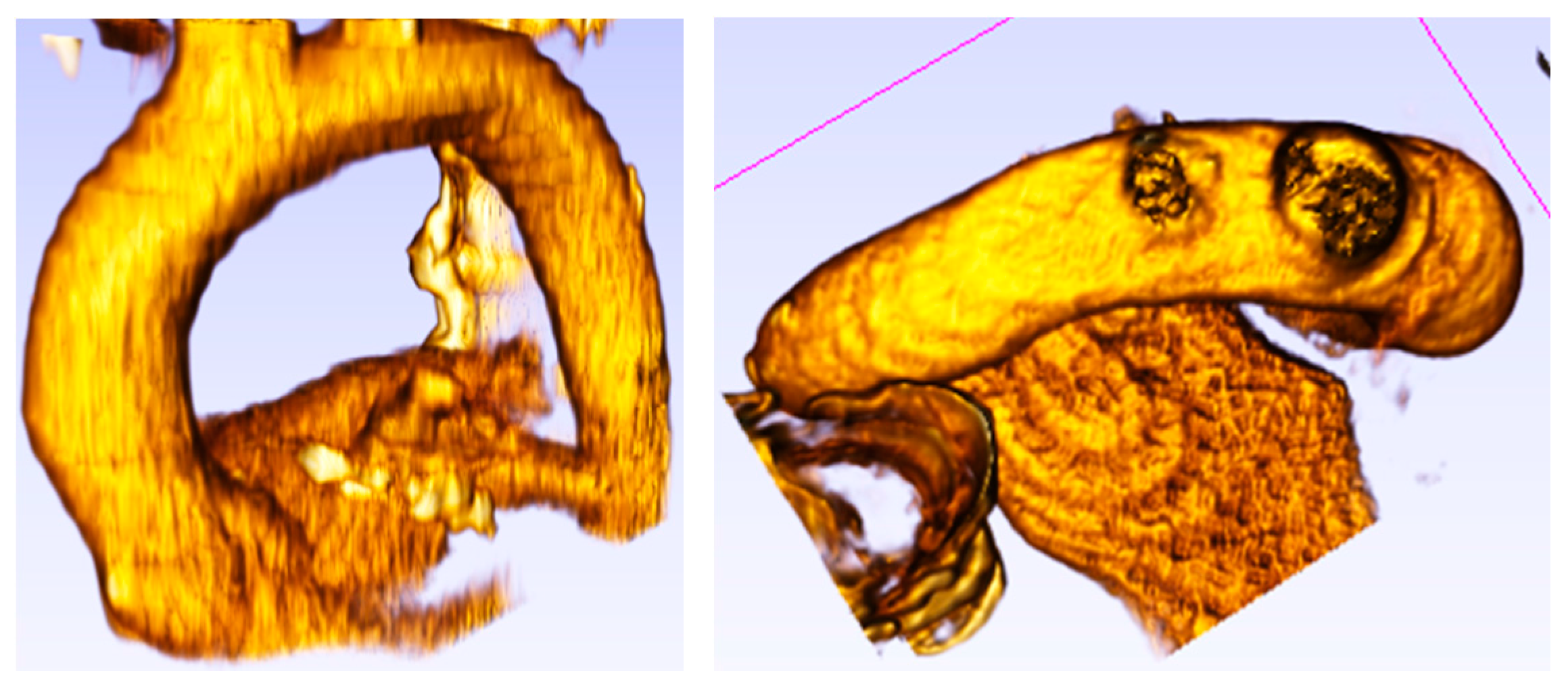
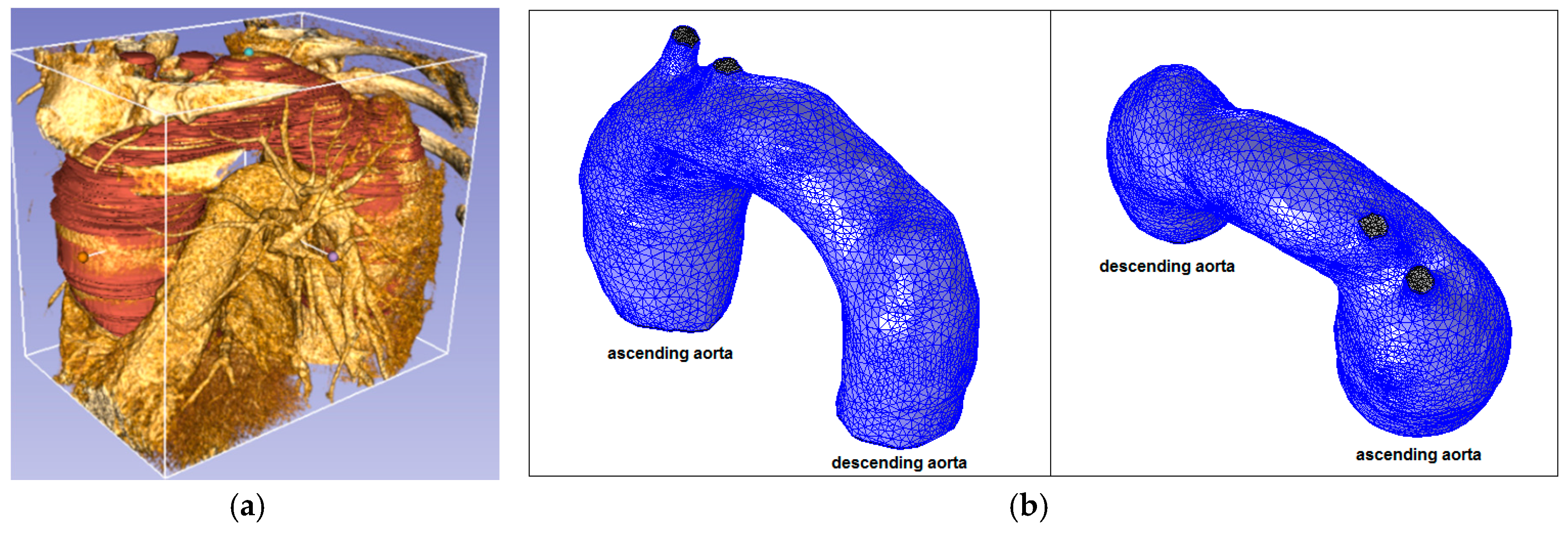
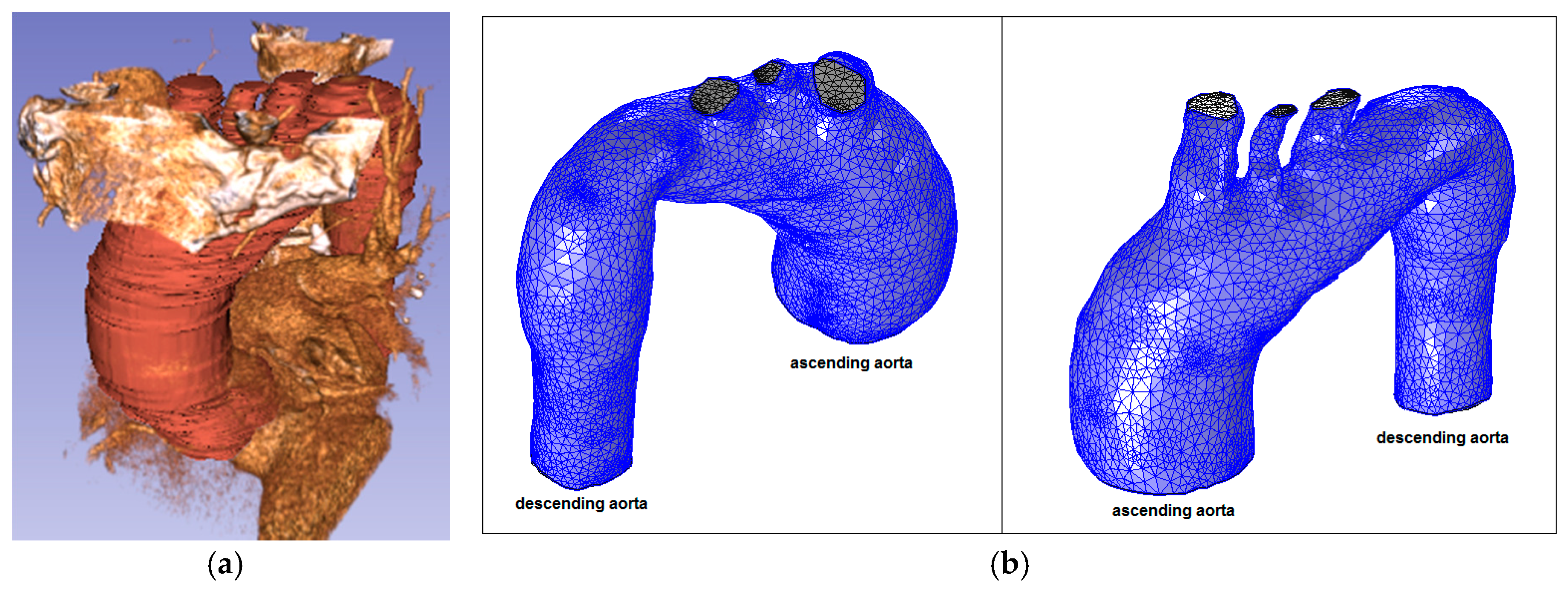
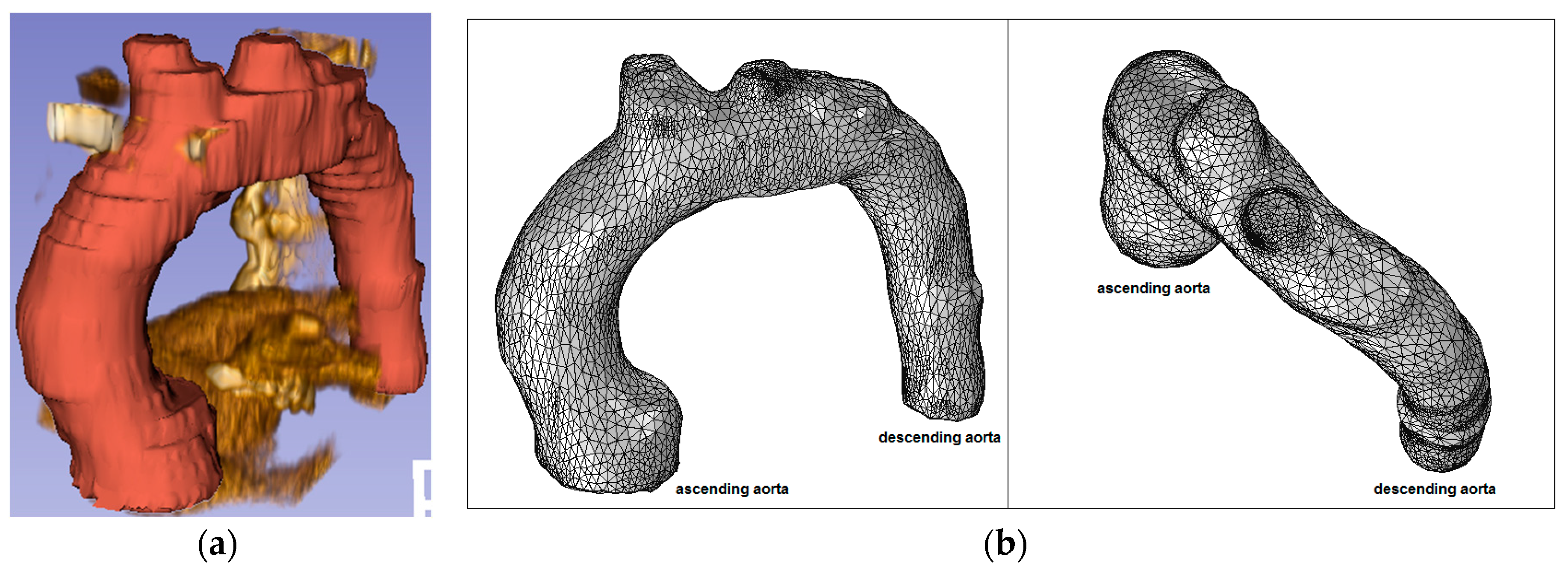


| Patient | (cm) | (cm) | (cm) | (cm) | (cm) | χ | β | γ | Type |
|---|---|---|---|---|---|---|---|---|---|
| Pilot | 2.80 | 1.40 | 1.40 | 2.80 | - | 1.00 | 1.00 | - | - |
| 1 | 3.54 | 2.06 | 2.70 | 4.76 | 6.92 | 1.35 | 0.76 | 0.69 | saccular with azimuthal symmetry (35% of deformation) |
| 2 | 2.69 | 0.56 | 3.33 | 3.88 | 11.53 | 1.44 | 0.17 | 0.34 | fusiform with only anterior wall dilated (44% of deformation) |
| Patients | Velocity Magnitude Range (m/s) | WSS Range (Pa) |
|---|---|---|
| Patient—pilot | 0.1–0.55 | 2–14 |
| 4 < 50% area < 6 (LWSS) | ||
| 8 < 50% area < 12 (HWSS) | ||
| Patient 1—TAA | 0.1–0.35 | 1–7 |
| 85% area < 5 (LWSS) | ||
| Patient 2—TAA | 0.1–0.60 | 0–14 |
| 0 < 60% area < 3 (LWSS) | ||
| 8 < 40% < 11 (HWSS) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simão, M.; Ferreira, J.; Tomás, A.C.; Fragata, J.; Ramos, H. Aorta Ascending Aneurysm Analysis Using CFD Models towards Possible Anomalies. Fluids 2017, 2, 31. https://doi.org/10.3390/fluids2020031
Simão M, Ferreira J, Tomás AC, Fragata J, Ramos H. Aorta Ascending Aneurysm Analysis Using CFD Models towards Possible Anomalies. Fluids. 2017; 2(2):31. https://doi.org/10.3390/fluids2020031
Chicago/Turabian StyleSimão, Mariana, Jorge Ferreira, António C. Tomás, José Fragata, and Helena Ramos. 2017. "Aorta Ascending Aneurysm Analysis Using CFD Models towards Possible Anomalies" Fluids 2, no. 2: 31. https://doi.org/10.3390/fluids2020031
APA StyleSimão, M., Ferreira, J., Tomás, A. C., Fragata, J., & Ramos, H. (2017). Aorta Ascending Aneurysm Analysis Using CFD Models towards Possible Anomalies. Fluids, 2(2), 31. https://doi.org/10.3390/fluids2020031







