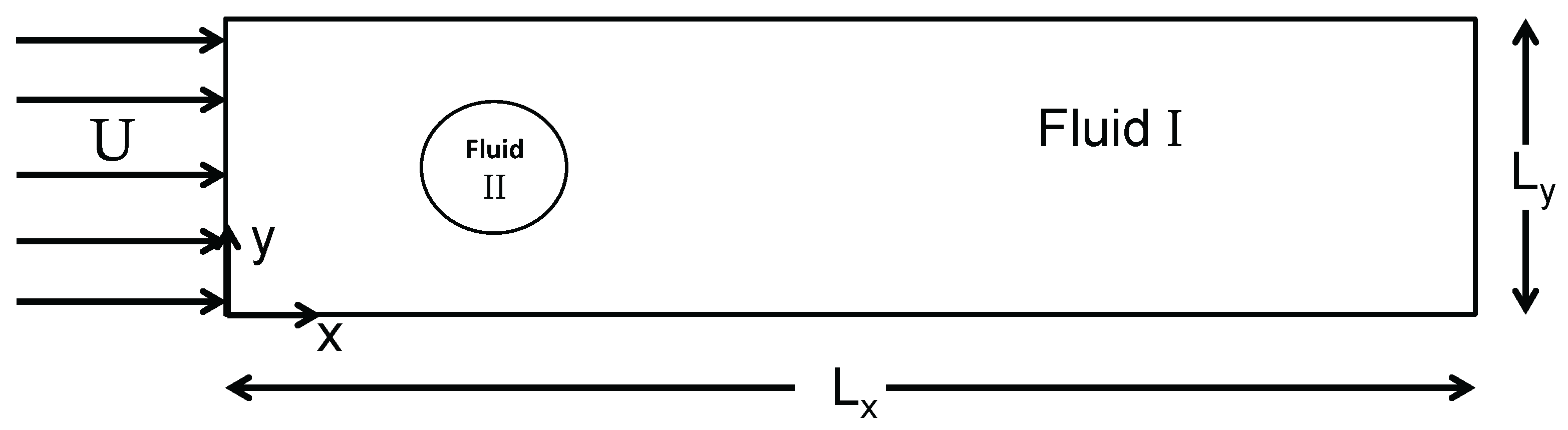
1. Introduction
Displacement of a less mobile fluid by a more mobile one in a porous medium results in a hydrodynamic instability, viscous fingering (VF). Its wide applicabilities, e.g., enhanced oil recovery [
1], CO
2 sequestration [
2], chromatographic separation [
3,
4], contaminant transport in aquifers [
5], mixing in low-Reynolds number flow [
6], intrinsic characteristics of nonlinear dynamics and pattern formation have fascinated active theoretical, numerical [
6,
7,
8,
9,
10,
11,
12,
13], and experimental [
14] researchers for more than half a decade. Both rectilinear and radial displacements have been investigated rigorously and have their own significance that can be investigated independently as well as comparatively. Here, we are interested in rectilinear displacements in porous media. The majority of the studies are focused on the case when the defending fluid is separated from the invading fluid by a flat interface. In many situations, e.g., aquifers, the contaminant can be of an arbitrary shape and miscible to the ambient fluid [
15]. When the underlying fluids are miscible to each other, the finger-like patterns that develop at the fluid–fluid interface depend, to a great extent, on the shape of the interface [
13], viscosity contrast [
1], and diffusion rate [
16]. As a consequence, mixing, spreading, and breakthrough time alter greatly [
6,
13,
15]. Pramanik et al. used the Fourier pseudospectral method to capture the dynamics of a more viscous blob in a homogeneous porous medium [
13], and the results are summarized in the
R-Pe parameter plane. Here,
R is the log-mobility ratio and Pe is the Péclet number. Depending upon the blob dynamics,
R-Pe plane was demarcated into three regions: lump-, comet-shaped deformations, and VF. Their studies were restricted to
, and Pe
, due to the limitations of the numerical convergence of the semi-implicit time integration of the pseudo-spectral method. The novelty of their work was identifying the re-entrance into the comet deformation region for large
R and fixed Pe, which is in strong contrast with the planar interface cases.
The dynamic viscosity of heavy oils is several orders magnitude larger than water or the conventional polymer used in polymer flooding oil recovery processes. Severe VF during water flooding of heavy oils leaves a large amount of residual oil in the reservoir [
17]. To the best of the authors’ knowledge, only experimental studies are conducted for very large viscosity contrast [
17]. This captivates us to numerically analyze miscible displacements, mixing, and spreading with very large viscosity contrasts. Various numerical schemes, e.g., finite difference (FD) [
7,
18], pseudospectral (PS) [
9,
11], finite element (FE) [
10], compact FD with alternating direction implicit (ADI) [
19], hybrid FD-PS [
20], finite volume (FV) [
6], etc., have been used for the nonlinear simulations of miscible VF. In spite of exhaustive numerical studies, miscible VF for large viscosity-contrast fluids are poorly explored. For large viscosity contrasts, the fluid velocity at the interface has sharp gradients. In these cases, one needs to solve a stiff system [
20] that limits the numerical convergence [
6]. This can be overcome through a suitable choice of the time-discretization method. Islam and Azaiez reported convergent numerical results for viscosity ratios of
. For water/polymer flooding of heavy oils, the viscosity ratios can go as high as
[
17]. We present numerical model using COMSOL Multiphysics software [
21] to obtain convergent numerical results for viscosity ratios of
.
Exploring the dynamics of the blob in the comet deformation region for very large
R is one of the motives of the present study. We have shown that for very large viscosity contrasts, variance of the transversely averaged concentration follows a power-law ∼
at later times. This power-law is larger than the one (
) for moderate viscosity contrast [
13]. The structure of the paper is as follows. The mathematical modeling and the methods used for the solution of the formulated problem are presented in
Section 2. In
Section 3, we present the results of our numerical experiments, followed by the discussion and conclusions of the results in
Section 4.
3. Results
In order to validate our COMSOL modeling, we first, qualitatively reproduce the results of [
13]. For a fixed value of Pe
, the spatio-temporal evolution of the circular blob for six different
Rs are shown in
Figure 2, which depict the re-entrance into the comet-shaped deformation region from the VF region, while increasing
R and keeping Pe fixed. In other words, not all unfavorable viscosity contrasts, but only a finite window of
R features VF.
For a given Pe, we define the upper limit of the VF-
R window as the critical log-mobility ratio,
, such that for all
(Pe) and the given Pe, only comet-shaped deformation is observed [
13]. In particular,
. In this paper, we primarily explore the dynamics of a more viscous blob for
, unless otherwise stated.
Figure 2 clearly depicts how increasing viscosity contrast favors and then inhibits VF. Here, we discuss the effect of
R for a fixed value of Pe = 1000. For
, convection is weaker than that required for the invading fluid to penetrate into the blob. As a result, the blob deforms into a lump and ultimately into a comet with a small tail. For
, the invading fluid penetrates into the blob, resulting in fingering instability at the rear interface and a tail formation at the frontal part of the blob. As we further increase
R beyond a critical value (
), the relative velocity of the two fluids increases significantly and the invading fluid prefentially flows around the blob, owing to its curvature [
13], and prevents VF. However, the tail formation persists and a long tail is observed at the frontal interface. This preferential flow is clearly visible in
Figure 2 at
s. The
Figure 2e,f depict how the dynamics of the blob change in the comet shape region while increasing the dynamic viscosity of the blob beyond the critical log-mobility ratio. For
, a tendency to feature VF is observed in the form of a lump (at
s), which ultimately changes into a comet with a wide, long tail (
Figure 2e). For
, the mobility of the blob reduces significantly, such that it remains at the same place over the time scale of significant downstream migration of the blob with
. However, the miscibility and a large relative velocity of the two fluids generate a long narrow tail. As a result, the dynamics of the blob can be described as a stagnant head comet with a downstream developing tail.
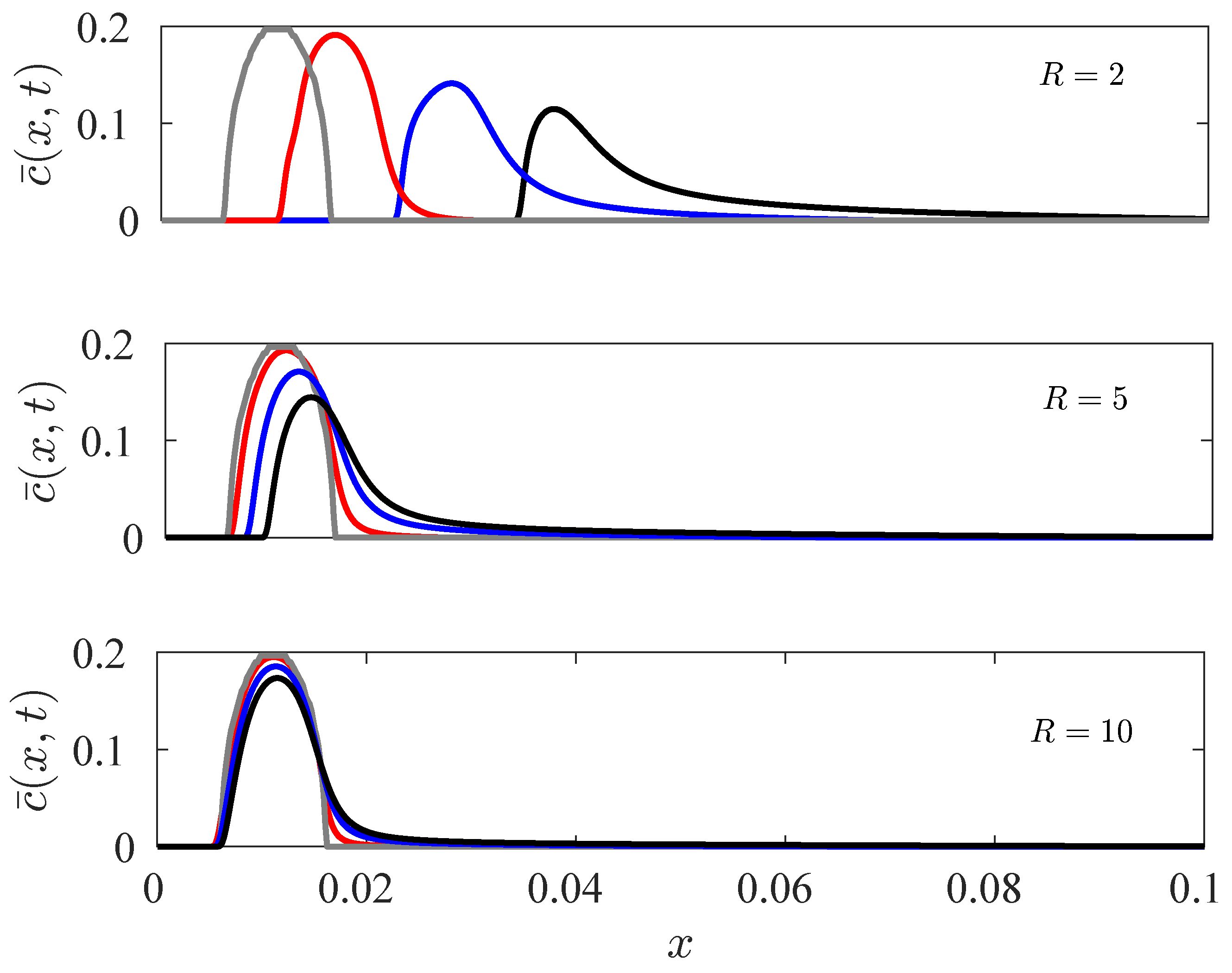
Next, we show that the qualitative features of comet shape blob can be captured from the transversely-averaged concentration,
The transversely-averaged concentration of the blob with different orders of viscosity ratio
and
are shown in
Figure 3.
The characteristics of the blob discussed above can also be described through
. Moreover, the transversely-averaged concentration clearly shows that the width of the tail decreases as the viscosity of the blob increases. A comparison of the position of the maxima at different times for each
R in
Figure 3 gives a lucid information about the relative mobility of the blobs. The gray line in
Figure 3 represents the transversely averaged concentration at
seconds for each
R. It ensures that the initial position of the blob for each
R simulation is the same and works as a reference with respect to which the relative position of the blobs at different times can be compared. It is to be noted that the flat top of the gray line is due to the approximation of a circular arc (of the blob) by rectangular mesh points. Through a grid independence test, we have ensured that the qualitative as well as quantitative dynamics remain unaltered due to this flat top of the gray line. As time progresses, diffusion smoothens the concentration gradient to make the curve smooth as is observed at later times. The increasing viscosity alters the relative velocity of the fluids.
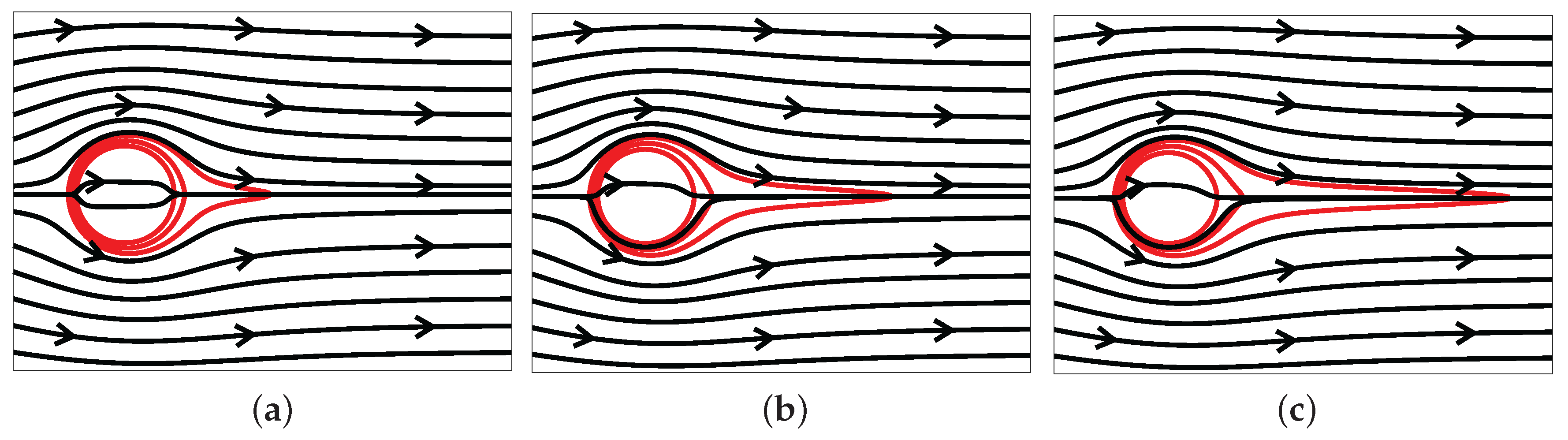
Streamlines are plotted (
Figure 4) to have an insight into the instantaneous velocity of fluid. The streamlines near the head of the highly viscous blob appear to be intersecting at a point, but they are actually very close. This is due to the high viscosity contrast, which results in a sudden decrease in the velocity of the fluid near the head. The ambient fluid cannot invade the blob and prefers to flow around it. This is depicted in terms of the sharp bend of the streamlines around the blob. The concentration contours (
Figure 4) help to clearly visualize this bend and the breaking in the left–right symmetry due to miscibility of the blob. Streamlines present within the blob (concentration contours) represent the movement of the blob, albeit very small. Thus, there exists no stagnation point, but a point of least velocity near the head of blob. The streamlines of very large viscosity contrast miscible flows exhibit following differences from the streamlines around an erodible body or a solid obstacle in Hele–Shaw cell [
25]. First, we discuss the differences between solid obstacle with circular cross section in a Hele–Shaw cell and very large viscosity contrast miscible blob in homogeneous porous media, since the mathematical formulations of the fluid flows in the two cases are analogous. In the former case, the streamlines are symmetric about both the longitudinal and transverse diameters of the circle. On the other hand, for the latter case, the left–right symmetry of the streamlines is broken due to the miscibility of the blob. Next, consider the comparisons between the cases of an erodible body in low-Reynolds number flow [
26] and very large viscosity contrasts miscible blob. In both the cases, the left–right symmetry of the streamlines are absent. However, unlike the former, downstream flow separation and upstream stagnation point are not observed in the latter case. This is attributed to the, albeit very small, non-zero fluid velocity within the miscible blob, but no fluid flow inside the erodible body. The upstream deformation of the erodible body or the miscible blob have the similarity that, in both the cases, it takes a streamlined topology. On the other hand, a long tail for the blob, but a flat interface [
26] for the erodible body in the downstream direction, marks a dissimilarity between the two.
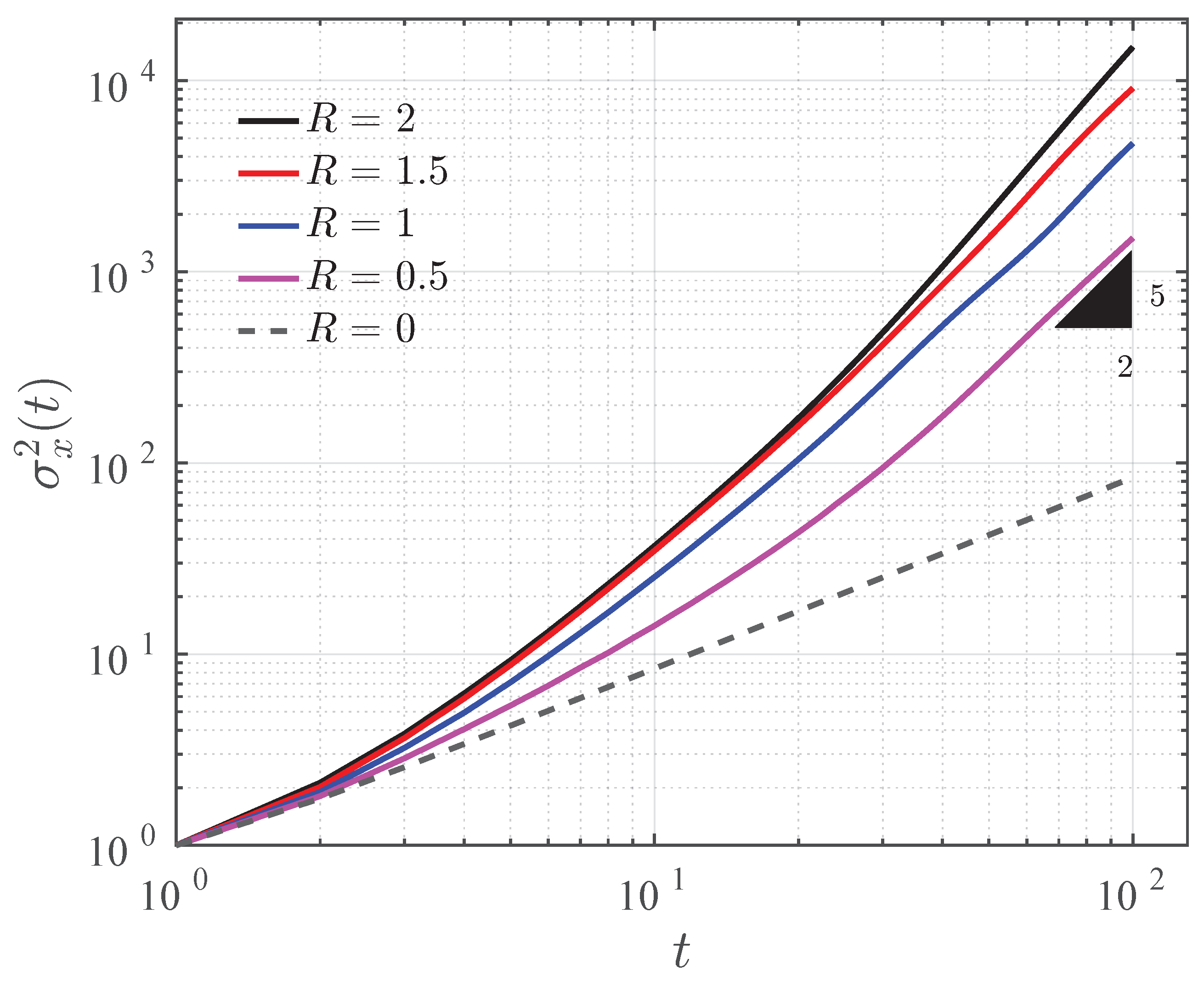
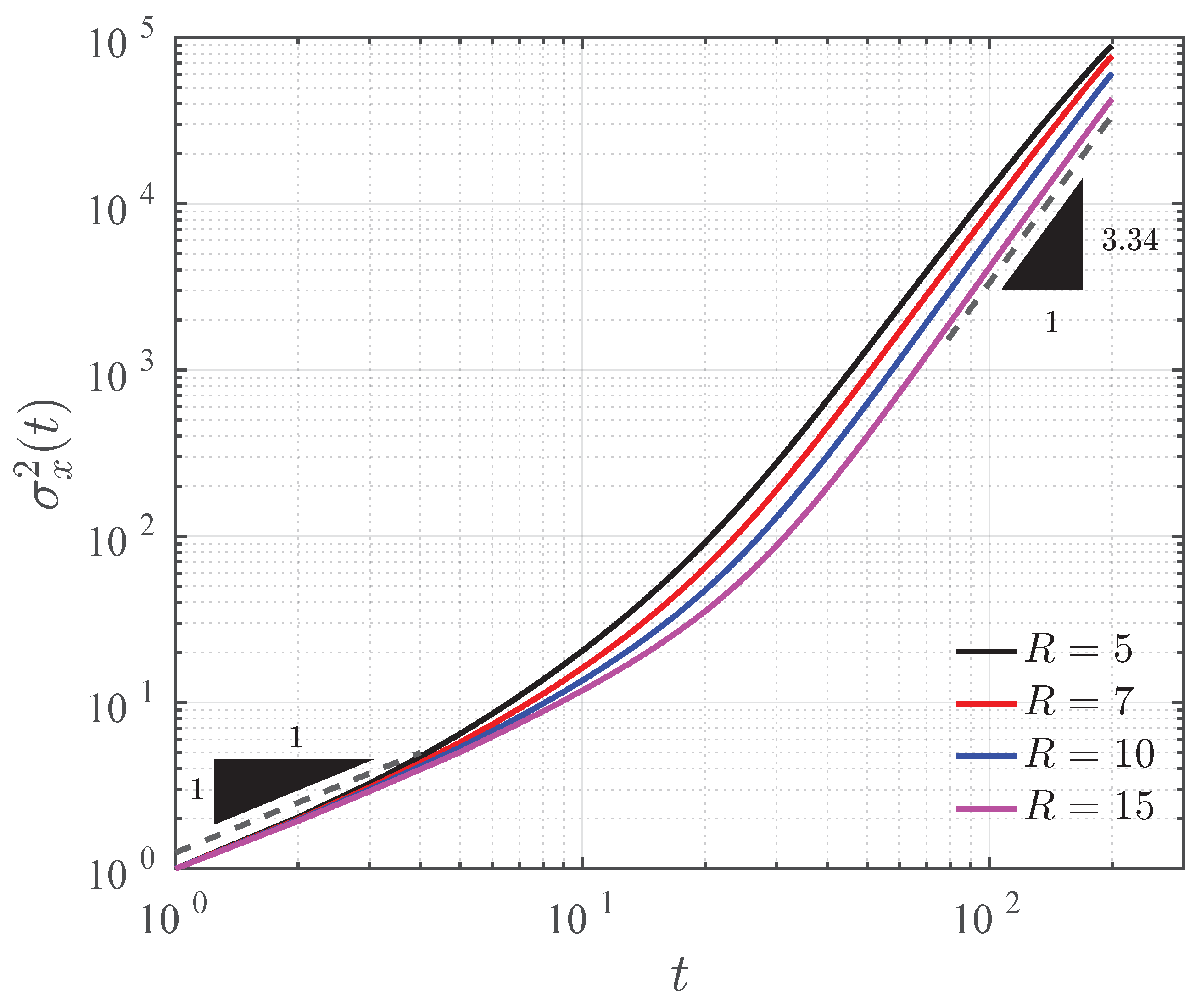
The stream-wise spreading of the blob is quantified in terms of the variance,
, [
13,
27] of the transversely-averaged concentration,
, defined as
Here,
is the mean of
. In order to refrain the numerical error to contaminate variance,
, we rescale the variance given by Equation (
13) as
Figure 5 and
Figure 6 show the log-log plot of the temporal evolution of the rescaled variance, which is denoted by the same notation as of the variance defined in Equation (
13). For
and Pe
, Pramanik et al. showed that
at early times, while at later times,
[
13]. We are successful at reproducing these power-law results using our COMSOL modeling (
Figure 5). This further confirms the validity of our COMSOL model. We are interested to know the power-law behavior of
for very large viscosity contrasts. For all values of
, early time behavior of
is identical to that of
. The instance of departure of
from the linear time variation depends on the value of
R. After that, there is a
R-dependent intermediate time interval for the transition from the linear time variation to another power-law variation of
. For viscosity ratio in the range
–
,
(see
Figure 6).
Furthermore, in order to quantify the left–right asymmetry of the blob, we measure a statistical quantity, the skewness [
28] of transversely-averaged concentration
,
The effect of
R on the asymmetry is examined by plotting skewness as a function of time in
Figure 7a, which shows that
increases with
t for all
R. This represents the asymmetry increases as time progresses in accordance with the increasing length of the downstream tail of the comet. Furthermore, at a fixed later time, skewness varies non-monotonically with
R as shown in
Figure 7b. This is a consequence of the re-entrance into the comet formation region for very high viscosity contrast. In the
comet formation region, a long tail is formed at the front interface, resulting in more asymmetry than that for
. However, for very high viscosity contrast
and even higher, the width of tail decreases, which causes a reduction in the asymmetry. Nevertheless, the asymmetry never vanishes, since the tail formation persists with viscosity contrast of all orders feasible with the current numerical computations. We also calculated the degree of mixing [
29,
30],
where
is the global variance of concentration, and
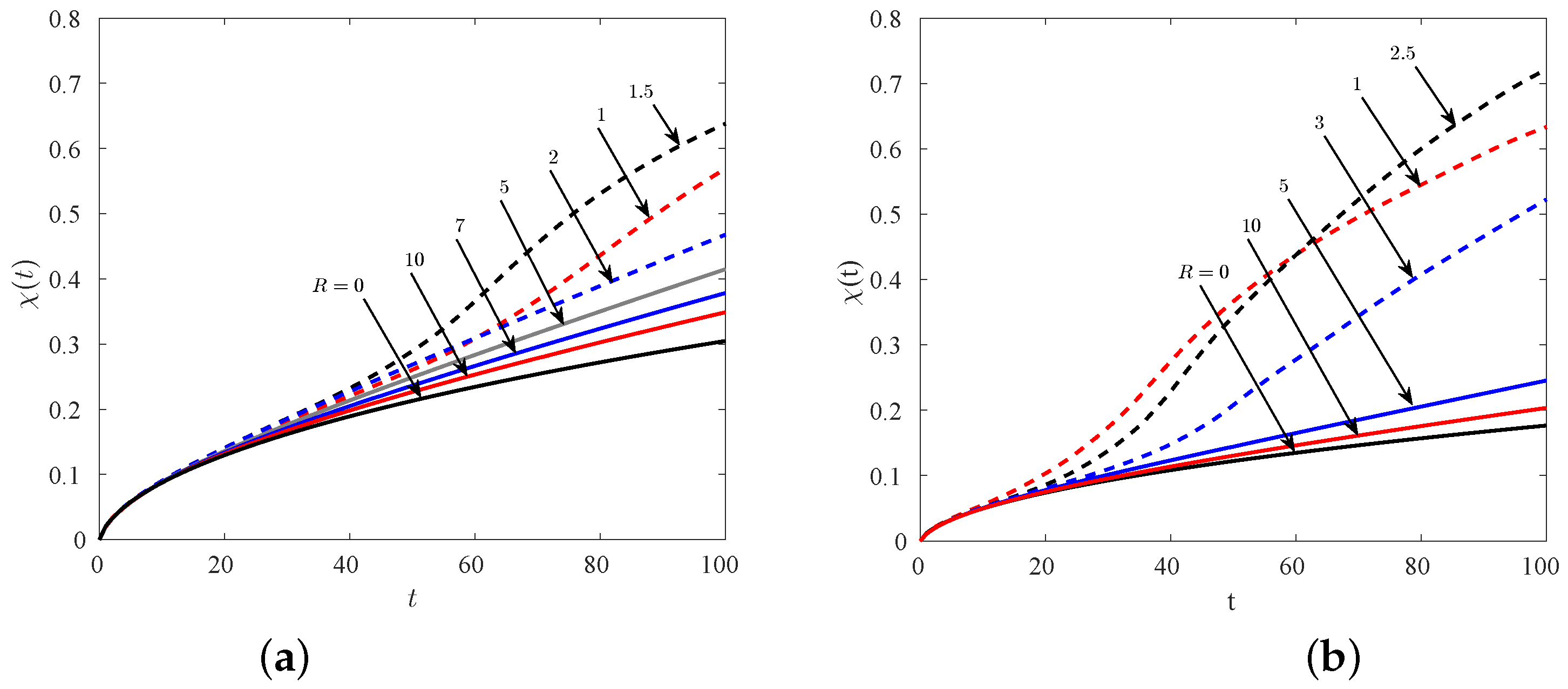
is its maximum value. This is a measure of mixing of the viscous blob with the ambient fluid.
In the present study, mixing is attributed to diffusive spreading, VF and tail formation.
Figure 8a shows the temporal evolution of
for a wide range of
R for
. This figure depicts that, at early times (
),
is almost identical for all
R, as, initially, diffusion dominates and mixing is due to diffusive spreading. At later times, the degree of mixing of the blob with the ambient fluid has a non-trivial dependence on
R. For
, the rear interface of the blob undergoes VF, in addition to a tail formation at the frontal interface. Consequently, the area of contact between the two fluids increases [
29], which eventually increases mixing. However, as
R is increased beyond
, the front interface deforms into a tail and no VF is observed. In addition, as is evident from
Figure 2 and
Figure 3, the width of the tail and hence the area of contact between the two fluids decreases, as we keep on increasing the viscosity contrast between the fluids. Ultimately, for
, the degree of mixing is found to approach the viscosity-matched case, for which mixing is only due to diffusive spreading, hence
is the minimum for this case
.
Figure 8b mimics the same qualitative features for
at different
R. However, a comparison of the corresponding curves for
in both the figures shows a smaller mixing for higher Pe. This is because, increasing Pe decreases the diffusion between the two fluids, which decreases the width of the tail and hence the mixing.
4. Discussion and Conclusions
Although numerical simulations of miscible VF remained in the forefront of active research over the decades, these studies remained restricted to either moderate diffusion or viscosity contrast. To the best of our knowledge, recent studies succeeded in capturing the VF dynamics for
[
20]. For either case of large
R or Pe, sharp velocity gradients at the finger tips cause problems with convergence of the numerical results. Here, we use an FEM-based COMSOL simulator and discuss some interesting and previously unexplored dynamics of miscible blobs in homogeneous porous media with very large viscosity contrasts.
Time discretization of the numerical scheme plays a very important role in deciding its fate (convergence or divergence). The explicit time discretization schemes are conditionally stable, allowing convergent results only for a limited value of the time or space discretization. Similarly, the semi-implicit time discretization schemes are found to show convergence only for some parameters. The Fourier pseudo-spectral method used by various researchers [
9,
13] to capture non-linear VF, is an example of the semi-implicit time discretization. This pseudo-spectral method converges only for
. Meiburg and Chen [
19] adapted a compact finite difference and the ADI method to simulate miscible VF in both homogeneous and heterogeneous porous media. They captured a new VF mechanism called side branching. However, they also could not go higher than
. The reason for this non-convergence was found to be the explicit nature of the scheme [
20]. In addition, when the viscosity contrast between the miscible fluids is high, there exists a sharp velocity gradient and slow concentration variation across the interface, making the problem stiff. Hence, for exploring the flow of the fluids with viscosity
, an implicit time-discretization with a stiff system solver may be helpful. In COMSOL, we used backward differentiation formulas of first and second orders, with the implicit time solvers known for their A-stability [
31]. Allowing the time stepping to be adaptive, and uniform spatial step size sufficient to capture the finest fingers and avoid numerical diffusion, helped us to obtain convergent results for very large viscosity contrast between the fluids (
). We showed that, for a high viscosity contrast, there exist remarkable similarities and dissimilarities between the flow around an erodible body and the flow of a less viscous fluid around a highly viscous miscible blob. Although there exists no stagnation point in the case of the latter, the huge viscosity contrast results in a considerable decrease in velocity near the interface. This decrease in velocity forms a reason for the non-existence of VF even with an unfavorable viscosity contrast for high viscosity blobs. Owing to miscibility, only a tail is observed at the frontal interface, motivating us to compare with the flow around erodible bodies. We also capture and discuss the breaking in the left–right symmetry of the streamlines around the blob, a distinction between the flow around highly viscous blob and the Hele–Shaw flow around a solid body, although both of the problems are mathematically analogous. In the presence of an unfavorable but very high viscosity contrast
or
, mixing and spreading of the blob is quantitatively similar to those of a blob in the ambient fluid of same viscosity, that is, when
. Initial time evolution of the variance of transversely averaged concentration (
Figure 6) and skewness (
Figure 7a) justify this. The spreading for a high viscous blob follows the power law
, and the degree of mixing varies non-monotonically with the log-mobility ratio
R. This can be attributed to the effect of curvature, which results in re-entrance into the comet formation regime, decreasing the area of contact and hence the degree of mixing with an increase in
R.
for the highly viscous blob approaches that for the viscosity matched case, independent of the Pe. In addition, it is found that there is no tendency of VF formation in the case of highly viscous blobs, as there is no lump formation initially, which is evident for blobs with log-mobility ratio
. Thus, we conclude that curvature plays a very important role in the displacement processes involving viscosity contrast, and the dynamics of a highly viscous blob can be explored further to compare to that of an erodible body and to understand heavy oil extractions.
Hence, the COMSOL simulations software used wisely can be applicable to understand fingering instability, mixing, and other qualitative as well as quantitative behaviors in the presence of additional disturbances to the system, such as dispersion anisotropy, permeability heterogeneity, heterogeneous porosity, velocity-dependent dispersion, adsorption, and many more, which may result in numerical instabilities to the spectral solution of the stream function formulation. An equation-based model using the COMSOL Multiphysics with more degrees of freedom in terms of the boundary conditions, domain discretization, and incorporating additional body (surface) forces into the transport equations will be considered in future research.