A Quasi-Mechanistic Mathematical Representation for Blood Viscosity
Abstract
:1. Introduction
1.1. Factors that Contribute to the Viscosity of Blood
1.2. The Krieger Model of Viscosity of Suspensions
2. Adaptation of the Krieger Viscosity Model for Blood
2.1. Plasma Viscosity
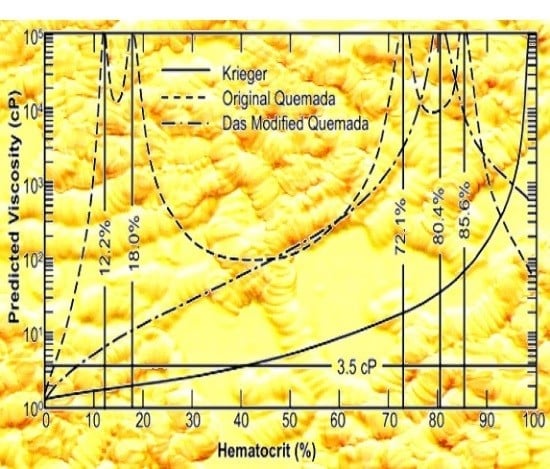
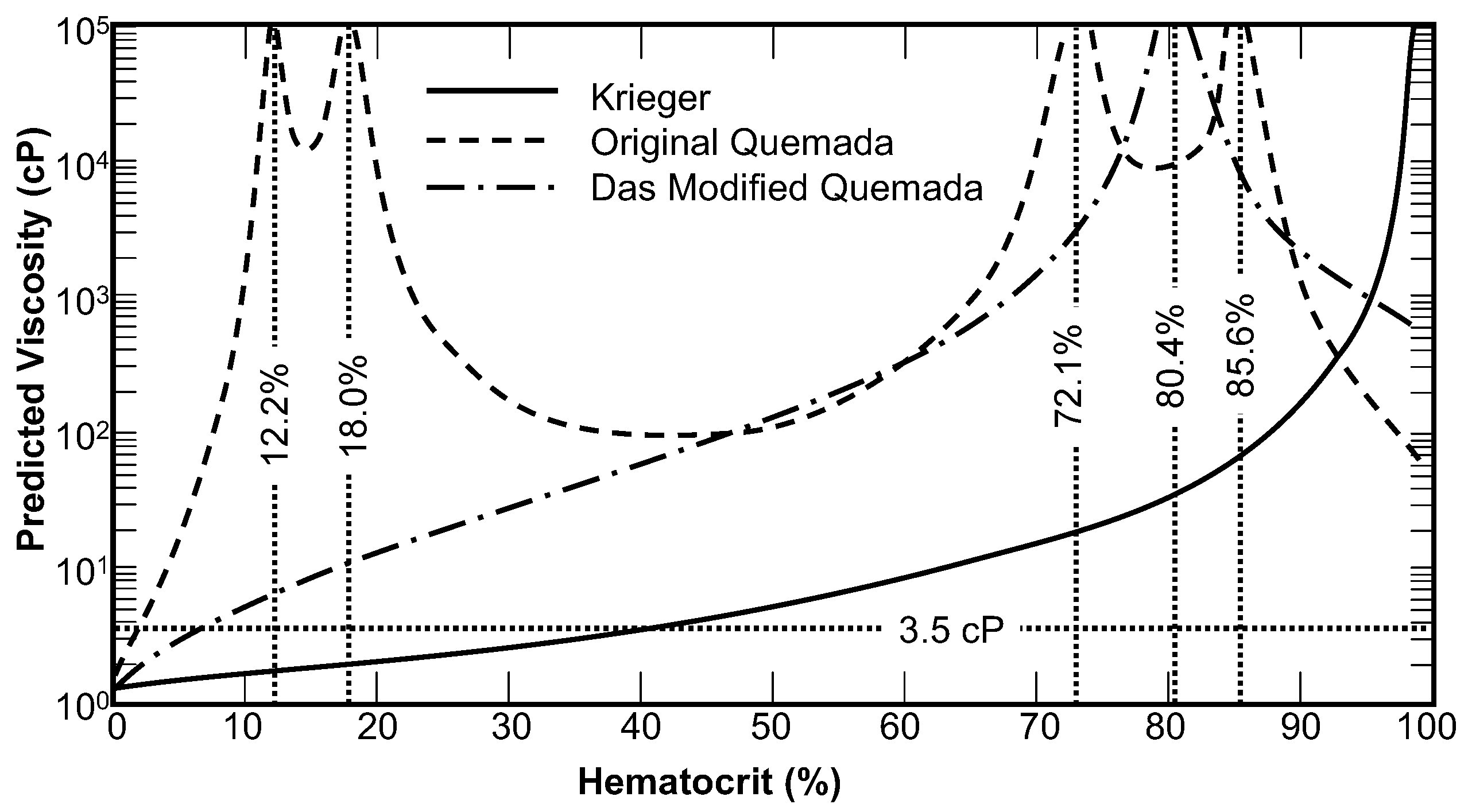
2.2. Critical Hematocrit
2.3. Krieger Exponent and Shear Thinning
3. Model Evaluation
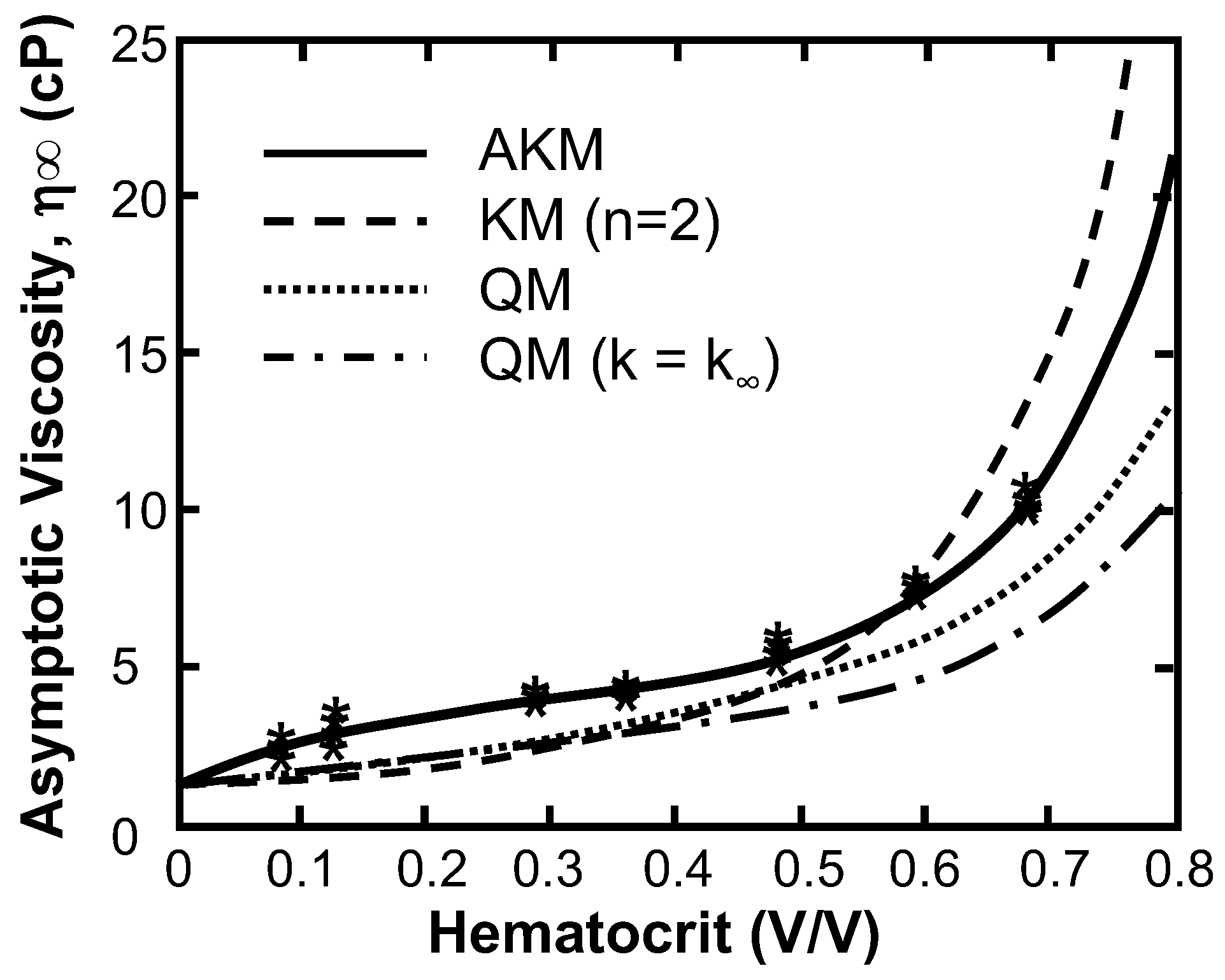
3.1. Parameter Estimation
3.2. Sensitivity Study
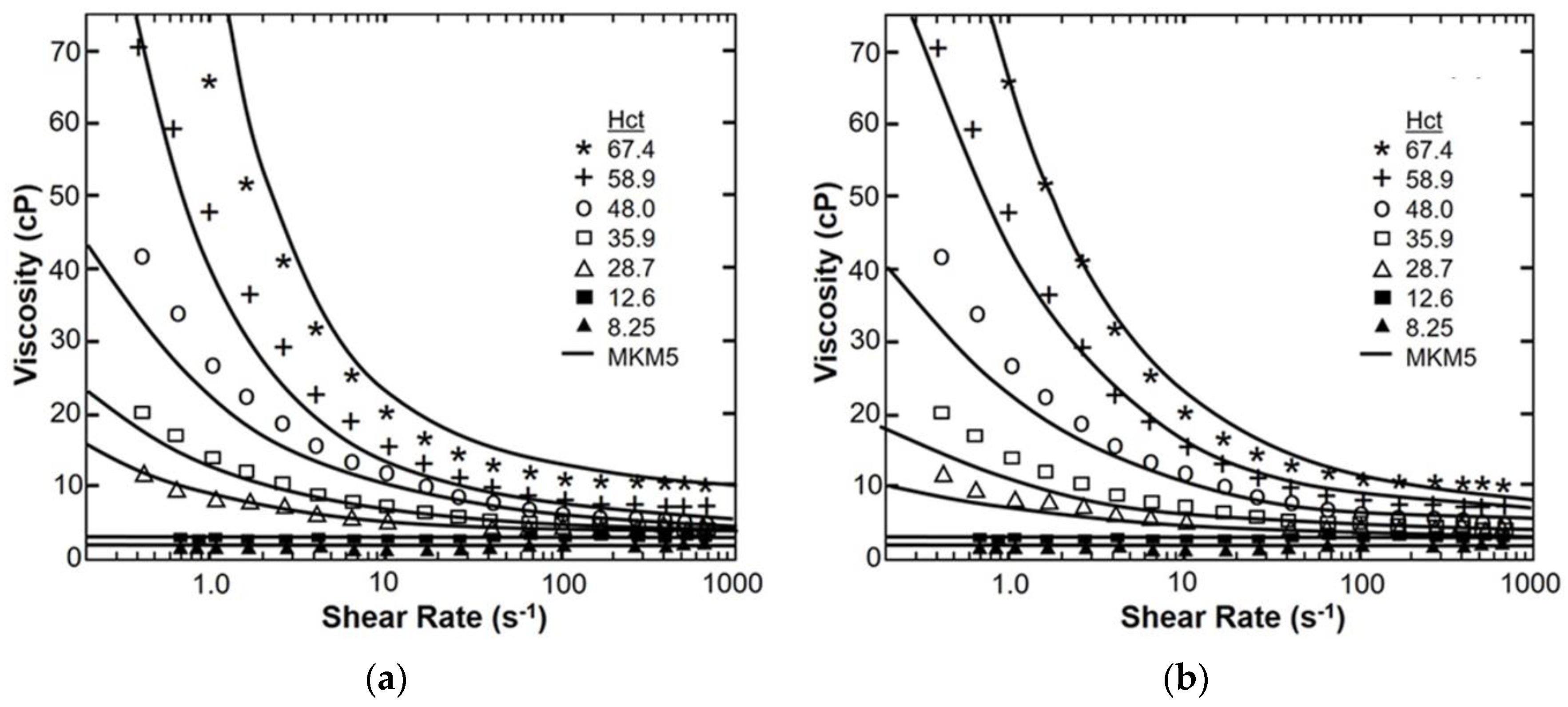
4. Results
Sensitivity Study of Shear Thinning Behavior in Tube Flow
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fahraeus, R.; Lindvist, T. The viscosity of the blood in narrow capillary tubes. Am. J. Physiol. Leg. Content 1931, 96, 562–568. [Google Scholar]
- Palmer, A.A. Axial drift of cells and partial plasma skimming in blood flowing through glass slits. Am. J. Physiol. Leg. Content 1965, 209, 1115–1122. [Google Scholar]
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [PubMed]
- Kim, N.J.; Diao, C.; Ahn, K.H.; Lee, S.J.; Kameneva, M.V.; Antaki, J.F. Parametric study of blade tip clearance, flow rate, and impeller speed on blood damage in rotary blood pump. Artif. Organs 2009, 33, 468–474. [Google Scholar] [CrossRef] [PubMed]
- Karino, T.; Goldsmith, H.L. Flow behaviour of blood cells and rigid spheres in an annular vortex. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1977, 279, 413–445. [Google Scholar] [CrossRef] [PubMed]
- Wootton, D.M.; Markou, C.P.; Hanson, S.R.; Ku, D.N. A mechanistic model of acute platelet accumulation in thrombogenic stenoses. Ann. Biomed. Eng. 2001, 29, 321–329. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Marhefka, J.N.; Shu, F.; Hund, S.J.; Kameneva, M.V.; Antaki, J.F. Micro-flow visualization of red blood cell-enhanced platelet concentration at sudden expansion. Ann. Biomed. Eng. 2008, 36, 1130–1141. [Google Scholar] [CrossRef] [PubMed]
- Sequeira, A.; Janela, J. An Overview of Some Mathematical Models of Blood Rheology. In A Portrait of State-of-the-Art Research at the Technical University of Lisbon; Pereira, M.S., Ed.; Springer: Lisbon, Portugal, 2007; pp. 65–87. [Google Scholar]
- Guyton, A.C. Textbook of Medical Physiology; Saunders: Philadelphia, PA, USA, 1981. [Google Scholar]
- Ballyk, P.D.; Steinman, D.A.; Ethier, C.R. Simulation of non-Newtonian blood flow in an end-to-side anastomosis. Biorheology 1994, 31, 565–586. [Google Scholar] [PubMed]
- Walburn, F.J.; Schneck, D.J. A constitutive equation for whole human blood. Biorheology 1976, 13, 201–210. [Google Scholar] [PubMed]
- Steffan, H.; Brandstätter, W.; Bachler, G.; Pucher, R. Comparison of Newtonian and Non-Newtonian Blood Flow in Stenotic Vessels using Numerical Simulation. In Biofluid Mechanics; Springer: Berlin, Heidelberg, 1990; pp. 479–485. [Google Scholar]
- Jung, J.; Hassanein, A. Three-phase CFD analytical modeling of blood flow. Med. Eng. Phys. 2008, 30, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Yeleswarapu, K.K.; Kameneva, M.V.; Rajagopal, K.R.; Antaki, J.F. The flow of blood in tubes: Theory and experiment. Mech. Res. Commun. 1998, 25, 257–262. [Google Scholar] [CrossRef]
- Quemada, D. Rheology of Concentrated Disperse Systems. II. Model for Non-Newtonian Shear Viscosity in Steady Flows. Rheol. Acta 1978, 17, 632–642. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Cokelet, G.R.; Brown, J.R.; Codd, S.L.; Seymour, J.D. Magnetic resonance microscopy determined velocity and hematocrit distrubutions in a Couette viscometer. Biorheology 2005, 42, 385–399. [Google Scholar] [PubMed]
- Das, B.; Johnson, P.C.; Popel, A.S. Effect of nonaxisymmetric hematocrit distribution on non-Newtonian blood flow in small tubes. Biorheology 1998, 35, 69–87. [Google Scholar] [CrossRef]
- Kameneva, M.V.; Ündar, A.; Antaki, J.F.; Watach, M.J.; Calhoon, J.H.; Borovetz, H.S. Decrease in red blood cell deformability caused by hypothermia, hemodilution, and mechanical stress: Factors related to cardiopulmonary bypass. ASAIO J. 1999, 45, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Eckmann, D.M.; Bowers, S.; Stecker, M.; Cheung, A.T. Hematocrit, volume expander, temperature, and shear rate effects on blood viscosity. Anesth. Analg. 2000, 91, 539–545. [Google Scholar] [CrossRef] [PubMed]
- Rosenkrantz, T.S. Polycythemia and hyperviscosity in the newborn. Semin. Thromb. Hemost. 2003, 29, 515–528. [Google Scholar] [PubMed]
- Rand, P.; Barker, N.; Lacombe, E. Effects of plasma viscosity and aggregation on whole-blood viscosity. Am. J. Physiol. Leg. Content 1970, 218, 681–688. [Google Scholar]
- Chien, S.; Usami, S.; Dellenback, R.J.; Gregersen, M.I.; Nanninga, L.B.; Guest, M.M. Blood viscosity: Influence of erythrocyte deformation. Science 1967, 157, 827–829. [Google Scholar] [CrossRef] [PubMed]
- Carr, R.; Cockelet, G.R. Rheology of suspensions of normal and hardened erythrocytes and their mixtures. J. Rheol. 1981, 25, 67–82. [Google Scholar] [CrossRef]
- Baskurtand, O.K.; Meiselman, H.J. Cellular determinants of low-shear blood viscosity. Biorheology 1997, 34, 235–247. [Google Scholar] [CrossRef]
- Snyder, G. Influence of temperature and hematocrit on blood viscosity. Am. J. Physiol. Leg. Content 1971, 220, 1667–1672. [Google Scholar]
- Chien, S.; Usami, S.; Taylor, H.M.; Lundberg, J.L.; Gregersen, M.I. Effects of hematocrit and plasma proteins on human blood rheology at low shear rates. J. Appl. Physiol. 1966, 21, 81–87. [Google Scholar] [PubMed]
- Armstrong, L.E. Hydration assessment techniques. Nutr. Rev. 2005, 63, S40–S54. [Google Scholar] [CrossRef] [PubMed]
- Rand, P.W.; Lacombe, E. Hemodilution, tonicity, and blood viscosity. J. Clin. Investig. 1964, 43, 2214–2226. [Google Scholar] [CrossRef] [PubMed]
- Sidel, V.W.; Solomon, A.K. Entrance of water into human red cells under an osmotic pressure gradient. J. Gen. Physiol. 1957, 41, 243–257. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, A.; Müller, P. Correlation of the internal microviscosity of human erythrocytes to the cell volume and the viscosity of hemoglobin solutions. Biochim. Biophys. Acta Mol. Cell Res. 1986, 885, 80–87. [Google Scholar] [CrossRef]
- Kameneva, M.V.; Antaki, J.F.; Borovetz, H.S.; Griffith, B.P.; Butler, K.C.; Yeleswarapu, K.K.; Watach, M.J.; Kormos, R.L. Mechanisms of red blood cell trauma in assisted circulation: Rheologic similarities of red blood cell transformations due to natural aging and mechanical stress. Asaio J. 1995, 41, M457–M460. [Google Scholar] [CrossRef] [PubMed]
- Rand, P.W.; Austin, W.H.; Lacombe, E.; Barker, N. pH and blood viscosity. J. Appl. Physiol. 1968, 25, 550–559. [Google Scholar] [PubMed]
- Reinhart, W.H.; Piety, N.Z.; Goede, J.S.; Shevkoplyas, S.S. Effect of osmolality on erythrocyte rheology and perfusion of an artificial microvascular network. Microvasc. Res. 2015, 98, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Keller, D.S.; Keller, D.V. The effect of particle size distribution on the antithixotropic and shear thickening properties of coal-water dispersions. J. Rheol. 1991, 35, 1583–1607. [Google Scholar] [CrossRef]
- Allende, M.; Kaylon, D.M. Assessment of particle-migration effects in pressure-driven viscometric flow. J. Rheol. 2000, 44, 79–89. [Google Scholar] [CrossRef]
- Huang, N.; Bonn, D. Viscosity of a dense suspension in Couette flow. J. Fluid Mech. 2007, 590, 497–507. [Google Scholar] [CrossRef]
- Jogun, S.; Zukoski, C.F. Rheology of dense suspensions of platelike particles. J. Rheol. 1996, 40, 1211–1232. [Google Scholar] [CrossRef]
- Bullard, J.W.; Pauli, A.T.; Garboczi, E.J.; Martys, N.S. A comparison of viscosity-concentration relationships for emulsions. J. Colloid Interface Sci. 2009, 330, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Niedzwiedz, K.; Buggisch, H.; Willenbacher, N. Extensional rheology of concentrated emulsions as probed by capillary breakup elongational rheometry (CaBER). Rheol. Acta 2010, 49, 1103–1116. [Google Scholar] [CrossRef]
- Lionberger, R.A. Shear thinning of colloidal dispersions. J. Rheol. 1998, 42, 843–863. [Google Scholar] [CrossRef]
- Heyes, D.M.; Sigurgeirsson, H. The Newtonian viscosity of concentrated stabilized dispersions: Comparisons with the hard sphere fluid. J. Rheol. 2004, 48, 223–248. [Google Scholar] [CrossRef]
- Mansour, M.H.; Bressloff, N.W.; Shearman, C.P. Red blood cell migration in microvessels. Biorheology 2010, 47, 73–93. [Google Scholar] [PubMed]
- Pal, R. Rheology of concentrated suspensions of deformable elastic particles such as human erythrocytes. J. Biomech. 2003, 36, 981–989. [Google Scholar] [CrossRef]
- Bowen, R.M. Theory of mixtures. In Continuum Physics III; Erningen, A.C., Ed.; Academic Press: New York, NY, USA, 1976; pp. 1–127. [Google Scholar]
- Ovarlez, G.; Bertrand, F.; Rodts, S. Local determination of the constitutive law of a dense suspension of noncolloidal particles through magnetic resonance imaging. J. Rheol. 2006, 50, 259–292. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Fradette, L.; Tanguy, P.A.; Bertrand, F.; Thibault, F.; Ritz, J.-B.; Giraud, E. CFD phenomenological model of solid–liquid mixing in stirred vessels. Comput. Chem. Eng. 2007, 31, 334–345. [Google Scholar] [CrossRef]
- Frith, W.J.; d’Haene, P.; Buscall, R.; Mewis, J. Shear thickening in model suspensions of sterically stabilized particles. J. Rheol. 1996, 40, 531–548. [Google Scholar] [CrossRef]
- Brooks, D.E.; Goodwin, J.W.; Seaman, G.V. Interactions among erythrocytes under shear. J. Appl. Physiol. 1970, 28, 172–177. [Google Scholar] [PubMed]
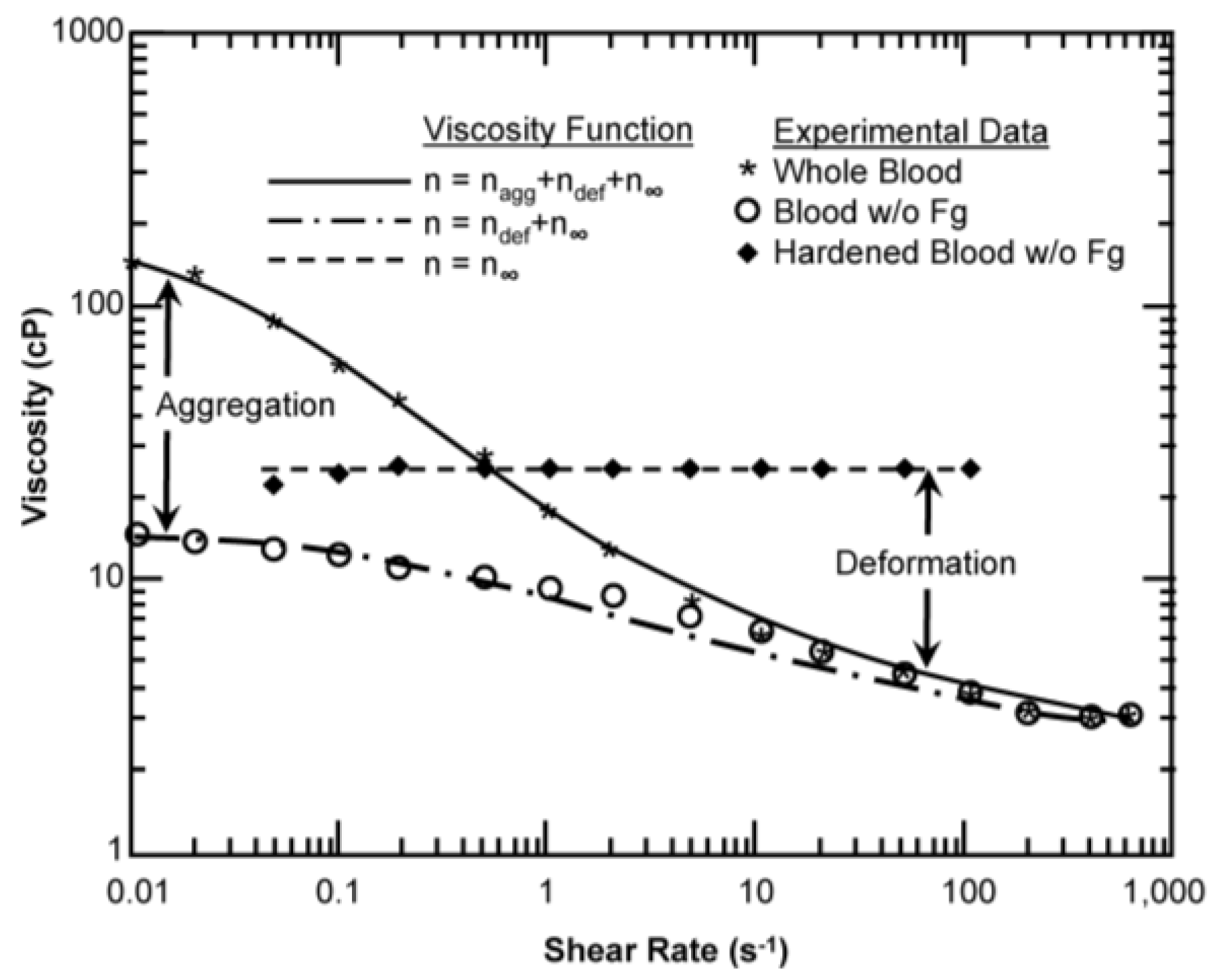
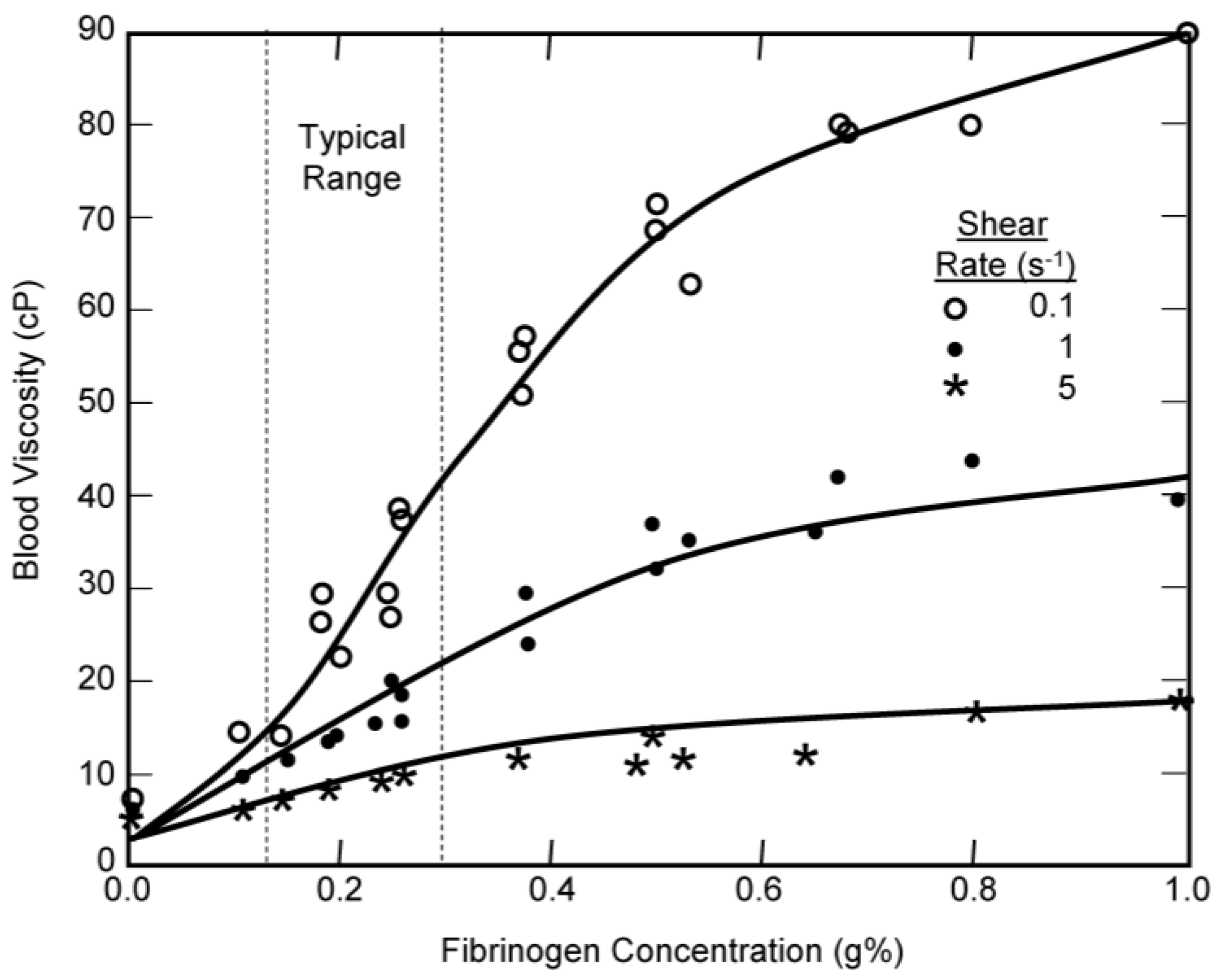
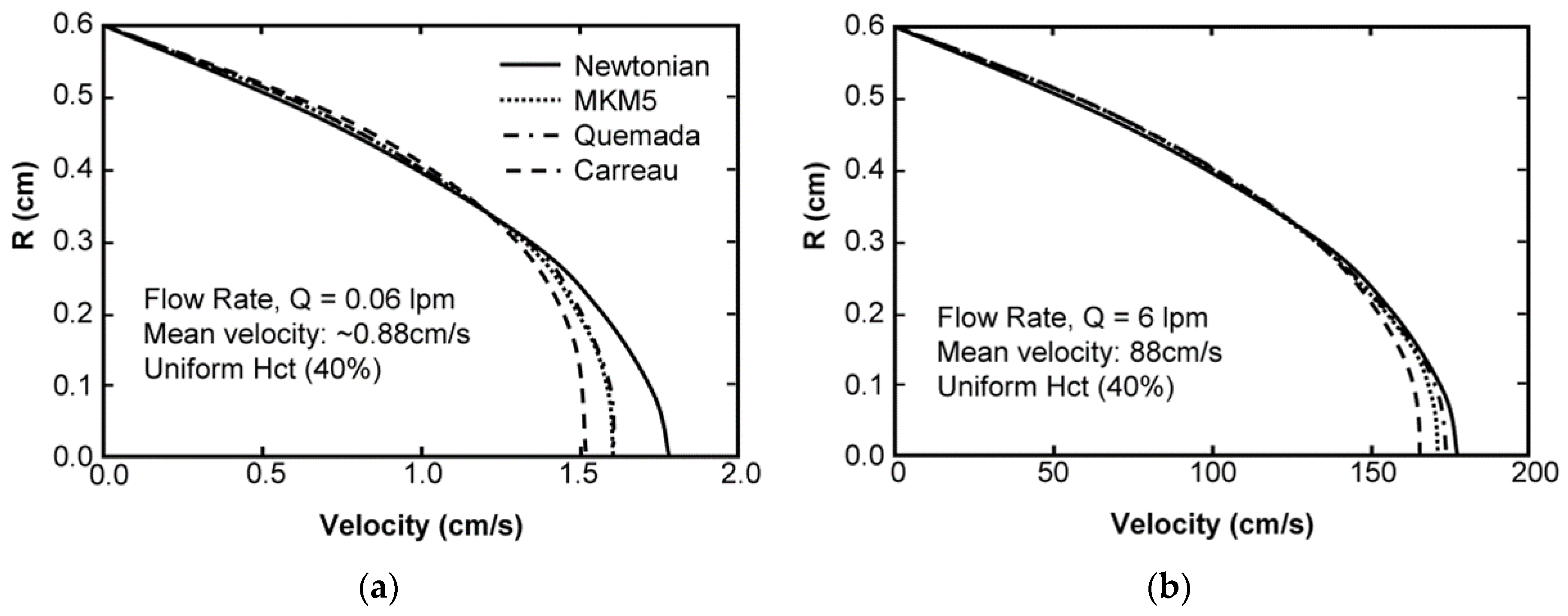
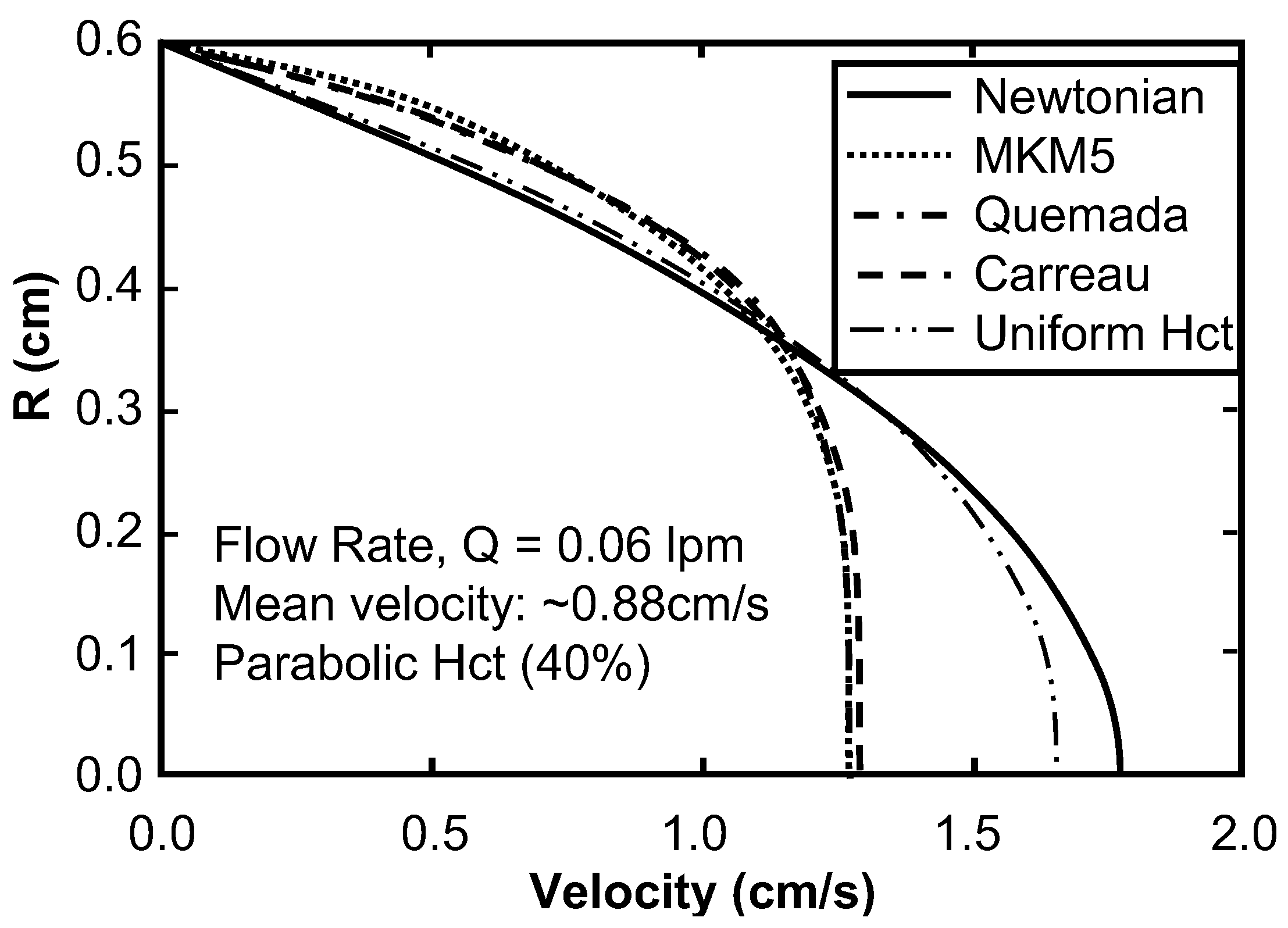
| Model | Equation | Shear Rate | Hematocrit | Proteins | Temperature | Asymptote LS/HS | Continuous | Legend |
|---|---|---|---|---|---|---|---|---|
| Newtonian [8] | – | – | – | – | –/X | X | (1) | |
| Asymptotic [9] | – | X | – | – | –/X | X | (2) | |
| Power-Law [8] | X | – | – | – | –/– | – | (3) | |
| Generalized Power-Law [10] | X | – | – | – | –/X | – | (4) | |
| Walburn-Schneck (WS) [11] | X | X | X | X | –/– | – | (5) | |
| Asymptotic Power-Law | X | X | X | X | –/X | X | (6) | |
| Cross, Modified Cross, Simplified Cross, Carreau, Carreau-Yasuda, Jung et al. [8,10,12,13] | X | – | – | – | X/X | X | (7) | |
| Powell-Eyring [8] | X | – | – | – | X/X | – | (8) | |
| Modified Powell-Eyring [10] | X | – | – | – | X/X | – | (9) | |
| Yeleswarapu [14] | X | – | – | – | X/X | X | (10) | |
| Quemada [15] | X | X | – | – | –/X | – | (11) | |
| Krieger [16] | – | X | – | – | X/X | X | (12) |
| Model | Coefficient Values | Ref. | Model | Coefficient Values | Ref. |
| Power-law | k = 0.42, | [8] | Walburn-Schneck (WS) | C1 = 0.00797, | [11] |
| C2 = 0.0608, | |||||
| n = 0.61 | C3 = 0.00499, | ||||
| C4 = 14.59 L/g | |||||
| Asymptotic | η0 = 0.014175, | [9] | Modified Cross | η∞ = 3.5 cP, | [8] |
| η1 = 0.05878, | Δη = 52.5 cP, | ||||
| η2 = 0.1598, | λ = 3.736 s, | ||||
| η3 = 0.31964 | m = 2.406, | ||||
| a = 0.254 | |||||
| Cross | η∞ = 3.5 cP, | [8] | Carreau-Yasuda | η∞ = 3.5 cP, | [8] |
| Δη = 52.5 cP, | Δη = 52.5 cP, | ||||
| λ = 1.007 s, | λ = 1.902 s, | ||||
| m = 1, | m = 1.25, | ||||
| a = 1.028 | a = 0.7588 | ||||
| Carreau | η∞ = 3.5 cP, | [8] | Modified Power-Erying | η∞ = 3.5 cP, | [10] |
| Δη = 52.5 cP, | Δη = 52.5 cP, | ||||
| λ = 3.313 s, | λ = 2.415 s, | ||||
| m = 2, | m = 1.089 | ||||
| a = 0.3216 | |||||
| Powell-Erying | η∞ = 3.5 cP, | [8] | Yeleswarapu | η∞ = 5.0 cP, | [14] |
| Δη = 52.5 cP, | Δη = 68.6 cP, | ||||
| λ = 5.383 s | λ = 14.81 s | ||||
| Simplified Cross | η∞ = 5 cP, | [12] | -- | ||
| Δη = 125 cP, | |||||
| λ = 8.0 s, | |||||
| m = 1, | |||||
| a = 1 | |||||
| Model | Coefficient Forms | Coefficients | Ref. | ||
| Generalized Power-Law | η∞ = 3.5, Δη = 25, Δn = 0.45, a = 50, b = 3, c = 50, d = 4. | [10] | |||
| Jung et al. Modified Carreau | η∞ = 0, λ = 0.1101 s, 6 s−1 Ko = 0, a1 = 0.1752, a2 = 0.4123, a3 = −0.4046, d1 = 16.305, d2 = −51.213, d3 = 122.28, 6 s−1 ko = 1, a1 = 0.8907, a2 = −1.0339, a3 = −0.4456, d1 = 9.7193, d2 = −22.454, d3 = 70.782 | [13] | |||
| Quemada Model (Cokelet) | ao = 3.874, a1 = −10.41, a2 = 13.80, a3 = −6.738, bo = 1.3435, b1 = −2.803, b2 = 2.711, b3 = −0.6479, co = −6.1508, c1 = 27.923, c2 = -25.60, c3 = 3.697 | [17] | |||
| Quemada Model (Das) | As above, except: | as above, except: ao = 0.275363 and a1 = 0.100158 | [18] | ||
| Model Parameter | AKM | AKM (Fixed Cells) | MKM5 | MKM9 | Agg/Def. Model | Fg Model |
|---|---|---|---|---|---|---|
| a | 1.70 (1.66–1.75) | 1.06 (0.944–1.18) | 0 | 0.686 (0.34–1.03) | 0.0974 | 1.30 |
| b | 9.86 (8.63–11.1) | −0.226−(0.201–0.251) | 8.71 (7.85–9.57) | 11.8 (4.11–19.5) | n/a | n/a |
| c | 6.07 (5.59–6.55) | −1.69−(1.54–1.85) | 2.87 (2.55–3.20) | 8.60 (3.42–13.8) | n/a | n/a |
| β | n/a | n/a | 8.23 (7.85–8.60) | n/a | n/a | n/a |
| λ | n/a | n/a | 108 (106–110) | 136 (120–152) | n/a | n/a |
| ν | n/a | n/a | 0.134 (0.122–0.146) | n/a | n/a | n/a |
| b1 | n/a | n/a | n/a | −9.11 −(10.7–7.48) | n/a | n/a |
| b2 | n/a | n/a | n/a | 13.0 (12.2–13.9) | n/a | n/a |
| n1 | n/a | n/a | n/a | 0.180 (0.090–0.269) | n/a | n/a |
| n2 | n/a | n/a | n/a | −0.170 −(0.304–0.035) | n/a | n/a |
| n3 | n/a | n/a | n/a | 0.124 (0.073–0.174) | n/a | n/a |
| βagg | n/a | n/a | n/a | n/a | 4.27 | n/a |
| λagg | n/a | n/a | n/a | n/a | 24.1 | 16.0 |
| νagg | n/a | n/a | n/a | n/a | 0.380 | 0.0895 |
| βdef | n/a | n/a | n/a | n/a | 4.36 | n/a |
| λdef | n/a | n/a | n/a | n/a | 5.44 | n/a |
| νdef | n/a | n/a | n/a | n/a | 0.120 | n/a |
| B1 | n/a | n/a | n/a | n/a | n/a | 6.26 |
| B2 | n/a | n/a | n/a | n/a | n/a | 5.54 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hund, S.J.; Kameneva, M.V.; Antaki, J.F. A Quasi-Mechanistic Mathematical Representation for Blood Viscosity. Fluids 2017, 2, 10. https://doi.org/10.3390/fluids2010010
Hund SJ, Kameneva MV, Antaki JF. A Quasi-Mechanistic Mathematical Representation for Blood Viscosity. Fluids. 2017; 2(1):10. https://doi.org/10.3390/fluids2010010
Chicago/Turabian StyleHund, Samuel J., Marina V. Kameneva, and James F. Antaki. 2017. "A Quasi-Mechanistic Mathematical Representation for Blood Viscosity" Fluids 2, no. 1: 10. https://doi.org/10.3390/fluids2010010
APA StyleHund, S. J., Kameneva, M. V., & Antaki, J. F. (2017). A Quasi-Mechanistic Mathematical Representation for Blood Viscosity. Fluids, 2(1), 10. https://doi.org/10.3390/fluids2010010