Large Eddy Simulation of Pulsatile Flow through a Channel with Double Constriction
Abstract
:1. Introduction
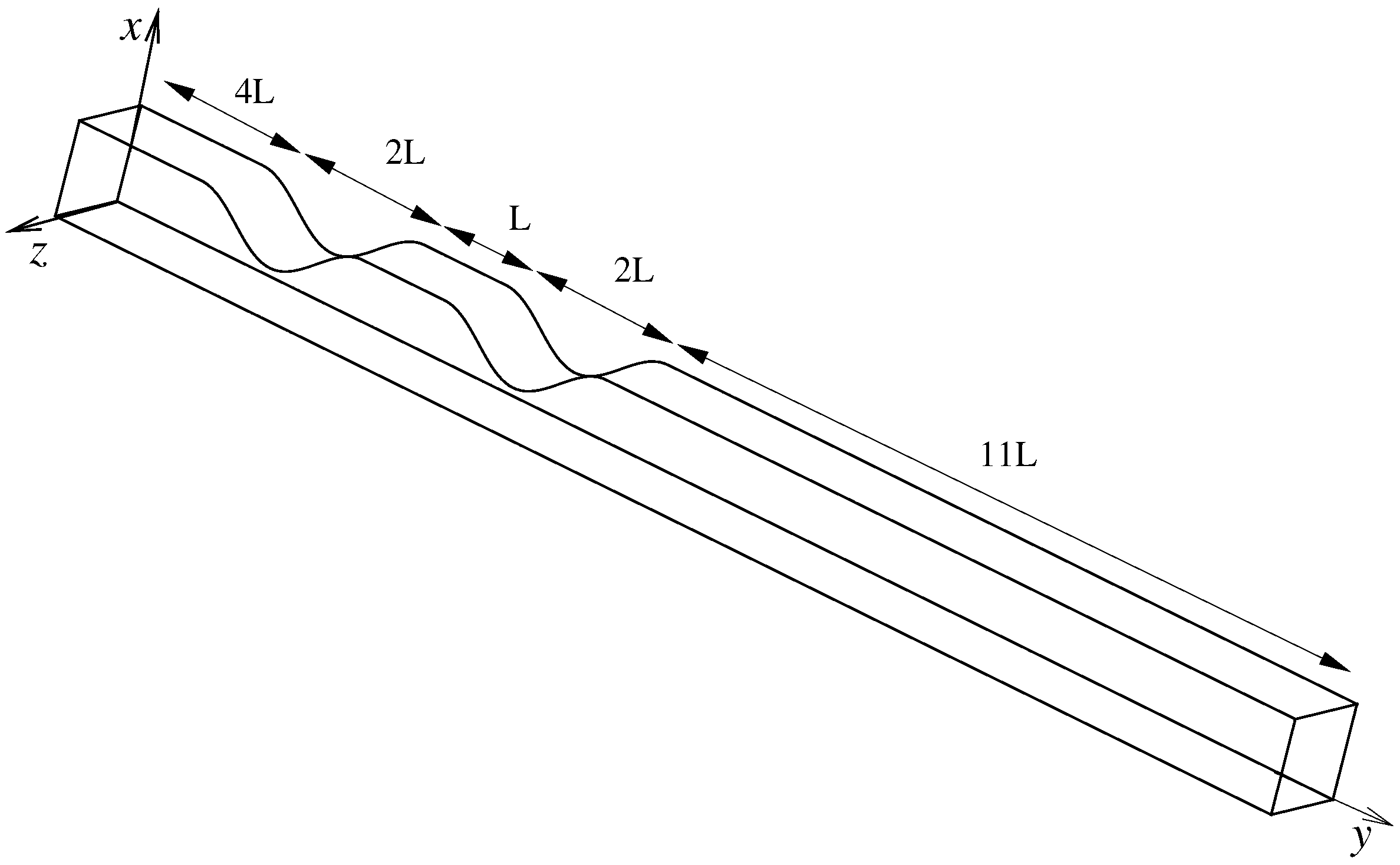
2. Formulation of the Problem
2.1. Boundary Conditions and Computational Parameters
2.2. Overview of Numerical Procedures
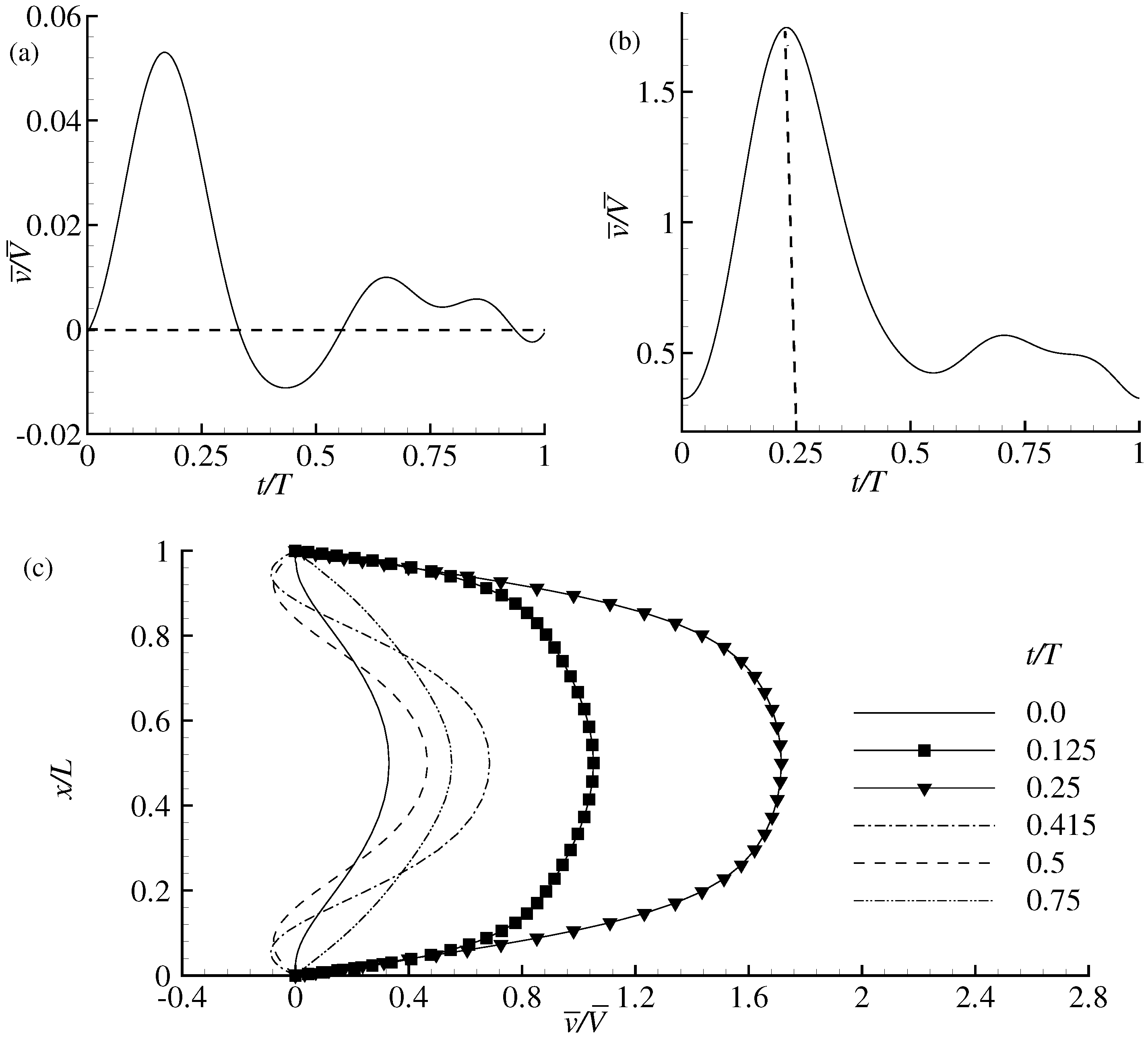
3. Data Processing
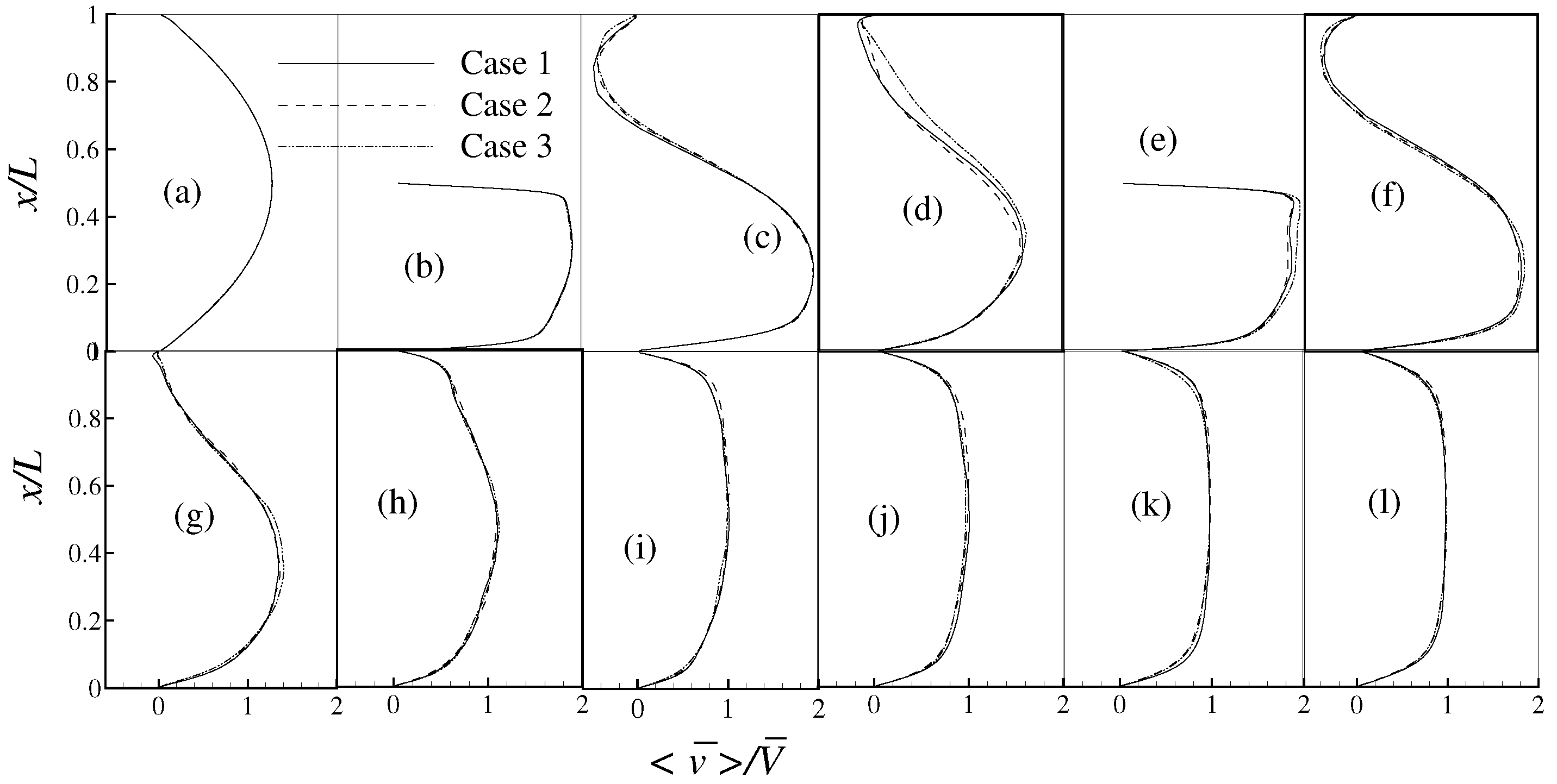
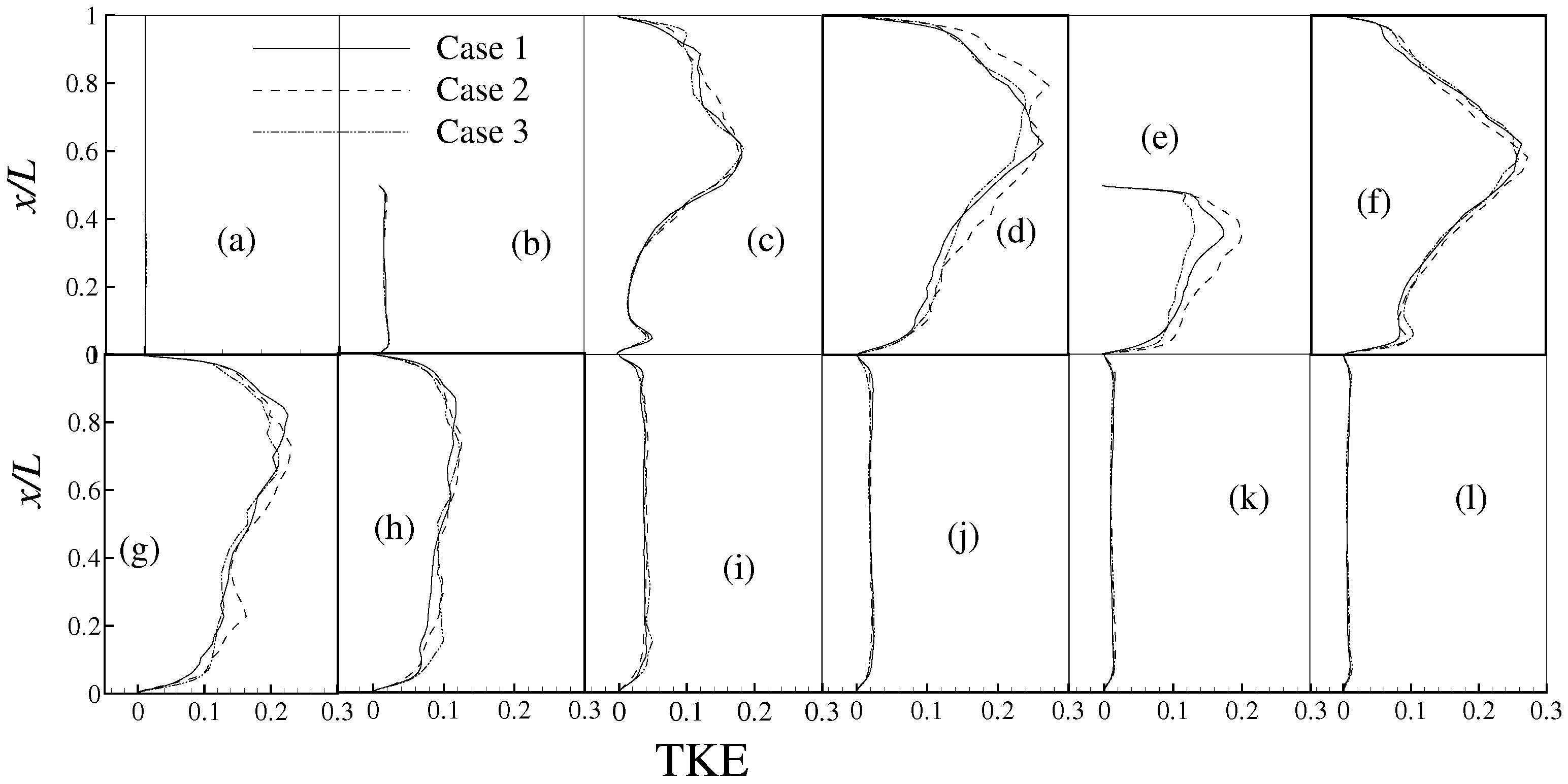
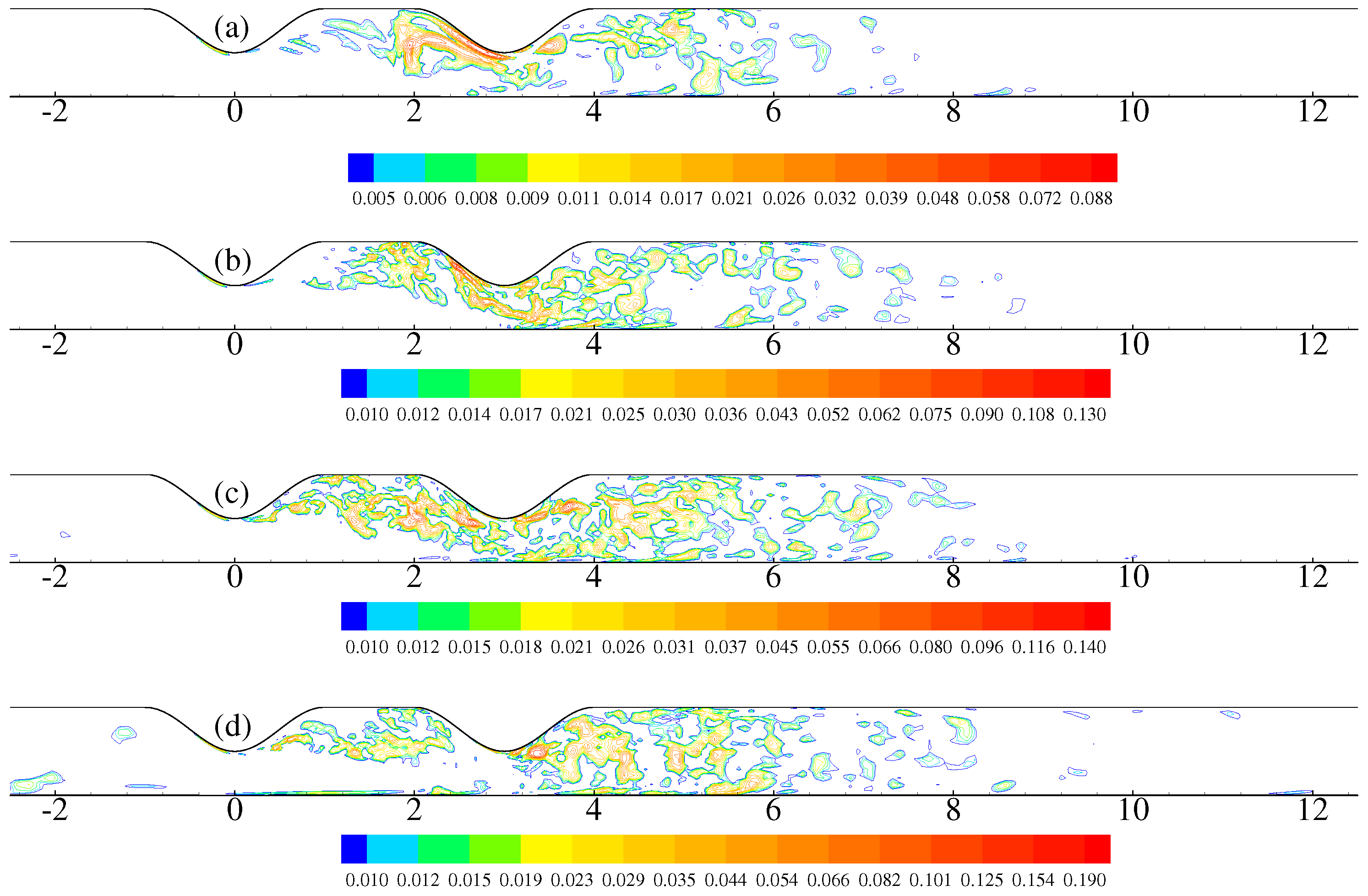
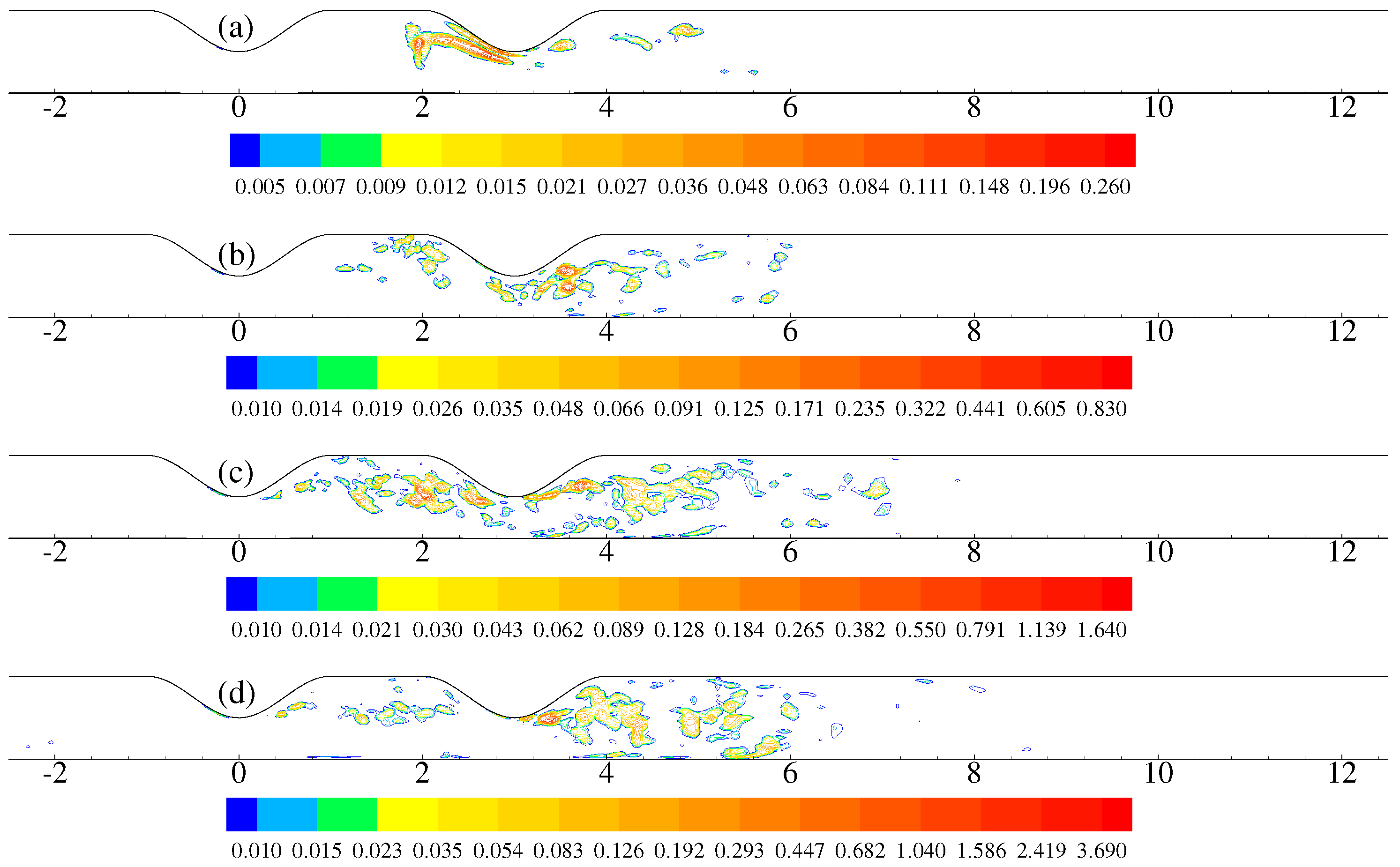
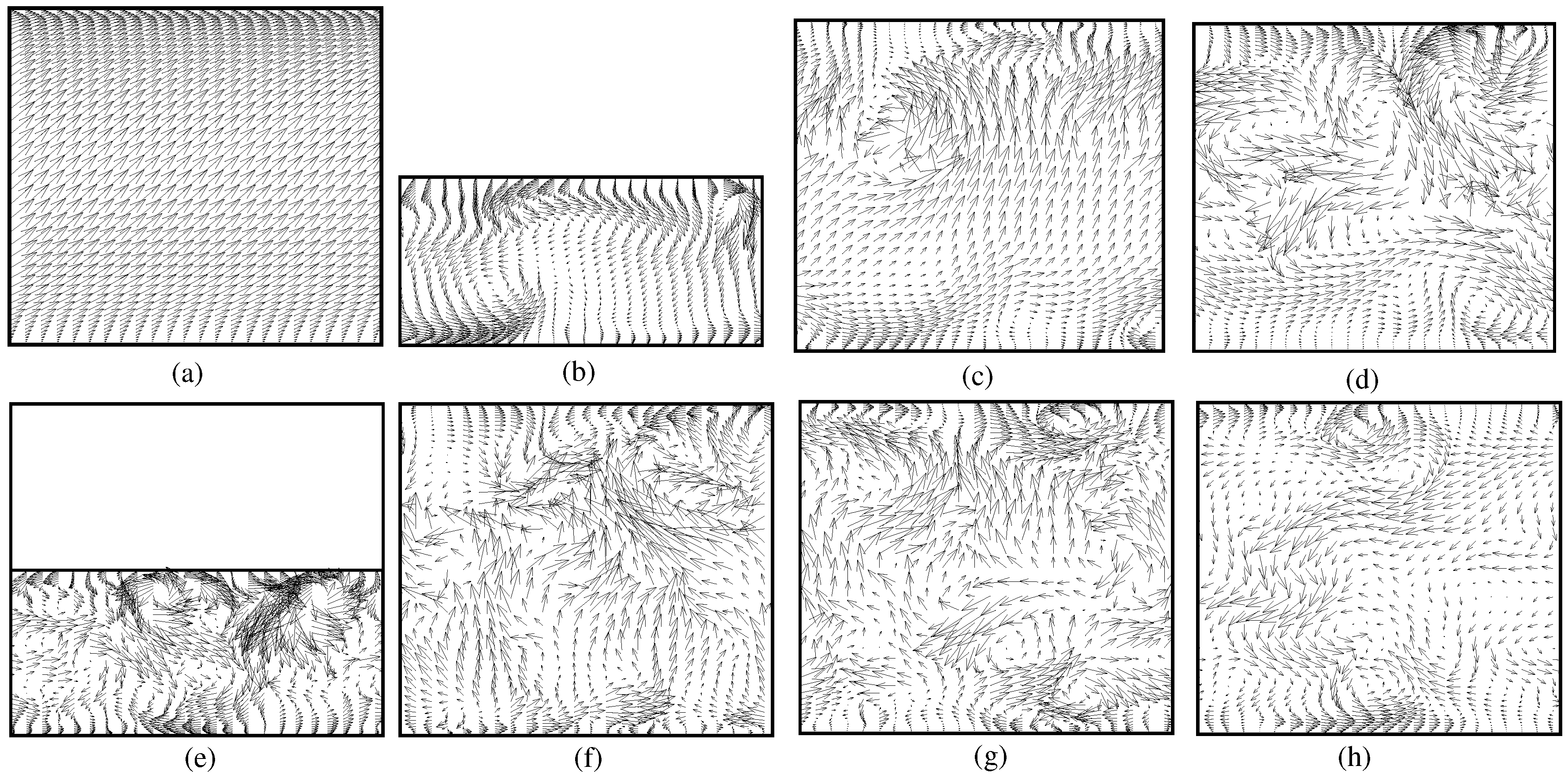
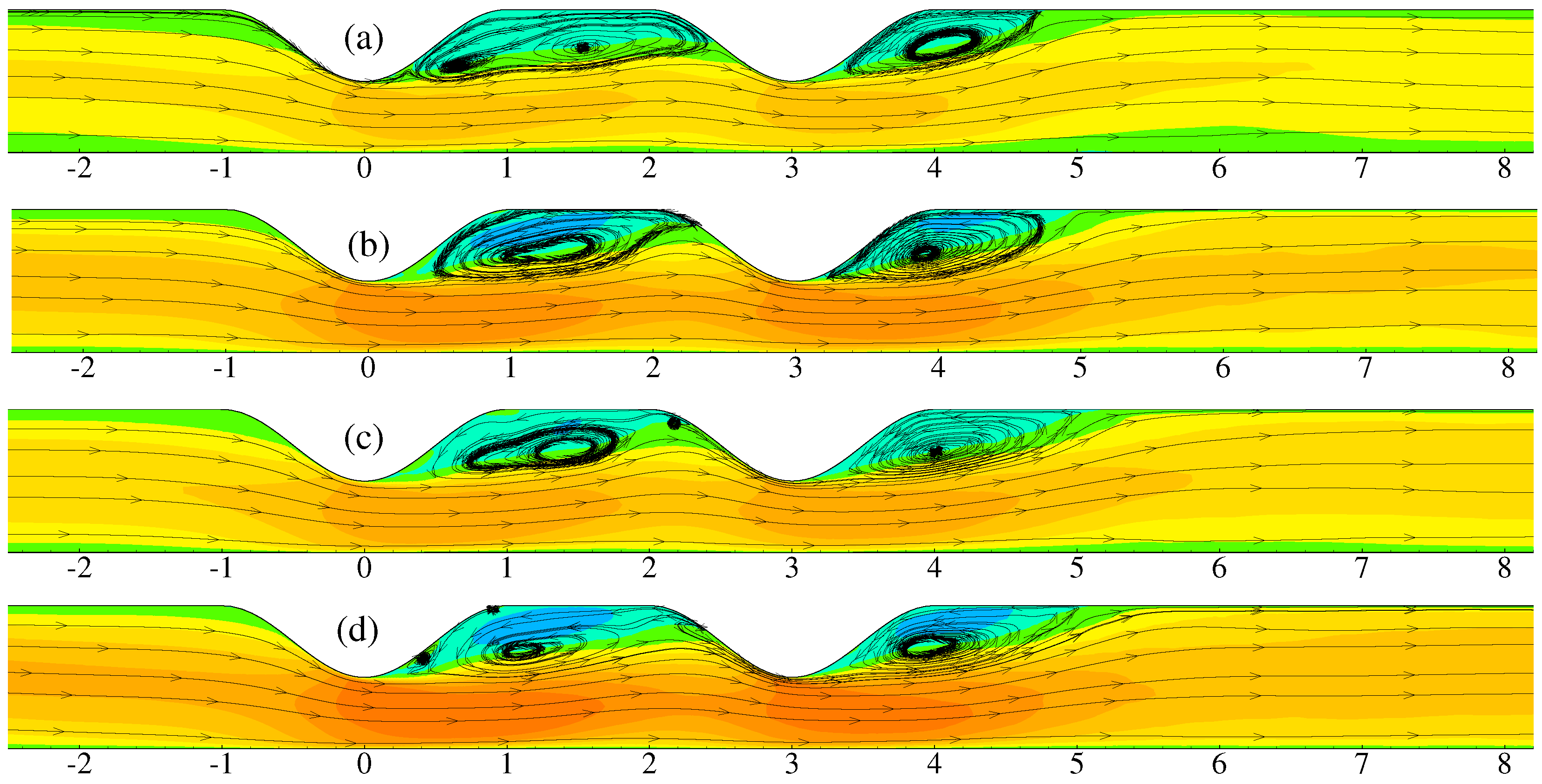
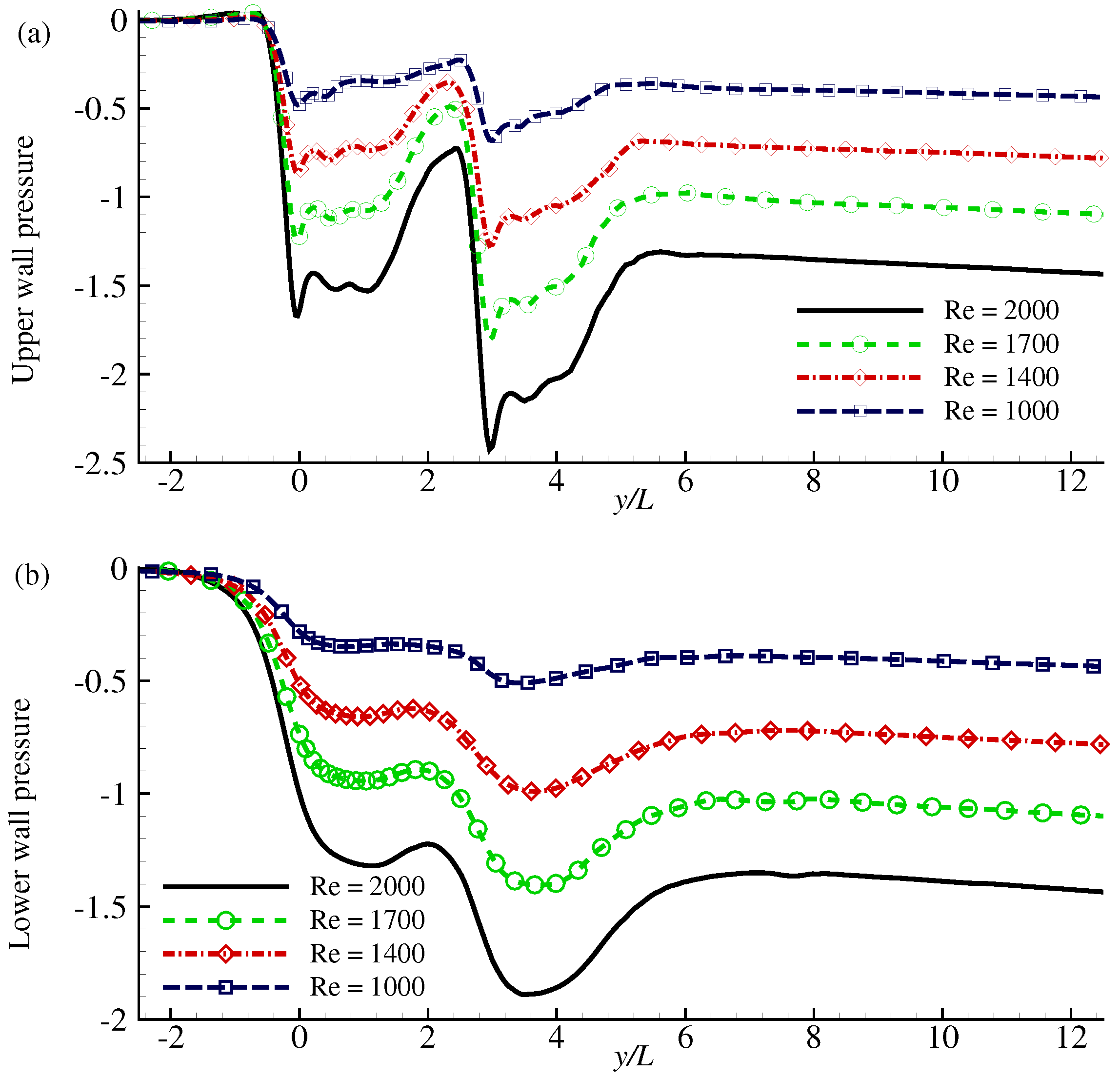
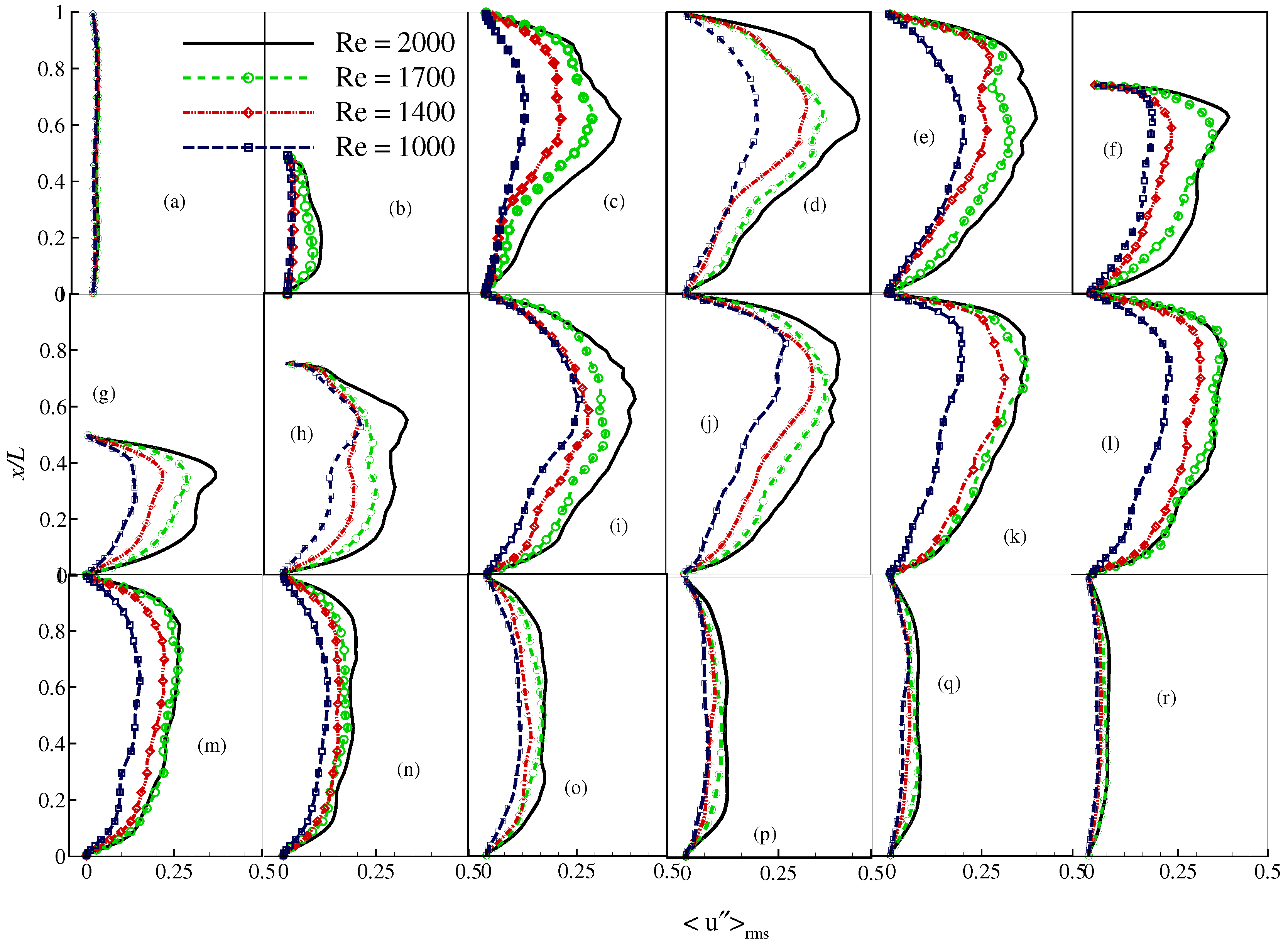
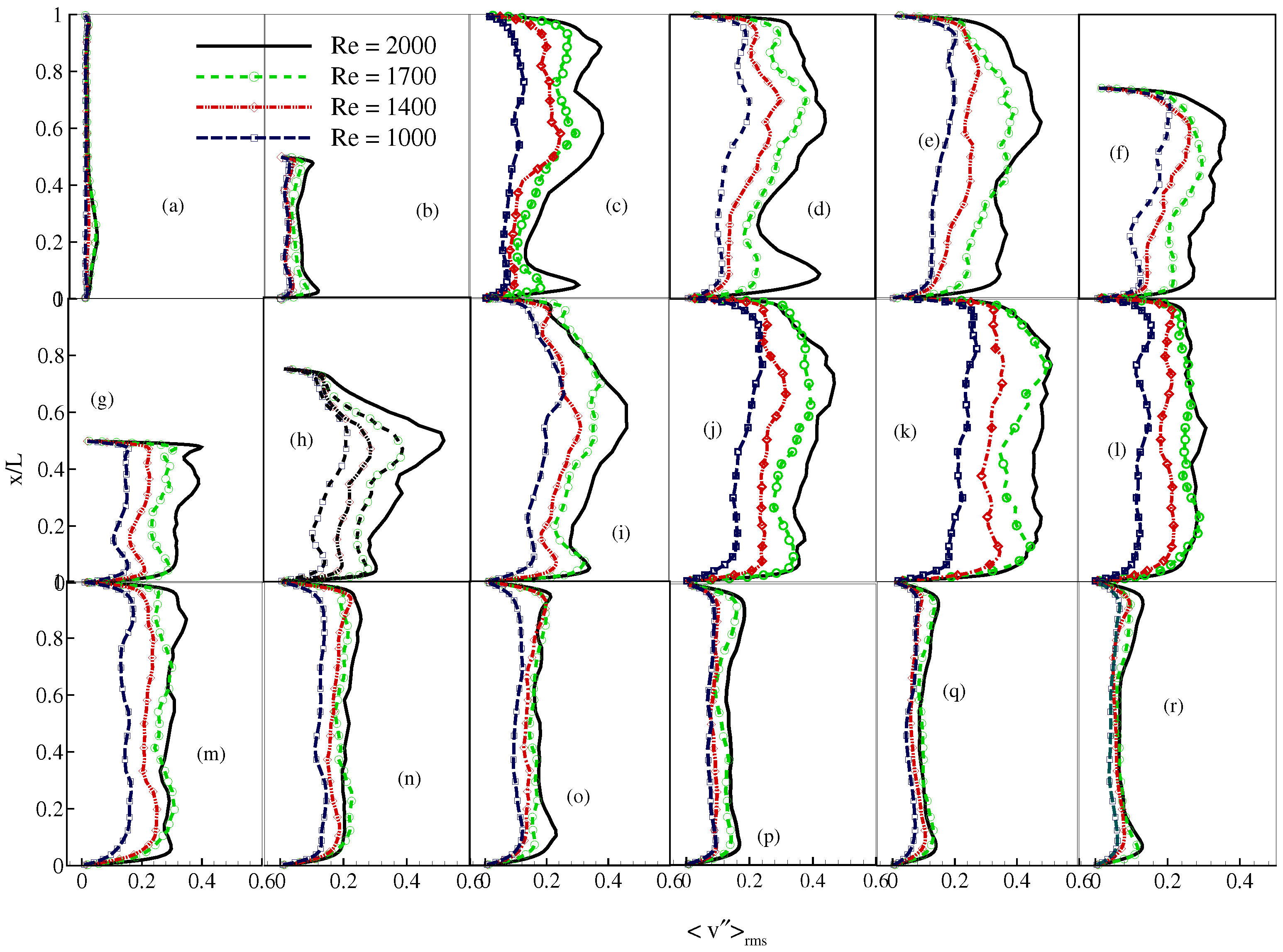
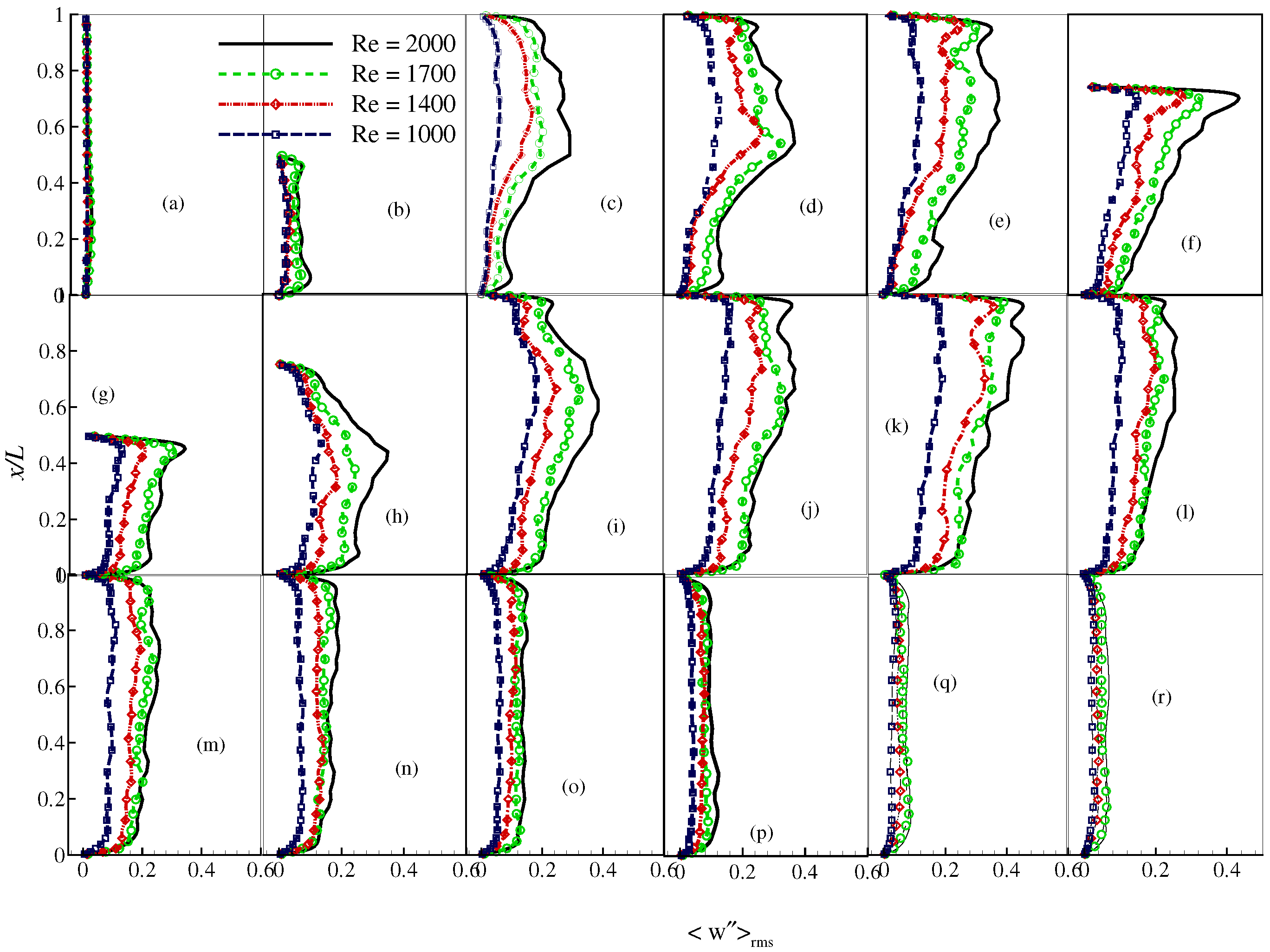
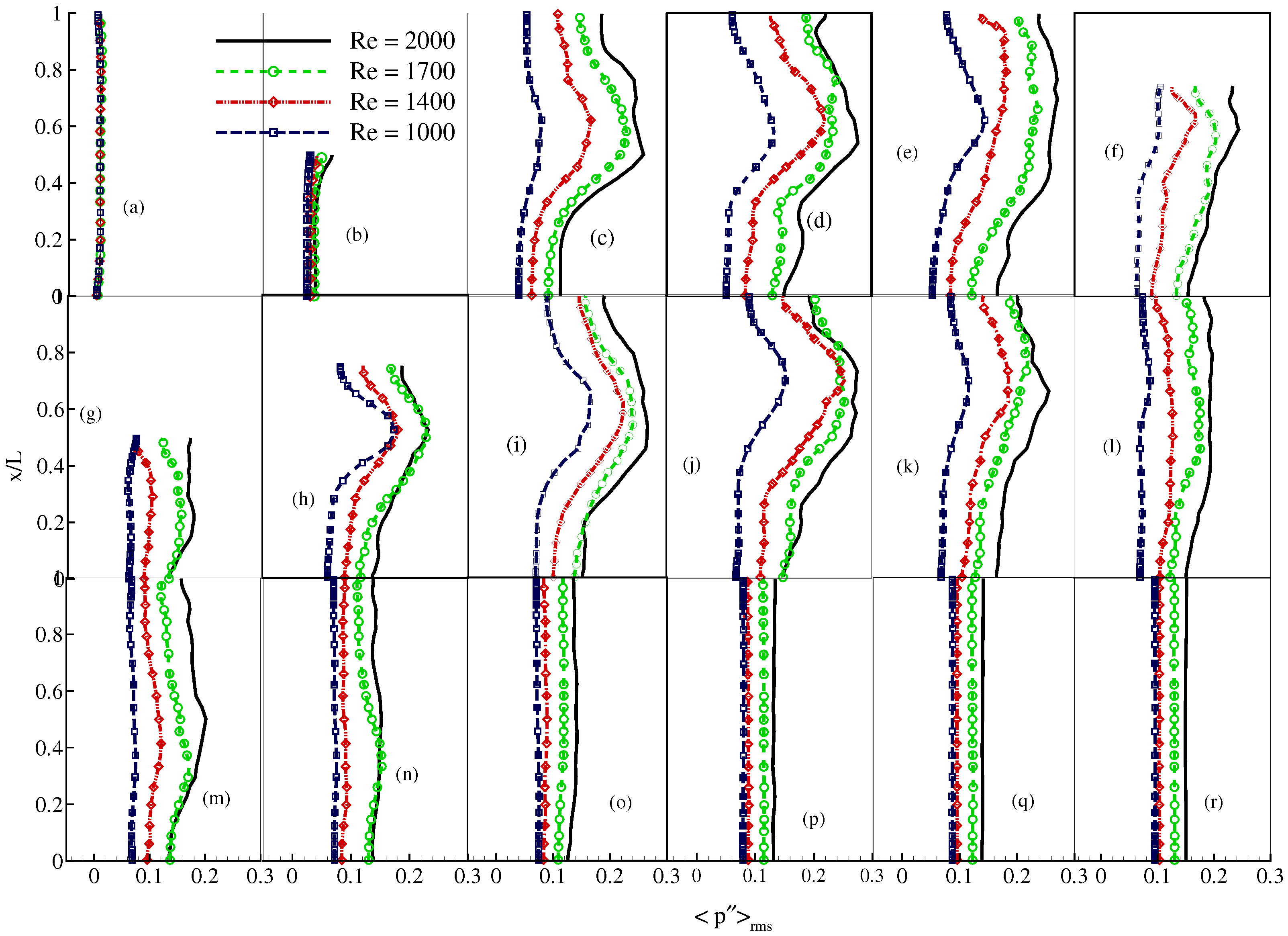
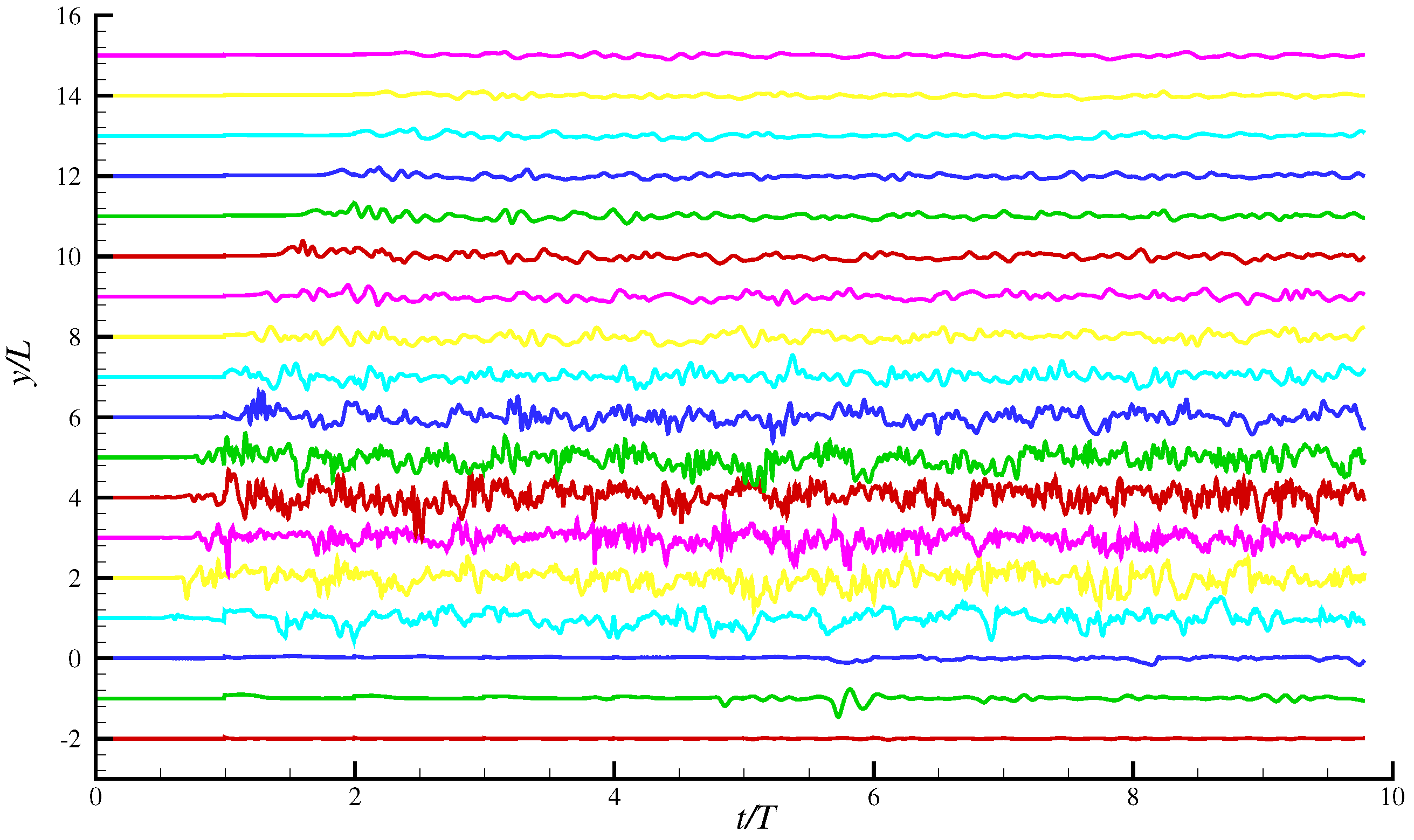
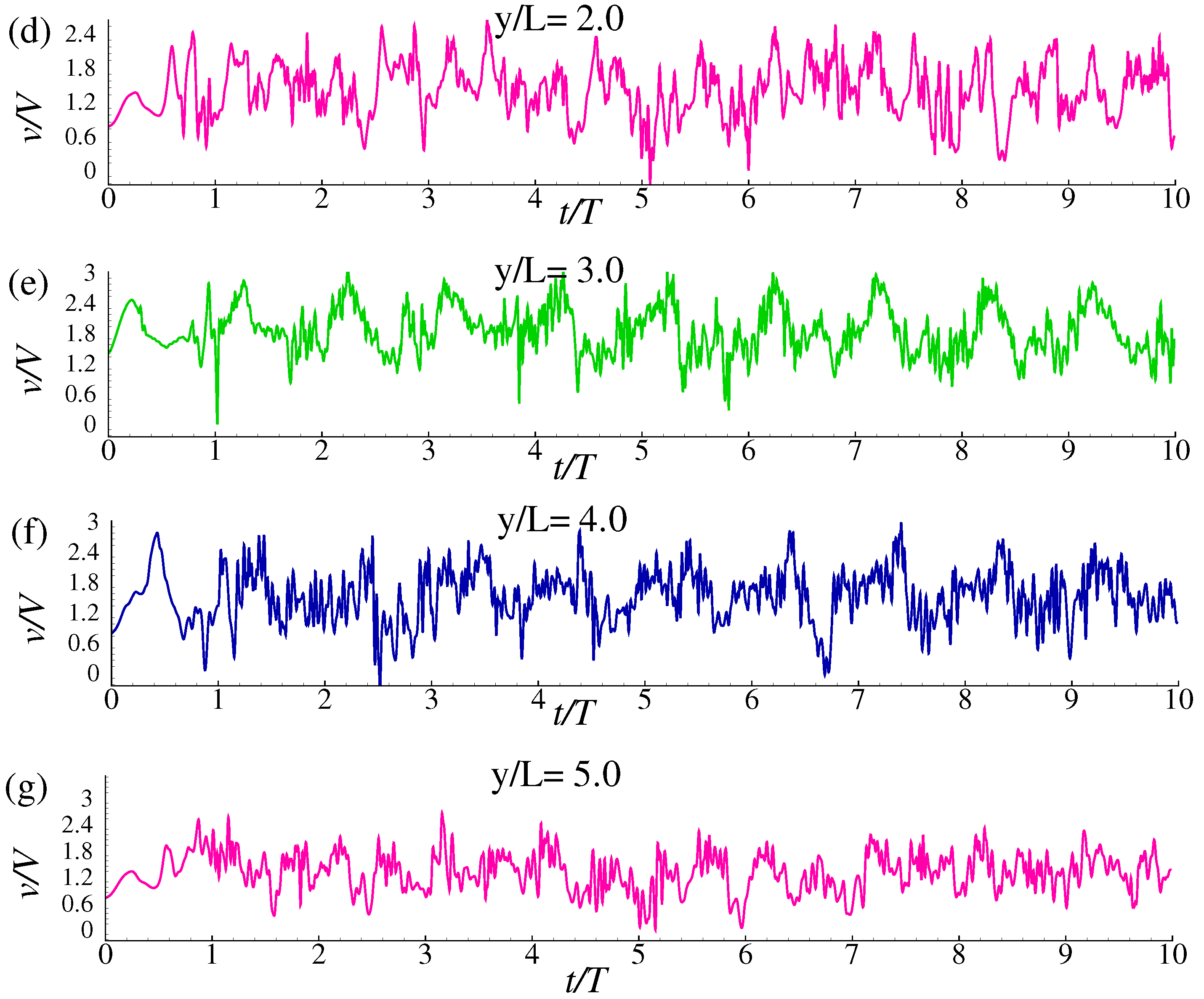
4. Results and Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Ku, D.N. Blood flows in arteries. Annu. Rev. Fluid Mech. 1997, 29, 399–434. [Google Scholar] [CrossRef]
- Khalifa, A.M.A.; Giddens, D.P. Analysis of disorder in pulsatile flows with application to poststenotic blood velocity measurement in dogs. J. Biomech. 1978, 11, 129–141. [Google Scholar] [CrossRef]
- Khalifa, A.M.A.; Giddens, D.P. Characterization and evolution of poststenotic flow disturbances. J. Biomech. 1981, 14, 279–296. [Google Scholar] [CrossRef]
- Clark, C. Turbulent velocity measurements in a model of aortic stenosis. J. Biomech. 1976, 9, 677–687. [Google Scholar] [CrossRef]
- O’Brien, V.; Ehrlich, L.W. Simple pulsatile flow in an artery with a constriction. J. Biomech. 1985, 18, 117–127. [Google Scholar] [CrossRef]
- Tutty, O.R. Pulsatile flow in a constricted channel. J. Biomech. Eng. 1992, 114, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Tu, C.; Delville, M.; Dheur, L.; Vanderschure, L. Finite element simulation of pulsatile flow throgh arterial stenosis. J. Biomech. 1992, 25, 1141–1152. [Google Scholar] [CrossRef]
- Deplano, V.; Siouffi, M. Experimental and numerical study of pulsatile flows through stenosis: Wall shear stress analysis. J. Biomech. 1999, 32, 1081–1090. [Google Scholar] [CrossRef]
- Damodaran, V.; Rankin, G.W.; Zhang, C. Numerical study of steady laminar flow through tube with multiple constriction using curvilinear co-ordinates. Int. J. Numer. Meth. Fluids 1996, 23, 1021–1041. [Google Scholar] [CrossRef]
- Zendehbudi, G.R.; Moayeri, M.S. Comparison of physiogical and simple pulsatile flows through stenosed ateries. J. Biomech. 1999, 32, 959–965. [Google Scholar] [CrossRef]
- Dvinsky, A.S.; Ojha, M. Simulation of three-dimensional pulsatile flow through an asymmetric stenosis. Med. Biol. Eng. Comput. 1994, 32, 138–142. [Google Scholar] [CrossRef] [PubMed]
- Long, Q.; Xu, X.Y.; Ramnarine, K.V.; Hoskins, P. Numerical investigation of physiological realistic pulsatile flow through arterial stenosis. J. Biomech. 2001, 34, 1229–1242. [Google Scholar] [CrossRef]
- Mallinger, F.; Drikakis, D. Laminar-to-turbulent transition in pulsatile flow through a stenosis. Biorheology 2002, 39, 437–441. [Google Scholar] [PubMed]
- Mallinger, F.; Drikakis, D. Instability in three-dimensional, unsteady, stenotic flows. Int. J. Heat Fluid Flow 2002, 23, 657–663. [Google Scholar] [CrossRef]
- Talukder, N.; Karayannacos, P.E.; Nerem, R.M.; Vasco, J.S. An experimental study of fluid mechanics of arterial stenosis. J. Biomech. Eng. 1977, 99, 74–82. [Google Scholar] [CrossRef]
- Lee, T.S.; Liao, W.; Low, H.T. Numerical simulation of turbulent flow through series stenoses. Int. J. Numer. Meth. Fluids 2003, 42, 717–740. [Google Scholar] [CrossRef]
- Lee, T.S.; Liao, W.; Low, H.T. Numerical study of physiological turbulent flows through series arterial stenoses. Int. J. Numer. Meth. Fluids 2004, 46, 315–344. [Google Scholar] [CrossRef]
- Varghese, S.S.; Frankel, S.H. Numerical Modeling of Pulsatile Turbulent Flow in Stenotic Vessels. J. Biomch. Eng. 2003, 125, 445–460. [Google Scholar] [CrossRef]
- Varghese, S.S.; Frankel, S.H.; Fischer, P.F. Direct numerical simulation of stenotic flows. Part 2. Pulsatile flow. J. Fluid Mech. 2007, 582, 281–318. [Google Scholar] [CrossRef]
- Scotti, A.; Piomelli, U. Turbulence models in pulsatile flow. AIAA J. 2002, 40, 537–544. [Google Scholar] [CrossRef]
- Paul, M.C.; Molla, M.M.; Roditi, G. Large-eddy simulation of pulsatile blood flow. Med. Eng. Phys. 2009, 31, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Paul, M.C.; Molla, M.M. Investigation of physiological pulsatile flow in a model arterial stenosis using large-eddy and direct numerical simulations. Appl. Math. Model. 2012, 36, 4393–4413. [Google Scholar] [CrossRef]
- Molla, M.M.; Paul, M.C.; Roditi, G. LES of additive and non-additive pulsatile flows in a model arterial stenosis. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 105–120. [Google Scholar] [CrossRef]
- Molla, M.M.; Wang, B.C.; Kuhn, D.C.S. Numerical study of pulsatile channel flows undergoing transition triggered by a modelled stenosis. Phys. Fluid 2012, 24, 121901. [Google Scholar] [CrossRef]
- Molla, M.M.; Hossain, A.; Wang, B.C.; Kuhn, D.C.S. Large-eddy simulation of pulsatile non-Newtonian flow in a constricted channel. Prog. Comput. Fluid Dyn. 2012, 12, 231–241. [Google Scholar] [CrossRef]
- Molla, M.M.; Paul, M.C. LES of non-Newtonian physiological blood flow in a model of arterial stenosis. Med. Eng. Phys. 2012, 34, 1079–1087. [Google Scholar] [CrossRef] [PubMed]
- Piomelli, U.; Liu, J. Large-eddy simulation of rotating channel flows using a localized dynamic model. Phys. Fluids 1995, 7, 839–848. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiment with the primitive equations. I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Piomelli, U.; Liu, J. Large-eddy simulation of rotating channels flows using a localized dynamic model. Phys. Fluids 1994, 7, 839–847. [Google Scholar] [CrossRef]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteris when the pressure gradient is known. J. Physiol. 1955, 155, 553–563. [Google Scholar] [CrossRef]
- Thomson, J.F.; Thames, F.; Mastin, C. Automatic numerical generation of body-fitted curvilinear coordinates system for field containing any number of arbitrary two dimensional bodies. J. Comput. Phys. 1974, 15, 299–319. [Google Scholar] [CrossRef]
- Morinishi, Y. Conservation Prperties of Finite Difference Schemes For Incompressible Flow; Center for Turbulence Research: Stanford, CA, USA, 1995; pp. 121–132. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Fow; Hemisphere Publishing Corporation: New York, NY, USA, 1980. [Google Scholar]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Vorst, H.A.D. BI-CGSTAB: A first and smoothly converging variant of BI-CG for the solution of the non-symmetric linear systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Kershaw, D.S. The Incomplete Cholesky-Cojugate Gradient method for the iterative solution of systems. J. Comput. Phys. 1978, 26, 43–65. [Google Scholar] [CrossRef]
- Jones, W.P.; di Mare, F.; Marquis, A.J. LES-BOFFIN: User’s Guide; Imperial College: London, UK, 2002. [Google Scholar]
- Sutera, S.P.; Mehrjardi, M.H. Deformation and fragmentation of human red blood cells in turbulent flow. Biophys. J. 1975, 15, 1–10. [Google Scholar] [CrossRef]
- Fry, D.L. Acute vascular endothelial changes associated with increases blood velocity gradients. Circ. Res. 1968, 22, 165–197. [Google Scholar] [CrossRef] [PubMed]
- Ask, P.; Hok, B.; Loyd, D.; Terio, H. Bio-acoustic signals from stenotic tube flow: State of the art and perspectives for future methodological development. Med. Biol. Eng. Comput. 1995, 33, 669–675. [Google Scholar] [CrossRef] [PubMed]




| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
| Case | |||||
|---|---|---|---|---|---|
| 0 | <2000 | 50 | 300 | 50 | |
| 1 | 2000 | 50 | 300 | 50 | |
| 2 | 2000 | 50 | 350 | 50 | |
| 3 | 2000 | 70 | 350 | 50 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molla, M.M.; Paul, M.C. Large Eddy Simulation of Pulsatile Flow through a Channel with Double Constriction. Fluids 2017, 2, 1. https://doi.org/10.3390/fluids2010001
Molla MM, Paul MC. Large Eddy Simulation of Pulsatile Flow through a Channel with Double Constriction. Fluids. 2017; 2(1):1. https://doi.org/10.3390/fluids2010001
Chicago/Turabian StyleMolla, Md. Mamun, and Manosh C. Paul. 2017. "Large Eddy Simulation of Pulsatile Flow through a Channel with Double Constriction" Fluids 2, no. 1: 1. https://doi.org/10.3390/fluids2010001
APA StyleMolla, M. M., & Paul, M. C. (2017). Large Eddy Simulation of Pulsatile Flow through a Channel with Double Constriction. Fluids, 2(1), 1. https://doi.org/10.3390/fluids2010001







