Influence of Boundary Conditions and Heating Modes on the Onset of Columnar Convection in Rotating Spherical Shells
Abstract
1. Introduction
- 1.
- For which values of and radius ratio are no-slip boundaries preferred over stress-free ones, and how does this depend on the choice of heating?
- 2.
- To what extent do mixed boundary conditions interpolate or alter the behaviour observed in the purely no-slip and purely stress-free cases?
- 3.
- How does the location of convective onset shift with radius ratio and , especially within the intermediate-shell range?
- To facilitate this exploration, we employ moderate Ekman numbers that permit extensive parametric coverage while retaining relevance to strongly rotating systems. Note that such systems are frequently referred to as “rapidly rotating” in the geophysical and planetary context but should not be confused with the rapid rotation regime in which stars become oblate spheroids. The results of our work offer a refined understanding of the convective onset problem and provide guidance on model selection for future investigations of nonlinear convection and magnetic field generation in spherical geometries.
2. Models and Methods
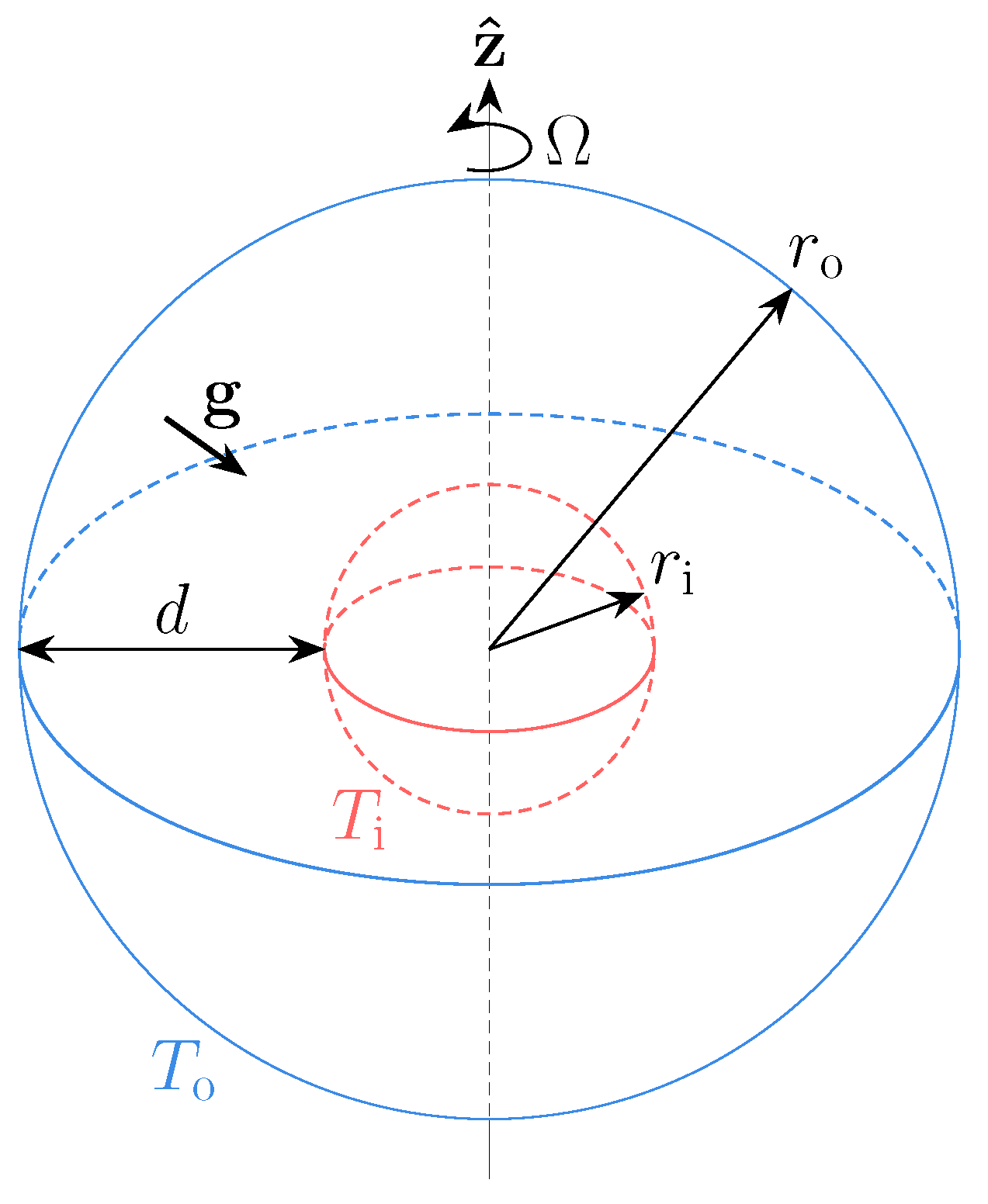
2.1. Baseline Linearised Model of Rotating Spherical Thermally-Driven Convection
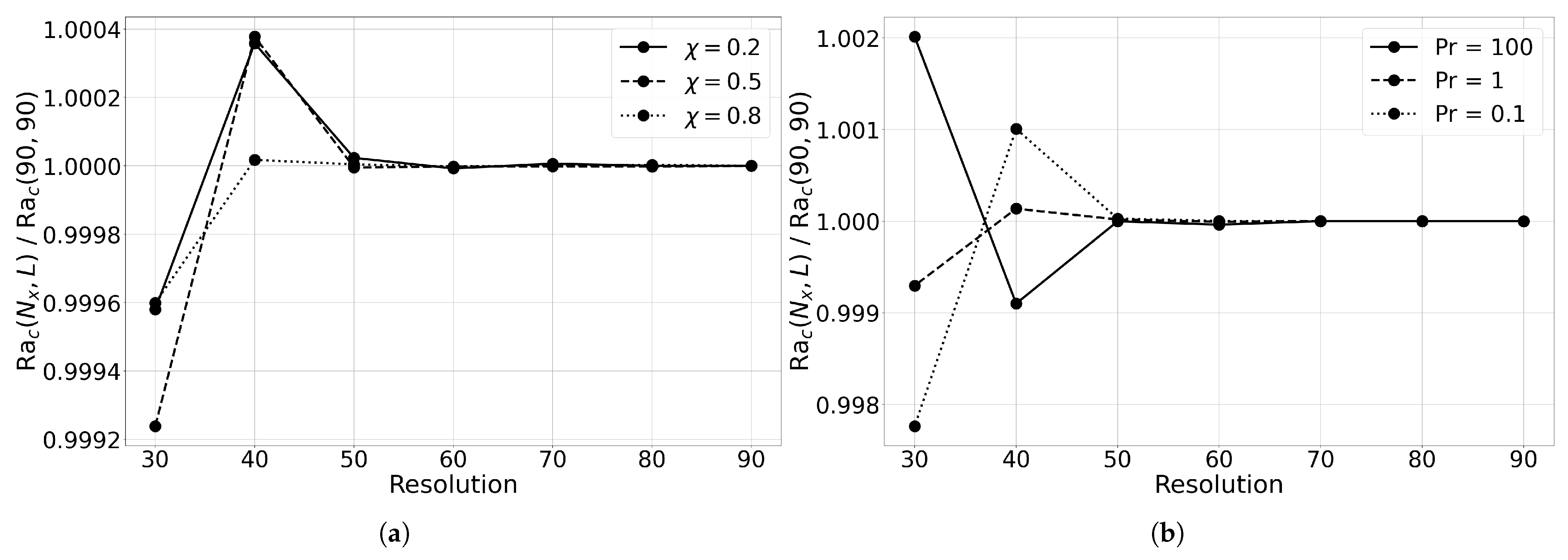
2.2. Numerical Method of Solution
2.3. Alternative Nondimensionalisations
3. Results
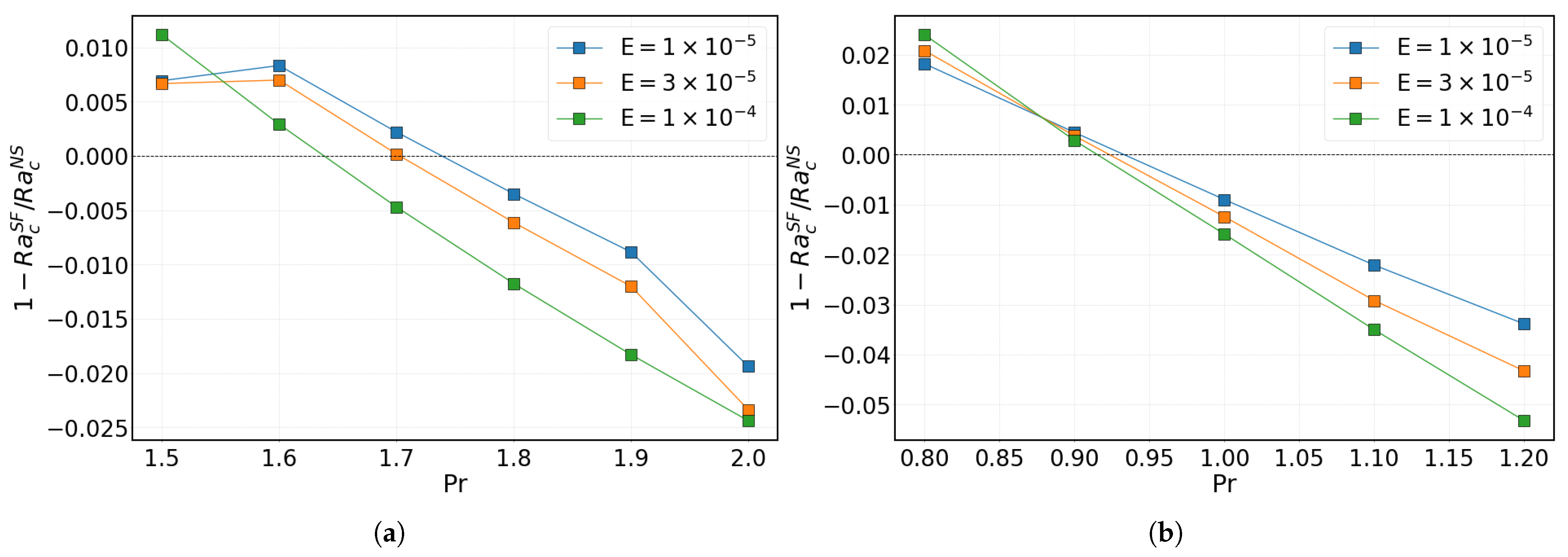
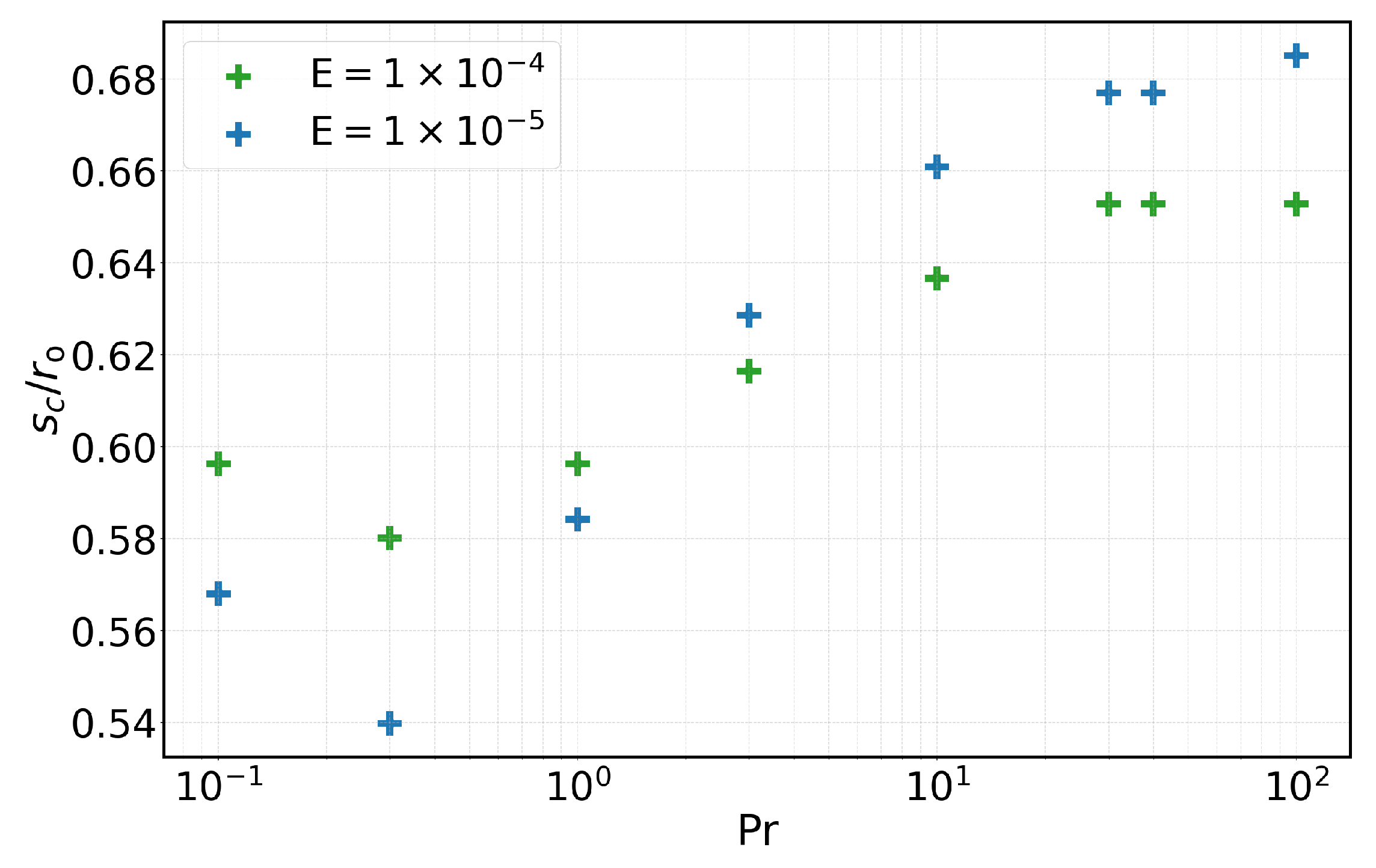
3.1. Dependence on the Prandtl Number
3.1.1. Effect of Mechanical Boundary Conditions
3.1.2. Effect of Heating Type
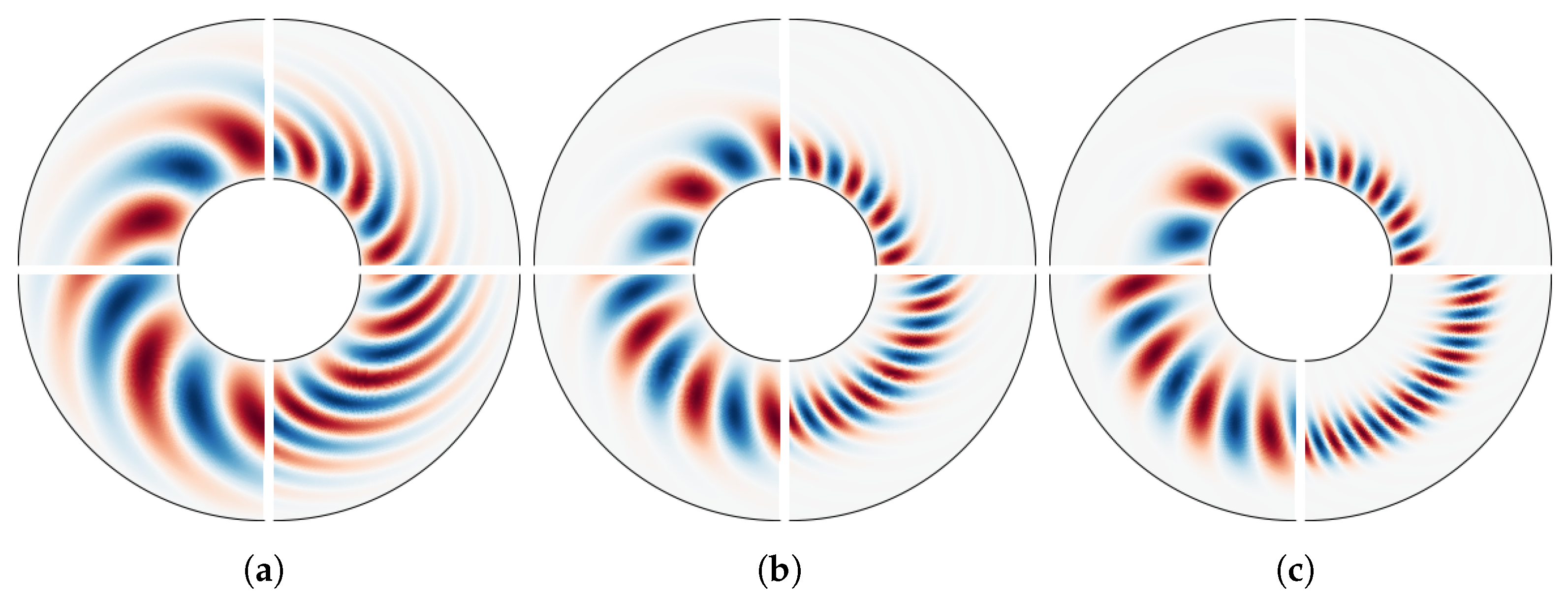
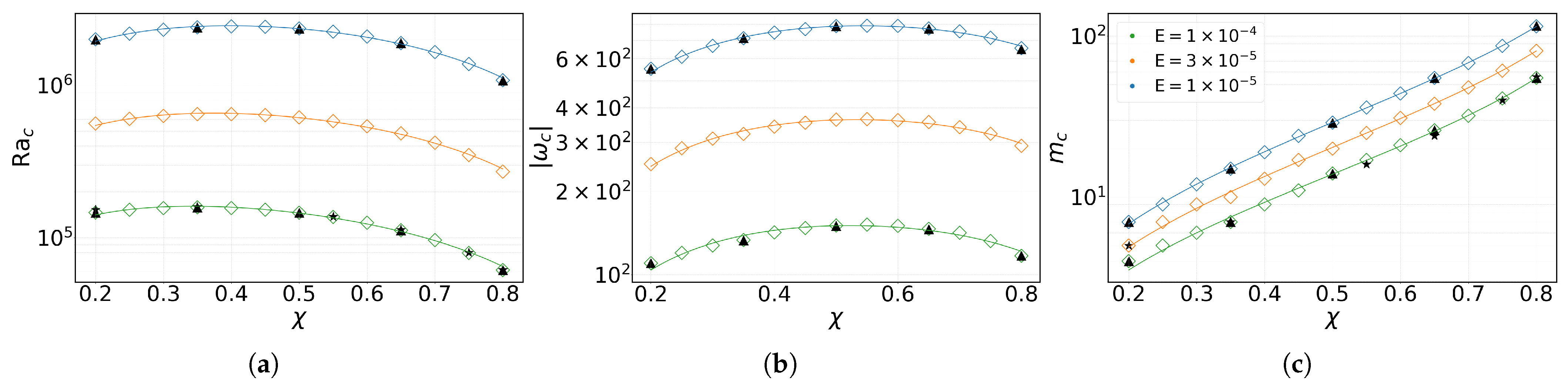
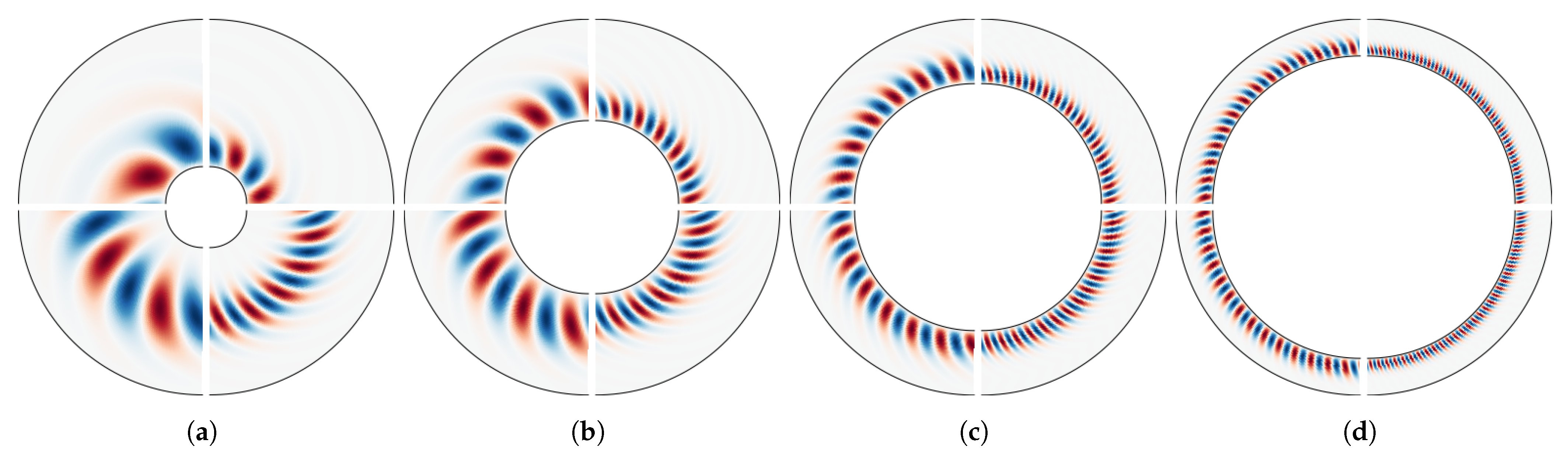
3.2. Dependence on Radius Ratio
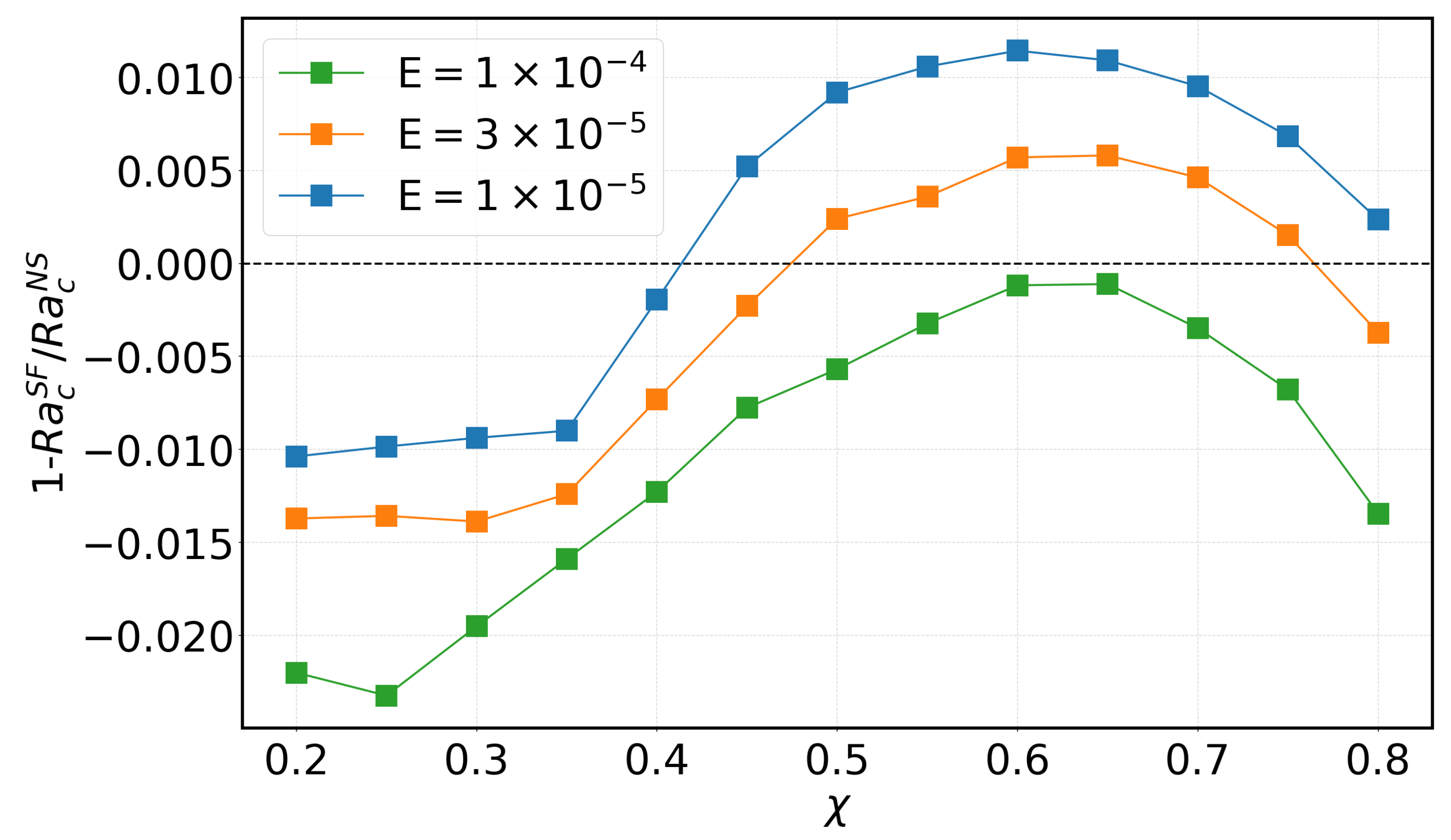
3.2.1. Effect of Mechanical Boundary Conditions
3.2.2. Effect of Heating Type
3.3. Dependence on Nondimensionalisation
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Poloidal–Toroidal Decomposition
Appendix A.2. Expansions in Trial Functions and Discretisation
Appendix A.3. Projection onto the Trial Functions and Matrix Expressions
Appendix B
References
- Busse, F.H.; Simitev, R.D. Planetary Dynamos. In Treatise on Geophysics; Elsevier: Amsterdam, The Netherlands, 2015; pp. 239–254. [Google Scholar] [CrossRef]
- Dormy, E. Rapidly Rotating Magnetohydrodynamics and the Geodynamo. Annu. Rev. Fluid Mech. 2025, 57, 335–362. [Google Scholar] [CrossRef]
- Charbonneau, P. Solar Dynamo Theory. Annu. Rev. Astron. Astrophys. 2014, 52, 251–290. [Google Scholar] [CrossRef]
- Jones, C.A. Planetary Magnetic Fields and Fluid Dynamos. Annu. Rev. Fluid Mech. 2011, 43, 583–614. [Google Scholar] [CrossRef]
- Tikoo, S.M.; Evans, A.J. Dynamos in the Inner Solar System. Annu. Rev. Earth Planet. Sci. 2022, 50, 99–122. [Google Scholar] [CrossRef]
- Tilgner, A.; Busse, F.H. Finite-amplitude convection in rotating spherical fluid shells. J. Fluid Mech. 1997, 332, 359–376. [Google Scholar] [CrossRef]
- Simitev, R.D.; Busse, F.H. Patterns of convection in rotating spherical shells. New J. Phys. 2003, 5, 97. [Google Scholar] [CrossRef]
- Christensen, U.R. Zonal flow driven by strongly supercritical convection in rotating spherical shells. J. Fluid Mech. 2002, 470, 115–133. [Google Scholar] [CrossRef]
- King, E.M.; Aurnou, J.M. Turbulent convection in liquid metal with and without rotation. Proc. Natl. Acad. Sci. USA 2013, 110, 6688–6693. [Google Scholar] [CrossRef]
- Fan, W.; Wang, Q.; Lin, Y. Scaling behaviour of rotating convection in a spherical shell with different Prandtl numbers. J. Fluid Mech. 2024, 998, A20. [Google Scholar] [CrossRef]
- Busse, F.H.; Simitev, R.D. Dynamos driven by convection in rotating spherical shells. Astron. Nachrichten Astron. Notes 2005, 326, 231–240. [Google Scholar] [CrossRef]
- Christensen, U.R.; Aubert, J. Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Int. 2006, 166, 97–114. [Google Scholar] [CrossRef]
- Simitev, R.D. Double-diffusive convection in a rotating cylindrical annulus with conical caps. Phys. Earth Planet. Inter. 2011, 186, 183–190. [Google Scholar] [CrossRef]
- Roberts, P.H. On the thermal instability of a rotating-fluid sphere containing heat sources. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1968, 263, 93–117. [Google Scholar] [CrossRef]
- Busse, F.H. Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 1970, 44, 441–460. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Clarendon: Oxford, UK, 1961. [Google Scholar]
- Soward, A.M. On the Finite amplitude thermal instability of a rapidly rotating fluid sphere. Geophys. Astrophys. Fluid Dyn. 1977, 9, 19–74. [Google Scholar] [CrossRef]
- Jones, C.A.; Soward, A.M.; Mussa, A.I. The onset of thermal convection in a rapidly rotating sphere. J. Fluid Mech. 2000, 405, 157–179. [Google Scholar] [CrossRef]
- Dormy, E.; Soward, A.M.; Jones, C.A.; Jault, D.; Cardin, P. The onset of thermal convection in rotating spherical shells. J. Fluid Mech. 2004, 501, 43–70. [Google Scholar] [CrossRef]
- Zhang, K. On coupling between the Poincaré equation and the heat equation. J. Fluid Mech. 1994, 268, 211–229. [Google Scholar] [CrossRef]
- Ardes, M.; Busse, F.; Wicht, J. Thermal convection in rotating spherical shells. Phys. Earth Planet. Inter. 1997, 99, 55–67. [Google Scholar] [CrossRef]
- Busse, F.H.; Simitev, R.D. Inertial convection in rotating fluid spheres. J. Fluid Mech. 2004, 498, 23–30. [Google Scholar] [CrossRef]
- Zhang, K.; Earnshaw, P.; Liao, X.; Busse, F.H. On inertial waves in a rotating fluid sphere. J. Fluid Mech. 2001, 437, 103–119. [Google Scholar] [CrossRef]
- Zhang, K.; Liao, X. A new asymptotic method for the analysis of convection in a rapidly rotating sphere. J. Fluid Mech. 2004, 518, 319–346. [Google Scholar] [CrossRef]
- Zhang, K.; Liao, X.; Busse, F.H. Asymptotic solutions of convection in rapidly rotating non-slip spheres. J. Fluid Mech. 2007, 578, 371–380. [Google Scholar] [CrossRef]
- Braginsky, S.I.; Roberts, P.H. Equations governing convection in earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 1995, 79, 1–97. [Google Scholar] [CrossRef]
- Soderlund, K.M.; Stanley, S.; Cao, H.; Calkins, M.A.; Browning, M.K. Puzzles in Planetary Dynamos: Implications for Planetary Interiors. Annu. Rev. Earth Planet. Sci. 2025, 53, 305–337. [Google Scholar] [CrossRef]
- Miesch, M.S.; Toomre, J. Turbulence, Magnetism, and Shear in Stellar Interiors. Annu. Rev. Fluid Mech. 2009, 41, 317–345. [Google Scholar] [CrossRef]
- Garcia, F.; Chambers, F.R.N.; Watts, A.L. Onset of low Prandtl number thermal convection in thin spherical shells. Phys. Rev. Fluids 2018, 3. [Google Scholar] [CrossRef]
- Silva, L.; Mather, J.F.; Simitev, R.D. The onset of thermo-compositional convection in rotating spherical shells. Geophys. Astrophys. Fluid Dyn. 2019, 113, 377–404. [Google Scholar] [CrossRef]
- Barik, A.; Triana, S.; Calkins, M.; Stanley, S.; Aurnou, J. Onset of convection in rotating spherical shells: Variations with radius ratio. Earth Space Sci. 2023, 10, e2022EA002606. [Google Scholar] [CrossRef]
- Morison, A.; Labrosse, S.; Deguen, R.; Alboussière, T. Onset of thermal convection in a solid spherical shell with melting at either or both boundaries. Geophys. J. Int. 2024, 238, 1121–1136. [Google Scholar] [CrossRef]
- Busse, F.H.; Simitev, R.D. Parameter dependences of convection-driven dynamos in rotating spherical fluid shells. Geophys. Astrophys. Fluid Dyn. 2006, 100, 341–361. [Google Scholar] [CrossRef][Green Version]
- Al-Shamali, F.; Heimpel, M.; Aurnou, J. Varying the spherical shell geometry in rotating thermal convection. Geophys. Astrophys. Fluid Dyn. 2004, 98, 153–169. [Google Scholar] [CrossRef]
- Silva, L.; Gupta, P.; MacTaggart, D.; Simitev, R.D. Effects of Shell Thickness on Cross-Helicity Generation in Convection-Driven Spherical Dynamos. Fluids 2020, 5, 245. [Google Scholar] [CrossRef]
- Davies, C.; Gubbins, D. A buoyancy profile for the Earth’ s core. Geophys. J. Int. 2011, 187, 549–563. [Google Scholar] [CrossRef]
- Jones, C.A.; Kuzanyan, K.M.; Mitchell, R.H. Linear theory of compressible convection in rapidly rotating spherical shells, using the anelastic approximation. J. Fluid Mech. 2009, 634, 291–319. [Google Scholar] [CrossRef]
- Gibbons, S.; Gubbins, D.; Zhang, K. Convection in rotating spherical fluid shells with inhomogeneous heat flux at the outer boundary. Geophys. Astrophys. Fluid Dyn. 2007, 101, 347–370. [Google Scholar] [CrossRef]
- Teed, R.J.; Dormy, E. Solenoidal force balances in numerical dynamos. J. Fluid Mech. 2023, 964, A26. [Google Scholar] [CrossRef]
- Net, M.; Garcia, F.; Sánchez, J. On the onset of low-Prandtl-number convection in rotating spherical shells: Non-slip boundary conditions. J. Fluid Mech. 2008, 601, 317–337. [Google Scholar] [CrossRef]
- Zhang, K. Convection in a rapidly rotating spherical shell at infinite Prandtl number: Steadily drifting rolls. Phys. Earth Planet. Inter. 1991, 68, 156–169. [Google Scholar] [CrossRef]
- Zhang, K.; Jones, C.A. The influence of Ekman boundary layers on rotating convection. Geophys. Astrophys. Fluid Dyn. 1993, 71, 145–162. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Beckers, J.M. The ekman layer. In International Geophysics; Elsevier: Amsterdam, The Netherlands, 2011; Volume 101, pp. 239–270. [Google Scholar] [CrossRef]
- Busse, F.H.; Cuong, P. Convection in rapidly rotating spherical fluid shells. Geophys. Astrophys. Fluid Dyn. 1977, 8, 17–41. [Google Scholar] [CrossRef]
- Zhang, K.; Greed, G. Convection in rotating annulus: An asymptotic theory and numerical solutions. Phys. Fluids 1998, 10, 2396–2404. [Google Scholar] [CrossRef]
- Seeley, W.; Coke, F.; Simitev, R.D.; Teed, R.J. Influence of Boundary Conditions and Heating Modes on Convective Onset in Rotating Spherical Shells. 2025. Available online: https://researchdata.gla.ac.uk/id/eprint/2015 (accessed on 1 September 2025).
- Blakely, R.J. Spherical Harmonic Analysis. In Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1995; pp. 100–127. [Google Scholar] [CrossRef]
- Busse, F.H.; Riahi, N. Patterns of convection in spherical shells. Part 2. J. Fluid Mech. 1982, 123, 283–301. [Google Scholar] [CrossRef]



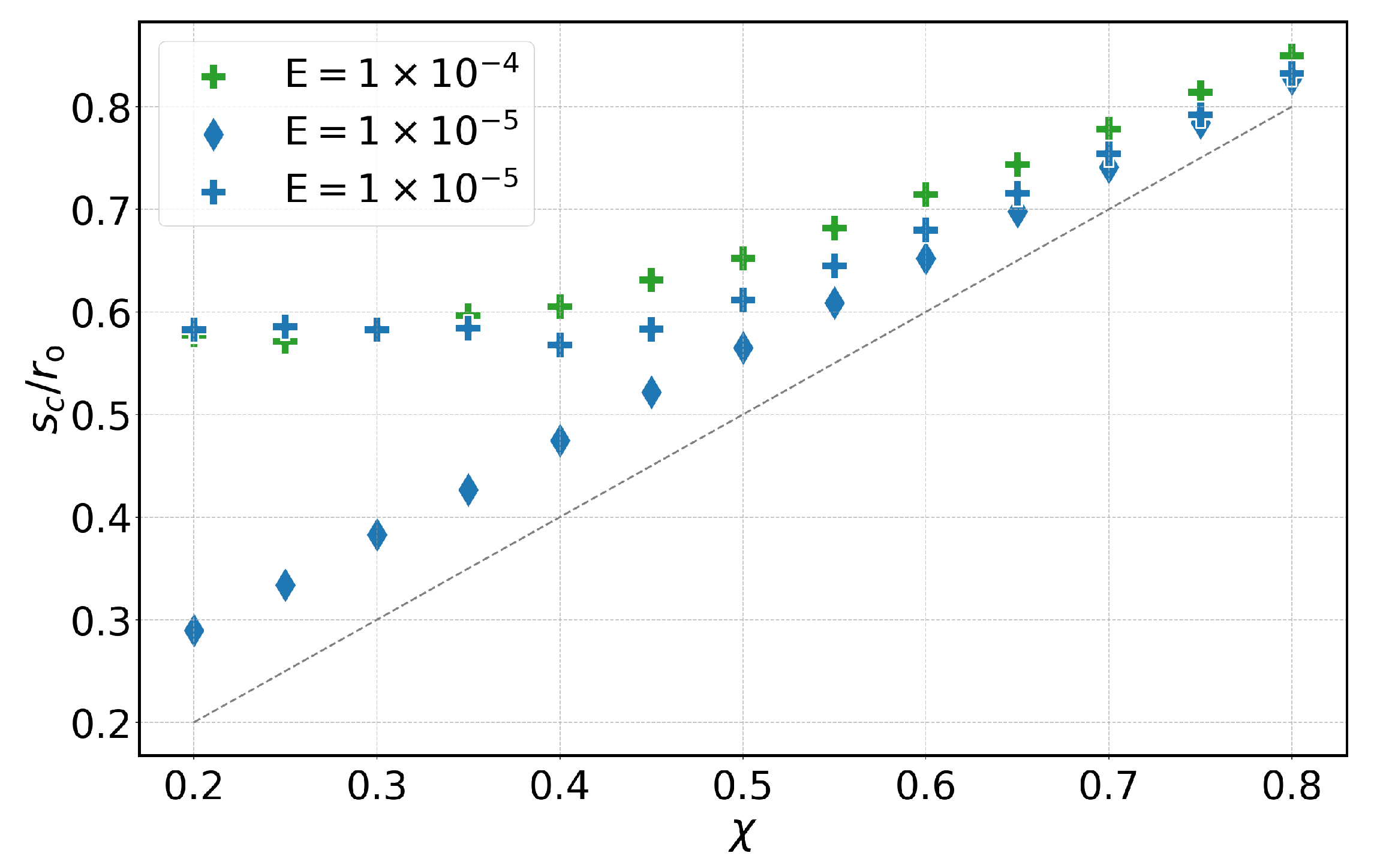
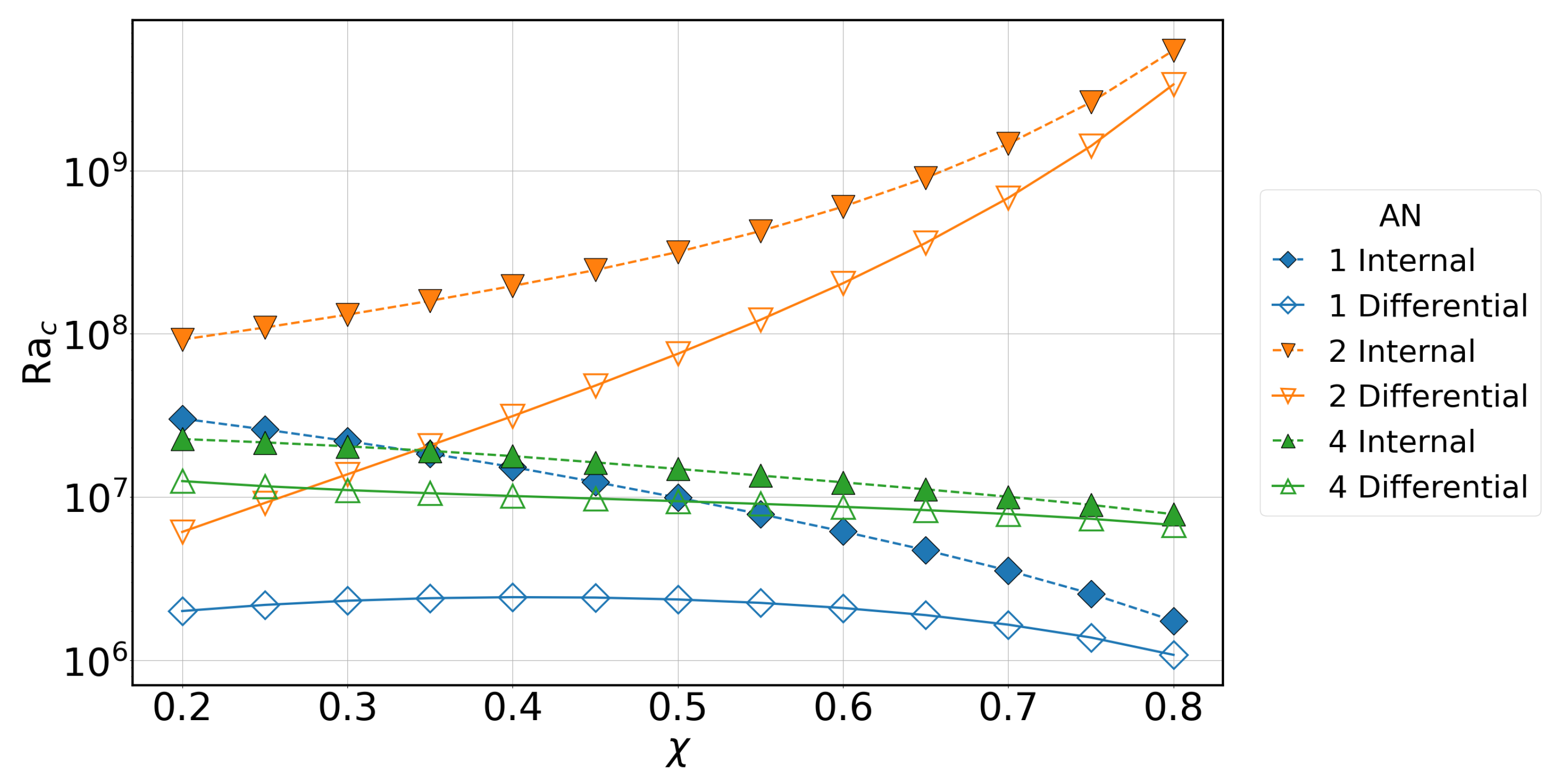
| AN-2 | AN-3 | AN-4 |
|---|---|---|
| E | ||||||
|---|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seeley, W.; Coke, F.; Simitev, R.D.; Teed, R.J. Influence of Boundary Conditions and Heating Modes on the Onset of Columnar Convection in Rotating Spherical Shells. Fluids 2025, 10, 237. https://doi.org/10.3390/fluids10090237
Seeley W, Coke F, Simitev RD, Teed RJ. Influence of Boundary Conditions and Heating Modes on the Onset of Columnar Convection in Rotating Spherical Shells. Fluids. 2025; 10(9):237. https://doi.org/10.3390/fluids10090237
Chicago/Turabian StyleSeeley, William, Francesca Coke, Radostin D. Simitev, and Robert J. Teed. 2025. "Influence of Boundary Conditions and Heating Modes on the Onset of Columnar Convection in Rotating Spherical Shells" Fluids 10, no. 9: 237. https://doi.org/10.3390/fluids10090237
APA StyleSeeley, W., Coke, F., Simitev, R. D., & Teed, R. J. (2025). Influence of Boundary Conditions and Heating Modes on the Onset of Columnar Convection in Rotating Spherical Shells. Fluids, 10(9), 237. https://doi.org/10.3390/fluids10090237







