Performance Analysis of Multi-Capillary Knudsen Heat Pumps

Abstract

The present work investigates the theoretical performance of the Knudsen heat pump (KHP), a novel heat pump concept in which the conventional mechanical compressor is replaced by a Knudsen compressor. This modification has the potential to reduce both maintenance requirements and energy consumption. The flow behavior within the Knudsen compressor, the core element of the KHP, is described using a simplified gas model derived from the formulation originally proposed by Muntz et al. The model predictions are initially validated against well-established data reported in the literature, and subsequently employed to analyze the performance of the KHP, with the final objective of enhancing its operational efficiency. To ensure the practical relevance of the performance assessment, the analysis is conducted using realistic geometrical and operational parameters derived from previously reported experimental studies of Knudsen compressors featuring rectangular or circular cross-sectional geometries. The results of this study suggest that, while the original KHP configuration exhibits limited performance, parametric analysis suggests the possibility to enhance its performance by more than 100% under optimal conditions, with additional factors identified that may enable further gains.

1. Introduction

The heat pump system is considered a vital thermal equipment that is present in a broad range of everyday applications [1]. Structurally, it consists of four fundamental components: a compressor, a condenser, an expansion valve, and an evaporator. Despite its wide-reaching utility, this device still faces crucial limitations worthy of special attention, e.g., the large proportion of energy consumption required to operate [2] and its implementation in remote or isolated domains, where it tends to operate under harsh conditions. These challenges arise mainly due to the configuration and functionality of the compressor. This justifies the need for novel solutions in the compressor working principle that could explore alternative operating concepts.

Among the suggested contemporary electromechanical technologies, the use of a Knudsen compressor (KC) [3] as the driving mechanism in heat pump systems is a promising solution (refer to [4] for a comprehensive review). Contrary to the conventional compressor that resorts to electrical energy to propel the mechanical parts and create a fluid flow rate, the KC generates useful work by harnessing thermal energy to power the system instead [2]. The physical working principle of the KC lies in the exploitation of a phenomenon known as thermal transpiration [5] to promote a rarefied gas flow inside the component.

Historically, the creation of a KC in the micro-regime was originally mentioned by Young [6], which holds a patent for it. However, the first micro-device actually fabricated is often credited to Vargo et al. [7]. Ever since its introduction, the KC has been the subject of numerous studies [8,9,10,11,12,13] and explored in multiple applications [14,15,16]. The Knudsen heat pump (KHP) system, which consists of a heat pump operated by a KC, is among one of the most promising technologies, with numerous successful prototypes reported [17,18,19]. More details on the underlying physical principles of KC, as well as its broad technological and application fields, can be found in the comprehensive review articles [20,21,22]. This work focuses on the KC element (with either a rectangular or a circular cross section) and its operating parameters, with the aim of enhancing the overall performance of the KHP device.

Given the complexity of the physical model that governs the gas flow in the KC, this study adopts the simplified formulation proposed by Muntz et al. [23]. Although simplified, this reduced model is shown to be valid through comparisons with solutions obtained from independent approaches. When applied to the KHP system, it yields valuable conclusions and practical guidelines regarding the optimal operating parameters that enhance the system efficiency.

The manuscript is organized as follows: Section 1 introduces the work. Namely, it describes the problem physics, the KC geometry and operation principle, and the study objectives. Section 2 concerns with the reduced flow model, which is the main theoretical tool used throughout the work. Particularly, its formulation, extension to different KC geometrical configurations, and verification against other models are discussed here. Section 3 covers the KHP, describing its individual elements and the main parameters assessed in the work analysis. Section 4 contains the main results of the work. Here, a detailed examination of the effect of the model parameters on the KHP performance is given. Finally, Section 5 concludes the work by summarizing the main findings and outlining directions for future research.

1.1. Rarefaction Regimes

A gas is denoted as rarefied when its density is low enough for the mean free path to be comparable to the characteristic length of the geometry. At the rarefaction limit, the surface collisions of the gas molecules tend to be much more frequent compared with its inter-molecular collisions [13].

The rarefaction level of a gas can be categorized into four regimes: the continuum/hydrodynamic regime, the slip regime, the transition regime, and the free molecular regime. The typical macro-scale flow is observed in the continuum/hydrodynamic regime, in which the gas is sufficiently dense for inter-molecular collisions to dominate. The thermal transpiration phenomenon, which is “invisible” at the macro-scale, manifests itself in a gas flow that can be located in either the slip, transition, or free molecular regimes [2].

The rarefaction regimes are characterized by the Knudsen number $Kn$. Figure 1 illustrates the $Kn$ range and the most suitable modeling approaches for each regime.

Figure 1. Overview of the range of Knudsen number and various model regimes. Adapted from [20].

The Knudsen number, given by Equation (1), quantifies the ratio between the mean free path $\lambda$, i.e., the average distance a moving particle travels between two consecutive collisions, and the characteristic length of the gas flow a, and it is expressed as follows [24]:

$$Kn={\displaystyle \frac{\lambda }{a}}$$

(1)

The rarefied gas flow in the Knudsen compressor is a type of problem that is usually modeled, assuming it falls into the slip regime ($0.01<Kn<0.1$). According to Figure 1, the Boltzmann equation is theoretically capable of encompassing all of the four regimes. However, solving it is a very complex task and, thus, hard to apply in typical engineering problems. To overcome this difficulty, a reduced flow model [23] is considered, which is able to predict the gas flow rate over the full spectrum of rarefaction regimes. This model is described in full details in Section 2.

1.2. Knudsen Compressor

Figure 2 illustrates two idealized configurations of a Knudsen compressor: the mono-capillary (Figure 2a) and the multi-capillary (Figure 2b).

Figure 2. Traditional Knudsen compressor configurations. Adapted from [21].

To optimize its performance, the Knudsen compressor is typically organized in several stages. Each stage comprises a capillary section (smaller cross section(s)) and a connector section (larger cross-section), both interconnected by a junction [13]. The flow is the result of a “competition” between the thermal transpiration contribution, promoted by a temperature gradient, and the classic Poiseuille flow contribution, promoted by a pressure gradient.

Positive temperature gradients and subsequent negative temperature gradients are applied in the capillary and connector sections, respectively, restricted between a low temperature value $T_L$ and a high temperature value $T_H$, thus resulting in a sawtooth-like distribution. The thermal transpiration flow contribution is therefore predominant in the capillary sections while the Poiseuille flow contribution is predominant in the connector sections of the compressor.

It should be taken into account that the Poiseuille flow is inevitable in the problem: introducing a positive temperature gradient in the system, in order to promote a thermal transpiration flow, consequently creates a pressure gradient that is also positive, according to the perfect gas law. This results in the undesirable Poiseuille contribution opposes the thermal transpiration contribution and negatively affects the overall flow.

The present work will focus only on the multi-capillary version of the Knudsen compressor, where each capillary section comprises several segments arranged in parallel.

1.3. Advantages and Disadvantages

As previously mentioned a heat pump whose compressor operates under the thermal transpiration phenomenon can bring unique advantages. For instance, when compared with the conventional mechanical compressor, the Knudsen compressor lacks moving components. This feature not only attenuates noise and vibrations but also eliminates the need to apply lubricants in the component, leading to an extension of its durability [18] and mitigation of maintenance requirements. Other relevant advantages consist of the following:

• The potential applicability of these compressors at low pressure requirements [2];
• The compact design owing to its micro/nano-scale configuration [2];
• The reliance on either waste heat deployed by other systems [18] or more environmentally friendly energy sources like solar energy [2] due to the nature of the energy input.

However, despite these advantages, the Knudsen heat pump has previously been proven to exhibit very low practical efficiency, as demonstrated by the results reported by Kugimoto et al. [19].

1.4. Objectives

The present work is set about studying the performance behavior of the Knudsen heat pump. For that, a numerical model [24,25,26,27,28,29,30] is first introduced, which aims to determine the value of relevant parameters in the rarefied gas flow typically found in Knudsen compressor elements, i.e., mass flow rate and pressure distribution. The results given by this model will further be used to predict the performance of a Knudsen heat pump that is composed of a multi-capillary Knudsen compressor. This study aims at finding optimal conditions that help improve the efficiency of this system. The results obtained here may serve as guidelines for possible innovative solutions in the design of the KHP technology.

2. Reduced Flow Rate Model

To study the functionality of the Knudsen compressor and, hence, the Knudsen heat pump, it is necessary to have theoretical models beforehand at our disposal that are simultaneously simple and reliable.

The simplified transport model referenced in the present work permits solving a rarefied gas flow in geometries subjected to temperature and pressure gradients. This model, henceforth labeled as the the Reduced Flow Rate model, or RFR model for short, has been originally proposed by Sharipov and co-workers [24,25,26,27,28,30] and later studied by Graur and co-workers [29]. This model, which is an extended version of the original RFR model proposed by [24,25,26,27,28,29,30], is applied for the Knudsen compressor geometry, taking as inspiration the already-existing version of the model proposed in the work of Aoki et al. [12,31].

The Reduced Flow Rate model is applicable to capillaries containing either a rectangular or a circular cross section, as well as capillaries with a constant or variable cross section along the longitudinal direction of the geometry. It uses an inversely related variant of the Knudsen number called the rarefaction parameter, $\delta$, see Equation (2), which is defined by [24]

$$\delta ={\displaystyle \frac{Pa}{\mu }}\sqrt{{\displaystyle \frac{m}{2k_{B}T}}}$$

(2)

Finally, it is worth underlining that, although it has benefits, the RFR model falls under idealized assumptions that simplify the calculations of the problem and may have a non-negligible impact (the work of Sharipov and Seleznev [24]; refer to these limitations in more detail). Future numerical and experimental research work should consider these assumptions when comparing and/or validating results.

2.1. Long Capillary Geometry

The long capillary geometry is composed of two reservoirs connected by a capillary of length L. This capillary has a wall temperature distribution $T_w\left(x\right)$ and features a characteristic dimension that can vary along the longitudinal direction $a\left(x\right)$, which is equal to (i) the radius for the circular cross section or (ii) the height for the rectangular cross section. The geometry is assumed to contain water vapor and is subjected to prescribed variations of pressure and temperature [24,29,30].

Figure 3 illustrates the considered problem, including the adopted coordinate system and the two types of cross sections studied. The nomenclature to be defined for the variables of the capillary extremities connecting the reservoirs shall henceforth follow the representation defined in it; that is, the pressure, temperature, characteristic dimension, and rarefaction parameter assigned to the left and right extremities are labeled as $P_I$, $T_I$, $a_I$, ${\delta }_I$, and $P_{II}$, $T_{II}$, $a_{II}$, ${\delta }_{II}$, respectively [24].

Figure 3. Long capillary geometry. Adapted from [24].

The RFR model focuses on solving Equation (3), which quantifies the balance between the thermal transpiration flow and the Poiseuille flow in the system [29]. In this equation, G corresponds to the reduced flow rate, $G_P\left(\delta \right)$ and $G_T\left(\delta \right)$ are the dimensionless coefficients of proportionality related to the Poiseuille flow and the thermal transpiration flow, in the given order, and $\varphi$ is a term equal to 2 or 3, depending on whether it is used for a rectangular cross-section capillary or a circular cross-section capillary, respectively.

$$G={\displaystyle \frac{L}{P_I}}{\left({\displaystyle \frac{a\left(x\right)}{a_I}}\right)}^{\varphi }\sqrt{{\displaystyle \frac{T_I}{T\left(x\right)}}}\left(-G_P{\displaystyle \frac{dP}{dx}}+G_T{\displaystyle \frac{P\left(x\right)}{T\left(x\right)}}{\displaystyle \frac{dT}{dx}}\right)$$

(3)

Figure 4a,b illustrate the reduced flow rate of Poiseuille and thermal transpiration flows, respectively, as a function of the rarefaction parameter $\delta$. It is observed that $G_P\left(\delta \right)$ is minimum at approximately $\delta =1$, while $G_T\left(\delta \right)$ monotonically decreases with the increase in $\delta$. This behavior determines the relevance of the thermal transpiration flow at moderate to low $\delta$.

Figure 4. Graphical representation of the dimensionless coefficients, $G_p$ and $G_T$, originally proposed by [24]. Panel (a): solid line—BGK model; crosses and circles—Boltzmann equation; given by [24]. Panel (b): solid line—BGK model; dashed line—BGK with recalculated $\delta$; squares—S-model; circles—Boltzmann equation; given by [24].

Owing to its non-linearity, Equation (3) shall be numerically solved. For that, we resort to the finite difference method following the works of Graur [29] and Sharipov [30]. The secant method is applied for the iterative process. The overall numerical scheme has been implemented in MATLAB, Version R2018b, [32], with its algorithmic flowchart presented in Appendix A.

Geometrical and operational conditions are applied in this model and quantified through ratios. The geometrical conditions consider the cross-section ratio $a{b}_{ratio}={\displaystyle \frac{a_{II}}{b}}$ (specifically for the rectangular cross-section studies), while the operating conditions account for the pressure ratio $P_{ratio}={\displaystyle \frac{P_{II}}{P_I}}$ and the temperature ratio $T_{ratio}={\displaystyle \frac{T_{II}}{T_I}}$.

The mass flow rate $\dot{M}$, in kg/s, given by Equation (4), is related to the reduced flow rate G according to

$$\dot{M}={\displaystyle \frac{G}{\frac{L}{A\times a_I\times P_I}\times \sqrt{\frac{2\times k\times T_I}{m}}}}$$

(4)

2.2. Knudsen Compressor Geometry

The RFR model will be applied to a multi-capillary Knudsen compressor consisting of several stages $N_{stages}$, as illustrated in Figure 5. Each stage is composed of a capillary section (A) of length $L^A=\gamma L_s$ and $N_{cap}$ capillaries of height $D^A$ and a connector section (B) of length $L^B=(1-\gamma )L_s$ and height $D^B$, where $L_s$ corresponds to the length of a single stage and $\gamma$ is the fraction of a single stage capillary section. The wall temperature along x forms a triangular distribution restricted between $T_L$ and $T_H$ [12,31], as shown in Figure 5. The total length of the compressor corresponds to L.

Figure 5. Multi-capillary Knudsen compressor. Adapted from [7].

$N_{cap}$ is defined so that the sum of all the capillary heights and of all the walls thicknesses separating each capillary ($a_c$) is equal to the connector section height. Each section of the compressor is solved separately using Equation (3) and considering the linear triangular temperature distribution. Assuming a coordinate system with its origin at a junction of a single arbitrary stage, as illustrated in Figure 6, the set of Equations (5) ensures the pressure and flow rate continuity across the junction.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & P^A{{|}_{x=0_{-}}=P^B|}_{x=0_{+}}\hfill \\ \hfill & G^A{|}_{x=0_{-}}={\displaystyle \frac{G^B{|}_{x=0_{+}}}{N_{cap}}}\hfill \end{array}\end{array}$$

(5)

Figure 6. Junction conditions. Adapted from [7].

An isometric view and two cross-section views of the rectangular and circular geometries, one along the xy plane and another along the yz plane (2D view), are illustrated in Figure 7 and Figure 8, respectively.

Figure 7. Illustration of the Knudsen multi-capillary compressor for the rectangular cross-section geometry.

Figure 8. Illustration of the Knudsen multi-capillary compressor for the circular cross-section geometry.

2.3. RFR Model Verification

The RFR model is first verified by comparing the results of the model shown in the previous sections against well-established literature results, namely, those reported by Aoki et al. [12,31]. Additionally, our verification study also includes comparisons with solutions of a Computational Fluid Dynamics (CFD) solver, namely, the COMSOL, Version 5.1, Multiphysics [33,34] slip–flow Navier–Stokes interface (hereafter, SF–NSE). The correspondence with these two sources is used as the primary measure for assessing the accuracy of our model.

For the verification study, we considered the data listed in Table 1 whose values follow [12,31]. The present analysis considers a mono-capillary Knudsen compressor geometry, as depicted in Figure 2a, where $a_{ratio}$ denotes the ratio between the characteristic dimensions of the capillary and connector sections.

Table 1. Data considered in the model verification study.

Parameters	Units	Cross Section
		Rectangular	Circular
$\varphi$	-	2	3
$N_{stages}$	-	10	10
$L^A$	m	0.5 × ${10}^{-3}$	0.5 × ${10}^{-3}$
$\gamma$	-	1/2	1/2
$a_{ratio}$	-	2	2
$a{b}_{ratio}$	-	0 (2D)	-
$T_{ratio}$	-	1.5	1.5
$P_{ratio}$	-	2	2
$a_I$	m	0.70 × ${10}^{-6}$	0.35 × ${10}^{-6}$
$T_I$	K	350	350
$N_{cap}$	-	1	1
$a_c$	-	3 × ${10}^{-6}$	3 × ${10}^{-6}$
${\delta }_I$	-	${\displaystyle \frac{\sqrt{\pi }}{2}}$	${\displaystyle \frac{\sqrt{\pi }}{2}}$

Results for the reduced flow rate G are summarized in Table 2, and the corresponding pressure distribution—expressed as the dimensionless pressure $\tilde{P}$ along the capillary—is shown in Figure 9 and Figure 10. Differences and similarities among them will be discussed below. Note that, to make the comparisons viable, the values reported in [12,31] had to be converted in terms of the reduced flow–rate metric G, given by Equation (6), which reads as follows:

$$G={\displaystyle \frac{2{\rho }^{\ast }{T}^{\ast }}{P^{\ast }}}\sqrt{{\displaystyle \frac{k_B{R}_s}{m}}}\tilde{M},$$

(6)

where ${\rho }^{\ast }$, $T^{\ast }$, and $P^{\ast }$ denote the reference mass density, temperature, and pressure of water vapor, respectively; $R_s$ is the specific gas constant; $k_B$ refers to the Boltzmann constant; m is the molecular mass; and $\tilde{M}$ is the non-dimensional mass flow rate retrieved from the cited works.

Table 2. RFR model verification results. Comparison of G predictions between different models.

Cross Section		G
Rectangular $a{b}_{ratio}=0.00$	RFR-KC	−0.0694
	[12]	−0.0677 (2.40%)
	SF-NSE	3.9391 (5775.94%)
Circular	RFR-KC	−0.0565
	[31]	−0.0671 (18.81%)
	SF-NSE	3.6638 (6584.60%)

Figure 9. RFR model verification results. $\tilde{P}$ profile for the Knudsen mono-capillary geometry with a rectangular cross section, as depicted in Figure 7.

Figure 10. RFR model verification results. $\tilde{P}$ profile for the Knudsen mono-capillary geometry with a circular cross section, as depicted in Figure 8.

The dimensionless pressure $\tilde{P}=P\left(x\right)/P_I$ exhibits a stage-wise triangular profile along $\tilde{x}=x/x_{II}$: each triangle corresponds to one of the ten repeated stages, with the first half arising in the capillary section and the second in the connector section.

The larger discrepancies observed in the SF–NSE solutions displayed in Figure 9 and Figure 10 are mainly attributed to the fact that CFD simulations have been performed for rarefaction parameters significantly outside the slip–flow regime. Given that the SF–NSE formulation considered by COMSOL is mainly applicable, and therefore accurate, within the slip–flow regime, its validity tends to degrade under these conditions, which explains the observed discrepancies. Another evident feature refers to the junction effects at the capillary–connector interfaces. They can be identified in Figure 9 and Figure 10 as small pressure jumps at these sites. Because both section lengths are short ($L_A=L_B=0.5\mathrm{mm}$), these interface effects are insufficiently damped. Unfortunately, extending the geometry to mitigate them does not seem feasible at present; for $N_{stages}=10$ COMSOL failed to converge or produced diverging solutions for longer L.

On the other hand, RFR–KC and Knudsen–diffusion predictions agree well—within $\approx 2–3\%$ for rectangular channels and $\approx 12–19\%$ for circular channels. The larger discrepancy in the circular mono-capillary case likely reflects limitations of the RFR–KC formulation, which justifies more in-depth investigations in a future study.

3. Knudsen Heat Pump

This section provides a brief overview on the operation principles and main parameters behind the Heat Pump Cycle. Then, it presents the mathematical model and the main input parameters considered in the KHP study. Finally, their relationship with respect to previously published studies is discussed. The results provided by the model will then be used to compute the energy transfer associated with the evaporator and the Knudsen compressor. Subsequently, the overall efficiency of the KHP will be estimated in order to assess the system performance.

3.1. Heat Pump Cycle

A heat pump system consists of a closed thermodynamic cycle whose main purpose is to maintain an enclosed space at a desirable temperature, different from the surrounding environment, by transferring heat from a source to a heat sink. Whether the objective is to cool or heat the enclosed space defines if the system acts as either a refrigeration cycle or a heat pump cycle, respectively [35].

Figure 11a shows an illustration of the heat pump cycle, and Figure 11b indicates the corresponding $log\left(P\right)-h$ diagram.

Figure 11. Heat pump cycle and corresponding process steps given in Equation (7). Adapted from [36]. $\dot{W}$: energy input to the compressor; $\dot{M}$: mass flow rate of the fluid in the system; ${\dot{Q}}_{EV}$ and ${\dot{Q}}_{CD}$: heat transferred in the evaporator and condenser; $T_{EV}$ and $T_{CD}$: temperatures of the enclosed spaces on the evaporator and condenser sides, respectively.

The thermo-physical processes taking place in the compressor, condenser, expansion valve, and evaporator are mathematically defined by the set of Equation (7), respectively, given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{W}& =\dot{M}(h_2-h_1)\hfill \\ \hfill {\dot{Q}}_{CD}& =\dot{M}(h_2-h_3)\hfill \\ \hfill h_3& =h_4\hfill \\ \hfill {\dot{Q}}_{EV}& =\dot{M}(h_1-h_4)\hfill \end{array}\end{array}$$

(7)

The coefficient of performance ($COP$) is a measure of the efficiency of the heat pump system. Depending on whether the system operates as a refrigeration or heat pump cycle, expressed by Equation (8) or Equation (9), respectively, this parameter quantifies the ratio between the energy desirably transferred—either from the enclosed space to the evaporator (${\dot{Q}}_{EV}$) or from the condenser to the enclosed space (${\dot{Q}}_{CD}$)—and the energy supplied to the compressor ($\dot{W}$). According to the systems mode of operation, this parameter is defined as follows:

$$CO{P}_{CD}={\displaystyle \frac{{\dot{Q}}_{CD}}{\dot{W}}}={\displaystyle \frac{h_2-h_3}{h_2-h_1}}$$

(8)

$$CO{P}_{EV}={\displaystyle \frac{{\dot{Q}}_{EV}}{\dot{W}}}={\displaystyle \frac{h_1-h_4}{h_2-h_1}}$$

(9)

For the performance study, the current work only focuses on the calculation of the coefficient of performance using ${\dot{Q}}_{EV}$ ($CO{P}_{EV}$), as the results for ${\dot{Q}}_{EV}$ and ${\dot{Q}}_{CD}$ and, consequently, $CO{P}_{EV}$ and $CO{P}_{CD}$ tend to be relatively close to each other.

3.2. KHP Energy Input

The present study is motivated by the work by Kugimoto et al. [19], which specifically emphasizes that, in practical applications, the total energy input should not be limited by the mechanical work required to drive the flow through the system, denoted above as $\dot{W}$, but must also include the thermal energy needed to offset continuous heat losses in the compressor. These losses arise from conduction along the longitudinal direction of the compressor, represented by ${\dot{Q}}_{conduction}$, and from radiation on the high-temperature side of the compressor, denoted as ${\dot{Q}}_{radiation}$.

The total conductive heat losses, in all stages of the Knudsen compressor, is expressed by Equation (10) in Watts (W) and its calculation follows [19]. However, unlike the methodology in [19], which presents the Knudsen compressor as a single capillary section (i.e., the membrane), the present work also incorporates conduction losses occurring within the connector sections.

$${\dot{Q}}_{conduction}=N_{stages}\left({\displaystyle \frac{{\kappa }^A{A}_w^A(T_H-T_L)}{L^A}}+{\displaystyle \frac{{\kappa }^B{A}_w^B(T_H-T_L)}{L^B}}\right)$$

(10)

In Equation (10), $\kappa$, $A_w$, and L represent the thermal conductivity, cross-section area, and length of the medium through which heat is conducted, respectively. This medium may refer to either the solid wall of the compressor or the water vapor within it. Recall from Section 2.2 that $T_H$ and $T_L$ correspond to the high and low temperatures of the compressor, while the superscripts A and B denote the capillary and connector sections, respectively.

Glass fiber, the material applied in the study performed by Kugimoto et al. [19], is also employed in the present work due to its low thermal conductivity, which helps minimize conductive heat losses. As reported in their study, the thermal conductivity of glass fiber is assumed to be $0.03$ W/(m·K) at 1 kPa and 324 K [19].

According to the database provided by the NIST Chemistry WebBook [37], the thermal conductivity of water vapor under these conditions is ≈0.02 W/(m·K). Knowing that the medium observed in the capillary section is composed of both solid wall (glass fiber) and water vapor, in order to simplify the calculation of ${\dot{Q}}_{conduction}$, the thermal conductivity of water vapor can be considered equal to that of the glass fiber. Accordingly, ${\kappa }^A={\kappa }^B$ = 0.03 W/(m·K) (note that the application of a low thermal conductive solid wall material, relative to that of water vapor, contradicts the thermal conductivity assumption stated in [24], so future work should be performed to verify the conformity of the application of low conductive materials using the RFR model).

Under the aforementioned assumption, the cross-section area $A_w$ will be identical in both sections, such that $A_w^A=A_w^B$.

The total radiative heat losses across all stages of the Knudsen compressor are calculated using Equation (11), expressed in Watts (W). In this equation, $\sigma$ denotes the Stefan–Boltzmann constant, $ϵ$ represents the emissivity of the solid wall material ($\approx 1$ as was assumed in [19]), and $T_{RT}$ is the room temperature, which can be considered equal to $T_L$ for simplicity (according to [19], $T_{RT}=294.37$ K).

$${\dot{Q}}_{radiation}=N_{stages}\sigma ϵA_w^A(T_H^4-T_{RT}^4)$$

(11)

Since the coefficient of performance indicated in Equation (9) takes solely into account the energy required to pump the flow in the system $\dot{W}$, and does not depend on the heat losses in the Knudsen compressor, a modified parameter that represents the KHP system performance in a more practical manner needs to be introduced into the study. This new parameter shall be denoted as $CO{P}_{practical}$ and is expressed by Equation (12). Equation (12) mathematically describes that the performance of the KHP is undesirably affected by the heat losses in the compressor. Following this new parameter, the $COP$ defined in Equation (9) shall henceforth be labeled the ideal coefficient of performance $CO{P}_{ideal}$.

$$CO{P}_{practical}={\displaystyle \frac{{\dot{Q}}_{EV}}{\dot{W}+{\dot{Q}}_{conduction}+{\dot{Q}}_{radiation}}}$$

(12)

3.3. KHP Analysis

The present study will investigate the influence of various input parameters on the flow rate ($\dot{M}$), the ideal coefficient of performance ($CO{P}_{ideal}$), and the practical coefficient of performance ($CO{P}_{practical}$) of a Knudsen heat pump. The goal is to identify optimal operating conditions that maximize $CO{P}_{practical}$, thereby enhancing the system’s overall efficiency. All geometric and operational parameters considered in this work are constrained to realistic values typically encountered in Knudsen compressor geometries.

To establish a comparative baseline, simulations are first conducted using realistic operating and geometric parameters. Table 3 summarizes key characteristics reported in previous related studies.

Table 3. KHP characteristics based on data reported in previous literature studies [14,17,19].

Article	Units	[19]	[14]	[17]
Fluid	-	Water vapor	Water vapor	Water vapor
KC type	-	Porous membrane	Porous membrane	Porous membrane
$N_{stages}$	-	1, 2	1, 2, 3, 4	1
KC length $L^A$	m	760 × ${10}^{-6}$	380 × ${10}^{-6}$	380 × ${10}^{-6}$
KC material	-	Glass fiber filter	Glass fiber filter	Glass fiber filter
Thermal conductivity $\kappa$	W/(m·K)	$0.03$	-	-
Pores size $a_I$	m	0.70 × ${10}^{-6}$	0.70 × ${10}^{-6}$	0.70 × ${10}^{-6}$
Cross-section area $A_w$	m2	78.5 × ${10}^{-4}$	4.9 × ${10}^{-4}$	4.9 × ${10}^{-4}$
$T_{ratio}$	-	494.77/294.46	324/295	433/293
$P_{ratio}$	-	930/876	3413/3333	1740/1700

For the present work, the parameters adopted for the baseline simulations are mainly drawn from the study by Kugimoto et al. [19]. Table 4 summarizes the selected parameters, where the values for $\gamma$, $N_{cap}$, and $a_c$ are assumed since the article [19] does not provide explicit data for these quantities. It is expected that the results to be presented here will differ from those reported in [19], primarily due to these geometry differences: the Knudsen compressor considered in the present study is modeled as a 2D configuration and does not fully match the geometry used in [19]. It should be noted that, for each study, all baseline parameters are held at their initial values, as listed in Table 4. By varying one parameter at a time, it becomes possible to isolate the marginal effect of each parameter analyzed.

Table 4. KHP baseline parameters.

Parameters	Units	Cross Section
		Rectangular	Circular
$\varphi$	-	2	3
$N_{stages}$	-	1	1
$L^A$	m	760 × ${10}^{-6}$	760 × ${10}^{-6}$
$\gamma$	-	1/10	1/10
$\kappa$	W/(m·K)	0.03	0.03
$a{b}_{ratio}$	-	1	-
$T_{ratio}$	-	494.77/294.46	494.77/294.46
$P_{ratio}$	-	930/876	930/876
$a_I$	m	0.70 × ${10}^{-6}$	0.35 × ${10}^{-6}$
$T_I$	K	294.46	294.46
$N_{cap}$	-	50	50
$a_c$	m	0.70 × ${10}^{-6}$	0.70 × ${10}^{-6}$
$A_w$	m2	78.5 × ${10}^{-4}$	78.5 × ${10}^{-4}$

Subsequently, a series of parametric studies will be conducted by systematically varying the baseline parameters to assess their individual impact on the mass flow rate and the KHP performance. An additional simulation scenario will be explored to further enhance performance metrics. Finally, simulations incorporating optimized parameters will be developed to evaluate enhancements in the results and performance of the system.

4. Results and Discussion

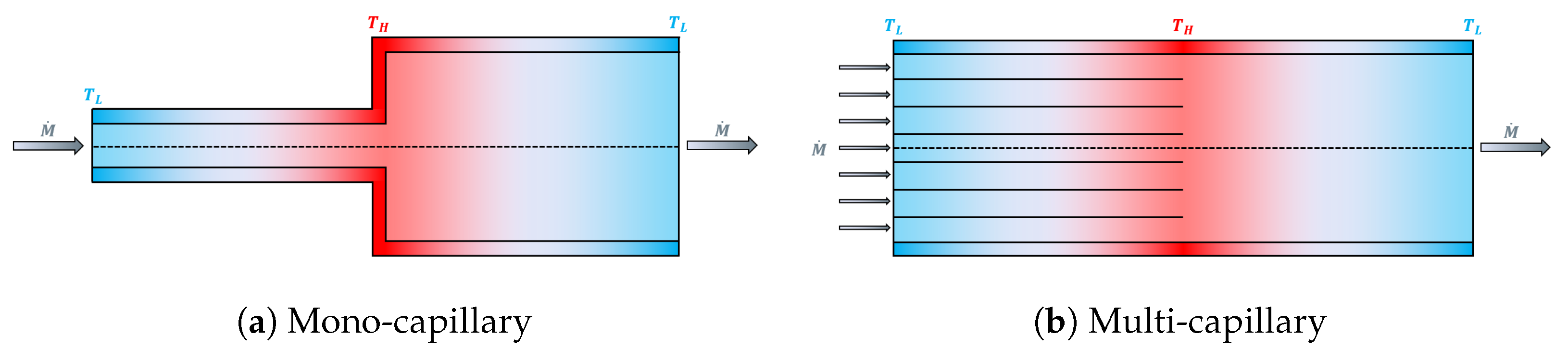
4.1. Baseline Simulations

Table 5 presents the results of the baseline simulations performed for a multi-capillary Knudsen compressor with a rectangular cross section and a circular cross section.

Table 5. KHP baseline simulations results.

Variables	Units	Cross Section
		Rectangular	Circular
$\dot{M}$	mg/s	1.164 × ${10}^{-7}$	5.273 × ${10}^{-10}$
${\dot{Q}}_{EV}$	W	2.892 × ${10}^{-7}$	1.310 × ${10}^{-9}$
$\dot{W}$	W	4.439 × ${10}^{-8}$	2.010 × ${10}^{-10}$
${\dot{Q}}_{conduction}$	W	$68.966$	$68.966$
${\dot{Q}}_{radiation}$	W	$23.328$	$23.328$
$CO{P}_{ideal}$	-	$6.514$	$6.514$
$CO{P}_{practical}$	-	3.133 × ${10}^{-9}$	1.419 × ${10}^{-11}$

These results help conclude that the heat pump coupled with a Knudsen compressor, with the currently chosen baseline parameters, cannot produce desirable results given their very small orders of magnitude, which consequently yields a poor performance.

To conclude this section, it is worth clarifying the lower $CO{P}_{practical}$ of the circular cross-section geometry, compared with the rectangular cross-section geometry, which is observed in the results. To begin with, let us recall that the mass flow rate is given by Equation (4), where L denotes the Knudsen compressor length, A gives the capillary cross-section area, $a_I$ is the characteristic dimension in the capillary section, $P_I$ is the pressure at the left extremity of the Knudsen compressor, $T_I$ gives the temperature at the left extremity of the Knudsen compressor, m is the molecular mass of water vapor, and G corresponds to the reduced flow rate. Thus, for fixed L, $P_I$, $T_I$, m, and G, we have $M\propto a_{I}A$. For the rectangular geometry, $A_{rect}=a_{I}b$, whereas for the circular geometry, $A_{circ}=\pi a_I^2$; here, $a_I$ is the characteristic dimension (height for the rectangular geometry, radius for the circular geometry) and $b=a_{II}/a{b}_{ratio}$ represents the width of the rectangular geometry. Because $a_{II}\gg a_I$ (the connector section is much wider than the capillary section), for $a{b}_{ratio}=1$, $b=a_{II}$, and consequently, $b\gg a_I$, $A_{rect}\gg A_{circ}$, and thus, it follows that $M_{rect}\gg M_{circ}$. Given that the mass flow rate is directly proportional to $CO{P}_{practical}$, the circular geometry exhibits a much smaller COP as a consequence of the lower $\dot{M}$.

4.2. Parametric Studies

Figure 12 presents the results of the parametric study performed for $a_I$ for 0 m $<a_I<20\times {10}^{-6}$ m, that is, the characteristic dimension of the capillary section.

Figure 12. $a_I$ parametric study.

Figure 12 evidences an increase in $\dot{M}$ and $CO{P}_{practical}$ at a micro-scale level, where $a_I$ becomes sufficiently small and thermal transpiration effects are predominant, thus positively influencing the flow. For the rectangular and circular geometries, both $\dot{M}$ and $CO{P}_{practical}$ reach their peak values at $a_I=12\times {10}^{-6}$ m and $a_I=11\times {10}^{-6}$ m, respectively. This is followed by a significant decrease in $\dot{M}$ and $CO{P}_{practical}$, where the Poiseuille contribution overcomes the thermal transpiration contribution, subsequently leading to negative values of $\dot{M}$ and $CO{P}_{practical}$ (the latter not being shown in the graph due to the logarithmic scale of the y-axis), indicating reversed flow directions uncharacteristic of heat pump systems. Thus, the range of $a_I$ values that leads to these reversed flow conditions should be avoided.

In contrast, $CO{P}_{ideal}$ remains constant and equal to $6.514$ for both cases throughout the variation of $a_I$, as $a_I$ does not influence enthalpy values within the KHP system. Based on these results, values of $a_I=12\times {10}^{-5}$ m (rectangular) and $11\times {10}^{-5}$ m (circular) were selected for the enhanced simulations, corresponding to the optimal $CO{P}_{practical}$ values within the studied range. These values fall into the typical micro-scale dimensions where the KC should operate, as indicated in previous studies [21,22].

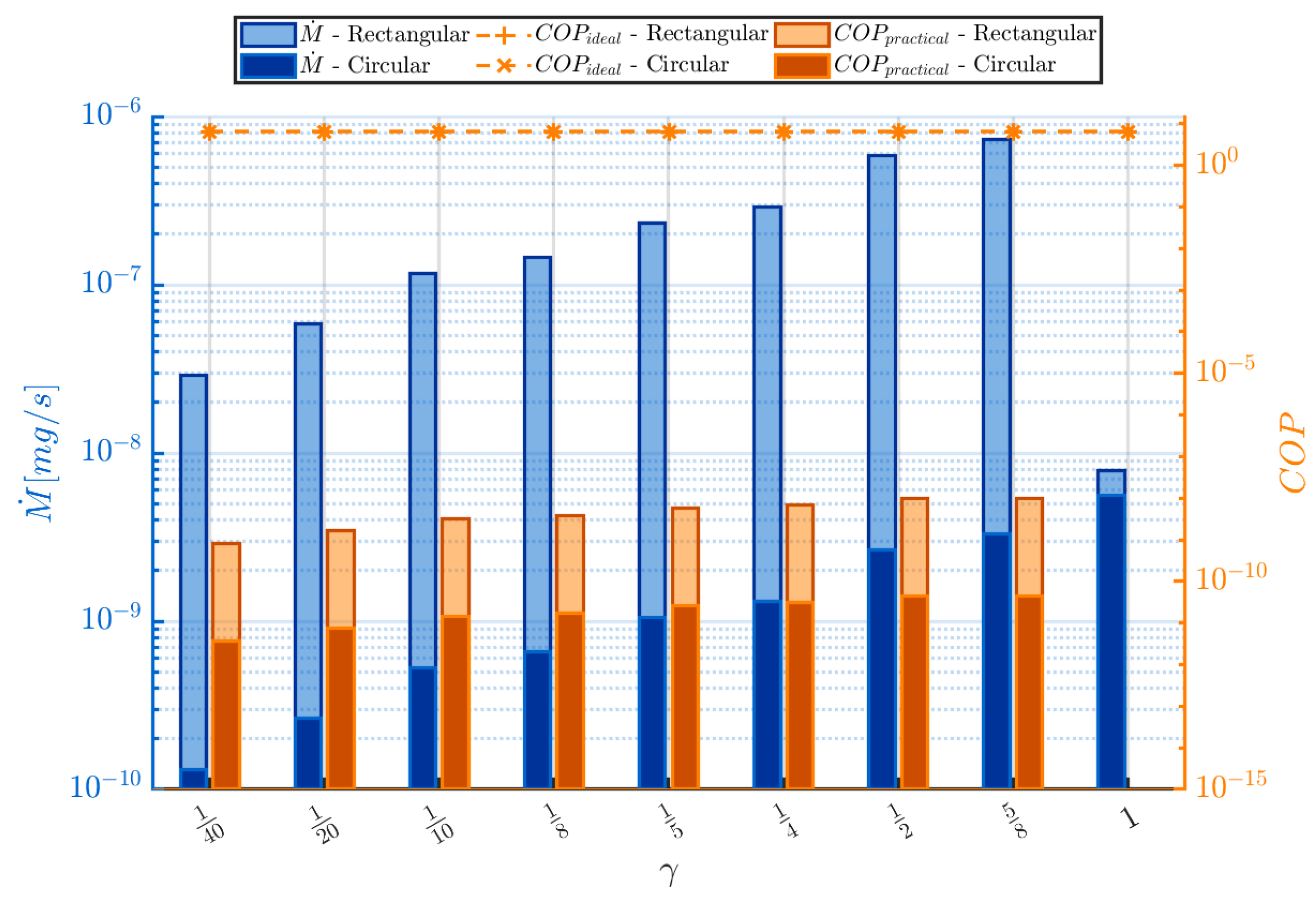
Figure 13 provides the graphical results developed during the parametric study of the characteristic dimension to width ratio $a{b}_{ratio}$ for a range of $0<a{b}_{ratio}<1$.

Figure 13. $a{b}_{ratio}$ parametric study.

While variations in $a{b}_{ratio}$ do not influence $CO{P}_{ideal}$, decreasing $a{b}_{ratio}$ results in an increase in both $\dot{M}$ and $CO{P}_{practical}$. This increase in $\dot{M}$ is attributed to the expansion of the rectangular cross-section area, primarily driven by an increase in the compressor width b. As $a{b}_{ratio}\to 0$, b, and consequently $\dot{M}$ and $CO{P}_{practical}$, tends towards infinity. As in the previous parametric study with $a_I$, $CO{P}_{ideal}$ remains constant at $6.514$, as $a{b}_{ratio}$ does not affect the enthalpy values in the KHP system. To comply with performance and geometric feasibility, a value of $a{b}_{ratio}=1\times {10}^{-4}$ was selected for the enhanced efficiency simulations, as it provides near-optimal results without requiring unrealistically large values for the compressor width b.

Figure 14 indicates the evolution of the results with capillary section fraction $\gamma$.

Figure 14. $\gamma$ parametric study.

The data depicted in Figure 14 shows that $\dot{M}$ is generally sensitive to variations in $\gamma$ across both geometric configurations, especially at $\gamma =1$. At this value, $\dot{M}$ decreases significantly in the rectangular geometry and increases in the circular geometry. Notably, $CO{P}_{ideal}$ is also not affected by variations of $\gamma$. Furthermore, the $CO{P}_{practical}$ collapses at $\gamma =1$, where the geometry is fully capillary. An optimal value of $\gamma ={\displaystyle \frac{5}{8}}$ has been selected for the enhanced efficiency simulations in both geometric cases, which corresponds to the $\gamma$ value that returns the highest $CO{P}_{practical}$.

Figure 15 presents the graphical results of the parametric study carried out for the number of capillaries $N_{cap}$.

Figure 15. $N_{cap}$ parametric study.

An increase in the number of capillaries positively influences $\dot{M}$ and $CO{P}_{practical}$ in both geometric configurations, leading to their asymptotic increase. As expected, $CO{P}_{ideal}$ remains unaffected, holding constant at $6.514$, indicating that it does not depend on $N_{cap}$. Based on these findings, $N_{cap}=2000$ has been selected for the enhanced efficiency simulations in both configurations, as further increase in this parameter yields negligible improvement of the KHP performance and would only increase the size and complexity of the Knudsen compressor.

Figure 16 outlines the results for the number of stages $N_{stages}$ parametric study.

Figure 16. $N_{stages}$ parametric study.

For both geometries, a notable decrease in the mass flow rate $\dot{M}$, and consequently $CO{P}_{practical}$, is observed with the increase in the number of stages $N_{stages}$, due to its inverse dependence on the total length of the Knudsen compressor L, which increases with the increase in $N_{stages}$ (refer to Equation (4)).

A similar trend is observed for both $CO{P}_{ideal}$ and $CO{P}_{practical}$, where a continuous decrease is observed with the increase in $N_{stages}$. Each additional stage increases the number of capillary sections requiring heat input and promotes conductive and radiative heat losses, thereby raising $\dot{W}$, ${\dot{Q}}_{conduction}$, and ${\dot{Q}}_{radiation}$. Since ${\dot{Q}}_{EV}$ is not affected, this imbalance leads to a reduction in both performance parameters.

Notably, as reported by Kugimoto et al. [19], the efficiency of a multi-stage Knudsen compressor scales inversely with the number of stages, such that the efficiency of an $N_{stages}$-stage compressor is approximately $1/N_{stages}$ of the efficiency of a single-stage unit. This theoretical prediction is qualitatively supported by the trend observed in the simulation results presented in Figure 16, where $CO{P}_{practical}$ drops as $N_{stages}$ increases, confirming the inverse efficiency relationship and reinforcing the impracticality of using a high number of stages from a performance standpoint.

For this study, $N_{stages}$ shall remain equal to 1 for the enhanced efficiency simulations in both geometric configurations.

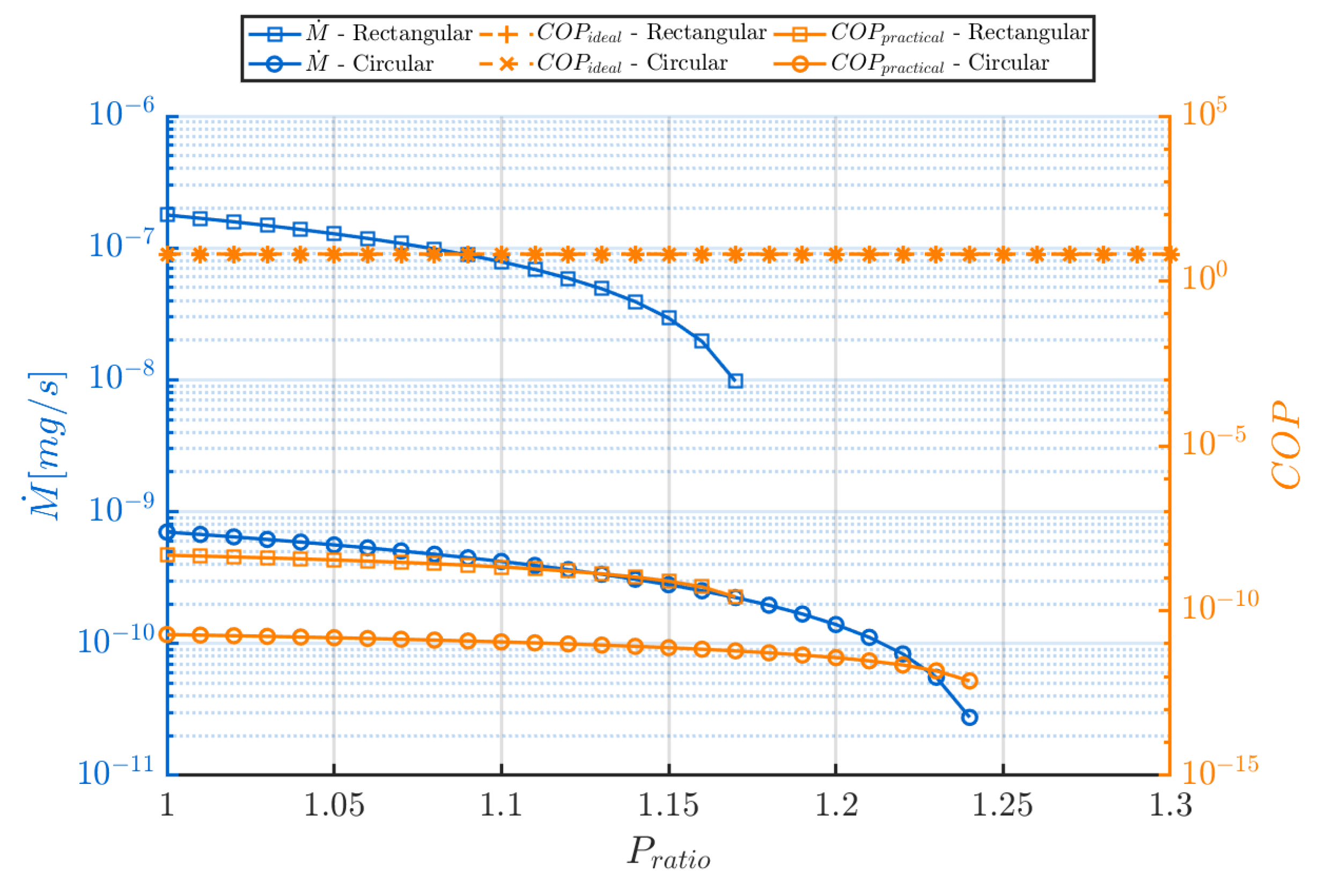
Figure 17 illustrates the results of the parametric study executed for the pressure ratio $P_{ratio}$.

Figure 17. $P_{ratio}$ parametric study.

The graphical results show that increasing the pressure ratio $P_{ratio}$ negatively impacts both $\dot{M}$ and $CO{P}_{practical}$. This trend is expected, as a pressure gradient within the Knudsen compressor enhances the Poiseuille flow contribution, which opposes the thermal transpiration-driven flow, thus shifting the net gas flow through the Knudsen heat pump system. For the rectangular and circular configurations, respectively, when $P_{ratio}>1.17$ and $P_{ratio}>1.24$, the flow direction reverses, causing $\dot{M}$ and $CO{P}_{practical}$ to become negative (although this is not visually evident in the plots due to the logarithmic y-axis scales).

In theory, optimal performance would be achieved when $P_{ratio}$ approaches unity, minimizing adverse Poiseuille flow, allowing thermal transpiration to dominate and for $CO{P}_{practical}$ to reach its most enhanced value. Unlike conventional heat pump systems, the KHP does not require an externally imposed pressure differential for operation, and a pressure gradient will be generated internally via thermal transpiration. Therefore, a value of $P_{ratio}={\displaystyle \frac{930}{876}}$, as initially chosen, shall remain for the enhanced efficiency simulations in order to maintain performance while satisfying practical constraints.

Figure 18 illustrates the results for the temperature ratio $T_{ratio}$ parametric study.

Figure 18. $T_{ratio}$ parametric study.

The results indicate that the mass flow rate $\dot{M}$ increases continuously with $T_{ratio}$ due to enhanced thermal transpiration effects induced by the growing temperature gradient across the system. For the rectangular and circular configurations, respectively, $CO{P}_{practical}$ reaches a peak at $T_{ratio}=1.6$ and $T_{ratio}=1.5$, before declining at further values of $T_{ratio}$. This decline in $CO{P}_{practical}$ beyond the optimal point is attributed to the disproportionate growth of $\dot{W}$, ${\dot{Q}}_{conduction}$, and ${\dot{Q}}_{radiation}$, which overcome the increase in ${\dot{Q}}_{EV}$.

In the case of $CO{P}_{ideal}$, a steady decrease is observed with increasing $T_{ratio}$, as the rise in $\dot{W}$ outweighs the gains in ${\dot{Q}}_{EV}$. Therefore, the optimal performance is achieved for the rectangular and circular configurations, respectively, at $T_{ratio}=1.6$ and $T_{ratio}=1.5$, which are selected for the enhanced efficiency simulations.

4.3. Heated Surface Coating

One of the main factors limiting the performance of the KHP refers to the thermal losses, which directly affect its efficiency. The material choice for the Knudsen compressor is therefore a critical design parameter, as it must address both conductive and radiative heat losses. In a study by Kugimoto et al. [19], a glass fiber membrane was employed as the material for the Knudsen compressor. While glass fiber exhibits relatively low thermal conductivity, its emissivity is extremely high, practically assumed to be $\approx 1$, meaning that radiative losses become predominant, thus significantly diminishing the KHP performance.

The present work considers the application of a low-emissivity flaky aluminum powder coating or silver nanoparticle coating on the heated wall of the Knudsen compressor, which can reduce surface emissivity to values of around 0.25 [38] and 0.015 [39], respectively, in order to overcome this limitation. By combining such a coating in the glass fiber surface, it is possible to suppress significant radiative losses.

Table 6 presents the impact of surface coating on ${\dot{Q}}_{radiation}$ and $CO{P}_{practical}$.

Table 6. KHP surface coating results.

Coating Type	Parameter	Units	Rectangular Cross Section		Circular Cross Section
			Result	Improvement	Result	Improvement
Al ($ϵ=0.25$)	${\dot{Q}}_{radiation}$	W	5.832	75.00%	5.832	75.00%
	$CO{P}_{practical}$	-	3.866 × ${10}^{-9}$	23.40%	1.751 × ${10}^{-11}$	2.26%
Ag ($ϵ=0.015$)	${\dot{Q}}_{radiation}$	W	0.350	98.50%	0.350	98.50%
	$CO{P}_{practical}$	-	4.172 × ${10}^{-9}$	33.16%	1.889 × ${10}^{-11}$	33.12%

The application of silver coating results in a dramatic reduction in radiative heat losses, with ${\dot{Q}}_{radiation}$ dropping 98.5% in both geometries when compared with the uncoated case. Aluminum, though less effective than silver, still provides a substantial 75% reduction.

In the rectangular cross section, silver coating improves $CO{P}_{practical}$ by 33.16%, while aluminum achieves a 23.40% improvement. For the circular geometry, performance gains are more modest due to inherently lower baseline COP values; nonetheless, silver still provides a 33.12% improvement compared with 2.26% for aluminum. These results confirm that minimizing surface emissivity via coating is an effective strategy for reducing radiative heat loss and enhancing overall system efficiency, particularly in rectangular geometries.

For the enhanced simulations, a surface coating using silver nanoparticles ($ϵ=0.015$) is selected, as it yields superior performance compared with the aluminum coating in terms of reduced radiative heat losses and improved overall system efficiency. It should be noted that economic and coating stability considerations are beyond the scope of this work and, thus, were not used as decisive factors for the choice of material. The material is selected solely in order to increase $CO{P}_{practical}$. While the total area to be coated in the KC is small (so material usage is minimal), deposition/processing can dominate cost. If investment if limited, aluminum (Al) provides a lower-cost alternative compared with silver with only a small increase in emissivity. Regarding stability, the layer is assumed to be protected against factors like dewetting that diminish the stability, using a thin Ti/Cr adhesion layer beneath it, therefore preserving its low emissivity. A detailed techno-economic analysis and an assessment of long-term coating stability shall be the subject of a future work.

4.4. Enhanced Setup

The following operating parameters are selected, as the optimal choices, from the preceding studies for the rectangular cross-section geometry: $a_I=12\times {10}^{-6}$ m; $a{b}_{ratio}=1\times {10}^{-4}$; $\gamma ={\displaystyle \frac{5}{8}}$; $N_{cap}=2000$; $N_{stages}=1$; $P_{ratio}={\displaystyle \frac{930}{876}}$, $T_{ratio}=1.6$; and, for the circular cross-section geometry: $a_I=11\times {10}^{-6}$ m; $\gamma ={\displaystyle \frac{5}{8}}$; $N_{cap}=2000$; $N_{stages}=1$; $P_{ratio}={\displaystyle \frac{930}{876}}$, $T_{ratio}=1.5$.

Table 7 presents the results obtained by using these parameters and the corresponding percentage comparison with the baseline simulations (Table 5).

Table 7. KHP outcomes using the enhanced parameters provided by the ensemble of parametric studies performed herein.

Variables	Units	Rectangular Cross Section		Circular Cross Section
		Enhanced Result	Percentage	Enhanced Result	Percentage
$\dot{M}$	mg/s	1123.30	≫100%	1.20 × ${10}^{-5}$	≫100%
${\dot{Q}}_{EV}$	W	2789.69	≫100%	2.98 × ${10}^{-5}$	≫100%
$\dot{W}$	W	376.02	≫100%	3.34 × ${10}^{-6}$	≫100%
${\dot{Q}}_{conduction}$	W	87.59	27.00%	73.00	5.85%
${\dot{Q}}_{radiation}$	W	0.28	−98.80%	0.20	−99.14%
$CO{P}_{ideal}$	-	7.408	13.72%	8.920	39.96%
$CO{P}_{practical}$	-	6.006	≫100%	4.069 × ${10}^{-7}$	≫100%

A comparison with the baseline simulations clearly highlights significant performance gains in the Knudsen heat pump resulting from the new implemented parameters, with the rectangular cross-section geometry influencing the most substantial improvements in the system.

For the rectangular cross section, nearly all performance metrics show marked enhancement. $\dot{M}$, and as a consequence ${\dot{Q}}_{EV}$, and $\dot{W}$ all increase by more than 100%. Additionally, radiative heat loss (${\dot{Q}}_{radiation}$) is reduced by 98.80%, promoted by the application of silver nanoparticle surface coatings in the Knudsen compressor. Both $CO{P}_{ideal}$ and $CO{P}_{practical}$ improve considerably, with the latter increasing from $3.133\times {10}^{-9}$ to 6.006. Conductive heat transfer (${\dot{Q}}_{conduction}$) is shown to increase by 27.09%, which comes from the cross-section area increase $A_w^A$ and $A_w^B$—mainly influenced by the increase in $a{b}_{ratio}$ and $N_{cap}$. Although an unfavorable outcome, this does not hinder the system’s efficiency, as evidenced by the substantial gain in $CO{P}_{practical}$, indicating an overall improvement in energy conversion performance.

The circular geometry also benefits from the applied enhancements, though the magnitude of improvement is comparatively lower. Increases of over 100% are observed in $\dot{M}$, ${\dot{Q}}_{EV}$, and $\dot{W}$, while radiative losses decrease by 99.14%, also due to surface coating using silver nanoparticles. Notably, the $CO{P}_{ideal}$ rises from 6.514 to 8.920—a 39.96% increase that even surpasses the 13.72% improvement observed for the rectangular configuration. However, $CO{P}_{practical}$ remains significantly lower than that of the rectangular case.

These results suggest that the rectangular geometry is more responsive to the applied enhancements. This is largely attributed to the modification of the $a{b}_{ratio}$ parameter, which strongly influences mass flow rate and, consequently, $CO{P}_{practical}$. Since $a{b}_{ratio}$ is unique to the rectangular configuration, its optimization led to substantial performance gains not observed in the circular configuration. Therefore, the rectangular Knudsen compressor demonstrates more advantageous characteristics for KHP applications.

5. Conclusions

The present work dealt with the performance analysis of the Knudsen heat pump. By carefully analyzing each of the most relevant parameters, it was possible to increase the performance of the KHP system. Although an improvement is evident for the circular cross-section geometry, it is not as significant as that for the rectangular cross-section geometry. The main reason for this limitation is the small mass flow rate yielded by the former geometry.

This study intends to promote the applicability of the Knudsen compressor as a novel approach for the heat pump technology. The use of the RFR model as means to solve the flow in the Knudsen compressor, in order to obtain results for the KHP, has enabled a deeper insight into the performance of the device and corresponding optimization. As energy management and miniaturized systems become critical, the Knudsen heat pump emerges as an innovative solution with future potential. Thus, continued research and development in this area should be incentivized to unlock new possibilities in thermal system designs.

Future work could include experimental validation of the current results using prototypes of the Knudsen compressor geometries considered herein. Additionally, the RFR model assumes that the wall material has sufficiently high thermal conductivity to allow a linear temperature distribution as an input condition; since glass fiber, which has very low thermal conductivity, was chosen for the wall material in this work, a dedicated analysis is needed to assess the appropriateness of applying the RFR model under such conditions.